Haryana State Board HBSE 10th Class Home Science Solutions Chapter 1 बाल विकास Textbook Exercise Questions and Answers.
Haryana Board 10th Class Home Science Solutions Chapter 1 बाल विकास
अति लघु उत्तरीय प्रश्न :
प्रश्न 1.
विकास से आप क्या समझते हैं ?
उत्तर :
विकास का अर्थ है कि अनेक कार्यों तथा कौशलों के लिए योग्यता अर्जित करना।
प्रश्न 2.
विकास कितने प्रकार का होता है ?
अथवा
विकास को कितनी श्रेणियों में बांटा गया है ?
उत्तर :
विकास निम्नलिखित प्रकार के होते हैं –
- शारीरिक
- गत्यात्मक
- सामाजिक
- संवेगात्मक
- भाषा
- ज्ञानात्मक।

प्रश्न 3.
किन-किन कारणों के कारण बच्चों का विकास उचित प्रकार से नहीं हो सकता ?
अथवा
कोई चार कारण बताएं, जिस कारण बच्चों का विकास उचित प्रकार से नहीं हो सकता।
उत्तर :
बच्चों का विकास कई कारणों से ठीक तरह नहीं होता जैसे –
- बच्चों को विरासत से ही कुछ कमियां मिली हों जैसे-बच्चा मंद बुद्धि हो सकता है, अंगहीन हो सकता है।
- बच्चे में अच्छे गुण होने के बावजूद उनको अच्छा वातावरण न मिल सकने के कारण भी उसके विकास में रुकावट डाल सकता है।
- कई बार घरेलू झगड़े भी बच्चे के विकास में रुकावट डालते हैं।
- बच्चे की रुचि से विपरीत उससे ज़बरदस्ती कोई कार्य करवाना जैसे किसी बच्चे को गाने-बजाने का शौक है तो उसे ज़बरदस्ती खेलने को कहा जाए।
- बचपन में बच्चे को माता-पिता का प्यार तथा देख-रेख न मिल सकना।
प्रश्न 4.
परिवार की खुशी बच्चों के भविष्य के साथ कैसे जुड़ी है ?
उत्तर :
प्रत्येक परिवार की खुशी, उम्मीद तथा भविष्य बच्चों से जुड़ा होता है। बच्चे ही देश का भविष्य होते हैं तथा परिवार में बच्चे यदि शारीरिक तथा मानसिक तौर पर स्वस्थ हो तो परिवार के लिए खुशी का कारण बनते हैं। परिवार खुश हो, तो बच्चों के विकास के लिए सहायक रहता है। यदि परिवार में लड़ाई-झगड़े हों अथवा परिवार आर्थिक पक्ष से तंग हो, तो इन बातों का बच्चों के भविष्य पर बुरा प्रभाव होता है।
प्रश्न 5.
बचपन को कितनी अवस्थाओं में बांटा जा सकता है ?
उत्तर :
बचपन को निम्नलिखित अवस्थाओं में बांटा जा सकता है –
- जन्म से दो वर्ष तक
- दो से तीन वर्ष तक
- तीन से छः वर्ष का बच्चा
- छ: से किशोरावस्था तक।

प्रश्न 6.
बच्चों को टीकों की बूस्टर दवा कब दिलाई जाती है ?
उत्तर :
छ: वर्ष का होने पर बच्चे को कई टीकों के बूस्टर डोज़ दिए जाते हैं ताकि उन्हें कई जानलेवा बीमारियों से बचाया जा सके।
प्रश्न 7.
कितनी आय का बच्चा कानुनी रूप से वयस्क समझा जाता है ?
उत्तर :
पहले 21 वर्ष के बच्चे को बालिग समझा जाता था, परन्तु अब 18 वर्ष के बच्चे को बालिग समझा जाता है जबकि 20 वर्ष की आयु तक उसका शारीरिक विकास होता रहता है।
प्रश्न 8.
समान-अन्तर खेल से क्या अभिप्राय है ?
उत्तर :
दो वर्ष तक के बच्चे में सहयोग की भावना अभी पैदा नहीं हुई होती। यदि ऐसे बच्चों को एक साथ बिठा भी दिया जाये तो वे स्वयं ही खेलते रहते हैं; एक-दूसरे से नहीं खेलते। ऐसी खेल को समान-अन्तर खेल कहा जाता है।
प्रश्न 9.
टैम्पर टैंट्रम से क्या अभिप्राय है ?
उत्तर :
कई बार बच्चे बहुत गुस्से हो जाते हैं तथा ज़मीन पर लेटते हैं। ऐसी अवस्था को टैम्पर टैंट्रम कहा जाता है।
प्रश्न 10.
माता-पिता बच्चे का सही मार्ग-दर्शन कैसे कर सकते हैं ?
उत्तर :
बच्चों में विभिन्न प्रकार की भावनाएं जैसे प्यार, गुस्सा, ईर्ष्या, डर, सहयोग आदि होती हैं। बच्चा अभी रो रहा होता है तथा अगले ही पल खिलखिला कर हंस रहा। होता है। उसकी भावनाएं बड़ी तेज़ी से बदलती हैं। उसकी बदलती भावनाओं को समझने के लिए हमें उनकी मनोवैज्ञानिक अवस्था को समझना आवश्यक है। बच्चों की विभिन्न भावनाओं को समझने के लिए मां-बाप उसका सही मार्ग-दर्शन कर सकते हैं।

प्रश्न 11.
बच्चों में झूठ बोलना, खर्चीलापन अथवा अहंकारी होना जैसी बुरी आदतें कैसे पैदा हो जाती हैं ?
उत्तर :
कई बार कई मां-बाप बच्चों पर अधिक सख्ती करते हैं तथा कई ज़रूरत से अधिक लाड-प्यार करते हैं। इन दोनों हालातों में बच्चे में ग़लत आदतें जैसे झठ बोलना, खर्चीलापन अथवा चोरी करना अथवा अहंकारी होना आदि पैदा हो जाती हैं।
प्रश्न 12.
11 से 12 वर्ष की आयु में लड़के-लड़कियां कौन-से खेल खेलते हैं ?
उत्तर :
लड़के क्रिकेट, कंचे, गुल्ली-डंडा, बॉस्केट बाल आदि खेलते हैं जबकि लड़कियां स्टापू, छुपा-छिपी तथा गोटियां आदि खेलती हैं।
प्रश्न 13.
बालक की वृद्धि तथा आहार (पोषण) में क्या सम्बन्ध है ?
उत्तर :
जब वृद्धि की गति तेज़ होती है, तो बालक को पोषक आहार की अधिक आवश्यकता होती है। पोषक आहार न मिलने से बालक के अंगों का विकास रुक जाता है।
प्रश्न 14.
बालक को शारीरिक वृद्धि को कैसे बढ़ाया जा सकता है ?
उत्तर :
1. उचित पोषक आहार देकर।
2. प्रोत्साहन द्वारा-बैठने, खड़े होने, चलने आदि के लिए प्रेरणा देकर।

प्रश्न 15.
‘संवेग’ का क्या अर्थ है ?
उत्तर :
संवेग का अर्थ उन अनुभूतियों से लिया जाता है जो व्यक्तियों को विभिन्न प्रकार से उत्तेजित करती हैं और उसमें हर्ष, क्रोध, भय एवं स्नेह का भाव पैदा करती हैं।
प्रश्न 16.
सामान्य शारीरिक विकास का प्रभाव बालक के किन व्यवहार क्षेत्र पर पड़ता है ?
उत्तर :
शारीरिक विकास का बालक के व्यवहार की गुणात्मकता और मात्रात्मकता दोनों पर गहरा प्रभाव पड़ता है। यह मुख्यतः चार क्षेत्रों पर पड़ता है –
- नाड़ी संस्थान
- मांसपेशियां
- अन्तः स्त्रावी ग्रंथियां
- शारीरिक संरचना।
प्रश्न 17.
बालक के सामान्य व्यवहार और शारीरिक विकास के विषय में कैरल का क्या मत है ?
उत्तर :
“बालक के दैहिक विकास और इसके सामान्य व्यवहार में घनिष्ठ सह-सम्बन्ध है। यदि हम समझना चाहते हैं कि भिन्न-भिन्न बालकों में क्या समानताएं हैं और क्या विषमताएं तथा आयु वृद्धि के साथ-साथ व्यक्ति में क्या-क्या परिवर्तन आते हैं तो हमें बालक के शारीरिक विकास का अच्छी प्रकार अध्ययन करना होगा।”
प्रश्न 18.
स्वस्थ बालक के लक्षण क्या हैं ?
उत्तर :
स्वस्थ बालक का चेहरा सदा खिला रहता है। उसकी आँखों में विशेष चमक रहती है। मन सदा कार्य के प्रति उत्साहित रहता है। शरीर क्रियाशील रहता है।

प्रश्न 19.
शारीरिक विकास को कौन-कौन से कारक प्रभावित करते हैं ?
अथवा
शारीरिक विकास को प्रभावित करने वाले चार कारक बताएँ।
उत्तर :
शारीरिक विकास को निम्नलिखित कारक प्रभावित करते हैं-परिवार, भौतिक वातावरण, जलवायु, भोजन, खेल, रोग, लैंगिक भिन्नता, संवेगात्मक तनाव।
प्रश्न 20.
बालक के शारीरिक विकास की कितनी अवस्थाएं हैं ?
उत्तर :
बालक के शारीरिक विकास की निम्नलिखित चार अवस्थाएं हैं –
- बालक का जन्म से 2 वर्ष तक विकास तेज गति से होता है।
- किशोरावस्था से पूर्व तक विकास की गति मंद होती है।
- किशोरावस्था में विकास तेजी से होता है।
- किशोरावस्था के बाद परिपक्वास्था तक विकास पुनः धीमी गति से होता है।
प्रश्न 21.
बच्चों के लिए व्यायाम क्यों आवश्यक है ?
उत्तर :
बच्चों के शारीरिक विकास एवं हड्डियों की सुदृढ़ता के लिए व्यायाम आवश्यक होता है। व्यायाम से शरीर स्वस्थ रहता है। बच्चे की आयु के बढ़ने के साथ-साथ उसके व्यायाम करने का ढंग भी बदलता जाता है। प्रारम्भ में शिशु अपने बिस्तर पर ही लेटा हुआ अपनी टांगें तथा बांहें फेंककर व्यायाम करता है। जब घुटनों के बल चलने लगता है तो वह चलकर, भागकर अथवा कूदकर व्यायाम करता है। बच्चे की देखभाल करने वालों को इस बात का ध्यान रखना चाहिए कि बच्चा हर रोज़ आवश्यकतानुसार व्यायाम करे ताकि उसका शरीर स्वस्थ रहे। व्यायाम करने से बच्चों को भूख भी अच्छी लगती है और वह रोगों से बचा रहता है।

प्रश्न 22.
बालक का रोगी होना उसके साधारण व्यवहार को कैसे प्रभावित करता –
उत्तर :
रोगी होने पर बालक का स्वभाव चिड़चिड़ा हो जाता है। बीमारी के पश्चात् वह हर समय कुछ-न-कुछ खाने की चीजें मांगता रहता है। इसलिए हमें बालक को स्वस्थ रखने का प्रयत्न करना चाहिए। रोगग्रस्त बालक का उचित उपचार करवाना चाहिए। स्वस्थ बालक का चेहरा प्रसन्न रहता है। उसकी आँखें चमकती रहती हैं तथा मन उत्साहित होता रहता है और शरीर क्रियाशील रहता है।
प्रश्न 23.
समुदाय में रहने पर बालक में कौन-कौन से अवगुण आ जाते हैं ?
उत्तर :
समुदाय में रहने पर बालक में निम्नलिखित अवगुण आ जाते हैं कसम खाना, गाली-गलौच करना, अश्लील व्यवहार करना, असत्य बोलना, बातों की उपेक्षा करना, नियमों का उल्लंघन करना, शरारत करना इत्यादि।
प्रश्न 24.
भाषा से क्या तात्पर्य है ?
उत्तर :
भाषा अपने विचारों को दूसरे व्यक्तियों तक पहुंचाने की योग्यता है। इसमें विचार, अनुभूति तथा संदेशवाहन को प्रतीकों द्वारा व्यक्त किया जाता है। इसके अन्तर्गत बोलना, लिखना, सुनना, पढ़ना, चेहरे के भाव, मुख मुद्रा, कला, आदि आते हैं। बोलना भाषा का एक अंग है और संदेश वहन करने का एक पक्ष है।
प्रश्न 25.
भाषा की विशेषताएं क्या हैं ?
उत्तर :
भाषा की कुछ विशेषताएं इस प्रकार हैं –
- प्रत्येक प्राणी की अपनी भाषा होती है।
- भाषा किसी की पैतृक सम्पत्ति नहीं है और न ही किसी वर्ग, जाति तथा समुदाय का एकाधिकार।
- भाषा अर्जित है।
- यह परिवर्तनशील होती हैं। देश, काल तथा परिस्थितियों के कारण इसमें परिवर्तन होता रहता है।
- भाषा का सम्बन्ध परम्पराओं से होता है।

प्रश्न 26.
भाषा विकास को प्रभावित करने वाले कारक क्या हैं ?
उत्तर :
भाषा विकास को प्रभावित करने वाले कारक हैं – व्यक्तित्व सम्बन्धी विशेषताएं, पारिवारिक सम्बन्ध, लिंग, सामाजिक-आर्थिक स्तर, निर्देशन, उत्प्रेरणा, सामाजिक अधिगम के स्तर हैं।
प्रश्न 27.
भाषा के विकास का स्वरूप क्या है ?
उत्तर :
भाषा को सामाजिक विकास का सबसे बड़ा साधन माना गया है। इसके विकास के स्वरूप को समझने के लिए निम्नलिखित बातों पर विचार करेंगे
1. संवेदनात्मक प्रतिक्रियाएँ-इसके अन्तर्गत देखना, सुनना आदि क्रियाएं आती हैं।
2. संवेदना क्रिया सम्बन्धी अनुक्रियाएँ-इसके अन्तर्गत बोलना, लिखना व चित्रांकन करना आदि आते हैं। बालक के मुख से सार्थक शब्द समूह को ही भाषा कहते हैं।
प्रश्न 28.
प्रयास और भूल द्वारा बच्चा किस प्रकार बोलना सीखता है ?
उत्तर :
अमेरिकन वैज्ञानिक डेशियल के अनुसार यदि बालक अनुकरण द्वारा बोलना सीखता, तो वह बहुत जल्दी सीख लेता। उनके अनुसार बालक प्रयास व भूल द्वारा बोलना सीखता है। जिस प्रकार बालक उंगलियों द्वारा किसी वस्तु को पकड़ने का प्रयत्न करता है, उसी प्रकार वह मुख से ध्वनियां निकालता है। माता-पिता उसे इन ध्वनियों का अनुकरण करने के लिए प्रोत्साहित करते हैं। इस प्रकार वह प्रयास और भूल द्वारा बोलना सीख जाता है।
प्रश्न 28.
(A) प्रत्येक व्यक्ति के जीवन में दाँत कितनी बार आते हैं ? उन्हें क्या कहते हैं ?
उत्तर :
शिशु के पहली बार दाँत छः से आठ महीने के मध्य निकलते हैं, इन्हें दूध के दाँत कहते हैं तथा दूसरी बार छः वर्ष की आयु में स्थायी दाँत निकलते हैं।
प्रश्न 29.
भाषा विकास का सीधा सम्बन्ध किससे है ?
उत्तर :
भाषा विकास का सीधा सम्बन्ध स्वर, यन्त्र, जीभ, गला और फेफड़ों की परिपक्वता से है। यदि बालक के ये अंग सामान्य रूप से विकसित होते हैं तो उसका भाषिक विकास संतोषजनक होता है। इसका सम्बन्ध दृष्टि, होंठ, ताल, दांत और नाक के विकास से भी है।

प्रश्न 30.
साहित्य को समाज का दर्पण क्यों कहा गया है ?
उत्तर :
भाषा सामाजिक सम्पर्क का सबसे बड़ा साधन है। इसके द्वारा सभी तरह की सांस्कृतिक उपलब्धियां सम्भव हो सकती हैं। इसके माध्यम से हम अपने विचार प्रकट कर सकते हैं। इससे ही साहित्य का आविर्भाव होता है। इसलिए साहित्य को समाज का दर्पण कहा गया है।
प्रश्न 31.
प्रेरणा द्वारा बालक किस प्रकार बोलना सीखता है ?
उत्तर :
बालक तब बोलता है जबकि बोले बिना उसका काम नहीं चलता। तोतली भाषा बोलने पर माता-पिता तो समझ लेते हैं। परन्तु बाहर जाने पर उसका मजाक उड़ाया जाता है। इसलिए वह शुद्ध बोलने का प्रयत्न करता है। दूसरे बालकों के साथ सामाजिक संबंध बनाने के लिए बालक अपनी आवश्यकताओं के पूरक शब्द को बोलने का प्रयास करता है।
प्रश्न 32.
बालक अनुकरण द्वारा किस प्रकार बोलना सीखता है ?
उत्तर :
बालक बबलाते समय मुँह से निकलने वाली ध्वनियों को दोहराता है। अन्य लोगों की मौजूदगी में वह उनकी बातों का अनुकरण करता है। छ: महीने की अवस्था के पश्चात् बालक ‘ना-ना-ना’, व ‘बा-बा-बा’ ध्वनियों का तथा ग्यारह महीने के पश्चात् बालक नाना, मामा, बाबा आदि शब्दों का अनुकरण करता है। इस प्रकार अनुकरण द्वारा बोलना सीख जाता है।
प्रश्न 33.
बच्चा सम्बद्धता द्वारा किस प्रकार अर्थ ग्रहण करता है ?
उत्तर :
बच्चे द्वारा बोले गये शब्द सम्बद्धता द्वारा निश्चित अर्थों को ग्रहण करते हैं। जिस प्रकार माता बच्चे के मुख से ‘बि’ सुनकर बिल्ली का खिलौना उसके पास लाकर “बिल्ली’ कहने के लिए उत्साहित करती है। बालक सामने बिल्ली देखता है और सुनता है। इस तरह निरर्थक ध्वनि ‘बि’ और ‘बिल्ली’ में सम्बद्धता स्थापित हो जाती है। माता की गैरहाज़िर में भी बालक बिल्ली को ‘बि’ पुकारता है।
प्रश्न 34.
बालक के क्रन्दन करने के क्या कारण हैं ?
उत्तर :
बालक के क्रन्दन करने के निम्नलिखित कारण हैं-भूख लगना, पेट में दर्द होना, सर्दी लगना, अधिक प्रकाश, अधिक अंधेरा आदि।

प्रश्न 35.
क्रन्दन ध्वनि (क्राइंग) क्या होती है ?
उत्तर :
बच्चों द्वारा रोने को क्रन्दन कहते हैं। बालक भूख, डर, पेट दर्द, अधिक प्रकाश, अधिक अंधेरा आदि होने पर क्रन्दन करता है।
प्रश्न 36.
समाजीकरण का क्या अर्थ है ?
उत्तर :
समाजीकरण का अर्थ है कि बालक को समाज के रीति-रिवाज, विश्वास, सामाजिक रस्में, जीवन मूल्य आदि तथा समाज में रहने का ज्ञान होना चाहिए।
प्रश्न 37.
अभिवृद्धि किसे कहते हैं ?
उत्तर :
अभिवृद्धि का सम्बन्ध शारीरिक आकार में बढ़ौत्तरी से है जैसे बालक का भार बढ़ना, लम्बाई बढ़ना, आदि।
प्रश्न 38.
अभिवृद्धि और विकास में एक अन्तर बताएं।
उत्तर :
अभिवृद्धि का अर्थ है शारीरिक आकार में बढ़ोत्तरी। यह विकास का ही एक पहलू है। विकास एक बढ़े दायरे वाला शब्द है, इसमें अभिवृद्धि भी आ जाती है तथा अन्य प्रकार का विकास जैसे संवेगात्मक, ज्ञानात्मक, तार्किक विकास आदि शामिल हैं। इनमें एक सबसे बड़ा अन्तर है कि अभिवृद्धि एक समय पर आकर रुक जाती है जब कि विकास मनुष्य के अन्तिम श्वास तक होता रहता है। अभिवृद्धि को देखा तथा मापा जा सकता है परन्तु विकास को मापना इतना सरल नहीं है।
प्रश्न 39.
अभिवृद्धि और विकास को प्रभावित करने वाले कारक कौन-कौन से
उत्तर :
अभिवृद्धि और विकास को प्रभावित करने वाले कारक है वंशानुक्रम तथा वातावरण।
प्रश्न 40.
बच्चों के किन्हीं दो संवेंगों के नाम लिखें। बालकों द्वारा उन्हें प्रदर्शित करने का कोई एक मुख्य तरीका भी बताएं।
उत्तर :
बच्चों के विभिन्न संवेग हैं-क्रोध, हर्ष, प्यार, डर आदि। शिशु चिल्लाकर या सांस रोककर अपने डर को प्रदर्शित करता है। हर्ष की स्थिति में बच्चा हंसता अथवा मुस्कराता है तथा ज़ोर से बाजू, टांगों को हिलाता है।

प्रश्न 41.
सामाजिक विकास को प्रभावित करने वाले मुख्य कारक कौन-से हैं ?
उत्तर :
सामाजिक विकास को प्रभावित करने वाले मुख्य कारक हैं-खेल, आर्थिक तथा सामाजिक स्तर, बाल समुदाय, शारीरिक व मानसिक विकास तथा परिवार आदि।
प्रश्न 42.
बचपनावस्था में शरीर की हड्डियों की संख्या …….. है जो कि किशोरावस्था तक ……….. रह जाती है।
उत्तर :
270, 206
प्रश्न 43.
बाल विकास बच्चों के कौन-से पहलू का अध्ययन करता है ?
उत्तर :
बाल विकास बच्चों की वृद्धि तथा विकास का अध्ययन है।
प्रश्न 44.
भाषा सीखने के प्रमुख अंग क्या हैं ?
उत्तर :
भाषा सीखने के प्रमुख अंग हैं-अनुकरण, वार्तालाप, कहानियां, प्रश्नोत्तर, खेल।
प्रश्न 45.
बाल्यावस्था के प्रमुख संवेगों को सूचीबद्ध कीजिए।
उत्तर :
भय, शर्मीलापन, परेशानी, चिन्ता, क्रोध, ईर्ष्या, जिज्ञासा, स्नेह आदि।

प्रश्न 46.
मां का दूध बच्चे के लिए क्यों आवश्यक है ?
उत्तर :
मां का दूध बच्चे के लिए एक प्रकार से पूर्ण आहार का कार्य करता है। उसको रोगों के प्रति प्रतिरोधक क्षमता बढ़ाने का कार्य करता है। बच्चे की भूख मिटती है। बच्चे को भावनात्मक संतुष्टि मिलती है। बच्चा अपनी मां के साथ जुड़ाव महसूस करता है। प्यार, स्नेह की भावना उत्पन्न होती है। मां को भी संतुष्टि मिलती है। बच्चे का विकास ठीक ढंग से होता है।
लघु उत्तरीय प्रश्न :
प्रश्न 1.
(क) बाल विकास से आप क्या समझते हो और पारिवारिक सम्बन्धों का महत्त्व बताएं।
(ख) वृद्धि एवं विकास दोनों कैसे अलग हैं ?
(ग) अभिवृद्धि और विकास में एक अन्तर बताएं।
उत्तर :
(क) बाल विकास बच्चों की वृद्धि तथा विकास का अध्ययन है। इसमें गर्भ अवस्था से लेकर बालिग होने तक की सम्पूर्ण वृद्धि तथा विकास का अध्ययन करते हैं। इनमें शारीरिक, मानसिक, व्यावहारिक एवं मनोवैज्ञानिक वृद्धि तथा विकास शामिल हैं। इसके अतिरिक्त बच्चों में पाई जाने वाली व्यक्तिगत भिन्नताएं, उनके साधारण तथा असाधारण व्यवहार तथा वातावरण का बच्चे पर प्रभाव को जानने की कोशिश भी की जाती है।
मनुष्य का बच्चा अपनी प्राथमिक आवश्यकताओं के लिए अपने आस-पास के लोगों पर अधिक समय के लिए निर्भर रहता है। बच्चे की ज़रूरतों को पूरा करने के लिए परिवार होता है। इन ज़रूरतों को किस तरह पूरा किया जाता है, इसका बच्चे के व्यक्तित्व पर प्रभाव पड़ता है तथा इसका बड़े होकर पारिवारिक रिश्तों पर भी प्रभाव पड़ता है।
मनुष्य के पारिवारिक रिश्ते उसके सामाजिक जीवन के लिए बहुत महत्त्वपूर्ण होते हैं। क्योंकि हम इस समाज में ही विचरते हैं, इसलिए हमारे पारिवारिक रिश्ते तथा परिवार से बाहर के रिश्ते हमारे जीवन की खुशी का आधार होते हैं। इस तरह बच्चे के विकास में पारिवारिक सम्बन्ध काफ़ी महत्त्व रखते हैं।

(ख) वृद्धि और विकास एक दूसरे से निम्नलिखित तरह से अलग हैं –
- शरीर के विभिन्न अंगों के आकार के बड़े होने को वृद्धि कहते हैं तथा गुणात्मक तत्त्वों के सुधार को विकास कहते हैं।
- वृद्धि विकास का ही एक हिस्सा है।
- विकास व्यक्तित्व के सभी क्षेत्रों में परिवर्तन लाता है।
- विकास के परिवर्तनों को मापना आसान नहीं है। परन्तु वृद्धि को देखा व मापा जा सकता है।
- विकास पूरा जीवन चलता है जबकि वृद्धि निर्धारित समय बाद रुक जाती है।
(ग) देखें भाग (ख)।
प्रश्न 2.
जन्म से दो वर्ष तक होने वाले शारीरिक विकास के पड़ावों का वर्णन करो।
उत्तर :
जन्म से दो वर्ष के दौरान होने वाले शारीरिक विकास निम्नलिखित अनुसार हैं
- 6 हफ्ते की आयु तक बच्चा मुस्कुराता है तथा किसी रंगीन वस्तु की ओर टिकटिकी लगाकर देखता है।
- 3 महीने की आयु तक बच्चा चलती-फिरती वस्तु से अपनी आँखों को घुमाने लगता है।
- 6 महीने का बच्चा सहारे से तथा 8 महीने का बच्चा बिना सहारे के बैठ सकता है।
- 9 महीने का बच्चा सहारे के बिना खड़ा हो सकता है।
- 10 महीने का बच्चा स्वयं खड़ा हो सकता है तथा सरल, सीधे शब्द जैसे-काका, पापा, मामा, टाटा आदि बोल सकता है।
- 1 वर्ष का बच्चा स्वयं उठकर खड़ा हो सकता है तथा उंगली पकड़कर अथवा स्वयं चलने लगता है।
- 12 वर्ष का बच्चा बिना किसी सहारे के चल सकता है तथा 2 वर्ष में बच्चा सीढ़ियों पर चढ़ सकता है।
प्रश्न 3.
स्कूल बच्चे के सामाजिक और मानसिक विकास में सहायक होता है। कैसे ?
उत्तर :
स्कूल में बच्चे अपने साथियों से पढ़ना तथा खेलना तथा कई बार बोलना भी सीखते हैं। इस तरह उनमें सहयोग की भावना पैदा होती है। बच्चा जब अपने स्कूल का कार्य करता है तो उसमें ज़िम्मेदारी का बीज बो दिया जाता है। जब वह अध्यापक का कहना मानता है तो उसमें बड़ों के प्रति आदर की भावना पैदा होती है। बच्चा स्कूल में अपने साथियों से कई नियम सीखता है तथा कई अच्छी आदतें सीखता है जो आगे चलकर उसके व्यक्तित्व को उभारने में सहायक हो सकती हैं।

प्रश्न 4.
बच्चों से मित्रतापूर्वक व्यवहार रखने से उनमें कौन-से सद्गुण विकसित होते हैं ? विस्तारपूर्वक लिखो।
उत्तर :
बच्चे के व्यक्तित्व तथा भावनात्मक विकास में माता-पिता के प्यार तथा मित्रतापूर्वक व्यवहार की बड़ी महत्ता है। माता-पिता के प्यार से बच्चे को यह विश्वास हो जाता है कि उसकी प्राथमिक ज़रूरतें उसके माता-पिता पूरी करेंगे। माता-पिता की ओर से बच्चे द्वारा पूछे गये प्रश्नों के उत्तर देने पर बच्चे का दिमागी विकास होता है। उसे स्वयं पर विश्वास होने लगता है। माता-पिता द्वारा बच्चे को कहानियां सुनाने पर उसका मानसिक विकास होता है।
कई बार बच्चा मां का कहना नहीं मानना चाहता तथा ज़बरदस्ती करने पर गुस्सा होता है। ऊँची आवाज़ में रोता है, हाथ-पैर मारता है तथा जमीन पर लोटने लग जाता है। ऐसी हालत में बच्चे को डांटना नहीं चाहिए तथा शांत होने पर उसे प्यार से माता-पिता द्वारा समझाया जाना चाहिए कि वह ऐसे ग़लत करता है। इस तरह बच्चे को पता चल जाता है कि माता-पिता उससे किस तरह के व्यवहार की उम्मीद करते हैं।
बच्चे से दोस्ताना व्यवहार रखने पर बच्चों को अपनी समस्याओं का हल ढूँढने के लिए ग़लत रास्तों पर नहीं चलना पड़ता अपितु उनमें विश्वास पैदा होता है कि माता-पिता उसे सही मार्ग बताएंगे। वह ग़लत संगति से बच जाता है। उसमें अच्छी रुचियां जैसे ड्राईंग, पेंटिंग, संगीत, अच्छी किताबें पढ़ना आदि पैदा होती हैं। वह अपनी शक्ति का प्रयोग अच्छे कार्यों में करता है। इस तरह वह एक अच्छा व्यक्तित्व बन कर उभरता है।
प्रश्न 5.
प्रारम्भिक वर्षों में माता-पिता बच्चे के व्यक्तित्व के विकास में किस प्रकार योगदान डालते हैं ?
उत्तर :
बच्चे के व्यक्तित्व को बनाने में माता-पिता का बड़ा योगदान होता है क्योंकि बच्चा जब अभी छोटा ही होता है तभी माता-पिता की भूमिका उसकी ज़िन्दगी में आरम्भ हो जाती है। बच्चे के प्रारम्भिक वर्षों में बच्चे को भरपूर प्यार देना, उस द्वारा किये प्रश्नों के उत्तर देना, बच्चे को कहानियां सुनाना आदि से बच्चे का व्यक्तित्व उभरता है तथा माता-पिता इसमें काफ़ी सहायक होते हैं।
प्रश्न 6.
बच्चों को टीके लगवाने क्यों जरूरी हैं ? बच्चों को कौन-से टीके किस आयु में लगवाने चाहिएं तथा क्यों ?
उत्तर :
बच्चों को कई खतरनाक जानलेवा बीमारियों से बचाने के लिए उन्हें टीके लगाये जाते हैं। इन टीकों का सिलसिला जन्म के पश्चात् आरम्भ हो जाता है। बच्चों को 2 वर्ष की आयु तक चेचक, डिप्थीरिया, खांसी, टिटनस, पोलियो, हेपेटाइटस, बी०सी०जी० तथा टी०बी० आदि के टीके लगवाये जाते हैं। छः वर्ष में बच्चों को कई टीकों की बूस्टर डोज़ भी दी जाती है।

प्रश्न 7.
बच्चे में तीन से छः वर्ष की आय तक होने वाले विकास का वर्णन करो।
उत्तर :
इस आयु में बच्चे की शारीरिक वृद्धि तेजी से होती है तथा उसकी भूख कम हो जाती है। वह अपना कार्य स्वयं करना चाहता है। बच्चे को रंगों तथा आकारों का ज्ञान हो जाता है तथा उसकी रुचि ड्राईंग, पेंटिंग, ब्लॉक्स से खेलने तथा कहानियां सुनने की ओर अधिक हो जाती है। बच्चा इस आयु में प्रत्येक बात की नकल करने लग जाता है।
प्रश्न 8.
दो से तीन वर्ष के बच्चे में होने वाले भावनात्मक विकास सम्बन्धी जानकारी दो।
उत्तर :
इस आयु के दौरान बच्चा मां की सभी बातें नहीं मानना चाहता। ज़बरदस्ती करने पर वह ऊंची आवाज़ में रोता है, ज़मीन पर लोटता है तथा हाथ-पैर मारने लगता है। कई बार वह खाना-पीना भी छोड़ देता है। माता-पिता को ऐसी हालत में चाहिए कि उसको न डांटें परन्तु जब वह शांत हो जाए तो उसे प्यार से समझाना चाहिए।
प्रश्न 9.
जन्म से दो वर्ष तक के बच्चे में सामाजिक तथा भावनात्मक विकास के बारे में आप क्या जानते हो ?
उत्तर :
इस आयु का बच्चा जिन आवाजों को सुनता है, उनका मतलब समझने की कोशिश करता है। वह प्यार तथा क्रोध की आवाज़ को समझता है। वह अपने आस-पास के लोगों को पहचानना आरम्भ कर देता है। जब बच्चे को अपने माता-पिता तथा परिवार के अन्य सदस्यों द्वारा पूरा लाड़-प्यार मिलता है तथा उसकी प्राथमिक आवश्यकताएं पूरी की जाती हैं तो उसे विश्वास हो जाता है कि उसकी ज़रूरतें उसके माता-पिता पूरी करेंगे। उसका इस तरह भावनात्मक तथा सामाजिक विकास आरम्भ हो जाता है।
प्रश्न 10.
दो से तीन वर्ष के बच्चे के विकास के बारे में तुम क्या जानते हो ?
उत्तर :
शारीरिक विकास – 2 से 3 वर्ष के बच्चे की शारीरिक तौर पर वृद्धि तेजी से होती है। शारीरिक विकास के साथ ही उसका सामाजिक विकास इस समय बड़ी तेजी से होता है।
मानसिक विकास – इस आयु का बच्चा नई चीजें सीखने की कोशिश करता है। वह पहले से अधिक बातें समझना आरम्भ कर देता है। वह अपने आस-पास के बारे में कई प्रकार के प्रश्न पूछता है। इस समय माता-पिता का कर्तव्य है कि वह बच्चे के प्रश्नों के उत्तर जरूर दें। बच्चे को प्यार से पास बिठा कर कहानियां सुनाने से उसका मानसिक विकास होता है।
सामाजिक विकास – इस आयु में बच्चे को दूसरे बच्चों की मौजूदगी का अहसास होने लग जाता है। अपनी मां के अतिरिक्त अन्य व्यक्तियों से भी प्यार करने लगता है। अब वह अपने कार्य जैसे भोजन करना, कपड़े पहनना, नहाना, बूट पालिश करना आदि स्वयं ही करना चाहता है।
भावनात्मक विकास – इस आयु में बच्चा मां की सभी बातें नहीं मानना चाहता। ज़बरदस्ती करने पर वह ऊँची आवाज़ में रोता, हाथ-पैर मारता तथा ज़मीन पर लेटने लगता है। कई-कई बार खाना-पीना भी छोड़ देता है। गुस्से की अवस्था में बच्चे को डांटना नहीं चाहिए तथा जब वह शांत हो जाये तो प्यार से उसे समझाना चाहिए। इस तरह बच्चे में माता-पिता के प्रति प्यार तथा विश्वास की भावना पैदा होती है तथा उसे यह अहसास होने लगता है कि उसके माता-पिता उससे किस तरह के व्यवहार की उम्मीद रखते हैं।

प्रश्न 11.
बच्चों की भावनात्मक देख-भाल के क्या लाभ हैं ?
उत्तर :
- इससे बच्चों में सुरक्षा का अनुभव तथा आत्म-विश्वास की भावना उत्पन्न होती है।
- इससे बच्चा मानसिक रूप में स्वस्थ रहता है तथा वह अपने आपको स्कूल, समाज तथा अपने साथियों में आसानी से ढाल लेता है।
- इससे बच्चों की मानसिक तथा मनोवैज्ञानिक ज़रूरतें पूरी होती हैं जिससे बच्चे में प्रशंसा तथा सन्तुष्टि के भाव पैदा होते हैं।
- इससे बच्चों में अच्छे व्यावहारिक गुण पैदा होते हैं तथा वह समाज में विचरण योग्य बनते हैं।
- जिन परिवारों में मानसिक रूप में स्वस्थ माहौल बना होता है वहां बच्चों की रुचियों तथा योग्यताओं में वृद्धि होती है।
प्रश्न 12.
बच्चों की भावनाएं विशेष रूप से कैसी होती हैं ?
उत्तर :
1. छोटे बच्चों की भावनाएं काफ़ी तेज़ होती हैं। वह छोटी-सी घटना से ही ज़ोर से रोने लग जाते हैं अथवा डर जाते हैं।
2. प्रत्येक बच्चे का स्वभाव दूसरे बच्चे से अलग होता है। विभिन्न स्थितियों में अलग-अलग बच्चों की अलग-अलग प्रतिक्रियाएं होती हैं जैसे बादलों के ज़ोर से गर्जन तथा बिजली के चमकने पर कई बच्चे तो डरकर रोने लगते हैं तथा कुछ बाहर निकलकर इस नज़ारे को देखना पसंद करते हैं।
3. बच्चे की भावना थोडी-थोडी देर में उभरती तथा समाप्त होती रहती है।
4. बच्चे की भावनाएं बहुत जल्दी बदलती हैं जैसे कई बार रोने के पश्चात् तुरन्त फिर हंसना आरम्भ कर देता है अथवा ईर्ष्या जाहिर करने के पश्चात् फिर प्यार की भावना दर्शाता है।
5. बच्चों की भावनाओं में आयु से अन्तर आ जाता है। कई भावनाएं छोटे बच्चों में बड़ी तेज़ होती हैं, पर आयु के साथ धीरे-धीरे कम होकर मद्धम पड़ जाती हैं अथवा पूर्णत: समाप्त हो जाती हैं।
6. बच्चे अपनी भावनाओं को छपा नहीं सकते। बच्चों की आन्तरिक भावनाओं का पता उनके व्यवहार से लग जाता है जैसे परीक्षाओं के दिनों में बच्चों को डर से भूख नहीं लगती।
प्रश्न 13.
छोटे बच्चों में प्यार की भावना कैसे उत्पन्न होती है ? वे किस भावना को कैसे प्रकट करते हैं ?
उत्तर :
बच्चे में प्यार की भावना ऐसे व्यक्ति के लिए पैदा होती है जो उसकी देखभाल करता है, उसकी ज़रूरतों की पूर्ति करता है और उसका पालन-पोषण करता है। ऐसा पहला व्यक्ति साधारणतः बच्चे की मां ही होती है जिससे बच्चा प्यार की भावना प्रकट करता है। फिर मां की गैर-मौजूदगी में किसी सम्बन्धी के लिए बच्चा प्यार की भावना प्रकट कर सकता है जो कि मां की तरह उसकी ज़रूरतों को पूरी करता है।
बहुत छोटे बच्चे अपनी प्यार की भावना प्रकट करने के लिए मुस्कराते हैं, हंसते हैं, अपनी बांहें उठा कर बुलाते हैं तथा अपने साथ खेलने वाले के चुम्बन लेते हैं। जब बच्चे 3 से 5 वर्ष के हो जाएं तो फिर उनकी रुचि अन्य सदस्यों में हो जाती है जो उनके साथ खेलते हैं अथवा उनमें रुचि लेते हैं। इस आयु में बच्चों को खिलौनों तथा जानवरों से काफ़ी प्यार होता है। बड़े होकर बच्चे अपने प्यार का इजहार करने से शर्माते हैं। किशोरावस्था में उनका अधिक प्यार अपने दोस्तों के प्रति हो जाता है। इस आयु में लड़के-लड़कियों का आपसी आकर्षण भी बढ़ता है।

प्रश्न 14.
माता-पिता बच्चों में मेल-जोल की भावना कैसे उत्पन्न कर सकते हैं ?
उत्तर :
जब बच्चा छोटा होता है तो उसमें सहयोग की भावना नहीं होती। यह भावना धीरे-धीरे उसमें विकसित होती है। जैसे-जैसे वह बड़ा होता जाता है उसको दूसरे बच्चों से चीजें, खिलौने आदि बांटने के बारे में पता चलता है। इस भावना को बच्चों में अच्छी तरह पैदा करने के लिए स्कूल में बच्चों को टोलियां बनाकर खेलने के लिए प्रेरित करना चाहिए। ऐसा ही घर में अथवा गली-मुहल्ले में जब बच्चा खेले तो करना चाहिए। मां-बाप को ‘मैं’ शब्द नहीं अपितु ‘हम’ शब्द सिखाना चाहिए। उसके आस-पास ऐसा माहौल बनाना चाहिए कि उसमें स्वयं सहयोग की भावना पैदा होनी चाहिए। ऐसी भावना रखने वाले बच्चे हमारे देश की धरोहर हैं।
प्रश्न 15.
बच्चों में क्रोध की भावना कब उत्पन्न होती है? इस पर कैसे नियन्त्रण किया जा सकता है ?
उत्तर :
बच्चों में गुस्सा तब पैदा होता है जब उन्हें उनकी मनपसंद वस्तु नहीं मिलती। वह तब भी गुस्सा करते हैं जब उनकी देखभाल करने वाला उनकी ओर ध्यान नहीं देता अथवा फिर उनसे उनकी मनपसंद वस्तु छीनने की कोशिश की जाती है। जब बच्चा स्कूल जाने लगता हो, वह धीरे-धीरे अपने गुस्से पर काबू पाना सीख लेता है तथा वह समाज में विचरण का तरीका सीख लेता है। कई बार बच्चा जब बहुत गुस्से होता है तो लोटने लगता है, तो उसे कुछ भी नहीं कहना चाहिए, जब वह शांत हो जाये, तो उसको प्यार से समझाना चाहिए।
इस तरह बच्चा स्वयं ही मां-बाप का व्यवहार देखकर शर्मिन्दगी महसूस करता है तथा स्वयं ही अपने आपको सुधारने की कोशिश करता है। घर में बच्चों पर अतिरिक्त रोक-टोक भी नहीं होनी चाहिए तथा न ही नाजायज़ सख्ती करनी चाहिए। इससे भी बच्चों में गैर-ज़रूरी गुस्सा तथा तनाव पैदा होता है। क्रोध एक नकारात्मक भावना है जहां तक हो सके कोशिश करो कि बच्चे में यह भावना न बढ़े-फूले।
प्रश्न 16.
विकास को प्रभावित करने वाले दो कारकों के नाम बताएँ।
उत्तर :
दो कारक हैं-आनुवंशिकता और वातावरण। आनुवंशिकता का अर्थ है वह लक्षण जो हमें माता-पिता से मिलते हैं जैसे आँखों का रंग, चेहरे की बनावट, लम्बाई, त्वचा का रंग आदि।
वातावरण का अर्थ है हमारे आसपास का वातावरण। यह दोनों ही कारक विकास में महत्त्वपूर्ण हैं। उदाहरण के लिए यदि बच्चा गूंगा पैदा हुआ है तो वातावरण चाहे कितना ही अच्छा क्यों न हो, बच्चे को बोलना नहीं सिखा सकता।
दूसरी तरफ अगर बच्चा बोल सकता है, पर उसका वातावरण ऐसा है कि जिसमें कोई भी उससे बोलता नहीं है। उसे बोलने के लिए प्रेरित नहीं करता, तो वह बोलने की क्षमता होते हुए भी बोलना नहीं सीख पाएगा। अत: व्यक्ति आनुवंशिकता एवं वातावरण दोनों का ही उत्पाद है।

प्रश्न 17.
शारीरिक विकास का क्या अर्थ है ? बच्चे का तीन साल तक के शारीरिक विकास का वर्णन करें।
उत्तर :
बच्चे की लम्बाई, भार, सामर्थ्य और उनके अंग प्रत्यंग में होने वाले परिवर्तनों को शारीरिक विकास कहा जाता है।
एक भारतीय बच्चा जन्म के समय औसतन 2/2 कि० ग्रा० का तथा 17” -19” लम्बा होता है। शैशव काल में उसकी वृद्धि बड़ी तीव्र होती है।
5 महीने में शिशु का वज़न दुगुना और 1 वर्ष पर तिगुना हो जाता है। पहले वर्ष में शिशु की लम्बाई 10”-12” तक बढ़ती है।
दो वर्ष का होते-होते शिशु अपनी होने वाली पूरी वयस्क लम्बाई का करीब आधा लम्बा हो जाता है।
पहले दो वर्षों की तीव्र वृद्धि बाद में कम हो जाती है। अब एक वर्ष में लम्बाई 2′”-3” बढ़ती है और वज़न में 212 कि० ग्रा० की वृद्धि होती है।
जैसे-जैसे शिशु बड़ा होता है उसकी हड्डियों की संख्या व मज़बूती बढ़ती जाती
7-8 महीनों में उसके दांत निकलने लगते हैं और 27 वर्ष तक बच्चे के 20 दूध के दांत निकल आते हैं।
प्रश्न 18.
गत्यात्मक विकास को परिभाषित करें एवं तीन साल तक के गत्यात्मक विकास को स्पष्ट करें।
उत्तर :
गत्यात्मक विकास का अर्थ है शारीरिक संचलन जैसे चलना, दौड़ना, सीढ़ी चढ़ना, वस्तु को पकड़ना आदि पर नियन्त्रण कर सकना।
गत्यात्मक विकास का क्रम इस प्रकार है –
सिर का नियन्त्रण – एक महीने पर होता है।
पलटना – 2-3 माह का होने पर बच्चा बगल से चित होने की अवस्था में पलटता है। छ: माह का होने पर पूरी तरह से पलटता है।
बैठना – 4-5 महीने का बालक सहारे के साथ बैठता है जबकि 6-7 महीने का होते-होते वह बिना सहारे बैठता है।
पकड़ना – 6-7 महीने का होने पर ही बच्चा पकड़ना सीखता है, खासकर वस्तुएँ।
खिसकना व घुटनों के बल चलना – 8-10 महीने का बच्चा हाथ व पैरों के बल चलने लगता है।
खड़े होना और चलना – 8 महीने का बच्चा सहारे के साथ खड़ा होता है और 12 महीने (1 वर्ष) का होने तक चल पड़ता है।
सीढ़ी चढ़ना – 13-14 महीने का बच्चा अपने हाथों व घुटनों के बल सीढ़ी चढ़ लेता है। 18 महीने का होते-होते वह बिना किसी सहारे के उतर चढ़ लेता है।

प्रश्न 18(A).
गत्यात्मक विकास का क्या अर्थ है ?
उत्तर :
देखें प्रश्न 18 का उत्तर।
प्रश्न 19.
गत्यात्मक विकास को कौन-से कारक प्रभावित करते हैं ?
उत्तर :
वे कारक निम्नलिखित हैं –
- बालक सरल बातें पहले सीखता है और कठिन बाद में, जैसे बच्चा पहले घसीटे मारता है फिर लाइनें बनाता है और अन्त में स्वर या व्यंजन लिखना सीखता है।
- अभ्यास गत्यात्मक विकास को प्रभावित करता है अर्थात् यदि किसी क्रिया में बालक को काफ़ी अभ्यास मिलता है वह उसे जल्दी सीख जाता है।
- आंख हाथ का समन्वय बालक की वृद्धि के साथ आता है अर्थात् बच्चा जैसे जैसे बड़ा होता है उसके आंख व हाथ में समन्वय आता है और वह धीरे-धीरे कठिन काम भी कर पाता है।
प्रश्न 20.
सामाजिक विकास क्या है ? बच्चे में होने वाले तीन साल तक के सामाजिक विकास को स्पष्ट करें।
अथवा
शैशव काल में बालक के सामाजिक विकास का उल्लेख करें।
अथवा
बालकों के सामाजिक विकास का उल्लेख करें।
उत्तर :
बच्चे का समायोजित व्यवहार करना सीखना ही उसका सामाजिक विकास है।
जन्म के समय सामाजिक व्यवहार – जन्म के समय बालक की लोगों में कोई रुचि नहीं होती। जब तक उसकी शारीरिक आवश्यकताएं पूरी होती हैं वह खुश रहता है व मनुष्यों व अन्य आवाज़ों में फर्क नहीं कर पाता।
2-3 महीने पर – बच्चा मनुष्यों व निर्जीव वस्तुओं में फर्क करना सीख लेता है। वह लोगों के साथ रहकर खुश होता है और अकेला होने पर रोता है।
3-4 महीने पर – आपके बात करने पर इस उम्र का शिशु मुस्कराएगा। इसे सामाजिक मुस्कराहट कहते हैं। अब बच्चा चाहेगा कि आप उसे उठाएँ। वह घर के परिचित चेहरों को पहचानने लगता है, जैसे – माता-पिता, दादा-दादी आदि।
6-7 महीने पर – बच्चा मुस्कराहट व डांट पर अलग-अलग प्रतिक्रिया करता है। उसे स्नेही व गुस्से भरी आवाज़ में अन्तर समझ आ जाता है।
8-9 महीने पर – 8-9 महीने का बच्चा बड़ों की बोली, हाव-भाव आदि की नकल करने लगता है। अब यदि उसे कोई अजनबी गोद में उठा ले तो वह रोने लगता है। 18 महीने तक उसकी यह ‘अजनबी चिन्ता’ खत्म हो जाती है। 2 साल पर-बच्चा साधारण निर्देशों का पालन करने लगता है और कुछ सरल कार्य भी करने लगता है।
2. साल के बाद – बच्चा जैसे ही घर से बाहर प्रैप्रेटरी स्कूल में जाता है वह बाहर के लोगों से सम्पर्क बनाना व तालमेल बिठाना सीखता है।

प्रश्न 21.
बालक के संवेगों के क्या लक्षण हैं ?
अथवा
बालकों के संवेंगों के लक्षण बताएं।
उत्तर :
बालक के संवेगों के निम्नलिखित लक्षण हैं –
- बच्चा संवेग अनुकरण द्वारा सीखता है अर्थात् देखकर सीखता है। यदि माँ बिल्ली से डरती है तो बच्चा भी डरेगा क्योंकि वह माँ का अनुकरण करता है।
- समान परिस्थितियों में बालकों का भिन्न संवेग प्रदर्शित होगा अर्थात् एक बालक अंधेरे से डरकर रोएगा, दूसरा दुबक कर बैठ जाएगा।
- बालकों के संवेग क्षणिक होते हैं अर्थात् बालक एक पल में रोता है तो दूसरे पल में हंसता है।
- बालकों के संवेग बहुत तीव्र होते हैं। अर्थात् वह छोटी-छोटी बातों पर रोते हैं या हंसते हैं।
प्रश्न 22.
आवश्यकता का क्या अर्थ है ?
उत्तर :
बच्चे के शरीर या दिमाग की साधारण स्थिति में परिवर्तन या बेचैनी को आवश्यकता’ कहते हैं। जब भी बच्चे की साधारण स्थिति में कोई परिवर्तन आता है, वह उसे बेचैन कर देता है। अतः वह रोता है। जब वह पुरानी अवस्था में आ जाता है तो वह खुश हो जाता है। बच्चे की मुख्य आवश्यकताएं हैं – (i) शारीरिक (ii) भावनात्मक (iii) ज्ञानात्मक।
प्रश्न 23.
ज्ञानात्मक आवश्यकता से आप क्या समझते हैं ?
उत्तर :
बच्चों में प्राकृतिक जिज्ञासा होती है कि अपने चारों ओर जो भी वह देखते हैं उसके बारे में जानना चाहते हैं। अतः उन्हें खोजबीन अवश्य करने दें। ऐसा करके वह खुद बहुत सी चीजें सीख जाते हैं। यदि उन्हें ऐसा करने से रोका जाएगा, तो वे नए चीजों के बारे में जानने की कोशिश छोड़ देंगे। उनकी जिज्ञासा कम हो जाएंगी। वह मन्द बुद्धि भी हो सकते हैं। अत: बच्चे की रुचि बनाए रखने के लिए यह आवश्यक है कि उसे नई चीजों के बारे में जानकारी हासिल करने दे परन्तु ध्यान रखें कि इस दौरान वह खुद को चोट न लगा ले।
प्रश्न 24.
शारीरिक विकास की अवस्थाएं बताइए।
उत्तर :
शारीरिक विकास की गति कभी तेज़ हो जाती है कभी मन्द। इसके निम्नलिखित चक्र होते हैं
- प्रथम चक्र – इसकी अवधि जन्म से 2 वर्ष तक होती है। इसमें वृद्धि की गति तेज़ होती है।
- द्वितीय चक्र – इसकी अवधि 2 वर्ष से यौवनारम्भ तक होती है। इसमें वृद्धि की गति मन्द होती है।
- तृतीय चक्र – इसकी अवधि यौवनारम्भ से लेकर 15-16 वर्ष की अवस्था तक होती है। इसमें वृद्धि की गति पुनः तेज़ हो जाती है।
- चतुर्थ चक्र-इसकी अवधि 16 वर्ष से परिपक्वावस्था तक होती है। इसमें वृद्धि की गति पुनः मन्द पड़ जाती है।

प्रश्न 25.
आयु वृद्धि के साथ-साथ बालक में क्या-क्या परिवर्तन होते हैं ?
उत्तर :
आयु वृद्धि के साथ – साथ बालक के स्नायु-मण्डल (नाड़ी संस्थान) तथा मांसपेशियों में विकास होता है जिसके फलस्वरूप उसकी क्रियात्मक क्षमताएं बढ़ती जाती हैं। जब बालक अपनी मांसपेशियों को नियंत्रित करना सीख जाता है, तब वह कई प्रकार के कार्यों को कर सकता है जैसे-खेलना, बैठना, खड़ा होना, सरकना, चलना, दौड़ना तथा कूदना आदि। इस नियन्त्रण शक्ति के आ जाने पर वह अपनी प्राण-रक्षा करने में सक्षम हो जाता है जैसे स्वयं मल-मूत्र का विसर्जन तथा हाथ-पैर के संचालन से अपने अन्य अंगों का बचाव इत्यादि।
प्रश्न 26.
बालक के विकास क्रम को प्रभावित करने वाले तत्त्व कौन-कौन से हैं?
उत्तर :
बालक के विकास क्रम को प्रभावित करने वाले तत्त्व निम्नलिखित हैं –
1. परिवार – थॉमसन, क्रामगन आदि विद्वानों के अनुसार बालकों का कद, अस्थियों की वृद्धि, लैंगिक परिपक्वता, दाँतों का विकास व खराब होना आदि बातें अनेक परिवारों में एक समान पाई जाती हैं।
2. लैंगिक भिन्नता – लड़के और लड़कियों के विकास क्रम में भी भिन्नता पाई जाती है।
3. देह की लम्बाई – क्रामगन तथा नारवल विद्वानों के मतानुसार बड़े बालक की अपेक्षा छोटा बालक अधिक समय तक बढ़ता है।
4. संवेगात्मक तनाव – संवेगात्मक तनाव बालक के विकास को रोक देता है।
5. ऋतु – जुलाई से दिसम्बर तक बालक का वज़न बढ़ता है। सितम्बर से दिसम्बर तक बालक की वज़न-वृद्धि की गति बहुत तेज़ होती है। फरवरी से जून काल की अपेक्षा इस काल में बालक का वज़न चार गुना बढ़ जाता है। अप्रैल से अगस्त तक बालक के कद में बढ़ोतरी होती है।
प्रश्न 27.
संवेग से आप क्या समझते हैं ? यह कितने प्रकार के होते हैं ?
उत्तर :
संवेग (Emotion) – संवेग अंग्रेज़ी शब्द इमोशन का पर्यायवाची है। इसका लेटिन रूप इमोवियर (emovere) है जिसका अर्थ है-हिला देना, उत्तेजित करना। जब भी संवेग की स्थिति आती है, व्यक्ति में बेचैनी आ जाती है। किसी भी परिस्थिति में व्यक्ति का व्यवहार, कोमलता, भय, क्रोध, विरोध, ईर्ष्या, ममता, सुख-दुःख आदि आन्तरिक वृत्तियों द्वारा प्रभावित होता है। इन्हीं आन्तरिक वृत्तियों को संवेग का नाम दिया जाता है।
संवेग निम्नलिखित प्रकार के होते हैं –
- भय
- क्रोध
- वात्सल्य
- घृणा
- करुणा
- आश्चर्य
- आत्माहीनता
- आत्माभिमान
- एकाकीपन
- भूख
- कामुकता
- कृतिभाव
- अधिकार भावना
- अमोद
- उत्साह
- आनन्द।

प्रश्न 28.
बालक के संवेगात्मक व्यवहार की विशेषताएँ बताइए।
उत्तर :
बालकों के संवेगात्मक व्यवहार की विशेषताएँ –
- बालकों के संवेग शारीरिक विकारों से सम्बन्धित रहते हैं।
- बालकों के संवेग थोड़ी देर ही रहते हैं।
- बालकों के संवेगों में उग्रता रहती है।
- बालकों के संवेग का रूप बदलता रहता है।
- बालकों के संवेग बार-बार प्रकट होते रहते हैं।
- भिन्न-भिन्न बालकों के संवेगात्मक व्यवहार में भिन्नता होती है।
- बालकों के संवेग जल्दी पहचान में आ जाते हैं।
- बालकों के संवेग आरोपित होते रहते हैं।
- बालकों के संवेगों की शक्ति में अन्तर आता रहता है।
- बालकों की संवेगात्मक अभिव्यक्ति में अन्तर आता रहता है।
प्रश्न 29.
संवेग की अवस्था में क्या परिवर्तन होते हैं ?
उत्तर :
क्रोध, भय, प्रेम, ईर्ष्या, जिज्ञासा, आनन्द, दया, संवेग की अवस्था में व्यक्ति में बाह्य और आन्तरिक दो प्रकार के परिवर्तन होते हैं।
1. बाह्य परिवर्तन – (1) इसके अन्तर्गत चेहरे की मुद्रा बदलना जैसे-हंसना, रोना, प्रेम आदि के भाव आते हैं। (2) शरीर के आसनों में परिवर्तन जैसे-खड़े होना, भागना, उछलना, हाथ-पैर फेंकना आदि आते हैं।
2. आन्तरिक परिवर्तन – इसके अन्तर्गत खून की गति में परिवर्तन, सांस का फूलना, हृदय की गति में परिवर्तन, पाचन क्रिया में गड़बड़ी आदि आते हैं।
प्रश्न 30.
बालक के विकास में संवेगों का योगदान बताइए।
उत्तर :
बालक के विकास में संवेगों का योगदान-शैशव काल में शिश में तीन प्रमुख संवेग दिखाई देते हैं-भय, क्रोध और प्रेम। भय और क्रोध की अभिव्यक्ति वह रो कर व्यक्त करता है। प्रेम-संवेग वह किलकारी मारकर व्यक्त करता है।
शिशु के प्रति स्नेह भाव के रूप में संवेग महत्त्वपूर्ण कार्य करते हैं। यदि शिशु की सुख-सुविधा का ख्याल रखा जाए तो उसके सामने भय-क्रोध की स्थिति नहीं आने पाती है। जब घर में दूसरे शिशु का जन्म हो तो यह ध्यान रखना चाहिए कि पहले बच्चे के मन में यह न आ जाए कि उसका महत्त्व घट गया है या वह प्रेम से वंचित हो गया है।
4 – 5 साल के बच्चों के संवेगों का पूर्ण विकास हो जाता है। यदि माता-पिता से पर्याप्त प्रेम व सहानुभूति प्राप्त होती रहे तो बच्चे संवेगों पर नियन्त्रण करना सीख लेते हैं और बालक का विकास अच्छी प्रकार होता रहता है। संवेग द्वारा जीवन रक्षा तथा संकट से उबारने का कार्य होता है। संवेग प्रेरक का कार्य भी करते हैं।

प्रश्न 31.
उन कारकों का वर्णन करो जो बालक के संवेगात्मक व्यवहार को प्रभावित करते हैं।
उत्तर :
बालक के संवेगात्मक व्यवहार को प्रभावित करने वाले कारक –
- अस्वस्थता – ज्वर, जुकाम, अपच, कुपोषण, दुखती आँख आदि के कारण बालक कमज़ोर और चिड़चिड़ा हो जाता है।
- थकान – बालक थकान की अवस्था में शीघ्र ही उत्तेजित हो जाता है।
- पारिवारिक स्थिति – माता-पिता के नौकरी करने से न चाहते हुए भी उसके बालक उपेक्षित रह जाते हैं।
- सामाजिक वातावरण – बालक परिवार में जैसा व्यवहार अपने बड़ों का देखता है, उसकी मनोवृत्ति भी वैसी ही हो जाएगी।
- बौद्धिक योग्यता – बुद्धिमान् बालकों में संवेगात्मक अस्थिरता अधिक पाई जाती है।
प्रश्न 32.
शारीरिक विकास और व्यवहार में क्या सम्बन्ध है ?
उत्तर :
शारीरिक विकास और व्यवहार में निम्नलिखित सम्बन्ध है –
- स्नायुमण्डल के विकास से मस्तिष्क का उचित विकास होता है। मस्तिष्क के विकास से मानसिक योग्यताओं का विकास होता है, जिससे अंगों के नियन्त्रण में सुविधा होती है।
- मांसपेशियों के विकास से बालक में गति करने की क्षमताएँ उत्पन्न होती हैं और अंगों में शक्ति बढ़ती है, इसलिए वह नए तरह के खेल-खेलकर खुशी प्राप्त कर सकता है।
- शारीरिक संरचना में परिवर्तन होने के परिणामस्वरूप बालक का व्यवहार बदल जाता है।
- स्वस्थ और अस्वस्थ शरीर वाले बालकों के व्यवहार में बहुत अन्तर आ जाता है। सामान्य स्वास्थ्य वाले बालक का व्यवहार ठीक होता है। अस्वस्थ बालक के व्यवहार में चिड़चिड़ापन, उदासी आदि आ जाती है।
प्रश्न 33.
पूर्व-विद्यालय काल में बच्चे के सामाजिक विकास पर प्रकाश डालिए।
उत्तर :
पूर्व-विद्यालय काल में दो से छ: साल तक के बच्चे आते हैं। इस उम्र के बच्चे हम-उम्र बच्चों के साथ अपनी चीज़ों को बाँटना और एक-दूसरे के साथ सहयोग करना सीखते हैं। 1 से 2 साल के बच्चे अपने आप अकेले ही खेलना अधिक पसन्द करते हैं। 2 साल के पश्चात् बच्चा समूह में खेलना पसन्द करता है। इस उम्र में हम-उम्र का साथ पसन्द करने लगते हैं। इस अवस्था के बालकों में कुछ आक्रामक प्रकृति भी पाई जाती है। बच्चों में पारस्परिक होड़ की भावना भी विकसित हो जाती है।
प्रश्न 34.
इनाम और दण्ड बच्चे के सामाजिक विकास को किस प्रकार प्रभावित करते हैं।
उत्तर :
इनाम और दण्ड की क्रिया भी बच्चे के सामाजिक विकास पर प्रभाव डालती है। प्रत्येक छोटी-सी बात के लिए बच्चे को डाँट-फटकार करते रहेंगे, तो बच्चा अवश्य ही हीनता का शिकार हो जाएगा और वे हर काम को करने से डरेगा कि कहीं उसको माता पिता से दण्ड न मिले। प्रत्येक छोटे-से कार्य पर बच्चे को शाबाशी या इनाम देना भी बच्चे को बिगाड़ देता है। इस प्रकार से इनाम और दण्ड में सन्तुलन होना चाहिए। सभी काम को इनाम या दण्ड से नहीं तोलना चाहिए। जब बच्चे को कभी-कभी प्रशंसा या इनाम मिलता है तो वह समझ जाता है कि वह जो कर रहा है। वह ठीक है और वह बार-बार करता है। इस प्रकार बालक उस व्यवहार को सीख जाता है।

प्रश्न 35.
(A) सीखने (Learning) की कुछ परिभाषाएं दीजिए।
(B) सीखना क्या है ?
(C) सीखने से क्या अभिप्राय है ?
उत्तर :
सीखने की कुछ परिभाषाएँ निम्नलिखित हैं –
1. जिस क्रिया से प्राणी अपने को वातावरण के अनुकूल बनाते हुए अनुभवों से अधिक लाभ उठाने की चेष्टा करता है, उसे सीखना कहते हैं। अतीत से लाभ उठाना सीखना है।
– डॉ० चौबे
2. सीखना वह प्रक्रिया है जिसके द्वारा व्यक्ति नवीन प्रकार के व्यवहारों को अर्जित करता है। सीखने में व्यक्ति या तो अपने जन्मजात व्यवहारों को परिवर्तित करता है या नवीन व्यवहार को अपनाता है।
– डगलस तथा हालैण्ड
3. सीखना व्यक्ति के कार्यों में स्थायी परिवर्तन लाना है जो निश्चित परिस्थितियों में या किसी इच्छा को प्राप्त करने अथवा किसी समस्या को सुलझाने के प्रयास में अभ्यास द्वारा लाया जाता है।
– बर्नहर्ट
4. अनुभव द्वारा व्यवहार में रूपान्तर लाना ही सीखना है।
– गेट्स
प्रश्न 36.
सीखने के सम्बन्ध में महत्त्वपूर्ण बातें क्या हैं ?
उत्तर :
सीखने के सम्बन्ध में महत्त्वपूर्ण बातें निम्नलिखित हैं –
- सीखने की प्रक्रिया बच्चे के जन्म से पूर्व माँ के भ्रूण (पेट) में ही आरम्भ हो जाती है।
- बाहरी वातावरण के आने पर बच्चा अधिकांश बातें सीख पाता है।
- अभ्यास द्वारा स्थायी परिवर्तन सीखता है।
- सीखने का क्रम चलता रहता है।
- कार्य के पूर्ण होने के द्वारा ही सीखने की क्रिया सम्भव हो पाती है।
- अतीत के अनुभवों से लाभ उठाना सीखना है।
- नवीन व्यवहारों को प्राप्त करना सीखना है।

प्रश्न 37.
बोलना सीखने के लिए आवश्यक बातें क्या हैं ?
उत्तर :
- मस्तिष्क का साहचर्य क्षेत्र और स्वर तन्त्र दोनों परिपक्व हों।
- बालक को बोलने के लिए प्रेरणा, प्रोत्साहन एवं अवसर प्राप्त हों और उसके बोलने का अभ्यास चलता रहे।
- अभिभावकों, संरक्षकों एवं माता-पिता को भूलकर भी ऐसे बच्चों के रोने अथवा संकेतों पर ध्यान नहीं देना चाहिए जो टूटी-फूटी भाषा बोलने लगे हों। यदि उनके मौन संकेतों के आधार पर उनकी आवश्यकताओं की पूर्ति हो जाएगी, तो उनका भाषा विकास कुछ अंश तक अवरुद्ध हो जाएगा।
- बालकों को शब्दों को सीखने के लिए उचित मार्गदर्शन या निर्देशन प्राप्त होना चाहिए।
- भाषा सिखाते समय निर्देशकों को चाहिए कि वे बालक के समक्ष “मॉडल शब्द” धीरे-धीरे, बारी-बारी से स्पष्ट एवं शुद्ध उच्चारण के साथ प्रस्तुत करें।
प्रश्न 38.
भाषा सीखने के प्रमुख अंग क्या हैं ?
उत्तर :
भाषा सीखने के प्रमुख अंग निम्नलिखित हैं –
1. अनुकरण – बच्चों में अनुकरण की प्रवृत्ति जन्म-जात होती है। यही कारण है कि माता-पिता, शिक्षक तथा अन्य साथियों की भाषा का बच्चे की भाषा पर गहरा प्रभाव पड़ता है। इस प्रकार बच्चा अनुकरण से भाषा सीखता है।
2. वार्तालाप – थोड़ा बड़ा बच्चा अपने साथियों के साथ टूटी-फूटी भाषा का प्रयोग करने लग जाता है। एक ही उम्र के बच्चे आपसी वार्तालाप से पर्याप्त मात्रा में भाषा सीखते हैं।
3. कहानियां – बच्चे कहानी सुनने के बहुत शौकीन होते हैं। घर के बड़े-बूढ़े सदस्य बच्चों को कहानियां सुनाते हैं। कहानियों से उन्हें आनन्द तो मिलता ही है साथ ही वे भाषा का बहुत कुछ बोलना भी सीख जाते हैं। माता-पिता व अन्य सदस्यों को चाहिए कि कहानी सुनाते समय भाषा की शुद्धता का ध्यान रखें अन्यथा बच्चा भी अशुद्ध भाषा सीखेगा।
4. प्रश्नोत्तर – बच्चों को प्रश्न पूछने की बहुत आदत होती है। बच्चे अपने से बड़ों तथा साथियों से बहुत प्रश्न पूछते हैं। बच्चे को प्रश्न का उचित उत्तर अवश्य देना चाहिए। प्रश्नों के उत्तर बच्चों को भाषा सीखने में अत्यधिक सहायता करते हैं।
5. खेल – कुछ खेल भी इस प्रकार के होते हैं जिनके निरन्तर प्रयोग से बच्चे भाषा को बोलना सीख जाते हैं। बच्चों को ऐसे खेलों के लिए प्रेरित किया जाना चाहिए।
प्रश्न 39.
भाषा विकास के सहायक अंगों का उल्लेख कीजिए।
उत्तर :
भाषा विकास के सहायक अंग हैं –
1. सुनने के द्वारा भाषा ज्ञान – बच्चे की सुनने की शक्ति जितनी अधिक प्रबल होगी, उतना ही भाषा को समझेगा। इस प्रकार लगातार सुनने और ज्ञान के आधार पर भाषा विकसित होती रहती है।
2. मुख के विभिन्न अंग – कंठ (गले) व जीभ के विकास पर भाषा का विकास निर्भर करता है। जैसे-जैसे बालक की आयु बढ़ती जाती है, उसके मुख के अंग भी विकसित होते जाते हैं। इन अंगों के पर्याप्त विकास के बाद बालक भाषा को समझने भी लगता है और बोलने भी लगता है।
3. अक्षर ज्ञान – पढ़ाई आरम्भ करने पर बच्चे को अक्षर ज्ञान कराया जाता है। विभिन्न ध्वनियों के लिए निश्चित अक्षर होते हैं और बच्चा इन्हें आँख के प्रयोग द्वारा सीखता है। लगातार वही अभ्यास करने पर वह जल्दी-जल्दी पढ़ने लगता है और आगे मौन रहकर भी पढ़ सकता है।
4. भाषा लेखन – पढ़ने के अभ्यास के बाद बच्चा उसी भाषा को लिखने का प्रयत्न करता है। लिखने में हाथ अंग का उपयोग होता है। बच्चा आँख से देखकर हाथ की शक्तियों से लिखता है। लेखन क्रिया में मानसिक शक्तियों का भी उपयोग होता है।

प्रश्न 40.
भाषा विकास का अर्थ बताएँ और बच्चे के 3 साल तक के भाषा विकास का विवरण दें।
उत्तर :
भाषा का अर्थ है शब्दों द्वारा की गई सम्प्रेषणा। भाषा के द्वारा ही सूचना एक व्यक्ति से दूसरे तक पहुंचाई जाती है।
जन्म से लेकर एक माह तक शिशु सिर्फ रोने की आवाज़ ही निकाल पाता है। 5-6 महीने का बच्चा बाबा-मामा जैसी ध्वनियां दोहराता है। इसे बैबलिंग कहते हैं। बैबलिंग में समूचे विश्व के शिशु एक जैसी ध्वनियां निकालते हैं।
1 वर्ष का बच्चा एक शब्द का उच्चारण करके पूरी बात समझाने की कोशिश करता है। उसके द्वारा कहे गए शब्द प्रायः किसी चीज़ के नाम होते हैं जैसे पापा, मामा आदि।
2 वर्ष का बच्चा दो शब्द जोड़कर वाक्य बनाता है जैसे ‘पापा आफिस’ ‘माँ-दूध’ आदि।
3 वर्ष का होने पर बच्चे छोटे-छोटे वाक्य बना लेते हैं जोकि 3-4 शब्दों से बने होते हैं। जैसे ‘मम्मी पानी दो’।
प्रश्न 41.
भाषा विकास के महत्त्व पर टिप्पणी लिखो।
उत्तर :
भाषा सामाजिक सम्पर्क का सबसे बड़ा साधन है। इसके द्वारा सभी तरह की सांस्कृतिक उपलब्धियां सम्भव हैं। इसके माध्यम से हम अपने विचारों को व्यक्त कर सकते हैं। इससे ही साहित्य का जन्म होता है। इसीलिए साहित्य को समाज का दर्पण कहा गया है। जैसा समाज होगा वैसा ही उसका साहित्य होगा। प्रसिद्ध वैज्ञानिक एमविल के मतानुसार किसी जाति के भाषा विकास का इतिहास उसके बौद्धिक विकास का इतिहास है। दूसरे प्राणियों की अपेक्षा मानव भाषा के कारण ही अधिक श्रेष्ठ माना गया है।
भाषा व सभ्यता का विकास साथ-साथ चलता है। शुरू में बालक स्थूल वस्तुओं को ही इस्तेमाल में लेता है। तत्पश्चात् वह भाषा का व्यवहार करने लगता है। शिक्षा का एक प्रधान उद्देश्य बालक को भाषा का समुचित ज्ञान कराना है। किसी भी व्यक्ति की बौद्धिक योग्यता का सर्वश्रेष्ठ माप उसका शब्द भण्डार ही है।
प्रश्न 42.
वंशानुक्रम बालक के वृद्धि और विकास को किस प्रकार प्रभावित करता है ?
उत्तर :
कोई भी बच्चा जब जन्म लेता है तो उसमें उसके माता तथा पिता के गुण होने अनिवार्य हैं। अर्थात् बच्चे की शक्ल-सूरत, चेहरे का रंग, नैन-नक्श, बाल, बोलचाल आदि पर माता-पिता के गुणों का प्रभाव होता है। बच्चों की लम्बाई, भार, डील-डौल भी वंशानुक्रम द्वारा प्रभावित होती है। इस प्रकार अभिवृद्धि का सीधा सम्बन्ध वंशानुक्रम से है तथा बच्चे में क्षमताओं का पैदा होना जैसे गणित में अच्छा होना, तार्किक शक्ति अधिक होना, वाक चातुर्य होना, संगीत, कलात्मक गुणों का होना आदि विकास के विभिन्न प्रकार भी वंशानुक्रम से प्रभावित हैं।

प्रश्न 43.
‘मील के पत्थर’ क्या है ? बाल्यावस्था में छोटे बच्चों के लिए इनका क्या महत्त्व है ?
उत्तर :
शिशु का जैसे-जैसे विकास होता है इसे मनोवैज्ञानिकों ने विभिन्न चरणों में बांटा है जिन्हें मील के पत्थर कहते हैं। इस प्रकार किसी भी शिशु की अभिवृद्धि तथा विकास उचित हो रहा है या नहीं इसके बारे में स्पष्ट हो जाता है। जैसे कितनी आयु में बच्चा चलना शुरू करेगा, कब बोलेगा, कितनी आयु में उसकी लम्बाई अथवा भार कितना होगा आदि विभिन्न मील के पत्थर हैं तथा बच्चे का विकास ठीक ढंग से हो रहा इससे भी अवगत करवाते हैं।
प्रश्न 44.
क्रोध संवेग के कारण बताएं।
उत्तर :
- अन्याय तथा अनाधिकार चेष्ट के प्रतिरोध में बालक क्रोध प्रकट करता है।
- क्षमता से बड़ा कार्य सौंप देने से।
- अभिभावक की अधीरता या चिड़चिड़ाहट।
- कपड़े पहनने की विधि कष्टदायक होना।
- भाई-बहिन व साथियों द्वारा चिढ़ाने पर।
- अत्यधिक थकान होने पर।
- बालक के काम में अनावश्यक रुकावट होने पर।
- शारीरिक दुर्बलता व रोग होने पर।
प्रश्न 45.
बालक क्रोध की अभिव्यक्ति कैसे करता है ?
उत्तर :
बालक द्वारा क्रोध की अभिव्यक्ति-बालक अपने क्रोध को निम्नलिखित प्रकार से व्यक्त कर सकता है –
- रोना
- चीखना-चिल्लाना
- दाँत पीसना
- सिर पटकना
- ज़मीन पर लेट जाना
- वस्तुओं को उठाकर फेंक देना
- गुस्से में मुख फाड़ना
- जीभ निकालना व थूकना।

दीर्घ उत्तरीय प्रश्न :
प्रश्न 1.
आधुनिक जीवन में बाल विकास का क्या महत्त्व है ?
उत्तर :
1. बाल विकास से हमें पता चलता है कि साधारणतः एक बच्चे से एक अवस्था में क्या आशा रखी जाए। यदि कोई बच्चा इस आशा से बाहर जाए तो उसकी ओर हमें विशेष ध्यान देना होगा।
2. बाल विकास की पढ़ाई से हमें बच्चों की ज़रूरतों सम्बन्धी जानकारी प्राप्त होती है। हम बच्चे के मनोविज्ञान को अच्छी तरह समझ कर उसका पालन-पोषण कर सकते हैं जिससे उसका बहुपक्षीय विकास अच्छे ढंग से हो सकता है।
3. बाल विकास के अध्ययन से हमें यह जानकारी मिलती है कि साधारण बच्चों से भिन्न बच्चों को किस तरह का वातावरण प्रदान करें कि वह हीन भावना का शिकार न हो जाएं जैसे शारीरिक अथवा मानसिक तौर पर विकलांग बच्चे, मन्द बुद्धि वाले बच्चे अपनी शारीरिक तथा मानसिक कमजोरियों से ऊपर उठकर अपना बहुपक्षीय विकास कर सकें।
4. बाल विकास पढ़ने से हमें वंश तथा वातावरण सम्बन्धी जानकारी भी मिलती है। एक-दो ऐसे महत्त्वपूर्ण पक्ष हैं जो बच्चे के विकास में बहुत योगदान डालते हैं। वंश से हमें बच्चे के उन गुणों के बारे पता चलता है जो बच्चों को अपने माता-पिता से जन्म से ही मिले होते हैं तथा जिन्हें बदला नहीं जा सकता जैसे नैन-नक्श, कद-काठ, बुद्धि आदि। बच्चे के इर्द-गिर्द को वातावरण कहा जाता है जैसे भोजन, अध्यापक, किताबें, खेलें, मौसम आदि। वातावरण बच्चे के व्यक्तित्व पर गहरा प्रभाव डालता हैं। अच्छा वातावरण बच्चे के व्यक्तित्व को उभारने में मदद करता है।

प्रश्न 2.
बाल विकास की शिक्षा के अन्तर्गत आपको किस के बारे में शिक्षा मिलती है ?
उत्तर :
बाल विकास के अध्ययन में बच्चों में पाई जाने वाली व्यक्तिगत भिन्नताएं, उनके साधारण तथा असाधारण व्यवहार तथा इर्द-गिर्द का बच्चे पर प्रभाव को जानने की कोशिश भी की जाती है।
प्रत्येक मनुष्य के व्यक्तित्व की जड़ें उसके बचपन में होती हैं। आजकल मनोवैज्ञानिक तथा समाज वैज्ञानिक किसी मनुष्य के व्यवहार को समझने के लिए उसके बचपन के हालातों की जांच-पड़ताल करते हैं। समाज वैज्ञानिक यह बात सिद्ध कर चुके हैं कि वे बच्चे जिन्हें बचपन में प्यार नहीं मिलता। बड़े होकर अपराधों की ओर रुचित होते हैं।
1. बच्चों की प्रवृत्ति को समझने के लिए-बाल विकास के अध्ययन से हम विभिन्न स्तरों पर बच्चों के व्यवहार तथा उनमें होने वाले परिवर्तनों से अवगत होते हैं। एक बच्चा विकास की विभिन्न स्थितियों से किस तरह गुज़रता है इसका पता बाल विकास के अध्ययन द्वारा ही चलता है।
2. बच्चे के व्यक्तित्व के विकास को समझने के लिए-बाल विकास अध्ययन बच्चे के व्यक्तिगत विकास तथा चरित्र निर्माण का ज्ञान उपलब्ध कराता है। ऐसे कौन-से तथ्य हैं जो भिन्न-भिन्न आयु के पड़ावों पर बच्चे के व्यक्तित्व को प्रभावित करते हैं तथा बच्चे के व्यक्तित्व के विकास में रुकावट डालने वाले कौन-से तत्त्व हैं, बाल विकास इनकी खोज करने के पश्चात् बच्चे की मदद करता है।
3. बच्चे के विकास के बारे जानकारी-गर्भ धारण से लेकर बालिग होने तक के शारीरिक विकास का अध्ययन बाल विकास का मुख्य भाग है। बाल विकास अध्ययन की मदद से बच्चे के शारीरिक विकास की रुकावटों तथा कारणों को अच्छी तरह समझ सकते हैं। बाल विकास बच्चे की शारीरिक विकास से सम्बन्धित समस्याओं को समझने में भी हमारी सहायता करता है।
4. बच्चे के लिए बढिया वातावरण पैदा करना-बच्चे के व्यवहार तथा रुचियों पर वातावरण का महत्त्वपूर्ण प्रभाव होता है। बाल विकास के अध्ययन से वातावरण के बच्चे पर पड़ रहे बुरे प्रभावों का पता चलता है। बच्चे के व्यक्तित्व के बढ़िया विकास के लिए बढ़िया वातावरण उत्पन्न करने सम्बन्धी मां-बाप तथा अध्यापकों को सहायता मिलती है।
5. बच्चों के व्यवहार को कन्ट्रोल करने के लिए-बच्चे का व्यवहार हर समय एक जैसा नहीं होता। बच्चे के व्यवहार से सम्बन्धित समस्याओं जैसे बिस्तर गीला करना, अंगूठा चूसना, डरना, झूठ बोलना आदि का कोई-न-कोई मनोवैज्ञानिक कारण अवश्य होता है। बाल विकास अध्ययन की सहायता से इन समस्याओं के कारणों को समझा तथा हल किया जा सकता है।
6. बच्चों का मार्ग-दर्शन-माता-पिता समय-समय पर बच्चों की रहनुमाई करते हैं। परन्तु आज-कल पढ़े-लिखे मां-बाप विशेषज्ञों से बच्चों का मार्ग-दर्शन करवाते हैं। यह मार्ग-दर्शन विशेषज्ञ मनोवैज्ञानिक विधियों द्वारा उसकी रुचियां, छुपी हुई क्षमता तथा झुकाव का पता लगाकर बच्चों का मनोवैज्ञानिक मार्ग-दर्शन करते हैं।
7. पारिवारिक जीवन को खुशियों भरा बनाने के लिए-बच्चे हर घर का भविष्य होते हैं। इसलिए उनका पालन-पोषण ऐसे वातावरण में होना चाहिए जो उनकी वृद्धि तथा विकास में सहायक हो। बाल विकास अध्ययन द्वारा हमें ऐसे वातावरण की जानकारी मिलती है। एक बढ़िया वातावरण में ही पारिवारिक प्रसन्नता तथा शान्ति उत्पन्न होती है।
उपरोक्त वर्णन से यह पता चलता है कि बाल विकास विज्ञान एक बहुत महत्त्वपूर्ण विषय है जिसकी सहायता से हम बच्चों के शारीरिक, मानसिक तथा भावनात्मक विकास से सम्बन्धित अनेकों पहलुओं से अवगत होते हैं। बच्चों के बचपन को खुशियों भरा बनाने के लिए यह विज्ञान बहुत लाभदायक है। खुशियों भरे बचपन वाले बच्चे ही भविष्य में स्वस्थ तथा प्रसन्न समाज रचेंगे। इस महत्त्वपूर्ण कार्य में बाल विकास विज्ञान की महत्त्वपूर्ण भूमिका है।

प्रश्न 3.
अभिवृद्धि और विकास के सिद्धान्तों को सूचीबद्ध करें व किन्हीं तीन का वर्णन करें। उदाहरण सहित स्पष्ट करें। .
अथवा
अभिवृद्धि और विकास के सिद्धान्त कौन-कौन से हैं ? उनमें से किन्हीं दो का वर्णन करें।
अथवा
विकास के सिद्धान्त उदाहरण सहित स्पष्ट करें।
उत्तर :
विकास कभी भी अव्यवस्थित तरीके से नहीं अपितु नियमानुसार चलता है। विकास के कुछ मुख्य सिद्धान्त इस प्रकार से हैं
1. विकास में परिवर्तन निहित है-विकास का अर्थ है परिवर्तन। हम परिवर्तन से ही ज्ञात कर सकते हैं कि शिशु में विकास हो रहा है। उदाहरणस्वरूप जब शिशु वयस्कता की ओर विकसित होता है। तब उसके शरीर की अपेक्षा उसका सिर छोटा हो जाता है जबकि जन्म पर सिर शरीर की तुलना से बड़ा होता है।
2. विभिन्न आयु स्तरों पर विकास की दर भिन्न होती है इसका अर्थ है कि कभी किसी उम्र में विकास तेजी से होता है। फिर धीमा पड़ जाता है और बाद में फिर तेजी पकड़ता है। उदाहरणस्वरूप पहले छः सालों में बच्चे का शारीरिक विकास बहुत तेजी से होता है। तत्पश्चात् 7-11 वर्ष तक विकास की गति कुछ धीमी हो जाती है। 12 वर्ष के बाद फिर तेज़ी से शारीरिक विकास होता है।
3. विकास क्रमागत और व्यवस्थित होता है-इसका अर्थ है कि विकास एक क्रम और व्यवस्था से चलता है। उदाहरण के लिए बच्चा पहले बैठना सीखता है, फिर खड़े होना और फिर चलना। बैठने से पहले वह चलना नहीं सीख सकता।
4. विकास सिर की ओर से प्रारम्भ होता है- इसका अर्थ है कि विकास सिर से शुरू होकर पैरों तक जाता है। उदाहरण के लिए बच्चा पहले सिर सम्भालना सीखता है, फिर बिस्तर पर लुढ़कना, बाद में बैठना, फिर खड़े होना और फिर चलना। अतः विकास प्रक्रिया सिर क्षेत्र से होती हुई धड़ तक जाती है और अन्त में निम्नतर क्षेत्र में जाती है अर्थात् पैरों में।
5. विकास केन्द्र से बाहर की ओर होता है-विकास प्रक्रिया पहले केन्द्र (Central portion) में होती है और तत्पश्चात् बाहर की ओर (Outside region)। उदाहरण के लिए बच्चा पहले चीज़ उठाने के लिए पूरी भुजा का प्रयोग करता है। फिर हाथ का, फिर उंगलियों का और अन्त में अंगूठे व उंगली का प्रयोग करता है।
6. विभिन्न व्यक्तियों में विकास की दर भिन्न होती है-दो बच्चे एक ही उम्र के . हो सकते हैं पर उनके विकास की दर एक सी कभी नहीं होती। उदाहरण के लिए आप दो चार साल के बच्चों को देखें। दोनों की लम्बाई में फर्क मिलेगा। दोनों का भाषा ज्ञान भिन्न होगा इत्यादि। यह अन्तर इसीलिए है क्योंकि दोनों की विकास की दर भिन्न है।

प्रश्न 4.
संवेगात्मक विकास का क्या अर्थ है ? बच्चे की तीन साल तक के संवेगात्मक विकास को स्पष्ट करें।
उत्तर :
संवेगात्मक विकास का अर्थ है, अपने संवेगों पर नियन्त्रण प्राप्त करना और समाज द्वारा अनुमोदित ढंग से उनकी अभिव्यक्ति करना।
जन्म के समय सभी संवेग बालक में विद्यमान नहीं होते पर धीरे-धीरे अंकुरित होते हैं। जन्म के समय सिर्फ ‘साधारण उद्वेग’ बच्चे में संवेग के रूप में विद्यमान होता है।
5 माह – प्रसन्नता व तकलीफ नामक संवेग प्रकट हो जाते हैं। जब बच्चा आरामदायक परिस्थिति में होता है, तो वह प्रसन्न होता है अन्यथा तकलीफ में होता है अर्थात् अपनी तकलीफ की अभिव्यक्ति करता है।
6 माह – भय नामक संवेग प्रकट हो जाते हैं। बालक ऊंचे स्थानों से डरता है। हवा में उछाले जाने पर भी डरता है। बड़ा होने पर वह चमकती बिजली, जानवर, शोर आदि से डरता है।
1 वर्ष – प्यार व क्रोध नामक संवेग प्रकट हो जाते हैं। मना किए जाने पर वह क्रोधित होता है और माता-पिता से प्यार प्रकट करता है, उनसे लिपटता है। अगर बच्चे को यह महसूस होता है कि माता-पिता उसे प्यार नहीं करते तो वह असुरक्षित महसूस करता है।
18 महीने पर ईर्ष्या नामक संवेग का विकास होता है। जब माता-पिता ज्यादा ध्यान छोटे भाई बहन पर देते हैं, तो बच्चा उनसे ईर्ष्या करने लगता है।
प्रश्न 5.
सामाजिक व्यवहार को कौन-से कारक प्रभावित करते हैं ?
उत्तर :
निम्नलिखित कारक सामाजिक व्यवहार को प्रभावित करते हैं –
- बच्चे बड़ों की नकल करके सीखते हैं। अत: बड़ों को सदा बच्चों के समक्ष अच्छा व्यवहार प्रदर्शित करना चाहिए।
- बालक इनाम व दण्ड द्वारा सीखते हैं। अतः अच्छे काम पर उन्हें इनाम दे। जैसे शाबाशी और गलत काम पर दण्ड दे ताकि वह उसे दुबारा न करे।
- माता – पिता का एक सम होना ज़रूरी है अर्थात् गलती पर दोनों ही बच्चे को रोकें और अच्छे काम के लिए दोनों ही शाबाशी दें।
- बहुत अधिक रोक-टोक बच्चे को आश्रित बना देती है। अतः हर काम के लिए बच्चे को मना न करें। उसे कुछ काम खुद करके सीखने दें।
- माता – पिता बच्चों का मार्ग-दर्शन प्यार से करें न कि डांट अथवा रोक-टोक के साथ।
माता-पिता बच्चों को समाज में सही व्यवहार करना सिखाते हैं। अतः वह समाजीकरण के कारक हैं। इसके अलावा बच्चे के दोस्त व नर्सरी स्कूल की अध्यापिका भी इसी श्रेणी में आते हैं।

प्रश्न 6.
बच्चे की शारीरिक आवश्यकताओं को संक्षेप में समझाएं।
अथवा
भोजन की आवश्यकता के अतिरिक्त बच्चों की और क्या क्या शारीरिक आवश्यकताएं होती हैं व उन्हें कैसे पूरा करना चाहिए ?
उत्तर :
ऐसी आवश्यकताएं जो बच्चे को जीवित रखने में सहायक होती हैं, शारीरिक आवश्यकताएं कहलाती हैं। ये निम्नलिखित प्रकार की होती हैं
1. भोजन की आवश्यकता – नवजात बच्चे का भोजन दूध होता है। जैसे-जैसे वह बड़ा होता है वह अतिरिक्त आहार लेने लगता है। बच्चे के लिए अच्छा आहार आवश्यक है क्योंकि वह बच्चे को
- स्वस्थ बनाता है।
- वृद्धि व विकास में मदद करता है।
- ऊर्जा प्रदान करता है।
- रोग के कीटाणुओं से बचाता है।
बच्चे को सही समय पर व अच्छा भोजन देना चाहिए।
2. नींद की आवश्यकता – एक नवजात शिशु करीब 20 घण्टे सोता है। जैसे-जैसे बच्चा वयस्क बन जाता है तो उसे 6-8 घण्टे की नींद चाहिए होती है। बच्चे को नींद आवश्यकतानुसार लेनी चाहिए। सोने से उसे आराम मिलता है व खोई हुई शक्ति वापिस आ जाती है।
3. शारीरिक व्यायाम की आवश्यकता – बच्चे को तन्दुरुस्त रहने के लिए व्यायाम की आवश्यकता है। व्यायाम सही विकास में मदद करता है। अत: बच्चों को मुक्त रूप से खेलने देना चाहिए पर उन पर निगरानी अवश्य रखें।
4. कपड़ों की आवश्यकता – बच्चों को मौसम के अनुसार कपड़ों की आवश्यकता होती है। गर्मियों में कॉटन, सर्दी में ऊनी। अत: उन्हें सही कपड़े पहनाने चाहिए। सर्दी में बच्चे को सिर्फ माँ से एक ज्यादा स्वेटर पहनाएँ। बच्चे को ढीले कपड़े पहनाएं।
5. बीमारियों से सुरक्षा की आवश्यकता – बच्चे के सही विकास के लिए आवश्यक है कि उसे बीमारियों से बचाया जाए। अत: उसे व उसके वातावरण को स्वच्छ रखें और उसे सही समय पर टीके लगवाएं।

प्रश्न 7.
बच्चों की भावनात्मक आवश्यकताएं कौन-सी हैं ?
उत्तर :
ये निम्नलिखित प्रकार की हैं –
1. प्यार की आवश्यकता – सभी बच्चों को स्नेह व प्यार की आवश्यकता होती है। अतः माता-पिता को अपने बच्चों को प्यार करना चाहिए। पर प्यार अन्धा नहीं होना चाहिए। माता-पिता से प्यार मिलने पर बच्चों में आत्म-विश्वास पैदा होता है। प्यार न मिलने पर बच्चे गैर-मिलनसार हो जाते हैं। अत: माता-पिता को अपने बच्चों के साथ अवश्य ही समय बिताना चाहिए। उसकी बातें सुननी चाहिए और उसे अच्छे कामों के लिए प्रेरित करना चाहिए। छोटे बच्चे के साथ शारीरिक सम्पर्क करना अति आवश्यक है।।
2. भावनात्मक सुरक्षा की आवश्यकता – बच्चे माता-पिता से यह समझना चाहते हैं कि वह क्या कर सकते हैं और क्या नहीं। अतः यदि माता-पिता उन्हें सही तरीके से समझाते हैं तो बच्चों में विश्वास व सुरक्षा की भावनाएं पैदा होती हैं। माता-पिता यदि बच्चों के अच्छे काम की प्रशंसा करते हैं व गलत काम की निन्दा करते हैं, तो वह बच्चे में सुरक्षा की भावना स्थापित करते हैं। यदि माता-पिता बच्चे के हर कार्य की उपेक्षा करते हैं और उनके कामों में उत्साह नहीं दिखाते तो बच्चे असुरक्षित महसूस करते हैं।
3. स्वतन्त्रता की आवश्यकता – स्वतन्त्रता का अर्थ है अपना काम खुद करना। बच्चे ज्यादातर अपना काम खुद करना चाहते हैं। बच्चों को अपने काम खुद करने दें। इससे उनमें आत्म-विश्वास पैदा होता है। अत: वह और भी कठिन कार्यों को करने की चेष्टा करते हैं। इससे उनका मानसिक विकास होता है। जब बच्चे कोई भी कार्य करें तो बड़े लोग आस-पास रह कर उन्हें देखते रहें ताकि बच्चे को चोट न लगे। यदि आप बच्चे को स्वतन्त्रता नहीं देंगे तो वह सदैव निर्भर रहेगा और उसका आत्म-विश्वास टूट जाएगा।
4. समायोजन की आवश्यकता – बच्चे धीरे-धीरे समायोजन (adjustment) सीखते हैं। धीरे-धीरे वह बड़े होते हैं तो ज्यादा समझदार होते हैं। वह अपनी चीजें दूसरों के साथ बांटकर खेलते हैं। जब बच्चा समायोजन स्थापित करता है तो –
1. वह अपने संवेगों पर नियन्त्रण करना सीख जाता है। दूसरे बच्चों के साथ खेलते हुए वह छोटी-छोटी बातों पर गुस्सा नहीं होता।
2. वह औरों के साथ अपनी चीजें बांटना सीखता है और सहनशील बनता है।
प्रश्न 8.
संवेगों के विकास में माता-पिता व परिवार के अन्य सदस्य किस तरह सहायता करते हैं ?
अथवा
संवेगों के विकास में माता-पिता किस तरह सहायता करते हैं ?
उत्तर :
बालक के संवेगों के विकास में माता-पिता का महत्त्वपूर्ण स्थान है। बालक सबसे ज्यादा स्नेह शुरू में अपनी माता से करता है। अधिक स्नेह या कम स्नेह दोनों ही बालक के लिए घातक सिद्ध होते हैं। इसलिए माता-पिता का यह कर्त्तव्य हो जाता है कि समय-समय पर बच्चे के प्रति स्नेह प्रदर्शित करते रहें।
क्रोध में यदि आक्रामकता अधिक हो, तो वह बच्चे के लिए घातक सिद्ध होता है। माता-पिता को चाहिए कि वे बालक के असन्तोष का पता लगाएँ, उसमें सहयोग की भावना विकसित करें, बालक को नेतृत्व का अवसर प्रदान करें, समय-समय पर उन्हें सामाजिक मान्यता प्रदान करें तथा समय-समय पर बालक की प्रशंसा व निन्दा करें।
माता-पिता को चाहिए कि वह बालक में नई वस्तु की रचना करने की प्रवृत्ति को विकसित करें। यदि इस प्रवृत्ति का दमन किया जाता है, तो बालक अपना आत्म-विश्वास खो बैठता है और उसमें कुंठाएं उत्पन्न हो जाती हैं।जिज्ञासा समस्त ज्ञान की जननी है। अत: इसे विकसित करने के लिए माता-पिता को चाहिए कि –
- बालकों को प्रश्न करने के लिए प्रोत्साहित करें।
- प्रश्न पूछने पर समस्या का समाधान प्यार सहित किया जाए, डांट-फटकार कर नहीं।
- प्रश्न का उत्तर बालक की रुचि, क्षमता तथा मानसिक स्तर के अनुसार हो।
- बालक को अनुभव प्रदान कर कुछ करके सीखने पर बल दिया जाए।
भय में बालक आत्म-विश्वास खो बैठता है। माता-पिता को चाहिए कि वह उसमें पलायन की प्रवृत्ति विकसित न होने दें। बच्चों को किसी वस्तु-स्थिति का भय न दिखाएं। मनोवैज्ञानिक ढंग से भयप्रद स्थितियों का सामना कराएं। एकान्त या अन्धकार में डरने वाले बच्चे को कभी भी एकान्त या अन्धकार में न छोड़ें। बच्चों को हर समय डांटना-पीटना नहीं चाहिए।
बालकों में ईर्ष्या का होना अच्छा नहीं। इसके लिए माता-पिता को इस भावना को विकसित होने से पूर्व ही उसे स्वस्थ दिशा प्रदान करनी चाहिए। इसके लिए बालक के स्वास्थ्य का पूरा ध्यान रखना चाहिए। उसकी दिनचर्या नियमित होनी चाहिए। बालक को उसके दोष के कारण उसे चिढ़ाना नहीं चाहिए। जब भी यह महसूस हो कि बालक ईर्ष्या की भावना से ग्रस्त है, कारणों की खोज कर ईर्ष्या भाव को समाप्त करना चाहिए।

प्रश्न 9.
भय क्या है ? भय को नियन्त्रित करने के मनोवैज्ञानिक उपाय दीजिए।
उत्तर :
भय (Fear) – भय की मूल प्रवृत्ति पलायन है जिसका प्रदर्शन बालक रोकर, चिल्लाकर, दौड़कर प्रकट करता है। बाल्यावस्था में भय तनाव के कारण होता है। प्रायः बजे नहाने, स्कूल जाने से, अप्रिय वस्तु खाने से डरते हैं। अधिक भय की प्रवृत्ति बालक के लिए हानिकारक होती है। पहले बच्चा प्रायः ऊंची आवाज़, अन्धेरा, अपरिचित व्यक्ति, जानवर, एकान्त, पीड़ा, पानी, ऊँचाई से डरता है। बड़े हो जाने पर भय काल्पनिक अधिक हो जाते हैं, जैसे- भूत का डर, चोर का डर, दुर्घटना का डर आदि।
भय को नियन्त्रित करने के मनोवैज्ञानिक उपाय –
1. मौखिक निराकरण विधि – इस विधि से बच्चे को समझाकर भयावह वस्त की निरर्थकता सिद्ध कर दी जाती है। समझाने पर बालक उस वस्तु या परिस्थिति से डरना छोड़ देता है।
2. ध्यानभंग विधि – इस विधि में बालक का ध्यान भयावह वस्तु से हटाकर किसी दूसरी जगह आकर्षित किया जाता है ताकि बच्चे के ध्यान से भयावह वस्तु हट जाए और वह दूसरी बातों की ओर सोचने लगे। जैसे यदि बच्चा किसी जानवर से डरता है, तो उसी क्षण बच्चे को कोई खिलौना देकर, मनोरम चित्र दिखाकर या किसी और वस्तु में ध्यान लगाकर उस जानवर का ध्यान हटाया जा सकता है।
3. अनाभ्यास विधि – इस विधि में बालक को भयावह परिस्थिति से उसी क्षण दूर ले जाकर उसकी उत्तेजना को समाप्त किया जाता है। इस सम्बन्ध में बच्चों को भूत-प्रेत की कहानियां नहीं सुनानी चाहिएं, अपितु वीरतापूर्ण कहानियां सुनाकर उसके भय की ग्रन्थि को दूर करना चाहिए।
4. प्रत्यक्ष साक्षात्कार – जो बच्चे किसी विशेष वस्तु या जानवर से डरते हैं, उन बच्चों को उसी विशेष वस्तु या जानवर के पास ले जाकर प्यार से, पुचकार कर साक्षात्कार कराना चाहिए। पहले उस जानवर का चित्र दिखाकर या खिलौना देकर उसे समझाना चाहिए फिर उस जानवर से साक्षात्कार कराकर उसके भय की ग्रन्थि का निवारण करना चाहिए।
प्रश्न 9.
(A) भय को नियंत्रित करने के दो मनोवैज्ञानिक उपाय बताएं।
उत्तर :
देखें उपरोक्त प्रश्न।
प्रश्न 10.
ईर्ष्या क्या है ? ईर्ष्या के निवारण के उपाय लिखिए।
उत्तर :
ईर्ष्या-यह क्रोध की उपशाखा है। ईर्ष्या सामाजिक परिस्थिति में उत्पन्न होने वाला व्यवहार है। बालक जब किसी व्यक्ति के व्यवहार में प्यार की कमी देखता है तो उसमें ईर्ष्या उत्पन्न हो जाती है। जब किसी भाई-बहन या दोस्त के कारण बालक अपने प्यार या किसी काम में बाधा महसूस करता है तो उसमें ईर्ष्या की भावना उत्पन्न हो जाती है। शैशवावस्था में बालक ईर्ष्या को रोकर, बाल खींचकर, कपड़े फाड़कर, ज़मीन पर लेटकर व्यक्त करता है। बाल्यावस्था में वह बड़ों की आज्ञा का उल्लंघन करके अथवा रोक कर इसे प्रकट करता है। तीव्र बुद्धि वाले बालकों में मन्द बुद्धि वाले बालकों की अपेक्षा ईर्ष्या कम होती है।
ईर्ष्या का निवारण – ईर्ष्या की भावना बच्चे के लिए घातक सिद्ध होती है। इसके निवारण के लिए निम्नलिखित साधनों को अपनाना चाहिए –
- बच्चे के स्वास्थ्य व उनकी आवश्यकताओं का ध्यान रखना चाहिए।
- बच्चों को नकारात्मक आदेश नहीं देना चाहिए।
- बच्चे को अधिक नहीं छेड़ना चाहिए नहीं, तो वह चिड़चिड़े स्वभाव का हो जाता है,
- यदि कोई बच्चा अपराध करता है तो अपराध की बुराई करनी चाहिए न कि बच्चे की।
- बच्चे की वस्तु को उसकी इच्छा के विरुद्ध किसी दूसरे बच्चे को नहीं देना चाहिए।
- बच्चे की दिनचर्या को मनोरंजक बनाना चाहिए। बच्चे को किसी-न-किसी खेल या कार्य में व्यस्त रखना चाहिए।
- अनावश्यक रूप से बच्चे की बुराई उसके सामने नहीं करनी चाहिए।

प्रश्न 11.
क्रोध संवेग के क्या कारण हैं ? बालक क्रोध की अभिव्यक्ति किस प्रकार करता है ? क्रोध की उपयोगिता क्या है ?
अथवा
क्रोध संवेग के क्या कारण हैं ? बालक क्रोध की अभिव्यक्ति किस प्रकार करता
उत्तर :
क्रोध-किसी क्रिया की सन्तुष्टि में जब कोई बाधा आती है, तो क्रोध उत्पन्न होता है। क्रोध में आक्रामकता का भाव होता है। बालक जितना हताश होगा उतना ही आक्रामक होगा। शारीरिक दुर्बलता के कारण अथवा रोग की हालत में बच्चा चिड़चिड़ा हो जाता है। उसको अधिक क्रोध आता है। क्रोध सदैव हानिकारक ही नहीं होता, कुछ परिस्थिति में क्रोध लाभदायक भी सिद्ध होता है। जैसे भय को दूर करने के लिए क्रोध का प्रयोग किया जाता है।
क्रोध संवेग के कारण –
- अन्याय तथा अनाधिकार चेष्ट के प्रतिरोध में बालक क्रोध प्रकट करता है।
- क्षमता से बड़ा कार्य सौंप देने से।
- अभिभावक की अधीरता या चिड़चिड़ाहट।
- कपड़े पहनने की विधि कष्टदायक होना।
- भाई-बहिन व साथियों द्वारा चिढ़ाने पर।
- अत्यधिक थकान होने पर।
- बालक के काम में अनावश्यक रुकावट होने पर।
- शारीरिक दुर्बलता व रोग होने पर।
बालक द्वारा क्रोध की अभिव्यक्ति – बालक अपने क्रोध को निम्नलिखित प्रकार से व्यक्त कर सकता है –
- रोना
- चीखना-चिल्लाना
- दाँत पीसना
- सिर पटकना
- ज़मीन पर लेट जाना
- वस्तुओं को उठाकर फेंक देना
- गुस्से में मुख फाड़ना
- जीभ निकालना व थूकना।
क्रोध की उपयोगिता – क्रोध केवल हानिकारक संवेग ही नहीं है वह उपयोगी भी होता है। जब क्रोध, दया व करुणा के साथ जागृत होता है, तो उपयोगी होता है। असामाजिक तत्त्वों तथा शत्रुओं के प्रति क्रोध प्रकट करना बालक की सामाजिक अच्छाई का रूप होता है। विपरीत परिस्थिति में क्रोध बालक को समुचित शक्ति भी प्रदान करता है।
प्रश्न 12.
संक्षिप्त टिप्पणी लिखिए –
1. स्नेह एवं ममता, 2. जिज्ञासा, 3. आनन्द एवं सुख।
उत्तर :
1. स्नेह एवं ममता – यह बालक का प्रारम्भिक संवेग है जिसे वह माँ, आया या परिवार के अन्य सदस्य, जो उसके सम्पर्क में आते हैं, के प्रति प्रकट करता है। प्रारम्भ में बालक सजीव एवं निर्जीव दोनों वस्तुओं से स्नेह करता है, क्योंकि वह दोनों में भेद नहीं समझता है। सवा साल बाद वह वस्तु और व्यक्ति में भेद समझने लगता है और उन्हीं से अधिक स्नेह करता है जिनके सम्पर्क में अधिक आता है। स्नेह के कारण व व्यक्ति को देखकर हँसता है, गोदी में जाता है, चिपक जाता है, हाथ फैलाता है व प्यार करता है।
2. जिज्ञासा – जिज्ञासा के साथ आश्चर्य का संवेग जुड़ा रहता है। बालक में प्रारम्भ से ही जिज्ञासा होती है और इसी जिज्ञासा के कारण वह ज्ञान प्राप्त करता है। बड़े होने पर भी यह मूल प्रवृत्ति विद्यमान रहती है। यहि बालक की जिज्ञासा को शान्त न किया जाए तो बालक सीखने की क्रिया में कोई उत्साह नहीं दिखाता है।
3. आनन्द एवं सुख – आनन्द का संवेग शिशु में 3-4 माह की आयु में देखा जाता है। इच्छा पूर्ति इस संवेग को उत्पन्न करती है। बालक की भूख मिटने पर, गोद में लेने पर, घुमाने पर, नया खिलौना लेने पर, सुन्दर चित्र देखकर हर्ष प्रकट करता है। आनन्द की अभिव्यक्ति बच्चे हाथ-पैर फेंककर, उछलकर, मुस्कराकर, हँसकर व्यक्त करते हैं।
शारीरिक और मानसिक स्वास्थ्य के लिए आनन्द श्रेष्ठ संवेग है। यह एक सामाजिक गुण भी है। बच्चे में आत्माभिमान की वृद्धि होती है। तनावों की कमी से बच्चों के व्यक्तित्व में निखार आता है।

प्रश्न 13.
सामाजिक विकास से आप क्या समझते हैं ? बालकों में सामाजिक विकास कब और कैसे विकसित होता है ?
उत्तर :
मनुष्य एक सामाजिक प्राणी है। जब बालक जन्म लेता है, तो वह अपनी हर आवश्यकता के लिए दूसरे व्यक्ति पर निर्भर रहता है। प्रत्येक सामाजिक प्राणी प्रत्यक्ष या अप्रत्यक्ष रूप से एक-दूसरे पर निर्भर करता है। हरलॉक के अनुसार, “कोई भी बालक सामाजिक पैदा नहीं होता। वह दूसरों के होते हुए भी अकेला ही होता है। समाज में दूसरों के सम्पर्क में आकर समायोजन की प्रक्रिया को सीखता है। इसलिए समाजीकरण की प्रक्रिया बालक के विकास के लिए अत्यन्त महत्त्वपूर्ण है।”
विभिन्न प्रकार की रुचियां, आदतों व व्यवहार में परिपक्वता विकसित होने को सामाजिक विकास कहा जाता है। शारीरिक विकास के साथ-साथ सामाजिक परिपक्वता आती है। सामाजिक गुणों को सीखने की प्रक्रिया को सामाजिक विकास अथवा समाजीकरण कहते हैं। बालक का जन्म से लेकर किशोरावस्था तक सामाजिक विकास बड़ी तीव्र गति से होता है। जब बालक जन्म लेता है तो पूर्ण असामाजिक होता है। दूसरे व्यक्तियों के सम्पर्क में आकर सामाजिकता का आरम्भ होता है।
तीन माह के बच्चे में सामाजिक विकास स्पष्ट दिखाई देने लगते हैं। इस समय वह अकेला रहने पर रोने लगता है और सबके बीच में प्रसन्न रहता है। व्यक्तियों की मुखमुद्रा को पहचानता है। दस माह का बालक बहुत कुछ सामाजिक प्रक्रिया सीख लेता है। हाथ मिलाना, नमस्ते करना। अब वह कुछ-कुछ अपना-पराया समझता है। पन्द्रह माह के बच्चे में सहयोग व भिन्नता दिखाई देने लगती हैं। वह अब संकेत पाकर आदेशों का पालन भी करने लगता है। दो साल का बालक खेलने के लिए अपनी साथी ढूँढता है और उसके व्यवहार में भी परिवर्तन। होने लगता है जो कि उसके सामाजिक विकास की ओर संकेत करते हैं। इस प्रकार से बालक का सामाजिक विकास जन्म के बाद प्रारम्भ होकर परिपक्वता तक विकसित होता है।
प्रश्न 14.
सामाजिक विकास को प्रभावित करने वाले तत्त्व लिखिए।
उत्तर :
सामाजिक विकास को प्रभावित करने वाले तत्त्व निम्नलिखित हैं –
1. नेतृत्व और सामाजिक विकास-बच्चों के किसी भी समूह में परस्पर का व्यवहार समानता का नहीं दिखाई पड़ता है। उनमें से एक अवश्य होता है, जो दूसरों का नेतृत्व करता है। लोकप्रियता और नेतृत्व साथ-साथ नहीं चलते। एक व्यक्ति लोकप्रिय होते हुए भी ज़रूरी नहीं कि नेता भी हो। परन्तु एक नेता सदैव लोकप्रिय होता है और समूह के अधिकांश लोग उसे जानते हैं।
नेतृत्व का प्रथम चिह्न 1 वर्ष की अवस्था में दिखाई देने लगता है। उदाहरण के लिए यदि एक खिलौना दूसरे बच्चे के पास है और एक बच्चे को वह अच्छा लगता है, तो उसे उससे छीनने का प्रयत्न करता है।
जिन बच्चों में नेतृत्व के गुण होते हैं, वे अन्य बच्चों से स्वभावतः बुद्धि, आकार और गुण में बड़े होते हैं। नेता बच्चा कड़ाई की प्रवृत्ति भी रखता है। नेतृत्व करने वाले बालकों को घर में स्वतन्त्रता मिली होती है।
2. संवेगात्मक व्यवहार और सामाजिक विकास-जो बालक चिड़चिड़े स्वभाव का तथा बात-बात पर रूठने वाला होता है, वह कभी भी लोकप्रिय नहीं हो सकता। इसके विपरीत हंसमुख तथा संवेगात्मक स्थिरता वाले बालक सभी को अपना मित्र बना लेते हैं। संवेगात्मक विकास तथा सामाजिक विकास साथ-साथ चलता है।
3. खेल और सामाजिक विकास-खेल बालक की कल्पनाओं, उसकी दया और सहयोग की भावना को दर्शाता है। खेल का प्रभाव बालक के सामाजिक जीवन पर प्रत्येक अवस्था में पड़ता है। कुशाग्र बुद्धि वाले अपने से बड़ों के साथ तथा मंद बुद्धि वाले अपने से छोटे के साथ खेलना पसन्द करते हैं। खेलने वाले सभी साथियों का प्रभाव भी बच्चे के सामाजिक विकास पर पड़ता है।
4. आर्थिक स्तर और सामाजिक विकास-माता-पिता के आर्थिक स्तर का बालक के सामाजिक विकास पर प्रभाव पड़ता है। निर्धन परिवार का बालक धनी परिवार के बच्चों के साथ रहते, पढ़ते हुए हीन भावना का शिकार हो जाता है। वह अपने कपड़ों की तुलना में हीनता का शिकार हो जाता है। आज हर बात का मूल्य पैसे से तोला जाता है तो निर्धन बालक के सामाजिक विकास का सन्तुलन कैसे रह सकता है।
5. बाल समुदाय और सामाजिक विकास-समुदाय में रहकर बालक समुदाय के नियमों का पालन करता है। वह बहुत-सी बातें सीखता है, जैसे – (i) अपनी आयु के बालकों के साथ समायोजन करना, (ii) ऐसा व्यवहार करना, जिन्हें लोग भी पसन्द करें, (iii) नवीन मूल्यों को ग्रहण करना, (iv) मित्रता, (v) संवेगात्मक सन्तोष द्वारा व्यक्तिगत स्वतन्त्रता, (vi) सामूहिक क्रियाओं द्वारा सामाजिक जीवन का आनन्द उठाना। समुदाय में रहकर बालक अच्छे व बुरे गुण दोनों सीखता है।
अच्छे गुण जैसे – (i) प्रजातन्त्र की भावना, (ii) निस्वार्थपन, (iii) सहयोग की भावना, (iv) न्याय तथा ईमानदारी, (v) साहस, (vi) सहनशीलता, (vii) आत्म नियन्त्रण, (viii) सामूहिक जीवन, (ix) दूसरों की भावनाओं का आदर करना।
बुरे गुण जैसे – (i) झूठ, (ii) गाली, (iii) कसमें खाना, (iv) गन्दे-गन्दे मज़ाक, (v) नियम तोड़ने की प्रवृत्ति, (vi) भागने की वृत्ति, (viii) बड़ों का अनादर करना, (viii) अल्पमत वालों की उपेक्षा।
6. शारीरिक व मानसिक विकास-जिन बालकों का शारीरिक विकास ठीक प्रकार से होता है उनमें सभी सामाजिक गुण शीघ्र और अच्छी तरह से विकसित होते हैं। जिनका शारीरिक विकास ठीक-से नहीं होता, कमज़ोर होते हैं, उनमें हीनता की भावना के कारण समाज में समायोजन ठीक प्रकार से नहीं होता। इसी प्रकार जिन बालकों का मानसिक विकास ठीक प्रकार से नहीं होता है, उनका समाज में समायोजन भी ठीक प्रकार से नहीं होता है। यह देखा गया है कि जिन बालकों का बुद्धि का स्तर सामान्य होता है, वे समाज में ठीक से समायोजन कर लेते हैं। जिन बालकों की बुद्धि तीव्र होती है या मन्द बुद्धि होती है, उनको समाज में समायोजन के लिए बहुत सी कठिनाइयों का सामना करना पड़ता है या वह समायोजन करने के लिए अपने को असमर्थ पाते हैं।
7. पारिवारिक प्रभाव-सामाजिक विकास में परिवार का बहुत बड़ा योगदान है। परिवार समाजीकरण का प्रमुख साधन है। परिवार के सदस्यों का भिन्न-भिन्न रूप होता है जो उसमें अनेक व्यक्तिगत एवं सामाजिक गुणों का विकास करते हैं। बहुत से सामाजिक गुण जैसे-सहानुभूति, प्रेम की भावना, उदारता, अनुदारता, न्याय-अन्याय, सत्य-असत्य आदि बालक परिवार से ही सीखता है।
उपरोक्त के अलावा माता-पिता का बालक के प्रति व्यवहार, बालकों का जन्म क्रम, प्रौढ़ सदस्यों की उपस्थिति, बालक का स्वास्थ्य, बालक का सौंदर्य, बालक की बुद्धि तथा विद्यालय का भी सामाजिक विकास पर प्रभाव पड़ता है।

प्रश्न 14A.
सामाजिक विकास को प्रभावित करने वाले कोई तीन कारक लिखें।
उत्तर :
देखें प्रश्न 14.
प्रश्न 15.
सामाजिक विकास की विशेषताएं लिखिए।
उत्तर :
सामाजिक विकास की विशेषताएं निम्नलिखित हैं –
1. आरम्भिक सामाजिक क्रियाएं-जन्म के बाद बालक का सामाजिक वातावरण उसकी माता व आस-पास का वातावरण होता है। वह माता का चेहरा देखकर मुस्कराता है। यही उसकी पहली सामाजिक अनुक्रिया है। बाद में अन्य व्यक्तियों के साथ उसका सम्पर्क बढ़ता है। अब वह अपने और पराये में अन्तर समझने लगता है और इस तरह से धीरे-धीरे बहुत-सी सामाजिक अनुक्रियाएं करने लगता है।
2. दसरे बालक के साथ अनक्रिया-दसरे बच्चों के सम्पर्क में आकर उनके व्यवहार के प्रति अनुक्रिया करता है। दो वर्ष का बालक देने-लेने वाले की अनुक्रिया समझने लगता है।
3. प्रतिरोधी व्यवहार नकारात्मक संवेगों के कारण बहुत से बालकों में प्रतिरोधी व्यवहार विकसित हो जाते हैं, जैसे-हठ करना, सिर हिला कर मना करना, अंगों में सख्ती से आना आदि।
4. सामाजिक प्रतिरोध – यह एक बौद्धिक प्रक्रिया है। बालक दूसरे व्यक्तियों के विचारों तथा अनुभूतियों को समझने लगता है व उनके प्रति उसमें संवेदना जागृत होती है। उसमें प्रतिद्वन्द्विता, सहयोग, अनिच्छापूर्वक कार्य करना आदि भाव विकसित हो जाते हैं।
5. लड़ाई-झगड़े – जैसे-जैसे बालक की सामूहिक क्रियाएं बढ़ती हैं उसमें लडाई झगडे की भावना का भी विकास होता है। कारण है उसके कार्यों की गति में अवरोध उत्पन्न होना। कभी-कभी बालक अपने सहयोगी के लिए या नकल के कारण लड़ाई झगड़ा कर बैठता है।
6. सहानुभूति – यह गुण प्रारम्भ से ही विकसित होने लगता है। सहानुभूति की भावना परिस्थिति के कारण उत्पन्न होती है। दूसरे बच्चे के शारीरिक या मानसिक दुःख को अनुभव कर बच्चा उसके प्रति सहानुभूति रखता है। सहानुभूतिपूर्ण व्यवहार में आयु एवं मानसिक परिपक्वता के साथ-साथ व्यक्तिगत भिन्नता पाई जाती है।
7. प्रतिस्पर्धा – अपने को आगे बढ़ाने में बालक सदा ही लगा रहता है और इसी भावना से प्रेरित हो उसमें प्रतिस्पर्धा विकसित होती है। किसी भी क्षेत्र में आगे बढ़ने के लिए यह गुण बहुत काम आता है।
8. सामहिक क्रियाएं – दो वर्ष का बालक खेलने के लिए साथ ढूंढने लगता है। बढ़ती अवस्था के साथ-साथ सामूहिक रूप से कार्य करने की प्रवृत्ति विकसित होती है। घर में भी अन्य सदस्यों के साथ मिलकर कार्य करना सीखता है।
9. सहयोग – सामाजिकता के लिए यह गुण अत्यन्त आवश्यक है। समूह में बिना सहयोग के गुण से व्यक्ति का समायोजन नहीं हो पाता। सहयोग की भावना से ही व्यक्ति में मित्र-शत्रु भाव उत्पन्न होता है।
10. नेतृत्व – यह एक सामाजिक गुण है। बालकों के समूह में उनका एक नेता अवश्य होता है। वही बालक नेता बनता है जिसका व्यक्तित्व अन्य सदस्यों से अच्छा होता है। जिस बालक में वीर-पूजा, कार्य-कुशलता गुण होते हैं तथा जिसका शारीरिक व मानसिक विकास ठीक होता है, भाषा-विकास अच्छा होता है ऐसे गुणों वाला बालक ही नेतृत्व को निभा पाता है। नेता बालक कई परिस्थितियों में नेतृत्व कर सकता है। उनमें सहयोग की भावना सबसे अधिक होती है।

प्रश्न 16.
शिशु अवस्था में क्या शारीरिक परिवर्तन होते हैं ?
उत्तर :
शिशु अवस्था जन्म से 2 वर्ष तक मानी जाती है। इस अवस्था में अग्रलिखित शारीरिक परिवर्तन होते हैं –
1. हड्डियां (Bones) – नवजात शिशु में 270 हड्डियां होती हैं। प्रारम्भ में शिशु की हड्डियां बहुत नर्म तथा कोमल होती हैं। प्रथम वर्ष में हड्डियों का विकास तीव्र गति से होता है। दूसरे वर्ष में यह अपेक्षाकृत मन्द गति से होता है।
2. लम्बाई (Height) – जन्म के समय से 2 वर्ष तक शिशु की लम्बाई में निम्नलिखित प्रकार बढ़ोत्तरी होती है –

3. वज़न (Weight) शिशु के वज़न का विकास निम्नलिखित प्रकार होता है –

4. हाथ और पैरों का अनुपात (Proportions of Arms and Legs) – जन्म के समय शिशु के हाथ-पैर छोटे-छोटे होते हैं। दो वर्ष की अवस्था तक हाथों की लम्बाई का विकास जन्म की अपेक्षा 60-70 प्रतिशत तक हो जाता है। नवजात शिशु के पैर मुड़े हुए होते हैं। पैरों की लम्बाई बढ़ने के साथ-साथ पैर सीधे भी हो जाते हैं। दो वर्ष की अवस्था तक पैर जन्म की अपेक्षा 40 प्रतिशत विकसित हो जाते हैं।
5. दाँत (Teeth) शिशु के प्रथम बार दाँत छ: से आठ महीने के मध्य निकलते हैं।
6. पाचन तन्त्र (Digestive System) – प्रारम्भ में पाचन तन्त्र की क्षमता का विकास तीव्र गति से होता है।
7. श्वसन तन्त्र (Respiratory System) – जन्म के समय फेफड़े छोटे होते हैं। दो वर्ष की अवधि में छाती और सिर की परिधि बराबर हो जाती है।

प्रश्न 17.
बाल्यावस्था में क्या शारीरिक परिवर्तन होते हैं ?
उत्तर :
(1) बाल्यावस्था 3 से 13 वर्ष तक होती है। इस अवस्था में अग्रलिखित शारीरिक परिवर्तन होते हैं –
1. हड्डियाँ (Bones) – बाल्यावस्था में अस्थिनिर्माण (Ossification) क्रिया चलती रहती है। इस अवस्था में हड़ियां काफ़ी कड़ी हो जाती हैं। इस अवस्था में प्रत्येक आयु स्तर पर लड़कों की अपेक्षा लड़कियों की हड्डियां अधिक कड़ी होती हैं।
2. लम्बाई (Height) बाल्यावस्था में लम्बाई का विकास निम्नलिखित प्रकार बताया जा सकता है –

लगभग 11 वर्ष की अवस्था में लड़कों की अपेक्षा लड़कियाँ कुछ अधिक लम्बी होती हैं।
3. वजन (Weight) बाल्यावस्था में वज़न का विकास निम्नलिखित प्रकार से होता है –
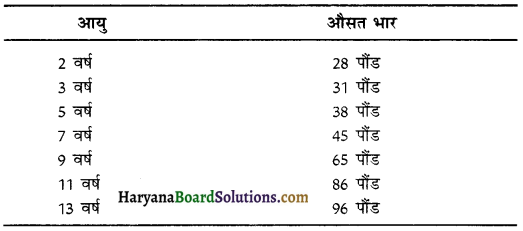
लगभग 6-7 वर्ष की अवस्था तक लड़कियों की अपेक्षा लड़के कुछ अधिक भारी हो जाते हैं। बाद की बाल्यावस्था में लड़कों की अपेक्षा लड़कियां कुछ अधिक भारी रहती हैं।
मांसपेशियां (Muscles) – 5 वर्ष की अवस्था तक मांसपेशियों का विकास शारीरिक अनुपात के अनुसार बढ़ता है। लगभग 5-6 वर्ष की अवस्था में मांसपेशियों का विकास तीव्र गति से होता है।
धड़ (Trunk) – 5 वर्ष की अवस्था तक गर्दन पतली और लम्बी दिखाई देने लगती है। बालक का धड़ 6 वर्ष की अवस्था तक जन्म की अपेक्षा दुगुना हो जाता है।
हाथ और पैर (Arms and Legs) – बाल्यावस्था में हाथ पतले रहते हैं परन्तु वयसन्धि अवस्था के आरम्भ होते ही इनकी मोटाई कुछ बढ़ने लगती है।
आठ वर्ष की अवस्था तक पैर 56% विकसित हो जाते हैं।
दांत (Teeth) – छः वर्ष की अवस्था में स्थायी दांत निकलना आरम्भ हो जाते हैं। लड़कियों में स्थायी दांत लड़कों की तुलना में शीघ्र निकलते हैं।
हृदय (Heart) – छ: वर्ष की अवस्था तक हृदय का भार जन्म की अपेक्षा 4-5 गुना हो जाता है। बारह वर्ष तक हृदय का भार जन्म की अपेक्षा सात गुना हो जाता है।
पाचन-तन्त्र (Digestive System) – वयसन्धि अवस्था प्रारम्भ होने तक पाचन-तन्त्र का विकास मन्द गति से होता है।
श्वसन-तन्त्र (Respiratory System) – बाल्यावस्था के अन्त तक छाती और सिर का अनुपात 3 : 2 हो जाता है।

प्रश्न 18.
बच्चों की शारीरिक आवश्यकताओं से आप क्या समझते हैं ? बच्चों की मुख्य शारीरिक आवश्यकताएं कौन-कौन सी हैं तथा इन्हें किस प्रकार पूरा किया जाना चाहिए ?
उत्तर :
बढते हए शिश की शारीरिक आवश्यकताएं निम्नलिखित हैं –
1. भोजन – जन्म से पूर्व भी बच्चे को भोजन की आवश्यकता होती है क्योंकि उसे जीवित रहना है और विकसित होना है। गर्भ में रहते हुए वह अपना भोजन बिना किसी परिश्रम के अपनी माता से प्राप्त करता रहता है। जन्म के बाद उसे अपनी हर आवश्यकता के लिए अभिभावकों पर निर्भर रहना पड़ता है और इन्हें पूरा करने के लिए स्वयं भी परिश्रम करना पड़ता है। भोजन बच्चे को शक्ति देता है, उसके दांत व हड्डियों को मजबूत बनाता है, खून एवं मांसपेशियों को बढ़ाता है और रोगों से शरीर की रक्षा करता है। मां का दूध बच्चे के लिए सर्वोत्तम आहार है। आयु बढ़ने के साथ-साथ दूध के अलावा कुछ अन्य प्रकार के भोज्य-पदार्थों की भी आवश्यकता होती है।
2. वस्त्र – शिशु के सर्वांगीण विकास में उसके वस्त्रों का भी समुचित स्थान है। वस्त्र बच्चे को मौसम के प्रतिकूल प्रभावों से बचाते हैं। गर्मी, सर्दी, बरसात के मौसम में अनुकूल वस्त्र पहनाए जाते हैं। कपड़ों से शरीर की सुन्दरता भी बढ़ती है। बच्चे को कोमल, हल्के, ढीले-ढाले तथा आरामदेह कपड़े पहनाने चाहिएं जिन्हें पहनकर वह स्वतन्त्रतापूर्वक हिल जुल सके।
3. शारीरिक सुरक्षा व स्वच्छता – बच्चे का शरीर आरम्भ में बहुत कमजोर होता . है। उसकी देख-भाल बहुत ही धैर्य और आराम से होनी चाहिए। बच्चे के शरीर को रोगों से सुरक्षित रखना चाहिए। उसकी देख-भाल स्वास्थ्यप्रद वातावरण में होनी चाहिए। उसके बाल, त्वचा, नाखून, दांत, नाक, कान तथा आंखों की आवश्यकतानुसार देख भाल होनी चाहिए। बच्चे के उचित पालन के लिए उसकी शारीरिक सफ़ाई की विशेष आवश्यकता होती है। बच्चे के लिए इस्तेमाल की जाने वाली वस्तुयें, जैसे-तौलिया, दूध की बोतल, खाने के बर्तन, बिस्तर, ब्रुश, कंघा, खिलौने, लंगोट या पोतड़े आदि की पूरी स्वच्छता रखनी चाहिए।
4. नींद – शिशु के उत्तम स्वास्थ्य के लिए परमावश्यक है कि उसे अच्छी प्रकार से नींद आए। जो शिशु पूर्णतः स्वस्थ है वह अपनी पूरी नींद लेता है और सोते समय बार-बार उठता नहीं है। नींद से बच्चे के शरीर को आराम मिलता है और उसकी खोई हुई शक्ति वापस आती है। अत: नींद एक शारीरिक आवश्यकता है।
5. व्यायाम – बच्चा बड़ा हो या छोटा, उसे व्यायाम करना आवश्यक होता है। व्यायाम से शरीर स्वस्थ रहता है। बच्चे की आयु के बढ़ने के साथ-साथ उसके व्यायाम करने का ढंग भी बदलता जाता है। प्रारम्भ में शिशु अपने बिस्तर पर ही लेटा हुआ अपनी टांगें तथा बांहें फेंककर व्यायाम करता है। जब घुटनों के बल चलने लगता है तो वह चलकर, भागकर अथवा कूदकर व्यायाम करता है। बच्चे की देख-भाल करने वाले को इस बात का ध्यान रखना चाहिए कि बच्चा हर रोज़ आवश्यकतानुसार व्यायाम करे ताकि उसका शरीर स्वस्थ रहे।

प्रश्न 19.
शिशु की भावनात्मक आवश्यकताओं का वर्णन कीजिए।
उत्तर :
भावनात्मक आवश्यकतायें बच्चे के व्यक्तित्व को बनाने में सहायक होती हैं इसलिए बच्चे के व्यक्तित्व को सन्तुलित बनाने के लिए इनकी पूर्ति करना अत्यन्त आवश्यक है। बच्चे की भावनात्मक आवश्यकतायें निम्नलिखित हैं –
1. अनुराग या प्रेम – बच्चे की यह भावनात्मक आवश्यकता बहुत गहरी होती है। प्रत्येक बच्चा अपने माता-पिता से प्यार तथा दुलार की आशा रखता है। माता-पिता या अभिभावक के प्यार भरे शब्द व मुस्कराहट बच्चे की इस आवश्यकता की पूर्ति करती है। बच्चे में इससे अपने प्रति विश्वास की भावना पैदा होती है। माता-पिता की डांट या थोड़ा सा भी अनादर बच्चे के इस विश्वास को ठेस पहुंचाता है और इसका प्रभाव उसके व्यक्तित्व पर पड़ता है।
2. भावनात्मक सुरक्षा – भावनात्मक सुरक्षा बच्चे को स्वतन्त्र एवं परिपक्व होने में सहायता देती है। अपने माता-पिता से मिले प्यार, दुलार, प्रशंसा, रुचि, आराम तथा दिलासा के आधार पर ही इस भावना का निर्माण होता है। कभी-कभी अधिक लाड़-प्यार से बच्चे बिगड़ भी जाते हैं। बच्चे को यह विश्वास बना रहना चाहिए कि उसके माता-पिता उसे प्यार करते हैं। उसे कभी यह अनुभव नहीं होना चाहिए कि घर में उसकी आवश्यकता नहीं है। कई घरों में विशेष रूप से ऐसा लड़कियों के साथ होता है।
3. सम्बद्धता – बच्चा अपने माता-पिता से प्रेम के साथ-साथ घर में अपना अस्तित्व भी चाहता है। वह घर में हर सदस्य से जुड़ा हुआ महसूस करना चाहता है। वह चाहता है कि घर के कार्यों में उसे भी सम्मिलित किया जाये। घर में उसकी ज़रूरत है इसका आभास उसे देते रहना चाहिए। कभी-कभी बच्चे से किसी बात की सलाह लेने से उसे खशी होती है।
4. अभिज्ञान – बच्चा भी आकर्षण केन्द्र बनकर लोगों का ध्यान अपनी ओर आकर्षित करके आनन्द का अनुभव करता है। उसे भी इच्छा रहती है कि कोई उसकी प्रशंसा करे। वह वही कार्य करना चाहता है जिससे वह प्रशंसा का भागी बन सके। उसकी यह भावना सदैव उसके साथ रहती है और वह सदैव उसे पाने के लिए प्रयत्नशील रहता है।
5. स्वतन्त्रता – बच्चे को प्रारम्भ में संसार का कोई अनुभव नहीं होता परन्तु रे-धीरे वह बहुत-सी बातें सीखता है, उसमें खोजने की भावना जन्म लेती है। जब वह अपने आपको किसी काम को कर सकने योग्य पाता है तो उसके मन में अपने आपके प्रति एक विश्वास जागता है। इस विश्वास के साथ-साथ वह आगे बढ़ने का प्रयत्न करता है। वह पहले से अधिक कठिन कार्य करने की इच्छा व्यक्त करता है। इस प्रकार बच्चे में स्वावलम्बन पैदा होता है। उदाहरण के तौर पर छोटे बच्चों में इस प्रकार के व्यवहार अक्सर देखने को मिलते हैं, जैसे वह स्वयं खाना चाहता है, स्वयं कपड़े पहनना चाहता है। बच्चे की इन इच्छाओं को दबाना नहीं चाहिए बल्कि उसे स्वयं काम करने देना चाहिए। परन्तु साथ-साथ इस बात का ध्यान भी रखना चाहिए कि स्वयं कार्य करता हुआ बच्चा कभी अपने आपको चोट न पहुंचाये।

प्रश्न 20.
शिश की सामाजिक आवश्यकताओं का उल्लेख कीजिए।
अथवा
बालक की प्रमुख सामाजिक आवश्यकताएँ कौन-कौन सी हैं ? वर्णन करो।
उत्तर :
मनुष्य एक सामाजिक प्राणी है। जब बालक जन्म लेता है तो वह अपनी हर आवश्यकता के लिए दूसरे व्यक्ति पर निर्भर करता है। प्रत्येक सामाजिक प्राणी प्रत्यक्ष या अप्रत्यक्ष रूप से एक-दूसरे पर निर्भर करता है। हरलॉक के अनुसार, “कोई भी बालक सामाजिक पैदा नहीं होता। वह दूसरों के होते हुए भी अकेला ही होता है। समाज में दूसरों के सम्पर्क में आकर समायोजन की प्रक्रिया को सीखता है। इसलिए समाजीकरण की प्रक्रिया बालक के विकास के लिए अत्यन्त महत्त्वपूर्ण है।” बढ़ते हुए बच्चे की सामाजिक
आवश्यकतायें निम्नलिखित हैं
1. आश्रितता – जब बच्चा अकेला होता है, तो रोता है। जब उसे गोद में लिया जाता है तो वह चिपटता है। कई लोगों के बीच में भी बच्चा प्रसन्न रहता है। इस प्रकार बालक की यह आवश्यकता आश्रितता की ओर संकेत करती है।
2. अनुकरण – बच्चा पहले मुखाकृतियों का, फिर हाव-भाव का, फिर भाषा और अन्त में सम्पूर्ण व्यवहार प्रतिमान का अनुकरण करना सीखता है। अनुकरण वह प्रक्रिया है जिसकी सहायता से बच्चा आगे चलकर सामाजिक प्राणी बनता है।
3. सहयोग – लगभग 12 वर्ष की अवस्था में यद्यपि बच्चों में दूसरे बच्चों के प्रति सहयोग के लक्षण दिखाई देते हैं, परन्तु दूसरे बच्चों की अपेक्षा वयस्क लोगों के प्रति बच्चों में सहयोग की अधिक इच्छा होती है।
4. शर्माहट – बालक जब लगभग 1 वर्ष का होता है तब उसमें शर्म के लक्षण दिखाई देते हैं, विशेष रूप से जब बालक के सामने कोई अपरिचित व्यक्ति आता है।
5. सहानुभूति – यह गुण प्रारम्भ से ही विकसित होने लगता है। सहानुभूति की भावना परिस्थिति के कारण उत्पन्न होती है। दूसरे बच्चे के शारीरिक या मानसिक दुःख को अनुभव कर बच्चा उसके प्रति सहानुभूति रखता है। सहानुभूतिपूर्ण व्यवहार में आयु एवं मानसिक परिपक्वता के साथ-साथ व्यक्तिगत भिन्नता पाई जाती है।
6. प्रतिस्पर्धा – अपने को आगे बढ़ाने में बालक सदा ही लगा रहता है और इसी भावना से प्रेरित हो उसमें प्रतिस्पर्धा विकसित होती है। किसी भी क्षेत्र में आगे बढ़ने के लिए यह गुण बहुत काम आता है।
7. सामूहिक क्रियाएं – दो वर्ष का बालक खेलने के लिए साथी ढूँढ़ने लगता है। बढ़ती अवस्था के साथ-साथ सामूहिक रूप से कार्य करने की प्रवृत्ति विकसित होती है। घर में भी अन्य सदस्यों के साथ मिलकर कार्य करना सीखता है।
8. सामाजिक अनुमोदन की इच्छा – सम्भवतः जब बच्चा बोलना भी नहीं जानता, तभी वह यह समझने लगता है कि वह प्रशंसा और ध्यान का केन्द्र है। बालक को सामाजिक अनुमोदन जैसे-जैसे प्राप्त होता जाता है, उसे प्रसन्नता और आनन्द प्राप्त होता जाता है। बहुत छोटा बच्चा यद्यपि अनजान व्यक्तियों से शर्माता है, परन्तु कुछ बड़ा बच्चा इन अनजान व्यक्तियों से अपने माता-पिता की अपेक्षा अधिक अनुमोदन प्राप्त करना चाहता है। जिस बच्चे में सामाजिक अनुमोदन की जितनी अधिक इच्छा होती है वह सामाजिक समायोजन उतनी ही जल्दी कर लेता है। वह शीघ्र ही समाज की प्रत्याशाओं के अनुसार व्यवहार अपना लेता है।

प्रश्न 21.
सामाजिक परिपक्वता के अध्ययन की कौन-कौन सी विधियाँ हैं ?
अथवा
सामाजिक परिपक्वता के अध्ययन की विधियों के नाम व उनके आविष्कारक बताएँ।
उत्तर :
प्रत्येक अवस्था में बालक को सामाजिक व्यवहार का अध्ययन अनेक विधियों द्वारा किया जाता है। ये विधियाँ दो प्रकार की हैं –
1. समाजमिति-इसके आविष्कारक श्री जे० एल० मोटनी हैं। इस नियम के अनुसार बालकों से पूछा जाता है कि वे किस प्रकार के बालकों के साथ बैठना या खेलना या काम करना पसन्द करेंगे। इसे एक रेखाचित्र पर अंकित करते हैं। एक वर्ष के बाद फिर इसी प्रकार का समाज रेखाचित्र तैयार करते हैं। इससे पता चलेगा कि उसका अन्य कौन-सा साथी लोकप्रिय बन गया है।
2. वाईनलैण्ड सामाजिक परिपक्वता माप-यह विधि प्रमाणीकृत कर ली गई है। इसके आविष्कारक डॉ० एडगर डोल हैं। इस नियम का प्रयोग विभिन्नावस्था के बालकों के सामाजिक व्यवहार का मापन करने के लिए किया जाता है। इसमें किशोरावस्था तक की 117 सामाजिक क्रियाओं को दिया गया है। इसके साथ ही सम्बन्धित रेखाचित्र भी दिए हैं जिसमें 31/2 वर्ष, 5 वर्ष, 8 वर्ष, 10 वर्ष तथा 12 से 15 वर्ष तक की अवस्था वाले बालकों की कार्यशक्ति प्रदर्शित की है।
31/2 वर्ष की अवस्था का बालक कैंची से कागज़ काटना, चम्मच का प्रयोग करना, पानी, गड्ढे और सीढ़ियों से अपने आप को बचाने आदि कार्य कर सकता है। 5 वर्ष की अवस्था का बालक वस्त्र पहनना, स्नानगृह में जाकर कपड़े उतारना, आँख-मिचौनी, कंकड पत्थर फेंकना और रस्सी कूदना आदि खेल खेलना तथा चित्र बनाना आदि कार्य कर सकता है। 8 वर्ष की अवस्था का बालक वयस्क के समान भोजन लेना, समय देखना, बाल संवारना तथा सामूहिक खेलों में भाग लेना शुरू कर देता है।
10 वर्ष की अवस्था का बालक दूध और आलू उबालना, जूस निकालना, बाजार से चीजें खरीदना, पैसे सुरक्षित रखना, सन्देश पहुँचाना आदि कार्य कर सकता है। 12 से 15 वर्ष की अवस्था का बालक कौशल सम्बन्धी खेलों में भाग लेना, साहित्यिक और सामाजिक समारोह में भाग लेना, ऋतु और अवसर के अनुसार कपड़े बदलना, घर और बगीचे सम्बन्धी कार्य करना आदि सभी कार्य करने की क्षमता रखता है।

प्रश्न 22.
बालक के आन्तरिक अवयवों के विकास के बारे में आप क्या जानते हैं ?
उत्तर :
बालक के आन्तरिक अवयवों के अन्तर्गत निम्नलिखित अवयव आते हैं –
- पाचन-तंत्र
- श्वसन-तंत्र
- हृदय
- मस्तिष्क
- परिवाही प्रणाली
- स्नायुमंडल
- मांसपेशियाँ
- चर्बी।
1. पाचन-तंत्र – बालक का पेट नालिका के आकार का होता है और एक वयस्क व्यक्ति का पेट थैली के आकार का होता है। वयस्क की अपेक्षा बालक को शीघ्र भूख लगती है क्योंकि बालकों की पाचन क्रिया तेज़ गति से चलती है। इसीलिए एक बालक को कई बार दूध पिलाना चाहिए। जन्म के समय बालक का पेट 1 औंस और 15 दिन के बाद 1/2 औंस और एक महीने के बाद 3 औंस वस्तु को ग्रहण करता है। बालकों के आहार में पौष्टिक तत्त्व 900 से 1200 कैलोरी तक होने चाहिएं।
2. श्वसन-तंत्र – नवजात बालक के फेफड़े छोटे आकार के होते हैं। दो साल की उम्र में फेफड़े व सिर दोनों का विकास समान होता है। परन्तु 13 साल के बालक के सीने का भार तो बढ़ता है परन्तु आकार वही रहता है। किशोरावस्था में फेफड़े का वज़न भी बढ़ जाता है। इस तरह श्वास लेने की क्षमता में भी वृद्धि होती है।
3. हृदय – नवजात बालक का हृदय छोटे आकार का होता है। लेकिन दैहिक भार के अनुपात में वह अधिक भारी होता है और किशोरावस्था तक शरीर का भार बढ़ जाता है। इस प्रकार किशोरावस्था में हृदय छोटा रह जाता है और नसें व नाड़ियाँ बढ़ जाती हैं। 6 साल की अवस्था में बालक के हृदय का भार जन्म से 4 से 5 गुना, 12 साल की उम्र में बालक के हृदय का भार जन्म से 7 गुना और वयस्कता की अवस्था में जन्म से 12 गुना हो जाता है।
4. मस्तिष्क – नवजात बालक के मस्तिष्क का भार 350 ग्राम होता है। जन्म से लेकर चार साल में बालक का मस्तिष्क अधिक तेज़ गति से विकास करता है। चार से आठ सालों में विकास धीमी गति से होता है और इसके पश्चात् किशोरावस्था तक मस्तिष्क के विकास की गति फिर तेज़ हो जाती है। 20 साल की आयु तक मस्तिष्क का पूर्ण विकास हो जाता है और इसलिए 20 साल के किशोर का मस्तिष्क सभी क्रियाएँ कर सकता है।
5. परिवाही प्रणाली – नवजात बालक की नाड़ी अधिक तेज़ गति से चलती है। जैसे जैसे बालक बड़ा होता है नाड़ी गति में कमी आ जाती है। बाल्यावस्था में रक्तचाप कम हो जाता है। उम्र वृद्धि के साथ रक्तचाप में भी वृद्धि आ जाती है। बाल्यावस्था में लड़के और लड़कियों का रक्तचाप समान रहता है। छोटे बालकों का तापमान भी स्थिर नहीं रहता है, वह बदलता रहता है। दोपहर व शाम की तुलना में सुबह तापमान कम रहता है।
6. स्नायुमंडल – स्नायुमंडल का निर्माण गर्भावस्था के पहले महीने से आरम्भ हो जाता है और गर्भ के छठे महीने तक एक अरब से ज्यादा स्नायुकोष मिलकर स्नायुमंडल का निर्माण करते हैं। जन्म से 3-4 सालों तक स्नायुमंडल का विकास तेज़ गति से होता है। उसके बाद विकास की गति धीमी पड़ जाती है। चार साल के बाद स्नायुमंडल का विकास मंद गति से होता रहता है।
7. मांसपेशियाँ – हृदय, पाचन-तंत्र और ग्रन्थियों का नियन्त्रण मांसपेशियों के द्वारा होता है। नवजात बालक की मांसपेशियों के तन्तु अविकसित होते हैं। नवजात बालक पराधीन एवं कमज़ोर होता है क्योंकि उसकी क्रियाओं में कोई तालमेल नहीं होता है। जन्म के समय मांसपेशियों का भार सम्पूर्ण दैहिक भार का 23% और 8 साल में दैहिक भार का 27%, 13 साल में दैहिक भार का 33% और 16 साल में सम्पूर्ण दैहिक भार का 44% हो जाता है। किशोरावस्था के पश्चात् लड़के एवं लड़कियों की मांसपेशियों में भिन्नता आ जाती है। लड़कों की मांसपेशियाँ ज्यादा मज़बूत और बड़ा होता है।
8. चर्बी – जन्म से लेकर नौ महीने तक चर्बी की मात्रा बहुत तेज़ गति से बढ़ती है। बालक के शरीर में चर्बी की मात्रा उसके वंशानुक्रम, शारीरिक रचना और भोजन पर निर्भर करती है। ग़रीब परिवारों के बालकों में चर्बी की मात्रा धीमी गति से बढ़ती है। एक साल के बाद 6 साल की उम्र तक चर्बी घटती है और 6 साल से 11 साल की उम्र तक चर्बी की मात्रा समान रहती है।

प्रश्न 23.
ज्ञानात्मक विकास का क्या अर्थ है ? तीन साल के बच्चे के अन्दर हुए ज्ञानात्मक विकास का विवरण दो।
उत्तर :
ज्ञानात्मक विकास में बच्चे की सोचने, तर्क करने, समस्याओं को हल करने की क्षमताओं का विकास होता है। जन्म से 3 वर्ष तक का ज्ञानात्मक विकास-सभी नवजात शिशु व्यवहार को दोहराना सीखते हैं। जैसे 2-3 माह का शिशु अपने होठों को इस प्रकार हिलाता है जैसे चूस रहा हो। वह इस क्रिया को तब भी करता है जब वह भूखा नहीं होता क्योंकि ऐसा करना उसे अच्छा लगता है। इन बच्चों को यदि खिलौने दिए जाए तो वह उसे हाथ में लेकर देखते हैं, चूसते हैं, रगड़ते हैं आदि। इस प्रकार की क्रियाओं से वह वस्तुओं के बारे में ज्यादा जानते व समझते हैं।
वस्तु स्थायित्व –
एक 5-6 माह के बालक को यदि कोई खिलौना दिखाकर छुपाया जाए तो वह उसे ज्यादा नहीं ढूँढ़ता। वह इसीलिए क्योंकि वह यह समझता है कि जो वस्तु को वह देख नहीं सकता वह है ही नहीं।
परन्तु 1\(\frac{1}{2}\) साल के बच्चे के साथ यदि ऐसा किया जाए तो वह खिलौना तुरन्त ढूँढ निकालेगा या आपसे वापिस मांगेगा। अत: नजरों से दूर होते ही किसी खिलौने अथवा वस्तु का बालक द्वारा न भूल जाने को ‘वस्तु स्थायित्व’ कहते हैं। लगभग 2 साल तक बच्चा यह सीख लेता है।
3 साल के बच्चे ऐसा सोचते हैं कि निर्जीव वस्तुओं में भी जान होती है। वे समझते हैं कि वस्तुओं में मानवीय गुण जैसे गुड़िया के पेट में दर्द होता है, मेज़ को चोट लगती है आदि छोटे बच्चे दूसरों का दृष्टिकोण नहीं समझ पाते। उदाहरण के लिए हम रोहन व उसके माँ के बीच हुए वार्तालाप पर नजर डालते हैं। रोहन कमरे में है और माँ रसोई में माँ।
रोहन दूध खत्म किया ?
रोहन : (जवाब में हाँ का सिर हिला देता है)।
माँ फिर पूछती है और रोहन फिर से सिर हिलाता है। वह यह बात नहीं समझता कि माँ को रसोई में उसका हिलता हुआ सिर नहीं बल्कि उसकी आवाज़ सुनाई देगी।
प्रश्न 24.
सीखना (Learning) क्या है ?
अथवा
सीखने की क्रिया को कितने भागों में बाँटा गया है ? उदाहरण सहित बताएँ।
उत्तर :
सीखने की क्रिया बालक के जन्म से ही आरम्भ हो जाती है। बालक जब माता के गर्भ में रहता है, तभी से उसमें कुछ चेतना आ जाती है और वह कभी-कभी बाहरी वातावरण की प्रतिक्रियाओं से प्रभावित हो जाया करता है।
सीखने की क्रिया को दो भागों में विभाजित किया जा सकता है –
1. जन्म-जात क्रिया
2. सीखना।
1. जन्म-जात क्रिया – ये वे क्रियायें हैं जो सभी प्राणियों में पाई जाती हैं। इन्हें सहज क्रियायें (Reflex actions) कहा जाता है। बालक पैदा होते ही छींकता है, खांसता है, मल त्याग आदि करता है, ये सभी क्रियाएं जन्मजात होती हैं। इन क्रियाओं को सीखने की क्रियाओं में नहीं रखा जा सकता क्योंकि इनके अर्जन में बच्चे को श्रम नहीं करना पड़ता
और वह इन्हें सीखने के लिए समाज के सहारे रहता है। वातावरण का प्रभाव इस क्रिया पर कुछ भी नहीं पड़ता।
2. सीखना – सीखना वह क्रिया है जिसके अभ्यास के फलस्वरूप बच्चे (या सीखने वाले) के व्यवहार में किसी प्रकार का स्थायी परिवर्तन होता है। इस परिवर्तन के फलस्वरूप ही वह अपने नये वातावरण में अभियोजित करने में समर्थ होता है।
इसे हम इस प्रकार समझ सकते हैं-यदि कोई बच्चा जलती लालटेन पर हाथ रखता है और जलन का अनुभव होते ही वह शीघ्र हाथ हटा लेता है, तो भविष्य में इस प्रकार की 2-4 गलतियों के बाद वह सीख जाता है कि जलती लालटेन पर उसका हाथ न पड़े। यहीं से बच्चे के सीखने की प्रक्रिया प्रारम्भ होती है। ऐसा ही उसके चलने-फिरने में भी होता है। जिस मार्ग में या वस्तु से टकराकर उसे चोट लगती है, वहां वह दुबारा नहीं जाना चाहता।
बालक जब पैदा होता है वह बोलना नहीं जानता। कुछ बड़ा होने पर वह बोलना सीख जाता है। बोलना सीख लेने पर उसके जीवन में एक नवीनता आती है और उसके व्यवहार में भी परिवर्तन आता है। इस प्रकार बच्चा चलना सीखता है और फिर चलने के द्वारा दौड़ना और उछलना सीखता है। इस प्रकार शारीरिक एवं मानसिक विकास के साथ-साथ उसका सीखने का क्रम भी चलता रहता है। बच्चा बार-बार गिरता है और चोट खाता है तब जाकर कहीं चलना सीखता है। अत: अपने को वातावरण के अनुकूल ढाल लेने की सफलता ही सीखना है।

प्रश्न 25.
सीखने की विधियों का उल्लेख कीजिए।
अथवा
सीखने की तीन विधियों का उल्लेख करें।
उत्तर :
बच्चा जब जन्म लेता है अर्थात् बाहरी वातावरण में प्रवेश करता है, उसी समय से वह विभिन्न विधियों द्वारा सीखना प्रारम्भ कर देता है। सीखने की विधियों द्वारा ही बच्चा चलना-फिरना, पढ़ना-लिखना और बोलना-चालना सीखता है। सीखने की प्रमुख विधियाँ निम्नलिखित हैं –
1. अभ्यास विधि
2. अनुकरण विधि
3. सम्बन्धीकरण विधि
4. आन्तरिक सूझ विधि।
1. अभ्यास विधि – इसे प्रयास और भूल की विधि भी कहते हैं। बच्चा अपने प्रारम्भिक ज्ञान को इसी विधि द्वारा प्राप्त करता है। जब बच्चा चलना सीखता है तब बार-बार गिरता है और उठता है। बच्चे का प्रयास तब तक जारी रहता है जब तक वह चलना सीख नहीं लेता। इसी प्रकार वह बैठना, उठना, खेलना, बढ़ना आदि इसी विधि द्वारा सीखता है।
2. अनुकरण विधि – घर में माता-पिता व अन्य सदस्यों को खाते-पीते, चलते फिरते, बात करते देखकर बच्चा उसका अनुकरण करता है। बच्चा बहुत-सा ज्ञान अनुकरण द्वारा प्राप्त करता है।
3. सम्बन्धीकरण विधि – इस विधि में स्वाभाविकता का अनुभव होता है। जैसे रोता हुआ बालक किसी के आने की आहट से रोना बन्द कर देता है। किसी स्त्री को देखकर बच्चा प्रसन्न हो उठता है क्योंकि वह स्त्री को माता के रूप में सोचता है। बच्चे को मां के आने से सन्तोष मिलता है क्योंकि उसे दूध पीने को मिलता है और उसकी भूख शांत होती है। यह एक स्वाभाविक उत्तेजना होती है।
4. आन्तरिक सूझ विधि – सीखने की यह भी एक महत्त्वपूर्ण विधि है। बच्चा जब किसी घोर आवश्यकता या संकट में पड़ जाता है तब उसे स्वयं ही कोई उपाय सूझ जाता है। इसमें संकेत अथवा अनुकरण की आवश्यकता नहीं पड़ती।
प्रश्न 26.
सीखने की क्रिया को कौन-से तत्त्व प्रभावित करते हैं ?
अथवा
सीखने की क्रिया को प्रभावित करने वाले छः तत्त्व बताएं।
उत्तर :
सीखना एक कला है। सीखने की कला में बहुत-से तत्त्व सहायक होते हैं। सीखने की क्रिया को प्रभावित करने वाले तत्त्व अग्रलिखित हैं –
1. प्रेरणा – नए कार्यों को सीखने के पीछे वास्तव में कोई-न-कोई प्रेरणा कार्य करती है। प्रेरित होकर ही बच्चा कोई नया कार्य सीखना चाहता है और प्रयास करता है। प्रेरणा से बच्चा क्रियाशील बनता है।
2. रुचि – बिना रुचि के कोई कार्य नहीं सीखा जा सकता। बच्चों में अभिरुचि उत्पन्न करके ही उन्हें बहुत-सी बातें सिखाई जाती हैं।
3. आत्म प्रगति का ज्ञान – जब बच्चे को पता चल जाता है कि किसी कार्य को करने या उसमें हिस्सा लेने में प्रगति है, तो स्वयं ही उसे सीखने की कोशिश करता है।
4. पुरस्कार व दण्ड – पुरस्कार व प्रतिष्ठा की प्राप्ति की प्रेरणा से बालक अधिक और कठिन कार्य भी पूरे कर लेते हैं, जैसे परीक्षा में पोजीशन प्राप्त करने के लिए पढ़ाई में कड़ी – मेहनत करते हैं। दण्ड का भय बच्चों को गलत बात सीखने से रोकता है। ….
5. प्रशंसा – प्रशंसा के लालच में बच्चे बहुत कार्य करना सीख जाते हैं।
6. संवेदना और प्रत्यक्षीकरण – आँख, कान, नाक, त्वचा तथा जीभ ये पाँच इन्द्रियां संवेदना के पांच द्वार हैं। इन्हीं के द्वारा प्रत्यक्षीकरण होता है। यदि हमारा कोई संवेदन अंग दोषपूर्ण होगा, तो उस अंग से कुछ सीखना प्रायः कठिन होगा।
7. थकान – बच्चा जब थका होता है, तब भी उसे कोई बात सीखने में अत्यन्त कठिनाई होती है।
8. आयु – सीखने का सम्बन्ध आयु से भी है। छोटे बच्चे को यदि संगीत या डांस सिखाया जाए, तो वह वयस्कों की तुलना में जल्दी सीख जाते हैं।
9. समय – विभिन्न कार्यों को सीखने के लिए विभिन्न समय होते हैं। जैसे पढ़ाई करने का उत्तम समय प्रातःकाल का बताया जाता है। 10. वातावरण – सीखने की प्रक्रिया पर वातावरण पर प्रभाव पड़ता है जैसे शोर-गुल में पढ़ा नहीं जा सकता। अधिक गर्मी और अधिक नमी भी बच्चों की कार्य-क्षमता को कम कर देती है।

प्रश्न 27.
बच्चे बोलना कैसे सीखते हैं ?
अथवा
बच्चे भाषा कैसे सीखते हैं ?
उत्तर :
बच्चा जिस समय पैदा होता है, वह जिह्वा से तो युक्त होता है परन्तु उसमें बोलने की क्षमता बिल्कुल नहीं होती। जन्म के बाद वह रोकर इस संसार में अपने आगमन की सूचना देता है। यह रोना ही उसकी वाक्-शक्ति की पहचान होती है। धीरे-धीरे उसके शारीरिक एवं मानसिक विकास के साथ-साथ उसकी वाक्-शक्ति का भी विकास होता है। सभी बच्चे एक ही अवस्था में बोलना नहीं सीखते। उनमें अन्तर होता है। बच्चे वाक्-शक्ति के विकास के पूर्व अपनी आवश्यकताओं को तीन रूपों में प्रकट करते हैं।
1. रुदन (रोना)
2. अस्पष्ट ध्वनि या अस्पष्ट शब्द बबलाना या बालालाप
3. संकेत या अंग विक्षेप या हाव-भाव
जीवन के प्रारम्भिक काल में शिशु अपनी आवश्यकता को रोकर ही प्रकट करता है। जब उसे भूख लगती है या जब वह गीले कपड़ों में लिपटा होता है या किसी रोग से पीड़ित होता है, तब वह अपनी व्यथा को रोकर ही व्यक्त करता है। भूख लगे रोते बच्चे को जब दूध पिलाया जाता है, तो वह तुरन्त प्रसन्न होकर हाथ-पैर चलाने लगता है। तीसरे सप्ताह के बाद बच्चे का रोना धीरे-धीरे कम हो जाता है।।
जब बच्चा डेढ़-दो मास का हो जाता है तब वह अपने कण्ठ से विशेष प्रकार की आवाज़ निकालता है जिसे बच्चे की किलकारी कहा जाता है। बाद में वह हा, हूँ तथा कुछ अस्पष्ट शब्दों का उच्चारण करने लगता है। परन्तु इस समय तक इन शब्दों का कोई अर्थ नहीं होता है। धीरे-धीरे खुशी की हालत में, जम्हाई लेते समय, छींकते समय तथा खांसते समय बच्चा कुछ ध्वनियां निकालता है। चार मास की आयु में ये ध्वनियां स्पष्ट सुनाई देने लगती हैं। बच्चे की ध्वनियों के विश्लेषण से ज्ञात होता है कि इन ध्वनियों में स्वर ही रहते हैं। जब बच्चे के सामने के दांत निकल आते हैं, तभी वह जीभ की नोंक, होंठों तथा दाँतों की सहायता से व्यंजन बोल सकने में समर्थ होता है।
एक वर्ष की आयु में बच्चा सभी स्वर तथा सीधे व्यंजन उच्चारित करने लगता है। धीरे-धीरे इन ध्वनियों की संख्या बढ़ती जाती है। इन ध्वनियों में एकरूपता भी आती जाती है। पहले पहल बच्चा व्यंजन और स्वर को मिलाकर बोलता है, जैसे-“ना” “मा” “गा” “दा” “बा”। बाद में अभ्यास के द्वारा बच्चा इन ध्वनियों को दोहराने लगता है जैसे-“ना-ना-ना-ना”, “मा-मा-मा-मा”, “दा-दा-दा-दा”, “गा-गा-गा-गा”, “बा बा-बा-बा” आदि। इसे बबलाना या बालालाप कहते हैं।
अभ्यास के द्वारा बच्चा अपनी आवाज़ को ऊँची या नीची भी कर सकता है। बबलाने की क्रिया द्वारा बच्चा अपने माता-पिता से वार्तालाप करने का प्रयास करता है। बबलाने से बच्चे को आनन्द की प्राप्ति भी होती है। इसके साथ-साथ बबलाने द्वारा बच्चा अपने स्वर यन्त्रों की मांसपेशियों को नियंत्रित करना भी सीखता है।
बोलना सीखने की तैयारी में तीसरी प्रधान क्रिया अंग विक्षेप या हाव-भाव है। बच्चा ध्वनियां निकालने के साथ-साथ अंग विक्षेप भी करता है। अंग विक्षेप में बच्चा सारा शरीर ही प्रयोग में लाता है। मनोवैज्ञानिकों के अनुसार, बच्चा अंग विक्षेप द्वारा अपनी बातें माता-पिता या बड़ों को समझाता है। यदि बच्चा इसमें सफल नहीं होता तो वह रोने लगता है उदाहरण के तौर पर भूख न होने पर मुँह से दूध बहने देना, मुस्कराना, हाथ फैलाना जिससे कोई गोदी में उठा ले, अनिच्छा प्रकट करने के लिए नहलाते या कपड़ा पहनाते समय रोना, कोई वस्तु पकड़ने के लिए हाथ आगे करना, गुस्से की अवस्था में हाथ-पैर पटकना या मुँह फुला लेना आदि।
जैसे-जैसे बच्चा बोलना सीखता है, अंग विक्षेपों की संख्या घटती जाती है, क्योंकि वह अब इन पर कम निर्भर करता है। 12 से 18 मास की आयु के बीच बच्चा बोलना सीखता है। एक वर्ष का बच्चा “ताता”, “पापा”, “दादा”, “मामा”, “बाबा” आदि शब्दों का अनुकरण कर सकता है। बाद में दो वर्ष की आयु तक वह दो-तीन संज्ञा शब्दों का वाक्य तोतली भाषा में बोलता है।
तीन वर्ष की आयु में बच्चा अपने बड़ों का अनुकरण करता हुआ पूरा वाक्य बोलने का प्रयत्न करता है। यही ऐसा समय होता है जब माता-पिता तथा परिवार के अन्य सदस्यों को शब्दों के उच्चारण व बोल-चाल का विशेष ध्यान रखना चाहिए, क्योंकि बच्चा उन्हीं उच्चारण का अनुकरण करता है जो घर में बोले जाते हैं। इस आयु में बच्चे का शब्द भण्डार बढ़ जाता है। लगभग 1000 शब्द का भण्डार उसके पास हो जाता है। पांच वर्ष की आयु में वह कहानी सुन तथा कह सकता है। इस प्रकार इन थोड़े-से-वर्षों में बच्चों का भाषा ज्ञान बहुत तीव्र गति से बढ़ता है।

प्रश्न 27(A).
बालालाप (बैबलिंग) क्या होती है ? बच्चे यह प्रायः किस आयु में शुरू करते हैं ?
उत्तर :
देखें प्रश्न 27 का उत्तर।
प्रश्न 28.
भाषा विकास को कौन-कौन से कारक प्रभावित करते हैं ?
अथवा
भाषा विकास को प्रभावित करने वाले तत्त्व कौन-कौन से हैं ?
अथवा
बच्चों के भाषा विकास में विभिन्नताएँ क्यों पाई जाती हैं ?
अथवा
भाषा विकास को प्रभावित करने वाले छः कारक बताएं।
उत्तर :
बालक का भाषा विकास कैसे और कितना होगा यह निम्नलिखित बातों पर निर्भर करता है –
1. स्वास्थ्य – दो साल तक की आयु में यदि बच्चा अधिक बीमार रहता है, तो उसका भाषा विकास निश्चित समय से देर में होता है।
2. सामाजिक आर्थिक स्थिति – जिन बालकों का सामाजिक आर्थिक स्तर ऊंचा होता है यह देखा गया है कि उनका भाषा विकास जल्दी और अच्छा होता है। वह अपने विचार ज्यादा अच्छी तरह से व्यक्त कर सकते हैं क्योंकि उनको वातावरण सम्बन्धी वह सभी उपकरण मिल जाते हैं जो भाषा विकास में सहायक होते हैं।
3. लिंग – प्रत्येक आयु में यह देखा गया है कि भाषा विकास में लड़कियां, लड़कों से आगे रहती हैं, वह बोलना जल्दी सीखती हैं, शब्द साफ़ और वाक्य लम्बे बना लेती हैं।
4. पारिवारिक सम्बन्ध – यदि मां के साथ बच्चे के सम्बन्ध अच्छे हैं, तो बालक का भाषा विकास भी ठीक होगा। जिस परिवार में बच्चों की देखभाल ठीक प्रकार से नहीं होती उन बच्चों में हीनता की भाषा के कारण बहुत-से भावना दोष विकसित हो जाते हैं, जैसे हकलाना आदि।
जो बच्चा परिवार में अकेला होता है उसकी तरफ़ माता-पिता भी अधिक ध्यान देते हैं। इसलिए उसका भाषा विकास भी अच्छा होता है।
5. व्यक्तित्व – बुद्धि के अलावा जो बालक शर्माते हैं या अन्तर्मुखी होते हैं उनका भाषा विकास ठीक से नहीं होता। जिन बच्चों का सामाजिक समायोजन ठीक से होता है उनका भाषा विकास भी और बच्चों से अच्छा होता है।
6. बुद्धि – बालक की जितनी अधिक तीव्र बुद्धि होगी उतना ही उसका भाषा विकास अच्छा होगा। बुद्धि से भाषा विकास का सीधा सम्बन्ध है। जो बालक मन्द बुद्धि वाले होते हैं उनका भाषा विकास न के बराबर होता है।
7. निर्देशन – जिन बालकों को अच्छे शिक्षक एवं अभिभावक मिल जाते हैं वे जल्दी-जल्दी भाषा सीखते है क्योंकि वे मॉडल शब्दों के द्वारा भाषा ज्ञान कराते हैं।
8. उत्प्रेरणा – उत्प्रेरक बालक से इशारों से बातचीत नहीं करते बल्कि वे शब्दों के द्वारा बालकों को अपनी भावनाओं को व्यक्त करने के लिए प्रेरित करते हैं। ऐसी उत्प्रेरणा से प्रेरित होकर बालकों का भाषा विकास तेजी से होता है।

प्रश्न 29.
भाषा विकास की अवस्थाओं का उल्लेख करो।
उत्तर :
भाषा विकास क्रम की अवस्थायें निम्नलिखित हैं –
1. ध्वनि पहचानना – नवजात शिशु ध्वनि को नहीं पहचान पाता। धीरे-धीरे वह ध्वनि को पहचानता है। उसके कानों में ध्वनि ग्रहण करने की शक्ति आ जाती है। 5-6 मास की अवस्था में पहुंचने पर शिशु ध्वनियों को पहचानने लगता है, जैसे धड़ाके की आवाज़ से वह चौंक पड़ता है और इधर-उधर देखने लगता है।
2. ध्वनि उच्चारण – ध्वनि को पहचानने के बाद ही ध्वनि उच्चारण करने की क्षमता आती है। 7-8 माह की अवस्था में बच्चा ध्वनि को पहचान कर मुस्कराता भी है। वह दूसरों के द्वारा बोले हुए शब्दों को सुन-सुनकर ही अधिकतर प्रयोग में आने वाले शब्दों को सीख लेता है।
3. शब्द उच्चारण की अवस्था – दो-तीन वर्ष की आयु में बच्चा कठिन शब्दों का उच्चारण भी करने लगता है। इसी अवस्था में माता-पिता उसे वस्तुओं की ओर संकेत करके उन वस्तुओं का नाम बताते हैं और खुद उच्चारण करके उससे कहलवाते हैं।
4. वाक्यों का प्रयोग – शब्दों के उच्चारण के बाद वाक्यों का नम्बर आता है। प्रारम्भ में बच्चा अस्पष्ट तथा असन्तुलित वाक्य बोलता है, किन्तु बाद में धीरे-धीरे वह स्पष्ट वाक्यों को भी बोलने लगता है।
5. लिखित भाषा का प्रयोग – बच्चा पहले बोलना सीखता है बाद में लिखना। लिखने से भाषा में परिपक्वता आती है। भाषा वही पूर्ण मानी जाती है जो बच्चा बोलना भी जानता हो और लिखना भी। भाषा की शुद्धता और सन्तुलन धीरे-धीरे बढ़ता जाता है।
6. भाषा विकास की पूर्ण अवस्था – भाषा विकास की पूर्णता का अर्थ है कि बालक भाषा को समझना, बोलना, पढ़ना और लिखना सभी कुछ जान जाए। भाषा की पूर्णता शीघ्र नहीं आती, धीरे-धीरे प्रयत्न तथा कोशिश के फलस्वरूप आती है। वैसे भाषा विकास से पूर्णता कभी नहीं आती, वह तो सदैव उन्नत अवस्था को प्राप्त होती रहती है।
प्रश्न 30.
भाषा के महत्त्व को स्पष्ट कीजिए।
उत्तर :
भाषा के महत्त्व को निम्नलिखित प्रकार व्यक्त किया जा सकता है –
1. प्रगति – भाषा, मानव जाति का इतिहास है। भाषा के माध्यम से व्यक्ति ने आज ज्ञान-विज्ञान के क्षेत्र में प्रगति की है। उसने भाषा की शक्ति के कारण स्वयं को समाज का सर्वोत्तम प्राणी सिद्ध किया है।
2. सामाजिक वंशक्रम की वाहक – आज हमारा प्राचीन साहित्य भाषा के माध्यम से ही सुरक्षित है।
3. सामाजिक सम्पर्क – भाषा सामाजिक सम्पर्क से विकसित होती है। भाषा के विकास के लिए समूह के सदस्य एक-दूसरे के प्रति प्रतिक्रिया करते हैं। क्रिया-प्रतिक्रिया के द्वारा ही समाज में प्रगति होती है।
4. सामाजिक तथा राष्ट्रीय एकता – भाषा सामाजिक तथा राष्ट्रीय एकता को बनाये रखने में एक कड़ी है। इसी से समाज तथा व्यक्ति एक राष्ट्र के रूप में जुड़े रहते हैं।
5. भाषा तथा विचार – भाषा तथा विचार का आपस में गहन सम्बन्ध है। विचार तभी विचार होता है जब उसकी मौखिक अथवा लिखित अभिव्यक्ति होती है।
6. मानव विकास की आधारशिला – भाषा ने व्यक्ति को विकास का आधार प्रदान किया है। जो व्यक्ति भाषा का संयत, संतुलित एवं प्रभावशाली उपयोग करना जानते हैं, वे अपने जीवन में विकास करते हैं।
7.संस्कृति का प्रतिबिम्ब – भाषा के विकास के साथ-साथ सभ्यता तथा संस्कृति भी विकसित हुई है। जिन समूहों की भाषा अविकसित है उनकी सभ्यता तथा संस्कृति भी अविकसित है। जनजातीय भाषा तथा संस्कृति इसके उदाहरण हैं।
8. साहित्य – भाषा और साहित्य का आपसी सम्बन्ध प्रगाढ़ है। किसी भी साहित्य को उसकी भाषा से आंका जाता है। भाषा ने ही वेद, वेदांग, उपनिषद् आदि महान् ग्रन्थ मानव समाज को दिये हैं।

प्रश्न 31.
बालक में सामान्य भाषा-दोष कैसे उत्पन्न होते हैं ? उन्हें कैसे दूर किया जाता है?
उत्तर :
बहुत से कारणों से बालक में कई भाषा-दोष उत्पन्न हो जाते हैं जो निम्नलिखित हैं
1. तुतलाना – जब बालक के ओंठ, तालू, जीभ, कंठ, कपाल की मांसपेशियों में सामूहिक रूप में सह-कार्य नहीं हो पाता तो यह दोष उत्पन्न होता है। कुछ बालक नकल करने की वजह से तुतलाते हैं, फिर उनको आदत पड़ जाती है। इसमें बच्चे ‘ट’, ‘ठ’, ‘ड’, ‘ढ’, ‘ण’, ‘र’, आदि वर्गों का उच्चारण दोषपूर्ण करते हैं। इसके बदले ट-त, ठ-थ, ड-ध, ण न, न-ल बोलते हैं। बालक को उचित निर्देश देकर व अभ्यास से इस दोष को दूर कर सकते हैं।
2. अशुद्ध शब्द का प्रयोग – यह दोष बालक दूसरे लोगों से सीखते हैं, जैसे ‘नखलऊ, लखनऊ’ और ‘छिकला, छिलका’ को बार-बार अभ्यास द्वारा यह दोष दूर किया जा सकता है। बड़ों को चाहिए कि वह बच्चों के सामने ऐसे न बोलें।
3. रुक-रुक कर बोलना – बहुत से बालकों के शब्द भण्डार में कमी होती है और वे रुक-रुक कर बोलते हैं। बालक को बोलते समय झिड़क कर उसे निराश न करें, वरन् उसे उचित शब्दों के चयन की सलाह देते रहें तो वह दोष दूर हो सकता है।
4. अनुनासिक उच्चारण – कई बार लाड़-प्यार के कारण बालक प्रत्येक शब्द में अनुस्वार लगाकर बोलते हैं और वही आदत बन जाती है जैसे-“हम नहीं खायेंगे”। यह दोष उचित निर्देश व स्नेह से समझाकर सुधार सकते हैं।
5. हकलाना-हकलाने में या तो एक ही स्वर बार-बार दोहराया जाता है। जैसे-क क क कमल या पा पा पा पानी अथवा आवाज़ का एकदम रुक जाना और आगे का अक्षर उच्चारित होना होता है।
हकलाने के प्रमुख कारण हो सकते हैं –
(i) बोलने का गलत तरीका सीख लेना।
(ii) संवेगात्मक तनाव।
(iii) मस्तिष्क सम्बन्धी असन्तुलन।
(iv) ध्वन्यात्मक विस्मृति।
(v) वंशानुक्रम।
(vi) अन्तःस्रावी ग्रंथियों का असंतुलन।
प्रश्न 32.
भाषा विकास की मापन विधियां कौन-सी हैं?
उत्तर :
बालक का भाषा विकास का मापन कई विधियों से किया जा सकता है। ये विधियां निम्नलिखित हैं
1. निर्धारित समय में बालक द्वारा प्रयुक्त शब्दों की गणना – इसमें 15 मिनट तक चुपचाप बालक द्वारा प्रयुक्त शब्दों को लिखा जाता है। इस प्रकार दो-तीन तालिकाएँ बनाकर आपस में तुलना की जाती है। इस आधार पर 7 वर्षीय बालक 36 शब्दों का, 14 वर्षीय लड़का अनुमानत: 160 शब्दों का उच्चारण करता है। 7 वर्षीय बालक की सम्पूर्ण प्रयोग शब्दावली 800 शब्दों की पाई गई और 14 वर्षीय लड़के की 3600 शब्दों की।
2. प्रयुक्त शब्दों की गणना – यह विधि अत्यंत सरल है। इस विधि में बालक के दिनभर के प्रयुक्त शब्दों को एक कॉपी में लिखते जाइए। इससे बालक की पूर्ण प्रयोग शब्दावली का पता लग सकता है।
3. प्रश्नावली – यह भी बुद्धि मापक परीक्षाओं का ही एक अंश होती है। इसके द्वारा अल्प समय में बालक के भाषा विकास की जानकारी, शब्दों की निश्चित संख्या के आधार पर की जा सकती है। इसमें बालकों से प्रश्नों द्वारा शब्दों के अर्थ पूछे जाते हैं।
एक शब्द/एक वाक्य वाले प्रश्न –
(क) निम्न का उत्तर एक शब्द में दें –
प्रश्न 1.
बचपन को कितनी अवस्थाओं में बांटा गया है ?
उत्तर :
चार।
प्रश्न 2.
लड़का कब बालिक (वयस्क) होता है ?
उत्तर :
21 वर्ष की आयु में।

प्रश्न 3.
जब बच्चा गुस्से से ज़मीन पर लोटता है, इसे क्या कहते हैं ?
उत्तर :
टैम्पर टैंट्रम।
प्रश्न 4.
भूख लगने अथवा पेट दर्द होने पर बच्चा क्या करता है ?
उत्तर :
क्रन्दन।
प्रश्न 5.
कितनी आयु में बच्चा बिना सहारे के चल सकता है ?
उत्तर :
12 वर्ष।
प्रश्न 6.
नवजात शिशु में कितनी हड्डियां होती हैं ?
उत्तर :
270.
प्रश्न 7.
शिशु के प्रथम बार दाँत कब निकल आते हैं ?
उत्तर :
छः से आठ महीने के मध्य।
प्रश्न 8.
नवजात बालक के मस्तिष्क का भार कितना होता है ?
उत्तर :
350 ग्राम।
प्रश्न 9.
जन्म के समय बालक का पेट कितनी वस्तु ग्रहण कर सकता है ?
उत्तर :
1 औंस।

प्रश्न 10.
एक नवजात शिशु लगभग कितने घण्टे सोता है ?
उत्तर :
20 घण्टे।
प्रश्न 11.
नवजात शिशु का जन्म के समय औसत भार कितना होता है ?
उत्तर :
6 से 8 पौंड।
प्रश्न 12.
आँखों के लिए कौन-सा विटामिन ज़रूरी है ?
उत्तर :
विटामिन ‘ए’।
प्रश्न 13.
हड्डियों के लिए कौन-सा खनिज लवण ज़रूरी है ?
उत्तर :
कैल्शियम।
(ख) रिक्त स्थान भरें –
1. ………… माह का बच्चा सरल, सीधे शब्द जैसे काका, मामा आदि बोल सकता है।
2. हड्डियों की मजबूती ……….. से आती है।
3. बच्चों को टीकों की बूस्टर दवा ……….. वर्ष का होने पर देनी होती है।
4. वृद्धि ………… का एक हिस्सा है।
5. जन्म के समय बच्चे में …………. विकास नहीं होता।
6. जन्म के समय बच्चे की औसत लम्बाई ………. होती है।
7. ………….. शारीरिक विकास को प्रभावित करती है।
उत्तर :
1. 10
2. कैल्शियम
3. छ:
4. विकास
5. सामाजिक
6. 19 से 20 इंच
7. खेल।

(ग) निम्न में ग़लत तथा ठीक बताएं –
1. समुदाय में रहने वाले बालक में अश्लील व्यवहार करना जैसे अवगुण आ जाते हैं।
प्रत्येक प्राणी की अपनी भाषा होती है। बच्चे दो-अढाई वर्ष तक शौच क्रिया पर नियन्त्रण कर लेते हैं।
हकलाने का एक कारण बोलने का ग़लत तरीका सीख लेना है।
5. बालकों के आहार में 5900 कैलोरी होनी चाहिए।
उत्तर :
1. ठीक
2. ठीक
3. ठीक
4. ठीक
5. गलत।
बहु-विकल्पीय प्रश्न –
प्रश्न 1.
बच्चा कितनी आयु में वयस्क होता है –
(A) 15 वर्ष
(B) 21 वर्ष
(C) 18 वर्ष
(D) 25 वर्ष।
उत्तर :
18 वर्ष।

प्रश्न 2.
भारतीय बच्चे का जन्म के समय लगभग भार होता है –
(A) 1 कि० ग्रा०
(B) 2.5 कि० ग्रा०
(C) 4 कि० ग्रा०
(D) 5 कि० ग्रा०।
उत्तर :
2.5 कि० ग्रा०।
प्रश्न 3.
……….. हड्डियों में मजबूती आती है –
(A) कैल्शियम से
(B) वसा से।
(C) लोहा से
(D) आयोडीन से।
उत्तर :
कैल्शियम से।
प्रश्न 4.
छोटे बच्चों में कौन-सी भावनाएं देखी जाती हैं –
(A) खुशी
(B) गुस्सा
(C) डर
(D) उपरोक्त सभी।
उत्तर :
उपरोक्त सभी।

प्रश्न 5.
बच्चे सहारा लेकर बैठने लगते हैं –
(A) 1 माह में
(B) 2 माह में
(C) 4 माह में
(D) 6 माह में।
उत्तर :
4 माह में।
प्रश्न 6.
शारीरिक विकास को प्रभावित करने वाले कारक हैं –
(A) वातावरण
(B) भोजन
(C) खेल
(D) उपरोक्त सभी।
उत्तर :
खेल।

प्रश्न 7.
ईर्ष्या नामक संवेग का विकास किस आयु में होता है –
(A) 1 माह
(B) 6 माह
(C) 18 माह
(D) 12 माह।
उत्तर :
18 माह।
प्रश्न 8.
बाल विकास किस बात का अध्ययन है :
(A) बच्चों की वृद्धि और विकास
(B) बच्चों का सामाजिक विकास
(C) बच्चों का संवेगात्मक विकास
(D) उपरिलिखित सभी।
उत्तर :
उपरिलिखित सभी।
प्रश्न 9.
मानवीय जीवन का आरम्भ कब शुरू होता है :
(A) जन्म के बाद
(B) जन्म के एक साल बाद
(C) जन्म के पांच साल बाद
(D) मां के गर्भ में।
उत्तर :
मां के गर्भ में।
प्रश्न 10.
मानवीय विकास के कितने पड़ाव होते हैं :
(A) छः
(B) चार
(C) दो
(D) आठ।
उत्तर :
चार।

प्रश्न 11.
टेम्पर टैंट्रम किसे कहा जाता है :
(A) खुश होकर ज़मीन पर लोटना
(B) गुस्सा जाहिर करने के लिए ज़मीन पर लोटना
(C) सोने से पहले ज़मीन पर लेटना
(D) नींद में जमीन पर लेटना।
उत्तर :
गुस्सा जाहिर करने के लिए ज़मीन पर लोटना।
प्रश्न 12.
मां का दूध बच्चे को क्यों पिलाना चाहिए :
(A) जीवित रहने के लिए
(B) बीमारियों से लड़ने की शक्ति पैदा करने के लिए
(C) भूख मिटाने के लिए
(D) उपरिलिखित सभी।
उत्तर :
उपरिलिखित सभी।
प्रश्न 13.
भाषा विकास कब सन्तोषजनक होता है :
(A) स्वर की परिपक्वता
(B) जीभ
(C) गला
(D) उपरिलिखित सभी।
उत्तर :
उपरिलिखित सभी।
प्रश्न 14.
वह कौन-सा कारण है जिससे बच्चे का विकास उचित प्रकार से नहीं होता :
(A) अच्छा वातावरण न होना
(B) मंदबुद्धि का होना
(C) माता-पिता का प्यार न मिलना
(D) उपरिलिखित सभी।
उत्तर :
उपरिलिखित सभी।

प्रश्न 15.
बच्चों को बूस्टर दवा (खुराक) कब दी जाती है :
(A) छः वर्ष का होने पर
(B) एक साल का होने पर
(C) दो साल का होने पर
(D) पांच साल का होने पर।
उत्तर :
छः वर्ष का होने पर।
प्रश्न 16.
बच्चा किस प्रकार बोलना सीखता है :
(A) अनुकरण द्वारा
(B) प्रेरणा द्वारा
(C) प्रयास और भूल द्वारा
(D) उपरिलिखित सभी।
उत्तर :
उपरिलिखित सभी।
प्रश्न 17.
वृद्धि ……………… का एक हिस्सा है :
(A) विकास
(B) व्यक्तित्व
(C) सीखने
(D) उपरिलिखित सभी।
उत्तर :
उपरिलिखित सभी।
प्रश्न 18.
बचपन में शरीर की हड्डियों की संख्या क्या होती है :
(A) 270
(B) 206
(C) 220
(D) 240.
उत्तर :
270.

प्रश्न 19.
वह कौन-सा कारक है जो शारीरिक विकास को प्रभावित करता है :
(A) वंशानुक्रम
(B) परिवार का आकार
(C) बुद्धि
(D) जन्म क्रम।
उत्तर :
वंशानुक्रम।
प्रश्न 20.
जन्म के समय बच्चे में सामाजिक विकास ……… होता है :
(A) पूर्ण
(B) नहीं
(C) सामान्य
(D) कम।
उत्तर :
नहीं।
प्रश्न 21.
जब बच्चे की आवश्यकताएं पूरी हो जाती हैं, तो क्या होता है :
(A) खुश
(B) रोना
(C) नाराज़
(D) गुस्सा होना।
उत्तर :
खुश।

प्रश्न 22.
बालक की अभिव्यक्ति के अन्य साधन कौन-से हैं :
(A) चित्रांकन
(B) हस्तकौशल
(C) संगीत
(D) उपरिलिखित सभी।
उत्तर :
उपरिलिखित सभी।
प्रश्न 23.
बच्चों की भावनाओं की क्या विशेषताएँ होती हैं :
(A) भावनाएं काफ़ी तेज़ होती हैं
(B) थोड़ी देर में उभरती और समाप्त होती हैं
(C) भावनाओं को छुपा नहीं सकते
(D) उपरिलिखित सभी।
उत्तर :
उपरिलिखित सभी।
प्रश्न 24.
जन्म के समय बच्चे का औसत भार कितना होता है :
(A) 2\(\frac{1}{2}\) किलो
(B) 3\(\frac{1}{2}\) किलो
(C) 4.0 किलो
(D) 5 किलो।
उत्तर :
2\(\frac{1}{2}\) किलो।
प्रश्न 25.
जन्म के समय बच्चे की औसत लम्बाई कितनी होती है :
(A) 15” – 20′”
(B) 17” – 19″
(C) 10” – 15”
(D) 25” – 30′”
उत्तर :
17” – 19″
प्रश्न 26.
किस आयु में बच्चे में दूध के दांत निकल आते हैं :
(A) 2\(\frac{1}{2}\) साल।
(B) 4\(\frac{1}{2}\) साल
(C) 1\(\frac{1}{2}\) साल
(D) 3 साल।
उत्तर :
(A) 2\(\frac{1}{2}\) साल।

प्रश्न 27.
दो वर्ष की आयु तक बच्चा कितने शब्द सीख लेता है :
(A) लगभग 272
(B) लगभग 400
(C) लगभग 500
(D) लगभग 1000.
उत्तर :
लगभग 272.
प्रश्न 28.
अभिवृद्धि का अर्थ है :
(A) शरीर के आकार और रूप में बढ़ोत्तरी
(B) बालक के क्रोध में बढ़ोत्तरी
(C) हस्तकला के क्षेत्र में बढ़ोत्तरी
(D) उपर्युक्त में से कोई नहीं।
उत्तर :
शरीर के आकार और रूप में बढ़ोत्तरी।
प्रश्न 29.
विभिन्न आयु स्तरों पर बालक के विकास की दर :
(A) एक-सी होती है
(B) भिन्न होती है
(C) उपर्युक्त दोनों होती है
(D) उपर्युक्त में से कोई नहीं होती।
उत्तर :
भिन्न होती है।
प्रश्न 30.
जन्म के समय एक बच्चे का औसत वजन कितना होता है ?
(A) 3.5 किग्रा
(B) 4 किग्रा
(C) 2.5 किग्रा
(D) 1.5 किग्रा।
उत्तर :
2.5 किग्रा।

प्रश्न 31.
विकास सदैव घटित होता है :
(A) केन्द्र से बाहर की ओर
(B) बाहर से केन्द्र की ओर
(C) दायीं ओर से बायीं ओर
(D) बायीं ओर से दायीं ओर।
उत्तर :
केन्द्र से बाहर की ओर।
प्रश्न 32.
विकास किस ओर से प्रारम्भ होता है ?
(A) पैरों की ओर से
(B) सिर की ओर से
(C) सिर और पैर दोनों ओर से
(D) धड़ की ओर से।
उत्तर :
सिर की ओर से।
प्रश्न 33.
बच्चे में तर्क करने की योग्यता को क्या कहते हैं ?
(A) सामाजिक विकास
(B) भाषा विकास
(C) मानसिक विकास
(D) उपर्युक्त सभी।
उत्तर :
मानसिक विकास।
प्रश्न 34.
बालकों के संवेगात्मक विकास के लक्षण क्या हैं ?
(A) भय
(B) प्यार
(C) क्रोध
(D) उपर्युक्त सभी।
उत्तर :
उपर्युक्त सभी।

प्रश्न 35.
वंशानुक्रम एवं वातावरण किसको प्रभावित करते हैं ?
(A) विकास को
(B) अभिवृद्धि को
(C) अभिवृद्धि और विकास को
(D) उपर्युक्त में से किसी को नहीं।
उत्तर :
अभिवृद्धि और विकास को।
प्रश्न 36.
अभिवृद्धि और विकास दोनों में क्या निहित है ?
(A) परिवर्तन
(B) सोचना
(C) योग्यता
(D) तर्क करना।
उत्तर :
परिवर्तन।
प्रश्न 37.
बच्चों को टीकों की बूस्टर दवा कब दिलाई जाती है ?
(A) छ: वर्ष का होने पर
(B) दो वर्ष का होने पर
(C) पाँच वर्ष का होने पर
(D) दस वर्ष का होने पर।
उत्तर :
छः वर्ष का होने पर।
प्रश्न 38.
किशोरावस्था में हड्डियों की संख्या कितनी होती है ?
(A) 206
(B) 216
(C) 236
(D) 276.
उत्तर :
206.

प्रश्न 39.
सीखने की क्रिया को कौन-सा तत्त्व प्रभावित करता है ?
(A) प्रेरणा
(B) रुचि
(C) प्रशंसा
(D) ऊपरलिखित सभी।
उत्तर :
ऊपरलिखित सभी।
प्रश्न 40.
बचपन में शरीर की हड़ियों की संख्या कितनी होती है ?
(A) 270
(B) 260
(C) 250
(D) 240.
उत्तर :
270.
प्रश्न 41.
बच्चों का विकास उचित प्रकार से क्यों नहीं हो पाता ?
(A) मंद बुद्धि के कारण
(B) अच्छा वातावरण न होने के कारण
(C) घरेलू झगड़े के कारण
(D) ऊपरलिखित सभी।
उत्तर :
ऊपरलिखित सभी।

प्रश्न 42.
जिन बालकों में संवेगात्मक नियंत्रण अधिक होता है, उनमें ……….. गुण अधिक पाए जाते हैं।
(A) सहनशीलता
(B) क्रोध
(C) जिज्ञासा
(D) प्यार।
उत्तर :
सहनशीलता।
प्रश्न 43.
बच्चों के शब्द भण्डार में व्यक्तिगत भिन्नता ……………. के कारण होती है।
(A) बुद्धि
(B) वातावरण
(C) प्रेरणा
(D) ऊपरलिखित सभी।
उत्तर :
ऊपरलिखित सभी।
प्रश्न 44.
यु का बच्चा कानूनी रूप से वयस्क समझा जाता है ?
(A) 21 वर्
कितनी आष
(B) 18 वर्ष
(C) 24 वर्ष
(D) 16 वर्ष।
उत्तर : 18 वर्ष।
प्रश्न 45.
बालक की शारीरिक वृद्धि को किस प्रकार बढ़ाया जा सकता है ?
(A) व्यायाम करने से
(B) आराम करने से
(C) उचित पौष्टिक आहार देकर
(D) कोई भी नहीं।
उत्तर :
उचित पौष्टिक आहार देकर।

प्रश्न 46.
किस आयु में बच्चा सीढ़ियाँ चढ़ना सीख लेता है ?
(A) 2 वर्ष में
(B) 1 वर्ष में
(C) 212 वर्ष में
(D) 3 वर्ष में।
उत्तर :
2 वर्ष में।
प्रश्न 47.
बच्चा दूसरों पर निर्भर होता है।
(A) जन्म से लेकर एक वर्ष तक
(B) जन्म से लेकर दो वर्ष तक
(C) जन्म से लेकर तीन वर्ष तक
(D) जन्म से लेकर छ: महीने तक।
उत्तर :
जन्म से लेकर दो वर्ष तक।
प्रश्न 48.
स्कूल में बच्चे का ………. विकास होता है।।
(A) मानसिक
(B) सामाजिक
(C) संवेगात्मक
(D) मानसिक तथा सामाजिक।
उत्तर :
मानसिक तथा सामाजिक।

प्रश्न 49.
बचपन में शरीर की हड्डियों की संख्या ……….. होती है।
(A) 240
(B) 270
(C) 276
(D) 280
उत्तर :
270.
प्रश्न 50.
बच्चे को कम-से-कम ………. महीने माँ का दूध अवश्य पिलाना चाहिए।
(A) दो
(B) छः
(C) चार
(D) आठ।
उत्तर :
छः।
प्रश्न 51.
………..वर्ष की अवस्था तक मस्तिष्क लगभग परिपक्व हो जाता है।
(A) 8
(B) 10
(C) 6
(D) 18
उत्तर :
8.

प्रश्न 52.
………..बुद्धि वाले बच्चों के दाँत देर से निकलते हैं।
(A) कम
(B) मध्यम
(C) कुशल
(D) इनमें से कोई नहीं।
उत्तर :
कम।
प्रश्न 53.
भाषा विकास का सीधा सम्बन्ध………… के परिपक्वता से होता है।
(A) स्वर
(B) जीव
(C) गला
(D) ये सभी।
उत्तर :
ये सभी।
प्रश्न 54.
बच्चों को बूस्टर दवा कितने वर्ष पर दी जाती है ?
(A) दो वर्ष
(B) पाँच वर्ष
(C) छ: वर्ष
(D) ग्यारह वर्ष।
उत्तर :
छः वर्ष।

प्रश्न 55.
वर्ष की अवस्था तक मस्तिष्क लगभग परिपक्व हो जाता है।
(A) 10
(B) 6
(C) 18
(D) 8
उत्तर :
8
प्रश्न 56.
…………. से विटामिन सी की प्राप्ति होती है।
(A) अण्डा
(B) दूध
(C) संतरा
(D) घी।
उत्तर :
संतरा।

बाल विकास HBSE 10th Class Home Science Notes
→ शारीरिक तथा मानसिक तौर पर स्वस्थ बच्चे ही देश का भविष्य हैं।
→ बच्चे के पालन-पोषण की प्रारम्भिक ज़िम्मेदारी उसके मां-बाप की होती है।
→ बाल विकास बच्चों की वृद्धि तथा विकास का अध्ययन है।
→ बाल विकास तथा बाल मनोविज्ञान का आपस में गहरा सम्बन्ध है।
→ मनुष्य के पारिवारिक रिश्ते उसके सामाजिक जीवन के लिए बहुत महत्त्वपूर्ण हैं।
→ सभी रिश्ते तथा सम्बन्ध मिलकर हमारे जीवन को आरामदायक बनाते हैं।
→ मानवीय जीवन का आरम्भ मां के गर्भ में आने से होता है।
→ मानवीय विकास के विभिन्न पड़ाव होते हैं; जैसे – बचपन, किशोरावस्था, प्रौढ़ावस्था तथा वृद्धावस्था।
→ बच्चा जन्म से लेकर दो वर्ष तक बेचारा-सा तथा दूसरों पर निर्भर होता है।
→ 12 वर्ष का बच्चा स्वयं चल सकता है और 2 वर्ष में बच्चा सीढ़ियां चढ़-उतर सकता है।
→ दो वर्ष के बच्चों को कई प्रकार की बीमारियों से बचाने के लिए टीके लगाए जाते हैं।
→ दो से तीन वर्ष का बच्चा नई चीजें सीखने की कोशिश करता है।
→ छ: वर्ष तक बच्चे की खाने, पीने, सोने, मल त्यागने तथा शारीरिक सफ़ाई की आदतें पक्की हो जाती हैं।
→ स्कूल में बच्चे का मानसिक तथा सामाजिक विकास होता है।
→ कई बार बच्चा गुस्सा जाहिर करने के लिए जमीन पर लेटता है, इस अवस्था को टेम्पर टैंट्रम कहा जाता है।
→ छोटे बच्चे को कम-से-कम छ: महीने मां का दूध अवश्य पिलाना चाहिए क्योंकि यह बच्चे में बीमारियों से लड़ने की शक्ति पैदा करता है।
→ 3-4 महीने के बच्चे को मां के दूध के साथ और खुराक भी देनी आरम्भ कर देनी चाहिए।
→ बच्चों की अच्छी आदतों का निर्माण मां-बाप के यत्नों पर निर्भर करता है।
→ बच्चों को खिलौने उनकी आयु के अनुसार ही मिलने चाहिएं।
→ खेलने से बच्चों का शारीरिक तथा मानसिक विकास होता है।
→ शारीरिक विकास का बालक के व्यवहार की गुणात्मकता और मात्रात्मकता, दोनों पर गहरा प्रभाव पड़ता है।
→ सामान्य शारीरिक विकास का प्रभाव बालक के व्यवहार के मुख्यतः चार क्षेत्रों पर पड़ता है –
- नाड़ी संस्थान
- मांसपेशियां
- अन्त: स्रावी ग्रन्थियां तथा
- शारीरिक संरचना।
→ बचपनावस्था में शरीर की हड्डियों की संख्या 270 होती है जो कि किशोरावस्था तक 206 रह जाती है।
→ वे बच्चे उन बच्चों की अपेक्षा अधिक लम्बे होते हैं जिनके परिपक्व होने की गति तीव्र होती है।
→ लगभग 17 वर्ष की अवस्था तक शरीर के विभिन्न अंगों का अनुपात वयस्क व्यक्तियों के समान हो जाता है।
→ प्रत्येक आयु के लड़कों के सिर लड़कियों की अपेक्षा कुछ बड़े होते हैं, परन्तु दोनों के विकास क्रम में कोई अन्तर नहीं होता है। 15 वर्ष के किशोर का सिर वयस्क व्यक्ति की अपेक्षा 98% होता है।
→ बालक के शरीर की लम्बाई और उसके पैरों की लम्बाई में हमेशा धनात्मक सह-सम्बन्ध होता है।
→ कम बुद्धि वाले बच्चों के दाँत देर से तथा अधिक बुद्धि वाले बच्चों के दाँत जल्दी निकलते हैं।
→आठ वर्ष की अवस्था तक मस्तिष्क लगभग परिपक्व हो जाता है। फिर भी मस्तिष्क का विकास किशोरावस्था तक चलता रहता है।
→शारीरिक विकास को प्रभावित करने वाले कारक हैं-वंशानुक्रम, भौतिक वातावरण, आहार, रोग, अन्तः स्त्रावी ग्रन्थियां, लिंग, संवेगात्मक व्यवधान, पारिवारिक प्रभाव तथा सामाजिक-आर्थिक स्तर।
→ बाल संवेगात्मकता को प्रभावित करने वाले कारक हैं-शारीरिक स्वास्थ्य, बुद्धि, लिंग, पिता-पुत्र सम्बन्ध, सामाजिक वातावरण, जन्म क्रम, परिवार का आकार, सामाजिक-आर्थिक स्तर, व्यक्तित्व।
→ बाल्यावस्था के कुछ प्रमुख संवेग हैं-भय, शर्मीलापन, परेशानी, चिन्ता, क्रोध, ईर्ष्या, जिज्ञासा तथा स्नेह।
→ जन्म के समय शिशु न सामाजिक होता है और न ही असामाजिक। आयु बढ़ने के साथ-साथ वह सामाजिक गुणों से सुशोभित होता जाता है और कुछ ही वर्षों बाद वह सामाजिक प्राणी कहलाने लगता है।
→ सामाजिक विकास का अर्थ उस योग्यता को अर्जित करना है जिसके द्वारा सामाजिक प्रत्याशाओं के अनुसार व्यवहार किया जा सके।
→ बचपनावस्था के कुछ सामाजिक व्यवहार हैं-अनुकरण, आश्रितता, ईर्ष्या, सहयोग, शर्माहट, ध्यान आकर्षित करना, अवरोधी व्यवहार।
→ पूर्व बाल्यावस्था के सामाजिक व्यवहार के कुछ प्रकार हैं-आक्रामकता, झगड़ा, चिढ़ाना, निषेधात्मक व्यवहार, सहयोग, ईर्ष्या, उदारता, सामाजिक अनुमोदन की इच्छा, आश्रितता, बालकों में भिन्नता, सहानुभूति।
→ उत्तर बाल्यावस्था में सामाजिक व्यवहार के कुछ प्रतिमान हैं-सामाजिक अनुमोदन, सुझाव ग्रहणशीलता, स्पर्धा और प्रतियोगिता, खेल, पक्षपात और सामाजिक विभेदीकरण, उत्तरदायित्व, सामाजिक सूझ, यौन विरोध भाव।
→ सामाजिक विकास को प्रभावित करने वाले मुख्य कारक हैं-शारीरिक बनावट और स्वास्थ्य, परिवार, पड़ोस, विद्यालय, मनोरंजन, व्यक्तित्व आदि।
→ विकास को निम्नलिखित श्रेणियों में बांटा जाता है –
- शारीरिक विकास
- गत्यात्मक विकास
- सामाजिक विकास
- संवेगात्मक विकास
- भाषा विकास
- ज्ञानात्मक विकास।
→ बच्चे के शरीर या दिमाग की साधारण स्थिति में परिवर्तन या बेचैनी को ‘आवश्यकता’ कहते हैं। बच्चे की आवश्यकताएं निम्नलिखित प्रकार की होती –
- शारीरिक
- भावनात्मक
- ज्ञानात्मक।
जब बच्चे की आवश्यकताएं पूरी हो जाती हैं, तो वह खुश हो जाता है।
→ भाषा सम्प्रेषण का माध्यम है, अत: इसका बालक के सामाजिक विकास में महत्त्वपूर्ण योगदान है।
→ भाषा के द्वारा बालक अपने आसपास के लोगों में सम्पर्क स्थापित करता है, अपने मनोभावों को व्यक्त करता है तथा दूसरों के मनोभावों के प्रति अपनी प्रतिक्रियाएं दिखाता है।
→ भाषा विकास का सीधा सम्बन्ध स्वर, यन्त्र, जीभ, गला और फेफड़ों की परिपक्वता से है। यदि बालक के ये अंग सामान्य रूप से विकसित होते हैं तो उसका भाषिक विकास सन्तोषजनक होता है। इसका सम्बन्ध दृष्टि, होंठ, ताल, दांत और नाक के विकास से भी है।
→ उद्दीपन अनुक्रिया के बीच साहचर्य स्थापित कर बालक को नए शब्द सिखलाए जा सकते हैं। यदि बालक के सामने बार-बार कलम दिखाकर ‘कलम-कलम’ का उच्चारण किया जाए, तो थोड़ी देर ठहरकर पुन: उसे कलम दिखाई जाए तो वह ‘कलम’ शब्द बोल लेगा। वह ‘कलम’ एक उद्दीपक वस्तु है।
→ एन० चॉस्की के अनुसार प्रत्येक बालक के व्यक्तित्व में भाषा सीखने की एक प्रकृति प्रदत्त क्षमता होती है।
→ बालकों का क्रन्दन एक प्रकार की भाषा है, जिसके द्वारा वे अपनी शारीरिक पीड़ा को अभिव्यक्ति करते हैं।
→ बालकों के शब्द भण्डार में व्यक्तिगत भिन्नता, बुद्धि, वातावरण, प्रेरणा और अधिगम के कारण होती है।
→ भाषा विकास को प्रभावित करने वाले कारक हैं-व्यक्तित्व सम्बन्धी विशेषताएं, पारिवारिक सम्बन्ध, लिंग, सामाजिक-आर्थिक स्तर, निर्देशन, उत्प्रेरणा तथा सामाजिक अधिगम के स्तर हैं।
![]()
![]()
![]()

![]()

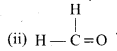

![]()
![]()
![]()
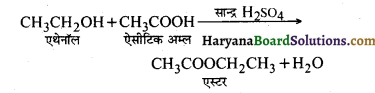
![]()