Class 10

Haryana State Board HBSE 10th Class Science Notes Chapter 2 Acids, Bases and Salts Notes.

Haryana Board 10th Class Science Notes Chapter 2 Acids, Bases and Salts

Understanding chemical Properties of Acids and Bases:

• In present times, 114 elements are known to us. These elements combine in several ways and give rise to a very large number of compounds.
• On the basis of their chemical properties all the compounds is can be divided into three groups. They are:

Acids: An acid is a compound having hydrogen which when dissolved in water releases i.e. dissociates hydrogen ions (H⁺) to be specific (H₃O⁺ ions). For example, hydrochloric acid (HCl), sulphuric acid (H₂SO₄), etc.

Bases: A base is a metal hydroxide substance which when dissolved in water release hydroxide (OH^–) ions. For example, sodium hydroxide (NaOH), calcium hydroxide (Ca(OH)₂), etc.

Salts: A salt is an ionic compound which is formed from the neutralization reaction of an acid and a base.

Olfactory Indicators: Olfactory means ‘relating to the sense of smell’. Those substances whose smell changes in acidic or basic solutions are called olfactory indicators.

Outcomes of certain important types of reactions:

Reaction of acid with metal:
When acid reacts with metal, metallic salt of that metal and hydrogen gas are produced.

Reaction of base with metal:
When a strong base reacts with certain metals, it produces salt and hydrogen gas.

Reaction of acid with metal carbonate or metal hydrogen carbonate:
When acids react with metal carbonate or metal hydrogen carbonate, most acids produce salt, water and carbon dioxide gas.

Reaction of acid with base:
When acid reacts with base, salt and water are produced. Since base neutralizes the effect of acid, this reaction is called neutralization reaction.

Reaction of acid with metal oxide:
When acid reacts with metal oxide, salt and water are produced.

Reaction of nonmetallic oxide with base:
When a non-metallic oxide reacts with base, the reaction gives out salt and water.

How Strong are Acid or Base Solutions?

Strong acids:
An acid which gets completely ionized completely in water or say which completely dissociates in water and produce a large amount of hydrogen [H⁺] ions (or say hydronium [H₂O⁺] ions) is called a strong acid.

Weak acids:
An acid which does not ionize completely (i.e. does not dissociate completely in water) and thus produce a small amount of hydrogen [H⁺] ions (or say H₂O⁺ ions) is called a weak acid.

Strong base:
A base, which completely ionizes in water and thus produces a large amount of hydroxide (OH^–) ions, is called a strong base or a strong alkali.

Weak base:
A base, which does not ionize completely in water and thus produces a small amount of hydroxide (OH^–) ions, is called a weak base or a weak alkali.

The methods of measuring the strength of an acid or a base:

• Through universal indicator and
• Through pH scale

pH scale:

• The pH scale measures concentration of hydrogen [H⁺] ions in the solution.
• The scale points range from O to 14. 0 means very acidic and 14 means very alkaline. Scale point 7 means neutral solution.

Importance of pH in everyday life:

• Importance of pH in existence of living beings,
• Importance of pH in soil,
• Importance of pH in digestion of food,
• Importance of pH in stopping tooth decay,
• Self-defence by animals and plats through Chemical warfare:

More About Salts

Salt:

• A salt is an ionic compound which is formed by the neutralization reaction of an acid and a base. Thus, we get salt when we react an acid with a base. When we dissolve a salt in water it will get ionized and release cation (i.e. the positive +ve ion) and anion (i.e. the negative – ve ion).
• In general, salts having same type of cations (+ve ions) or anions (-ve) belong to the same family.

Some Important Salts:

Read More:

KOTAKBANK Pivot Point Calculator

Haryana State Board HBSE 10th Class Science Notes Chapter 12 Electricity Notes.

Haryana Board 10th Class Science Notes Chapter 12 Electricity

Electric Current and Circuit

• Electric charge and conduction of electricity:
• ‘Charge’ or ‘electric charge’ is the fundamental quantity of electricity.
• Electric charge or simply charge is of two types, (1) Positive (+) charge and (2) negative (-) charge.
• If electric charge flows through a conductor such as metal wire, we say that there is electric current in the conductor. The S.l. unit of electric charge is columb ‘C’.
• An electron possesses a ‘negative charge of  6 x 10^-19 C whereas a proton possesses a ‘positive charge of 6 x 10^-19 C’.
• Free (or conducting) electrons are responsible for conducting electricity or say conduction.
• Electric current can flow very easily through material which contain a large number of free electrons. Hence such a material is called a conductor. For example, metals such as copper, silver and aluminium are conductors.

Electric current:
The rate of flow of electric charge is known as electric current. In other words, the net quantity of electric charge that flows through any cross­section of a conductor is known as the electric current.

Thus, electric current \(=\frac{\text { Quantity of electric charge }}{\text { Time }}\)

If Q is the amount of electric charge passing through any cross-section of a conductor in time then, electric current \((I)=\frac{Q}{t}\)

SI unit of electric current is Coulomb/second (C/s). Electric current is also measured in Ampere (A).

Electric circuit:
A continuous and closed path along which electric current flows is called an electric circuit.

Electric Potential and Potential Difference

Electric potential difference:
The amount of work done to take a unit positive charge from a given point say A to point B in a circuit carrying some current is known as the electrical potential difference between the two points.

Thus, electric potential difference
\((V)=\frac{\text { Work done }(W)}{\text { Electric charge }(Q)}\) \(V=\frac{W}{Q}\)

In practice, electric potential difference is known as voltage. Its S.I unit is joule/coulomb or volt (V).

If the work done to bring 1 coulomb electric charge from one point to another is 1 joule, then the potential difference between these two points is called 1 volt.
\(\text { Thus, } 1 \text { volt }=\frac{1 \text { joule }}{1 \text { Coulomb }} \quad \mathrm{~V}=1 \mathrm{JC}^{-1}\)

Ohm’s law:

• In a definite physical situation, the electric current (I) flowing through the conductor is directly proportional to the potential difference (V) applied across it, provided its temperature and other physical conditions remain same.
• Thus, I α V or say V α I.
  ∴ V = I R (where, R is the proportionality by constant and it represents resistance R of the circuit)
• The SI unit of resistance (R) is volt/ampere which is called ohm and it is denoted by Ω. (Omega).
  ∴ \(1 \mathrm{Ohm}(\Omega)=\frac{1 \text { volt }(\mathrm{V})}{1 \text { ampere }(\mathrm{l})}\)

Factors on which the Resistance of a Conductor Depends

The resistance (R) of a conductor is directly proportional to the length of the conductor and inversely proportional to the area of its cross-section.

Resistance R α length l and also R α \(\frac{1}{A}\)
∴ \(\mathrm{R} \alpha \frac{1}{\mathrm{~A}}=\rho \frac{1}{\mathrm{~A}}\)

∴ \(R \alpha \frac{1}{A}=\rho \frac{1}{A}\) (where ρ (rho) is constant and called the resistivity of conducting material.)
We can also say, \(\rho=\mathrm{R} \frac{\mathrm{A}}{l}\)

The S.l unit of resistivity ρ =Ωm (Ohm meter)

At constant temperature, the resistance of a conductor depends on:

• Length (L) i.e. R α L,
• Area of cross-section (A) i.e. \(R \propto \frac{1}{A}\) and
• Nature of material.

Combining all these factors we get:
\(R \propto \frac{L}{A} \text { or say } R=\rho \frac{L}{A}\)

Resistance of a Sprem of Resistors

Joining resistors in a series connection:

• When two or more resistors are connected end- to-end consecutively, such a connection is called a series connection.
• In a series connection, equivalent resistance
  R_s = R₁ + R₂ + R₃

Joining resistors in a parallel connection:
When two or more resistors are connected between the same two points of a circuit, they are said to be connected in a parallel connection (because they are connected in parallel and not end-to-end).

In a parallel connection, equivalent resistance is denoted as \(\frac{1}{R_p}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}\)

Heating effect of electric current:

• When electric current is passed through a high resistance wire, the resistance wire becomes hot and produces heat. Here, electrical energy is converted into heat energy which is known as the heating effect of electric current.
• The energy spent by the source of the work done by the source can be calculated as
  W=l.R x I.t =l²Rt.
  Thus, heat energy (H) = I²Rt

Practical Applications of Heating Effect of Electric Current

Practical (daily life) applications of heating effect of electric current:

• Household heating appliances: Electric iron, toaster, sandwich maker, room heater, electric kettle, etc. all such appliances make use of heating effect of electric current.
• Electric bulbs: When electricity is passed through the filament of the electric bulbs, the bulbs light up. Here, heating effect is used foremitting light.
• Electric fuse: Electric tuse is a safety device which works on the heating effect of electric current.

Electric power:

• The electrical energy consumed (or heat energy generated) in unit time is called electric power.
• In other words, electric power is the rate of electric energy. It is denoted by R.

∴ Power P \(\mathrm{P}=\frac{\text { Electric energy consumed }}{\text { Time }}\)
\(=\frac{W}{t}=\frac{l^2 R t}{t}\)
(∴ W = electrical energy = I²Rt)
∴ P=I²R

The SI unit of power is joule/second or watt (W).
Practical unit of electrical energy:
Power \(\mathrm{P}=\frac{\text { electric energy }(\mathrm{W})}{\text { time }(\mathrm{t})}\)
∴ Electrical energy (W) = Power (P) x time (t)
= watt x second
= joule

Thus, the unit of electrical energy is watt. second.
The larger unit of electrical energy is kWh.
1 kWh = 1000 watt x 3600 seconds
= 3.6 x 10⁶ joules (J)

Read More:

BHEL Pivot Point Calculator

Haryana State Board HBSE 10th Class Science Notes Chapter 5 Periodic Classification of Elements Notes. BANKBARODA Pivot Point Calculator

Haryana Board 10th Class Science Notes Chapter 5 Periodic Classification of Elements

Making Order Out of Chaos – Early Attempts at the Classification of Elements

Need of classifying elements:
Classifying the elements help us to understand their properties and produce various products.

Dobereiner’s classification of elements
(Dobereiner’s triads):
In 1817, German chemist Johann Wolfgang Dobereiner started classifying elements on the basis of their chemical properties.

Law of Triads:
If three elements are arranged in the increasing order of their atomic masses, the atomic mass of the intermediate (i.e. second) element would be almost equal to the average of atomic masses of first and third elements. This is known as Law of Triads. It was given by Dobereiner.

Limitation of Dobereiner’s classification :

• Certain elements could not be classified by Dobereiner’s method.
• Only a limited number of elements could be classified into triads.

The three triads identified by Doberiner:

• Lithium, Sodium and Potassium
• Chlorine, Bromine and Iodine
• Calcium, Strontium and Barium.

Newlands’ Law of Octaves:

• When elements are arranged in the increasing
  order of their atomic masses, properties of every 8th element are found to be similar to the properties of the first element.
• In 1866, a scientist named John Newlands arranged the elements in the increasing order of their atomic masses.
• During this arrangement, he found properties of every 8th element to be similar i.e. property of 1st and then 8th element would be similar. This periodicity pattern was known as the Law of Octaves (octaves = eight).

Limitation of Newlands’ Law of Octaves:

1. The law was applicable only upto calcium.
2. Newlands thought that there were only 56 elements in nature. He also thought that no more elements would be discovered in the future.
3. In order to fit elements any how into his table, Newlands adjusted two elements in the slot even if the properties of elements did not match with other elements.

Making Order Out of Chaos Mendeleev \ Periodic Table

Mendeleev’s Periodic Table:

1. In 1869, Russian chemist Dmitri Ivanovich Mendeleev started his work of classifying 63 elements known to man.

2. Mendeleev started by examining the relationship of

• ‘Atomic mass of an element’ with
• ‘Physical property of the element’ and
• Chemical property of the element.

3. Through this classification, he concluded that “The properties of elements are periodic function (i.e. periodic in nature) of their atomic mass.” This law came to be known as Mendeleev’s Periodic Law

Criteria used by Mendeleev for developing periodic table:

• The properties of elements are the periodic function of their atomic masses. Hence, arranging elements in the increasing order of their atomic masses.
• Elements with similar properties are arranged in the same group.
• The formula of oxides and hydrides formed by an element.

Anomalies (irregularities) of Mendeleev’s Periodic Table:

• Sequence of few elements was inverted,
• Gaps were kept at few places

Limitations of Mendeleev’s Periodic Table:

• The position of hydrog en could not be correctly assigned,
• The table could not assign proper position for the isotopes of various elements
• Some elements were not arranged on the basis of their increasing atomic mass. This posed a question as to how many elements could still take the place between two elements.

Making Order out of Chaos – The Modern Periodic Table:

Periodic table:
The Periodic Table is a chart in which all the elements known to us are arranged in a systematic manner.

Modern Periodic Law:
Properties of elements are a periodic function of their atomic numbers.

Arrangement of elements in groups and periods in Modern Periodic Table:

(a) Placement of an element in a group:
Elements are placed in a particular group on the basis of the ‘valence electrons’ i.e. elements having same number of valence electrons will be placed in same group.

(b) Placement of an element in a period:
Within a horizontal period, as one moves from left to right, the ‘elements have same number of shells’ but, ‘different valence electrons’. Moreover, on moving left to right, the number of electrons of valence shell increase by 1 unit.

Thus, elements having same number of shells are placed in the same period. For example, Na, Mg, Al, Si, etc. have 3 shells and hence are placed in the 3rd period.

Trends in the Modern Periodic Table Periodic properties:

The properties which are determined by the electronic configuration of elements or which depend on the electroninc configuration of elements are known as periodic properties.

Trends of change in (1) Valency, (2) Atomic size and (3) Metallic and non-metallic properties in groups and periods:

Characteristic	Groups	Periods
1. Valency	All the elements of a group have same valency.	On moving from left to right, the valency of elements increase from 1 to 4 and then goes on decreasing to O (zero).
2. Atomic size (Radius of atom)	As we move down in a group, the size of atoms i.e. atomic size increase	On moving from left to right in a period, the size of the atoms decrease.
3. Metallic and Non-metallic properties	Going down in the group, the metallic property of elements increase	On moving left to right in a period, the metallic property of elements decreases while non-metallic property increases.

Metalloids or semi-metallic elements:

1. Elements which possess properties of both metals and non-metals are known as metalloids or semi- metallic elements.
2. In the Modern Periodic Table, a zig-zag line separates metals and non-metals. The border line elements such as boron (B), silicon (Si), germanium (Ge), arsenic (As), antimony (Sb), tellurium (Te) and polonium (Po) on this zig-zag line are known as metalloids or semi-metals.

Haryana State Board HBSE 10th Class Maths Solutions Chapter 3 दो चर वाले रैखिक समीकरण युग्म Ex 3.3 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.3

प्रश्न 1.
निम्नलिखित रैखिक समीकरण युग्म को प्रतिस्थापन विधि से हल कीजिए-
(i) x + y = 14
x – y = 4
(ii) s – t = 3
\(\frac{s}{3}+\frac{t}{2}\) = 6
(iii) 3x – y = 3
9x – 3y = 9
(iv) 0.2x + 0.3y = 1.3
0.4x + 0.5y = 2.3
(v) √2x + √3y = 0
√3 x – √8y = 0
(vi) \(\frac{3 x}{2}-\frac{5 y}{3}\) = -2
\(\frac{x}{3}+\frac{y}{2}=\frac{13}{6}\)
हल :
(i) यहाँ पर
x + y = 14 ……….. (i)
y = 14-x
तथा x – y = 4 ………….. (ii)
y = 14 – x को समीकरण (ii) में प्रतिस्थापित करने पर,
x – (14 – x) = 4
या x – 14 + x = 4
या 2x = 4 + 14
या 2x = 18
या x = \(\frac{18}{2}\) =9
x का मान समीकरण (i) में प्रतिस्थापित करने पर,
9 + y = 14
y = 14 – 9 = 5
अतः अभीष्ट हल x = 9 व y = 5

(ii) यहाँ पर s – 1 = 3… (i)
s = 3+t
तथा \(\frac{s}{3}+\frac{t}{2}\) = 6 … (ii)
2s + 3t = 36 (दोनों ओर 6 से गुणा करने पर) … (ii)

s = 3 + t को समीकरण (ii) में प्रतिस्थापित करने पर, .
2 (3 + t) + 3t = 36
6 + 2t + 3t = 36
5t = 36 – 6
5t = 30
या t = \(\frac{30}{5}\) = 6
t का मान समीकरण (i) में प्रतिस्थापित करने पर,
s – 6 = 3
या s = 3 + 6 = 9
अतः अभीष्ट हल s = 9 व 1 = 6

(iii) यहाँ पर 3x – y = 3 … (i)
y = 3x – 3
तथा 9x – 3y = 9 … (ii)
y = 3x – 3 को समीकरण (ii) में प्रतिस्थापित करने पर,
या 9x – 3 (3x – 3) = 9
या 9x – 9x + 9 = 9
9 = 9
यह कथन x के प्रत्येक मान के लिए सत्य है।
अतः समीकरण (i) व (ii) के अपरिमित रूप से अनेक हल हैं।

(iv) यहाँ पर
0.2x + 0.3y = 1.3… (i)
x = \(\frac{1.3-0.3 y}{0.2}\)1.3 – 0.3y
तथा 0.4x + 0.5y = 2.3… (ii)
x = [atex]\frac{1.3-0.3 y}{0.2}[/latex] को समीकरण (ii) में प्रतिस्थापित करने पर,
0.4( [atex]\frac{1.3-0.3 y}{0.2}[/latex] ) + 0.5y = 2.3
या 2 (1.3 – 0.3y) + 0.5y = 2.3
या 2.6 – 0.6y + 0.5y = 2.3
या -0.1y = 2.3 – 2.6
या – 0.1y = – 0.3
या y =[atex]\frac{-0.3}{-0.1}[/latex] = 3
y का मान समीकरण (i) में प्रतिस्थापित करने पर,
या 0.2x + 0.3 (3) = 1.3
या 0.2x + 0.9 = 1.3
या 0.2x = 1.3 – 0.9
या 0.2x = 0.4
या x = \(\frac{0.4}{0.2}\) = 2
अतः अभीष्ट हल x = 2 व y = 3

(v) यहाँ पर
√2x- √3y = 0 ……(i)

या -3y – 4y = 0 [दोनों ओर √2 से गुणा करने पर]
या -7y = 0
या y = [ltex]\frac{0}{7}[/latex] = 0
y का मान समीकरण (i) में प्रतिस्थापित करने पर,
√2x + √3 (0) = 0
या √2x + 0 = 0
√2x = 0
x = \(\frac{0}{\sqrt{2}}\)
अतः अभीष्ट हल x = 0 व y = 0

(vi) यहाँ पर
\(\frac{3 x}{2}-\frac{5 y}{3}\) = -2
9x – 10y = -12 (दोनों ओर 6 से गुणा करने पर) …(i)
x = \(\frac{10 y-12}{9}\)
तथा \(\frac{x}{3}+\frac{y}{2}=\frac{13}{6}\)
2x + 3y = 13 (दोनों ओर 6 से गुणा करने पर) ………………(ii)
x = \(\frac{10 y-12}{9}\)को समीकरण (ii) में प्रतिस्थापित करने पर,
\(2\left(\frac{10 y-12}{9}\right)\) + 3y = 13

या \(\frac{20 y-24}{9}\) + 3y = 13
या 20y – 24 + 27y = 117 (दोनों ओर 9 से गुणा करने पर)
या 47 y= 117 + 24
या y = \(\frac{141}{47}\) = 3
y का मान समीकरण (i) में प्रतिस्थापित करने पर,
9x – 10 (3) = – 12
9x = – 12 + 30
9x = 18
x = \(\frac{18}{9}\)= 2
अतः अभीष्ट हल x = 2 व y =3

प्रश्न 2.
2x + 3y = 11 और 2x-4y = -24 को हल कीजिए और इससे ‘m’ का वह मान ज्ञात कीजिए जिसके लिए y= me +3 हो।
हल :
यहाँ पर 2x + 3y = 11 …………… (i)
x = \(\frac{11-3 y}{2}\)
तथा 2x–4y = – 24 …. (ii)
x = \(\frac{11-3 y}{2}\) को समीकरण (ii) में प्रतिस्थापित करने पर,
2(\(\frac{11-3 y}{2}\)) – 4y = – 24
या 11 – 3y – 4y = – 24
या  -7y = – 24-11
या y = \(\frac{-35}{-7}\) = 5
y का मान समीकरण (i) में प्रतिस्थापित करने पर,
2x + 3 (5) = 11
या  2x = 11-15
या x = \(\frac{-4}{2}\) =-2
अब x = – 2 व y = 5 को y = mx + 3 में प्रतिस्थापित करने पर प्राप्त होगा,
या 5 = m (-2)+3
या 5 = – 2m +3
या 2m = 3-5
या m = \(\frac{-2}{2}\) = -1
अतः अभीष्ट हल x = – 2, y= 5 व m = – 1

प्रश्न 3.
निम्नलिखित समस्याओं में रैखिक समीकरण युग्म बनाइए और उनके हल प्रतिस्थापन विधि द्वारा ज्ञात कीजिए-
(i) दो संख्याओं का अंतर 26 है और एक संख्या दूसरी संख्या की तीन गुनी है। उन्हें ज्ञात कीजिए।
(ii) दो संपूरक कोणों में बड़ा कोण छोटे कोण से 18 डिग्री अधिक है। उन्हें ज्ञात कीजिए।
(iii) एक क्रिकेट टीम के कोच ने 7 बल्ले तथा 6 गेदें 3800 रु० में खरीदीं। बाद में, उसने 3 बल्ले तथा 5 गेंदें 1750 रु० में खरीदी। प्रत्येक बल्ले और प्रत्येक गेंद का मूल्य ज्ञात कीजिए।
(iv) एक नगर में टैक्सी के भाड़े में एक नियत भाड़े के अतिरिक्त चली गई दूरी पर भाड़ा सम्मिलित किया जाता है। 10 km दूरी के लिए भाड़ा 105 रु० है तथा 15 km के लिए भाड़ा 155 रु० है। नियत भाड़ा तथा प्रति km भाड़ा क्या है? एक व्यक्ति को 25 km यात्रा करने के लिए कितना भाड़ा देना होगा?
(v) यदि किसी भिन्न के अंश और हर दोनों में 2 जोड़ दिया जाए, तो वह \(\frac{9}{11}\) हो जाती है। यदि अंश और हर दोनों में 3 जोड़ दिया जाए, तो वह \(\frac{5}{6}\) हो जाती है। वह भिन्न ज्ञात कीजिए।
(vi) पाँच वर्ष बाद जैकब की आयु उसके पुत्र की आयु से तीन गुनी हो जाएगी। पाँच वर्ष पूर्व जैकब की आयु उसके पुत्र की आयु की सात गुनी थी। उनकी वर्तमान आयु क्या है?
हल :
(i) यहाँ पर
माना बड़ी संख्या = x .
व छोटी संख्या = y
प्रश्नानुसार रैखिक युग्म होंगे, x -y = 26 …………(1)
तथा x = 3y ………(ii)
x = 3y को समीकरण (i) में प्रतिस्थापित करने पर,
3y – y =
या 2y = 26
या y = \(\frac{26}{2}\) = 13
y का मान समीकरण (ii) में प्रतिस्थापित करने पर,
x = 3(13)
x = 39
अतः अभीष्ट संख्याएँ = 39 व 13

(ii) यहाँ पर
माना बड़ा कोण = x
व छोटा कोण = y
प्रश्नानुसार रैखिक युग्म होंगे, x = y + 18° ……(i)
तथा x+ y = 180°(:: संपूरक कोणों का योग 180° होता है) …………… (ii)
x =y + 18° को समीकरण (ii) में प्रतिस्थापित करने पर,
(y+ 18°) + y = 180°
या 2y = 180° – 18°
या y = \(\frac{162^{\circ}}{2}\) = 81°
y का मान समीकरण (i) में प्रतिस्थापित करने पर,
x = 81° + 18° = 99°
अतः अभीष्ट कोण = 99° व 81°

(iii) यहाँ पर
माना क्रिकेट के 1 बल्ले का मूल्य = x रु०
तथा क्रिकेट की 1 गेंद का मूल्य = y रु०
प्रश्नानुसार रैखिक युग्म होंगे, 7x+ 6y = 3800 ………….(i)
तथा 3x + 5y = 1750 ………………(ii)
x = \(\frac{1750-5 y}{3}\)
x = \(\frac{1750-5 y}{3}\) को समीकरण (i) में प्रतिस्थापित करने पर,
7( \(\frac{1750-5 y}{3}\)) + 6y = 3800
या 7(1750 – 5y) + 18y = 11400 (दोनों ओर 3 से गुणा करने पर)
या 12250-35y + 18y = 11400
या – 17y = 11400-12250
या y = \(\frac{-850}{-17}\) = 50
y का मान समीकरण (ii) में प्रतिस्थापित करने पर,
3x + 5(50) = 1750
या 3x = 1750 – 250
या x = \(\frac{1500}{3}\) = 500
अतः क्रिकेट के एक बल्ले का मूल्य = 500 रु०
तथा क्रिकेट की एक गेंद का मूल्य = 50 रु०

(iv) यहाँ पर
माना टैक्सी का नियत भाड़ा = x रु०
तथा अतिरिक्त प्रति कि०मी० भाड़ा = y रु०
प्रश्नानुसार रैखिक युग्म होंगे,
x + 10y = 105 ………….(i)
तथा x + 15y = 155 …………..(ii)
x = 155 – 15y
x = 155-15y को समीकरण (i) में प्रतिस्थापित करने पर,
155 – 15y + 10y = 105
या -5y = 105 – 155
या y = \(\frac{-50}{-5}\) = 10
y का मान समीकरण (ii) में प्रतिस्थापित करने पर,
x + 15(10) = 155
या x = 155-150 = 5
अतः टैक्सी का नियत भाड़ा = 5 रु० ।।
तथा अतिरिक्त प्रति कि०मी० का भाड़ा = 10 रु०
25 कि०मी० यात्रा करने के लिए दिया जाने वाला भाड़ा = x + 25y
= [5+ 25 (10)] रुपए
= [5+ 250] रुपए
= 255 रुपए

(v) यहाँ पर
माना भिन्न का अंश = x
व भिन्न का हर = y
तो भिन्न = x/y
प्रश्नानुसार रैखिक युग्म होंगे, \(\frac{x+2}{y+2}=\frac{9}{11}\)
11x + 22 = 9y+ 18
11x – 9y = 18 – 22
11x – 9y = -4 ………….(i)
तथा \(\frac{x+3}{y+3}=\frac{5}{6}\)
6x + 18 = 5y + 15
6x-5y = 15-18
6x – 5y = -3
= 5y-3
x =\(\frac{5 y-3}{6}\) ……………(ii)
x = \(\frac{5 y-3}{6}\)को समीकरण (i) में प्रतिस्थापित करने पर,
11 (\(\frac{5 y-3}{6}\)) -9y = -4
या 11(5y – 3) – 54y = – 24 (दोनों ओर 6 से गुणा करने पर)
या 55y – 33 – 54y = -24
या y = 33 – 24 = 9

y का मान समीकरण (ii) में प्रतिस्थापित करने पर,
6x – 5(9) = -3
या 6x = 45 -3
या x = \(\frac{42}{6}\) = 7
अतः अभीष्ट भिन्न = \(\frac{7}{9}\)

(vi) यहाँ पर
माना जैकब की वर्तमान आयु = x वर्ष
पुत्र की वर्तमान आयु = y वर्ष
प्रश्नानुसार रैखिक युग्म होंगे,
x + 5 = 3 (y+5)
x + 5 = 3y + 15
x = 3y + 15 – 5
x = 3y + 10……………(i)
x – 5 = 7(y – 5)
x – 5 = 7y – 35
x = 7y – 35 + 5
x = 7y – 30 ……………(ii)

x = 7y – 30 को समीकरण (i) में प्रतिस्थापित करने पर,
या 7y – 30 = 3y + 10
या 7y – 3y = 10+30
या 4y = 40
या y = 40/4 = 10

y का मान समीकरण (ii) में प्रतिस्थापित करने पर
x = 7(10)-30
= 70 – 30 = 40
जब की वर्तमान आयु = 40 वर्ष
व पुत्र की वर्तमान आयु = 10 वर्ष

Haryana State Board HBSE 10th Class Maths Solutions Chapter 3 दो चर वाले रैखिक समीकरण युग्म Ex 3.5 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.5

प्रश्न 1.
निम्नलिखित रैखिक समीकरणों के युग्मों में से किसका एक अद्वितीय हल है, किसका कोई हल नहीं है या किसके अपरिमित रूप से अनेक हल हैं। अद्वितीय हल की स्थिति में, उसे वज्र-गुणन विधि से ज्ञात कीजिए।
(i) x – 3y – 3 = 0
3x – 9y – 2 = 0
(ii) 2x + y =5
3x + 2y = 8
(iii) 3x – 5y = 20
6x – 10y = 40
(iv) x – 3y – 7 = 0
3x – 3y – 15 = 0
हल :
(i) यहाँ पर x – 3y – 3 = 0 ….(i)
3x – 9y – 2 = 0 ….(ii)
a₁ = 1; b₁ = -3; c₁ = -3
a₂ = 3; b₂ = – 9; c₂ = -2

इसलिए दिए गए रैखिक समीकरण युग्म का कोई हल नहीं है।

(ii) यहाँ पर
2x + y-5 = 0
व 3x + 2y – 8 = 0
a₁ = 2; b₁ = 1; c₁ = -5
a₂ = 3; b₂ = 2; c₂ = – 8

इसलिए दिए गए रैखिक समीकरण युग्म का अद्वितीय हल है।

अब वज्र-गुणन विधि से हल करने के लिए

x = 2 और y =1
अतः अभीष्ट हल x = 2 व y=1

(iii) यहाँ पर
3x – 5y – 20 = 0 …………….(i)
6x – 10y – 40 = 0 …………….(ii)
a₁ = 3; b₁ = -5; c₁ = – 20
a₂ = 6; b₂ = – 10; c₂ = – 40

इसलिए दिए गए रैखिक समीकरण युग्म के अपरिमित रूप से अनेक हल हैं।

(iv) यहाँ पर
x – 3y – 7 = 0
3x – 3y – 15 = 0
a₁ = 1; b₁ = -3; c₁ = – 7
a₂ = 3; b₂ = -3; c₂ = – 15

इसलिए दिए गए रैखिक समीकरण युग्म का अद्वितीय हल है।

अब वज्र-गुणन विधि से हल करने के लिए

x = 4 और y = -1
अतः अभीष्ट हल x = 4 व y = – 1

प्रश्न 2.
(i) a और b के किन मानों के लिए, निम्न रैखिक समीकरणों के युग्म के अपरिमित रूप से अनेक हल होंगे?
2x + 3y = 7
(a – b)x + (a + b)y = 3a + b -2

(ii) k के किस मान के लिए, निम्न रैखिक समीकरणों के युग्म का कोई हल नहीं है?
3x + y = 1
(2k – 1)x + (k – 1)y = 2k + 1
हल :
(i) यहाँ पर 2x + 3y – 7 = 0 …………..(i)
व . (a – b)x + (a + b)y – (3a + b – 2) = 0 …………..(ii)
a₁ = 2; b₁ = 3; c₁ = -7 .
a₂ = a – b; b₂ = a + b; c₂ = – (3a + b -2)
दिए गए रैखिक समीकरण युग्म के अपरिमित रूप से अनेक हल के लिए आवश्यक है कि,

2(a + b) = 3(a – b) व -2 (3a + b – 2) = -7(a – b)
या 2a + 2b = 3a-36 व -6a-2b + 4 = – 7a + 7b
या 3a – 3b – 2a – 2b = 0 व – 6a – 2b + 4 + 7a – 7b = 0
या a – 5b = 0 व a – 9b + 4 = 0
अर्थात् a – 5b = 0 …………(1)
व a – 9b + 4 = 0…(ii)

अब वज्र-गुणन विधि से हल करने के लिए

a = 5 व b = 1
अतः अभीष्ट मान a = 5 व b = 1 के लिए रैखिक समीकरण युग्म के अपरिमित रूप से अनेक हल होंगे।

(ii) यहाँ पर
3x + y – 1 = 0 …(i)
व (2k – 1)x + (k – 1) – (2k + 1) = 0 …(ii)
4₁ = 3; b₁ = 1; csub>1 = -1
a₂ = 2k- 1; b₂ = k- 1; c₂ = – (2k + 1)
दिए गए रैखिक समीकरण युग्म के कोई भी हल न होने के लिए आवश्यक है कि,
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
\(\frac{3}{2 k-1}=\frac{1}{k-1}\)
या 3(k – 1) = 1(2k– 1)
या 3k – 3 = 2k – 1
या 3k – 2k = -1 +3
या k = 2
अतः अभीष्ट मान k = 2 के लिए रैखिक समीकरण युग्म का कोई भी हल नहीं होगा।

प्रश्न 3.
निम्नलिखित रैखिक समीकरणों के युग्म को प्रतिस्थापन एवं वज्र-गुणन विधियों से हल कीजिए। किस विधि को आप अधिक उपयुक्त मानते हैं?
8x + 5y = 9
3r + 2y = 4
हल :
यहाँ पर
8x + 5y – 9 = 0 ………………..(i)
3x + 2y – 4 = 0 ………………….(ii)
प्रतिस्थापन विधि से हल करने के लिए समीकरण (i) से y = \(\frac{9-8 x}{5}\)
y = \(\frac{9-8 x}{5}\) को समीकरण (ii) में प्रतिस्थापित करने पर,
3x + 2(\(\frac{9-8 x}{5}\)) -4 = 0
या 15x + 2(9 – 8x) – 20 = 0 (दोनों ओर 5 से गुणा करने पर)
या 15x + 18 – 16x – 20 = 0
या -x – 2 = 0
या x = -2
x का मान समीकरण (i) में प्रतिस्थापित करने पर,
8(-2) + 5y – 9 = 0
या 5y = 9 + 16
या y =\(\frac{25}{5}\) = 5
अतः अभीष्ट हल x = -2 व y = 5

वज्र-गुणन विधि से हल करने के लिए-

अतः अभीष्ट हल x = -2 व y = 5
अतः वज्र-गुणन विधि अधिक उपयुक्त है।

प्रश्न 4.
निम्नलिखित समस्याओं में रैखिक समीकरणों के युग्म बनाइए और उनके हल (यदि उनका अस्तित्व हो) किसी बीजगणितीय विधि से ज्ञात कीजिए
(i) एक छात्रावास के मासिक व्यय का एक भाग नियत है तथा शेष इस पर निर्भर करता है कि छात्र ने कितने दिन भोजन लिया है। जब एक विद्यार्थी A को, जो 20 दिन भोजन करता है, 1000 रु० छात्रावास के व्यय के लिए अदा करने पड़ते हैं, जबकि एक विद्यार्थी B को, जो 26 दिन भोजन करता है छात्रावास के व्यय के लिए 1180 रु० अदा करने पड़ते हैं। नियत व्यय और प्रतिदिन के भोजन का मूल्य ज्ञात कीजिए।
(ii) एक भिन्न \(\frac{1}{3}\) हो जाती है, जब उसके अंश से 1 घटाया जाता है और वह \(\frac{1}{4}\) हो जाती है। जब हर में 8 जोड़ दिया जाता है। वह भिन्न ज्ञात कीजिए।
(iii) यश ने एक टेस्ट में 40 अंक अर्जित किए, जब उसे प्रत्येक सही उत्तर पर 3 अंक मिले तथा अशुद्ध उत्तर पर 1 अंक की कटौती की गई। यदि उसे सही उत्तर पर 4 अंक मिलते तथा अशुद्ध उत्तर पर 2 अंक कटते, तो यश 50 अंक अर्जित करता। टेस्ट में कितने प्रश्न थे?
(iv) एक राजमार्ग पर दो स्थान A और B, 100 km की दूरी पर हैं। एक कार A से तथा दूसरी कार B से एक ही समय चलना प्रारंभ करती है। यदि ये कारें भिन्न-भिन्न चालों से एक ही दिशा में चलती हैं, तो वे 5 घंटे पश्चात मिलती हैं और यदि ये विपरीत दिशा में चलती हैं तो वे 1 घंटे पश्चात् मिलती हैं। दोनों कारों की चाल ज्ञात कीजिए।
(v) एक आयत का क्षेत्रफल 9 वर्ग इकाई कम हो जाता है, यदि उसकी लंबाई 5 इकाई कम कर दी जाती है और चौड़ाई 3 इकाई बढ़ा दी जाती है। यदि हम लंबाई को 3 इकाई और चौड़ाई को 2 इकाई बढ़ा दें, तो क्षेत्रफल 67 वर्ग इकाई बढ़ जाता है। आयत की विमाएँ ज्ञात कीजिए।
हल :
(i) यहाँ पर
माना छात्रावास का मासिक नियत व्यय = x रु०
व छात्र के प्रतिदिन के भोजन का व्यय = y रु०
प्रश्नानुसार रैखिक समीकरण युग्म होंगे,
x + 20y = 1000 (विद्यार्थी A के लिए) …………….(i)
x + 26y = 1180 (विद्यार्थी B के लिए) ………..(ii)
समीकरण (ii) को समीकरण (i) में से घटाने पर

y का मान समीकरण (i) में प्रतिस्थापित करने पर,
x + 20(30) = 1000
x = 1000 – 600 = 400
अतः छात्रावास का मासिक नियत व्यय = 400 रु०
व छात्र के प्रतिदिन के भोजन का व्यय = 30 रु०

(ii) यहाँ पर
माना भिन्न = \(\frac{x}{y}\)
प्रश्नानुसार रैखिक समीकरण युग्म होंगे,
\(\frac{x-1}{y}=\frac{1}{3}\)
3x – 3 = y
3x – y = 3 …………………(i)
\(\frac{x}{y+8}=\frac{1}{4}\)
या 4x = y +8
या 4x -y = 8
समीकरण (ii) को समीकरण (i) में से घटाने पर,

या x = 5

x = 5 x का मान समीकरण (i) में प्रतिस्थापित करने पर,
3(5) – y = 3:
या -y = 3 – 15
या -y = – 12
या y = 12
अतः अभीष्ट भिन्न = \(\frac{5}{12}\)

(iii) यहाँ पर
माना यश के टेस्ट में सही उत्तरों की संख्या = x
व यश के टेस्ट में अशुद्ध उत्तरों की संख्या = y
प्रश्नानुसार रैखिक समीकरण युग्म होंगे,
3x – y = 40 ……………(i)
व 4x – 2y = 50
2x – y = 25
समीकरण (ii) को समीकरण (i) में से घटाने पर,

x का मान समीकरण (i) में प्रतिस्थापित करने पर,
3(15) – y = 40
या -y = 40 – 45
या -y = -5
या y = 5
अतः   प्रश्नों की कुल संख्या = x +y = 15 + 5 = 20

(iv) यहाँ पर
माना स्थान A से चलने वाली कार की चाल = u km/h
व स्थान B से चलने वाली कार की चाल = v km/h
स्थान A से चलने वाली कार द्वारा 5 घंटे व 1 घंटे में क्रमशः तय दूरी = 5u km व u km
स्थान B से चलने वाली कार द्वारा 5 घंटे व 1 घंटे में क्रमशः तय दूरी = 5v km व v km
प्रश्नानुसार रैखिक समीकरण युग्म होंगे,
5u – 5v = 100
या u – v = 20 (दोनों ओर 5 से भाग करने पर) …………..(i)
u + v = 100 …..(ii)
समीकरण (i) व समीकरण (ii) को जोड़ने पर
2u = 120
या u = \(\frac{120}{2}\) = 60
u का मान समीकरण (ii) में प्रतिस्थापित करने पर,
60 +v = 100
या v = 100 -60 = 40
अतः स्थान A से चलने वाली कार की चाल = 60 km/h
व स्थान B से चलने वाली कार की चाल = 40 km/h

(v).यहाँ पर
माना आयत की लंबाई = x इकाई
तथा आयत की चौड़ाई = y इकाई
तो आयत का क्षेत्रफल = xy वर्ग इकाई
प्रश्नानुसार रैखिक समीकरण युग्म होंगे, ..
(x -5) (y + 3) = xy – 9
या xy + 3x – 5y – 15 = xy – 9
या xy + 3x – 5y-xy = – 9 + 15
या 3x – 5y = 6 …………(i)
(x + 3) (y + 2) = xy + 67
या xy + 2x + 3y + 6 = xy + 67
या xy + 2x + 3y – xy = 67 – 6
या 2x + 3y = 61 …………..(ii)
समीकरण (i) को 3 से तथा समीकरण (ii) को 5 से गुणा करके परस्पर जोड़ने से,

या x = \(\frac{323}{19}\) = 17
x का मान समीकरण (ii) में प्रतिस्थापित करने पर,
2(17) + 3y = 61
या 3y = 61 – 34
या y = \(\frac{27}{3}\) = 9
अतः आयत की लंबाई = 17 इकाई
व आयत की चौड़ाई = 9 इकाई

Haryana State Board HBSE 10th Class Maths Solutions Chapter 3 दो चर वाले रैखिक समीकरण युग्म Ex 3.4 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 3 दो चर वाले रैखिक समीकरण युग्म Exercise 3.4

प्रश्न 1.
निम्नलिखित समीकरणों के युग्म को विलोपन विधि तथा प्रतिस्थापना विधि से हल कीजिए। कौन-सी विधि अधिक उपयुक्त है?
(i) x +y = 5 और 2x – 3y =4
(ii) 3x + 4y = 10 और 2x – 2y = 2
(iii) 3x – 5y – 4 = 0 और 9x = 2y + 7
(iv) \(\frac{x}{2}+\frac{2 y}{3}\) = -1 और x – \(\frac{y}{3}\) = 3
हल :
(i) यहाँ पर
x + y = 5 …………(i)
2x – 3y = 4 ………….(ii)

विलोपन विधि से हल
समीकरण (i) को 3 से गुणा करके समीकरण (ii) में जोड़ने पर प्राप्त होगा,

प्रतिस्थापन विधि से हल

समीकरण (i) से x = 5-y को समीकरण (ii) में प्रतिस्थापित करने पर,
2 (5-7)-3y = 4
या10 – 2y – 3y = 4
-5y = 4 – 10
या y = \(\frac{-6}{-5}=\frac{6}{5}\)
y का मान समीकरण (i) में प्रतिस्थापित करने पर,
x + \(\frac{6}{5}\) = 5
x = 5 – \(\frac{6}{5}=\frac{25-6}{5}=\frac{19}{5}\)
अतः अभीष्ट हल x = \(\frac{19}{5}\) y = \(\frac{6}{5}\)
दोनों ही विधियाँ उपयुक्त हैं।

(ii) यहाँ पर
3x + 4y = 10 ………..(i)
2x-2y = 2 …………..(ii)

विलोपन विधि से हल
समीकरण (ii) को 2 से गुणा करके समीकरण (i) में जोड़ने पर प्राप्त होगा,

या x = \(\frac{14}{7}\) = 2
‘x का मान समीकरण (i) में रखने पर,
3(2) +4y = 10
या 4y = 10-6
या y = 4/4 = 1
अतः अभीष्ट हल x = 2 व y = 1

प्रतिस्थापन विधि से हल
समीकरण (i) से x = \(\frac{10-4 y}{3}\)
x = \(\frac{10-4 y}{3}\) का मान समीकरण (ii) में रखने पर,
2 (\(\frac{10-4 y}{3}\)) -29 – 2
या 2 (10 -4y)- 6y = 6 (दोनों ओर 3 से गुणा करने पर)
या 20 – 8y – 6y = 6
या – 14y = 6 – 20
या y = -14/-14 = 1
y का मान समीकरण (1) में प्रतिस्थापित करने पर,
3x +4 (1) = 10
या 3x = 10 – 4
या x = \(\frac{6}{3}\) = 2
अतः अभीष्ट हल x = 2 व y = 1
दोनों ही विधियाँ उपयुक्त हैं।

(iii) यहाँ पर
3x – 5y – 4 = 0
या 3x – 5y = 4 ………….(i)
9x = 2y+7
या 9x – 2y = 7 …………(ii)

विलोपन विधि से हल

समीकरण (i) को 3 से गुणा करके उसमें से समीकरण (ii) घटाने पर,

प्रतिस्थापन विधि से हल
समीकरण (i) से x = \(\frac{4+5 y}{3}\)
x = \(\frac{4+5 y}{3}\) का मान समीकरण (ii) में प्रतिस्थापित करने पर,
9 (\(\frac{4+5 y}{3}\)) – 2y = 7
3 (4 + 5y) – 2y = 7
12 + 15y – 2y = 7
13y = 7 – 12
y = \(\frac{-5}{13}\)
y का मान समीकरण (i) में प्रतिस्थापित करने पर,

अतः अभीष्ट हल x = \(\frac{9}{13}\) व y = \(\frac{-5}{13}\)
दोनों ही विधियाँ उपयुक्त हैं।

(iv) यहाँ पर
\(\frac{x}{2}+\frac{2 y}{3}\) = -1
या 3x +4y = – 6 (दोनों ओर 6 से गुणा करने पर) …………..(i)
तथा x – \(\frac{y}{3}\) = 3
3x – y = 9 (दोनों ओर 3 से गुणा करने पर)

विलोपन विधि से हल

क्योंकि समीकरण (i) व (ii) में x के गुणांक समान हैं इसलिए समीकरण (ii) को समीकरण (i) में से घटाने पर,

या y = \(\frac{-15}{5}\) = -3
y का मान समीकरण (i) में रखने पर,
3x +4(- 3) = -6
या 3x= -6 + 12
या x = 6/3 = 2
अतः अभीष्ट हल x = 2 व y = – 3

प्रतिस्थापन विधि से हल
समीकरण (ii) से x = \(\frac{9+y}{3}\)
x = \(\frac{9+y}{3}\) को समीकरण (1) में प्रतिस्थापित करने पर,
3(\(\frac{9+y}{3}\)) +4y = – 6
9 + y + 4y = -6
5y = -6-9
y = \(\frac{-15}{5}\) =-3
y का मान समीकरण (1) में प्रतिस्थापित करने पर,
3x +4 (-3) = -6
3x = -6+ 12.
x = \(\frac{6}{3}\) = 2
अतः अभीष्ट हल x = 2 व y = -3
दोनों ही विधियाँ उपयुक्त हैं।

प्रश्न 2.
निम्नलिखित समस्याओं में रैखिक समीकरणों के युग्म बनाइए और उनके हल (यदि उनका अस्तित्व हो) विलोपन विधि से ज्ञात कीजिए-
(i) यदि हम अंश में 1 जोड़ दें तथा हर में से 1 घटा दें, तो भिन्न 1 में बदल जाती है। यदि हर में 1 जोड़ दें, तो यह 1/2 हो जाती है। वह भिन्न क्या है?
(ii) पाँच वर्ष पूर्व नूरी की आयु सोनू की आयु की तीन गुनी थी। दस वर्ष पश्चात्, नूरी की आयु सोनू की आयु की दो गुनी हो जाएगी। नूरी और सोनू की आयु कितनी है?
(iii) दो अंकों की संख्या के अंकों का योग 9 है। इस संख्या का नौ गुना, संख्या के अंकों को पलटने से बनी संख्या का दो गुना है। वह संख्या ज्ञात कीजिए।
(iv) मीना 2000 रु० निकालने के लिए एक बैंक गई। उसने खजाँची से 50 रु० तथा 100 रु० के नोट देने के लिए कहा। मीना ने कुल 25 नोट प्राप्त किए। ज्ञात कीजिए कि उसने 50 रु० और 100 रु० के कितने-कितने नोट प्राप्त किए?
(v) किराए पर पुस्तकें देने वाले किसी पुस्तकालय का प्रथम तीन दिनों का एक नियत किराया है तथा उसके बाद प्रत्येक अतिरिक्त दिन का अलग किराया है। सरिता ने सात दिनों तक एक पुस्तक रखने के लिए 27 रु० अदा किए, जबकि सूसी ने एक पुस्तक पाँच दिनों तक रखने के 21 रु० अदा किए। नियत किराया तथा प्रत्येक अतिरिक्त दिन का किराया ज्ञात कीजिए।
हल :
(i), यहाँ पर
माना भिन्न = \(\frac{x}{y}\),
प्रश्नानुसार रैखिक समीकरण होगी, \(\frac{x+1}{y-1}\) = 1
x +1 = y-1
x – y = -1 – 1
x – y = -2 …………..(i)
\(\frac{x}{y+1}=\frac{1}{2}\)
या 2x = y +1
2x -y = 1 …….(ii)
समीकरण (ii) को समीकरण (i) में से घटाने पर,

या x = 3
x का मान समीकरण (i) में रखने पर,
3-y = – 2
या -y = -2 – 3
या -y = -5
या y = 5
अतः अभीष्ट भिन्न = \(\frac{3}{5}\)

(ii) यहाँ पर
माना नूरी की वर्तमान आयु = x वर्ष
व सोनू की वर्तमान आयु = y वर्ष
प्रश्नानुसार रैखिक समीकरण होगी, x-5 = 3 (y-5)
x-5 = 3y- 15
या x – 3y = – 15 +5
या 3y = – 10
तथा x+ 10 = 2 (y + 10)
या x + 10 = 2y + 20
या x – 2y = 20 – 10
या x – 2y = 10
समीकरण (ii) को समीकरण (i) में से घटाने पर,

या y = 20
y का मान समीकरण (i) में रखने पर,
x – 3 (20) = – 10
x = – 10 + 60
x = 50
अतः नूरी की वर्तमान आयु = 50 वर्ष
व सोनू की वर्तमान आयु = 20 वर्ष

(iii) यहाँ पर
माना दो अंकों की संख्या की इकाई का अंक = x
व दो अंकों की संख्या की दहाई का अंक = y
संख्या = x + 10y
अंक पलटने पर प्राप्त संख्या = 10x +y
प्रश्नानुसार रैखिक समीकरण होगी, xy = 9
तथा 9 (x + 10y) = 2 (10x + y)
या 9x + 90y = 20x +2y
या 20x – 9x +2y – 90y = 0
या 11x – 88y = 0
या x – 8y = 0 (दोनों ओर 11 से भाग करने पर)
समीकरण (ii) को समीकरण (i) में से घटाने पर,

या y = 9/9
y = 1
y का मान समीकरण (i) में रखने पर,
x + 1 = 9
x = 9-1 = 8
अतः अभीष्ट संख्या = x + 10y = 8 + 10 (1) = 18

(iv) यहाँ पर
माना 50 रु० वाले नोटों की संख्या = x
व 100 रु० वाले नोटों की संख्या = y
प्रश्नानुसार रैखिक समीकरण होगी x + y = 25
व 50x + 100y = 2000
या x + 2y = 40 (दोनों ओर 50 से भाग देने पर)
समीकरण (ii) को समीकरण (i) में से घटाने पर,

या y = 15
y का मान समीकरण (i) में रखने पर,
x+ 15 = 25
x = 25 – 15 = 10
अतः 50 रु० वाले नोटों की संख्या = 10
व 100 रु० वाले नोटों की संख्या = 15

(v) यहाँ पर
माना पुस्तक का प्रथम 3 दिन का नियत किराया = x रु०
व पुस्तक का प्रत्येक अतिरिक्त दिन का किराया = y रु०
प्रश्नानुसार रैखिक समीकरण होगी, x +4y = 27 (सरिता के लिए) ………….(i)
व x + 2y = 21(सूसी के लिए) ……………(ii)
समीकरण (ii) को समीकरण (1) में से घटाने पर,

2y = 6
y = 6/2
y = 3
y का मान समीकरण (i) में रखने पर,
x +4 (3) = 27 या
या x = 27-12 = 15
x = 15
अतः पुस्तक का प्रथम 3 दिन का नियत किराया = 15 रु०
पुस्तक का प्रत्येक अतिरिक्त दिन का किराया = 3 रु०

Haryana State Board HBSE 10th Class Sanskrit Solutions Shemushi Chapter 11 प्राणेभ्योऽपि प्रियः सुहृदः Textbook Exercise Questions and Answers.

Haryana Board 10th Class Sanskrit Solutions Shemushi Chapter 11 प्राणेभ्योऽपि प्रियः सुहृदः

HBSE 10th Class Sanskrit प्राणेभ्योऽपि प्रियः सुहृदः Textbook Questions and Answers

प्रश्न 1.
अधोलिखितप्रश्नानाम् उत्तराणि संस्कृतभाषया लिखत
(अधोलिखित प्रश्नों के उत्तर संस्कृतभाषा में लिखिए-)
(i) चन्दनदासः कस्य गृहजनं स्वगृहे रक्षति स्म ?
(ii) तृणानां केन सह विरोधः अस्ति ?
(iii) कः चन्दनदासं द्रष्टुमिच्छति ?
(iv) पाठेऽस्मिन् चन्दनदासस्य तुलना केन सह कृता ?
(v) प्रीताभ्यः प्रकृतिभ्यः प्रतिप्रियं के इच्छन्ति ?
(vi) कस्य प्रसादेन चन्दनदासस्य वणिज्या अखण्डिता ?
उत्तराणि:
(i) चन्दनदासः अमात्यराक्षसस्य गृहजनं स्वगृहे रक्षति स्म।
(ii) तृणानानाम् अग्निना सह विरोधः अस्ति।
(iii) चाणक्यः चन्दनदासं द्रष्टुमिच्छति।
(iv) पाठेऽस्मिन् चन्दनदासस्य तुलना शिविना सह कृता।
(v) प्रीताभ्यः प्रकृतिभ्यः प्रतिप्रियं राजानः इच्छन्ति।
(vi) आर्यस्य प्रसादेन चन्दनदासस्य वणिज्या अखण्डिता।

प्रश्न 2.
स्थूलाक्षरपदानि आधृत्य प्रश्ननिर्माणं कुरुत(स्थूलपदों के आधार पर प्रश्ननिर्माण कीजिए-)
(i) शिविना विना इदं दुष्करं कार्यं कः कुर्यात्।
(ii) प्राणेभ्योऽपि प्रियः सुहृत्।।
(ii) आर्यस्य प्रसादेन मे वणिज्या अखण्डिता।
(iv) प्रीताभ्यः प्रकृतिभ्यः राजानः प्रतिप्रियमिच्छन्ति।
(v) तृणानाम् अग्निना सह विरोधो भवति।
उत्तराणि-(प्रश्ननिर्माणम्)
(i) केन विना इदं दुष्करं कार्यं कः कुर्यात् ?
(ii) प्राणेभ्योऽपि प्रियः कः ?
(iii) कस्य प्रसादेन मे वणिज्या अखण्डिता ?
(iv) प्रीताभ्यः प्रकृतिभ्यः के प्रतिप्रियमिच्छन्ति ?
(v) केषाम् अग्निना सह विरोधो भवति ?

प्रश्न 3.
निर्देशानुसारं सन्धिं/सन्धिविच्छेदं कुरुत
(निर्देशानुसार सन्धि/सन्धिविच्छेद कीजिए-)
(क) यथा- कः + अपि – कोऽपि
प्राणेभ्यः + अपि – …………….
…………….. + अस्मि – सज्जोऽस्मि।
आत्मनः + …………….. – आत्मनोऽधिकारसदृशम्
(ख) यथा- सत् + चित् – सच्चित्
शरत् + चन्द्रः – कदाचित् + च
उत्तराणि
(क) यथा- कः + अपि – कोऽपि
प्राणेभ्यः + अपि – प्राणेभ्योऽपि
सज्जः + अस्मि – सज्जोऽस्मि।
आत्मनः + अधिकारसदृशम् – आत्मनोऽधिकारसदृशम्
(ख) यथा-. सत् + चित्
सच्चित् शरत् + चन्द्रः – शरच्चन्द्रः
कदाचित् + च – कदाचिच्च।

प्रश्न 4.
अधोलिखितवाक्येषु निर्देशानुसारं परिवर्तनं कुरुत
(अधोलिखित वाक्यों में निर्देश के अनुसार परिवर्तन कीजिए-)
यथा-प्रतिप्रियमिच्छन्ति राजानः। प्रतिप्रियमिच्छति राजा। (एकवचने)
(i) सः प्रकृतेः शोभां पश्यति (बहुवचने)
(ii) अहं न जानामि। (मध्यमपुरुषैकवचने)
(iii) त्वं कस्य गृहजनं स्वगृहे रक्षसि ? (उत्तमपुरुषैकवचने)
(iv) कः इदं दुष्करं कुर्यात् ? (प्रथमपुरुषैबहुवचने)
(v) चन्दनदासं द्रष्टुमिच्छामि। (प्रथमपुरुषैकवचने)
(vi) राजपुरुषाः देशान्तरं व्रजन्ति। (प्रथमपुरुषैकवचने)
उत्तराणि
(i) ते प्रकृतेः शोभां पश्यन्ति।
(ii) त्वं न जानासि।
(iii) अहं कस्य गृहजनं स्वगृहे रक्षामि ?
(iv) के इदं दुष्करं कुर्युः ?
(v) चन्दनदासं द्रष्टुमिच्छति।
(vi) राजपुरुषः देशान्तरं व्रजति।

प्रश्न 5.
कोष्ठकेषु दत्तयोः पदयोः शुद्धं विकल्पं विचित्य रिक्तस्थानानि पूरयत
(कोष्ठक में दिए गए पदों में से शुद्ध विकल्प चुन कर रिक्तस्थानों की पूर्ति कीजिए-)
(i) ……….. विना इदं दुष्करं कः कुर्यात्। (चन्दनदासस्य / चन्दनदासेन)
(ii) …………… इदं वृत्तान्तं निवेदयामि। (गुरवे / गुरोः)
(ii) आर्यस्य ………… अखण्डिता मे वणिज्या। (प्रसादात् / प्रसादेन)
(iv) अलम् ………..। (कलहेन / कहलात्)
(v) वीरः ………. बालं रक्षति। (सिंहेन / सिंहात्)
(vi) ………… भीतः मम भ्राता सोपानात् अपतत्। (कुक्कुरेण / कुक्कुरात्)
(vii) छात्रः …………….. प्रश्नं पृच्छति। (आचार्यम् / आचार्येण)
उत्तराणि
(i) चन्दनदासेन विना इदं दुष्करं कः कुर्यात् ।
(ii) गुरवे इदं वृत्तान्तं निवेदयामि।
(iii) आर्यस्य प्रसादेन अखण्डिता मे वणिज्या।
(iv) अलं कलहेन।
(v) वीरः सिंहात् बालं रक्षति।
(vi) कुक्कुरात् भीतः मम भ्राता सोपानात् अपतत्।
(vii) छात्रः आचार्य प्रश्नं पृच्छति।।

प्रश्न 6.
अधोदत्तमञ्जूषातः समुचितपदानि गृहीत्वा विलोमपदानि लिखत
(नाचे दी गई मञ्जूषा से समुचित पद लेकर विलोम पद लिखिए-)
आदरः असत्यम् गुणः पश्चात् तदानीम् तत्र
(i) अनादरः ………………………………..
(ii) दोषः ………………………………..
(iii) पूर्वम् ………………………………..
(iv) सत्यम् ………………………………..
(v) इदानीम् ………………………………..
(vi) अत्र ………………………………..
उत्तराणि
(i) अनादरः – आदरः
(ii) दोषः – गुणः
(iii) पूर्वम् – पश्चात्
(iv) सत्यम् – असत्यम्
(v) इदानीम् – तदानीम्
(vi) अत्र – तत्र

प्रश्न 7.
उदाहरणमनुसृत्य अधोलिखितानि पदानि प्रयुज्य पञ्चवाक्यानि रचयत
(उदाहरण के अनुसार अधोलिखित पदों का प्रयोग करके पाँच वाक्य बनाइए-)
यथा निष्क्रम्य- शिक्षिका पुस्तकालयात् निष्क्रम्य कक्षां प्रविशति।
(i) उपसृत्य ………………………………..
(ii) प्रविश्य ………………………………..
(iii) द्रष्टुम् ………………………………..
(iv) इदानीम् ………………………………..
(v) अत्र ………………………………..
उत्तराणि-(वाक्यप्रयोगः)
(i) उपसृत्य – बालक: मातरम् उपसृत्य प्रणमति।
(ii) प्रविश्य – बालकाः उद्याने प्रविश्य क्रीडन्ति।
(iii) द्रष्टुम् – त्वं किं द्रष्टुम् इच्छसि ?
(iv), इदानीम् – इदानीम् अहं चलचित्रं द्रष्टुम् इच्छामि।
(v) अत्र – अत्र चलचित्रगृहं नास्ति।

योग्यताविस्तारः
कविपरिचयः’मुद्राराक्षसम्’ इति नाम्नः नाटकस्य प्रणेता विशाखदत्तः आसीत्। सः राजवंशे उत्पन्नः आसीत्। तस्य पिता भास्करदत्तः महाराजस्य पदवी प्राप्नोत्। विशाखदत्तः राजनीतेः न्यायस्य ज्योतिषविषयस्य च विद्वान् आसीत्। वैदिकधर्मावलम्बी भूत्वाऽपि सः बौद्धधर्मस्य अपि आदरमकरोत्।

कवि परिचय-‘मुद्राराक्षसम्’ इस नाम के नाटक के रचयिता विशाखदत्त थे। वे राजवंश में उत्पन्न हुए थे। उनके पिता भास्करदत्त ने महाराज की पदवी प्राप्त की थी। विशाखदत्त राजनीति, न्याय और ज्योतिष विषय के विद्वान् थे। वैदिक धर्मावलम्बी होकर भी वे बौद्धधर्म का भी आदर करते थे।

ग्रन्थपरिचयः- ‘मुद्राराक्षसम्’ एकम् ऐतिहासिकं नाटकम् अस्ति। दशाङ्केषु विरचिते अस्मिन्नाटके चाणक्यस्य राजनीतिककौशलस्य बुद्धिवैभवस्य राष्ट्रसञ्चालनार्थम् कूटनीतीनाम् निदर्शनमस्ति। अस्मिन्नाटके चाणक्यस्यामात्यराक्षसस्य च कूटनीत्योः संघर्षः।

‘मुदाराक्षसम्’ एक ऐतिहासिक नाटक है। दश अंकों में रचित इस नाटक में चाणक्य के राजनीतिक कौशल, बुद्धि वैभव और राष्ट्र संचालन के लिए उनकी कूटनीतियों का निदर्शन है। इस नाटक में चाणक्य और अमात्य राक्षस की कूटनीतियों का संघर्ष है।

भावविस्तार:
चाणक्य-चाणक्यः एकः विद्वान् ब्राह्मणः आसीत्। तस्य पितृप्रदत्तं नाम विष्णुगुप्तः आसीत्। अयमेव ‘कौटिल्य’ इति नाम्ना प्रसिद्धः केषाञ्चित् विदुषाम् इदमपि मतमस्ति यत् राजनीतिशास्त्रे कुटिलनीतेः प्रतिष्ठापनाय तस्याः स्व-जीवने उपयोगाय च अयं ‘कौटिल्यः’ इत्यपि कथ्यते। चणकनामकस्य कस्यचित् आचार्यस्य पुत्रत्वात् ‘चाणक्यः’ इति नाम्ना स प्रसिद्धः जातः । नन्दानां राज्यकालः शतवर्षाणि पर्यन्तम् आसीत्। तेषु अन्तिमेषु द्वादशवर्षे एतेन सुमाल्यादीनाम् अष्टनन्दानां संहारः कारितः तथा च चन्द्रगुप्तमौर्यः नृपत्वेन राजसिंहासने स्थापितः। अयमेकः महान् राजनीतिज्ञः आसीत्। एतेन भारतीयशासनव्यवस्थायाः प्रामाणिकतत्त्वानां वर्णनेन युक्तं “अर्थशास्त्रम्” इति अतिमहत्त्वपूर्णः ग्रन्थः रचितः।

चन्द्रगुप्तमौर्यः-चन्द्रगुप्तः महापद्मनन्दस्य मुरायाः च पुत्रः आसीत्। चाणक्यस्य मार्गदर्शने अनेन चतुर्विंशतिवर्षपर्यन्तं राज्यं कृतम्।। राक्षसः-नन्दराज्ञः स्वामिभक्तः चतुरः प्रधानामात्यः आसीत्। चन्दनदासः-कुसुमपुर-नाम्नि नगरे महामात्यस्य राक्षसस्य प्रियतमं पात्रं मित्रञ्च आसीत्। स मणिकारः श्रेष्ठी च आसीत्। अस्यैव गृहात् राक्षसः सपरिवार: नगरात् बहिरगच्छत्।
चाणक्य-चाणक्य एक विद्वान ब्राह्मण था। उसके पिता द्वारा दिया गया नाम विष्णुगुप्त था। यह ही कौटिल्य इस नाम से प्रसिद्ध हुआ। कुछ विद्वानों का यह भी मत है कि राजनीति शास्त्र में कूटनीति की प्रतिष्ठापना के लिए और उसका अपने जीवन में उपयोग करने के लिए इन्हें ‘कौटिल्य’ कहा जाता है।

चणक नामक किसी आचार्य का पुत्र होने के कारण वे ‘चाणक्य’ इस नाम से प्रसिद्ध हुए। नन्दों का राज्य काल 100 वर्षों तक रहा। उनमें अन्तिम 12 वर्षों में इन (चाणक्य) के द्वारा सुमाल्य आदि आठ नन्दों का विनाश करवाया गया और चन्द्रगुप्त मौर्य को राजा के रूप में राजसिंहासन पर बैठाया गया। ये एक महान् राजनीतिज्ञ थे। इन्होंने भारतीय शासन व्यवस्था का प्रामाणिक तत्त्वों के वर्णन से युक्त अर्थशास्त्र नामक अत्यन्त महत्त्वपूर्ण ग्रन्थ की रचना की। चन्द्रगुप्त मौर्य-चन्द्रगुप्त महापद्मनन्द और मुरा का पुत्र था। चाणक्य के मार्गदर्शन में इसने 24 वर्ष तक राज्य किया।
राक्षस-राजा नन्द का स्वामीभक्त चतुर प्रधान अमात्य था। चन्दनदास-कुसुमपुर नामक नगर में महामात्य राक्षस का सबसे प्रिय पात्र और मित्र था। वह सुवर्णकार और सेठ था। इसी के घर से राक्षस परिवार सहित नगर से बाहर गया था।

भाषिक विस्तारः
1. पृथक् और विना शब्दों के योग में द्वितीया तृतीया और पंचमी तीनों विभक्तियों का प्रयोग
यथा-जलं विना जीवनं न सम्भवति। द्वितीया
जलेन विना जीवनं न सम्भवति । तृतीया
जलात् विना जीवनं न सम्भवति। पञ्चमी
परिश्रमं पृथक् नास्ति सुखम्। द्वितीया
परिश्रमात् पृथक् नास्ति सुखम्। पञ्चमी

2. अनीयर् प्रत्ययप्रयोगः
अत्यादरः – शङ्कनीयः
जन्तुशाला – दर्शनीया
याचकेभ्यः दानं – दानीयम्
वेदमन्त्राः – स्मरणीयाः
पुस्तकमेलापके पुस्तकानि – क्रयणीयानि।
(क) अनीयर् प्रत्ययस्य प्रयोगः योग्यार्थे भवति।
(ख) अनीयर् प्रत्यये ‘अनीय’ इति अवशिष्यते।
(ग) अस्य रूपाणि त्रिषु लिङ्गेषु चलन्ति।
यथा-
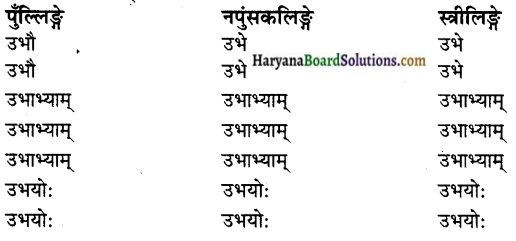
पुंल्लिङ्गे स्त्रीलिङ्गे नपुंसकलिङ्गे
पठनीयः पठनीया पठनीयम्
इनके रूप क्रमशः देववत्, लतावत् तथा फलवत् चलेंगे।

3. उभ सर्वनामपदम् पुल्लिङ्गे नपुंसकलिङ्गे

HBSE 10th Class Sanskrit प्राणेभ्योऽपि प्रियः सुहृदः Important Questions and Answers

प्रश्न 1.
अधोलिखितानां वाक्यानां/सूक्तीनां भावार्थं हिन्दीभाषायां लिखत
(अधोलिखित वाक्यों/सूक्तियों के भावार्थ हिन्दीभाषा में लिखिए-)
(क) अत्यादरः शङ्कनीयः’।
(अत्यधिक आदर सन्देह पैदा करता है)
भावार्थ :-‘अत्यादरः शङ्कनीयः’ यह सूक्ति हमारी पाठ्यपुस्तक ‘शेमुषी भाग-2’ में संकलित ‘प्राणेभ्योऽपि प्रियः सुहृद्’ पाठ से उद्धृत की गयी है। यह पाठ महाकवि विशाखदत्त के ‘मुद्राराक्षसम्’ नाटक से लिया गया है। उपर्युक्त सूक्ति में अत्यधिक आदर को सन्देह का कारण बतलाया गया है।
इस सूक्ति का भावार्थ यह है कि यदि कोई व्यक्ति बिना कारण आपके प्रति अत्यधिक आदर प्रदर्शित करता है या जो व्यक्ति अब तक आपके प्रति तटस्थ या शत्रुतापूर्ण व्यवहार करता था और अब अचानक अतीव आदर प्रदर्शित करने लगा है तो समझ लो कि दाल में कुछ काला है। अर्थात् आदर प्रदर्शित करने वाला व्यक्ति कोई न कोई चाल चलने वाला है। पाठ में जब चाणक्य अपने शत्रु (राक्षस) के मित्र चन्दनदास के प्रति अतीव आदरपूर्ण व्यवहार करने लगता है तब चन्दनदास यह कहता है कि चाणक्य में एकाएक आया यह परिवर्तन अवश्य ही इनकी कोई कपटी चाल का हिस्सा है।
भाव यह कि हमें अचानक अत्यधिक आदर करने वाले व्यक्ति के प्रति सचेत होकर रहना चाहिए।

(ख) प्रीताभ्यः प्रकृतिभ्यः प्रतिप्रियमिच्छन्ति राजानः।
(प्रसन्न हुई प्रजाओं से राजा लोग बदले में अपना हित भी करवाना चाहता है)
भावार्थ :-उपर्युक्त सूक्ति हमारी पाठ्यपुस्तक ‘शेमुषी भाग-2’ में संकलित ‘प्राणेभ्योऽपि प्रियः सुहृद्’ पाठ से उद्धृत की गयी है। यह पाठ महाकवि विशाखदत्त के नाटक ‘मुद्राराक्षसम्’ से संकलित है। सूक्ति में राजा और प्रजा के पारस्परिक सम्बन्धों के विषय में बतलाया गया है।
प्रदत्त सूक्ति का भाव यह है कि राजा अपनी प्रजाओं की हर प्रकार की रक्षा करता है और यदि प्रजाएँ राजा के प्रशासन से सर्वथा प्रसन्न हैं तो राजा भी यह आशा करता है कि प्रजायें भी राजा की इच्छा के अनुसार कार्य करें। पाठ में चाणक्य चन्दनदास से पूछता है कि क्या आपका व्यापार ठीक चल रहा है। चन्दनदास कहता है कि बिल्कुल ठीक चल रहा है। चन्द्रगुप्त मौर्य के राज्य में हमें कोई कठिनाई नहीं है। चाणक्य कहता है कि यदि आप उनके प्रशासन से प्रसन्न हैं; तो आप भी राजा का कुछ हित कीजिए। अर्थात् राजा नन्द के मन्त्री राक्षस के जो परिवार चन्दनदास के पास रह रहा है; वह उस परिवार को वर्तमान के राजा चन्द्रगुप्त मौर्य को सौंप दे।
भाव यह कि राजा और प्रजा का पारस्परिक सम्बन्ध उपकार एवं प्रत्युपकार “Give and take” पर आधारित होता है।

कीदृशस्तृणानामग्निना सह विरोधः।
प्रसंग :-“कीदृशस्तृणानामग्निना सह विरोधः” यह सूक्ति हमारी संस्कृत की पाठ्यपुस्तक “शेमुषी भाग-2′ में मुद्राराक्षस नाटक से संकलित पाठ “प्राणेभ्योऽपि प्रियः सुहृद्” से उद्धृत की गयी है। इसमें बड़ों के साथ छोटे कैसे शत्रुता मोल ले सकते हैं; इस तथ्य को प्रकट किया गया है।
सरलार्थ :-तिनकों का अग्नि के साथ विरोध सम्भव नहीं है।
भावार्थ :-ऊपर लिखित सक्ति का भावार्थ यह है कि बड़े छोटों से वैर करें यह तो समझ आ जाता है क्योंकि ऐसा करने पर वे उन्हें सजा आदि देने का सामर्थ्य रखते हैं; परन्तु छोटे बड़ों के साथ वैर या द्वेष रखें यह सम्भव नहीं है क्योंकि उनके पास बड़ों को दण्डित करने का सामर्थ्य नहीं होता है। पाठ में चाणक्य चन्दनदास को कहता है कि आप राजा अर्थात् चन्द्रगुप्त मौर्य का विरोध करना छोड़ दो तब चन्दनदास कहता है कि आप यह क्या कह रहे हैं; मैं राजा का विरोध क्यों करूँगा क्योंकि क्या कभी तिनके अग्नि का विरोध कर सकते हैं अर्थात् कभी नहीं।
अतः जहाँ सूर्य को दीपक दिखाने जैसी बात हो या दो पक्षों में बहुत बड़ा अन्तर हो वहाँ उपर्युक्त सूक्ति का प्रयोग किया जाता है।

(ग) शिरसि भयम् अतिदूरं प्रतिकारः।
(चाणक्य चन्दनदास को धमकी देते हुए कहता है कि-भय आपके सिर पर मण्डरा रहा है और उसका उपाय बहुत दूर है)
भावार्थ :-‘शिरसि भयम् अतिदूरे प्रतिकारः’ यह सूक्ति हमारी संस्कृत की पाठ्यपुस्तक ‘शेमुषी भाग-2’ में संकलित पाठ ‘प्राणेभ्योऽपि प्रियः सुहृद्’ पाठ से उद्धृत की गयी है। इसमें अप्रस्तुत की अपेक्षा प्रस्तुत से लाभ उठाने की बात कही गयी है।
सूक्ति का भावार्थ यह है कि चन्दनदास तुम जिस व्यक्ति (मन्त्री राक्षस) के लिए कार्य कर रहे हो; वह यहाँ नहीं है और आपकी इस समय कोई सहायता भी नहीं कर सकता है जबकि यदि तुम अपने घर पर छुपे हुए मन्त्री के परिवार को हमें सौंप देते हो तो हम आपको सजा देने की अपेक्षा पुरस्कृत भी कर सकते हैं। अब आप निर्णय करो कि वर्तमान का लाभ उठाना है या भविष्य के साथ चिपके रहना है। इस सूक्ति का प्रयोग वर्तमान और भविष्य में से एक का चुनाव करने के विकल्प के रूप में किया जाता है।

सुलभेष्वर्थलाभेषु परसंवेदने जने ।
क इदं दुष्करं कुर्यादिदानीं शिविना विना ॥

प्रसंग :-उपर्युक्त सूक्ति हमारी संस्कृत की पाठ्यपुस्तक ‘शेमुषी भाग-2’ में मुद्राराक्षस नाटक से उद्धृत पाठ ‘प्राणेभ्योऽपि प्रियः सुहृद्’ से ली गयी है। इसमें चन्दनदास की मित्र के प्रति निष्ठा को देखकर उसकी प्रशंसा में कहता है कि आपने तो परोपकार में राजा शिवि की भान्ति आदर्श प्रस्तुत कर दिया।
सरलार्थ :-चाणक्य चन्दनदास की मित्र के प्रति निष्ठा को देखकर कहता है कि-दूसरों की वस्तु के समर्पित करने पर बहुत धन प्राप्त होने की स्थिति में भी दूसरों की वस्तु के सुरक्षा रूपी कठिन कार्य को ‘शिवि’ को छोड़कर तुम्हारे अतिरिक्त दूसरा कौन कर सकता है।
भावार्थ :-ऊपर लिखित सूक्ति का भाव यह है कि धन लोभ का त्याग करके भी धरोहर की रक्षा करना किसी विरले ही महापुरुष के वश की बात होती है। चाणक्य कहता है कि चन्दनदास मन्त्री राक्षस के परिवार को चन्द्रगुप्त मौर्य को सौंप देने पर आप धन और पद की प्राप्ति कर सकते हैं तथापि आप अपनी धरोहर की रक्षा के प्रति वचनबद्ध हैं। ऐसी निष्ठा या तो हमने शिवि द्वारा कबूतर रक्षण में देखी थी या फिर आज आप में देख रहे हैं।
संसार में ऐसे लोग भी विद्यमान हैं जो सब कुछ त्याग कर भी अपने वचन पर अडिग रहते हैं।

प्रश्न 2.
स्थूलपदानि आधृत्य प्रश्ननिर्माणं कुरुत
(स्थूलपदों के आधार पर प्रश्ननिर्माण कीजिए-)
(क) अत्यादरः शङ्कनीयः।
(ख) प्रीताभ्यः प्रकृतिभ्यः प्रतिप्रियमिच्छन्ति राजानः।
(ग) राजनि अविरुद्धवृत्तिर्भव।
(घ) सन्तमपि गेहे अमात्यराक्षस्य गृहजनं न समर्पयामि।
(ङ) नन्दस्यैव अर्थसम्बन्धः प्रीतिम् उत्पादयति।
उत्तराणि-(प्रश्ननिर्माणम्)
(क) अत्यादरः कीदृशः?
(ख) प्रीताभ्यः प्रकृतिभ्यः प्रतिप्रियमिच्छन्ति के?
(ग) कस्मिन् अविरुद्धवृत्तिर्भव?
(घ) सन्तमपि गेहे कस्य गृहजनं न समर्पयामि?
(ङ) नन्दस्यैव अर्थसम्बन्धः किम् उत्पादयति?

प्रश्न 3.
अधोलिखित-प्रश्नानां प्रदत्तोत्तरविकल्पेषु शुद्धं विकल्पं विचित्य लिखत
(अधोलिखित प्रश्नों के उत्तर के लिए दिए गए विकल्पों में से शुद्ध विकल्प चुनकर लिखिए-)
(क) ‘कदाचिच्च’ पदस्य सन्धिविच्छेदोऽस्ति
(i) कदाचित् + च
(ii) कदाचिच् + च
(iii) कदा + चिच्च
(iv) कदाचित + च।
उत्तरम्:
(i) कदाचित् + च।

(ख) ‘प्राणेभ्यः + अपि’ अत्र सन्धियुक्तपदम्
(i) प्राणेभ्योरपि
(ii) प्राणेभ्योऽअपि
(iii) प्राणेभ्योष्वपि
(iv) प्राणेभ्योऽपि।
उत्तरम्:
(iv) प्राणेभ्योऽपि।

(ग) ‘गृहजनम्’ अस्मिन् पदे कः समासोऽस्ति ?
(i) बहुव्रीहिः
(ii) तत्पुरुषः
(ii) अव्ययीभावः
(iv) द्वन्द्वः ।
उत्तरम्:
(ii) तत्पुरुषः

(घ) ‘अपरिक्लेशः’ इति पदस्य समास-विग्रहः
(i) अपरः क्लेशः
(ii) क्लेशम् अनतिक्रम्य
(iii) न परिक्लेशः
(iv) अपरिहार्यः क्लेशः।
उत्तरम्:
(iii) न परिक्लेशः

(ङ) ‘द्रष्टुम्’ इति पदे कः प्रत्ययः ?
(i) त्व
(ii) तल्
(iii) तुमुन्
(iv) क्ता।
उत्तरम्:
(iii) तुमुन्

(च) ………. प्रचीयन्ते संव्यवहारणां वृद्धिलाभाः ?
(रिक्तस्थानपूर्तिः अव्ययपदेन)
(i) अपि
(ii) ह्यः
(iii) न
(iv) च।
उत्तरम्:
(i) अपि

(छ) मम विद्यालये ……… प्रमुखं प्रवेशद्वारम् अस्ति।
(रिक्तस्थानपूर्तिः उचितसंख्यापदेन)
(i) एकम्
(ii) एका
(iii) चतस्रः
(iv) शताधिकम्।
उत्तरम्:
(i) एकम्।

(ज) आर्यस्य प्रसादेन कस्य वणिज्या अखण्डिता ?
(i) अमात्यराक्षसस्य
(ii) चाणक्यस्य
(iii) चन्दनदासस्य
(iv) चन्द्रगुप्तस्य।
उत्तरम्
(iii) चन्दनदासस्य।

(झ) तृणानां केन सह विरोधः भवति ?
(i) जलेन
(ii) अग्निना
(iii) वायुना
(iv) पशुना।
उत्तरम्:
(i) अग्निना

(ज) ‘आर्येण’ अत्र का विभक्तिः प्रयुक्ता ?
(i) प्रथमा
(ii) सप्तमी
(iii) तृतीया
(iv) चतुर्थी।
उत्तरम्:
(iii) तृतीया।

यथानिर्देशम् उत्तरत
(ट) ‘भीताः’ इति पदस्य प्रकृति-प्रत्ययौ लिखत।
(ठ) ‘ननु भवता प्रष्टव्याः स्मः। (अत्र किम् अव्ययपदं प्रयुक्तम्)
(ड) ‘राजनि अविरुद्धवृत्तिर्भव। (‘भव’ अत्र कः लकारः प्रयुक्तः ?)
(ढ) अयम् विद्यालयः 12 कक्षापर्यन्तः अस्ति। (अङ्कस्थाने संस्कृतसंख्यावाचक-विशेषणं लिखत)
(ण) प्राचार्यस्य 2 सहायकौ उपप्राचार्यों स्तः। (अङ्कस्थाने संस्कृतसंख्यावाचकविशेषणं लिखत)
(त) शिविना विना इदं दुष्करं कः कुर्यात्। (रेखाङ्कितपदेन प्रश्ननिर्माणं कुरुत)
उत्तराणि-
(ट) ‘भीताः’ – भी + क्त।
(ठ) ‘ननु’ इति अव्ययपदं प्रयुक्तम्।
(ड) ‘भव’ अत्र लोट् लकारः प्रयुक्तः ।
(ढ) अयम् विद्यालयः द्वादश-कक्षापर्यन्तः अस्ति।
(ण) प्राचार्यस्य द्वौ सहायकौ उपप्राचार्यों स्तः।
(त) केन विना इदं दुष्करं कः कुर्यात् ?

प्राणेभ्योऽपि प्रियः सुहृदः पठित-अवबोधनम्

निर्देशः-अधोलिखितं गद्यांशं पठित्वा एतदाधारितान् प्रश्नानाम् उत्तराणि संस्कृत-पूर्णवाक्येन लिखत
(अधोलिखित गद्यांश को पढ़कर इन पर आधारित प्रश्नों के उत्तर संस्कृत के पूर्ण वाक्य में लिखिए-)

1. चाणक्यः – वत्स ! मणिकारश्रेष्ठिनं चन्दनदासमिदानीं द्रष्टुमिच्छामि। शिष्यः
शिष्यः – तथेति (निष्क्रम्य चन्दनदासेन सह प्रविश्य) इतः इतः श्रेष्ठिन् (उभौ परिक्रामत:)
शिष्यः – (उपसृत्य) उपाध्याय ! अयं श्रेष्ठी चन्दनदासः।
चन्दनदासः -जयत्वार्यः।
चाणक्यः – श्रेष्ठिन् ! स्वागतं ते। अपि प्रचीयन्ते संव्यवहारणां वृद्धिलाभाः ?
चन्दनदासः – (आत्मगतम्) अत्यादरः शङ्कनीयः। (प्रकाशम्) अथ किम्। आर्यस्य प्रसादेन अखण्डिता मे वणिज्या।
चाणक्यः – भो श्रेष्ठिन् ! प्रीताभ्यः प्रकृतिभ्यः प्रतिप्रियमिच्छन्ति राजानः।
चन्दनदासः – आज्ञापयतु आर्यः, किं कियत् च अस्मजनादिष्यते इति।
चाणक्यः – भो श्रेष्ठिन् ! चन्द्रगुप्तराज्यमिदं न नन्दराज्यम्। नन्दस्यैव अर्थसम्बन्धः प्रीतिमुत्पादयति। चन्द्रगुप्तस्य तु भवतामपरिक्लेश एव।
चन्दनदासः – (सहर्षम्) आर्य ! अनुगृहीतोऽस्मि।

पाठ्यांश-प्रश्नोत्तर
(क) पूर्णवाक्येन उत्तरत
(i) चाणक्यः कं द्रुष्टुम् इच्छति ?
(ii) आर्यस्य प्रसादेन कस्य वणिज्या अखण्डिता ?
(iii) अनुगृहीतः कः भवति ?
(iv) कस्य एव अर्थसम्बन्धः प्रीतिम् उत्पादयति ?
(v) अत्यादरः कीदृशः ?
(vi) चन्दनदासः कः अस्ति ?
(vii) किम् इच्छन्ति राजानः ?
उत्तराणि:
(i) चाणक्यः चन्दनदासं द्रुष्टुम् इच्छति।
(ii) आर्यस्य प्रसादेन चन्दनदासस्य वणिज्या अखण्डिता।
(iii) अनुगृहीतः चन्दनदासः भवति।
(iv) नन्दस्य एव अर्थसम्बन्धः प्रीतिम् उत्पादयति।
(v) अत्यादरः शङ्कनीयः।
(vi) चन्दनदासः मणिकारश्रेष्ठी अस्ति।
(vii) प्रीताभ्यः प्रकृतिभ्यः प्रतिप्रियम् इच्छन्ति राजानः ।

(ख) निर्देशानुसारम् उत्तरत
(i) ‘परिक्रामतः’ अत्र कः उपसर्गः प्रयुक्तः ?
(ii) ‘अखण्डिता वणिज्या’-अत्र विशेष्यपदं किम् ?
(ii) ‘व्यापाराणाम्’ इत्यर्थे प्रयुक्तं पदं किम् ?
(iv) ‘अस्मज्जनादिष्यते’-अत्र ‘अस्मत्’ इति सर्वनाम कस्मै प्रयुक्तम् ?
(v) ‘दरिद्रः’ इत्यस्य प्रयुक्तं विलोमपदं किम् ?
उत्तराणि:
(i) परि।
(ii) वणिज्या।
(iii) संव्यवहाराणाम्।
(iv) चन्दनदासाय।
(v) श्रेष्ठी।

हिन्दीभाषया पाठबोधः

शब्दार्था:-मणिकारश्रेष्ठिनम् = (रत्नकारं वणिजम्) मणियों का व्यापारी । निष्क्रम्य = (बहिर्गत्वा) बाहर निकलकर। परिक्रामतः = (परिभ्रमणं कुर्वतः) (दोनों) परिभ्रमण करते है। उपसृत्य = (समीपं गत्वा) पास जाकर। प्रचीयन्ते =(वृद्धिं प्राप्नुवन्ति) बढ़ते हैं । संव्यवहाराणाम् = (व्यापाराणाम्) व्यापारों का। आत्मगतम् = (स्वगतम्) मन-ही-मन। प्रकाशम् = (प्रकटरूपे) प्रकट रूप में। शङ्कनीयः = (सन्देहास्पदम्) शंका करने योग्य। प्रसादेन = (कृपया) कृपा से। अखण्डिता = (निर्बाधा) बाधारहित । वणिज्या = (वाणिज्यम्) व्यापार । प्रीताभ्यः = (प्रसन्नाभ्यः) प्रसन्नजनों के प्रति। प्रतिप्रियम् = (प्रत्युपकारम्) उपकार के बदले किया गया उपकार। अपरिक्लेशः = (दु:खाभाव:) दुःख का अभाव।

प्रसंगः-प्रस्तुत गद्यांश हमारी पाठ्य पुस्तक ‘शेमुषी द्वितीयो भागः’ के ‘प्राणेभ्योऽपि प्रियः सुहृद्’ नामक पाठ से लिया गया है। चाणक्य से भेंट करने के लिए उनकी अनुमति से सेठ चन्दनदास को चाणक्य के सामने लाया जाता है और चाणक्य उसका बहुत आदर करते हुए चन्द्रगुप्त के राज्य में उसके व्यापार की वृद्धि के बारे में पूछता है। इसी का वर्णन प्रस्तुत नाटयांश में है।

सरलार्थः
चाणक्य – पुत्र ! मैं इस समय सुवर्ण व्यापारी सेठ चन्दनदास को देखना (मिलना) चाहता हूँ।
शिष्य – ठीक ही (बाहर निकलकर चन्दनदास के साथ प्रवेश करके) इधर से इधर से सेठ जी ( दोनों घूमते हैं)।
शिष्य – (पास जाकर) उपाध्यायजी ! ये सेठ चन्दनदास हैं।
चन्दनदास – आर्य की जय हो।
चाणक्य – सेठ जी ! आपका स्वागत है। क्या आपके व्यापार-कार्यों की लाभवृद्धियाँ हो रही हैं ?
चन्दनदास – (मन-ही-मन) अत्यधिक आदर शङ्का (सन्देह) के योग्य है। (प्रकट रूप में) और क्या! आर्य की कृपा से मेरा व्यापार परिपूर्ण है।
चाणक्य – अरे सेठ जी ! राजा प्रसन्न हुई अपनी प्रजा से बदले में प्रिय चाहते हैं। अर्थात् राजा का तुम्हारे प्रति जो मृदु व्यवहार है, उसके बदले में वे भी आपसे कुछ प्रिय व्यवहार चाहते हैं।
चन्दनदास – आर्य आज्ञा करें, इस व्यक्ति से क्या और कितना चाहते हैं ?
चाणक्य – अरे सेठजी ! यह चन्द्रगुप्त का राज्य है, न कि नन्द का राज्य। धन का सम्बन्ध नन्द के लिए ही प्रीति उपजाता है। चन्द्रगुप्त के लिए तो आपका दुःख रहित होना ही प्रीतिदायक है।
चन्दनदास – (हर्ष के साथ) आर्य ! अनुगृहीत हुआ हूँ।

भावार्थ:-भाव यह है कि चाणक्य चन्दनदास को आदरपूर्वक मिलने के लिए बुलाता है। चन्दनदास अपने प्रति चाणक्य के अति आदर को शंका की दृष्टि से देखता है। चाणक्य उससे पूछता है कि चन्द्रगुप्त के राज्य में उसका व्यापार फल-फूल रहा है या नहीं। चन्दनदास कहता है कि बिल्कुल ठीक चल रहा है। चन्द्रगुप्त मौर्य के राज्य में हमें कोई कठिनाई नहीं है। चाणक्य कहता है कि यदि आप उनके प्रशासन से प्रसन्न हैं; तो आप भी राजा का कुछ हित कीजिए। क्योंकि राजा और प्रजा का पारस्परिक सम्बन्ध उपकार एवं प्रत्युपकार “Give and take” पर आधारित होता है।
नोट-संस्कृत में वाक्य के आरम्भ में आने वाला ‘अपि’ शब्द प्रश्नवाचक होता है-अपि = किम्। जैसे-अपि कुशलोऽसि ?
‘क्या आप कुशल हैं ?’

2. चाणक्यः भो श्रेष्ठिन् ! स चापरिक्लेशः कथमाविर्भवति इति ननु भवता प्रष्टव्याः स्मः।
चन्दनदासः – आज्ञापयतु आर्यः।
चाणक्यः – राजनि अविरुद्धवृत्तिर्भव।
चन्दनदासः – आर्य ! कः पुनरधन्यो राज्ञो विरुद्ध इति आर्येणावगम्यते ?
चन्दनदासः – (कर्णो पिधाय) शान्तं पापम्, शान्तं पापम्। कीदृशस्तृणानामग्निना सह विरोध: ?
चाणक्यः – अयमीदृशो विरोधः यत् त्वमद्यापि राजापथ्यकारिणोऽमात्यराक्षसस्य गृहजनं स्वगृहे रक्षसि।
चन्दनदासः – आर्य ! अलीकमेतत्। केनाप्यनार्येण आर्याय निवेदितम्।
चाणक्यः – भो श्रेष्ठिन् ! अलमाशङ्कया। भीताः पूर्वराजपुरुषाः पौराणामनिच्छतामपि गृहेषु गृहजनं निक्षिप्य देशान्तरं व्रजन्ति। ततस्तत्प्रच्छादनं दोषमुत्पादयति।

पाठ्यांश-प्रश्नोत्तर
(क) पूर्णवाक्येन उत्तरत
(i) कस्मिन् अविरुद्धवृत्तिः भवेत् ?
(ii) तृणानां केन सह विरोधः भवति ?
(ii) राजापथ्यकारी कः अस्ति ? ।
(iv) चन्दनदासः कस्य गृहजनं रक्षति ?
(v) के देशान्तरं व्रजन्ति?
(vi) चाणक्येन राज्ञः विरुद्धः अधन्यः कः अवगम्यते ?
(vii) केषां गृहजनं स्वगृहे प्रच्छादनं दोषम् उत्पादयति ?
उत्तराणि
(i) राजनि अविरुद्धवृत्तिः भवेत्।
(ii) तृणानां अग्निना सह विरोधः भवति।
(iii) राजापथ्यकारी अमात्यराक्षसः अस्ति।
(iv) चन्दनदासः कस्य गृहजनं रक्षति।
(v) पूर्वराजपुरुषाः देशान्तरं व्रजन्ति।
(vi) चाणक्येन राज्ञः विरुद्धः अधन्यः चन्दनदासः अवगम्यते।
(vii) पूर्वराजपुरुषाणां गृहजनं स्वगृहे प्रच्छादनं दोषम् उत्पादयति।

(ख) निर्देशानुसारम् उत्तरत
(i) ‘असत्यम्’ इत्यर्थे प्रयुक्तं पदं किम् ?
(ii) ‘राजहितकारिणः’ इत्यस्य प्रयुक्तं विलोमपदं किम् ?
(ii) ‘भीताः पूर्वराजपुरुषाः’ अत्र विशेषणपदं किम् ?
(iv) ‘निक्षिप्य’ अत्र कः प्रत्ययः प्रयुक्तः ?
(v) ‘केनाप्यनार्येण’ अत्र सन्धिच्छेदं कुरुत।
उत्तराणि
(i) अलीकम्।
(ii) राजापथ्यकारिणः ।
(iii) भीताः ।
(iv) ल्यप् ।
(v) केन + अपि + अनार्येण।

हिन्दीभाषया पाठबोधः
शब्दार्थाः-आविर्भवति = (अवतारणाम् करोति) अवतरित करना, उपस्थित करना। आज्ञापयतु = (आदिशतु) आदेश कीजिए। अर्थसम्बन्धः = (धनस्य सम्बन्धः) धन का सम्बन्ध । परिक्लेशः = (दुःखम्) दुःख । प्रष्टव्याः = (प्रष्टुं योग्याः) पूछने योग्य। अविरुद्धवृत्तिः = (अविरुद्धस्वभाव:) विरोधरहित स्वभाववाला। अवगम्यते = (ज्ञायते) जाना जाता है। पिधाय = (आच्छाद्य) बन्दकर। राजापथ्यकारिणः = (नृपापकारकारिणः) राजाओं का अहित करने वाले। अलीकम् = (असत्यम्) झूठ। अनार्येण = (दुष्टेन) दुष्ट के द्वारा। पौराणाम् = (नगरवासिनाम्) नगर के लोगों के। अनिच्छताम् = (न इच्छताम्) न चाहते हुओं का। निक्षिप्य = (स्थापयित्वा) रखकर। व्रजन्ति = (गच्छन्ति) जाते हैं। प्रच्छादनम् = (आच्छादनम्) छिपाना।

प्रसंग:-प्रस्तुत गद्यांश हमारी पाठ्य पुस्तक ‘शेमुषी द्वितीयो भागः’ के ‘प्राणेभ्योऽपि प्रियः सुहृद्’ नामक पाठ से लिया गया है। चाणक्य सेठ चन्दनदास से बातचीत करते हुए स्पष्ट करता है कि राजा का अहित करने वाले के परिवार को अपने घर में आश्रय देना दण्डनीय अपराध है और अमात्य राक्षस के परिवार को छिपाकर तुमने भी यह अपराध किया है। इसी का वर्णन प्रस्तुत नाट्यांश में है।

सरलार्थ:
चाणक्य – अरे सेठ जी ! और वह दुःख का अभाव कैसे पैदा होता है, बस यही आपसे पूछा जाना है।
चन्दनदास – आज्ञा कीजिए आर्य।
चाणक्य – राजा के प्रति उसके अनुकूल व्यवहार वाले होओ।
चन्दनदास – आर्य ! फिर कौन अभागा राजा के विरुद्ध आचरण करने वाला जाना गया है ?
चाणक्य – पहले तो आप ही हैं।
चन्दनदास – (कानों पर हाथ रखकर) पाप शान्त हो, पाप शान्त हो-अग्नि के साथ तिनकों का कैसा विरोध ?
चाणक्य – यह विरोध ऐसे है कि तुम आज भी राजा का अहित करने वाले अमात्य राक्षस के परिवार के लोगों की अपने घर में रक्षा कर रहे हो।
चन्दनदास – आर्य, यह झूठ है। किस दुष्ट के द्वारा आर्य को निवेदन किया गया है।
चाणक्य – अरे सेठ जी । आशका मत करो। डरे हुए पूर्व राजपुरुष नगरवासियों के न चाहते हुए भी उनके घरों में (अपने) परिवार के लोगों को रखकर परदेश को चले जाते हैं। इसी से उनको छिपाना दोष उत्पन्न करता है। अर्थात् इस प्रकार राजा के अहितैषी राजपुरुषों के परिवारजनों को छिपाना अपराध है।

भावार्थ:-भाव यह है कि चाणक्य चन्दनदास को कहता है कि वह आज भी राजा का अहित करने वाले अमात्य राक्षस के परिवार के लोगों की अपने घर में रक्षा कर रहा है और इस प्रकार राजा का अहित चाहने वाले राजपुरुषों के परिवारजनों को छिपाना अपराध है।

3. चन्दनदासः – एवं नु इदम्। तस्मिन् समये आसीदस्मद्गृहे अमात्यराक्षसस्य गृहजन इति।
चाणक्यः – पूर्वम् ‘अनृतम्’, इदानीम् “आसीत्” परस्परविरुद्ध वचने।
चन्दनदासः – आर्य ! तस्मिन् समये आसीदस्मद्गृहे अमात्यराक्षस्य गृहजन इति।
चाणक्यः – अथेदानी क्व गतः ?
चन्दनदासः – न जानामि।
चाणक्यः – कथं न ज्ञायते नाम ? भो श्रेष्ठिन् शिरसि भयम् अतिदूरं तत्प्रतिकारः।
चन्दनदासः – आर्य ! किं मे भयं दर्शयसि ? सन्तमपि गेहे अमात्यराक्षस्य गृहजनं न समर्पयामि, किं पुनरसन्तम् ?
चाणक्यः – चन्दनदास ! एष एव ते निश्चयः ?
चन्दनदासः – बाढम् एष एव मे निश्चयः।
चाणक्यः – (स्वगतम् ) साधु ! चन्दनदास साधु। सुलभेष्वर्थलाभेषु परसंवेदने जने। क इदं दुष्करं कुर्यादिदानीं शिविना विना॥

पाठ्यांश-प्रश्नोत्तर

(क) पूर्णवाक्येन उत्तरत
(i) तस्मिन् समये कस्य गृहे अमात्य-राक्षसस्य गृहजनः आसीत् ?
(ii) पूर्वम् ‘अनृतम्’, इदानीं किम् ?
(iii) कस्य प्रतिकारः अतिदूरम् अस्ति ?
(iv) भयं कः दर्शयति ?
(v) केन विना इदं दुष्करं कुर्यात् ?
उत्तराणि:
(i) तस्मिन् समये चन्दनदासस्य गृहे अमात्य-राक्षसस्य गृहजनः आसीत्।
(ii) पूर्वम् ‘अनृतम्’, इदानीं किम् ‘आसीत्’ ।
(iii) भयस्य प्रतिकारः अतिदूरम् अस्ति।
(iv) भयं चाणक्यः दर्शयति।
(v) शिविना विना इदं दुष्करं कुर्यात्।

(ख) निर्देशानुसारम् उत्तरत
(i) ‘परस्परविरुद्धे वचने’ अत्र विशेषणपदं किम् ?
(ii) ‘कुत्र’ इत्यर्थे अत्र प्रयुक्तम् अव्ययपदं किम् ?
(iii) ‘सन्तम्’ इत्यस्य प्रयुक्तं विलोमपदं किम् ?
(iv) ‘एष एव मे निश्चयः’ अत्र ‘मे’ इति सर्वनाम कस्मै प्रयुक्तम् ?
(v) ‘सुलभेष्वर्थलाभेषु’ अत्र सन्धिच्छेदं कुरुत।
उत्तराणि:
(i) परस्परविरुद्ध।
(ii) क्व।
(ii) असन्तम्।
(iv) चन्दनदासाय।
(v) सुलभेषु + अर्थलाभेषु।

हिन्दीभाषया पाठबोधः
शब्दार्थाः-अमात्यः = (मन्त्रीं) मन्त्री। प्रतिकारः = (प्रतिशोधार्थं कृता क्रिया) बदले की कार्यवाही। असन्तम् = (न निवसन्तम्) न रहने वाले। बाढम् = (आम्) हाँ। संवेदने = (समर्पणे कृते सति) समर्पण कर देने पर। जने = (लोके) संसार में। शिविना = (शिवि-नृपेण) राजा शिवि के द्वारा।

प्रसंगः-प्रस्तुत गद्यांश हमारी पाठ्य पुस्तक ‘शेमुषी द्वितीयो भागः’ के ‘प्राणेभ्योऽपि प्रियः सुहृद्’ नामक पाठ से लिया गया है। चन्दनदास के परस्पर विरुद्ध वचनों में भी चाणक्य जब यह स्पष्ट कर देते हैं कि अमात्य राक्षस के परिवार को उसने अपनी सुरक्षा में रखा हुआ हैं तो चन्दनदास राजदण्ड की बात सुनकर भी निर्भय होकर कहता है कि घर में होने पर भी मैं अमात्य राक्षस के परिवार को राजा के लिए समर्पित न करता। फिर घर में न होने पर उसे दिया ही कैसे जा सकता है ? इसी का वर्णन प्रस्तुत नाट्यांश में है।

सरलार्थः
चन्दनदास – हाँ ऐसा ही है। तब मेरे घर में अमात्य राक्षस का परिवार था।
चाणक्य -पहले ‘झूठ’, अब ‘था’ ऐसे दो परस्पर विपरीत वचन।
चन्दनदास – आर्य ! उस समय मेरे घर में अमात्य राक्षस का परिवार था।
चाणक्य – तो अब कहाँ गया ?
चन्दनदास – नहीं जानता हूँ।
चाणक्य – क्यों नहीं जानते। अरे सेठ जी ! (भय) सिर पर है, उसका प्रतिकार (निवारण) बहुत दूर।
चन्दनदास – आर्य ! क्या मुझे भय दिखा रहे हो ? घर में होने पर भी अमात्य राक्षस के परिजन को नहीं देता, फिर न होने पर तो बात ही क्या ?
चाणक्य – चन्दनदास ! यही तुम्हारा निश्चय है ?
चन्दनदास – हाँ यही मेरा निश्चय है।
चाणक्य – (मन-ही-मन) धन्य ! चन्दनदास धन्य!
श्लोकान्वयः – परस्य संवेदने अर्थलाभेषु सुलभेषु इदं दुष्करं कर्म जने (लोके) शिविना विना कः कुर्यात् ।
संस्कृतेऽर्थः – परस्य परकीयस्य अर्थस्य संवेदने समर्पणे कृते सति अर्थलाभेषु सुलभेषु सत्सु स्वार्थं तृणीकृत्य
परसंरक्षणरूपमेवं दुष्करं कर्म जने (लोके) एकेन शिविना विना त्वदन्यः कः कुर्यात् । शिविरपि कृते युगे कृतवान् त्वं तु इदानीं कलौ युगे करोषि इति ततोऽप्यतिशयित-सुचरितत्वमिति भावः।

श्लोक का सरलार्थ:-दूसरों की वस्तु को समर्पित करने पर बहुत धन प्राप्त होने की स्थिति में भी दूसरों की वस्तु की सुरक्षा रूपी कठिन कार्य को एक शिवि को छोड़कर तुम्हारे अलावा दूसरा कौन कर सकता है ?

भावार्थ:-भाव यह है कि चन्दनदास के परस्पर विरुद्ध वचनों के आधार पर चाणक्य जब यह स्पष्ट कर देता है कि अमात्य राक्षस के परिवार को उसने अपनी सुरक्षा में रखा हुआ है तो चन्दनदास राजदण्ड की बात सुनकर भी निर्भय होकर कहता है कि घर में होने पर भी मैं अमात्य राक्षस के परिवार को राजा के लिए समर्पित न करता। फिर घर में न होने पर उसे दिया ही कैसे जा सकता है ?
प्रस्तुत श्लोक के माध्यम से महाकवि विशाखदत्त ने बड़े ही संक्षिप्त शब्दों में चन्दनदास के गुणों का वर्णन किया है। इसमें कवि ने कहा है कि दूसरों की वस्तु की रक्षा करनी कठिन होती है। यहाँ चन्दनदास के द्वारा अमात्य राक्षस के परिवार की रक्षा का कठिन काम किया गया है। न्यायसंरक्षण को महाकवि भास ने भी दुष्कर कार्य मानते हुए स्वप्नवासवदत्तम् में कहा है-‘दुष्करं न्यासरक्षणम्’।

निष्कर्षः- चन्दनदास अगर अमात्य राक्षस के परिवार को राजा को समर्पित कर देता, तो राजा उससे प्रसन्न भी होता और बहुत-सा धन पारितोषिक के रूप में देता, पर उसने भौतिक लाभ व लोभ को दरकिनार करते हुए अपने प्राणप्रिय मित्र के परिवार की रक्षा को अपना कर्तव्य माना और इसे निभाया भी। कवि ने चन्दनदास के इस कार्य की तुलना राजा शिवि के कार्यों से की है जिन्होंने अपने शरणागत कपोत की रक्षा के लिए अपने शरीर के अंगों को काटकर दे दिया था। राजा शिवि ने तो सत्युग में ऐसा किया था, परन्तु चन्दनदास ने ऐसा कार्य इस कलियुग में किया है, इसलिए वह और भी अधिक प्रशंसा का पात्र है।

प्राणेभ्योऽपि प्रियः सुहृदः (प्राणों से भी प्यारा मित्र) Sumarry in Hindi

प्राणेभ्योऽपि प्रियः सुहृदः पाठ-परिचय

‘मुद्राराक्षसम्’ महाकवि विशाखदत्त द्वारा रचित राजनीति पर केन्द्रित एक महत्त्वपूर्ण नाटक है। इस नाटक में आठ अंक हैं। जिनमें चन्द्रगुप्त मौर्य के शासन को चाणक्य द्वारा स्थापित करने का कथानक है। कूटनीतिज्ञ चाणक्य की बुद्धि से चन्द्रगुप्त न केवल पाटलिपुत्र का राज्य प्राप्त करता है अपितु अपनी कूटनीति के बल पर ही चाणक्य नन्द वंश के अति गुणवान् स्वामिभक्त महा-मन्त्री राक्षस को भी चन्द्रगुप्त का मन्त्री बनाने के लिए विवश कर देता है। राक्षस को वश में करने में चाणक्य की कूटनीति, गुप्तचर व्यवस्था तथा राक्षस की मुद्रा से अंकित एक पत्र की महत्त्वपूर्ण भूमिका होती है। मुद्रा के द्वारा राक्षस को वश में करने के कारण ही इस नाटक का नाम ‘मुद्राराक्षसम्’ रखा गया है।
पाठ के रूप में प्रस्तुत नाट्यांश ‘प्राणेभ्योऽपि प्रियः सुहृद्’ इसी ‘मुद्राराक्षसम्’ नाटक के प्रथम अङ्क से उद्धृत किया गया है। नन्दवंश का विनाश करने के बाद उसके हितैषियों को खोज-खोजकर पकड़वाने के क्रम में चाणक्य, अमात्य राक्षस एवं उसके कुटुम्बियों की जानकारी प्राप्त करने के लिए चन्दनदास से वार्तालाप करता है, किन्तु चाणक्य को अमात्य राक्षस के विषय में कोई सुराग न देता हुआ चन्दनदास अपनी मित्रता पर दृढ़ रहता है। उसके मैत्री-भाव से प्रसन्न होता हुआ भी चाणक्य जब उसे राजदण्ड का भय दिखाता है, तब चन्दनदास राजदण्ड भोगने के लिए भी सहर्ष प्रस्तुत हो जाता है। इस प्रकार अपने सुहृद् के लिए प्राणों का भी उत्सर्ग करने के लिए तत्पर चन्दनदास अपनी सुहृद्-निष्ठा का एक ज्वलन्त उदाहरण प्रस्तुत करता है।

प्राणेभ्योऽपि प्रियः सुहृदः पाठस्य सारांश:

‘प्राणेभ्योऽपि प्रियः सुहृद्’ यह पाठ महाकवि विशाखदत्त द्वारा रचित ‘मुद्राराक्षसम्’ नामक नाटक से लिया गया है। प्रस्तुत पाठ में राक्षस के मित्र सेठ चन्दनदास का अपने मित्र के प्रति प्रगाढ़ प्रेम दर्शाया गया है। पाठ का सार इस प्रकार है

चाणक्य को अपने गुप्तचरों द्वारा यह पता चल जाता है कि पूर्व राजा नंद के विश्वासपात्र मन्त्री राक्षस के परिवार को राजधानी के एक सेठ चन्दनदास ने अपने घर में छिपाकर रखा हुआ है। चाणक्य अपने शिष्यों के द्वारा पूछताछ के लिए सेठ चन्दनदास को बुलवाता है और बड़े आदर के साथ उसके व्यापार का कुशल पूछता है। उत्तर में चन्दनदास अपने व्यापार वृद्धि पर प्रसन्नता प्रकट करता है। चाणक्य चन्दनदास से कहता है कि अमात्य राक्षस राजा चन्द्रगुप्त का हितैषी नहीं है और विद्रोही राजपुरुषों के परिवार को अपने घर में छिपाकर रखना एक अपराध है।

आपने अमात्य राक्षस के परिवार को अपने घर में छिपाकर यह अपराध किया है। जिसके दंड से बचना कठिन है। चन्दनदास निर्भयतापूर्वक कहता है कि यदि मेरे पास अमात्य राक्षस का परिवार हो भी, तो भी मैं उसे राजा के लिए समर्पित नहीं करूँगा, फिर मेरे पास तो है ही नहीं। चाणक्य मन ही मन चन्दनदास की मित्रता पर प्रसन्न होता है और उसे बधाई देता है कि अपने मित्र के जिस परिवार को सौंपकर इस सेठ को पर्याप्त धन लाभ हो सकता है यह सेठ चन्दनदास उस परिवार को सौंपने को तैयार नहीं है शरण में आए हुए की रक्षा अपने प्राणों से भी बढ़कर करना यह राजा शिवि के अतिरिक्त और कौन कर सकता है। दूसरे शब्दों में सेठ चन्दनदास को राजा शिवि के समान शरणागत की रक्षा करने वाला मानकर चाणक्य ने उसकी प्रशंसा की है और चन्दनदास ने भी अपने प्राणों की बाजी लगाकर अपने मित्र के परिवार की रक्षा करके सिद्ध कर दिया कि मित्र प्राणों से भी प्रिय होता है।

Haryana State Board HBSE 10th Class Sanskrit Solutions Apathit Avabodhanam अपठित-अवबोधनम् Exercise Questions and Answers.

Haryana Board 10th Class Sanskrit अपठित-अवबोधनम्

1. प्रदत्तगद्यांशं पठित्वा अधोलिखित प्रश्नानाम् उत्तराणि लिखत
द्वापरयुगे हस्तिनापुरे शान्तनुः नाम नृपतिः अभवत्। शान्तनोः पुत्रस्य नाम देवव्रतः आसीत्। गंगायाः पुत्रत्वात् तस्य नाम ‘गांगेय’ इत्यपि आसीत्। सः पराक्रमी आसीत्। सः बालब्रह्मचारी, पितृभक्तश्च आसीत्।

(क) शान्तनुः कुत्र राजा आसीत् ?
(ख) देवव्रतः कस्य पुत्रः आसीत् ?
(ग) देवव्रतः कीदृशः आसीत् ?
(घ) पितृभक्तः कः आसीत् ?
(ङ) ‘इत्यपि’ पदे सन्धिच्छेदं कुरुत। (H.B. 2014-A)
उत्तराणि
(क) शान्तनुः हस्तिनापुरे राजा आसीत्।
(ख) देवव्रतः शान्तनोः पुत्रः आसीत्।
(ग) देवव्रतः पराक्रमी, बालब्रह्मचारी, पितृभक्तश्च आसीत्।
(घ) पितृभक्तः देवव्रतः आसीत्।
(ङ) ‘इत्यपि’ = इति + अपि।

2. प्रदत्तगद्यांशं पठित्वा अधोलिखित प्रश्नानाम् उत्तराणि लिखत
एकस्मिन् वने एकः वृक्षः आसीत्। वृक्षे एकः खगः अवसत्। वृक्षे स सुन्दरं नीडम् अरचयत्। तत्र दम्पती उषित्वा शावकानां रक्षाम् अकुरुताम्। एकदा महती वर्षा अभवत्। तदा तत्र एकः वानरः आगच्छत्। खगः तम् अवदत्। त्वं कथं न नीडं रचयसि ? वानरः क्रुद्ध्वा नीडम् अत्रोटयत्।

(क) वृक्षः कुत्र आसीत् ?
(ख) खगः कम् अवदत् ?
(ग) वानरः क्रुद्ध्वा किम् अकरोत् ?
(घ) दम्पती केषां रक्षाम् अकुरुताम् ?
(ङ) ‘आसीत्’ क्रिया पदे क: लकारः ? (H.B. 2014-B)
उत्तराणि
(क) वृक्षः वने आसीत्।
(ख) खगः वानरम् अवदत्।
(ग) वानरः क्रुद्ध्वा नीडम् अत्रोटयत्।
(घ) दम्पती उषित्वा शावकानां रक्षाम् अकुरुताम्।
(ङ) ‘आसीत्’ क्रिया पदे कः लकारः। ।

3. प्रदत्तगद्यांशं पठित्वा अधोलिखितप्रश्नानाम् उत्तराणि लिखत
आचार्यः गुरुः भवति। गुरवः पूज्याः भवन्ति। संसारे गुरून् विना किमपि कार्यं न सिध्यति। अतः गुरवः महत्त्वपूर्णाः सन्ति। गुरवः शिष्याणां हिताय यत् यत् शुभं कथयन्ति तत् तत् वाक्यमेव उपदेशो भवति। अतः आचार्य देवो भव।

(क) गुरवः कीदृशाः भवन्ति ?
(ख) गुरून् विना किं न सिध्यति ?
(ग) गुरवः केषां हिताय उपदिशन्ति ?
(घ) ‘किमपि’ इति पदे सन्धिच्छेदं कुरुत।
(ङ) ‘विना’ योगे का विभक्तिः भवति ? (H.B. 2014-C)
उत्तराणि:
(क) गुरवः पूज्याः भवन्ति।
(ख) गुरून् विना किमपि कार्यं न सिध्यति।
(ग) गुरवः शिष्याणां हिताय उपदिशन्ति।
(घ) ‘किमपि’ = किम् + अपि।
(ङ) ‘विना’ योगे द्वितीया/तृतीया/पञ्चमी विभक्तिः भवति।

4. अधोलिखितम्-अनुच्छेदं पठित्वा प्रदत्तप्रश्नानाम् उत्तराणि संस्कृतपूर्णवाक्येन लिखतअहम् एकः छिन्नद्रुमः अस्मि। ह्यः वने एक: नरः आगच्छत्। सः काष्ठाय मम शरीरम् अच्छिनत्। छेदनेन मे शरीरे अनेके व्रणाः जाताः । छुरिकायाः प्रहारम् शरीरात् अश्रुरूपाः जलबिन्दवः अपतन्। अकथनीया मम पीड़ा। हृदयं विदीर्णं जातम्। अश्रुभिः कण्ठः अवरुद्धः । मम अन्तकालः समीपे एव तिष्ठति। काष्ठानि एकत्रीकृत्य सः तु अगच्छत्। परं कोऽस्ति अत्र व्यथा कथाश्रवणाय ?

प्रश्नाः
(i) एषः अनुच्छेदः कस्य आत्मकथां कथयति।
(ii) कदा वने एकः नरः आगच्छत्।।
(iii) सः नरः किमर्थं वृक्षस्य शरीरं अच्छिनत् ?
(iv) छेदनेन वृक्षस्य शरीरे के जाताः ?
(v) वृक्षस्य अश्रुभिः किम् अभवत् ?
उत्तराणि:
(i) एषः अनुच्छेदः एकस्य छिन्नस्य द्रुमस्य आत्मकथां कथयति।
(ii) ह्यः वने एक: नरः आगच्छत् ।
(iii) सः नरः काष्ठाय वृक्षस्य शरीरम् अच्छिनत्।
(iv) छेदनेन वृक्षस्य शरीरे व्रणाः जाताः।।
(v) वृक्षस्य अश्रुभिः जलबिन्दवः अपतन्।

5. अधोलिखितम्-अनुच्छेदं पठित्वा प्रदत्तप्रश्नानाम् उत्तराणि संस्कृतपूर्णवाक्येन लिखत
प्रकृतिः मनुष्यस्य उपकारिणी। मनुष्यैः सह तस्याः शाश्वतः सम्बन्धः। सा विविधरूपेषु अस्मिन् जगति आत्मानं प्रकटयति। विविधाः ओषधयः सकलानि खनिजानि च प्रकृतेः एव शोभा। सा तु नित्यं एव एतैः साधनैः सर्वेषाम् उपकारं करोति, परम् अधन्यः अयं जनः कृतज्ञतां विहाय असाधुसेवितं पथं गच्छति, विविधानि कष्टानि च अनुभवति।

प्रश्नाः-
(i) मनुष्यैः सह कस्याः शाश्वतः सम्बन्धः ?
(ii) प्रकृतिः विविधरूपेषु कुत्र आत्मानं प्रकटयति ?
(iii) प्रकृतेः का शोभा अस्ति ?
(iv) प्रकृति कस्य उपकारिणी अस्ति ?
(v) अधन्यः अयं जनः कृतज्ञतां विहाय किं करोति ?
उत्तराणि:
(i) मनुष्यैः सह प्रकृत्याः शाश्वतः सम्बन्धः ।
(ii) प्रकृतिः विविधरूपेषु जगति आत्मानं प्रकटयति।
(iii) विविधाः ओषधयः सकलानि खनिजानि च प्रकृतेः शोभा अस्ति।
(iv) प्रकृतिः मनुष्यस्य उपकारिणी अस्ति।
(v) अधन्यः अयं जनः कृतज्ञतां विहाय असाधुसेवितं पथं गच्छति।

6. अधोलिखितम्-अनुच्छेदं पठित्वा प्रदत्तप्रश्नानाम् उत्तराणि संस्कृतपूर्णवाक्येन लिखत
अस्माकं देशे अनेकानि राज्यानि सन्ति। तेषु हरियाणा राज्य अति लघुराज्यं वर्तते। अस्य उदयः 1966 तमे वर्षे नवम्बर मासस्य प्रथमे दिनाङ्के अभवत्। हरियाणाप्रदेश: वीराणां भूमिः कथ्यते। अस्य कुरुक्षेत्रे नगरे महाभारतस्य युद्धम् अभवत्। श्रीकृष्ण अर्जुनाय गीतायाः उपदेशम् अत्रैव अयच्छत्। इदं राज्यं कृषिप्रधान राज्यम् अस्ति। अस्य भूमिः अति उपजाऊ: अस्ति। अस्य कृषकाः अतीव परिश्रमं कुर्वन्ति। जनाः साधारणं जीवनं व्यतीतं कुर्वन्ति।

(क) हरियाणा राज्यं कीदृक् राज्यं वर्तते ?
(ख) हरियाणा केषां भूमिः कथ्यते ?
(ग) अस्य कृषकाः किं कुर्वन्ति ?
(घ) अस्य कुरुक्षेत्रनगरे किम् अभवत् ?
(ङ) जनाः कीदृशं जीवन व्यतीतं कुर्वन्ति ?
उत्तरम्
(क) हरियाणा राज्यं लघुराज्यं राज्यं वर्तते।
(ख) हरियाणा वीराणां भूमिः कथ्यते।
(ग) अस्य कृषकाः अतीव परिश्रमं कुर्वन्ति।
(घ) अस्य कुरुक्षेत्रनगरे महाभारतस्य युद्धम् अभवत्।
(ङ) जनाः साधारणं जीवन व्यतीतं कुर्वन्ति।

7. अधोलिखितम्-अनुच्छेदं पठित्वा प्रदत्तप्रश्नानाम् उत्तराणि संस्कृतपूर्णवाक्येन लिखत
निरपराधानां प्राणिनां हिंसनं न कर्तव्यम्, इत्यहिंसायाः भावः। भारतवर्षेऽहिंसायाः स्थानं महत्त्वपूर्णमस्ति। अहिंसाधर्मस्यैव पालनेन भगवतो बुद्धस्य गणना दशावतारेषु क्रियते। भगवान् महावीरोऽपि अहिंसायाः पोषक: आसीत्। अहिंसायाः पालनं मनसा, वाचा, कर्मणा च कर्तव्यम्। निरपराधस्य कस्यापि जन्तोः हिंसनं नूनं निन्दनीयम्।

प्रश्ना:-
(i) अहिंसायाः पालनं कथं कर्तव्यम् ?
(ii) भारतवर्षे कस्याः स्थानं महत्त्वपूर्णमस्ति ?
(iii) अहिंसाधर्मस्यैव पालनेन कस्य गणना दशावतारेषु क्रियते ?
(iv) क: अहिंसायाः पोषकः आसीत् ?
(v) केषां हिंसनं न कर्तव्यम् ?
उत्तराणि
(i) अहिंसायाः पालनं मनसा, वाचा, कर्मणा च कर्तव्यम्।
(ii) भारतवर्षेऽहिंसायाः स्थानं महत्त्वपूर्णमस्ति।
(iii) अहिंसाधर्मस्यैव पालनेन भगवंतो बुद्धस्य गणना दशावतारेषु क्रियते।
(iv) भगवान् महावीरोऽपि अहिंसायाः पोषकः आसीत्।
(v) निरपराधानां प्राणिनां हिंसनं न कर्तव्यम्।

8. अधोलिखितम्-अनुच्छेदं पठित्वा प्रदत्तप्रश्नानाम् उत्तराणि संस्कृतपूर्णवाक्येन लिखत
अद्य भोजनालये पाचकः बहुव्यञ्जनानि पचति। चुल्यामग्निः सम्यक् न ज्वलति। धूमोऽपि मन्दं मन्दं बहि: चारों खण्डों की परीक्षोपयोगी सामग्री नि:सरति । स्थाल्यां बहुमोदकाः सन्ति। कटाहे तप्तं घृतं वर्तते, जलपात्रेषु जलं न दृश्यते। पीठेषु मनुष्या: नोपविष्टाः सन्ति। काष्ठधारः अस्ति, तस्योपरि दधिपात्रं विद्यते।

प्रश्ना:-
(i) स्थाल्यां के सन्ति ?
(ii) कुत्र जलं न दृश्यते ?
(iii) कटाहे कीदृशं घृतं वर्तते ?
(iv) अद्य भोजनालये पाचक: कानि पचति ?
(v) धूमोऽपि कथं बहि: निःसरति ?
उत्तराणि:
(i) स्थाल्यां बहुमोदकाः सन्ति
(ii) जलपात्रेषु जलं न दृश्यते।
(iii) कटाहे तप्तं घृतं वर्तते।।
(iv) अद्य भोजनालये पाचक: बहुव्यञ्जनानि पचति।
(v) धूमोऽपि मन्दं मन्दं बहिः निःसरति।

9. अधोलिखितम्-अनुच्छेदं पठित्वा प्रदत्तप्रश्नानाम् उत्तराणि संस्कृतपूर्णवाक्येन लिखत
स्वस्थं पर्यावरणं अस्माकं जीवनस्य आधारोऽस्ति पर्यावरणस्य आधारः पुष्पिता: पल्लविताः वृक्षाः भवन्ति। वृक्षाः ऑक्सीजन प्रदाय पर्यावरणं स्वस्थं कुर्वन्ति। वृक्षाः पर्यावरणं संतुलितं कुर्वन्ति। ते यथाकालम् मेघानाम् वर्षणे सहायकाः भवन्ति। वृक्षाः पुष्पाणां फलानाम् औषधीनाम् च आगाराः सन्ति। वृक्षपादपानाम् हरीतिमा, तेषां पुष्पाणाम् शोभा, पक्षिणाम् कलरवः च शुष्कहृदयानपि रसविभोरान् कुर्वन्ति।

प्रश्ना:
(i) कस्य आधारः वृक्षाः भवन्ति ?
(ii) वृक्षाः किं प्रदाय पर्यावरणं स्वस्थं कुर्वन्ति ?
(iii) वृक्षाः यथाकालं केषां वर्षणे सहायकाः भवन्ति ?
(iv) वृक्षाः कस्य आगाराः सन्ति ?
(v) वृक्षाणां शोभाः पक्षिणां कलरवः च किं कुर्वन्ति ?
उत्तराणि
(i) पर्यावरणस्य आधारः वृक्षाः भवन्ति।
(ii) वृक्षाः आक्सीजनं प्रदाय पर्यावरणं स्वस्थं कुर्वन्ति।
(iii) वृक्षाः यथाकालं मेघानां वर्षणे सहायकाः भवन्ति।
(iv) वृक्षाः पुष्पाणां फलानाम् औषधीनाम् च आगाराः सन्ति।
(v) वृक्षाणां शोभाः पक्षिणां कलरवः च शुष्कहृदयान् अपि रसविभोरान् कुर्वन्ति।

10. अधोलिखितम्-अनुच्छेदं पठित्वा प्रदत्तप्रश्नानाम् उत्तराणि संस्कृतपूर्णवाक्येन लिखतदक्षिणभारते सागरमध्ये एकं लघुद्वीपं वर्तते। तस्मिन् द्वीपे सागरतरङ्गैः क्षाल्यमानं प्राचीनं नगरं कन्याकुमारी इति अस्ति। एषा कन्याकुमारी त्रयाणां सागराणां सङ्गमस्थली। समुद्रजले प्रतिबिम्बितं सूर्योदयस्य दृश्यम् अद्भुतम् एव। सूर्यस्य क्रमश: अरुणा पीता धवला च शोभा दर्शकान् मन्त्रमुग्धान् करोति। सागरस्य लहरीभिः क्षिप्तानां चित्र-विचित्रवर्णानां शुक्तीनां वृष्टिः इव भवति।

प्रश्नाः
(i) सागरमध्ये एकं लघुद्वीपं कुत्र वर्तते ?
(ii) तस्मिन् द्वीपे सागरतरङ्गः क्षाल्यमानं किम् कन्याकुमारी इति अस्ति ?
(iii) एषा कन्याकुमारी केषाम् सइगमस्थली अस्ति ?
(iv) समुद्रजले प्रतिबिम्बितं सूर्योदयस्य दृश्यम् कीदृशं भवति ?
(v) सूर्यस्य कीदृशी शोभा दर्शकान् मन्त्रमुग्धान् करोति ?
उत्तराणि:
(i) सागरमध्ये एकं लघुद्वीपं दक्षिण भारते वर्तते।।
(ii) तस्मिन् द्वीपे सागरतरङ्गैः क्षाल्यमानं प्राचीनं नगरं कन्याकुमारी इति अस्ति।
(iii) एषा कन्याकुमारी त्रयाणां सागराणां सइगमस्थली अस्ति।
(iv) समुद्रजले प्रतिबिम्बितं सूर्योदयस्य दृश्यम् अद्भुतं भवति।
(v) सूर्यस्य क्रमशः अरुणा पीता धवला च शोभा दर्शकान् मन्त्रमुग्धान् करोति।

11. अधोलिखितम्-अनुच्छेदं पठित्वा प्रदत्तप्रश्नानाम् उत्तराणि संस्कृतपूर्णवाक्येन लिखत-
एकस्मिन् देवालये ताम्रचूडः नाम परिव्राजक: वसति स्म। स च प्रत्यहं भिक्षाटनं कृत्वा जीविकानिर्वाहं करोति। सर्वां भिक्षां भिक्षापात्रे निधाय नागदन्ते अवलम्ब्य रात्रौ स्वपिति। अथ एकदा मूषकाः स्वस्वामिनम् अकथयन्-स्वामिन्। वयं भिक्षां भक्षयतुं न शक्नुमः। भवान् तत्र आरोढुं समर्थः। अतः कृपां कुरु। मूषक-स्वामी भिक्षापात्रं समारुह्य मूषकेभ्यः भिक्षान्नम् अयच्छत्। परिव्राजकः अचिन्तयत् – कथमेनं मारयेयम्। सः जर्जरवंशम् आनीय पुनः पुनः ताडयति। एकदा तस्य मित्रं तत्र आगच्छत् । स परिव्राजकम् अवदत् — यदि त्वं मद्वचनं न शृणोषि तर्हि अन्यत्र यास्यामि । परिव्राजक: उवाच् मा एवं वद। अहं मूषकेण त्रस्तः किं कुर्याम् ?

प्रश्ना:
(i) ताम्रचूड: नाम परिव्राजकः कुत्र वसति स्म ?
(ii) ताम्रचूड: सर्वां भिक्षां किं कृत्वा रात्रौ स्वपिति ?
(iii) मूषक-स्वामी किं कृत्वा मूषकेभ्यः भिक्षान्नम् अयच्छत् ?
(iv) परिव्राजक: किं आनीय पुनः पुनः ताडयति ?
(v) परिव्राजक: किमर्थं मित्रस्य वचनं न शृणोति ?
उत्तराणि:
(i) ताम्रचूड: नाम परिव्राजकः एकस्मिन् देवालये वसति स्म।
(ii) ताम्रचूड: सर्वां भिक्षां भिक्षापात्रे निधाय नागदन्ते अवलम्ब्य रात्रौ स्वपिति।
(iii) मूषक-स्वामी भिक्षापात्रं समारुह्य मूषकेभ्यः भिक्षान्नम् अयच्छत् ।
(iv) परिव्राजक: जर्जनवंशम् आनीय पुनः पुनः ताडयति।
(v) परिव्राजक: मूषकेण त्रस्तः, अतएव मित्रस्य वचनं न शृणोति।

12. अधोलिखितम्-अनुच्छेदं पठित्वा प्रदत्तप्रश्नानाम् उत्तराणि संस्कृतपूर्णवाक्येन लिखत
एकदा प्रात:काले बालः सिद्धार्थः उपवने भ्रमणम् अकरोत्। तदा गगने कस्यचित् व्याधस्य बाणेन एकः हंसः विद्धः अभवत्, सः च प्रकम्पमान: सिद्धार्थस्य उपवने अपतत् सिद्धार्थः धावित्वा हंसम् उपागच्छत्। हंसः पीडया व्यथितः आसीत्। सः हंसस्य शरीरात् बाणं बहिः अकरोत् । तदा देवदत्तः तत्र आगतः। सः अकथयत् – अयं मम हंसः अस्ति यतः अयं मया एव बाणेन विद्धः आसीत्। उभौ स्वपक्षे निर्णयं प्राप्तुं न्यायालयं गतौ। न्यायाधीशः अकथयत् – अ पक्षी तस्मै दास्यते यस्य समीपे मया मुक्तः अयं गमिष्यति। तदा राज्ञा मुक्तः सः हंसः सिद्धार्थम् उपागच्छत्। सिद्धार्थः तं गृहीत्वा गगने अमुञ्चत्।

प्रश्ना:
(i) बालः सिद्धार्थः कुत्र भ्रमणम् अकरोत् ?
(ii) गगने हंसः केन विद्धः अभवत् ?
(iii) ‘अयं मम हंसः अस्ति’ इति कः अवदत् ?
(iv) उभौ किमर्थम् न्यायालयं गतौ ?
(v) राज्ञा मुक्तः सः हंसः कम्’ उपागच्छत् ?
उत्तराणि
(i) बालः सिद्धार्थः उपवने भ्रमणम् अकरोत्।
(ii) गगने हंसः कस्यचित् व्याधस्य बाणेन विद्धः अभवत् ।
(iii) ‘अयं मम हंसः अस्ति’ इति सिद्धार्थः अवदत्।
(iv) उभौ स्वपक्षे निर्णयं प्राप्तुं न्यायालयं गतौ ?
(v) राज्ञा मुक्तः सः हंसः सिद्धार्थम् उपागच्छत् ?

13. अधोलिखितम्-अनुच्छेदं पठित्वा प्रदत्तप्रश्नानाम् उत्तराणि संस्कृतपूर्णवाक्येन लिखत
एक: शशक: कच्छपम् अवदत् – त्वं शनैः शनैः चलसि। अहं तु तीव्र धावामि। कच्छपः अवदत् – रे । शशक ! अहं शनैः शनैः चलामि परम आलस्यं न करोमि । तयोः मध्ये अयं समयः अभवत् – मार्गस्य अन्ते यः जलाशयः अस्ति, तत्र यः पूर्वं गमिष्यति सः विजयी भविष्यति । शशक: अधावत् -परं कच्छप: मन्दं मन्दम् अचलत्। किञ्चित् दूरं गत्वा शशक: वृक्षस्य छायायां विश्रामम् अकरोत्। श्रान्तः सः शीघ्रं गाढनिद्रायां सुप्तः। कच्छपः शशकं सुप्तं दृष्ट्वा अग्रे अचलत्। शशकः चिरात् निद्रां त्यक्त्वा यदा जलाशयस्य समीप प्राप्तः तदा तत्र स्थितः कच्छपः वदति-“ये सततं कार्ये संलग्नाः, तेषाम् एव विजयः भवति।

प्रश्ना:
(i) शशककच्छपमध्ये कः तीव्र धावति ?
(ii) कच्छपशशकमध्ये कः समयः अभवत् ?
(iii) शशकः कुत्र विश्रामं अकरोत् ?
(iv) शशक: जलाशयस्य समीपं कदा प्राप्तः ?
(v) केषाम् सततम् विजयः भवति ? (H.B. 2007-C)
उत्तराणि
(i) शशककच्छपमध्ये शशकः तीव्र धावति।
(ii) तयोः मध्यं अयं समयः अभवत् – मार्गस्य अन्ते यः जलाशयः अस्ति, तत्र यः पूर्वं गमिष्यति सः विजयी भविष्यति।।
(iii) शशक: वृक्षस्य छायायां विश्राम अकरोत्।
(iv) यदा कच्छपः विजय प्राप्तः तत्पश्चात् शशक: जलाशयस्य समीपं प्राप्तः।
(v) ये सततं कार्ये संलग्नाः भवन्ति, तेषाम् एव विजयः भवति।

अभ्यासार्थम्

1. अधोलिखितम्-अनुच्छेदं पठित्वा प्रदत्तप्रश्नानाम् उत्तराणि संस्कृतपूर्णवाक्येन लिखत
महर्षेः दयानन्दस्य जन्मनाम मूलशंकरः आसीत्। अयं महात्मा गुजरातप्रान्तस्य मौर्वी राज्ये टंकारा ग्रामे औदीच्यब्राह्मणकुले जन्म अलभत। अस्य पितुः नाम अम्बाशंकरः आसीत्। अस्मिन् कुले शिवपूजा महती भक्तिरूपेण भवति स्म। अम्बाशंकरः स्वपुत्रमपि शिवभक्तं द्रष्टुम् ऐच्छत्। पश्चात् एष संस्कृतस्य महान् विद्वान् अभवत्। वेदेषु अस्य अपारनिष्ठा आसीत्। एष एव श्रेष्ठसमाज-निर्माणाय आर्यसमाजस्य स्थापनाम् अकरोत्।

प्रश्नाः
(i) महर्षेः दयानन्दस्य जन्मनाम किम् आसीत् ?
(ii) कस्मिन् कुले महर्षेः दयानन्दस्य जन्म अभवत् ?
(iii) अस्य कुले कस्य पूजा भवति स्म ?
(iv) अम्बाशंकरः कस्य नाम आसीत् ?
(v) महर्षिः द्रयानन्दः आर्यसमाजस्य स्थापनाम् किमर्थम् अकरोत् ?

(2) अधोलिखितम्-अनुच्छेदं पठित्वा प्रदत्तप्रश्नानाम् उत्तराणि संस्कृतपूर्णवाक्येन लिखत
प्रकृतिः मनुष्यस्य उपकारिणी। मनुष्यैः सह तस्याः शाश्वत: सम्बन्धः । सा विविधरूपेषु अस्मिन् जगति आत्मानं प्रकटयति। विविधाः ओषधयः सकलानि खनिजानि च प्रकृतेः एव शोभा। सा तु नित्यम् एव एतैः साधनैः सर्वेषाम् उपकारं करोति, परम् अधन्यः अयं जनः कृतज्ञतां विहाय असाधुसेवितं पथं गच्छति, विविधानि कष्टानि च अनुभवति । नरः शाश्वतं सुखं वाञ्छति चेत् तर्हि प्रकृतेः प्रतिकूलं कदापि न आचरेत्।

प्रश्नाः-
(i) मनुष्यैः सह कस्याः शाश्वतः सम्बन्धः ?
(ii) प्रकृतिः विविधरूपेषु कुत्र आत्मानं प्रकटयति ?
(iii) प्रकृतेः का शोभा अस्ति ?
(iv) प्रकृति कस्य उपकारिणी अस्ति ?
(v) नरः शाश्वतं सुखं वाञ्छति चेत् तर्हि किं कदापि न आचरेत् ?

3. अधोलिखितम्-अनुच्छेदं पठित्वा प्रदत्तप्रश्नानाम् उत्तराणि संस्कृतपूर्णवाक्येन लिखत
अहं पाटलपुष्पम् अस्मि। दिने रविकिरणा: मां विकासयन्ति रात्रौ ज्योत्स्ना मां लालयति। मम अनेके वर्णाः-श्वेतः, पीतः, नारङ्गः, अरुणः, पाटलश्च । एतेषु रक्तिमः वर्णः जनेभ्यः सर्वाधिकं रोचते। वरवध्वोः जयमालयोः अहं विलसामि। अहं मृदुना सुगन्धेन वातावरणं सुरभितं करोमि । मम स्वल्पकालजीवनमपि लोकहितम् आतनोति अतः पूर्णविकसितं मे रूपम् अभिनन्दन्ति जनाः।

प्रश्ना :
(i) पाटलपुष्पम् कुत्र विलसति ?
(ii) दिने के पाटलपुष्पं विकासयन्ति ?
(iii) रात्रौ पाटलपुष्पं का लालयति ?
(iv) पाटलपुष्पस्य कति वर्णाः भवन्ति ?
(v) पाटलपुष्पस्य कं रूपं जनाः अभिनन्दन्ति ?

4. अधोलिखितम्-अनुच्छेदं पठित्वा प्रदत्तप्रश्नानाम् उत्तराणि संस्कृतपूर्णवाक्येन लिखत-
कस्मिंश्चित् नगरे एकः नसीमः नाम धनिकः वसति। नसीमः अतीव उदारपुरुषः आसीत्। सः सदैव निर्धनेभ्यः धनम्, वस्त्रहीनेभ्यः च वस्त्रम् यच्छति। एकदा तस्य प्रदेशे वर्षा न अभवत्। अन्नस्य तु तस्मिन् प्रदेशे अभावः एव अभवत्। तदा स: नसीमः सर्वेभ्य: जनेभ्यः अन्नदानम् अकरोत्। सः प्रतिदिनम् निर्धनेभ्यः अन्नम् भोजनम् च यच्छति। तस्य नगरे कोऽपि जनः क्षुधया पीडितः न अभवत्। एकदा नसीमः मार्गे काष्ठभारं वहन् एकम् वृद्धम् अपश्यत्। सः तम् अपृच्छत्-“त्वम् भोजनाय नसीमस्य गृहे किमर्थम् न गच्छसि ? वृथा वृद्धावस्थायाम् अपि श्रमम् करोषि इति”। वृद्धः अवदत् “श्रम एव मम जीवनम् न तु हस्तप्रसारणम्”।

(क) नसीमः कीदृशः पुरुषः आसीत् ?
(ख) स: केभ्यः धनम् यच्छति ?
(ग) नसीमः भारवहन् कम् अपश्यत् ?
(घ) तस्य नगरे कोऽपि जनः कया पीड़ितः न अभवत् ?
(ङ) अस्य अनुच्छेदस्य उचितं शीर्षकं लिखत।

5. अधोलिखितम्-अनुच्छेदं पठित्वा प्रदत्तप्रश्नानाम् उत्तराणि संस्कृतपूर्णवाक्येन लिखत
एक: कर्तव्यपरायणः नगररक्षकः आसीत्। यदा सः इतस्ततः अभ्रमत् तदा एकम् वृद्धम् महापुरुषम् अपश्यत्। सः वृद्धः आम्रवृक्षस्य आरोपणे लीनः आसीत्। इदम् दृष्ट्वा सः नगररक्षकः तम् अवदत्-“भवान् किमर्थम् वृथा परिश्रमम् करोति ? यतः यदा एषः वृक्ष: फलिष्यति तदा भवान् जीवितः न भविष्यति, अतः अलं श्रमेण” । वृद्धः महापुरुषः हसित्वा अवदत्”पश्यतु भवान् एतान् फलयुक्तान् वृक्षान्, एतेषाम् आरोपणम् मया न कृतम् परं अहम् फलानि खादित्वा सन्तुष्ट: भवामि। अतः यदा मम आरोपितस्य वृक्षस्य फलानि अन्ये खादिष्यन्ति, अहम् पुनः प्रसन्नः भविष्यामि”। महापुरुषस्य वचनम् श्रुत्वा नगररक्षकः अचिन्तयत्-“अहम् अपि वृक्षान् आरोपयिष्यामि”।

(क) नगररक्षकः कीदृशः आसीत् ?
(ख) सः कीदृशम् महापुरुषम् अपश्यत् ?
(ग) वृद्धः महापुरुषः कस्य आरोपणे लीनः आसीत् ?
(घ) कस्य वचनम् श्रुत्वा नगररक्षकः अचिन्तयत् ?
(ङ) अस्य अनुच्छेदस्य उचितं शीर्षकं लिखत।

6. अधोलिखितम्-अनुच्छेदं पठित्वा प्रदत्तप्रश्नानाम् उत्तराणि संस्कृतपूर्णवाक्येन लिखत
एक: कृषक: तस्य भार्या च प्रतिदिनम् स्वक्षेत्रे कार्यम् अकुरुताम्। एकदा यदा कृषक: खनित्रेण भूमिम् खनति स्म तदा सः एकम् स्वर्णस्य महाकुम्भम् प्राप्नोति। कुम्भे च स्वर्णमुद्राः आसन्। तौ प्रसन्नौ भूत्वा गृहे अगच्छताम्। अग्रिमे दिवसे कृषकस्य भार्या स्वसख्यै सर्वम् न्यवेदयत्। जनाः कृषकम् कथयन्ति धनम् राजकोषे यच्छ। यदा रात्रौ तस्य पत्नी स्वपिति स्म तदा कृषक: अनेकानि मिष्ठान्नानि क्रीत्वा सूत्रखण्डै: बद्ध्वा उद्यानस्य वृक्षेषु लम्बयत। यदा तस्य पत्नी वृक्षेषु मिष्ठान्नानि फलितानि सन्ति । सर्वे जनाः हसित्वा गच्छन्ति। कृषक: तु कथयति-“मम भार्या तु अद्यत्वे कल्पनालोके एव विचरति। स्वर्णकुम्भः अपि तस्याः कल्पना एव”।

(क) कृषकः प्रतिदिनम् कुत्र कार्यम् अकरोत् ?
(ख) क्षेत्रे कृषक: किम् प्राप्नोति ?
(ग) धनम् राजकोषे प्रयच्छ इति के कथयन्ति ?
(घ) कृषक: केन भूमिम् खनति ?
(ङ) अस्य अनुच्छेदस्य उचितं शीर्षकं लिखत।

7. अधोलिखितम्-अनुच्छेदं पठित्वा प्रदत्तप्रश्नानाम् उत्तराणि संस्कृतपूर्णवाक्येन लिखत
अस्माकं जन्मभूमिः भारतवर्षमस्ति। देशोऽयमतिरमणीयः वर्तते। देवाः अप्यस्य दर्शनोत्सुकाः भवन्ति। अस्य भूमिः विविधानि फलानि अन्नानि च उत्पादयति। भारतस्योत्तरस्यां दिशि नगाधिराजो हिमालयः शोभते। दक्षिणस्यां च दिशि सागरः पादक्षालनं करोति। षड्ऋतवोऽत्र क्रमशः आगच्छन्ति। अत्र अनेकाः भाषाः, विविधाः सम्प्रदायाः, विभिन्नाः जातयश्च सन्ति, पुनरपि अनेकतायामप्येकता सर्वत्र दृश्यते।

(i) भारतस्योत्तरस्यां दिशि कः शोभते ?
(ii) भारतभूमिः कानि उत्पादयति ?
(iii) . देशोऽयं कीदृशः वर्तते ?
(iv) दक्षिणस्यां दिशि कः पादक्षालनं करोति ?
(v) कति ऋतवोऽत्र क्रमशः आगच्छन्ति ?

Haryana State Board HBSE 10th Class Maths Solutions Chapter 10 वृत्त Ex 10.2 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 10 वृत्त Exercise 10.2

प्रश्न 1.
एक बिंदु Q से एक वृत्त पर स्पर्श रेखा की लंबाई 24 cm तथा Q की केंद्र से दूरी 25 cm है। वृत्त की त्रिज्या है
(A)7 cm
(B) 12 cm
(C) 15 cm
(D) 24.5 cm
हल :
(A)7 cm

कारण-दिए गए वृत्त का केंद्र 0 लेने पर QT वृत्त की स्पर्श रेखा तथा OT वृत्त की त्रिज्या है परंतु त्रिज्या और स्पर्श रेखा के बीच 90° का कोण होता है।
अतः OQ = 25cm
QT = 24cm
अतः वृत्त की त्रिज्या (OT) = \(\sqrt{(\mathrm{OQ})^{2}-(\mathrm{QT})^{2}}\)
= \(\sqrt{(25)^{2}-(24)^{2}}\)
= \(\sqrt{625-576}=\sqrt{49}\)
= 7cm

प्रश्न 2.
संलग्न आकृति में, यदि TP, TQ केंद्र 0 वाले किसी वृत्त पर दो स्पर्श रेखाएँ इस प्रकार हैं कि ∠POQ = 110°, तो ∠PTQ बराबर है
(A) 60°
(B) 70°
(C) 80°
(D) 90°
हल :
(B)70°

कारण-क्योंकि स्पर्श रेखा और त्रिज्या के बीच का कोण 90° होता है।
∠OPT = 90° व ∠OQT = 90°
∠POQ = 110° व ∠PTQ = ?
चतुर्भुज POQT में,
∠PTQ + ∠OPT + ∠POQ + ∠OQT = 360°
∠PTQ+ 90° + 110° + 90° = 360°
∠PTO+290° = 3600
∠PTQ = 360° – 290° = 70°

प्रश्न 3.
यदि एक बिंदु P से 0 केंद्र वाले किसी वृत्त पर PA, PB स्पर्श रेखाएँ परस्पर 80° के कोण पर झुकी हों, तो ∠POA बराबर है-
(A)50°
(B) 60°
(C) 70°
(D) 80°
हल :
(A)50°

कारण-यहाँ पर, PA और PB स्पर्श रेखाएँ हैं जो केंद्र O वाले वृत्त पर स्थित हैं।
हम जानते हैं कि वृत्त की त्रिज्या और स्पर्श रेखा के बीच 90° का कोण होता है।
∠OAP = 90° व ∠OBP = 90°
ΔPAO और ΔPBO में,
PA = PB (बाह्य बिंदु से समान स्पर्श रेखाएँ)
OA = OB (वृत्त की त्रिज्याएँ)
OP = OP (उभयनिष्ठ)
ΔPAO ≅ ΔΡΒΟ (sss सर्वांगसमता)
∠APO = ∠BPO = \(\frac{1}{2}\) x 80° = 40°
अब ΔPAO में,
∠OAP + ∠POA + ∠APO = 180°
90° + ∠POA + 40° = 180°
∠POA = 180° – 130° = 50°

प्रश्न 4.
सिद्ध कीजिए कि किसी वृत्त के किसी व्यास के सिरों पर खींची गई स्पर्श रेखाएँ समांतर होती हैं।
हल :

दिया है-एक वृत्त C(O, R) का कोई व्यास AOB है जिसके सिरों A और B पर क्रमशः स्पर्श रेखाएँ PQ और RS खींची गई हैं।
सिद्ध करना है-PQ || RS
प्रमाण-हम जानते हैं कि स्पर्श रेखा और त्रिज्या के बीच बनने वाला कोण 90° होता है।
∴ ∠PAB = 90° व ∠ABS = 90°
∠PAB = ∠ABS
परंतु ये एकांतर कोण हैं।
∴ PQ || RS [इति सिद्धम्]

प्रश्न 5.
सिद्ध कीजिए कि स्पर्श बिंदु से स्पर्श रेखा पर खींचा गया लंब वृत्त के केंद्र से होकर जाता है।
हल :

माना केंद्र O वाले वृत्त की एक स्पर्श रेखा AB है जो वृत्त को P पर स्पर्श करती है। यदि संभव हो तो PQ ⊥ AB जो केंद्र से नहीं गुजरता है।
हम जानते हैं कि स्पर्श बिंदु पर स्पर्श रेखा और त्रिज्या लंबवत् होती है।
AB ⊥ OP
∠OPB = 90°
∠QPB = 90° (रचना से)
∠QPB = ∠OPB
परंतु यह असंभव है, क्योंकि एक भाग पूरे के समान नहीं हो सकता। इसलिए हमारी कल्पना गलत है।
अतः स्पर्श बिंदु पर स्पर्श रेखा पर खींचा गया लंब वृत्त के केंद्र से गुजरता है।

प्रश्न 6.
एक बिंदु A से, जो एक वृत्त के केंद्र से 5 cm दूरी पर है, वृत्त पर स्पर्श रेखा की लंबाई 4 cm है। वृत्त की त्रिज्या ज्ञात कीजिए।
हल :

हम जानते हैं कि स्पर्श बिंदु पर स्पर्श रेखा और त्रिज्या लंबवत होते हैं।
∴ ∠OPA = 90°
OA = 5cm
PA = 4cm
समकोण ΔOPA में,
OP = \(\sqrt{(\mathrm{OA})^{2}-(\mathrm{PA})^{2}}\)
= \(\sqrt{(5)^{2}-(4)^{2}}\)
= \(\sqrt{25-16}=\sqrt{9}\) = 3 cm
अतः वृत्त की त्रिज्या = 3cm

प्रश्न 7.
दो संकेंद्रीय वृत्तों की त्रिज्याएँ 5 cm तथा 3 cm हैं। बड़े वृत्त की उस जीवा की लंबाई ज्ञात कीजिए जो छोटे वृत्त को स्पर्श करती हो।
हल :

माना, दिए गए दो संकेंद्रीय वृत्तों का केंद्र 0 है तथा AB बड़े वृत्त की जीवा है जो छोटे वृत्त को बिंदु P पर स्पर्श करती है।
OP तथा OA को मिलाओ।
हम जानते हैं कि स्पर्श रेखा और त्रिज्या परस्पर लंबवत् होती है।
∴ ∠OPA = 90°
OP = 3 cm
OA = 5 cm

अब AB = 2 x AP = 2 x 4 cm = 8 cm
अतः जीवा AB की लंबाई = 8 cm

प्रश्न 8.
एक वृत्त के परिगत एक चतुर्भुज ABCD खींचा गया है (देखिए संलग्न आकृति)। सिद्ध कीजिए-
AB + CD = AD + BC
हल :

दिया है-ABCD एक चतुर्भुज है जो वृत्त को P, Q, R तथा S पर स्पर्श करता है।
सिद्ध करना है-AB + CD = AD + BC
प्रमाण-हम जानते हैं कि वृत्त के किसी बाह्य बिंदु से खींची गई स्पर्श रेखाएँ समान .. होती हैं।
AP = AS ………….(i)
BP = BQ ……..(ii)
CR = CQ ……..(iii)
DR = DS ……..(iv)
समीकरण (i), (ii), (iii) व (iv) को जोड़ने पर,
___AP + BP + CR + DR = AS + BQ + CQ + DS
या (AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
या AB + CD = AD + BC [इति सिद्धम् ]

प्रश्न 9.
संलग्न आकृति में XY तथा X’Y’, O केंद्र वाले किसी वृत्त पर दो समांतर स्पर्श रेखाएँ हैं और स्पर्श बिंद्र C पर स्पर्श रेखा AB,XY को A तथा X’Y’ को B पर प्रतिच्छेद करती है। सिद्ध कीजिए कि ∠AOB = 90° है।
हल :

दिया है-XY और X’Y’ केंद्र 0 वाले वृत्त की दो समांतर स्पर्श रेखाएँ हैं तथा स्पर्श बिंदु C वाली एक अन्य स्पर्श रेखा AB, XY को A पर तथा X’Y’ को B पर प्रतिच्छेद करती है। OA और OB को मिलाने पर ∠AOB प्राप्त होता है।
सिद्ध करना है-∠AOB = 90°
रचना-O और C को मिलाइए। इसी प्रकार स्पर्श रेखाओं XY और X’Y’ के स्पर्श बिंदु P और Q को 0 से मिलाएँ।
प्रमाण-क्योंकि XY स्पर्श रेखा है और OP एक त्रिज्या है।
∠OPA = 90° ………….(i)
इसी प्रकार, AB स्पर्श रेखा है और OC एक त्रिज्या है।
∠OCA = 90° ……..(ii)
अब समकोण AOPA और समकोण AOCA में,
AP = AC (बाह्य बिंदु से एक ही वृत्त की स्पर्श रेखाएँ)
∠OPA = ∠OCA (प्रत्येक 90°)
OA = OA (उभयनिष्ठ)
अतः ∆OPA = missing ∆OCA (समकोण-कर्ण भुजा सर्वांगसम नियम से)
∠POA = ∠COA ……..(iii)
इसी प्रकार ∠QOB = ∠COB ……………(iv)
समीकरण (ii) व (iv) से,
∠POA + ∠QOB = ∠COA + ∠COB = 180° [∵ POQ एक सरल रेखा है]
∠COA + ∠COB = 90°
∠AOB = 90° [इति सिद्धम् ]

प्रश्न 10.
सिद्ध कीजिए कि किसी बाह्य बिंदु से किसी वृत्त पर खींची गई स्पर्श रेखाओं के बीच का कोण स्पर्श बिंदुओं को मिलाने वाले रेखाखंड द्वारा केंद्र पर अंतरित कोण का संपूरक होता है।
हल :

दिया है-एक वृत्त पर एक बाह्य बिंदु P से PA तथा PB दो स्पर्श रेखाएँ खींची गई हैं।
सिद्ध करना है- ∠APB + ∠AOB = 180°
रचना-A व B को वृत्त के केंद्र 0 से मिलाओ।
प्रमाण-क्योंकि PA स्पर्श रेखा है और OA त्रिज्या है।
OA ⊥ PA
∴ ∠PAO = 90° …………(i)
इसी प्रकार, ∠PBO = 90° …….(ii)
चतुर्भुज PAOB में,
∠APB + ∠PAO + ∠AOB + ∠PBO = 360°
∠APB + 90° + ∠AOB + 90° = 360°
∠AOB + ∠APB = 360° – 90° – 90° = 180°
अतः एक वृत्त पर एक बाह्य बिंदु से खींची गई स्पर्श रेखाओं के बीच कोण का स्पर्श बिंदुओं को मिलाने वाले रेखाखंड द्वारा केंद्र पर अंतरित कोण का संपूरक होता है। [इति सिद्धम्]

प्रश्न 11.
सिद्ध कीजिए कि किसी वृत्त के परिगत समांतर चतुर्भुज समचतुर्भुज होता है।
हल :

दिया है-एक समानांतर चतुर्भुज ABCD की चारों भुजाएँ एक वृत्त C (O, r) को बिंदुओं पर स्पर्श करती हैं।
सिद्ध करना है-ABCD एक समचतुर्भुज है।
प्रमाण-क्योंकि ABCD एक समांतर चतुर्भुज है।
∴ AB = CD तथा AD = BC
हम जानते हैं कि किसी वृत्त पर बाह्य बिंदु से खींची गई स्पर्श रेखाएँ समान होती है।
∴ AP = AS …..(i) [बिंदु A से वृत्त पर स्पर्श रेखाएँ]
BP = BQ ……(ii) [बिंदु B से वृत्त पर स्पर्श रेखाएँ]
CR = CQ …..(iii) [बिंदु C से वृत्त पर स्पर्श रेखाएँ]
DR = DS …..(iv) [बिंदु D से वृत्त पर स्पर्श रेखाएँ]
समीकरण (i), (ii), (iii) व (iv) को जोड़ने पर,
AP + BP + CR + DR = AS + BQ + CQ + DS
(AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
AB + CD = AD + BC
AB + AB = BC + BC
[:: AB = CD, BC = AD]
2AB = 2BC
AB = BC
इसलिए समानांतर चतुर्भुज ABCD में AB = BC = CD = AD
अतः ABCD एक समचतुर्भुज है। [इति सिद्धम्]

प्रश्न 12.
4 cm त्रिज्या वाले एक वृत्त के परिगत एक त्रिभुज ABC इस प्रकार खींचा गया है कि रेखाखंड BD और DC (जिनमें स्पर्श बिंदु D द्वारा BC विभाजित है) की लंबाइयाँ क्रमशः 8 cm और 6 cm हैं (देखिए संलग्न आकृति)। भुजाएँ AB और AC ज्ञात कीजिए।
हल :

माना, ∆ABC का अंतः केंद्र 0 इस प्रकार है कि
OD = OE = OF = 4 cm
BD = BE = 8 cm
(बाह्य बिंदु B से स्पर्श रेखाएँ)
CD = CF = 6 cm (बाह्य बिंदु C से स्पर्श रेखाएँ)
माना AF = AE = x cm (बाह्य बिंदु A से स्पर्श रेखाएँ)
अब AB = AE + BE = (x + 8) cm
AC = AF + CF = (x +6) cm
BC = CD + BD = 6 + 8 = 14 cm
अब ∆ABC में,

परंतु ∆ABC का क्षेत्रफल = (∆BOC + ∆AOC + ∆AOB) का क्षेत्रफल
= \(\frac{1}{2}\) x BC x OD + \(\frac{1}{2}\) x AC x OF + \(\frac{1}{2}\) x AB x OE
= \(\frac{1}{2}\) x 14 x 4 + \(\frac{1}{2}\) x (x + 6) x 4 + \(\frac{1}{2}\) x (x + 8) x 4
= 28 + (2x + 12) + (2x + 16)
= 4x + 56 …..(ii)
समीकरण (i) व (ii) की तुलना से,
\(\sqrt{48 x(x+14)}\) = 4x + 56
दोनों ओर का वर्ग करने पर,
48x(x + 14) = (4x + 56)²
48x(x + 14) = 16(x + 14)²
3x(x + 14) = (x + 14)²
3x = (x + 14)
या 3x-x = 14
या 2x = 14
या x = 14/2 = 7
अतः AB = x +8 = 7+ 8 = 15 cm
x + 6 = 7+ 6 = 13 cm

प्रश्न 13.
सिद्ध कीजिए कि वृत्त के परिगत बनी चतुर्भुज की आमने-सामने की भुजाएँ केंद्र पर संपूरक कोण अंतरित करती हैं।
हल :

दिया है-एक वृत्त C(O, R) जोकि एक चतुर्भुज ABCD की भुजाओं AB, BC, CD और DA को क्रमशः बिंदुओं P, Q, R और S पर स्पर्श करता है।
सिद्ध करना है-∠AOB + ∠COD = 180° तथा ∠BOC + ∠AOD = 180°
रचना-OP, OQ, OR तथा OS को मिलाइए।
प्रमाण-हम जानते हैं कि बाह्य बिंदु से किसी वृत्त पर खींची गई दोनों स्पर्श रेखाएँ वृत्त के केंद्र पर समान कोण अतरित करती हैं।
∠1 = ∠2 ……(1) [∵ AP = AS]
∠3 = ∠4 ……(ii) [∵ BP = BQ]
∠5 = ∠6 ……(iii) [∵ CQ=CR]
∠7 = ∠8 …….(iv) [∵ DR = DS]
हम जानते हैं कि बिंदु O पर बने सभी कोणों का योग चार समकोण है।
∠1 + ∠2 + ∠3 + ∠4+ ∠5 + ∠6 + ∠7+ ∠8 = 360°
2(∠2 + ∠3 + ∠6 + ∠7) = 360° तथा ∠(∠1 + ∠8 + ∠4+ ∠5) = 360°
[समीकरण (i) से (iv) का प्रयोग करने पर]
∠2 + ∠3 + ∠6 + ∠7 = 180° तथा ∠1 + ∠8 + ∠4 + ∠5 = 180°
(∠2 + ∠3) + (∠6 + ∠7) = 180° तथा (∠1 + ∠8) + (∠4 + ∠5) = 180°
∠AOB + ∠COD = 180° [:: ∠2 + ∠3 = ∠AOB तथा ∠6 + ∠7 = ∠COD]
तथा ∠AOD + ∠BOC = 180° ∠1+ ∠8 = ∠AOD तथा ∠4+ ∠5 = ∠BOC ] [इति सिद्धम्]

Haryana State Board HBSE 10th Class Maths Solutions Chapter 11 रचनाएँ Ex 11.2 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 11 रचनाएँ Exercise 11.2

प्रश्न 1.
6 cm त्रिज्या का एक वृत्त खींचिए। केंद्र से 10 cm दूर स्थित एक बिंदु से वृत्त पर स्पर्श रेखा युग्म की रचना कीजिए और उनकी लंबाइयाँ मापिए।
हल :

रचना के चरण
(1) O को केंद्र मानकर 6 cm त्रिज्या की चाप द्वारा एक वृत्त खींचिए।
(2) O से 10 cm की दूरी पर एक बिंदु P लीजिए।
(3) O व P को मिलाइए।
(4) OP को बिंदु M पर समद्विभाजित कीजिए।
(5) अब M को केंद्र मानकर तथा OM को त्रिज्या लेकर एक वृत्त खींचिए जो दिए हुए वृत्त को Q तथा R पर प्रतिच्छेदित करे।
(6) PQ तथा PR को मिलाइए। यही PQ तथा PR वृत्त की अभीष्ट स्पर्श रेखाएँ हैं।
(7) मापने पर PQ = PR = 8 cm है।

प्रश्न 2.
4 cm त्रिज्या के एक वृत्त पर 6 cm त्रिज्या के एक संकेंद्रीय वृत्त के किसी बिंदु से एक स्पर्श रेखा की रचना कीजिए और उसकी लंबाई मापिए। परिकलन से इस माप की जाँच भी कीजिए।
हल :

रचना के चरण-
(1) O को केंद्र मानकर 4 cm त्रिज्या तथा 6 cm त्रिज्या की चाप द्वारा दो संकेंद्रीय वृत्त खींचिए।
(2) बड़े वृत्त की परिधि पर एक बिंदु P अंकित करें।
(3) OP को मिलाकर इसका लंब समद्विभाजक M प्राप्त कीजिए।
(4) अब M को केंद्र मानकर तथा OM को त्रिज्या लेकर एक वृत्त खींचिए जो छोटे वृत्त को Qतथा R पर प्रतिच्छेद करे।
(5) PQ तथा PR को मिलाइए। यही PQ तथा PR छोटे वृत्त की अभीष्ट स्पर्श रेखाएँ हैं।
(6) मापने पर PQ = PR = 4.5 cm (लगभग) है।
जाँच-OQ को मिलाकर समकोण ΔPQO प्राप्त कीजिए।
अब समकोण ΔPQO में,
OQ = 4 cm, OP = 6 cm
PQ = \(\sqrt{(O P)^{2}-(O Q)^{2}}=\sqrt{(6)^{2}-(4)^{2}}\)
= \(\sqrt{36-16}=\sqrt{20}\) = 4.47 cm = missing 4.5 cm

प्रश्न 3.
3 cm त्रिज्या का एक वृत्त खींचिए। इसके किसी बढ़ाए गए व्यास पर केंद्र से 7 cm की दूरी पर स्थित दो बिंदु P और Q लीजिए। इन दोनों बिंदुओं से वृत्त पर स्पर्श रेखाएँ खींचिए।
हल :

रचना के चरण-
(1) O को केंद्र मानकर 3 cm त्रिज्या की चाप द्वारा एक वृत्त खींचिए।
(2) वृत्त के एक व्यास AOB को P और Qतक इस प्रकार बढ़ाए कि OP= OQ = 7 cm हो।
(3) OP तथा OQ के लंब समद्विभाजक क्रमशः M, तथा M, प्राप्त कीजिए।
(4) अब M, को केंद्र तथा M₁P को त्रिज्या मानकर एक वृत्त खींचिए जो दिए
गए वृत्त को T₁, व T₂, पर प्रतिच्छेद करे।
(5) PT₁ तथा PT₂ को मिलाइए। इस प्रकार PT₁ तथा PT₂ बिंदु P से स्पर्श रेखाएँ हैं।
(6) इसी प्रकार M₂ को केंद्र तथा M₂Q को त्रिज्या मानकर एक वृत्त खींचिए जो दिए गए वृत्त को T₃ व T₄ पर प्रतिच्छेद करे।
(7) QT₃ तथा QT₄ को मिलाइए। इस प्रकार QT₃ तथा QT₄ बिंदु Q से स्पर्श रेखाएँ हैं।

प्रश्न 4.
5 cm त्रिज्या के एक वृत्त पर ऐसी दो स्पर्श रेखाएँ खींचिए, जो परस्पर 60° के कोण पर झुकी हों।
हल :

रचना के चरण-
(1) O को केंद्र मानकर 5 cm त्रिज्या लेकर एक वृत्त खींचिए।
(2) वृत्त की किसी त्रिज्या OR से 120° का कोण लेकर एक त्रिज्या OQ खींचिए।
(3) वृत्त की त्रिज्याओं OR तथा OQ के बिंदु R तथा Q पर 90° का कोण बनाइए।
(4) इस प्रकार PR तथा PQ वृत्त की अभीष्ट स्पर्श रेखाएँ हैं जो 60° के कोण पर झुकी हैं।

प्रश्न 5.
8 cm लंबा एक रेखाखंड AB खींचिए। A को केंद्र मानकर 4 cm त्रिज्या का एक वृत्त तथा B को केंद्र लेकर 3 cm त्रिज्या का एक अन्य वृत्त खींचिए। प्रत्येक वृत्त पर दूसरे वृत्त के केंद्र से स्पर्श रेखाओं की रचना कीजिए।
हल :

रचना के चरण-
(1) पैमाने की सहायता से AB = 8 cm लंबा एक रेखाखंड खींचिए।
(2) A को केंद्र मानकर 4 cm त्रिज्या की परकार द्वारा एक वृत्त खींचिए जो AB को O पर मिले।
(3) इसी प्रकार B को केंद्र मानकर 3 cm त्रिज्या की परकार द्वारा एक वृत्त खींचिए।
(4) स्पष्टत बिंदु ० रेखाखंड AB का मध्य-बिंदु है। अब O को केंद्र तथा OA या OB को त्रिज्या मानकर एक वृत्त खींचिए जो केंद्र B वाले वृत्त को T₁ व T₂ तथा केंद्र A वाले वृत्त को T₃ व T₄ पर प्रतिच्छेद करता है।
(5) AT₁, AT₂, BT₃ तथा BT₄ को मिलाने पर वांछित स्पर्श रेखाएँ प्राप्त हो जाती हैं।

प्रश्न 6.
माना ABC एक समकोण त्रिभुज है, जिसमें AB = 6 cm, BC = 8 cm तथा ∠B = 90° है। B से AC पर BD लंब है। बिंदुओं B, C, D से होकर जाने वाला एक वृत्त खींचा गया है। A से इस वृत्त पर स्पर्श रेखा की रचना कीजिए।
हल :

रचना के चरण-
(1) पैमाने की सहायता से BC = 8 cm लंबा एक रेखाखंड खींचिए।
(2) B पर 90° का कोण बनाइए तथा BA = 6 cm काटिए।
(3) A और C को मिलाकर समकोण ΔABC प्राप्त कीजिए।
(4) बिंदु B से BD ⊥ AC खींचिए जो AC को D पर काटे।
(5) अब D को केंद्र तथा DA या DB या DC को त्रिज्या लेकर एक वृत्त खींचिए।
(6) A पर AT ⊥ AD खींचिए जो वृत्त की स्पर्श रेखा होगी।

प्रश्न 7.
किसी चूड़ी की सहायता से एक वृत्त खींचिए। वृत्त के बाहर एक बिंदु लीजिए। इस बिंदु से वृत्त पर स्पर्श रेखाओं की रचना कीजिए।
हल :
im 7
रचना के चरण-
(1) एक चूड़ी लेकर उसे अपनी कॉपी पर रखकर पैंसिल की सहायता से एक वृत्त खींचिए।
(2) वृत्त के बाहर दिए बिंदु A से एक छेदक रेखा ARS खींचिए तथा इसे C तक इस प्रकार बढ़ाइए कि AR = AC हो।
(3) अब CS को व्यास मानकर एक अर्धवृत्त की रचना कीजिए।
(4) बिंदु A पर AB ⊥ AS खींचिए जो अर्धवृत्त को B पर प्रतिच्छेद करे।
(5) अब A को केंद्र तथा AB को त्रिज्या मानकर एक चाप लगाइए जो दिए गए वृत्त को T₁ व T₂ पर प्रतिच्छेदं करे।
(6) AT₁ तथा AT₂ को मिलाने पर वांछित स्पर्श रेखाएँ प्राप्त होती हैं।

Haryana State Board HBSE 10th Class Maths Solutions Chapter 11 रचनाएँ Ex 11.1 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 11 रचनाएँ Exercise 11.1

प्रश्न 1.
7.6 cm लंबा एक रेखाखंड खींचिए और इसे 5 : 8 अनुपात में विभाजित कीजिए। दोनों भागों को मापिए।
हल :
रचना के चरण-

(1) पैमाने की सहायता से 7.6 cm लंबा एक रेखाखंड AB खींचिए।
(2) AB से एक न्यून कोण बनाती हुई किरण AX खींचिए।
(3) किरण AX पर 13(5 + 8) बिंदु A₁,A₂,A₃, A₄,A₅,A₆,A₇,A₈,A₉,A₁₀,A₁₁,A₁₂, और A₁₃ इस प्रकार अंकित कीजिए कि AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅ = A₅A₆ = A₆A₇ = A₇A₈ = A₈A₉ = A₉A₁₀ = A₁₀A₁₁ = A₁₁A₁₂ =A₁₂A₁₃ हो।
(4) A₁₃B को मिलाइए।
(5) A₅ से A₅P || A₁₃B खींचने के लिए बिंदु A₅ पर ∠AA₅P = ∠AA₁₃B बनाइए।
(6) इस प्रकार प्राप्त बिंदु P अभीष्ट बिंदु है जो AB को 5 : 8 के अनुपात में विभाजित करता है।
(7) पैमाने की सहायता से दोनों भागों को मापने पर AP= 2.9 cm तथा PB = 4.7 cm (लगभग) प्राप्त होते हैं।
प्रतिपादन (Justification)-त्रिभुज ABA₁₃; में AP || A₁₃B है।
अतः आधारभूत समानुपातिका प्रमेय से,
\(\frac{\mathrm{AP}}{\mathrm{PB}}=\frac{\mathrm{AA}_{5}}{\mathrm{~A}_{5} \mathrm{~A}_{13}}\)
\(\frac{\mathrm{AP}}{\mathrm{PB}}=\frac{5}{8}\)
AP : PB = 5:8

प्रश्न 2.
4 cm, 5 cm और 6 cm भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर इसके समरूप एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की 2/3 गुनी हों।
हल :

रचना के चरण-
(1) पैमाने की सहायता से 6 cm लंबा एक रेखाखंड BC खींचिए।
(2) B को केंद्र तथा त्रिज्या 5 cm लेकर एक चाप BC के ऊपर की ओर लगाइए।
(3) C को केंद्र तथा त्रिज्या 4 cm लेकर एक चाप BC के ऊपर की ओर लगाइए जो चरण (2) की चाप को A पर प्रतिच्छेद करें।
(4) AB तथा AC को मिलाकर अभीष्ट ΔABC प्राप्त कीजिए।
(5) अब BC के नीचे की ओर एक न्यून कोण CBX बनाइए।
(6) किरण BX पर तीन बिंदु B₁, B₂, तथा B₃, इस प्रकार अंकित कीजिए। कि BB₁ = B₁B₂ = B₂B₃, हो। .
(7) B₃C को मिलाइए।
(8) B₂ से B₂D||B₃C खींचने के लिए बिंदु B₂ पर ∠BB₂D = ∠BB₃C. बनाइए तथा B.D को मिलाइए।
(9) अब बिंदु D से DE || AC खींचने के लिए ∠BDE = ∠BCA बनाइए जो AB को E पर काटे।
इस प्रकार EBD वांछित त्रिभुज है जिसकी भुजाएँ दी गई ΔABC की भुजाओं की 2/3 गुनी है।
प्रतिपादन (Justification)-ΔABC में DE || AC है।
ΔABC ~ ΔEBD (AAA समरूपता से)
\(\frac{E B}{A B}=\frac{B D}{B C}=\frac{D E}{A C}=\frac{2}{3}\)

प्रश्न 3.
5 cm, 6 cm और 7 cm भुजाओं वाले एक त्रिभुज की रचना कीजिए, और फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की 7/5 गुनी हों।
हल :

रचना के चरण-
(1) एक त्रिभुज ABC बनाइए जिसकी भुजाएँ AB = 7 cm, BC = 6 cm तथा AC = 5 cm हों।
(2) बिंदु A से एक किरण AX, रेखाखंड AB के साथ न्यून कोण बनाते हुए खींचिए।
(3) किसी चाप की परकार खोलकर रेखा AX को सात बराबर AX₁, X₁X₂, X₂X₃, X₃X₄, X₄X₅, X₅X₆, X₆X₇ भागों में बाँटिए।।
(4) X₅ को B से मिलाइए।
(5)X₇ से X₇B’||X₅B खींचिए जो AB को बढ़ाने पर B’पर मिले।
(6) B’ से B’C’ || BC खींचिए जो AC को बढ़ाने पर C’ पर मिले।
(7) इस प्रकार ΔAB’ C’ अभीष्ट त्रिभुज है जिसकी भुजाएँ ΔABC की भुजाओं का 7/5 वां भाग हैं।
प्रतिपादन (Justification)-ΔAB’C’ में BC || B’C’ है। ΔABC ~ ΔAB’ C’ (AAA समरूपता से)
\(\frac{A B^{\prime}}{A B}=\frac{B^{\prime} C^{\prime}}{B C}=\frac{A C^{\prime}}{A C}=\frac{7}{5}\)

प्रश्न 4.
आधार 8 cm तथा ऊँचाई 4 cm के एक समद्विबाहु त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ इस समद्विबाहु त्रिभुज की संगत भुजाओं की 1\(\frac{1}{2}\) गुनी हो।
हल :

रचना के चरण-
(1) पैमाने की सहायता से 8 cm लंबा एक रेखाखंड BC खींचिए।
(2) BC रेखाखंड का लंब समद्विभाजक PQ खींचिए जो BC को M पर मिले।
(3) M को केंद्र मानकर 4 cm त्रिज्या की परकार से AM = 4 cm काटिए।
(4) AB तथा AC को मिलाकर अभीष्ट ΔABC प्राप्त कीजिए।
(5) अब BC को D तक इस प्रकार बढ़ाइए कि BD = 12 cm प्राप्त हो क्योंकि (8 x \(\frac{3}{2}\)) = 12cm होता है।
(6) D से DE || AC खींचने के लिए ∠BDE = ∠BCA बनाइए जो BA को बढ़ाने पर E पर मिले।
(7) इस प्रकार EBD अभीष्ट त्रिभुज है जिसकी संगत भुजाएँ समद्विबाहु त्रिभुज ABC की भुजाओं का \(\frac{3}{2}\) गुना है।
प्रतिपादन (Justification)-ΔEBD में AC || DE है।
ΔEBD ~ ΔABC (AAA समरूपता से)
\(\frac{\mathrm{EB}}{\mathrm{AB}}=\frac{\mathrm{DE}}{\mathrm{CA}}=\frac{\mathrm{BD}}{\mathrm{BC}}=\frac{12}{8}=\frac{3}{2}\)

प्रश्न 5.
एक त्रिभुज ABC बनाइए, जिसमें BC = 6 cm,AB = 5 cm और ∠ ABC = 60° हो। फिर एक त्रिभुज की रचना कीजिए, जिसकी भुजाएँ ΔABC की संगत भुजाओं की \(\frac{3}{4}\) गुनी हो।
हल :

रचना के चरण
(1) पैमाने की सहायता से 6 cm लंबा एक रेखाखंड BC खींचिए।
(2) बिंदु B पर परकार की सहायता से ZXBC = 60° बनाइए।
(3) B को केंद्र मानकर 5 cm की त्रिज्या वाली परकार द्वारा BA = 5cm काटिए।
(4) AC को मिलाकर ΔABC प्राप्त कीजिए।
(5) अब BC के नीचे की ओर एक न्यून कोण CBY बनाइए।
(6) किरण BY पर चार बिंदु B₁, B₂, B₃, व B₄ इस प्रकार अंकित करें कि BB₁ = B₁B₂ = B₂B₃ = B₃B₄ हों।
(7) B₄C को मिलाइए।
(8) B₃ से B₃D || B₄C खींचने के लिए ∠ BB₃D = ∠ BB₄C बनाइए जो BC को D पर काटे।
(9) अब Dसे DE ||AC खींचने के लिए ∠ BDE =∠ BCA बनाइए जो AB को E पर मिले।
इस प्रकार EBD वांछित त्रिभुज है जिसकी भुजाएँ दी गई ΔABC की भुजाओं की 3/4 गुनी हैं।
प्रतिपादन (Justification)-ΔABC में DE || AC
ΔEBD ~ ΔABC (AAA समरूपता से)
\(\frac{E B}{A B}=\frac{B D}{B C}=\frac{D E}{C A}=\frac{3}{4}\)

प्रश्न 6.
एक त्रिभुज ABC बनाइए, जिसमें BC=7 cm, ∠B= 45°, ∠A= 105° हो। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ ΔABC की संगत भुजाओं की \(frac{4}{3}\) गुनी हों।
हल :

रचना के चरण
(1) पैमाने की सहायता से 7 cm लंबा एक रेखाखंड BC खींचिए।
(2) परकार की सहायता से ∠B = 45° व ∠C = 180° –
(∠A + ∠B) = 180° – (45° + 105°) = 30° की रचना कीजिए। जो परस्पर बिंदु A पर मिले।
(3) BC के नीचे की ओर एक न्यून कोण बनाती हुई किरण BX खींचिए।
(4) किरण BX पर चार बिंदु B₁, B₂, B₃, व B₄ इस प्रकार B
अंकित करें कि BB₁ = B₁B₂ = B₂B₃ = B₃B₄ हों।
(5) B₃C को मिलाइए।
(6) बिंदु B₄ से B₄D ||B₃C खींचने के लिए ∠BB₃C = ∠BB₄D खींचिए जो BC को बढ़ाने पर D पर मिले।
(7) अब बिंदु D से DE || AC खींचने के लिए ∠BDE = ∠BCA बनाइए जो BA को बढ़ाने पर E पर मिले।
इस प्रकार BED अभीष्ट त्रिभुज है जिसकी भुजाएँ त्रिभुज ABC की भुजाओं की \(frac{4}{3}\) गुनी हैं।
प्रतिपादन (Justification)-ΔEBD में AC || DE
ΔABC ~ ΔEBD (AAA समरूपता से)
\(\frac{E B}{A B}=\frac{B D}{B C}=\frac{D E}{C A}=\frac{4}{3}\)

प्रश्न 7.
एक समकोण त्रिभुज की रचना कीजिए, जिसकी भुजाएँ (कर्ण के अतिरिक्त) 4 cm तथा 3 cm लंबाई की हों। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की \(frac{5}{3}\) गुनी हों।
हल :

रचना के चरण-
(1) पैमाने की सहायता से 4 cm लंबा एक रेखाखंड BC खींचिए।
(2) बिंदु B पर परकार की सहायता से 90° का कोण बनाइए।
(3) B को केंद्र तथा 3 cm त्रिज्या के परकार खोलकर, BA = 3 cm काटिए।
(4) AC को मिलाइए जिससे अभीष्ट त्रिभुज ABC प्राप्त हो।
(5) BC के नीचे की ओर एक न्यून कोण बनाती हुई किरण BX खींचिए।
(6) किरण BX पर पाँच बिंदु B₁, B₂, B₃, B₄ तथा B₅, इस प्रकार अंकित करें । कि BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ हों।
(7) B₃C को मिलाइए तथा B₅ से B₅D || B₃C खींचने के लिए ∠BB₅D = ∠BB₃C बनाइए जो BC को बढ़ाने पर D पर मिले।
(8) अब बिंदु D से DE || CA खींचने के लिए ∠BDE = ∠BCA बनाइए जो BA को बढ़ाने पर E पर काटे।
इस प्रकार EBD अभीष्ट त्रिभुज है जिसकी भुजाएँ ΔABC की भुजाओं की \(frac{5}{3}\) गुनी हैं।