HBSE 10th Class Maths Solutions Chapter 6 त्रिभुज Ex 6.4

Haryana State Board HBSE 10th Class Maths Solutions Chapter 6 त्रिभुज Ex 6.4 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 6 त्रिभुज Exercise 6.4

नोट : यह प्रश्नावली निम्नलिखित प्रमेय पर आधारित है।
प्रमेय 6.6 : दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात इनकी संगत भुजाओं के अनुपात के वर्ग के बराबर होता है।
हल :
दिया है : AABC और ΔPQR इस प्रकार है कि ΔABC ~ΔPQR

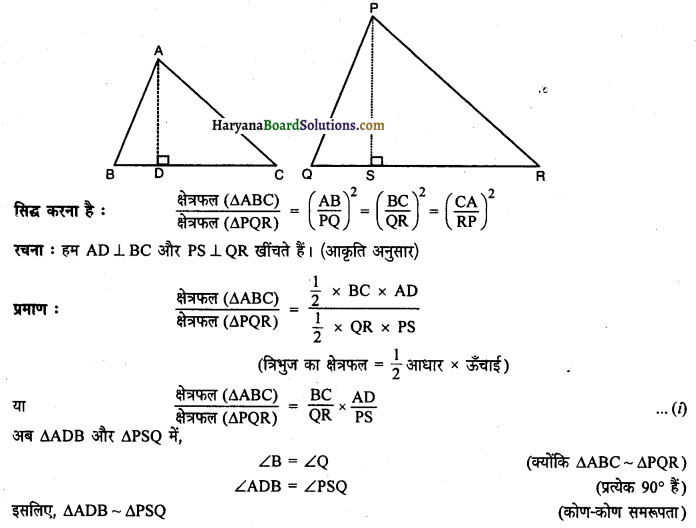
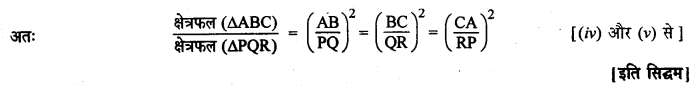
प्रश्न 1.
मान लीजिए ΔABC ~ΔDEF है और इनके क्षेत्रफल क्रमशः 64cm² और 121cm² हैं। यदि EF= 15.4cm हो, तो BC ज्ञात कीजिए।
हल :
क्योंकि ΔABC ~ΔDEF
ΔABC का क्षेत्रफल = 64cm²
और ΔDEF का क्षेत्रफल = 121cm²
EF = 15.4cm

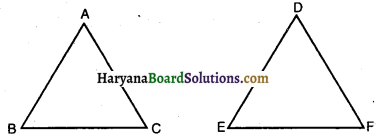
हम जानते हैं कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के अनुपात के वर्ग के बराबर होता है।

∴ अतः BC = 11.2 cm

प्रश्न 2.
एक समलंब ABCD जिसमें AB || DC है, के विकर्ण परस्पर बिंदु पर प्रतिच्छेद करते हैं। यदि AB = 2 CD हो तो त्रिभुजों AOB और COD के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हल :

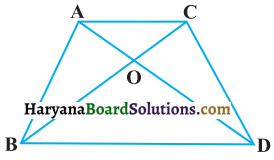
दिया है : ABCD एक समलंब है जिसमें AB || DC और AB = 2CD है।
सिद्ध करना है : ΔAOB का क्षेत्रफल :ΔCOD का क्षेत्रफल = ?
प्रमाण : ΔAOB और ΔCOD में,
∠AOB = ∠COD (शीर्षाभिमुख कोण)
∠OAB = ∠OCD (एकांतर कोण)
∠OBA = ∠ODC (एकांतर कोण)
ΔAOB ~ ΔCOD. (कोण-कोण-कोण समरूपता नियम से)
हम जानते हैं कि समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के अनुपात के वर्ग के बराबर होता है।

अतः ΔAOB का क्षेत्रफल : ΔCOD का क्षेत्रफल = 4:1

प्रश्न 3.
संलग्न आकृति में एक ही आधार BC पर दो त्रिभुज ABC और DBC बने हुए हैं। यदि AD, BC को 0 पर प्रतिच्छेद करे, तो दर्शाइए कि
दिशाइए कि \(\frac{\operatorname{ar}(\triangle \mathrm{ABC})}{\operatorname{ar}(\triangle \mathrm{DBC})}=\frac{\mathrm{AO}}{\mathrm{DO}}\) है।
हल :

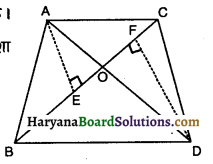
दिया है : ΔABC और ΔDBC समान आधार BC पर हैं परंतु विपरीत दिशा में हैं।
सिद्ध करना है : \(\frac{\operatorname{ar}(\triangle \mathrm{ABC})}{\operatorname{ar}(\triangle \mathrm{DBC})}=\frac{\mathrm{AO}}{\mathrm{DO}}\)
रचना : AE ⊥ BC और DF ⊥ BC खींचो।
प्रमाण: ΔAEO और ΔDFO में
∠AOE = ∠DOF (शीर्षाभिमुख कोण)
∠AEO = ∠DFO (प्रत्येक 90°)
कोण-कोण समरूपता गुणधर्म से,
ΔAEO ~ ΔDFO

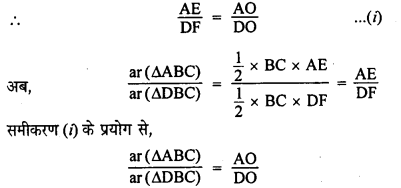
प्रश्न 4.
यदि दो समरूप त्रिभुजों के क्षेत्रफल बराबर हों, तो सिद्ध कीजिए कि वे त्रिभुज सर्वांगसम होते हैं।
हल :
दिया है : ΔABC ~ ΔPQR तथा क्षेत्रफल ΔABC = क्षेत्रफल ΔPQR
सिद्ध करना है : ΔABC = ΔPQR

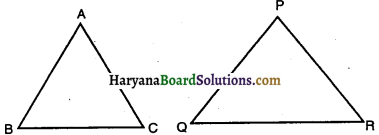
प्रमाण : हम जानते हैं कि दो समरूप त्रिभुजों का क्षेत्रफल उनकी संगत भुजाओं के अनुपात के वर्ग के बराबर होता है।
\(\therefore \quad \frac{\triangle \mathrm{ABC} \text { का क्षेत्रफल }}{\triangle \mathrm{PQR} \text { का क्षेत्रफल }}=\left(\frac{\mathrm{AB}}{\mathrm{PQ}}\right)^{2}=\left(\frac{\mathrm{BC}}{\mathrm{QR}}\right)^{2}=\left(\frac{\mathrm{CA}}{\mathrm{PR}}\right)^{2}\)
परंतु ΔABC का क्षेत्रफल = ΔPQR का क्षेत्रफल (दिया है)
\(\therefore \quad\left(\frac{\mathrm{AB}}{\mathrm{PQ}}\right)^{2}=\left(\frac{\mathrm{BC}}{\mathrm{QR}}\right)^{2}=\left(\frac{\mathrm{CA}}{\mathrm{PR}}\right)^{2}=1\)
\(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BC}}{\mathrm{QR}}=\frac{\mathrm{CA}}{\mathrm{PR}}=1\)
AB = PQ, BC = QR, CA = PR
अतः ΔABC = ΔPQR (भुजा-भुजा-भुजा सर्वांगसमता नियम से) [इति सिद्धम]

प्रश्न 5.
एक त्रिभुज ABC की भुजाओं AB, BC और CA के मध्य-बिंदु क्रमशः D, E और F हैं। ADEF और AABC के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हल :

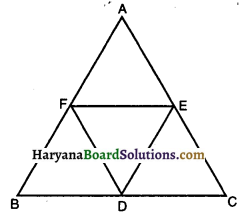
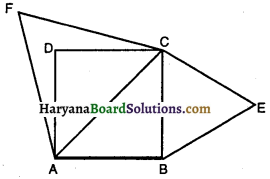
दिया है : ΔABC, जिसकी भुजाओं BC, CA और AB के मध्य-बिंदु क्रमशः D, E और F है।
सिद्ध करना है : ΔDEF और ΔABC के क्षेत्रफलों में क्या अनुपात है।
प्रमाण : क्योंकि ΔABC में D व E क्रमशः BC व CA के मध्य-बिंदु हैं।
∴ DE || AB तथा DE = \(\frac{1}{2}\)AB
इसी प्रकार EF = \(\frac{1}{2}\)BC व DF = \(\frac{1}{2}\) CA
अतः ΔABC और ΔDEF में,
\(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{\mathrm{CA}}{\mathrm{DF}}\) (प्रत्येक – 2/1)
∴ ΔABC ~ ΔDEF (भुजा-भुजा-भुजा समरूपता नियम से)
परंतु दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के अनुपात के वर्ग के बराबर होता है,

अतः ΔABC का क्षेत्रफल : ΔDEF का क्षेत्रफल = 4:1

प्रश्न 6.
सिद्ध कीजिए कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात इनकी संगत माध्यिकाओं के अनुपात का वर्ग होता
हल :
दिया है : ΔABC ~ ΔPQR तथा AD व PS क्रमशः त्रिभुज ABC और PQR की दो माध्यिकाएँ हैं।
सिद्ध करना है :

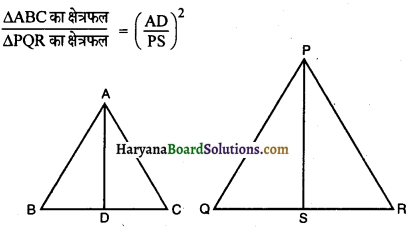
प्रमाण : हम जानते हैं कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के अनुपात के वर्ग के बराबर होता है।
\(\frac{\triangle \mathrm{ABC} \text { का क्षेत्रफल }}{\triangle \mathrm{PQR} \text { का क्षेत्रफल }}=\left(\frac{\mathrm{AB}}{\mathrm{PQ}}\right)^{2}\)
अब ΔABC ~ ΔPQR (दिया है)

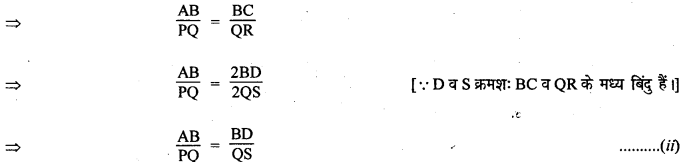
अतः ΔABD व ΔPQS में,
∠B = ∠Q [∵ ΔABC ~ ΔPQS]

प्रश्न 7.
सिद्ध कीजिए कि एक वर्ग की किसी भुजा पर बनाए गए समबाहु त्रिभुज का क्षेत्रफल उसी वर्ग के एक विकर्ण पर बनाए गए समबाहु त्रिभुज के क्षेत्रफल का आधा होता है।
हल :

दिया है : ABCD एक वर्ग है जिसकी भुजा BC पर समबाहु ΔBCE तथा विकर्ण AC पर समबाहु AACF बनाए गए हैं।
सिद्ध करना है : ΔBCE का क्षेत्रफल = \(\frac{1}{2}\)(ΔACF का क्षेत्रफल)
प्रमाण : क्योंकि ABCD एक वर्ग है।
∴ AB = BC = CD = DA
तथा AC = √2 BC [∵ वर्ग का विकर्ण = 2 वर्ग की भुजा]
अब क्योंकि ΔBCE व ΔACF समबाहु त्रिभुजें हैं इसलिए दोनों के तीनों कोण समान होंगे। अतः ΔBCE ~ ΔACF, हम जानते हैं कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के अनुपात के वर्ग के बराबर होता है।


ΔBCE का क्षेत्रफल = \(\frac{1}{2}\) (ΔACF का क्षेत्रफल) [इति सिद्धम]

नोट : प्रश्न 8 व 9 में से सही उत्तर चुनिए और अपने उत्तर का औचित्य दीजिए-

प्रश्न 8.
ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य-बिंदु है। त्रिभुजों ABC और BDE के क्षेत्रफलों का अनुपात है-
(A)2:1 (B)1:2 (C)4:1 (D) 1 : 4
हल :

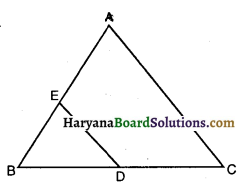
क्योंकि ΔABC और ΔBDE दोनों ही समबाहु त्रिभुजें हैं इसलिए दोनों के तीनों कोण समान होंगे। अतः
ΔABC ~ ΔBDE
हम जानते हैं कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के अनुपात के वर्ग के बराबर होता है।

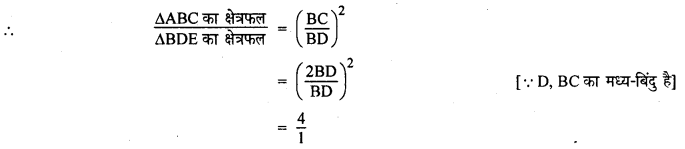
अतः ΔABC का क्षेत्रफल : ΔBDE का क्षेत्रफल = 4 : 1
∴ सही उत्तर (C) है।

प्रश्न 9.
दो समरूप त्रिभुजों की भुजाएँ 4:9 के अनुपात में हैं। इन त्रिभुजों के क्षेत्रफलों का अनुपात है
(A)2:3 (B) 4:9 (C)81 : 16 (D) 16 : 81
हल :
क्योंकि हम जानते हैं कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के अनुपात के वर्ग के बराबर होता है।
∴ इन त्रिभुजों के क्षेत्रफलों का अनुपात = (4)² : (9)^{2 = 16 : 81}