HBSE 10th Class Maths Solutions Chapter 6 त्रिभुज Ex 6.6

Haryana State Board HBSE 10th Class Maths Solutions Chapter 6 त्रिभुज Ex 6.6 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 6 त्रिभुज Exercise 6.6

प्रश्न 1.
संलग्न आकृति में PS कोण QPR का समद्विभाजक है। सिद्ध कीजिए कि \(\frac{\mathbf{Q S}}{\mathbf{S R}}=\frac{\mathbf{P Q}}{\mathbf{P R}}\) है।


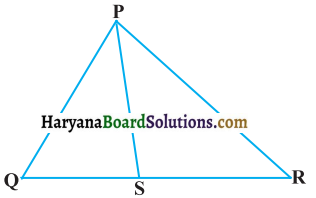
हल : दिया है : ΔPQR में भुजा PS, ∠QPR का समद्विभाजक है जो QR को S पर मिलता है। अर्थात्
∠QPS = ∠SPR
सिद्ध करना है : \(\frac{\mathrm{QS}}{\mathrm{SR}}=\frac{\mathrm{PQ}}{\mathrm{PR}}\)
रचना : R से RT || SP खींचो जो QP को बढ़ाने पर T पर मिले।
प्रमाण : क्योंकि PS || TR तथा PR तिर्यक रेखा इन्हें काटती है।
∠SPR = ∠PRT (एकांतर कोण युग्म) …. (i)
∠QPS = ∠PTR (संगत कोण युग्म) …………….(ii)
परंतु ∠QPS = ∠SPR (दिया है)
∠PRT = ∠PTR (समीकरण (i) व (ii) से)
PT = PR …. (iii) (क्योंकि समान कोणों की सम्मुख भुजाएँ समान होती हैं)
अब ΔQRT में,
PS || TR (रचना से)
\(\frac{\mathrm{QS}}{\mathrm{SR}}=\frac{\mathrm{PQ}}{\mathrm{PT}}\) (आधारभूत आनुपातिक प्रमेय से)
\(\frac{\mathrm{QS}}{\mathrm{SR}}=\frac{\mathrm{PQ}}{\mathrm{PR}}\)(समीकरण (iii) से) [इति सिद्धम]

प्रश्न 2.
संलग्न आकृति में D त्रिभुज ABC के कर्ण AC पर स्थित एक बिंदु है जबकि BD ⊥ AC तथा DM ⊥ BC और DN ⊥ AB है। सिद्ध कीजिए कि
(i) DM² = DN x MC
(ii) DN² = DM x AN

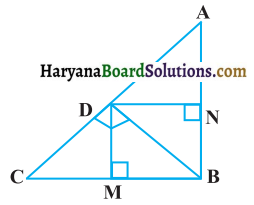
हल :
दिया है : ABC एक समकोण त्रिभुज है जिसमें ∠ABC = 90°, BD ⊥ AC, DM ⊥ BC व DN ⊥ AB है।
(i) सिद्ध करना है : DM² = DN x MC
प्रमाण : समकोण ΔBDC में DM ⊥ BC है,
∴ ΔDMC ~ ΔBMD
\(\frac{\mathrm{DM}}{\mathrm{BM}}=\frac{\mathrm{MC}}{\mathrm{DM}}\) (समरूप त्रिभुजों की संगत भुजाएँ)
DM² = BM x MC
परंतु BMDN एक आयत है जिसमें BM = DN
अतः DM² = DN X MC [इति सिद्धम]

(ii) सिद्ध करना है : DN² = DM x AN
प्रमाण : समकोण ΔBDA में DN ⊥ AB है
ΔBDN ~ ΔADN
अतः \(\frac{\mathrm{DN}}{\mathrm{BN}}=\frac{\mathrm{AN}}{\mathrm{DN}}\)
या DN² = BN x AN
परंतु BMDN एक आयत है जिसमें BN = DM
अतः DN² = DM XAN [इति सिद्धम]

प्रश्न 3.
संलग्न आकृति में ABC एक त्रिभुज है जिसमें ∠ABC > 90° है तथा AD ⊥ CB है। सिद्ध कीजिए कि AC² = AB² + BC² + 2 BC. BD है।

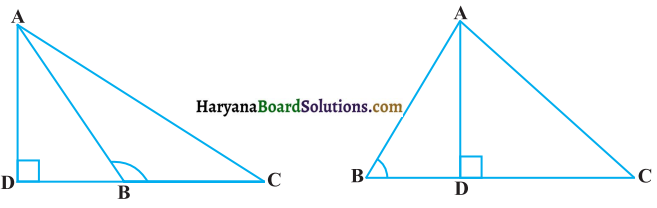
हल :
दिया है : एक ΔABC में ∠ABC > 90° तथा AD बढ़ी हुई भुजा CB पर लंब है।
सिद्ध करना है : AC² = AB² + BC² + 2BC.BD
प्रमाण : समकोण ΔADB में पाइथागोरस प्रमेय से
AB² = AD² + DB² …………..(i)
इसी प्रकार समकोण ΔADC में पाइथागोरस प्रमेय से
AC² = AD² + DC²
AC² = AD² + (DB + BC)²
AC² = AD² + DB² + BC² + 2 DB . BC
AC² = AB² + BC² + 2 DB . BC (समीकरण (i) से)
अतः AC² = AB² + BC² + 2 BC. BD [इति सिद्धम]

प्रश्न 4.
संलग्न आकृति में ABC एक त्रिभुज है जिसमें ∠ABC < 90° है तथा AD ⊥ BC है। सिद्ध कीजिए कि AC2 = AB+ BC2 – 2 BC. BD है।

हल :
दिया है : ΔABC में ∠B < 90° और AD ⊥ BC
सिद्ध करना है : AC² = AB² + BC² – 2BC.BD
प्रमाण : समकोण ΔABD में,
AB² = AD² + BD² ….(i)
समकोण ΔADC में,
AC² = AD² + DC²
AC² = AD² + (BC – BD)² (:: DC = BC – BD)
AC² = AD² + BC² + BD² – 2BC.BD
AC² = (AD² + BD²)+ BC² – 2BC.BD
AC² = AB² + BC² – 2BC.BD (i) से] [इति सिद्धम]

 

प्रश्न 5.
संलग्न आकृति में AD त्रिभुज ABC की एक माध्यिका है तथा AM ⊥ BC है। सिद्ध कीजिए कि-
(i) AC² = AD² + BC.DM + \(\left(\frac{B C}{2}\right)^{2}\)
(ii) AB² = AD² – BC.DM + \(\left(\frac{B C}{2}\right)^{2}\)
(iii) AC² + AB² = 2AD² + \(\frac{1}{2}\)BC²

हल :
दिया है : ΔABC में AD एक माध्यिका है तथा AM ⊥ BC है।
(i) सिद्ध करना है : AC² = AD² + BC.DM + \(\left(\frac{B C}{2}\right)^{2}\)
प्रमाण : समकोण ΔAMD में पाइथागोरस प्रमेय से,
AD² = AM² + MD² ……………(i)
समकोण ΔAMC में पाइथागोरस प्रमेय से,
AC² = AM² + (MC)²
= AM² + (MD + CD)²
= AM² + MD² + CD² + 2MD.CD [∵ BC = 2CD व समीकरण (i) से]
= AD² + \(\left(\frac{B C}{2}\right)^{2}\) + MD.BC
AC² = AD² + BCDM + \(\left(\frac{B C}{2}\right)^{2}\)
AC² = AD² + BC.DM + \(\left(\frac{B C}{2}\right)^{2}\)
[इति सिद्धम]….(ii)

(ii) सिद्ध करना है : AB² = AD² – BC.DM + \(\left(\frac{B C}{2}\right)^{2}\)
प्रमाण : समकोण ΔAMD में पाइथागोरस प्रमेय से,
AD² – AM² + DM²
समकोण AAMB में पाइथागोरस प्रमेय से,
AB² = AM² + BM²
= AM² + (BD – DM)²
= AM² + BD² – 2BD.DM + DM²
= (AM² + DM²) + \(\left(\frac{B C}{2}\right)^{2}\) -(2BD).DM
= AD² – BCDM + \(\left(\frac{B C}{2}\right)^{2}\) [∵ BD = BC/2 व समीकरण (i) से]
अतः AB² = AD² – BCDM + \(\left(\frac{B C}{2}\right)^{2}\) [इति सिद्धम] ….(iv)

(iii) सिद्ध करना है : AC² + AB² = 2AD² + \(\frac{1}{2}\)BC²
प्रमाण : समीकरण (ii) व (iv) को जोड़ने पर,
AC² + AB² = 2AD² + 2 \(\left(\frac{B C}{2}\right)^{2}\)
= 2AD² + \(\frac{1}{2}\) BC²
अतः AC² + AB² = 2AD² + \(\frac{1}{2}\)BC² [इति सिद्धम]

प्रश्न 6.
सिद्ध कीजिए कि एक समांतर चतुर्भुज के विकर्णों के वर्गों का योग उसकी भुजाओं के वर्गों के योग के बराबर होता है।

हल :
दिया है : ABCD एक समांतर चतुर्भुज है जिसके विकर्ण AC तथा BD परस्पर बिंदु O पर समद्विभाजित करते हैं।
सिद्ध करना है : AB² + BC² + CD² + DA² = AC² + BD²
प्रमाण : हम जानते हैं कि समांतर चतुर्भुज ABCD के विकर्ण AC व BD / परस्पर समद्विभाजित करते हैं।
इसलिए BO त्रिभुज ABC की माध्यिका तथा Do त्रिभुज ADC की माध्यिका है।
AB² + BC² = 2BO² + \(\frac{1}{2}\)AC²
DA² + CD² = 2DO² + \(\frac{1}{2}\)AC²
समीकरण (i) व (ii) को जोड़ने पर,
AB² + BC² + CD² + DA² = 2(BO² + DO²) + AC²
= \(2\left[\left(\frac{1}{2} \mathrm{BD}\right)^{2}+\left(\frac{1}{2} \mathrm{BD}\right)^{2}\right]+\mathrm{AC}^{2}\)
= \(2\left[\frac{1}{4} \mathrm{BD}^{2}+\frac{1}{4} \mathrm{BD}^{2}\right]+\mathrm{AC}^{2}\)
= 2 x \(\frac{1}{2}\)BD² + AC²
= BD² + AC²
अतः AB² + BC² + CD² + DA² = AC² + BD² [इति सिद्धम]

प्रश्न 7.
संलग्न आकृति में एक वृत्त की दो जीवाएँ AB और CD परस्पर बिंदु Pपर . प्रतिच्छेद करती हैं। सिद्ध कीजिए कि.
(i) ΔAPC ~ΔDPB
(ii) AP.PB = CP.DP

हल :
दिया है : एक वृत्त की दो जीवाएँ AB और CD परस्पर वृत्त के अंतर बिंदु P पर प्रतिच्छेद करती हैं।
सिद्ध करना है : (i) ΔAPC ~ΔDPB
(ii) AP.PB = CP.DP
रचना : AC और BD को मिलाइए।
प्रमाण : (i) ΔAPC और ΔDPB में,
∠PCA = ∠PBD (एक ही वृत्तखंड के कोण)
∠APC = ∠DPB (शीर्षाभिमुख कोण)
ΔAPC ~ ΔDPB (कोण-कोण समरूपता नियम से) [इति सिद्धम]

(ii) क्योंकि . ΔAPC ~ ΔDPB (प्रमाणित)
\(\frac{\mathrm{AP}}{\mathrm{DP}}=\frac{\mathrm{CP}}{\mathrm{PB}}\) (समरूप त्रिभुजों के संगत भाग)
या AP.PB = CP.DP [इति सिद्धम]

प्रश्न 8.
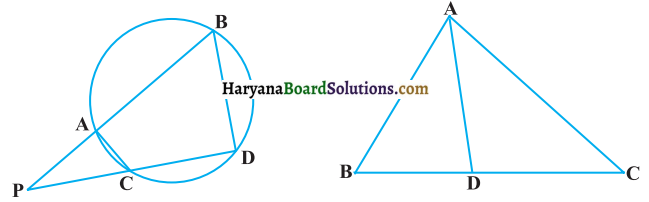
संलग्न आकृति में एक वृत्त की दो जीवाएँ AB और CD बढ़ाने पर परस्पर बिंदु Pपर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि
(i) ΔPAC ~ΔPDB
(ii) PA.PB = PC.PD

हल :
दिया है एक वृत्त की दो जीवाएँ AB और CD बढ़ाने पर परस्पर वृत्त के बाहर बिंदु P पर प्रतिच्छेद करती हैं।
सिद्ध करना है :
(i) ΔPAC ~ΔPDB ..
(ii) PA.PB = PC.PD
रचना : AC और BD को मिलाओ।
प्रमाण : (i) बिंदु P वृत्त के बाहर स्थित है।
∠PAC + ∠CAB = 180° ….(i) (रखिक युग्म)
और, ∠CAB + ∠PDB = 180° …(ii) (चक्रीय चतुर्भुज के सम्मुख कोण)
समीकरण (i) व (ii) से,
∠PAC + ∠CAB = ∠CAB+ ∠PDB
∠PAC = ∠PDB
अब त्रिभुजों PAC तथा PDB में,
∠PAC = ∠PDB (प्रमाणित)
∠APC = ∠DPB (उभयनिष्ठ कोण)
ΔPAC ~ ΔPDB (कोण-कोण समरूपता) [इति सिद्धम ]

(ii) क्योंकि
ΔPAC ~ ΔPDB(प्रमाणित)
\(\frac{\mathrm{PA}}{\mathrm{PD}}=\frac{\mathrm{PC}}{\mathrm{PB}}\) (समरूप त्रिभुजों के संगत भाग)
PA.PB = PC.PD [इति सिद्धम].

प्रश्न 9.
संलग्न आकृति में त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि \(\frac{\mathrm{BD}}{\mathrm{CD}}=\frac{\mathrm{AB}}{\mathrm{AC}}\) है। सिद्ध कीजिए कि AD, कोण BAC का समद्विभाजक है।
हल :
दिया है : ΔABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि-
\(\frac{\mathrm{BD}}{\mathrm{CD}}=\frac{\mathrm{AB}}{\mathrm{AC}}\)
सिद्ध करना है : AD, ∠BAC का समद्विभाजक है।
रचना : भुजा BA को E तक इस प्रकार बढ़ाओ कि AE = AC हो तथा CE को मिलाओ।

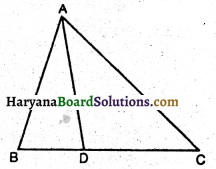
प्रमाण : ΔAEC में AE = AC (रचना से)
∠AEC= ∠ACE (समान भुजाओं के सम्मुख कोण) ….(i)
\(\frac{\mathrm{BD}}{\mathrm{CD}}=\frac{\mathrm{AB}}{\mathrm{AC}}\) (दिया है)
(∵ AE = AC रचना से)
DA || CE (आधारभूत आनुपातिकता प्रमेय का विलोम)
अब DA || CE तथा CA व AE एक तिर्यक रेखा है इसलिए
∠BAD = ∠AEC (संगत कोण युग्म) ….(ii)
∠DAC = ∠ACE (एकांतर कोण युग्म) ………….(iii)
अब समीकरण (i), (ii) व (iii) की तुलना से,
∠BAD = ∠DAC
अतः AD, ∠BAC का समद्विभाजक है। [इति सिद्धम]

प्रश्न 10.
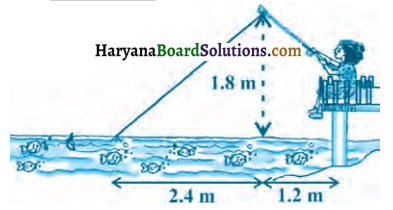
नाज़िमा एक नदी की धारा में मछलियाँ पकड़ रही है। उसकी मछली पकड़ने वाली छड़ का सिरा पानी की सतह से 1.8m ऊपर है तथा डोरी के निचले सिरे से लगा काँटा पानी के सतह पर इस प्रकार स्थित है कि उसकी नाजिमा से दूरी 3.6m है और छड़ के सिरे के ठीक नीचे पानी के सतह पर स्थित बिंदु से उसकी दूरी 2.4m है। यह मानते हुए कि उसकी डोरी (उसकी छड़ के सिरे से काँटे तक) तनी हुई है, उसने कितनी डोरी बाहर निकाली हुई है (देखिए संलग्न आकृति)? यदि वह डोरी को 5cm/s की दर से अंदर खींचे, तो 12 सेकंड के बाद नाजिमा की काँटे से क्षैतिज दूरी कितनी होगी?

हल :
प्रश्नानुसार, यहाँ पर हम AC ज्ञात करना चाहते हैं जबकि AB = 2.4m व BC = 1.8m है।
समकोण ΔABC में पाइथागोरस प्रमेय से,
(AC)² = (AB)² + (BC)²
= (2.4)² + (1.8)²
= 5.76 + 3.24
= 9.00
AC = 3m
अतः तनी हुई डोरी का जितना भाग पानी से बाहर है = 3m
डोरी को अंदर खींचने की दर = 5 cm/s
12 सेकंड में खींची डोरी की लंबाई = 5 x 12 = 60cm
= 0.6m
जितनी डोरी बाहर शेष है = (3 – 0.6)m = 2.4m

इस स्थिति में,
(PB)² = (PC)² – (BC)²
= (2.4)² – (1.8)²
= 5.76 – 3.24
= 2.52
PB = 1.59m (लगभग)
अतः नाजिमा की काँटे से क्षैतिज दूरी = (1.59 + 1.2)m
= 2.79m (लगभग)