Haryana State Board HBSE 9th Class Maths Notes Chapter 4 Linear Equations in Two Variables Notes.
Haryana Board 9th Class Maths Notes Chapter 4 Linear Equations in Two Variables
Introduction
In previous classes, we have learnt about the linear equation in one variable. We recall that an equation is a statement of equality which involves one or more unknown quantities known as variables. An equation is called linear equation in one variable or an equation of degree one in one variable, if only a single variable with degree one occurs in the equation. For example x + 5 = 0, 5y + 3 = 13, 3(x + 2) = x + 4, etc. The value of a variable which satisfied a linear equation is known as its solution. If ax + b = 0 is linear equation in one variable, where a, b are real numbers and a ≠ 0, then x = \(\frac{-b}{a}\) is its solution.
In this chapter, we shall use this knowledge in solving linear equations in two variables x and y of the form ax + by + c = 0, where a, b, c are real numbers and a ≠ 0, b ≠ 0.
Rene Descartes (1596 – 1650), a French philosopher and mathematician introduced that a point P in the plane can be specified with two real numbers, also called coordinates of the point P. This concept of coordinates will help us to represent linear equations graphically.
Key Words
→ Perpendicular: A right angle to a line or surface, whereas vertical means at right angles to the earth’s surface. Symbol used for this perpendicular is ⊥.
→ Parallel: Extending in the same direction and always remaining equidistant.
→ Real Number: A number which is a rational number or the limit of a sequence of rational numbers. It includes the irrational number such as \(\sqrt{2}\), \(\sqrt{3}\), \(\sqrt[3]{2}\) and π. A concrete representation of real numbers is provided by the decimal number system; other number systems are possible, such as the binary number system. The real number is what is often understood by “Number” in ordinary mathematics.
→ Variable: A quantity which, throughout a mathematical calculation or investigation, is capable of varying or does not vary in value. A quantity which may assume a succession of values.
→ Graph: A geometric representation of a relationship between two variables, usually in rectangular coordinate system.
→ Statement: A sentence which can be judged to be true or false is known as a statement.
![]()
Basic Concepts
1. Linear Equations: An equation of the form ax + by + c = 0, where a, b, c are real numbers and a ≠ 0, b ≠ 0 is called a linear equation in two variables, x and y are known as variables. For example:
(i) 2x + 3y = 5
(ii) – 5x + 2y = -9
(iii) \(\frac{2 x}{3}+\frac{3 y}{2}-5=0\)
(iv) \(\sqrt{3}\)x + \(\sqrt{2}\)y – \(\sqrt{5}\) = 0.
The following equations are not linear equations in two variables:
(i) \(\frac{1}{x}\) + y = 5
(ii) \(\sqrt{x}\) + \(\sqrt{y}\) – 6 = 0
(iii) x2 + y – 7 = 0
(iv) x-1 + y-1 – 4 = 0.
Notes:
1. In the linear equation ax + by + c = 0, a is the coefficient of x, b is the coefficient of y and c is the constant term.
2. In the linear equation ax + by + c = 0, if we have a = 0, b ≠ 0 then equation will be 0 × x + by + c = 0 i.e., by + c = 0 and if we have b = 0, a ≠ 0, then equation will be ax + 0 × y + c = 0 i.e., ax + c = 0.
In both cases, we get a linear equation in one variable. This is why put the condition that both a and b are non-zero. However, in Cartesian situations we shall allow one of the two coefficients to be zero.
3. The standard form of the linear equation is ax + by + c = 0.
Solution of a linear equation:
We know that every linear equation in one variable has unique solution Now, we will examine the solutions of a linear equation in two variables x and y is of the form ax + by + c = 0, where a, b, c are real numbers and a ≠ 0, b ≠ 0. Any pair of values of x and y which satisfies the given linear equation is called a solution of the linear equation.
Let us consider the equation 2x + 3y = 12.
Substitute x = 3 and y = 2 in the above equation, we get
L.H.S. = 2 × 3 + 3 × 2 = 6 + 6 = 12
R.H.S. = 12
Therefore, (3, 2) is a solution of the linear equation, with the value of x first and value of y second.
But, (2, 3) is not a solution of the above linear equation because on putting x = 2, y = 3, we get
L.H.S. = 2 × 2 + 3 × 3 = 4 + 9 = 13
R.H.S. = 12
L.H.S. ≠ R.H.S.
![]()
Graph of a Linear Equation in Two Variables:
We have obtained the solutions of a linear equation in two variables algebraically. In this section, we will learn the method of a sketching the graph of a linear equation in two variables x and y i.e., the graph of the equation of the form ax + by + c = 0, where a ≠ 0, b ≠ 0.
We have learnt in previous section that any pair of values of x and y, which satisfies the given equation is called a solution of the equation.
Now consider a linear equation 3x + 2y = 8. First of all we find different solutions of this equation, x = 0, y = 4; x = 2, y = 1; x = 4, y = -2 and x = 6, y = -5 are all solutions of this equation.
We will prepare a table of values of (x, y) as follows:
| x | 0 | 2 | 4 | 6 |
| y | 4 | 1 | -2 | -5 |
Now we plot these points on a graph paper and then join these points to form the line l.
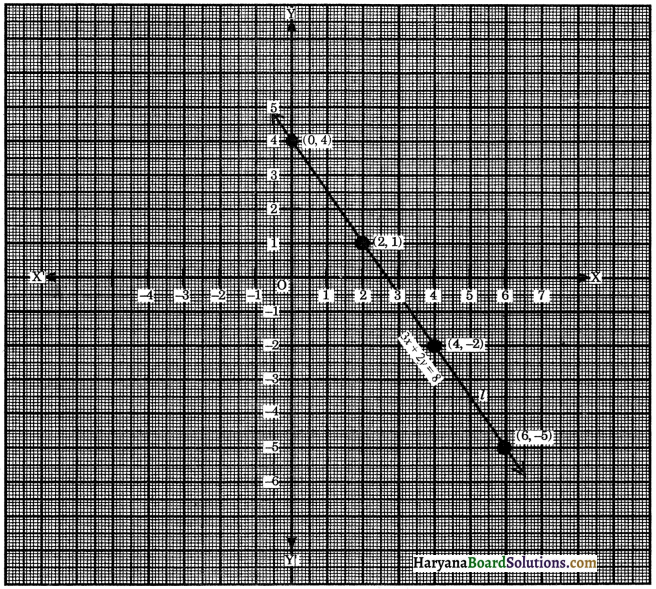
This line is called the graph of the linear equation 3x + 2y = 8.
Remarks:
1. Every point whose co-ordinates satisfy the equation lie on the straight line ‘l'(graph).
2. Every point (α, β) on the line ‘l’ gives a solution x = α, y = β of linear equation.
3. Any point which does not lie on the line ‘l’ is not a solution of the equation.
4. The reason that a, degree one, equation ax + by + c = 0 is called a linear equation is that its geometrical representation is a straight line.
Working method for sketching the graph of a linear equation in two variables x and y.
Step I. Express y in term of x i.e., y = \(-\left(\frac{a x+c}{b}\right)\).
Step II. Choose at least three convenient values of x and find the corresponding values of y, satisfying the given equation.
Step III. Prepare the table of values of x and y.
Step IV. Plot the ordered pair (x, y) from the table on a graph paper.
Step V. Join these three points by a straight line.
The line obtained is the graph of the equation ax + by + c = 0.
![]()
Equations of Lines Parallel to the x-axis and y-Axis:
In figure 4.20 we have a straight line m parallel to x-axis. The line, meeting the y-axis at a distance of 3 units from the origin. We observe that y co-ordinate of each point on line m is 3. Line m can be express in one variable as y = 3 and express in two variables as 0.x + 1, y = 3. So, we conclude that y = a, (where a is a real number) represents a straight line parallel to x-axis at a distance a from it.

Similarly in figure 4.21 line n parallel to y-axis. It can be express in one variable as x = 2 and express in two variables as 1.x + 0.y = 2. So, we conclude that x = a (where a is a real number) represents a straight line parallel to the y-axis at a distance a from it.

Some special Types of Linear Equations:
(a) Equation of the x-axis is y = 0, (b) Equation of the y-axis is x = 0, which are shown in the figure 4.22.

Read More: