HBSE 10th Class Maths Solutions Chapter 11 रचनाएँ Ex 11.1

Haryana State Board HBSE 10th Class Maths Solutions Chapter 11 रचनाएँ Ex 11.1 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 11 रचनाएँ Exercise 11.1

प्रश्न 1.
7.6 cm लंबा एक रेखाखंड खींचिए और इसे 5 : 8 अनुपात में विभाजित कीजिए। दोनों भागों को मापिए।
हल :
रचना के चरण-

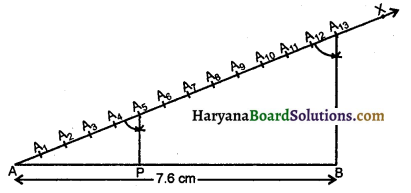
(1) पैमाने की सहायता से 7.6 cm लंबा एक रेखाखंड AB खींचिए।
(2) AB से एक न्यून कोण बनाती हुई किरण AX खींचिए।
(3) किरण AX पर 13(5 + 8) बिंदु A₁,A₂,A₃, A₄,A₅,A₆,A₇,A₈,A₉,A₁₀,A₁₁,A₁₂, और A₁₃ इस प्रकार अंकित कीजिए कि AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅ = A₅A₆ = A₆A₇ = A₇A₈ = A₈A₉ = A₉A₁₀ = A₁₀A₁₁ = A₁₁A₁₂ =A₁₂A₁₃ हो।
(4) A₁₃B को मिलाइए।
(5) A₅ से A₅P || A₁₃B खींचने के लिए बिंदु A₅ पर ∠AA₅P = ∠AA₁₃B बनाइए।
(6) इस प्रकार प्राप्त बिंदु P अभीष्ट बिंदु है जो AB को 5 : 8 के अनुपात में विभाजित करता है।
(7) पैमाने की सहायता से दोनों भागों को मापने पर AP= 2.9 cm तथा PB = 4.7 cm (लगभग) प्राप्त होते हैं।
प्रतिपादन (Justification)-त्रिभुज ABA₁₃; में AP || A₁₃B है।
अतः आधारभूत समानुपातिका प्रमेय से,
\(\frac{\mathrm{AP}}{\mathrm{PB}}=\frac{\mathrm{AA}_{5}}{\mathrm{~A}_{5} \mathrm{~A}_{13}}\)
\(\frac{\mathrm{AP}}{\mathrm{PB}}=\frac{5}{8}\)
AP : PB = 5:8

प्रश्न 2.
4 cm, 5 cm और 6 cm भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर इसके समरूप एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की 2/3 गुनी हों।
हल :

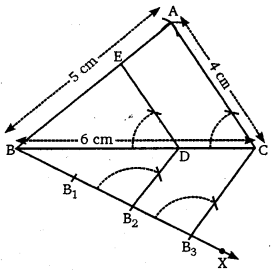
रचना के चरण-
(1) पैमाने की सहायता से 6 cm लंबा एक रेखाखंड BC खींचिए।
(2) B को केंद्र तथा त्रिज्या 5 cm लेकर एक चाप BC के ऊपर की ओर लगाइए।
(3) C को केंद्र तथा त्रिज्या 4 cm लेकर एक चाप BC के ऊपर की ओर लगाइए जो चरण (2) की चाप को A पर प्रतिच्छेद करें।
(4) AB तथा AC को मिलाकर अभीष्ट ΔABC प्राप्त कीजिए।
(5) अब BC के नीचे की ओर एक न्यून कोण CBX बनाइए।
(6) किरण BX पर तीन बिंदु B₁, B₂, तथा B₃, इस प्रकार अंकित कीजिए। कि BB₁ = B₁B₂ = B₂B₃, हो। .
(7) B₃C को मिलाइए।
(8) B₂ से B₂D||B₃C खींचने के लिए बिंदु B₂ पर ∠BB₂D = ∠BB₃C. बनाइए तथा B.D को मिलाइए।
(9) अब बिंदु D से DE || AC खींचने के लिए ∠BDE = ∠BCA बनाइए जो AB को E पर काटे।
इस प्रकार EBD वांछित त्रिभुज है जिसकी भुजाएँ दी गई ΔABC की भुजाओं की 2/3 गुनी है।
प्रतिपादन (Justification)-ΔABC में DE || AC है।
ΔABC ~ ΔEBD (AAA समरूपता से)
\(\frac{E B}{A B}=\frac{B D}{B C}=\frac{D E}{A C}=\frac{2}{3}\)

प्रश्न 3.
5 cm, 6 cm और 7 cm भुजाओं वाले एक त्रिभुज की रचना कीजिए, और फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की 7/5 गुनी हों।
हल :

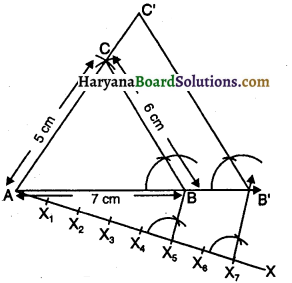
रचना के चरण-
(1) एक त्रिभुज ABC बनाइए जिसकी भुजाएँ AB = 7 cm, BC = 6 cm तथा AC = 5 cm हों।
(2) बिंदु A से एक किरण AX, रेखाखंड AB के साथ न्यून कोण बनाते हुए खींचिए।
(3) किसी चाप की परकार खोलकर रेखा AX को सात बराबर AX₁, X₁X₂, X₂X₃, X₃X₄, X₄X₅, X₅X₆, X₆X₇ भागों में बाँटिए।।
(4) X₅ को B से मिलाइए।
(5)X₇ से X₇B’||X₅B खींचिए जो AB को बढ़ाने पर B’पर मिले।
(6) B’ से B’C’ || BC खींचिए जो AC को बढ़ाने पर C’ पर मिले।
(7) इस प्रकार ΔAB’ C’ अभीष्ट त्रिभुज है जिसकी भुजाएँ ΔABC की भुजाओं का 7/5 वां भाग हैं।
प्रतिपादन (Justification)-ΔAB’C’ में BC || B’C’ है। ΔABC ~ ΔAB’ C’ (AAA समरूपता से)
\(\frac{A B^{\prime}}{A B}=\frac{B^{\prime} C^{\prime}}{B C}=\frac{A C^{\prime}}{A C}=\frac{7}{5}\)

प्रश्न 4.
आधार 8 cm तथा ऊँचाई 4 cm के एक समद्विबाहु त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ इस समद्विबाहु त्रिभुज की संगत भुजाओं की 1\(\frac{1}{2}\) गुनी हो।
हल :

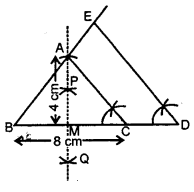
रचना के चरण-
(1) पैमाने की सहायता से 8 cm लंबा एक रेखाखंड BC खींचिए।
(2) BC रेखाखंड का लंब समद्विभाजक PQ खींचिए जो BC को M पर मिले।
(3) M को केंद्र मानकर 4 cm त्रिज्या की परकार से AM = 4 cm काटिए।
(4) AB तथा AC को मिलाकर अभीष्ट ΔABC प्राप्त कीजिए।
(5) अब BC को D तक इस प्रकार बढ़ाइए कि BD = 12 cm प्राप्त हो क्योंकि (8 x \(\frac{3}{2}\)) = 12cm होता है।
(6) D से DE || AC खींचने के लिए ∠BDE = ∠BCA बनाइए जो BA को बढ़ाने पर E पर मिले।
(7) इस प्रकार EBD अभीष्ट त्रिभुज है जिसकी संगत भुजाएँ समद्विबाहु त्रिभुज ABC की भुजाओं का \(\frac{3}{2}\) गुना है।
प्रतिपादन (Justification)-ΔEBD में AC || DE है।
ΔEBD ~ ΔABC (AAA समरूपता से)
\(\frac{\mathrm{EB}}{\mathrm{AB}}=\frac{\mathrm{DE}}{\mathrm{CA}}=\frac{\mathrm{BD}}{\mathrm{BC}}=\frac{12}{8}=\frac{3}{2}\)

प्रश्न 5.
एक त्रिभुज ABC बनाइए, जिसमें BC = 6 cm,AB = 5 cm और ∠ ABC = 60° हो। फिर एक त्रिभुज की रचना कीजिए, जिसकी भुजाएँ ΔABC की संगत भुजाओं की \(\frac{3}{4}\) गुनी हो।
हल :

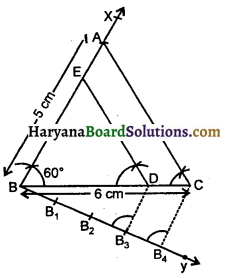
रचना के चरण
(1) पैमाने की सहायता से 6 cm लंबा एक रेखाखंड BC खींचिए।
(2) बिंदु B पर परकार की सहायता से ZXBC = 60° बनाइए।
(3) B को केंद्र मानकर 5 cm की त्रिज्या वाली परकार द्वारा BA = 5cm काटिए।
(4) AC को मिलाकर ΔABC प्राप्त कीजिए।
(5) अब BC के नीचे की ओर एक न्यून कोण CBY बनाइए।
(6) किरण BY पर चार बिंदु B₁, B₂, B₃, व B₄ इस प्रकार अंकित करें कि BB₁ = B₁B₂ = B₂B₃ = B₃B₄ हों।
(7) B₄C को मिलाइए।
(8) B₃ से B₃D || B₄C खींचने के लिए ∠ BB₃D = ∠ BB₄C बनाइए जो BC को D पर काटे।
(9) अब Dसे DE ||AC खींचने के लिए ∠ BDE =∠ BCA बनाइए जो AB को E पर मिले।
इस प्रकार EBD वांछित त्रिभुज है जिसकी भुजाएँ दी गई ΔABC की भुजाओं की 3/4 गुनी हैं।
प्रतिपादन (Justification)-ΔABC में DE || AC
ΔEBD ~ ΔABC (AAA समरूपता से)
\(\frac{E B}{A B}=\frac{B D}{B C}=\frac{D E}{C A}=\frac{3}{4}\)

प्रश्न 6.
एक त्रिभुज ABC बनाइए, जिसमें BC=7 cm, ∠B= 45°, ∠A= 105° हो। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ ΔABC की संगत भुजाओं की \(frac{4}{3}\) गुनी हों।
हल :

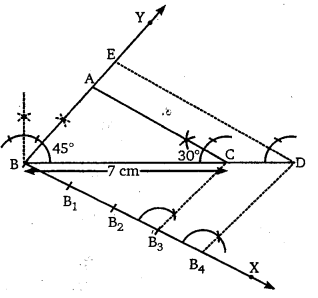
रचना के चरण
(1) पैमाने की सहायता से 7 cm लंबा एक रेखाखंड BC खींचिए।
(2) परकार की सहायता से ∠B = 45° व ∠C = 180° –
(∠A + ∠B) = 180° – (45° + 105°) = 30° की रचना कीजिए। जो परस्पर बिंदु A पर मिले।
(3) BC के नीचे की ओर एक न्यून कोण बनाती हुई किरण BX खींचिए।
(4) किरण BX पर चार बिंदु B₁, B₂, B₃, व B₄ इस प्रकार B
अंकित करें कि BB₁ = B₁B₂ = B₂B₃ = B₃B₄ हों।
(5) B₃C को मिलाइए।
(6) बिंदु B₄ से B₄D ||B₃C खींचने के लिए ∠BB₃C = ∠BB₄D खींचिए जो BC को बढ़ाने पर D पर मिले।
(7) अब बिंदु D से DE || AC खींचने के लिए ∠BDE = ∠BCA बनाइए जो BA को बढ़ाने पर E पर मिले।
इस प्रकार BED अभीष्ट त्रिभुज है जिसकी भुजाएँ त्रिभुज ABC की भुजाओं की \(frac{4}{3}\) गुनी हैं।
प्रतिपादन (Justification)-ΔEBD में AC || DE
ΔABC ~ ΔEBD (AAA समरूपता से)
\(\frac{E B}{A B}=\frac{B D}{B C}=\frac{D E}{C A}=\frac{4}{3}\)

प्रश्न 7.
एक समकोण त्रिभुज की रचना कीजिए, जिसकी भुजाएँ (कर्ण के अतिरिक्त) 4 cm तथा 3 cm लंबाई की हों। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की \(frac{5}{3}\) गुनी हों।
हल :

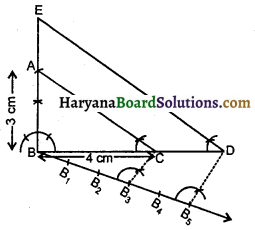
रचना के चरण-
(1) पैमाने की सहायता से 4 cm लंबा एक रेखाखंड BC खींचिए।
(2) बिंदु B पर परकार की सहायता से 90° का कोण बनाइए।
(3) B को केंद्र तथा 3 cm त्रिज्या के परकार खोलकर, BA = 3 cm काटिए।
(4) AC को मिलाइए जिससे अभीष्ट त्रिभुज ABC प्राप्त हो।
(5) BC के नीचे की ओर एक न्यून कोण बनाती हुई किरण BX खींचिए।
(6) किरण BX पर पाँच बिंदु B₁, B₂, B₃, B₄ तथा B₅, इस प्रकार अंकित करें । कि BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ हों।
(7) B₃C को मिलाइए तथा B₅ से B₅D || B₃C खींचने के लिए ∠BB₅D = ∠BB₃C बनाइए जो BC को बढ़ाने पर D पर मिले।
(8) अब बिंदु D से DE || CA खींचने के लिए ∠BDE = ∠BCA बनाइए जो BA को बढ़ाने पर E पर काटे।
इस प्रकार EBD अभीष्ट त्रिभुज है जिसकी भुजाएँ ΔABC की भुजाओं की \(frac{5}{3}\) गुनी हैं।