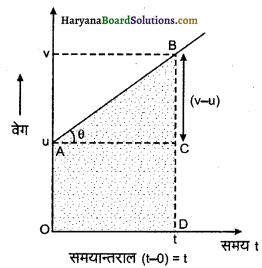
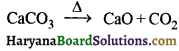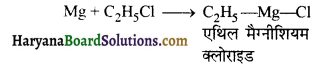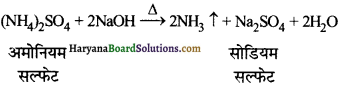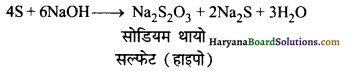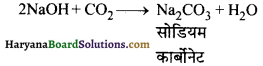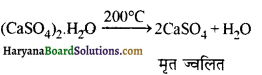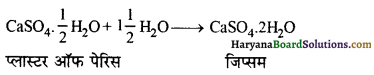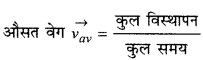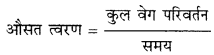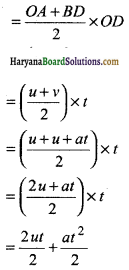Haryana State Board HBSE 11th Class Chemistry Important Questions Chapter 10 s-ब्लॉक तत्त्व Important Questions and Answers.
Haryana Board 11th Class Chemistry Important Questions Chapter 10 s-ब्लॉक तत्त्व
बहुविकल्पीय प्रश्न:
1. क्षार धातुएँ हैं-
(1) Na व K
(2) Mg व Ca
(3) Cu व Mg
(4) Al व Fe
उत्तर:
(1) Na व K
2. सोडियम धातु को इसमें सुरक्षित रखा जाता है-
(1) बेन्जीन
(2) कैरोसीन
(3) ऐल्कोहॉल
(4) टॉलूईन।
उत्तर:
(2) कैरोसीन
3. निम्न में से कौन-सी धातु कमरे के ताप पर जल से क्रिया करती है-
(1) चाँदी
(2) लोहा
(3) ऐल्यूमिनियम
(4) सोडियम।
उत्तर:
(4) सोडियम।
4. कौन-सा तत्व ऑक्सीजन की प्रचुरता में गरम करने पर सुपर-ऑक्साइड बनाता है-
(1) Li
(2) Na
(3) K
(4) Ca
उत्तर:
(3) K

5. सोडियम, लीथियम की तुलना में जल से बहुत तीव्रता से अभिक्रिया करता है, क्योंकि-
(1) इसका परमाणु भार अधिक है
(2) यह अधिक विद्युत-धनी है
(3) यह अधिक विद्युत-ऋणी है
(4) इसमें अधिक संयोजकता इलेक्ट्रॉन हैं।
उत्तर:
(2) यह अधिक विद्युत-धनी है
6. निम्न में से किसकी हाइड्रेशन ऊर्जा अधिकतम है-
(1) H+
(2) Na+
(3) K+
(4) Rb+
उत्तर:
(1) H+
7. KO2 किसका उदाहरण है-
(1) सब ऑक्साइड
(2) सुपर ऑक्साइड
(3) सामान्य ऑक्साइड
(4) परॉक्साइड
उत्तर:
(2) सुपर ऑक्साइड
8. सीजियम ऑक्साइड है-
(1) प्रबल क्षारीय
(2) अम्लीय
(3) दुर्बल क्षारीय
(4) उभयधर्मी।
उत्तर:
(1) प्रबल क्षारीय
9. निम्न में से कौन-सा धातु कार्बोनेट गरम करने पर अपघटित होता है-
(1) Li2CO3
(2) Na2CO3
(3) K2CO3
(4) Rb2CO3
उत्तर:
(1) Li2CO3
10. भार-धातुओं के प्रबल अपचायक होने का कारण है-
(1) बड़ी परमाणु त्रिज्या
(2) बड़ी आयनिक त्रिक्या
(3) कम विद्युत श्रूपात्मकता
(4) कम प्रथम आयनन ऊर्जा।
उत्तर:
(4) कम प्रथम आयनन ऊर्जा।
11. क्षारीय धातुओं में से धातु जो रेडियो एक्टिव है-
(1) Cs
(2) Fr
(3) Rb
(4) Li
उत्तर:
(2) Fr
12. निम्न में से सबसे हल्का तत्व है-
(1) Na
(2) Ca
(3) Li
(4) Mg
उत्तर:
(3) Li
13. जब K को तेजी से वायु में गर्म किया जाता है तो प्राप्त होता है-
(1) K2O
(2) KO2
(3) K2O2
(4) KO
उत्तर:
(2) KO2
14. Na+ और K+ की अपेक्षा Li+ की आयनिक चालकता कम है, क्योंकि-
(1) Li+ का आयनन विभव कम है
(2) Li+ का आवेश घनत्व उच्व है
(3) Li+ की जलयोजन प्रवृत्ति उज्ञ है
(4) उपरोक्त में से कोई नहां।
उत्तर:
(3) Li+ की जलयोजन प्रवृत्ति उज्ञ है
15. निम्न क्षार धातु आयनों में से किसकी जलीय विलयन में चालकता न्यूनवम होती है-
(1) Rb+
(2) Cs+
(3) Li+
(4) Na+
उत्तर:
(3) Li+
16. परॉक्साइड बनाने वाले तत्वों का समूह है-
(1) Li, Na, K
(2) Na, K, Mg
(3) H, Na, Ba
(4) H, Li , Mg
उत्तर:
(3) H, Na, Ba
17. इलेक्ट्रोड विभव के आधार पर जलीय विलयन में सर्बोंत्तम अपचायक है-
(1) Li
(2) Na
(3) K
(4) Rb
उत्तर:
(1) Li
18. सहसंयोजक प्रकृति का क्लोराइड है-
(1) BaCl2
(2) NaCl
(3) CaCl2
(4) BeCl2
उत्तर:
(4) BeCl2
19. उभयधर्मी ऑक्साइड का उदाइरण है-
(1) MgO
(2) Na2O
(3) BeO
(4) BaO
उत्तर:
(3) BeO
20. प्रयोगशाला में निर्जलीकारक के रूप में प्रयुक्त होने वाला यौगिक है-
(1) NaCl
(2) CaCl2
(3) MgCl2
(4) KCl
उत्तर:
(2) CaCl2
21. निम्न धातु कार्बोनेट्टों में कौन-सा गर्म करने पर धातु देता है-
(1) MgCO3
(2) Ag2CO3
(3) K2CO3
(4) FeCO3
उत्तर:
(2) Ag2CO3
22. धावन सोड़ा का सूत्र है-
(1) Na2CO3.7H2O
(2) Na2CO3. H2O
(3) Na2CO3.10H2O
(4) Na2CO3
उत्तर:
(3) Na2CO3.10H2O
23. बेकिंग सोडा है-
(1) Na2CO3
(2) NaHCO3
(3) Na2SO4
(4) K2CO3
उत्तर:
(3) Na2SO4
24. सान्द्र जलीय NaOH विलयन निम्न में से किस मिश्रण को अलग कर सकता है-
(1) Al3+ तथा Sn2+
(2) Al3+ तथा Fe3+
(3) Al3+ तथा Zn2+
(4) Zn2+ तथा Pb2+
उत्तर:
(2) Al3+ तथा Fe3+
25. जिंक की क्रिया कास्टिक सोडा विलयन की अधिकता से कराने पर प्राप्त होता है-
(1) Zn(OH)2
(2) ZnO
(3) Na2ZnO2
(4) ZnH2
उत्तर:
(3) Na2ZnO2
26. सॉल्वे प्रक्रम में Na2CO3 के अवक्षेपण का कारण है-
(1) अमोनिया से क्रिया
(2) ताप में कमी
(3) ब्राइन बिलयन में समआयन प्रभाव
(4) CO2 की क्रिया।
उत्तर:
(3) ब्राइन बिलयन में समआयन प्रभाव
27. सोडियम को शुष्क वायु में जलाने पर प्राप्त होता है-
(1) Na2O
(2) Na2O2
(3) NaO2
(4) Na3N
उत्तर:
(4) Na3N

28. NaCl को जल में घोलने पर सोडियम आयन हो जाता है-
(1) औँक्सीकृत
(2) अपचयित
(3) जल-अपघटित
(4) जलयोजित।
उत्तर:
(1) औँक्सीकृत
29. क्रिस्टल कार्बोनेट होता है-
(1) NaCO3
(2) Na2CO3.2H2O
(3) Na2CO3.H2O
(4) Na2CO3.10H2O
उत्तर:
(3) Na2CO3.H2O
30. गर्म सान्द्र NaOH विलयन के साथ ब्रोमीन की क्रिया से प्राप्त होता है-
(1) NaBrO
(2) NaBrO
(3) NaBrO
(4) NaBrO
उत्तर:
(3) NaBrO
31. सोडा लाइम है-
(1) Na2CO3 + Ca
(2) NaOH + NaHCO3
(3) NaOH + CaO
(4) NaOH + Na2CO3
उत्तर:
(3) NaOH + CaO
32. ब्राद्वन होता है-
(1) Na2CO3 का सान्द्र विलयन
(2) Na2SO4 का सान्द्र विलयन
(3) NaCl का सान्द्र विलयन
(4) फिटकरी का सान्द्र विलयन।
उत्तर:
(3) NaCl का सान्द्र विलयन
33. सोद्धा ऐश है-
(1) Na2CO3.H2O
(2) NaOH
(3) NaHCO2
(4) शुष्क Na2CO3
उत्तर:
(4) शुष्क Na2CO3
34. पोटेंशियम नाइट्रेट गर्म करने पर क्या बनाता है-
(1) K2O
(2) KO2
(3) K2O2
(4) KNO2
उत्तर:
(4) KNO2
35. निम्न में से कौन-सी धातु गर्म सान्द्र कॉस्टिक सोद्धा विलयन में नहीं घुलती है-
(1) Zn
(2) Zn
(3) Al
(4) Fe
उत्तर:
(4) Fe
36. पीले फॉस्फोरस को सान्द्र सोडियम हाइड्रॉक्साइड विलयन के साथ गर्म करने पर कौन सा पदार्थ बनता है?
(1) NaPO3 और NaH2PO4
(2) PH3 और NaH3PO3
(3) PH3 और NaH3PO2
(4) Na2HPO3 और Na2HPO4
उत्तर:
(3) PH3 और NaH3PO2
37. धावन सोडा का सूत्र है-
(1) Na2CO3
(2) Na3CO3.H2O
(3) Na2CO3.5H2O
(4) Na2CO3.10H3O
उत्तर:
(4) Na2CO3.10H3O
38. निम्न में से कौन-सा कथन सत्य है-
(1) लीथियम कार्बोनेट जल में विलेय होता है
(2) Na, K तथा NH4 के कार्बोनेट जल में विलेय होते हैं
(3) Ca, Sr तथा Ba के कार्बोनेट जल में विलेय होते हैं
(4) Mg तथा Cu के बेसिक कार्बोनेट जल में विलेय होते हैं।
उत्तर:
(2) Na, K तथा NH4 के कार्बोनेट जल में विलेय होते हैं
39. निम्न में से कौन-सा लवण बुन्सन की अदीप्त ज्वाला को बेंगनी रंग प्रदान करता है-
(1) NaCl
(2) BaCl2
(3) CaCl2
(4) KCl
उत्तर:
(4) KCl
40. आग बुझाने वाले यन्त्रों में H2SO4 तथा निम्न में से क्या होता है ?
(1) NaHCO3 तथा Na2CO3
(2) NaHCO3 विलयन
(3) Na2CO3
(4) CaCO3
उत्तर:
(1) NaHCO3 तथा Na2CO3
41. सोडियम कार्बोनेट बनता है-
(1) कोल्बे विधि द्वारा
(2) सॉल्वे प्रक्रम द्वारा
(3) नेल्सन विधि द्वारा
(4) सम्पर्क विधि द्वारा।
उत्तर:
(2) सॉल्वे प्रक्रम द्वारा
42. सोडियम धातु को निम्न में से किसके अन्तर्गत संचित नहीं किया जाता है-
(1) बेन्जीन
(2) कैरोसीन
(3) ऐल्कोहॉल
(4) टॉलूईन।
उत्तर:
(3) ऐल्कोहॉल
43. निम्न में से कौन-सी क्षारीय धातु नहीं है-
(1) Rb
(2) Cs
(3) Fr
(4) Rn
उत्तर:
(4) Rn
44. निम्न में से कौन-सा कमरे के ताप पर द्रव है-
(1) Na
(2) Fr
(3) Ce
(4) Os
उत्तर:
(2) Fr
45. क्षारीय मृदा धातुएँ सम्बन्धित हैं, आवर्त सारणी के –
(1) s- ब्लॉक से
(2) p-ब्लॉक से
(3) d- ब्लॉक से
(4) f-ब्लॉक से ।
उत्तर:
(1) s- ब्लॉक से
46. क्षारीय मृदा धातुओं के कार्बोनेटों के ऊष्मीय स्थायित्व का घटता हुआ क्रम है-
(1) BaCO3 > SrCO3 > CaCO3 > MgCO3
(2) BaCO3 > SrCO3 > MgCO3 > CaCO3
(3) CaCO3 > SrCO3 > MgCO3 > BaCO3
(4) MgCO3 > CaCO3 > SrCO3 > BaCO3
उत्तर:
(2) BaCO3 > SrCO3 > MgCO3 > CaCO3
47. प्रथम आयनन विभव को प्रदर्शित करने वाला सही क्रम है-
(1 ) K > Na > Ni
(2) Be> Mg > Ca
(3) B > C>N
(4) Ge > Si > C
उत्तर:
(2) Be> Mg > Ca
48. बढ़ते हुये आयनिक गुण का सही क्रम है-
(1) BeCl2 < MgCl2 < CaCl2 < BaCl2
(2) BeCl2 < MgCl2 < BaCl2 < CaCl2
(3) BeCl2 < BaCl2 < MgCl2 < CaCl2
(4) BeCl2 < CaCl2 < MgCl2 < BaCl2
उत्तर:
(1) BeCl2 < MgCl2 < CaCl2 < BaCl2
49. क्षारीय मृदा धातुओं में से वह तत्व जो मुख्यतः सह-संयोजक
यौगिक बनाता है-
(1) Ba
(2) Sr
(3) Ca
(4) Be
उत्तर:
(4) Be
50. एक धात्विक ऑक्साइड का सूत्र MO है इसके फॉस्फेट का होगा –
(1) M3(PO4)2
(2) MPO4
(3) M3PO4
(4) M2(PO4)3
उत्तर:
(1) M3(PO4)2
51. जिप्सम है-
(1) MgSO4.7H2O
(2) CuSO4.5H2O
(3) CaSO4.5H2O
(4) Na2SO4.10H2O
उत्तर:
(3) CaSO4.5H2O
52. मैग्नीशियम का निष्कर्षण करते हैं-
(1) कार्नेलाइट के विद्युत अपघटन से
(2) टैल्क के जलीय अपघटन से
(3) मैग्नेसाइट के ताप – अपघटन से
(4) उपर्युक्त सभी से।
उत्तर:
(1) कार्नेलाइट के विद्युत अपघटन से
53. दुर्बलतम क्षार है-
(1) Be(OH)2
(2)Mg(OH)2
(3) NaOH
(4) KOH
उत्तर:
(1) Be(OH)2
54. एप्सम का सूत्र है-
(1) MgSO4
(2) MgSO4.7H2O
(3) CaSO4.2H2O
(4) CaSO4
उत्तर:
(2) MgSO4.7H2O
55. कपड़ा धोने का सोडा होता है-
(1) Na2CO3.10H2O
(2) Na2CO3. H2O
(3) Na2CO3.5H2O
(4) Na2CO3
उत्तर:
(1) Na2CO3.10H2O
56. सबसे अधिक धनात्मक क्षारीय मृदा धातु है-
(1) Be
(2) Mg
(3) Ca
(4) Ba
उत्तर:
(4) Ba
57. निम्न में से किसका आयनन विभव अधिकतम है-
(1) Be
(2) Mg
(3) Ca
(4) Ba
उत्तर:
(1) Be
58. निम्न में से कौन-सा धातु कार्बोनेट गर्म करने पर अपघटित होता है-
(1) MgCO3
(3) K2CO3
(2) Na2CO3
(4) Rb2 CO3
उत्तर:
(1) MgCO3
59. कैल्सियम लवण ज्वाला में रखने से कौन-सा रंग प्रदान करता है-
(1) लाल
(2) हरा
(3) सफेद
(4) गुलाबी
उत्तर:
(1) लाल

60. कौन – सा क्विक लाइम है-
(1) Ca(OH)2
(2) CaO
(3) CaCO3
(4) Ca(OH)2 + H2O
उत्तर:
(2) CaO
61. नाइट्रोलिम होता है-
(1) Ca(NO3)2
(2) Ca(CN)2
(3) CaCN2 + C
(4) CaCN2
उत्तर:
(3) CaCN2 + C
62. सीमेन्ट निर्माण में निम्न में से कौन सा कच्चे माल के रूप में प्रयोग किया जाता है-
(1) चूने का पत्थर, क्ले एवं रेत
(2) चूने का पत्थर, जिप्सम एवं रेत
(3) चूने का पत्थर, जिप्सम एवं ऐलुमिना
(4) चूने का पत्थर, क्ले एवं जिप्सम ।
उत्तर:
(4) चूने का पत्थर, क्ले एवं जिप्सम ।
63. प्लास्टर ऑफ पेरिस है-
(1) CaSO4.2H2O
(2) MgSO4.7H2O
(3) KCl.MgCl2.6H2O
(4) CaSO4.1/2H2O
उत्तर:
(4) CaSO4.1/2H2O
64. जिप्सम का सूत्र है-
(1) MgSO4.2H2O
(2) CaSO4.2H2O
(3) CaSO4.3H2O
(4) 2CaSO4
उत्तर:
(2) CaSO4.2H2O
65. जल की अत्यंत सूक्ष्म मात्रा को अवशोषित करने के लिए सर्वोत्तम अभिकर्मक है-
(1) सिलिका जैल
(2)CaCl2
(3) Mg(ClO4)2
(4) H2SO4
उत्तर:
(1) सिलिका जैल
66. एप्सम लवण है-
(1) CaSO4.2H2O
(2) SrSO4
(3) BaSO4
(4) MgSO4.7H2O
उत्तर:
(4) MgSO4.7H2O
67. सीमेन्ट का जमकर कठोर होने का कारण है-
(1) निर्जलीकरण
(2) जलयोजन व जलअपघटन
(3) जलअपघटन
(4) बहुलीकरण।
उत्तर:
(3) जलअपघटन
68. बुझा हुआ चूना है-
(1) CaO
(2) Ca(OH)2
(3) CaCO3
(4) CaCl2
उत्तर:
(2) Ca(OH)2
69. प्लास्टर ऑफ पेरिस कठोर हो जाता है-
(1) CO2 को पृथक् करने पर
(2) CaCO2 में परिवर्तित होकर
(3) जल से संयुक्त होने पर
(4) जल को पृथक् करने पर ।
उत्तर:
(3) जल से संयुक्त होने पर
70. चूने का दूध है-
(1) CaO
(2) Ca(OH)2 का जलीय विलयन
(3) Ca(OH)2
(4) Ca(OH)2 का जलीय निलम्बन |
उत्तर:
(4) Ca(OH)2 का जलीय निलम्बन |
71. प्लास्टर ऑफ पेरिस जल के साथ कठोर पुँज में परिवर्तित हो जाता है, इसका संघटन है-
(1) CaSO4
(2) CaSO4. H2O
(3) CaSO4. 2H2O
(4) CaSO4.Ca(OH)2
उत्तर:
(3) CaSO4. 2H2O
72. निर्जल मैग्नीशियम क्लोराइड MgCl2.2H2O को गर्म करके तैयार किया जा सकता है-
(1) शुष्क हाइड्रोजन क्लोराइड गैस की धारा में
(2) कार्बन के साथ
(3) जब तक कि यह गल न जाये
(4) चूने के साथ ।
उत्तर:
(1) शुष्क हाइड्रोजन क्लोराइड गैस की धारा में
73. सीमेन्ट का जमना है-
(1) ऊष्माक्षेपी अभिक्रिया
(2) ऊष्माशोषी अभिक्रिया
(3) न तो ऊष्माक्षेपी न ही ऊष्माशोषी
(4) इनमें से कोई नहीं।
उत्तर:
(1) ऊष्माक्षेपी अभिक्रिया
74. पोर्टलैण्ड सीमेण्ट (नूने को छोड़कर) का बहुत बड़ा अंश है-
(1) ऐलुमिना
(2) सिलिका
(3) आयरन ऑक्साइड
(4) मैग्नीशिया ।
उत्तर:
(2) सिलिका
75. MgCi2 तथा MgO का मिश्रण कहलाता है-
(1) पोर्टलैण्ड सीमेण्ट
(2) सोरेल सीमेन्ट
(3) दिक् लवण
(4) इनमें से कोई नहीं ।
उत्तर:
(2) सोरेल सीमेन्ट
76. निम्न में से कौन सी धातु क्लोरोफिल में पायी जाती है-
(1) Mg
(2) Be
(3) Ca
(4) इनमें से कोई नहीं।
उत्तर:
(1) Mg
77. मोर्टार (गारा) मिश्रण है-
(1) बुझा चूना, रेत तथा जल
(2) बुझा चूना, प्लास्टर ऑफ पेरिस तथा जल
(3) मैग्नीशियम क्लोराइड, टार तथा चूना
(4) चूना, पोर्टलैण्ड सीमेण्ट तथा जल ।
उत्तर:
(1) बुझा चूना, रेत तथा जल
78. फ़्लैश बल्ब का तार किसका बना होता है ?
(1) Mg
(2) Ba
(3) Ag
(4) Cu
उत्तर:
(1) Mg
79. आतिशबाजी में गहरा लाल रंग किस मूलक की उपस्थिति के कारण होता है-
(1) Na
(2) Ba
(3) K
(4) Sr
उत्तर:
(4) Sr
80. निम्न में कौन – सा बेराइट है-
(1) BaO
(2) BaCO3
(3) BaSO4
(4) BaCl2.2H2O.
उत्तर:
(3) BaSO4
81. मोर्टार में रेत का कार्य है-
(1) कठोरता को कम करना
(2) पदार्थ को ठोस बनाना
(3) पदार्थ के लचीलेपन को कम करना
(4) अधिक सिकुड़न को रोकना जिसके कारण दरार पड़ जाती है ।
उत्तर:
(4) अधिक सिकुड़न को रोकना जिसके कारण दरार पड़ जाती है ।
82. बुझा हुआ चूना निम्न में से किसके उत्पादन में प्रयोग होता है-
(1) सीमेण्ट
(2) वर्णक
(3) दवाईयाँ
(4) अग्निसह ईंटें ।
उत्तर:
(1) सीमेण्ट
83. गैसों को सुखाने में प्रयुक्त किया जाता है-
(1) CaCO3
(3) NaHCO3
(2) Na2CO3
(4) CaO
उत्तर:
(4) CaO
84. लिथोफोन एक मिश्रण है-
(1) BaCl2 + ZnS
(2) BaSO4 + ZnS
(3) BaSO4 + ZnSO4
(4) BaO2 + ZnSO4
उत्तर:
(2) BaSO4 + ZnS
अति लघु उत्तरीय प्रश्न:
प्रश्न 1.
लीथियम का एक उपयोग बताइए ।
उत्तर:
मिश्र धातु बनाने में।
प्रश्न 2.
सोडियम का एक प्रमुख उपयोग दीजिए ।
उत्तर:
सोडियम वाष्प लैम्प बनाने में।
प्रश्न 3.
कौन-से क्षारीय मृदा तत्व ज्वाला को रंग प्रदान करते हैं?
उत्तर:
Ca, Sr तथा Ba |
प्रश्न 4.
बेरीलियम हाइड्राइड की प्रकृति क्या है?
उत्तर:
बहुलक प्रकृति होती है।
प्रश्न 5.
बेरीलियम हैलाइड किस प्रकार के होते हैं?
उत्तर:
आयनिक प्रकृति के होते हैं।
प्रश्न 6.
क्षार धातुएँ प्रबल अपचायक क्यों होती हैं ?
उत्तर:
क्षार धातुओं का परमाणु आकार अपने आवर्त के सभी तत्वों से बड़ा होने के कारण ये धातुएँ अपने बाह्य कक्ष का इलेक्ट्रॉन आसानी से त्याग देती हैं। अतः ये प्रबल अपचायक होती हैं।
प्रश्न 7.
Na, K, Rb और Cs वायु में खुले क्यों नहीं रखे जाते हैं?
उत्तर:
ये सभी तत्व अति क्रियाशील हैं तथा वायु की ऑक्सीजन के साथ ऑक्साइड बनाते हैं।
प्रश्न 8.
क्षार धातुएँ अधिक मुलायम क्यों होती हैं ?
उत्तर:
क्षार धातुओं में संकुलन ढीला-ढाला होता है तथा जालक में काफी रिक्त स्थान होता है। इसीलिए ये मुलायम होती हैं।
प्रश्न 9.
लीथियम सहसंयोजक यौगिक क्यों बनाता है?
उत्तर:
लीथियम का छोटा आकार, अधिक नाभिकीय आवेश और अधिक ध्रुवण क्षमता के कारण यह सहसंयोजक यौगिक बनाता है।
प्रश्न 10.
क्षार धातुएँ द्वितीय आयन क्यों नहीं बनाती हैं?
उत्तर:
क्षार धातएँ अपना संयोजी इलेक्टॉन त्यागकर स्थायी अक्रिय गैस विन्यास प्राप्त कर लेती हैं जो अति कठिनाई से टूटता है । अत: क्षार धातुएँ द्विधनात्मक आयन नहीं बनाती हैं।
प्रश्न 11.
वर्ग 1 के तत्व क्षार धातुएँ क्यों कहलाते हैं?
उत्तर:
वर्ग 1 के तत्व क्षार धातुएँ कहलाते हैं; क्योंकि इनके हाइड्रॉक्साइड विलेय क्षारक हैं जो क्षार (alkalies) कहलाते हैं। इसके अतिरिक्त इन तत्वों की राख (ash) प्रकृति में क्षारीय होती है।

प्रश्न 12.
क्षार धातुओं की आयनन ऊर्जा कम क्यों होती है ?
उत्तर:
क्षार धातुओं की आयनन ऊर्जा इनके बड़े परमाणु आकार के कारण कम होती है। ये सरलता से इलेक्ट्रॉन त्याग देते हैं ।
प्रश्न 13.
क्षार धातुओं की आयनन ऊर्जा परमाणु क्रमांक में वृद्धि के साथ क्यों घटती है?
उत्तर:
परमाणु क्रमांक बढ़ने पर परमाणु आकार बढ़ता है जिससे संयोजी इलेक्ट्रॉनों तथा नाभिक के बीच आकर्षण बल घटता है। अतः वर्ग में नीचे जाने पर अर्थात् परमाणु क्रमांक में वृद्धि होने पर आयनन ऊर्जा घटती है।
प्रश्न 14.
उन क्षार धातुओं के नाम लिखें जो वायु की अधिकता में गरम करने पर सुपर ऑक्साइड बनाती हैं?
उत्तर:
K, Rb और Cs |
प्रश्न 15.
उस धातु का नाम लिखें जो जल की सतह पर उससे बिना अभिक्रिया करे तैरती है।
उत्तर:
Li.
प्रश्न 16.
क्षार धातुओं में उन धातुओं के नाम बताएँ जो द्रव अवस्था में पायी जाती हैं।
उत्तर:
Cs और Fr.
प्रश्न 17.
उस मुख्य कारक को लिखें जिसकी वजह से लीथियम असंगत व्यवहार करता है।
उत्तर:
इसकी उच्च ध्रुवणता शक्ति (charge / size अनुपात ) ।
प्रश्न 18.
निम्न को उनके सह संयोजक गुण के आधार पर घटते हुये क्रम में व्यवस्थित करें।
MCI, MBr, MF, MI जहाँ (M= क्षार धातुएँ)
उत्तर:
जैसे-जैसे ऋण आयनों का आकार बढ़ता जाता है वैसे-वैसे इनका सहसंयोजक गुण भी बढ़ता जाता है।
MI > MBr > MC1 > MF
प्रश्न 19.
समूह-1 के तत्वों को क्या कहते हैं ?
उत्तर:
क्षार धातुएँ।
प्रश्न 20.
उस क्षार धातु का नाम लिखें जो Mg से विकर्ण सम्बन्ध प्रदर्शित करती है।
उत्तर:
Li |
प्रश्न 21.
सोडियम धातु को मिट्टी के तेल में क्यों रखा जाता है?
उत्तर:
सोडियम धातु अत्यधिक क्रियाशील होती है तथा यह नमी, ऑक्सीजन एवं CO2 के साथ क्रिया करके NaOH, Na2O तथा Na2CO3 बनाती है। अत: इसे नमी तथा वायु से बचाने के लिये मिट्टी के तेल में रखा जाता है।
प्रश्न 22.
सोडियम तथा पोटैशियम के मुख्य अयस्कों के नाम
लिखें।
उत्तर:
Na – NaCl
K – KCl
प्रश्न 23.
प्रकाश विद्युत सेल में हम क्षार धातुओं का प्रयोग क्यों करते हैं ?
उत्तर:
क्योंकि इनके आयनन विभव का मान कम होता है।
प्रश्न 24.
Na (11) तथा K (19) का इलैक्ट्रॉनिक विन्यास लिखें।
उत्तर:
Na(11) → 1s2 2s2 2p63s1
K (19) → 1s2 2s2 2p63s23p64s1
प्रश्न 25.
क्षार धातुओं के गलनांक एवं क्वथनांक कम क्यों होते हैं?
उत्तर:
क्योंकि इनका आकार बड़ा होता है एवं इनमें उपस्थित धात्विक बंध भी कमजोर होते हैं।
प्रश्न 26.
क्षार धातुओं के घनत्व कम क्यों हैं?
उत्तर:
बड़े आकार एवं कमजोर घात्विक बन्ध के कारण क्षार धातुओं के घनत्व काफी कम होते हैं।
प्रश्न 27.
Na और K को हम उनके गलित ……………….. के …………….. अपचयन द्वारा प्राप्त कर सकते हैं।
उत्तर:
अयस्कों, वैद्युतीय।
प्रश्न 28.
Na+…………………. ‘परमाणु के साथ समइलैक्ट्रॉनिक है।
उत्तर:
नियॉन (Ne) ।
प्रश्न 29. सोडियम का आयनन विभव K से………………. होता है।
उत्तर:
अधिक ।
प्रश्न 30.
क्षार धातुओं के यौगिक प्रायः विलेय होते हैं क्योंकि वे के होते हैं ?
उत्तर:
आयनिक प्रकृति ।
प्रश्न 31.
किस क्षार धातु के आयन की ध्रुवणता सबसे अधिक होती है।
उत्तर:
लीथियम ।
प्रश्न 32.
भारतीय साल्टपीटर किसे कहते हैं?
उत्तर:
KNO3 भारतीय साल्टपीटर कहलाता है ।
प्रश्न 33.
सोडियम हाइड्रॉक्साइड के औद्योगिक निर्माण में सह-उत्पाद कौन-सा होता है ?
उत्तर:
क्लोरीन ।
प्रश्न 34.
200°C तक गर्म ठोस कॉस्टिक सोडा पर CO गैस प्रवाहित करने पर क्या प्राप्त होता है?
उत्तर:
HCOONa (सोडियम फॉमेट)
प्रश्न 35.
सोडियम कार्बोनेट के जलीय विलयन के क्षारीय होने का क्या कारण है?
उत्तर:
क्योंकि यह जल अपघटित होकर सोडियम हाइड्रॉक्साइड एवं कार्बोनिक अम्ल बनाता है। NaOH एक प्रबल क्षार है जबकि कार्बोनिक अम्ल एक दुर्बल अम्ल है जिस कारण से इसका जलीय विलयन क्षारीय हो जाता है।
प्रश्न 36.
जब K को तेजी से वायु में गर्म किया जाता है तो क्या प्राप्त होता है?
उत्तर:
KO2 (पौटेशियम सुपरऑक्साइड)
प्रश्न 37.
नौसादर क्या होता है?
उत्तर:
NH4Cl को नौसादर कहते हैं।
प्रश्न 38.
धावन सोडे को गर्म करने पर क्या प्राप्त होता है?
उत्तर:
केवल जल वाष्प प्राप्त होती है।
प्रश्न 39.
रिक्त स्थानों की पूर्ति कीजिए-
(i) Na2CO3.10H2O को………………. कहते हैं।
उत्तर:
धावन सोडा ।
(ii) LiNO3 अपघटित होकर………………. एवं………………. देता है जबकि अन्य सभी क्षारीय धातुओं के नाइट्रेट अपघटित होकर……………….व………………. देते हैं।
उत्तर:
LiNO3 अपघटित होकर NO2 एवं O2 देता है जबकि अन्य सभी क्षारीय धातुओं के नाइट्रेट अपघटित होकर धातु नाइट्राइट व O2 देते हैं।
(iii) Li2CO3 गर्म करने पर……………….एवं………………. में अपघटित होता है।
उत्तर:
Li2CO3 गर्म करने पर Li20 एवं O2 में अपघटित होता है जबकि अन्य क्षारीय धातु कार्बोनेट गर्म करने पर अपघटित नहीं होते हैं।
(iv) क्षार धातुएँ मर्करी में घुलकर उसके साथ मिश्र धातु बनाती है जिन्हें……………….कहते हैं।
उत्तर:
अमलगम ।
(v) क्षार धातु धनात्मक आयन का आकार जितना छोटा होता है उतना ही………………. जलयोजन होता है।
उत्तर:
अधिक ।
(vi) अमोनिया में संतृप्त NaCl के विलयन को………………. कहते हैं।
उत्तर:
अमोनियामय ब्राइन ।
(vii) द्रव अमोनिया में क्षार धातुएँ नीला रंग देती हैं, इसका कारण उसमें उपस्थित………………. है ।
उत्तर:
अमोनिएटेड इलेक्ट्रॉन ।
प्रश्न 40.
वर्ग-1 के तत्वों में ऊपर से नीचे चलने पर घनत्व बढ़ता जाता है लेकिन किस तत्व पर यह क्रम विचलित होता है ?
उत्तर:
K तत्व पर यह क्रम विचलित होता है।
प्रश्न 41.
किन तत्वों का घनत्व पानी से कम है ?
उत्तर:
Li, Na तथा K ।
प्रश्न 42.
वर्ग-1 के तत्वों में प्रबलतम धनविद्युती तत्व कौन-सा होगा ?
उत्तर:
Cs (सीजियम) ।
प्रश्न 43.
वर्ग-1 की धातुओं में से कौन-सी धातु कठोर है ?
उत्तर:
Li (लीथियम)।
प्रश्न 44.
वर्ग-1 की धातुओं में से कौन-सी धातु नर्म है ?
उत्तर:
Cs (सीजियम)।

प्रश्न 45.
वर्ग-1 की धातुओं में से वह कौन-सी धातु है जिसे चाकू से नहीं काटा जा सकता है ?
उत्तर:
Li (लीथियम)।
प्रश्न 46.
वर्ग- 1 में कौन-सी धातु द्रव अवस्था में पायी जाती है ?
उत्तर:
सीजियम (Cs) ।
प्रश्न 47.
कौन-सी धातु का प्रयोग फोटो इलेक्ट्रिक सेल में करते हैं ?
उत्तर:
सीजियम का प्रयोग फोटो इलेक्ट्रिक सेल में किया जाता है।
प्रश्न 48.
वर्ग- 1 के धातुओं के धनायन की प्रकृति कैसी होती है ?
उत्तर:
वर्ग-1 के धातुओं के धनायन की प्रकृति प्रतिचुम्बकीय होती है।
प्रश्न 49.
वर्ग-1 की धातुओं में से किस धातु धनायन की जलयोजन ऊर्जा का मान अधिकतम होता है ?
उत्तर:
Li+ की जलयोजन ऊर्जा का मान अधिकतम होता है।
प्रश्न 50.
वर्ग-1 की धातुओं के जलयोजित धनायनों की आयनिक चालकता का क्रम लिखें।
उत्तर:
\(\mathrm{Li}_{(a q)}^{+}<\mathrm{Na}_{(a q)}^{+}<\mathrm{K}_{(a q)}^{+}<\mathrm{Rb}_{(a q)}^{+}<\mathrm{Cs}_{(a q)}^{+}\) जलयोजित धनायनों की आयनिक चालकता का क्रम
प्रश्न 51.
वर्ग-1 के तत्वों में किस तत्व की आयनन एन्थैल्पी सर्वाधिक है ?
उत्तर:
Li (लीथियम)।
प्रश्न 52.
वर्ग-1 के तत्वों में कौन-सी धातुएँ संकुल हाइड्राइड बनाती हैं ?
उत्तर:
LiAlH4 एवं NaBH4 (अर्थात् Li एवं Na) ।
प्रश्न 53.
वर्ग-1 के तत्वों के हाइड्रॉक्साइड में कौन प्रबलतम क्षार है ?
उत्तर:
CsOH (सीजियम हाइड्रॉक्साइड)।
प्रश्न 54.
सुपरऑक्साइड आयन को किससे प्रदर्शित करते हैं ?
उत्तर:
O2– (सुपरऑक्साइड) ।
प्रश्न 55.
परॉक्साइड एवं ऑक्साइड आयन को किससे प्रदर्शित करते हैं।
उत्तर:
परॉक्साइड (O22- तथा ऑक्साइड (O2-) ।
प्रश्न 56.
वर्ग- 1 के तत्वों के हाइड्रॉक्साइडों की प्रबलता को घटते क्रम में व्यवस्थित करें।
उत्तर:
CsOH > RbOH > KOH > NaOH > LiOH (प्रबलता का क्रम)।
प्रश्न 57.
वर्ग-1 में कौन-सा तत्व नाइट्रोजन से क्रिया कर नाइट्राइड बनाता है ?
उत्तर:
लीथियम |
प्रश्न 58.
सोडियम हाइड्रॉक्साइड को दाहक सोडा (caustic soda) क्यों कहते हैं ?
उत्तर:
क्योंकि यह त्वचा पर फफोले (blisters) डालता है।
प्रश्न 59.
काली राख (Black ash) किसे कहते हैं ?
उत्तर:
Na2CO3 व CaS के मिश्रण को काली राख कहते हैं।
प्रश्न 60.
हल्की क्षार धातुओं जैसे Li, Na, K आदि का घनत्व जल से कम होता है, क्यों ?
उत्तर:
क्योंकि इन धातुओं का परमाणु-आयतन जल से अधिक होता है।
प्रश्न 61.
क्षार धातुएँ विद्युत व ऊष्मा की अच्छी चालक हैं, स्पष्ट करो ।
उत्तर:
क्योंकि इनका संयोजी इलेक्ट्रॉन नाभिक से कम शक्ति के द्वारा जुड़ा होता है।
प्रश्न 62.
क्षार धातुओं को मिट्टी के तेल या पैराफीन में क्यों रखते हैं ?
उत्तर:
क्योंकि ये जल एवं वायु से क्रिया कर लेती हैं।
प्रश्न 63.
क्रिस्टल कार्बोनेट व धावन सोडा दोनों सोडियम के कार्बोनेट हैं। इन दोनों में क्या अन्तर है ?
उत्तर:
सोडियम कार्बोनेट के मोनोहाइड्रेट को क्रिस्टल कार्बोनेट व डेका हाइड्रेट को धावन सोडा कहते हैं।
क्रिस्टल कार्बोनेट – Na2CO3.H2O
धावन सोडा – Na2CO3.10H2O
प्रश्न 64.
क्षार धातुओं के सुपरऑक्साइड रंगीन व अनुचुम्बकीय होते हैं, क्यों ?
उत्तर:
सुपर ऑक्साइडों में तीन इलेक्ट्रॉनों का एक बन्ध होता है जिसमें अयुग्मित इलेक्ट्रॉन होते हैं। इस कारण यह अनुचुम्बकीय व रंगीन होते हैं।
प्रश्न 65.
Li अपने वर्ग के अन्य तत्वों की अपेक्षा वर्ग II-A के Mg से अधिक समानता रखता है, क्यों ?
उत्तर:
Li+ व Mg+ की ध्रुवण क्षमता लगभग समान होने के कारण Li व Mg के लवणों के गुणों में समानता पायी जाती है।
प्रश्न 66.
NaOH को वायु में रखने पर यह पहले द्रव बनाता है। फिर ठोस हो जाता है, क्यों ?
उत्तर:
NaOH, वायु की CO2 व नमी को अवशोषित कर लेता है। पहले यह NaOH का संतृप्त विलयन बनाता है फिर CO2 से क्रिया करके Na2CO3 बनाता है । यह अविलेय होने के कारण ठोस Na2CO3 में परिवर्तित हो जाता है।
प्रश्न 67.
शुद्ध NaCl प्रस्वेद्य (deliquescent) नहीं है, परन्तु घर पर प्रयोग होने वाला नमक वर्षा के दिनों में नमी युक्त हो जाता है।
उत्तर:
घर पर प्रयोग होने वाले नमक में MgCl2 अशुद्धि के रूप में होता है जो कि एक प्रस्वेद्य यौगिक है।
प्रश्न 68.
शुष्क चूना क्या है? यह कैसे बनाया जाता है ?
उत्तर:
शुष्क चूना कैल्सियम ऑक्साइड (CaO) है। इसे चूना पत्थर (कैल्सियम कार्बोनेट) को गर्म करके बनाया जाता है।
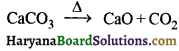
प्रश्न 69.
BeCl2 कार्बनिक विलायकों में विलेय क्यों होता है?
उत्तर:
BeCl2 सहसंयोजी यौगिक है; इसलिए यह कार्बनिक विलायकों में विलेय होता है।
प्रश्न 70.
शुष्क चूने से प्रारम्भ करके बुझा चूना कैसे बनाया जाता है ? क्या अभिक्रिया ऊष्माक्षेपी होगी या ऊष्माशोषी ?
उत्तर:
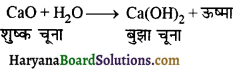
जब शुष्क चूने को जल में डाला जाता है, यह कैल्सियम हाइड्रॉक्साइड बनाता है। यह अभिक्रिया ऊष्माक्षेपी होती है।
प्रश्न 71.
उस क्षार धातु का नाम बताइए जो मैग्नीशियम के साथ विकर्ण सम्बन्ध प्रदर्शित करती है ?
उत्तर:
लीथियम ।
प्रश्न 72.
निम्नलिखित में विभेद करने के लिए एक अभिकर्मक अथवा एक प्रक्रम बताइए-
(i) BeSO4 तथा BaSO4
(ii) Be(OH)2 तथा Ba(OH)2
उत्तर:
(i) BeSO4 जल में विलेय है, जबकि BaSO4 नहीं है ।
(ii) Be(OH)2, NaOH में विलेय है, जबकि Ba(OH)2 अविलेय है।
प्रश्न 73.
बेरिलियम वर्ग IIA तथा ऐलुमिनियम IIIB में विद्यमान है, परन्तु फिर भी इनके गुणों में समानता का प्रमुख कारण क्या है?
उत्तर:
बेरिलियम वर्ग IIA तथा ऐलुमिनियम वर्ग IIIB में उपस्थित हैं, परन्तु इनके गुणों में समानता का कारण इनमें विकर्ण सम्बन्ध का होना है।
प्रश्न 74.
क्षारीय मृदा धातुओं के हाइड्रॉक्साइडों की जल में विलेयता वर्ग में नीचे जाने पर पर क्यों बढ़ती है?
उत्तर:
क्षारीय मृदा धातुओं में ऋणायन समान हों तो धनायन की त्रिज्या जालक एन्थैल्पी को प्रभावित करती है। चूँकि बढ़ती हुई आयनिक त्रिज्या के साथ जलयोजन एन्थैल्पी की तुलना में ऋणात्मक एन्थैल्पी तेजी से कम होती है; अतः वर्ग के नीचे जाने पर विलेयता बढ़ती जाती है।

प्रश्न 75.
क्षारीय मृदा धातुओं के कार्बोनेटों एवं सल्फेटों की जल में विलेयता वर्ग में ऊपर से नीचे क्यों घटती है?
उत्तर:
ऋणायन का आकार धनायन की तुलना में बहुत अधिक है एवं जालक एन्थैल्पी वर्ग में लगभग स्थिर रहती है। चूँकि वर्ग में जलयोजन ऊर्जा का मान ऊपर से नीचे घटता है अतः धातु कार्बोनेट एवं सल्फेटों की विलेयता वर्ग में नीचे जाने पर घटती है।
प्रश्न 76.
उच्च ताप पर नाइट्रोजन के साथ कौन सी धातु सीधे संयोग कर सकती है ?
उत्तर:
Mg.
प्रश्न 77.
क्षारीय मृदा धातुओं में वे कौन-सी धातुएँ हैं जो ज्वाला परीक्षण नहीं देती हैं।
उत्तर:
Be, Mg.
प्रश्न 78.
मैग्नीशियम की दो मिश्र धातुएँ बताइए ।
उत्तर:
मैग्नेलियम : Al Mg
डूरेल्यूमिन : Mg Al Mn Cu Si
प्रश्न 79.
ग्रिगनार्ड अभिकर्मक का सूत्र लिखिए यह कैसे प्राप्त किया जाता है?
उत्तर:
R = CH3, C2H5 आदि X = हैलोजन) ऐल्किल हैलाइड के ईथरीय विलयन में मैग्नीशियम हैलाइड मिलाने पर ऐल्किल मैग्नीशियम हैलाइड बनता है जिसे ग्रिगनार्ड अभिकर्मक कहते हैं।
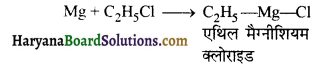
प्रश्न 80.
कैल्सियम का कौन-सा यौगिक धातु कर्म में गालक के रूप में प्रयुक्त होता है ?
उत्तर:
CaO.
प्रश्न 81.
दो उभयधर्मी ऑक्साइडों के नाम लिखिए ।
उत्तर:
- बेरीलियम ऑक्साइड (BeO)
- ऐल्यूमिनियम ऑक्साइड (Al2O3)
प्रश्न 82.
मैग्नीशियम रिबन के टुकड़े को नाइट्रोजन में गर्म करके जल में ठण्डा करने पर कौन सी गैस प्राप्त होती है ?
उत्तर:
अमोनिया (NH3)
प्रश्न 83.
वर्ग-2 के तत्वों को क्षारीय मृदा धातुएँ क्यों कहते हैं ?
उत्तर:
क्योंकि इनके ऑक्साइड क्षारीय होते हैं और मृदा (earth, SiO2) की तरह अगलनीय होते हैं।
प्रश्न 84.
क्षारीय मृदा धातुएँ प्रतिचुम्बकीय क्यों होती हैं ?
उत्तर:
क्षारीय मृदा धातुओं के तत्वों में कोई भी अयुग्मित इलेक्ट्रॉन नहीं होता है। अतः ये प्रतिचुम्बकीय होती हैं।
प्रश्न 85.
निर्जल CaSO4 निर्जलीकारक (drying agent) की तरह प्रयोग होता है, क्यों ?
उत्तर:
निर्जल CaSO4 जल को अवशोषित कर लेता है तथा हाइड्रेटेड सल्फेट CaSO4.2H2O बनाता है।
प्रश्न 86.
सीमेन्ट में चूने की मात्रा परिवर्तित करने पर क्या प्रभाव पड़ता है ?
उत्तर:
सीमेन्ट में यदि चूने की मात्रा कम कर दी जाये तो दुर्बल सीमेन्ट बनता है जो शीघ्रता से जमता है। जबकि सीमेन्ट में चूने की मात्रा अधिक होने पर सीमेन्ट के जमने पर दरारें पड़ जाती हैं।
प्रश्न 87.
सीमेन्ट में यदि सिलिका की मात्रा बढ़ा दी जाये तो क्या होगा ?
उत्तर:
सीमेन्ट में सिलिका की मात्रा अधिक बढ़ा देने पर दुर्बल सीमेण्ट का निर्माण होता है।
प्रश्न 88.
सीमेन्ट को बनाते समय क्लिंकर में जिप्सम क्यों मिलाते हैं ?
उत्तर:
क्योंकि जिप्सम मिलाने पर सीमेन्ट के जमने की दर कम हो जाती है एवं सीमेन्ट कठोर भी हो जाता है ।
प्रश्न 89.
मोर्टार किसे कहते हैं ?
उत्तर:
सीमेण्ट, रेत एवं पानी का मिश्रण मोर्टार कहलाता है।
प्रश्न 90.
कैल्सियम के उस हैलाइड का नाम बताएँ तो जल में अविलेय है ?
उत्तर:
कैल्सियम फ्लुओराइड (CaF2).
प्रश्न 91.
वह कौन-सी क्षारीय मृदा धातु है, जिसके तार खींचे जा सकते हैं ?
उत्तर:
Mg धातु के तार खींचे जा सकते हैं।
प्रश्न 92.
ज्वाला को हरा रंग प्रदान करने वाली क्षारीय मृदा धातु कौन-सी है।
उत्तर:
बेरियम (Ba).
प्रश्न 93.
वह कौन-सी क्षारीय मृदा धातुएँ हैं जो कि ज्वाला को रंग नहीं देती हैं ?
उत्तर:
Be (बेरीलियम) तथा Mg ( मैग्नीशियम) ।
प्रश्न 94.
क्षार धातुओं में किस तत्व की आयनन एन्थैल्पी उच्चतम है ?
उत्तर:
लीथियम (Li) धातु की आयनन एन्थैल्पी उच्चतम होती है।
प्रश्न 95.
जैव उपयोगिता वाले चार धात्विक आयन बताएँ ।
उत्तर:
Na+, K+, Mg2+ एवं Ca2+
प्रश्न 96.
उभयधर्मी क्षारीय मृदा धातु के हाइड्रॉक्साइड का सूत्र लिखें।
उत्तर:
बेरीलियम हाइड्रॉक्साइड [Be(OH)2]
प्रश्न 97.
बेरीलियम ऑक्साइड (BeO) का क्वथनांक उच्च होता है, क्यों ?
उत्तर:
क्योंकि बेरीलियम ऑक्साइड बहुलक के रूप में रहता है। इस कारण इसका क्वथनांक उच्च होता है ।
प्रश्न 98.
डोलोमाइट का सूत्र क्या है ?
उत्तर:
MgCO3. CaCO3
प्रश्न 99.
टूटी हड्डियों पर प्लास्टर चढ़ाने हेतु उपयोगी पदार्थ का नाम व सूत्र दें।
उत्तर:
टूटी हड्डियों पर प्लास्टर ऑफ पेरिस (CaSO4.2H2O) का प्लास्टर चढ़ाया जाता है।
प्रश्न 100.
धातुकर्म में गालक के रूप में Ca का कौन-सा यौगिक प्रयोग किया जाता है ?
उत्तर:
कैल्सियम ऑक्साइड (CaO) को गालक के रूप में प्रयोग किया जाता है।
प्रश्न 101.
संगमरमर के पत्थर का सूत्र क्या है ?
उत्तर:
कैल्सियम कार्बोनेट (CaCO3).
प्रश्न 102.
एप्सम लवण का सूत्र क्या है ?
उत्तर:
MgSO4 . 7H2O.
प्रश्न 103.
कार्नेलाइट का सूत्र क्या है ?
उत्तर:
KCl. MgCl2:6H2O
प्रश्न 104.
मृत जल प्लास्टर (Dead Burnt Plaster) किसे कहते हैं ?
उत्तर:
निर्जल CaSO4 को मृत जल प्लास्टर कहा जाता है।

प्रश्न 105.
कैल्सियम के दो अयस्कों के नाम लिखें।
(1) फ्लोरेपेटाइट : 3Ca3(PO4)2.CaF2
(2) फैल्सपार : CaF2
प्रश्न 106.
क्या होता है जब Mg के नाइट्रेट को गर्म करते हैं ?
उत्तर:
मैग्नीशियम के नाइट्रेट को गर्म करने पर यह विघटित हो जाता है तथा ऑक्साइड, नाइट्रोजन डाइऑक्साइड एवं ऑक्सीजन गैस बनाता है।

प्रश्न 107.
क्या होता है जब बिना बुझे चूने को सिलिका के साथ गरम करते हैं ?
उत्तर:
बिना बुझे चूने को सिलिका के साथ गर्म करने पर कैल्सियम सिलिकेट का सफेद मिश्रण प्राप्त होता है।

प्रश्न 108.
क्या होता है जब कैल्सियम नाइट्रेट को गर्म करते हैं ?
उत्तर:
कैल्सियम नाइट्रेट को गर्म करने पर यह CaO, NO2 एवं O2 में टूट जाता है।

प्रश्न 109.
क्या होता है जब Cl2 की बुझे हुए चूने से क्रिया होती है ?
उत्तर:
CaOCl2 बनता है
\(2 \mathrm{Ca}(\mathrm{OH})_2+2 \mathrm{Cl}_2 \longrightarrow \mathrm{CaCl}_2+\mathrm{CaOCl}_2+2 \mathrm{H}_2 \mathrm{O}\)
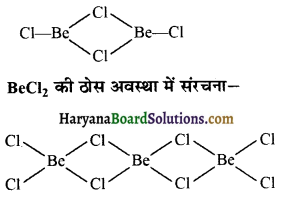
प्रश्न 110.
BeCl2 की वाष्प प्रावस्था एवं ठोस प्रावस्था की संरचना बनाएँ।
उत्तर:
BeCl2 की वाष्प अवस्था में संरचना-
प्रश्न 111.
पोटैशियम की तुलना में सोडियम अधिक उपयोगी क्यों है ?
उत्तर:
K की प्रकृति वाष्पशील होती है जिसके कारण K पोटैशियम तुलना में कम उपयोगी होता है। मुख्य रूप से Na का उपयोग अपचायक के रूप में, N तथा S के आंकलन में तथा Na का वाष्प लैम्प बनाने में किया जाता है।
प्रश्न 112.
BeO जल में अविलेय है जबकि BeSO4 जल में विलेय है, क्यों ?
उत्तर:
कैडी एवं ऐल्से के नियमानुसार समान को समान विलेय करता है (like dissolves like) चूँकि BeO एक आयनिक यौगिक है अत: यह जल में विलेय यौगिक है।
प्रश्न 113.
क्या होता है जब मैग्नीशियम सल्फेट को गर्म करते हैं ?
उत्तर:
MgSO4 को गर्म करने पर MgO, SO2 तथा O2 बनता है।

प्रश्न 114.
s – ब्लॉक के तत्व दुर्बल प्रकार के संकुल बनाते हैं।
उत्तर:
s – ब्लॉक के तत्व दुर्बल प्रकार के संकुल बनाते हैं क्योंकि इनके भीतरी कोश में इलेक्ट्रॉन उपस्थित होते हैं अर्थात् आन्तरिक कोश भरे होते हैं जबकि बाहरी कोश में एक अथवा दो ही इलेक्ट्रॉन होते हैं।
प्रश्न 115.
क्या होता है जब CaO की क्रिया H2SO4 से होती है ?
उत्तर:
CaO की क्रिया H2SO4 से होने पर कैल्सियम सल्फेट बनता है।
\(\mathrm{CaO}+\mathrm{H}_2 \mathrm{SO}_4 \longrightarrow \mathrm{CaSO}_4+\mathrm{H}_2 \mathrm{O}\)
प्रश्न 116.
क्षारीय मृदा धातुओं के भौतिक गुण जैसे – घनत्व, गलनांक, क्वथनांक, विशिष्ट ऊष्मा आदि में क्रमिक परिवर्तन नहीं होता है, क्यों ?
उत्तर:
इन तत्वों के भौतिक गुणों में क्रमिक परिवर्तन नहीं होता है। इसका कारण इन तत्वों के ठोस अवस्था में भिन्न-भिन्न धातु जालक का होना है।
प्रश्न 117.
CaCl2 को निर्जलीकारक की भाँति क्यों प्रयोग करते हैं ?
उत्तर:
CaCl2 की जल के साथ प्रबल बन्धुता होती है। इसी के कारण यह निर्जलीकारक की भाँति प्रयुक्त होता है।
प्रश्न 118.
निर्जल कैल्सियम सल्फेट को प्लास्टर ऑफ पेरिस की भाँति प्रयोग क्यों नहीं कर सकते हैं ?
उत्तर:
क्योंकि निर्जल कैल्सियम सल्फेट जल से क्रिया करके जमता नहीं है।
प्रश्न 119.
सीमेन्ट का जमना क्या है ?
उत्तर:
सीमेन्ट में जल मिलाकर छोड़ देने पर कुछ समय पश्चात् एक कठोर पदार्थ बन जाता है इसे ही सीमेन्ट का जमना ( setting) कहते हैं।
प्रश्न 120.
कंक्रीट क्या है ?
उत्तर:
सीमेन्ट, रेत व पत्थर के छोटे टुकड़े (रोड़ी) और पानी के मिश्रण को कंक्रीट कहा जाता है।
प्रश्न 121.
प्रबलित कंक्रीट क्या है ?
उत्तर:
लोहे के सरियों का जाल बनाकर उसमें कंक्रीट भरने से प्रबलित कंक्रीट प्राप्त होती है।
प्रश्न 122.
क्षार धातुओं की अपेक्षा क्षारीय मृदा धातुओं के ऑक्साइडों की क्रियाशीलता कम होती है, क्यों ?
उत्तर:
क्योंकि वायु में रखने पर क्षारीय मृदा धातुओं के ऑक्साइड धीरे-धीरे परॉक्साइड में ऑक्सीकृत होते रहते हैं ।
लघु उत्तरीय प्रश्न:
प्रश्न 1.
विकर्ण सम्बन्ध से आप क्या समझते हैं ? समझाइए ।
उत्तर:
विकर्ण सम्बन्ध (Diagonal Relation ) – आवर्त सारणी मेंs एवं p ब्लॉक का प्रथम तत्व अपने समूह के अन्य तत्वों से गुणों में काफी भिन्नता प्रदर्शित करता है। द्वितीय आवर्त के तत्व अपने वर्ग के तत्वों से तो भिन्नता रखते हैं परन्तु तृतीय आवर्त के तत्वों के गुणों से समानता प्रदर्शित करते हैं। तत्वों के इस गुण को विकर्ण सम्बन्ध कहते हैं।
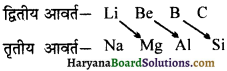
यह तत्व परस्पर विकर्ण सम्बन्ध प्रदर्शित करते हैं क्योंकि इन तत्वों की परमाणु त्रिज्या एवं विद्युत ऋणता के मान लगभग समान होते हैं।

प्रश्न 2.
Li क्षार धातुओं में प्रबलतम अपचायक है । क्यों ?
उत्तर:
सभी क्षार धातुओं का मानक आयनन विभव अधिक ऋणात्मक होने के कारण इन धातुओं में इलेक्ट्रॉन त्यागने की प्रबलतम प्रवृत्ति होती है। Li का आयनन विभव अन्य सभी क्षार धातुओं की तुलना में सर्वाधिक ऋणात्मक होता है क्योंकि Li+ आयन की हाइड्रेशन ऊर्जा अधिक एवं आयनिक त्रिज्या बहुत कम होती है।

अतः क्षार धातुओं में Li सबसे प्रबलतम अपचायक है।
प्रश्न 3.
लिथियम धातु के पाँच मुख्य उपयोग लिखिए ।
उत्तर:
लिथियम के उपयोग-
- कॉपर, निकिल आदि धातुओं के शुद्धिकरण में अशुद्धि पृथक्कारक के रूप में प्रयोग होता है।
- मिश्र धातुओं की तनन क्षमता बढ़ाने के लिए लीथियम का उपयोग होता है।
- रॉकेट एवं मिसाइल के नोदन में आवश्यक ताप नाभिकीय ऊर्जा उत्पन्न करने में लीथियम का उपयोग होता है।
- इसका समस्थानिक (7Li) प्राथमिक शीतलक के रूप में नाभिकीय रिएक्टर में प्रयोग होता है।
- लीथियम के कुछ यौगिक अपचायक के रूप में, वात रोग के उपचार में एवं कीटाणुनाशक के रूप में प्रयुक्त होते हैं।
प्रश्न 4.
लीथियम एवं सोडियम के चार-चार खनिजों के नाम सूत्र सहित लिखें।
उत्तर:
लीथियम के खनिज-
- स्पोडुमीन – Li Al Si2 O6
- लैपिडोलाइड – K2 Li3 Al4 Si O2
- पेटेलाइट – Li Al Si4O11
- ट्रिफिलाइट – Li3. Na3. Fe3. Mn3( PO3)4
सोडियम के खनिज-
- चिली साल्टपीटर – NaNO3
- सब्ज मिट्टी – Na2CO3
- बोरेक्स – Na2B4O7. 10H2O
- नेट्रान (उत्फुल्ल सोडा ) – Na2CO3. H2O
प्रश्न 5. सोडियम धातु के कोई पाँच उपयोग लिखें।
उत्तर:
सोडियम धातु के उपयोग-
- सोडियम युक्त यौगिकों के निर्माण में। उदाहरण – Na2O2,NaCN
- विलायकों (कार्बनिक) के निर्जलीकरण की क्रिया में ।
- सोडियम निष्कर्ष बनाने में (जो कार्बनिक यौगिकों में तत्वों की पहचान करने के लिए सहायक होता है । )
- धातुओं के निष्कर्षण (Extraction) में। उदाहरण- बोरॉन, सिलिकॉन, मैग्नीशियम ।
- घने कोहरे के पार देखने के लिए सोडियम वाष्प लैंप के निर्माण में।
प्रश्न 6.
उन धातुओं के नाम लिखें जो निम्नलिखित यौगिकों (खनिजों) में पायी जाती हैं?
(अ) चिली साल्ट पीटर (Chile Salt petre) (ब) मार्बल (स) एप्सोमाइट (द) बॉक्साइट
उत्तर:
(अ) चिली साल्ट पीटर – Na
(ब) मार्बल – Ca
(स) एप्सोमाइट – Mg
(द) बॉक्साइट – Al
प्रश्न 7.
क्षार धातुओं एवं क्षारीय मृदा धातुओं के चार गुणों की तुलना करें।
उत्तर:
| क्षार धातुएँ |
क्षारीय मृदा धातुएँ |
| 1. ये मुलायम धातु होती हैं। |
1. ये क्षार धातुओं से कठोर होती हैं। |
| 2. ये +1 ऑक्सीकरण संख्या प्रदर्शित करती हैं। |
2. ये +2 ऑक्सीकरण संख्या प्रदर्शित करती हैं। |
| 3. Li2CO3 को छोड़कर इन धातुओं के कार्बोनेट जल में विलेय होते हैं। |
3. इनके कार्बोनेट जल में अविलेय हैं। |
| 4. Li को छोड़कर, अन्य धातुएँ जटिल यौगिक नहीं बनाती हैं। |
4. ये जटिल यौगिक बनाती हैं। |
प्रश्न 8.
केवल क्षार धातुओं एवं क्षारीय मृदा धातुओं के ही हाइड्राइड ज्ञात हैं क्यों? इनके दो उदाहरण भी दें।
उत्तर:
कम आयनन विभव होने के कारण क्षार धातुओं एवं क्षारीय मृदा धातुओं में अधिक विद्युत धनात्मक गुण होता है, जिसके कारण ये आयनिक हाइड्राइड बनाती हैं उदाहरण – NaH, CaH2, KH आदि ।
प्रश्न 9.
क्षार धातुओं का अमोनिया में विलयन नीले रंग का दिखाई पड़ता है, क्यों ?
उत्तर:
नीला रंग अमोनियामय इलेक्ट्रॉन की उपस्थिति के कारण दिखाई देता है। यह दृश्य प्रकाश उत्पन्न होने के कारण होता है।
Na + (x + y) NH3 → Na+ (NH3)x + e– (NH3)y अमोनियामय इलेक्ट्रॉन
प्रश्न 10.
क्षार धातुओं को उनकी जल के साथ अभिक्रियाशीलता के आधार पर बढ़ते हुये क्रम में व्यवस्थित करें एवं कारण भी बताएँ ?
उत्तर:
Li< Na<K< Rb < Cs < Fr
क्षार धातुओं की अभिक्रियाशीलता उपरोक्त दिये गये क्रम के अनुसार बढ़ती जाती है क्योंकि इनका आकार बढ़ता है, आयनन विभव का मान घटता जाता है जिसके कारण इनकी अभिक्रियाशीलता बढ़ती जाती है।
प्रश्न 11.
निम्न का मिलान करें-
| (अ) (आयन) |
(ब) (ऑक्सीकरण संख्या) |
| 1. परऑक्साइड |
(i) +1 |
| 2. बाइकार्बोनेट |
(ii) +2 |
| 3. अमोनियम |
(iii) +3 |
| 4. फास्फेट |
(iv) -3 |
|
(v) -1 |
|
(vi) -2 |
उत्तर:
1. (iv), 2. (v), 3. (i), 4. (iv)
प्रश्न 12.
निम्न का मिलान करें-
| धातु |
प्राप्त होती है |
| 1. Na |
(i) एल्बॉइट (Albite) |
| 2. Mg |
(iii) बॉक्साइट (Bauxite) |
| 3. Ca |
(iii) टैल्क (Talc) |
| 4. Al |
(v) सिनेबार (Cinnabar) |
उत्तर:
1.(i), 2.(iii), 3(iv), 4.(ii)
प्रश्न 13.
निम्न में किस प्रकार विभेद करेंगे।
(अ) KNO3 एवं LiNO3
(ब) Na2CO3 एवं NaHCO3
उत्तर:
(अ) KNO3 एवं LiNO3 – LiNO3 को गर्म करने पर लाल भूरे रंग की NO2 की घूम्र प्राप्त होती है जबकि KNO3 ‘अपघटित होकर रंगहीन O2 गैस देता है।
\(4 \mathrm{LINO}_3 \longrightarrow 2 \mathrm{Li}_2 \mathrm{O}+4 \mathrm{NO}_2 \uparrow+\mathrm{O}_2\) भूरे रंग की गैस
\(2 \mathrm{KNO}_3 \longrightarrow 2 \mathrm{KNO}_2+\mathrm{O}_2 \uparrow\)
(ब) Na2CO3 एवं NaHCO3 – NaHCO3 को गर्म करने पर CO2 गैस प्राप्त होती है जो चूने के पानी में प्रवाहित करने पर चूने के पानी को दूधिया कर देती है। जबकि Na2CO3 को गर्म करने पर यह अपघटित नहीं होते हैं।
\(2 \mathrm{NaHCO}_3 \longrightarrow \mathrm{Na}_2 \mathrm{CO}_3+\mathrm{CO}_2+\mathrm{H}_2 \mathrm{O}\)
प्रश्न 14.
क्या होता है जब सोडियम सल्फेट के विलयन को बेरियम नाइट्रेट के जलीय विलयन में प्रवाहित करते हैं।
उत्तर:
बेरियम सल्फेट का सफेद अवक्षेप प्राप्त होता है।

प्रश्न 15.
क्या होता है जब-
(अ) क्लोरीन गैस को गर्म और सान्द्र NaOH विलयन में प्रवाहित किया जाता है ?
(ब) क्लोरीन गैस को ठण्डे एवं तनु NaOH विलयन में प्रवाहित करते हैं ।
उत्तर:
(अ) सोडियम क्लोरेट बनता है।

प्रश्न 16.
क्या होता है जब-
(अ) सोडियम हाइड्रॉक्साइड विलयन टिन क्लोराइड विलयन में मिलाया जाता है।
(ब) जिंक सल्फेट विलयन में सोडियम हाइड्रॉक्साइड विलयन धीरे-धीरे मिलाते हैं।
उत्तर:
(अ) टिन क्लोराइड के विलयन में NaOH मिलाने पर पहले स्टैनस हाइड्रॉक्साइड का सफेद अवक्षेप प्राप्त होता है जो NaOH की अधिकता में धुलकर सोडियम स्टैनाइट बनाता है।

(ब) जिंक सल्फेट विलयन की NaOH से क्रिया कराने पर पहले जिंक हाइड्रॉक्साइड का सफेद अवक्षेप प्राप्त होता है, जो NaOH की अधिकता में घुलकर सोडियम जिंकेट बनाता है ।
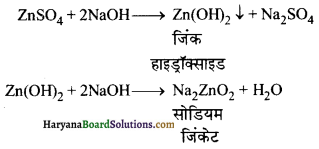
प्रश्न 17.
क्या होता है जब-
(अ) अमोनियम सल्फेट के विलयन में कॉस्टिक सोडा विलयन मिलाते हैं।
(ब) सल्फर को कॉस्टिक सोडा विलयन के साथ उबालते हैं। (स) पीला फॉस्फोरस NaOH विलयन के साथ क्रिया करता है।
उत्तर:
(अ) अमोनियम सल्फेट के विलयन में कॉस्टिक सोडा विलयन मिलाते हैं तो अमोनिया गैस निकलती है।
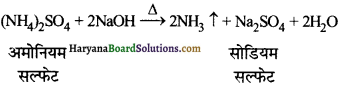
(ब) सल्फर को कॉस्टिक सोडा विलयन के साथ उबालते हैं तो सोडियम थायोसल्फेट प्राप्त होता है।
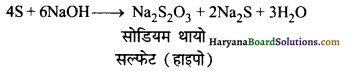
(स) पीले फॉस्फोरस की NaOH विलयन के साथ क्रिया से फॉस्फीन (PH3) प्राप्त होती है।

प्रश्न 18.
क्या होता है जब-
(अ) अमोनियाकृत ब्राइन में CO2 गैस प्रवाहित होती है।
(ब) कास्टिक सोडा CO3 से क्रिया करता है।
(स) गर्म सोडियम हाइड्रॉक्साइड विलयन में एल्यूमीनियम मिलाया जाता है।
उत्तर:
(अ) अमोनियाकृत ब्राइन में CO2 प्रवाहित करने पर सोडियम बाइकार्बोनेट प्राप्त होता है।

(ब) कास्टिक सोडा की क्रिया CO2 से कराने पर Na2CO3 प्राप्त होता है।
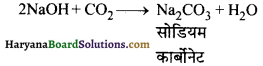
(स) गर्म सोडियम हाइड्राक्साइड विलयन में एल्यूमीनियम मिलाने पर सोडियम मेटाएल्युमिनेट प्राप्त होता है।

प्रश्न 19.
निम्न को कैसे प्राप्त करोगे-
(अ) धावन सोडा से खाने का सोडा ।
(ब) सोडियम क्लोराइड से क्लोरीन ।
(स) ऐल्युमिनियम क्लोराइड से सोडियम मेटा ऐल्युमिनेट ।
उत्तर:
(अ) धावन सोडा से खाने का सोडा – जब धावन सोडा के विलयन में CO2 गैस प्रवाहित की जाती है तो खाने का सोडा बनता है।
\(\mathrm{Na}_2 \mathrm{CO}_3+\mathrm{CO}_2+\mathrm{H}_2 \mathrm{O} \longrightarrow 2 \mathrm{NaHCO}_3 \downarrow\) खाने का सोडा
(ब) सोडियम क्लोराइड से क्लोरीन – सोडियम क्लोराइड से क्लोरीन बनाने के लिये गलित NaCl का विद्युत अपघटन करते हैं।

(स) ऐलुमिनियम क्लोराइड से सोडियम मेटा ऐलुमिनेट – सर्वप्रथम AlCl3 की क्रिया NaOH से कराते हैं तो Al(OH)3 अवक्षेपित होता है। फिर इसमें NaOH अधिकता में डालते है तो सोडियम मेटा ऐल्युमिनेट बनता है।
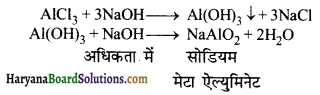
प्रश्न 20.
बेरिलियम तथा ऐलुमिनियम में विकर्ण सम्बन्ध की व्याख्या करे ।
उत्तर:
- ऐलुमीनियम के समान बेरिलियम शीघ्रता से अम्लों से प्रभावित नहीं होता है, क्योंकि धातु की सतह पर ऑक्साइड की फिल्म उपस्थित होती है। अतः ये H2 को मुक्त नहीं करते हैं।
- दोनों ही H2O से अभिक्रिया नहीं करते हैं।
- दोनों के क्लोराइड सहसंयोजी होते हैं तथा कार्बनिक विलायकों में घुलनशील होते हैं तथा दोनों वाष्पीय अवस्था में द्विलक के रूप में रहते हैं।

- दोनों ही लुइस अम्ल की तरह कार्य करते हैं अर्थात् दोनों ही e– युग्म को ग्रहण कर सकते हैं। इनका उपयोग फ्रीडेल-क्राफ्ट के उत्प्रेरक (Friedel Carft Catalyst) के रूप में होता है।
- क्षार की अधिकता में बेरीलियम हाइड्रॉक्साइड घुल जाता है और बेरिलेट (Bcryllate) आयन [Be(OH4)]2 देता है। ठीक इसी प्रकार ऐलुमीनियम हाइड्रॉक्साइड ऐलुमिनेट (Aluminate) आयन [Al(OH)4]– देता है।
- बेरीलियम एवं ऐलुमीनियम आयन जटिल यौगिक (Complexes) बनाने की प्रबल प्रवृत्ति रखते हैं। जैसे- BeF22-, AlF63- |

प्रश्न 21.
क्षार धातुओं में लीथियम के असंगत व्यवहार की विवेचना कीजिए |
उत्तर:
लीथियम का व्यवहार अपने समूह के अन्य तत्वों से भिन्न होता है। निम्नलिखित कारणों से लीथियम असंगत या असामान्य व्यवहार पदर्शान करता है।
- इनके परमाणु एवं आयन (Li+) का असाभान्य छोटा आकार
- उच्च ध्रुवण क्षमता (अर्थात् आवेश/त्रिज्या अनुपात)
- अधिक आयनन ऊर्जा एवं इलेक्ट्रॉन ऋणात्मकता
- d-कक्षकों का न होना।
- अधिक जलयोजन ऊर्जा।
लीथियम एवं अन्य क्षार धातुओं में असमानताओं के मुख्य बिन्दु:
लीथियम एवं अन्य क्षार धातुओं में असमानताओं के मुख्य बिन्दु निम्न हैं-
1. लीथियम अत्यधिक कठोर होता है जबकि अन्य मुलायम।
2. इसका गलनांक एवं क्वथनांक अन्य की अपेक्षा अधिक होता है।
3. लीथियम नाइट्रेट गरम करने पर लीथियम ऑक्साइड (Li2O) देता है जबकि अन्य क्षार धातुओं के नाइट्रेट विघटित होकर नाइट्राइट बनाते हैं।
\(4 \mathrm{LiNO}_3 \longrightarrow 2 \mathrm{Li}_2 \mathrm{O}+4 \mathrm{NO}_2+\mathrm{O}_2\)
\(2 \mathrm{NaNO}_3 \longrightarrow 2 \mathrm{NaNO}_2+\mathrm{O}_2\)
4. अन्य क्षार धातुओं के फ्लुओराइड एवं ऑक्साइड की तुलृना में LiF एवं Li2O जल में कम विलेय है।
5. लीथियम ऐसिटिलीन से अभिक्रिया करके एसिटि-लाइट नहीं बनाता है जबकि अन्य क्षार धातुएँ ऐसा करती हैं।

6. लीथियम हाइड्रोजन कार्बोनेट ठोस अवस्था में प्राप्य नहीं है। जबकि अन्य क्षाः धातु ठोस हाइड्रोजन कार्बोनेट बनाते हैं।
7. LiCl प्रस्वेद्य (Deliquescent) है एवं हाइड्रेट, LiCl.2H2O के रूप में क्रिस्टलित होता है जबकि अन्य धातुएँ हाइड्रेटड क्लोराइड नही। बनाते हैं।
8. लीथियम हवा के साथ दहन करने पर मोनोऑक्साइड (Li2O) बनाता है तथा यह नाइट्रोजन के साथ अभिक्रिया करके नाइट्राइड Li3N भी बनाता है जब्रकि अन्य नहीं बनाते।
\(6 \mathrm{Li}+\mathrm{N}_2 \longrightarrow 2 \mathrm{Li}_3 \mathrm{~N}\)
\(6 \mathrm{Na}+\mathrm{N}_2 \longrightarrow\) अभिक्रिया नहीं
9. लीथियम कार्बोनेट को गर्म करने पर Li2O तथा CO2 प्राप्त होती है जबकि अन्य क्षार धातुओं के कार्बोनेट विघटित नहीं होते हैं।
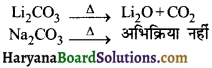
10. लीथियम कार्बन के साथ कार्बाइड बनाता है जबकि अन्य नह
\(4 \mathrm{Li}+\mathrm{C} \longrightarrow \mathrm{Li}_4 \mathrm{C}\) (लीथियम कार्बाइड)
11. लीथियम ब्रोमीन से बहुत धीरे-धीरे अभिक्रिया करके ब्रोमाइ वनाता है जबकि अन्य क्षार धातुएँ ब्रोमीन से तीव्रता के साथ अभिक्रि करती हैं।
12. लीथियम आयन कार्ब लीथियम यौगिक (organo-lithium compounds) बनाता है, जबकि अन्य नहीं।
13. Li2SO4 द्विक-लवण (double salt) नहीं बनाता जबकि अन्य श्षार धातुएँ द्विक-लवण बनाती हैं।
14. लीथियम अमोनिया के साथ लीथियम इमाइड (imide) Li2NH बनाता है जबकि अन्य क्षार धातुएँ एमाइड (amide) बनाती हैं।
प्रश्न 22.
कॉस्टनर कैलनर सेल विधि से कॉस्टिक सोडा कैसे प्राप्त करेंगें ?
उत्तर:
- यह एक सफेद क्रिस्टलीय ठोस है, जो कि 591 K ताप पर गलता है।
- NaOH के क्रिस्टल प्रस्वेद्य (deliquescent) होते हैं।
- वायुमण्डल में दीर्घकाल तक खुला छोड़ने पर विलयन की सतह पर Na2CO3 की एक सफेद पपड़ी बन जाती है क्योंकि NaOH वायुमण्डल से CO2 को अवशोषित कर लेता है।
\(2 \mathrm{NaOH}+\mathrm{CO}_2 \longrightarrow \mathrm{Na}_2 \mathrm{CO}_3+\mathrm{H}_2 \mathrm{O}\)
- इसके जलीय विलयन में साबुन जैसा स्पर्श होता है तथा इसका स्वाद कड़वा होता है।
- NaOH प्रबल क्षार की तरह कार्य करता है, यह HCl से क्रिया करके उसे उदासीन कर देता है।
\(\mathrm{NaOH}+\mathrm{HCl} \longrightarrow \mathrm{NaCl}+\mathrm{H}_2 \mathrm{O}\)
प्रश्न 23.
सॉल्वे प्रक्रम द्वारा सोडियम कार्बोनेट का निर्माण किया जाता है, किन्तु पोटैशियम कार्बोनेट का निर्माण नहीं किया जाता, क्यों ? समझाइए ।
उत्तर:
सॉल्वे प्रक्रम से Na2CO3 बनाने में प्राप्त माध्यमिक उत्पाद NaHCO3 अल्प विलेय होने के कारण अवक्षेपित हो जाता है। इसे अलग करके व सुखाकर निस्तापन (calcination) करके Na2CO3 प्राप्त कर लिया जाता है।
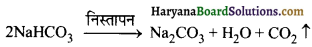
इसके विपरीत पोटैशियम बाइकार्बोनेट (KHCO3) अति विलेय होने के कारण अलग नहीं किया जा सकता है। अतः प्रक्रम से Na2CO3 का निर्माण सम्भव है, परन्तु K2CO3 का निर्माण सम्भव नहीं है।
प्रश्न 24.
सोडियम कार्बोनेट के विभिन्न रूप क्या हैं? इन पर ताप का प्रभाव बताइए ।
उत्तर:
सोडियम कार्बोनेट निम्नलिखित चार प्रकार का होता है-
- निर्जल Na2CO3, जिसको सोडा ऐश कहते हैं ।
- सोडियम कार्बोनेट मोनोहाइड्रेट (Na2CO3. H2O)
- सोडियम कार्बोनेट हेप्टाइड्रेट (NaCO3. 7H2O)
- सोडियम कार्बोनेट डेकाहाइड्रेट (Na2CO3. 10H2O) इसे धावन सोडा भी कहते हैं।
इस पर ताप का प्रभाव निम्नांकित प्रकार से है-

प्रश्न 25.
प्लास्टर ऑफ पेरिस के जमने की रासायनिक अभिक्रिया का समीकरण दीजिए ।
उत्तर:
प्लास्टर ऑफ पेरिस जमकर कड़ा छिद्रयुक्त ठोस बन जाता । इसे प्लास्टर ऑफ पेरिस का जमना कहते हैं। वस्तुत: यह अभिक्रिया प्लास्टर ऑफ पेरिस का जिप्सम से परिवर्तन है ।
(CaSO4)2.H2O + 3H2O2→2(CaSO4.2H2O) जिप्सम
प्रश्न 26.
सीमेन्ट के निर्माण में प्रयुक्त किए जाने वाले कच्चे पदार्थों के नाम लिखिए।
उत्तर:
सीमेन्ट निर्माण में प्रयुक्त कच्चे एर्थ निम्नलिखित हैं-
- कैल्सियम युक्त पदार्थ – चूने का पत्थर, चॉक, संगमरमर आदि ।
- मृण्मय पदार्थ – मिट्टी, स्लेट, सिलिका, ऐलुमिना, आयरन ऑक्साइड आदि ।
- 2% – 3% जिप्सम ।
प्रश्न 27.
क्लिंकर ( Clinker) क्या है ? इससे सीमेन्ट कैसे बनाया जाता है ?
अथवा
क्लिंकर पर टिप्पणी लिखिए ।
उत्तर:
सीमेन्ट के कच्चे पदार्थों से बने मिश्रण को सीमेन्ट की भट्टी में डालकर गर्म करने के बाद छोटी-छोटी गोलियों के रूप में प्राप्त पदार्थ को क्लिंकर कहते हैं । क्लिंकर, डाइकैल्सियम सिलिकेट, ट्राइकैल्सियम सिलिकेट, टाइकैल्सियम ऐलुमिनेट तथा टेट्राकैल्सियम ऐलुमिनोफेराइट का मिश्रण है। क्लिंकर में 2-3% जिप्सम मिलाकर इसको पीसकर प्रयोग करने – योग्य सीमेण्ट प्राप्त किया जाता है जिसको पोर्टलैण्ड सीमेण्ट कहते हैं।
प्रश्न 28.
सीमेन्ट के प्रयोग में बालू का क्या उपयोग होता है?
उत्तर:
सीमेण्ट जल या नमी के प्रति अति सुग्राही है। नमी के कारण इसमें आन्तरिक प्रतिबल उत्पन्न हो जाता है जिससे इसमें दरार पड़ जाती है और इसकी क्षमता कम हो जाती है। बालू मिलाने से सीमेन्ट में आन्तरिक प्रतिबल उत्पन्न नहीं होता जिससे सीमेन्ट में दरार नहीं पड़ती हैं।
प्रश्न 29.
गोर्टार, गारा, कंक्रीट व प्रबलित कंक्रीट से क्या तात्पर्य है?
अथवा
कंक्रीट और प्रबलित कंक्रीट क्या है?
उत्तर:
(अ) मोर्टार (Mortar) – मोर्टार बुझे चूने [Ca(OH)2], बालू (SiO2) तथा जल के मिश्रण की एक लेई (paste) है। वायु में खुला रहने पर इस लेई से जल उड़ जाता है और वायु से CO2 गैस अवशोषित करके कैल्सियम कार्बोनेट बनने के कारण वह कठोर हो जाता है ।
(ब) गारा ( Slurry) – पिसे हुए चूने के पत्थर तथा घुले मृत्तिका के टुकड़ों के गाढ़े जलीय मिश्रण को गारा कहते हैं। इसको सीमेण्ट की भट्टी में डालकर क्लिंकर तैयार करते हैं।
(स) कंक्रीट (Concrete ) – कंकड़, पत्थर या ईंट के टूटे टुकड़ों के साथ सीमेण्ट तथा बालू को जल में मिलाकर तैयार किए मिश्रण को कंक्रीट कहते हैं। इसके जमने से ठोस संरचना प्राप्त होती है।
(द) प्रबलित कंक्रीट (Reinforced concrete ) – पत्थर के छोटे-छोटे टुकड़ों, सीमेन्ट तथा बालू के जल में बने सीमेण्ट कंक्रीट मिश्रण को तार की जाली या लोहे की छड़ों के बीच चारों ओर भरकर कठोर तथा मजबूत संरचना हेतु जमाया जाता है, उसे प्रबलित कंक्रीट कहते हैं ।

प्रश्न 30.
सीमेन्ट के जमने का कारण बताइए या सीमेन्ट किस प्रकार कठोर हो जाता है?
अथवा
सीमेन्ट के जमने प्पणी लिखिए।
उत्तर:
सीमेन्ट में जल मिलाकर छोड़ देने पर कुछ समय बाद यह कठोर पदार्थ बन जाता है। इसे सीमेन्ट का जमना ( setting) कहते हैं । जब सीमेन्ट जमता है तो निम्नलिखित अभिक्रियाएँ होती हैं-
(अ) जलयोजन (Hydration) – डाइ व ट्राइकैल्सियम सिलिकेट तथा ट्राइकैल्सियम ऐलुमिनेट का जलयोजन होकर उनके कोलॉइडी (colloidal) जेल बन जाते हैं।

(ब) जल अपघटन (Hydrolysis ) — ट्राइकैल्सियम सिलिकेट और ट्राइकैल्सियम ऐलुमिनेट का जल अपघटन होकर कैल्सियम और ऐलुमिनियम हाइड्रॉक्साइड बनते हैं।
\(3 \mathrm{CaO} \cdot \mathrm{Al}_2 \mathrm{O}_3+6 \mathrm{H}_2 \mathrm{O} \longrightarrow 3 \mathrm{Ca}(\mathrm{OH})_2+2 \mathrm{Al}(\mathrm{OH})_3\) इस प्रकार ट्राइकैल्सियम सिलिकेट का आंशिक जल – अपघटन होता है।
(स) ट्राइकैल्सियम ऐलुमिनेट शीघ्र जमने वाला पदार्थ है । जिप्सम की उपस्थिति में इसके जमने की दर धीमी हो जाती है। जिप्सम के साथ निम्नलिखित अभिक्रिया होती है और कैल्सियम सल्फोऐलुमिनेट बनता है-
\(3 \mathrm{CaO} \cdot \mathrm{Al}_2 \mathrm{O}_3+3 \mathrm{CaSO}_4+2 \mathrm{H}_2 \mathrm{O} \longrightarrow 3 \mathrm{CaOAl}_2 \mathrm{O}_3 \cdot 3 \mathrm{CaSO}_4 \cdot 2 \mathrm{H}_2 \mathrm{O}\)
अतः जिप्सम का कार्य सीमेन्ट के जमने की दर कम करना है। इससे सीमेण्ट कठोर हो जाता है।
प्रश्न 31.
सीमेन्ट क्या है? इसके मुख्य अवयव क्या हैं?
अथवा
सीमेन्ट के निर्माण में प्रयुक्त होने वाले पदार्थों के नाम लिखिए।
उत्तर:
सीमेन्ट (Cement ) — डाइकैल्सियम सिलिकेट (2CaO.SiO2), ट्राइकैल्सियम सिलिकेट (3CaO.SiO2), ट्राइ – कैल्सियम ऐलुमिनेट (3CaO.Al2O3) तथा जिप्सम (CaSO4.2H2O) की उचित मात्रा पर प्राप्त मिश्रण सीमेन्ट कहलाता है। इसके मुख्य अवयव हैं – चूना (CaO), सिलिका (SiO2), ऐलुमिना (Al2O3), आयरन ऑक्साइड (Fe2O3), मैग्नीशियम ऑक्साइड (MgO) और सल्फर ट्राइ-ऑक्साइड (SO3)।
प्रश्न 32.
सीमेन्ट क्लिंकर के मुख्य अवयव क्या हैं? इसमें जिप्सम क्यों मिलाया जाता है?
उत्तर:
सीमेन्ट क्लिंकर के मुख्य अवयव निम्नलिखित हैं-
- डाइकैल्सियम सिलिकेट (2CaO.SiO2)
- ट्राइकैल्सियम सिलिकेट (3CaO.SiO2)
- ट्राइकैल्सियम ऐलुमिनेट (3CaO.Al2O3)
- टेट्राकैल्सियम ऐलुमिनोफेराइट (4CaO.Al2O3.Fe2O3)
सीमेन्ट क्लिंकर जल के प्रति अति सुग्राही होता है तथा नमी और जल के सम्पर्क में आकर जम जाता है। इसकी जमने की क्षमता को शिथिल करने के लिए मन्दक पदार्थ मिलाए जाते हैं। जिप्सम एक मन्दक पदार्थ है। इसके मिलाने से सीमेन्ट क्लिंकर के जमने की क्षमता मन्द हो जाती है और अधिक जल के सम्पर्क में आने पर ही यह जमता है।
प्रश्न 33.
चूने के पत्थर के औद्योगिक उपयोग बताइए ।
उत्तर:
- सीमेन्ट के निर्माण में ।
- बिना बुझा तथा बुझा चूना बनाने में ।
- धातुकर्म में गालक के रूप में।
- संगमरमर के रूप में भवन निर्माण में ।
- खड़िया के रूप में पेण्ट, डिस्टैम्पर, टूथ पेस्ट, सौन्दर्य प्रसाधन सामग्री बनाने में।
- औषधियों के निर्माण में, ग्राइप वाटर के रूप में।
प्रश्न 34.
प्लास्टर ऑफ पेरिस से क्या समझते हो ? इसके बनाने की विधि, एक गुण व उपयोग दीजिए ।
उत्तर:
कैल्सियम सल्फेट हेमी हाइड्रेट को प्लास्टर ऑफ पेरिस कहते हैं। इसका सूत्र (CaSO4)2.H2O या CaSO4 + \(\frac { 1 }{ 2 }\)H2O है। जिप्सम को 390K पर गर्म करने पर प्लास्टर ऑफ पेरिस प्राप्त होता है।
\(2 \mathrm{CaSO}_4 \cdot 2 \mathrm{H}_2 \mathrm{O} \longrightarrow\left(\mathrm{CaSO}_4\right)_2 \cdot \mathrm{H}_2 \mathrm{O}+3 \mathrm{H}_2 \mathrm{O}\)
यह एक सफेद चूर्ण है। जल के साथ कठोर हो जाता है।
\(\left(\mathrm{CaSO}_4\right)_2 \cdot \mathrm{H}_2 \mathrm{O}+3 \mathrm{H}_2 \mathrm{O} \longrightarrow 2 \mathrm{CaSO}_4 \cdot 2 \mathrm{H}_2 \mathrm{O}\)
इसका उपयोग प्लास्टर चढ़ाने तथा मूर्तियाँ, खिलौने आदि बनाने के काम किया जाता है।
प्रश्न 35.
कैल्सियम हाइड्रॉक्साइड कैसे प्राप्त किया जाता है ? इसकी CO2, Cl2 से क्या अभिक्रिया होती है ? इसके दो उपयोग दीजिए ।
उत्तर:
बनाने की विधि – CaO की जल से अभिक्रिया होने पर कैल्सियम हाइड्रॉक्साइड बनता है।
CaO + H2O → Ca(OH)2 + 67 KJ/Mole
CO2 से अभिक्रिया – चूने के पानी में CO2 गैस प्रवाहित करने पर कैल्सियम कार्बोनेट बनता है जिससे विलयन दूधिया हो जाता है। अधिक CO2 प्रवाहित करने पर विलयशील कैल्सियम बाइकार्बोनेट बनता है जिससे दूधियापन समाप्त हो जाता है।
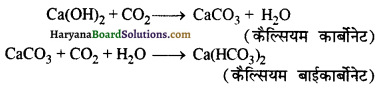
क्लोरीन से क्रिया- (i) शुष्क बुझे चूने पर C करने पर विरंजक चूण जातो
Ca(OH)2 + Cl2 → HOCl2 + H2O
(ii) ठण्डे चूने के पानी में Cl2 प्रवे करने पर कैल्सियम हाइपोक्लोराइड तथा कैल्सियम क्लोराइड बन्ना
2Ca(OH)2 + 2Cl2 → Ca(OC)2 + 2H2 + CaCl2
(iii) गर्म चूने के पानी में Cl2 प्रवाहित करने पर `ल्सियम क्लोरेट तथा कैल्सियम क्लोराइड बनता है।
6Ca(OH)2 + 6Cl2 → Ca(ClO3)2 + 5CaCl2 +6H2O
उपयोग- (1) विरंजक चूर्ण बनाने में ।
(2) सोडियम कार्बोनेट के निर्माण में ।
प्रश्न 36.
निम्न को कैसे बनाओगे- (अ) प्लास्टर ऑफ पेरिस से जिप्सम (ब) जिप्सम से प्लास्टर ऑफ पेरिस
उत्तर:
(अ) प्लास्टर ऑफ पेरिस से जिप्सम

(ब) जिप्सम से प्लास्टर ऑफ पेरिस
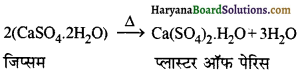
(अ) जिप्सम को 200°C तक गरम करते हैं ।
उत्तर:
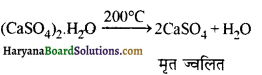
(ब) कार्बन डाई ऑक्साइड गैस को चूने के पानी में प्रवाहित करते हैं।
उत्तर:
Ca(OH)2 + CO2 → CaCO3 + H2O
(स) प्लास्टर ऑफ पेरिस की क्रिया जल से होती है।
उत्तर:
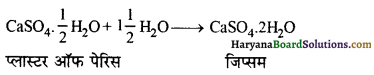
विस्तृत उत्तरीय प्रश्न:
प्रश्न 1.
एक अकार्बनिक यौगिक (X) जलाने पर सुनहरी पीली ज्वाला देता है और निम्न अभिक्रियाएँ प्रदर्शित करता है।
(i) जिंक पाउडर, यौगिक (X) के सान्द्र जलीय घोल के साथ उबालने पर घुल जाता है और हाइड्रोजन निकलती है।
(ii) X के जलीय घोल को स्टैनस क्लोराइड के जलीय घोल में मिलाने पर पहले एक सफेद अवक्षेप प्राप्त होता है, जो (X) के विलयन की अधिकता में घुल जाता है। (X) को पहचानिए तथा (i) और (ii) पदों पर होने वाली अभिक्रियाओं के समीकरण दीजिए।
उत्तर:
X = सोडियम हाइड्रॉक्साइड
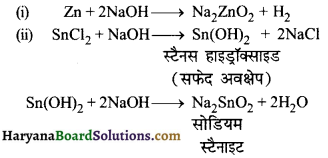
2. (i) सोडियम सल्फाइट तथा सोडियम सल्फाइड के एक सान्द्र विलयन में गैस (B) प्रवाहित करने पर अकार्बनिक यौगिक (A) बनता है।
(ii) (A) को तनु AgNO3 के विलयन में डालने पर सफेद अवक्षेप प्राप्त होता है जो शीघ्र ही काले रंग के यौगिक (C) में बदल जाता है।
(iii) FeCl3 की 2 या 3 बूँदें (A) के विलयन की अधिकता में डालने पर एक बैंगनी रंग का यौगिक (D) बनता है। यह रंग शीघ्र ही गायब हो जाता है।
(iv) A के विलयन को CuCl2 के विलयन में डालने पर पहले एक सफेद अवक्षेप बनता है जोकि (A) की अधिकता में घुलकर यौगिक (E) बनाता है। (A) से (E) तक को पहचानिए तथा (i) से (iv) पदों पर होने वाली अभिक्रियाओं के रासायनिक समीकरण दीजिए।
उत्तर:

Read More:
LUPIN Pivot Point Calculator
![]()
![]()
![]()




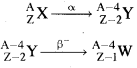





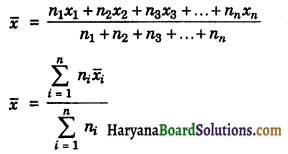
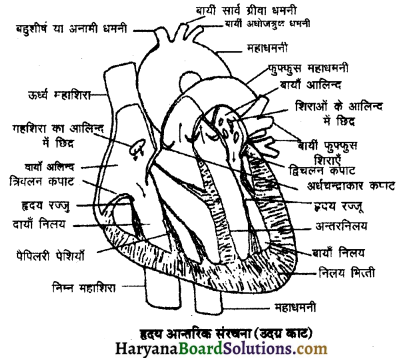
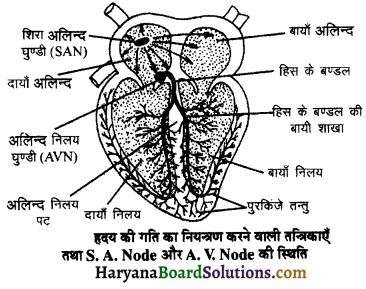
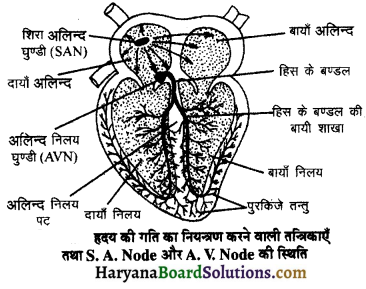
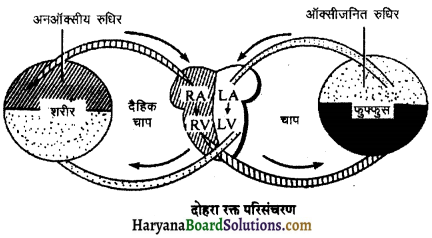
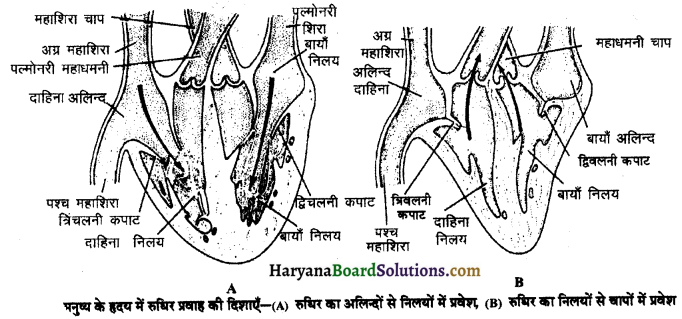 (2) अलिन्दों का प्रफुंचन (Atrial Systole)-जैसे ही अलिन्दों का अनुशिथिलन समाप्त होता है दोनों अलिन्द एक साथ संकुचित होते हैं। यह अवस्था निल़य प्रकुंचन कहलाती है जो लगभग 0.1 सेकण्ड तक रहती है। इस संकुचन के फलस्वरूप लगभग 25% ही रुधिर जो अलिन्दों में बचा रहता है, निलयों में आता है। इस प्रकार दोनों निलय रुधिर से पूर्णतया भर जाते हैं।
(2) अलिन्दों का प्रफुंचन (Atrial Systole)-जैसे ही अलिन्दों का अनुशिथिलन समाप्त होता है दोनों अलिन्द एक साथ संकुचित होते हैं। यह अवस्था निल़य प्रकुंचन कहलाती है जो लगभग 0.1 सेकण्ड तक रहती है। इस संकुचन के फलस्वरूप लगभग 25% ही रुधिर जो अलिन्दों में बचा रहता है, निलयों में आता है। इस प्रकार दोनों निलय रुधिर से पूर्णतया भर जाते हैं।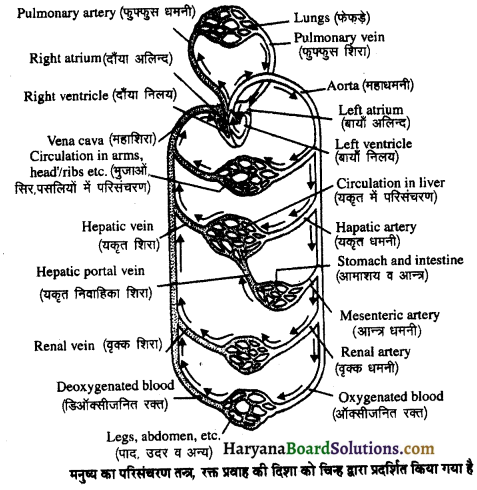




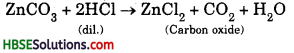

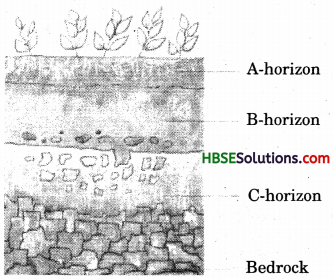 Soil profile
Soil profile