Author name: Bhagya

Haryana State Board HBSE 10th Class Maths Notes Chapter 7 Coordinate Geometry Notes.

Haryana Board 10th Class Maths Notes Chapter 7 Coordinate Geometry

Introduction
We have studied in previous classes that how to locate the position of a point in co-ordinate plane of two dimensions in terms of two co-ordinates. The distance of a point from the y-axis is called its x-co-ordinate or abscissa. The distance of a point from the x-axis is called its y co-ordinate or ordinate. The coordiantes of a point on the x-axis are of the form (x, 0), and of a point on the y-axis are of the form (0, y).

In is chapter, we shall extend our knowledge by learning how to find the distance between the two points whose co-ordinates are given, and to find the area of the triangle formed by three given points. We shall also learn about how to find the co-ordinates of the point which divides a line segment joining two given points in a given ratio.

1. Plane-It is a flat surface, which extends indefinitely in all directions. The surface of a sheet of paper, the surface of a smooth green board, the surface of a smooth table top are some examples of a plane.
2. Co-ordinate axes-To locate the position of a point in a plane, two mutually perpendicular lines are drawn. One of them is horizontal known as x-axis and other is vertical known as y-axis. These axes are combindely called co-ordinate axes.
3. Origin-The point of intersection of two Axes is called origin.
4. Quadrants-The axes divide a plane into four parts called quadrants.
5. Collinear points-If three or more pointa lie on the same line, they are called collinear points. Otherwise, they are called non-collinear points.

Distance Formula
a₁ = a = 0
Let P (x₁, y₁) and Q(x₂, y₂) be the given points in the plane. Draw PS ⊥ x-axis, QT ⊥ x-axis and PR ⊥ QT from P, Q and P respectively. Then
OS = x₁, OT = x₂, PS = y₁, QT = y₂
PR = ST = OT – OS = x₂ – x₁ and QR = QT – RT = y₂ – y₁
ΔQRP is a right angled triangle, right angled at R.

∴ PQ² = PR² + QR² [By Pythagoras theorem]
PQ² = (x₂ – x₁)² + (y₂ – y₁)²
PQ = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)
Hence, distance between any two points
\(=\sqrt{\begin{array}{r}
(\text { difference of abscissa })^2+ \\
\text { (difference of ordinates) }^2
\end{array}}\)
It is called the distance formula.
Remark: (i) The distance of a point P(x, y) from the origin O(0, 0) is given by
OP = \(\sqrt{(x-0)^2+(y-0)^2}=\sqrt{x^2+y^2}\)

(ii) If three points A, B and C are collinear then AB + BC = AC.
(iii) Properties of different types of quadrilaterals
(a) Square : In a square, all sides and diagonals are equal
(b) Rectangle : In a rectangle opposite sides and diagoals are equal.
(c) Parallelogram : In a parallelogram opposite sides are equal.
(d) Paralleogram but not a rectangle : In this case opposite sides are equal but diagonals are not equal
(e) Rhombus but not a square : In this case all sides are equal, but diagonals are not equal.

Section Formula
By section formula we find out the coordinates of the point which divides the line segment joining the two given points in a given ratio internally.
Let P(x, y) be the point dividing the line segment joining the points. A(x₁, y₁) and B(x₂, y₂) internally in the ratio m₁ : m₂.

Draw AL ⊥ OX; PM ⊥ OX, BN ⊥ OX, Also draw AK ⊥ PM and PQ ⊥ BN. Then, OL = x₁, OM = x, AL = y₁, PM = y and BN = y₂. ON = x₂.
AK = LM = OM – OL = x – x₁
PQ = MN = ON – OM
= x₂ – x
PK = PM – KM = y – y₁
BQ = BN – QN = y₂ – y
In right ΔAKP and ΔPQB.
∠AKP = ∠PQB (Each is 90°)
∠AKP = ∠BPQ (Corresponding ∠s)
ΔAKP ~ ΔPQB [By AA similarity criterion]


Remarks: (1) If P is the mid point of AB then m₁ : m₂ = 1 : 1.
Then co-ordinates of P are
\(\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\)
(2) If the ratio in which P divides AB is k : 1. Then the coordiantes of the point P are
\(\left(\frac{k x_2+x_1}{k+1}, \frac{k y_2+y_1}{k+1}\right)\)

Co-ordinates of the Centroid of a Triangle
Let A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) be the vertices of a given ΔABC. Let D be the mid point of BC. Let G(x, y) be centroid of the triangle as shown in figure.
Co-ordinates of the point D are \(\left(\frac{x_2+x_3}{2}, \frac{y_2+y_3}{2}\right)\)
Since centroid divides each median in the ratio 2 : 1.

∴ G divides AD in the ratio 2 : 1

Hence, the coordinates of the centroid of the triangle are \(\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right)\)

Area of Triangle
Let A(x₁, y₁) B(x₂, y₂) and C(x₃, y₃) be the vertices of the given ΔABC. Draw BL, AM and CN perpendicular to the x-axis.
Then, LM = (x₁ – x₂), LN = (x₃ – x₂)
MN = (x₃ – x₁)
Now, Area of ΔABC = ar(Trap BLMA) + ar(Trap AMNC) – ar(Trap BLNC)

Since, the area is never negative, we have
Area (ΔABC) = \(\frac{1}{2}\)[(x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]

Condition for the collinearity of three points
If three points A (x₁, y₁), B (x₂, y₂) and C(x₃, y₃) are collinear.
Then Area of ΔABC = 0

⇒ \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)
⇒ x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)
= 0
Remark : To find the area of a polygon we divide it in triangles and take numerical value of the area of each of the triangles.

Haryana State Board HBSE 10th Class Maths Notes Chapter 9 त्रिकोणमिति का अनुप्रयोग Notes.

Haryana Board 10th Class Maths Notes Chapter 9 त्रिकोणमिति का अनुप्रयोग

→ उन्नयन कोण- यदि वस्तु हमारी आँख के स्तर से ऊपर हो अर्थात् आँख की क्षैतिज रेखा से ऊपर हो तो हमें वस्तु को देखने के लिए अपनी आँखों को ऊपर की ओर उठाना पड़ेगा। इस प्रक्रिया में हमारी दृष्टि रेखा क्षतिज रेखा से एक कोण से ऊपर की ओर घूम जाती है। इस कोण को, वस्तु का उन्नयन कोण (Angle of elevation) कहते हैं।

→ अवनमन कोण-यदि वस्तु हमारी आँख के स्तर से नीचे हो अर्थात् वस्तु हमारी आँख की क्षैतिज रेखा से नीचे हो तो हमें वस्तु को देखने के लिए अपनी आँख को नीचे की ओर झुकाना पड़ेगा। इस प्रक्रिया में हमारी दृष्टि रेखा क्षैतिज रेखा से एक कोण पर नीचे की ओर घूम जाती है। इस कोण को वस्तु का अवनमन कोण (Angle of depression) कहा जाता है।

→ सर्वसमिका-एक या अधिक चरों वाले उस समीकरण को सर्वसमिका कहा जाता है जोकि संबंधित सभी मानों के लिए संतुष्ट हो जाता है अर्थात् चरों के सभी मानों के लिए समीकरण का बायाँ पक्ष, दाएं पक्ष के समान होता है।

प्रमुख त्रिकोणमितीय कोणों के मान निम्नलिखित सारणी में दिए गए हैं-

Haryana State Board HBSE 10th Class Maths Notes Chapter 14 Statistics Notes.

Haryana Board 10th Class Maths Notes Chapter 14 Statistics

Introduction
In the earlier classes, we have already learnt about the representation of given data into ungrouped as well as grouped frequency distributions and its representation through various graphs such as bar graphs, histograms, frequency polygons etc and you have also studied about measures of central tendency such as mean, median and mode of an ungrouped data. In this chapter, we shall learn how to calculate mean, median and mode for the grouped data. We shall also discuss the concept of cumulative frequency distribution and learn how to draw cumulative frequency curves, called Ogives.

1. Statistics: The branch of mathematics in which we study to extract meaningful information from the collected data. It is the area of study dealing with the presentation, analysis and interpretation of the data. It seems to have been derived from the Latin word ‘status’ or German word ‘statistik’ or Italian word ‘statista’.
2. Data: The facts or figures, which are numerical or otherwise, collected with a definite purpose are called data. Data is the plural form of the Latin word datum.
3. Observation: Every factor figure of the data is called an observation.
4. Frequency: The number of times a particular observation occurs is called the frequency of the observation.
5. Grouped frequency distribution: If the data are very large and the range is large, we put the data in groups of suitable size and mention the frequency of each group. Such a distribution is called grouped frequency distribution.

6. An inclusive frequency distribution: The upper limit of one class does not coincide with the lower limit of the next class. Such as, 1 – 10, 11 – 20, ……… is known as an inclusive frequency distribution.
7. An exclusive frequency distribution: The upper limit of one class coincides with the lower limit of the next class such as 1 – 10, 10 – 20, ……… is known as an exclusive frequency distribution.
8. Measures of Central Tendency: The numerical expressions which represent the characteristic of a group are called Measures of Central Tendency or Average. Mean, Median and Mode are three measures of central tendency (averages).
9. Class interval: Each group into which the raw data is condensed is called a class interval. Each class is bounded by two figures, which are called the class limits. The figures on the left side of the classes are called lower limits while figures on the right are known as upper limits.
10. Class size: The difference between the true upper limit and true lower limit of a class is called its class size.
11. Class Mark: The class mark of the class interval is the value midway between its true lower limit and true upper limit.
Class mark of a class = \(\frac{\text { True upper limit + True lower limit }}{2}\)
12. Cumulative Frequency: The cumulative frequency of a class interval is the sum of frequencies of all classes up to that class (including the frequency of that particular class).
13. Mean of grouped data: We know that if x₁, x₂, x₃, ………., x_n be n observations with respective frequencies f₁, f₂, f₃, …….., f_n, their mean is given by
\(\bar{x}=\frac{f_1 x_1+f_2 x_2+f_3 x_3+\ldots \ldots+f_n x_n}{f_1+f_2+f_3+\ldots \ldots+f_n}\)
We can write this in short form
\(\bar{x}=\frac{\sum_{i=1}^n f_i x_i}{\sum_{i=1}^n f_i}\)
It is more briefly written as \(\bar{x}=\frac{\Sigma f_i x_i}{\Sigma f_i}\), It is understood that varies from 1 to n. The Greek letter ‘Σ’ (capital sigma) is particularly used for writing summations.
With this assumption we can have the following three methods to calculate the mean of grouped data.

(a) Direct Method
1. For each class, find the class mark x_i, as
\(x_i=\frac{\text { lower limit }+\text { upper limit }}{2}\)
2. Find the product of each x_i with the corresponding fi, and find the algebraic sum of these products, i.e. Σf_ix_i.
3. Find the sum of all the frequencies i.e., Σf_i
4. Calculate the value of \(\bar{x}\), using the formula.
\(\bar{x}\) = \(\frac{\Sigma f_i x_i}{\Sigma f_i}\)

(b) Assumed Mean Method (Shortcut Method)
In case the values of the variable are very large in magnitude ie., the values of xi are very large in magnitude then computation of the mean \(\bar{x}\) becomes rather tedious and lengthy. To make calculation easier we use assumed mean method to find \(\bar{x}\).

Here, we choose an arbitrary constant a, also called assumed mean and subtract it from each of the value x_i. The reduced value d_i = x_i – a is called the deviation of x from a.

While using this method, we go through the following steps:
1. For each class interval find class mark x_i, as x_i = \(\frac{1}{2}\)(lower limit + upper limit)
2. Assume a suitable value of x_i in the middle of x_i‘ s as the assumed mean.
3. Find out the deviations of the mid value of each from the assumed mean (d_i = x_i – a).
4. Calculate the product of deviation (d_i) with corresponding frequency (f_i) for each class.
5. Find the algebraic sum of these products ie., Σf_id_i.
6. Find the sum of all the frequencies ie., Σf_i
7. Calculate the value of \(\bar{x}\), using the formula
\(\bar{x}\) = \(a+\frac{\sum f_i d_i}{\sum f_i}\)

(c) Step Deviation Method
The shortcut method discussed is further simplified or calculations are reduced to a great extent by adopting step deviation method. Scaling down the deviation (from the assumed mean) by a step (further dividing by a common factor), will reduce the calculation to a minimum.

Here we choose an arbitrary constant a (also called assumed mean) and subtract it from each of the value x_i. The reduced value (x_i – a) is called the deviation of x_i from ‘a’. These deviations are then divided by constant h, where h is the suitable divisor of all the d_i‘s.

In this method; we go through the following steps:
1. For each class interval, calculate the class mark x_i by using the formula,
x_i = \(\frac{1}{2}\)(lower limit + upper limit)
2. Choose the assumed mean ‘a’ in the middle of x_i.
3. Calculate the values of d_i (d_i = x_i – a)
4. Calculate the values of u_i {u_i = \(\frac{x_i-a}{h}\), where h is the class width}
5. Find the product of each u_i with the corresponding f_i.
6. Find the algebraic sum of these products i.e. Σf_iu_i
7. Find the sum of all the frequencies i.e., Σf_i.
8. Calculate the mean \(\bar{x}\) by using formula.
\(\bar{x}\) = \(a+\left(\frac{\Sigma f_i u_i}{\Sigma f_i}\right) h\)

Mode of Grouped Data
Recall from class IX that the mode of statistical data is the value among the observations which occurs most frequently. In other words, mode of a statistical data is the value of the observations which has maximum frequency.

In a grouped frequency distribution, it is not possible to determine the mode by looking at the frequencies. Here, we can only locate a class with the maximum frequency, called the modal class. The mode of grouped data is a value inside the modal class, and is given by the formula.
Mode = \(l+\left(\frac{f_1-f_0}{2 f_1-f_0-f_2}\right) \times h\)
Where,
l = Lower limit of the modal class
f₁ = Frequency of the modal class
f₀ = Frequency of the class preceding the modal class
f₂ = Frequency of the class succeeding the modal class
h = Size of the class interval (assuming all class sizes to be equal)

Remark: In some cases, It is possible that more than one value may have the same maximum frequency. In such a case the data is said to be multimodal. Though grouped data can also be multimodal, we shall restrict ourselves to unimodal data only i.e. the data having a single mode.

Median of Grouped Data
Median of a distribution is the value of the middle-most observation which divides it exactly in two equal parts when the data are arranged in ascending (or descending order).

(a) Median of an ungrouped data:
Arrange the data in ascending or descending order. Let the total number of observations be n
(i) If n is odd, the median is the value of the \(\left(\frac{n+1}{2}\right)^{\text {th }}\) observation.
(ii) If n is even, the median is mean of the \(\left(\frac{n}{2}\right)^{\text {th }}\) and \(\left(\frac{n}{2}+1\right)^{\text {th }}\) observations.

(b) Median of discrete series:
Arrange the terms in ascending or descending order. Then prepare a cumulative frequency distribution table. Let the total frequency be n
(i) If n is odd, then median = size of the \(\left(\frac{n+1}{2}\right)^{\text {th }}\) term.
(ii) If n is even then
median = \(\frac{1}{2}\)[size of the \(\left(\frac{n}{2}\right)^{\text {th }}\) term + size of the \(\left(\frac{n}{2}+1\right)^{\text {th }}\) term]

(c) Cumulative frequency distribution:
The frequencies are expressed as cumulative total against the class intervals in cumulative frequency distribution. It is of two types:
For example
(i) Less than type :

(ii) More than type :

(d) Median of grouped or continuous frequency distribution:
In order to calculate the median of the grouped data or continuous frequency distribution, we go through the following ahead steps:
(1) Prepare a cumulative frequency distribution and obtain n = Σf_i
(2) Find \(\frac{n}{2}\)
(3) Locate the class whose cumulative frequency is greater than (and nearest to) \(\frac{n}{2}\). This class is the median class.
(4) Calculate the median using the formula given by:
Median = \(l+\left(\frac{\frac{n}{2}-c f}{f}\right) \times h\)
Where l = lower limit of median class
n = number of observations
c_f = Cumulative frequency of class preceding the median class
f = frequency of median class
h = class size (assuming class size to be equal)

(e) Empirical relation between mean, median and mode.
3 Median = Mode + 2 Mean

Graphical Representation of Cumulative Frequency Distribution
In class IX, we have learnt about representing statistical data by using bar graphs, histograms and frequency polygons. In this section, we shall learn about to represent cumulative frequency distribution through cumulative frequency curves or ogives.

As we already know that cumulative frequency distribution are of two types, namely, less than type and more than type, accordingly there are two types of cumulatives frequency curves (or ogives).
(a) Less than ogive:
To draw a less than ogive, we go through the following steps:

• Prepare a less than cumulative frequency distribution from the given ordinary frequency distribution.
• Mark the upper class limits along the x-axis choosing a suitable scale.
• Mark the cumulative frequencies along the y-axis choosing a suitable scale.
• On joining these points successively by a free hand smooth curve, we get a cumulative frequency curve or an ogive (of less than type).

(b) More than ogive:
To draw a more than ogive, we go through the following steps:

• Prepare a more than frequency distribution from the given ordinary frequency distribution.
• Mark the lower class limits along the x-axis choosing a suitable scale.
• Mark the cumulative frequencies along the y-axis choosing a suitable scale.
• On joining these points successively by free hand smooth curve, we get a cumulative frequency curve or an ogive of more than type.

Remark 1: Draw any one of the two types of ogives for the given distribution. Take a point P(0, \(\frac{n}{2}\)) on the y-axis and draw PM || x-axis cutting the above curve at a point M. Again draw MN perpendicular to x-axis, cutting the x-axis at point N. Then median = x co-ordinate of point N.

Remark 2: Draw both types of ogives i.e., less than type and more than type for the given distribution on the same graph paper. Mark A as the point of intersection of these two ogives. Draw AP perpendicular to x-axis, cutting x-axis at P. Then median = x co-ordinate of point P.

Remark 3: For drawing ogive, it should be ensured that the class intervals are continuous.

Haryana State Board HBSE 10th Class Maths Notes Chapter 9 Some Applications of Trigonometry Notes.

Haryana Board 10th Class Maths Notes Chapter 9 Some Applications of Trigonometry

Introduction
We have studied about trigonometric ratios in earlier classes. In this chapter, we shall use the trigonometric ratios, to solve the problems regarding the heights and distances of various objects. Two common terms used in this chapter are angle of elevation and angle of depression.
1. Elevation: The height to which something is raised above a point of reference.
2. Depression: The depth to which something is lowered below a point of reference.
3. Line of sight: The line drawn from the eye of an observer to the point in the object viewed by the observer.
4. Complementary angles: Two angles having a sum of 90°, are called complementary angles.

5. Speed = Distance/Time
6. Alternate interior angle: The pair of angles on opposite sides of the transversal but inside the two lines are called alternate interior angles.
If the two lines are parallel, then the alternate interior angles formed are equal.

Heights and Distances
Angle of Elevation: If a person is looking up at an object, the acute angle measured from the horizontal level to the line of sight when the object being viewed is called the angle of elevation. Here

O is the point of observation, P is the position of the object, OP is the line of sight. OA is horizontal level and α is the angle of elevation.

Angle of Depression: The angle between the line of sight and horizontal level through the eye of the observer, when the object being viewed is below the horizontal level is called angle of depression. Here position of observer is at O. OM is the horizontal level through O. OP is the line of sight. β is the angle of depression when the object at P is observed from O.

Remarks:
(a) Numerically the angle of elevation is equal to the angle of depression.
(b) The angle of elevation and angle of depression both are measured with the horizontal.
(c) The angle of elevation or depression increases as the observer moves towards the object.

Haryana State Board HBSE 10th Class Maths Notes Chapter 8 त्रिकोणमिति का परिचय Notes.

Haryana Board 10th Class Maths Notes Chapter 8 त्रिकोणमिति का परिचय

→

→ विभिन्न त्रिकोणमितीय अनुपातों में संबंध-
cosec θ = \(\frac{1}{\sin \theta}\);
sec θ = \(\frac{1}{\cos \theta}\);
cot θ = \(\frac{1}{\tan \theta}\);
tan θ = \(\frac{\sin \theta}{\cos \theta}\);
cot θ = \(\frac{\cos \theta}{\sin \theta}\).

→ मूलभूत त्रिकोणमितीय सर्वसमिकाएँ-
मुख्य सूत्र
(i) sin² θ + cos² θ = 1
(ii) sec² θ = 1 + tan² θ
(iii) cosec² θ = 1 + cot² θ
मुख्य सूत्र से प्राप्त अन्य सूत्र
(i) sin² θ = 1 – cos² θ
cos² θ = 1 – sin² θ
(ii) sec² θ – tan² θ = 1
sec² θ – 1 = tan² θ
(iii) cosec² θ – cot² θ = 1
cosec² θ – 1 = cot² θ

→ पूरक कोणों के त्रिकोणमितीय अनुपात- समकोण ΔABC में यदि 0° ≤ θ ≤ 90°
तो,
(i) sin (90° – θ) = \(\frac{\mathrm{AB}}{\mathrm{AC}}\) = cos θ,
(ii) cos (90° – θ) = \(\frac{\mathrm{BC}}{\mathrm{AC}}\) = sin θ,
(iii) tan (90° – θ) = \(\frac{\mathrm{AB}}{\mathrm{BC}}\) = cotθ,
(iv) cot (90° – θ) = \(\frac{\mathrm{BC}}{\mathrm{AB}}\) = tan θ,
(v) sec (90° – θ) = \(\frac{\mathrm{AC}}{\mathrm{BC}}\) = cosec θ.
(vi) cosec (90° – θ) = \(\frac{\mathrm{AC}}{\mathrm{AB}}\) = sec θ.

→ sin A या cos A का मान कभी भी 1 से अधिक नहीं होता, जबकि sec A या cosec A का मान सदैव 1 से अधिक या 1 के बराबर होता है।

→ विशिष्ट कोणों के त्रिकोणमितीय अनुपात-

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 15 प्रायिकता Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 15 प्रायिकता

परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न:

प्रश्न 1.
टायर बनाने वाली एक कंपनी तय की गई उन दूरियों का एक रिकार्ड रखती थी, जिसके पहले टायर को बदल देने की आवश्यकता पड़ी। सारणी में 1000 स्थितियों के परिणाम दिखाए गए हैं।

यदि आप इस कंपनी से एक टायर खरीदते हैं, तो इस बात की प्रायिकता क्या होगी कि
(i) 4000 कि०मी० की दूरी तय करने से पहले ही इसे बदलना आवश्यक होगा?
(ii) यह 9000 कि०मी० से भी अधिक दूरी तक चलेगा?
(iii) 4000 कि०मी० और 14000 कि०मी० के बीच की कोई दूरी तय करने के बाद इसे बदलना आवश्यक होगा?
हल :
संभाव्य परिणामों की कुल संख्या = 20 + 210 + 325 + 445 = 100
(i) उस टायर की बारंबारता, जिसे 4000 कि०मी० की दूरी तय करने से पहले बदलना आवश्यक हो, 20 है।
अतः, P (4000 कि०मी० की दूरी तय करने से पहले टायर बदलना आवश्यक हो)
= \(\frac{20}{1000}\) = 0.02

(ii) उस टायर की बारंबारता जो 9000 कि०मी० से भी अधिक दूरी तय करेगा = 325 + 445 = 770
अतः,P (टायर 9000 कि०मी० से भी अधिक दूरी तक चलेगा) = \(\frac{770}{1000}\) = 0.77

(iii) उस टायर की बारंबारता जिसे 4000 कि०मी० और 14000 कि०मी० के बीच की दूरी तय कर लेने के बाद बदलना आवश्यक होगा = 210 + 325 = 535
अतः, P (4000 कि०मी० और 14000 कि०मी० के बीच की कोई दूरी तय करने के बाद टायर को बदलना आवश्यक हो)
= \(\frac{535}{1000}\) = 0.535.

प्रश्न 2.
एक थैले में 3 लाल, 5 काली और 4 सफेद गेंदें हैं। थैले में से एक गेंद यादृच्छया निकाली गई। निकाली गई गेंद के
(i) सफेद?
(ii) लाल?
(iii) काली? होने की प्रायिकता क्या है?
हल :
(i) थैले में 4 सफेद गेंद हैं। तो सफेद गेंद निकलने की 4 संभावनाएं हैं और थैले में से एक गेंद की संभावित परिणाम की संभावना 12 है।

∴ P (सफेद गेंद निकालना) = \(\frac{4}{12}=\frac{1}{3}\)

(ii) P (लाल गेंद निकालना) = \(\frac{3}{12}=\frac{1}{4}\)

(iii) P (काली गेंद निकालना) = \(\frac{5}{12}\)

प्रश्न 3.
एक थैले में 3 लाल और 2 नीली गोलियां हैं। एक गोली यादृच्छया (at random) निकाली जाती है। नीली गोली के निकलने की प्रायिकता क्या है?
हल :
गोली को यादृच्छिक रूप से निकालने का अर्थ है कि परिणाम सम-संभावी हैं।
परिणामों की कुल संख्या = 3 + 2 = 5
चूंकि थैले में 2 नीली गोलियां हैं, अतः कुल 5 परिणाम में ।
से, अनुकूल परिणाम = 2
इसलिए, P (एक नीली गोली) = \(\frac{2}{5}\)

प्रश्न 4.
1 से 30 तक अंकित टिकटों को अच्छी तरह से मिलाकर एक बॉक्स में डाला जाता है तथा उसमें से एक टिकट निकाली जाती है। प्रायिकता (probability) ज्ञात कीजिए, जबकि टिकट पर अंकित अंक
(i) अभाज्य संख्या हो,
(ii) सम पूर्ण वर्ग हो,
(iii) 7 से भाज्य संख्या हो।
हल :
संभाव्य परिणामों की कुल संख्या = 30
(i) 1 से 30 तक अंकित टिकटों में अभाज्य संख्या वाले टिकट = 2, 3, 5, 7, 11, 13, 17, 19, 23, 29
अतः अनुकूल परिणामों की कुल संख्या = 10
∴ अभाज्य संख्या वाला टिकट निकलने की प्रायिकता = \(\frac{10}{30}=\frac{1}{3}\)

(ii) संपूर्ण वर्ग वाले टिकट = 4, 16
अतः अनुकूल परिणामों की संख्या = 2
∴ सम पूर्ण वर्ग वाले टिकट निकलने की प्रायिकता = \(\frac{2}{30}=\frac{1}{15}\)

(iii) 7 से भाज्य संख्या वाले टिकट = 7, 14, 21, 28
अतः अनुकूल परिणामों की संख्या = 4
∴ 7 से भाज्य संख्या वाले टिकट निकलने की प्रायिकता = \(\frac{4}{30}=\frac{2}{15}\)

प्रश्न 5.
रिक्त स्थानों की पूर्ति कीजिए :
(i) निश्चित घटना की प्रायिकता ___________ होती है।
(ii) असंभव घटना की प्रायिकता ___________ होती है।
(iii) किसी घटना (निश्चित और असंभव के अतिरिक्त) की प्रायिकता ___________ के बीच में होती है।
(iv) एक पासे को एक बार उछाला गया। अभाज्य संख्या प्राप्त होने की प्रायिकता ___________ है।
हल :
(i) 1
(ii) 0
(iii) 0 और 1
(iv) \(\frac{1}{2}\)

प्रश्न 6.
एक विद्यार्थी द्वारा मासिक यूनिट परीक्षा में प्राप्त किए गए अंकों का प्रतिशत नीचे दिया गया है-

इन आंकड़ों के आधार पर इस बात की प्रायिकता ज्ञात कीजिए कि एक यूनिट परीक्षा में वह विद्यार्थी 70% से अधिक अंक प्राप्त करता है।
हल :
यहाँ पर,
कुल संभाव्य परिणामों की संख्या = यूनिट (I + II + III + IV + V) = 5
70% से अधिक अंक प्राप्त करने के अनुकूल परिणामों की संख्या = यूनिट (II + III + V) = 3
∴ P (70% से अधिक प्राप्त करना) = \(\frac{3}{5}\) = 0.6

प्रश्न 7.
52 पत्तों की ताश की गड्डी से चिड़ी के बादशाह, बेगम और गुलाम को अलग करके शेष को अच्छी तरह से फेंट दिया गया है। शेष पत्तों में से एक पत्ता निकाला जाता है। निम्न की प्राप्ति की प्रायिकता ज्ञात कीजिए :
(i) पान
(ii) बादशाह।
हल :
(i) बादशाह, बेगम और गुलाम को अलग करके शेष बचे पत्तों की संख्या = 52 – 3 = 49 पत्ते
अब 49 पत्तों में 13 पान के पत्ते हैं।
अर्थात अनुकूल परिणामों की संख्या = 13
तथा संभाव्य परिणामों की कुल संख्या = 49
अब, P (पान) = अनुकूल परिणामों की संख्या / संभाव्य परिणामों की कुल संख्या
= \(\frac{13}{49}\)

(ii) 49 पत्तों में 3 बादशाह हैं क्योंकि 1 बादशाह को निकाल दिया गया है।
∴ अनुकूल परिणामों की संख्या = 3
अब, P (बादशाह) = अनुकूल परिणामों की संख्या / संभाव्य परिणामों की कुल संख्या
= \(\frac{3}{49}\)

Multiple Choice Questions with Answers:

प्रश्न 1.
किसी घटना के घटने की प्रायिकता होती है-
(A) 0 से 0.5 के बीच
(B) 0 से 1 के बीच
(C) 0 से 2 के बीच
(D) 0 से 5 के बीच
उत्तर-
(B) 0 से 1 के बीच

प्रश्न 2.
एक सिक्के को 1000 बार उछालने पर निम्नलिखित बारम्बारताएँ प्राप्त हुईं- चित – 455; पट – 545. इसमें पट प्राप्ति की प्रायिकता होगी-
(A) \(\frac{91}{200}\)
(B) \(\frac{1}{2}\)
(C) \(\frac{109}{200}\)
(D) 0
उत्तर-
(C) \(\frac{109}{200}\)

प्रश्न 3.
उपरोक्त प्रश्न नं० 2 में एक चित के आने की घटना की प्रायिकता है-
(A) 0.455
(B) 4.55
(C) 5.45
(D) 0.545
उत्तर-
(A) 0.455

प्रश्न 4.
दो सिक्कों को एक साथ 500 वार उछालने पर हमें प्राप्त होता है। दो चितः 105 बार; एक चित :275 वार; कोई भी चित नहीं-120 बार। इसमें एक चित के आने की घटना की प्रायिकता है-
(A) 0.275
(B) 2.75
(C) 0.55
(D) 0.21
उत्तर-
(C) 0.55

प्रश्न 5.
उपरोक्त प्रश्न नं0 4 में दो चित के आने की घटना की प्रायिकता है-
(A) 0.21
(B) 0.105
(C) 0.55
(D) 0.24
उत्तर-
(A) 0.21

प्रश्न 6.
उपरोक्त प्रश्न नं० 4 में कोई भी चित नहीं आने की घटना की प्रायिकता है-
(A) 0.21
(B) 0.12
(C) 0.55
(D) 0.24
उत्तर-
(D) 0.24

प्रश्न 7.
एक क्रिकेट मैच में एक महिला बल्लेबाज खेली गई 30 गेंदों में 6 बार चौका मारती है, चौका मारे जाने की प्रायिकता
(A) \(\frac{4}{5}\)
(B) \(\frac{3}{5}\)
(C) \(\frac{1}{5}\)
(D) \(\frac{2}{5}\)
उत्तर-
(C) \(\frac{1}{5}\)

प्रश्न 8.
एक क्रिकेट मैच में, एक महिला बल्लेबाज खेली गई 30 गेदों में 6 बार चौका मारती है। चौका न मारे जाने की प्रायिकता होगी-
(A) \(\frac{4}{5}\)
(B) \(\frac{3}{5}\)
(C) \(\frac{1}{5}\)
(D) \(\frac{2}{5}\)
उत्तर-
(A) \(\frac{4}{5}\)

प्रश्न 9.
तीन सिक्कों को एक साथ 200 बार उछाला गया है तथा इनमें विभिन्न परिणामों की बारम्बारताएँ हैं :

28 यदि तीनों सिक्कों को पुनः एक साथ उछाला जाए, तो दो चित के आने की प्रायिकता होगी
(A) \(\frac{23}{200}\)
(B) \(\frac{9}{25}\)
(C) \(\frac{77}{200}\)
(D) \(\frac{7}{50}\)
उत्तर-
(B) \(\frac{9}{25}\)

प्रश्न 10.
एक थैले में 3 लाल, 5 काली और 4 सफेद गेंदें हैं। थैले में से एक गेंद यदृच्छया निकाली गई। निकाली गई गेंद के सफेद होने की प्रायिकता होगी-
(A) \(\frac{5}{12}\)
(B) \(\frac{1}{4}\)
(C) \(\frac{1}{3}\)
(D) \(\frac{1}{2}\)
उत्तर-
(C) \(\frac{1}{3}\)

प्रश्न 11.
एक थैले में 3 लाल, 5 काली और 4 सफेद गेंदें हैं। थैले में से एक गेंद यदृच्छया निकाली गई। निकाली गई गेंद के लाल होने की प्रायिकता होगी-
(A) \(\frac{1}{5}\)
(B) \(\frac{3}{5}\)
(C) शून्य
(D) \(\frac{2}{5}\)
उत्तर-
(B) \(\frac{3}{5}\)

प्रश्न 12.
एक थैले में 3 लाल और 2 नीली गोलियां हैं। एक गोली यदृच्छया (at random) निकाली जाती है। नीली गोली के निकलने की प्रायिकता होगी
(A) \(\frac{1}{5}\)
(B) \(\frac{3}{5}\)
(C) शून्य
(D) \(\frac{2}{5}\)
उत्तर-
(D) \(\frac{2}{5}\)

प्रश्न 13.
सारणी-

इस सारणी में एक विद्यार्थी द्वारा 20 से कम अंक प्राप्त करने की प्रायिकता होगी
(A) \(\frac{7}{90}\)
(B) \(\frac{17}{90}\)
(C) \(\frac{7}{10}\)
(D) \(\frac{27}{90}\)
उत्तर-
(A) \(\frac{7}{90}\)

प्रश्न 14.
प्रश्न नं0 13 की सारणी के अनुसार एक विद्यार्थी द्वारा 60 या उससे अधिक अंक प्राप्त करने की प्रायिकता होगी
(A) \(\frac{15}{90}\)
(B) \(\frac{23}{90}\)
(C) \(\frac{8}{90}\)
(D) \(\frac{67}{90}\)
उत्तर-
(B) \(\frac{23}{90}\)

प्रश्न 15.
प्रश्न नं० 13 की सारणी के अनुसार एक विद्यार्थी द्वारा 70 या उससे अधिक अंक प्राप्त करने की प्रायिकता होगी-
(A) \(\frac{15}{90}\)
(B) \(\frac{23}{90}\)
(C) \(\frac{8}{90}\)
(D) \(\frac{82}{90}\)
उत्तर-
(C) \(\frac{8}{90}\)

प्रश्न 16.
प्रश्न नं० 13 की सारणी के अनुसार एक विद्यार्थी द्वारा 30 से कम अंक प्राप्त करने की प्रायिकता होगी-
(A) \(\frac{7}{90}\)
(B) \(\frac{10}{90}\)
(C) \(\frac{3}{90}\)
(D) \(\frac{17}{90}\)
उत्तर-
(D) \(\frac{17}{90}\)

प्रश्न 17.
सांख्यिकी के बारे में विद्यार्थियों का मत जानने के लिए 200 विद्यार्थियों का सर्वेक्षण किया गया। प्राप्त आंकड़ों को नीचे दी गई सारणी में लिख लिया गया है-

प्रायिकता ज्ञात कीजिए कि यदृच्छया चुना गया विद्यार्थी सांख्यिकी पसंद करता है
(A) \(\frac{27}{40}\)
(B) \(\frac{13}{40}\)
(C) 1
(D) शून्य
उत्तर-
(A) \(\frac{27}{40}\)

प्रश्न 18.
अच्छी प्रकार से फेंटी गई, 52 पत्तों की ताश की गड्डी में से एक पत्ता खींचा गया है। एक इक्के की प्राप्ति की प्रायिकता होगी-
(A) \(\frac{1}{52}\)
(B) \(\frac{2}{26}\)
(C) \(\frac{1}{13}\)
(D) \(\frac{3}{52}\)
उत्तर-
(C) \(\frac{1}{13}\)

प्रश्न 19.
एक मौसम केंद्र के रिकॉर्ड को देखने से पता चलता है कि पिछले 250 क्रमागत दिनों में किए गए मौसम पूर्वानुमानों में से 175 बार उसके पूर्वानुमान सही रहे हैं। एक दिए हुए दिन पर पूर्वानुमान के सही होने की प्रायिकता होगी-
(A) 0.3
(B) 0.7
(C) 0.5
(D) 0.4
उत्तर-
(B) 0.7

प्रश्न 20.
एक विद्यार्थी द्वारा मासिक यूनिट परीक्षा में प्राप्त किए गए अंकों का प्रतिशत नीचे दिया गया है-

इन आंकड़ों के आधार पर इस बात की प्रायिकता क्या होगी कि एक यूनिट परीक्षा में वह विद्यार्थी 70% से अधिक अंक प्राप्त करता है-
(A) 0.6
(B) 0.4
(C) 0.5
(D) 0.2
उत्तर-
(A) 0.6

प्रश्न 21.
निश्चित घटना की प्रायिकता _____________ होती है।
(A) शून्य
(B) शून्य से 1 के बीच
(C) \(\frac{1}{2}\)
(D) 1
उत्तर-
(D) 1

प्रश्न 22.
असम्भव घटना की प्रायिकता _____________ होती है।
(A) एक
(B) \(\frac{1}{2}\)
(C) शून्य
(D) \(\frac{3}{2}\)
उत्तर-
(C) शून्य

प्रश्न 23.
एक पासे को एक बार उछाला गया। अभाज्य संख्या प्राप्त होने की प्रायिकता होगी
(A) \(\frac{1}{2}\)
(B) \(\frac{1}{3}\)
(C) \(\frac{2}{3}\)
(D) \(\frac{1}{6}\)
उत्तर-
(A) \(\frac{1}{2}\)

प्रश्न 24.
1 से 30 तक अंकित टिकटों को अच्छी तरह से मिलाकर एक बॉक्स में डाला जाता है तथा उसमें से एक टिकट निकाली जाती है। निकाली गई टिकट पर अंकित अंक 7 से भाज्य संख्या होने की प्रायिकता होगी-
(A) \(\frac{1}{30}\)
(B) \(\frac{1}{15}\)
(C) \(\frac{2}{15}\)
(D) \(\frac{1}{10}\)
उत्तर-
(C) \(\frac{2}{15}\)

प्रश्न 25.
आटे की उन ग्यारह थैलियों में, जिन पर 5 कि०ग्रा० अंकित है, वास्तव में आटे के निम्नलिखित भार (कि०ग्रा० में) हैं:
4.97 5.05 5.08 5.03 5.00 5.06 5.08 4.98 5.04 5.07 5.00
यादृच्छया चुनी गई एक थैली में 5 कि०ग्रा० से अधिक आटा होने की प्रायिकता होगी-
(A) \(\frac{7}{11}\)
(B) \(\frac{6}{11}\)
(C) \(\frac{5}{11}\)
(D) \(\frac{10}{11}\)
उत्तर-
(A) \(\frac{7}{11}\)

प्रश्न 26.
एक सिक्के को एक बार उछालने पर पट प्राप्त करने की प्रायिकता होती है-
(A) \(\frac{1}{2}\)
(B) \(\frac{1}{3}\)
(C) \(\frac{2}{3}\)
(D) \(\frac{1}{6}\)
उत्तर-
(A) \(\frac{1}{2}\)

Haryana State Board HBSE 10th Class Maths Notes Chapter 8 Introduction to Trigonometry Notes.

Haryana Board 10th Class Maths Notes Chapter 8 Introduction to Trigonometry

Introduction
In our daily life we measure the distances or heights by using some mathematical techniques which come under a branch of mathematics called trigonometry The word trigonometry is derived from the Greek words tri means three), gon (means sides), metron (means measure). Thus, trigonometry is the study of relationship between the sides and angles of a triangle Early even today trigonometrical technique used to find out the distances of the stars and planets from the Earth by astronomers. It is also used in Engineering and Physical science. In the present chapter, we shall study some ratios of the sides of a right triangle with respect to its acute angles, called trignometric ratios of the angle or briefly T-ratios. We shall also calculate the values of the trigonometric ratios for some specific angles, define them for angles 0° and 90° and establish some identities involving these ratios called trigonometric identities.

1. Trigonometry: Trigonometry is the study of relationship between the sides and angles of a triangle.
2. Trigonometric Ratios: The trigonometric ratios of an acute angle in a right triangle express the relationship between the angle and the length of its sides.
3. Trigonometrie Identity: An equation involving trigonometrie ration of an angle is cnlled a trigonometric identity, if it is true for all values of the angles involved.
4. sin θ: sin θ is the abbreviation used for sine of angle θ.
5. cos θ: cos θ is the abbreviation used for cosine of angle θ.
6. tan θ: tan θ is the abbreviation used for tangent of angle θ.
7. cosec θ: cosec θ is the abbreviation used for cosecant of angle θ.
8. sec θ: sec θ is the abbreviation used for secant of angle θ.
9. cot θ: cot θ is the abbreviation used for cotangent of angle θ.
10. Complementary angles: Two angles having sum 90° are called complementary angles.

Trigonometric Ratios
We shall define the trigonometric ratios for an acute angle of a right angled triangle. Let us take a right triangle ABC right angled at B.
Here, ∠CAB and ∠ACB both are acute angles.
The side BC which is opposite to the ∠A we call it the opposite side to ∠A and side AB which is adjacent to ∠A is called adjacent side to ∠A and AC is the hypotenuse of right triangle.

There are six trigonometric ratios of ∠A in right triangle ABC which are defined as follows:


The ratios defined above are generally written in short form as sin A, cos A, tan A, cosec A, sec A and cot A respectively and ratios cosec A, sec A, and cot A are respectively the reciprocals of the ratios sin A, cos A and tan A.
Note: Position of the sides changes when we consider ∠C in place of ∠A as follows:

1. sine C = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
2. consine C = \(\frac{\mathrm{BC}}{\mathrm{AC}}\)
3. tangent C = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
4. cosecant C = \(\frac{\mathrm{AC}}{\mathrm{AB}}\)
5. secant C = \(\frac{\mathrm{AC}}{\mathrm{BC}}\)
6. cotangent C = \(\frac{\mathrm{BC}}{\mathrm{AB}}\)
So, the trigonometric ratios of an acute angle in a right triangle express the relationship between the angles and lengths of its sides.

Remark:
(1) sin A is not the product of ‘sin’ and A. The symbol ‘sin’ separated from the angle A has no meaning. Similarly, cos A is not the Product of cos’and A. Similar interpretations follows for other trigonometric ratios also.
(2) Since the hypotenuse is the longest side in a right triangle, the value of sin A or cos A is always less than 1 (or in particular, equal to 1).
(3) The values of cosec A and sec A cannot be smaller than 1.

(a) Relationship between the trignometric ratios of an angle:
Consider a right triangle ABC in which ∠B = 90° and ∠A = θ
Then, tan θ = \(\frac{\mathrm{BC}}{\mathrm{AB}}\)

Trigonometric Ratios of Some Specific Angles
In this section, we will find the values of the trigonometric ratio of 30°, 45°, 60°, 90° and 0°.
(a) Trigonometric Ratios of 30° and 60°

Consider an equilateral ΔABC with each side of length 2a. We know that each angle of an equilateral triangle is 60°. Therefore, ∠A = ∠B = ∠C = 60°. Draw AD ⊥ BC.
We know that in equilateral Δ, the perpendicular from vertex on the base, bisects the bruse and also the vertical angle.
∴ D is the midpoint of BC
⇒ BD = DC = a.
Also, AD is the bisector of ∠A,
∴ ∠BAD = ∠CAD = \(\frac{60^{\circ}}{2}\) = 30°
Now, in right ΔADB,
AB² = BD² + AD²
[By Pythagoras theorem]
(2a)² = a² + AD²
4a² = a² + AD²
AD² = 4a² – a² = 3a²
AD = \(\sqrt{3}\)a
Trigonometric Ratios of 30°
In right ΔADB, we have
Base (AD) = \(\sqrt{3}\)a, Perpendicular (BD) = a, Hypotenuse (AB) = 2a and ∠BAD = 30°.

Trigonometric Ratios of 60°
In right ΔABD, we have
Base (BD) = a, Perpendicular (AD) = \(\sqrt{3}\)a, Hypotenuse (AB) = 2a and ∠ABD = 60°.

(b) Trigonometric Ratios of 45°
Consider a right triangle ABC, right angled at B such that ∠A = 45°.
∵ ∠A + ∠B + ∠C = 180°
[sum of ∠s of a triangle]
⇒ 45° + 90° + ∠C = 180°
⇒ ∠C + 135° = 180°
⇒ ∠C = 180° – 135°
= 45°
∴ ∠A = ∠C
⇒ AB = BC

Let AB = BC = a. Then,
AC² = AB² + BC²
[By Pythagoras theorem]
AC² = a² + a²
AC² = 2a²
AC = \(\sqrt{2}\)a
Now, in right ΔABC, we have
∠A = 45°, Base (AB) = a, Perpendicular (BC) = a, Hypotenuse (AC) = \(\sqrt{2}\)a.

(c) Trigonometric Ratios of 0° and 90°
Let ∠BAC = θ be an acute angle and let P be a point on its side AB. Draw PM ⊥ AC.
It is evidence from ΔPMA, that as becomes smaller and smaller, line segment PM also becomes smaller and smaller, and finally when θ becomes 0°, the point P will coincide with M. Consequently, we have,
PM = 0, AP = AM


(Not defined)
From ΔPMA, it is evident that as θ increases, the line segment AM becomes smaller and smaller and finally when θ becomes 90°, the point M will coincide A. Consequently, we have
AM = 0, AP = PM

Table of Values of Trigonometric ratios of 0°, 30°, 45°, 60° and 90°

Trigonometric Ratios of Complementary Angles
Complementary Angles: Two angles are said to be complementary, if their sum is 90°.
Thus, θ and (90° – θ) are complementary angles.
Trigonometric Ratios of Complementary Angles:

Consider a ΔOMP such that ∠M = 90°, ∠POM = 0.
Then, ∠OPM = (90° – θ) is its o complementary angle.
For the reference angle θ, we have

For the reference angle (90° – θ), we have
Base = PM, Perpendicular = OM and Hypotenuse = OP.

From (1) and (2), we get
sin (90° – θ) = cos θ
cos (90° – θ) = sin θ
tan (90° – θ) = cot θ
cosec (90° – θ) = sec θ
sec (90° – θ) = cosec θ
cot (90° – θ) = tan θ

Trigonometric Identities
An equation involving trigonometric ratios of an angle is called a trigonometric identity, if it is true for all values of the angles involved.
Fundamental Trigonometric Identities
1. sin² θ + cos² θ = 1
2. sec² θ = 1 + tan² θ
3. cosec² θ = 1 + cot² θ
In right ΔABC, right angled at B, we have
BC² + AB² = AC² ……(1) [By Pythagoras theorem]

1. Dividing each term of (1) by AC², we get

These fundamental identities can be expressed in the following forms:
(i) sin² θ = 1 – cos² θ
or sin θ = \(\sqrt{\left(1-\cos ^2 \theta\right)}\)
(ii) cos² θ = 1 – sin² θ
or cos θ = \(\sqrt{\left(1-\sin ^2 \theta\right)}\)
(iii) sec² θ – tan² θ = 1
(iv) tan² θ = sec² θ – 1
or tan θ = \(\sqrt{\sec ^2 \theta-1}\)
(v) cosec² θ – cot² θ = 1
(vi) cot² θ = cosec² θ – 1
or cot θ =

Haryana State Board HBSE 10th Class Maths Notes Chapter 7 निर्देशांक ज्यामिति Notes.

Haryana Board 10th Class Maths Notes Chapter 7 निर्देशांक ज्यामिति

→ निर्देशांक अक्ष-X’OX तथा Y’OY को निर्देशांक अक्ष (Coordinate Axes) कहते हैं। X’OX को x-अक्ष, Y’OY को y-अक्ष तथा O को मूल बिंदु (Origin point) कहते हैं। चूँकि X’OX तथा Y’OY परस्पर लंब हैं, अतः X’OX तथा Y’OY को कभी-कभी समकोणिक अक्ष (Perpendicular Axes) भी कहते हैं।

→ चतुर्थांश-लंबवत् रेखाएं X’OX तथा Y’OY तल को चार भागों में विभक्त करती हैं, जिन्हें चतुर्थांश (Quadrant) कहते हैं। XOY, YOX’, X’OY’ और Y’OX को क्रमशः प्रथम, द्वितीय, तृतीय और चतुर्थ चतुर्थांश कहते हैं। हम OX, OY दिशाओं को प्रायः धनात्मक और OX’, OY’ को ऋणात्मक लेते हैं। चतुर्थांशों में स्थित बिंदुओं के निर्देशांक इस प्रकार हैं-

→ दो बिंदुओं के बीच की दूरी-दो बिंदुओं P (x₁, y₁) तथा Q(x₂, y₂) के बीच की दूरी के लिए सूत्र निम्नलिखित है-
PQ = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)

→ बिंदु P(x, y) की मूल बिंदु O(0, 0) से दूरी निम्न होती है-
OP = \(\sqrt{x^2+y^2}\)

→ विभाजन सूत्र- बिंदु P, जो बिंदुओं A (x₁, y₁) और B(x₂, y₂) को मिलाने वाले रेखाखंड को m₁ : m₂ के अनुपात में आंतरिक रूप में विभाजित करता है, के निर्देशांक-
\(\left(\frac{m_1 x_2+m_2 x_1}{m_1+m_2}, \frac{m_1 y_2+m_2 y_1}{m_1+m_2}\right)\)

→ बिंदुओं P (x₁, y₁) और Q (x₂, y₂) को जोड़ने वाले रेखाखंड PQ के मध्य-बिंदु के निर्देशांक \(\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\) होते हैं।

→ बिंदुओं (x₁, y₁), (x₂, y₂) और (x₃, y₃) से बनने वाले त्रिभुज का क्षेत्रफल व्यंजक \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₁(y₃ – y₁) + x₃(y₁ – y₂)] का संख्यात्मक मान होता है।

Haryana State Board HBSE 10th Class Maths Notes Chapter 15 प्रायिकता Notes.

Haryana Board 10th Class Maths Notes Chapter 15 प्रायिकता

→ घटना E की सैद्धांतिक (या परंपरागत) प्रायिकता P(E) को निम्नलिखित रूप में परिभाषित किया जाता है-

जहाँ हम कल्पना करते हैं कि प्रयोग के सभी परिणाम समप्रायिक हैं।

→ एक निश्चित या निर्धारित घटना की प्रायिकता 1 होती है।

→ एक असंभव घटना की प्रायिकता 0 होती है।

→ घटना E की प्रायिकता एक ऐसी संख्या P(E) है कि 0 ≤ P(E) ≤ 1

→ वह घटना जिसका केवल एक ही परिणाम हो एक प्रारंभिक घटना कहलाती है। किसी प्रयोग की सभी प्रारंभिक घटनाओं की प्रायिकता का योग 1 होता है।

→ किसी भी घटना E के लिए P(E) + P(\(\bar{E}\)) = 1 होता है, जहाँ E घटना ‘E नहीं’ को व्यक्त करता है। E और \(\bar{E}\) पूरक घटनाएँ कहलाती हैं।

Haryana State Board HBSE 10th Class Maths Notes Chapter 14 सांख्यिकी Notes.

Haryana Board 10th Class Maths Notes Chapter 14 सांख्यिकी

→ सांख्यिकी- सांख्यिकी वह विज्ञान है, जो संख्यात्मक आंकड़ों के संग्रह, प्रस्तुतीकरण एवं विश्लेषण की उपयोगी विधियों एवं तकनीकों का अध्ययन करती है तथा उन पर आधारित निष्कर्ष निकालती है।

→ सांख्यिकी आंकड़ों का निरूपण- साठिाकी आंकड़ों को निरूपित करने के लिए निम्नलिखित प्रकार के आलेखों या आरेखों का उपयोग किया जाता है-

• आयतचित्र,
• वारंवारता बहुभुज,
• वारंवारता बक,
• दंड आरेख,
• चित्रालेख,
• पाई चार्ट या वृत्तीय आरेख।

→ अवर्गीकृत आंकड़ों का माध्य (समांतर माण)-सांख्यिकी आंकड़ों का आदर्श मापक ‘माध्य’ होता है क्योंकि माध्य अथवा औसत ज्ञात करने के लिए सभी आंकड़ों को निरूपित किया जाता है। इसे \(\bar{x}\) द्वारा प्रकट किया जाता है तथा प्राप्त आंकड़ों का माध्य सभी प्रेक्षणों के योग को प्रेक्षणों की संख्या से भाग देकर ज्ञात किया जाता है।
यदि n प्रेक्षण x₁, x₂, x₃, …….., x_n हो तो,

→ वर्गीकृत आंकड़ों के माध्य का परिकतन-इसकी निम्नलिखित दो विधियों हैं-
(a) प्रत्यक्ष विपि : यदि घर x के x₁, x₂, x₃, ………, x_n अलग-अलग मान हों तथा इनकी संगत वारंवारता f₁, f₂, f₃, …….., f_n हो तो,

(b) कथित माध्य विधि : यदि बारंबारताएँ अधिक हों तो गणना कठिन हो जाती है और तब इस विधि का प्रयोग करते हैं। इस विधि में हम एक खेच्छ अचर मान ‘a’ को लेते हैं (ध्यान रहे कि ‘a’ का गान x का वह मान लेना चाहिए, जो बंटन के मध्य भाग में हो)। ‘a’ के मान को x_i में से घटाते जाते हैं। पटाने पर प्राप्त मान (x – a) को विषलन मान ‘d’ कहते हैं अर्थात d_i = x_i – a तो माध्य \(\bar{x}\) = a + \(\bar{d}\), जहाँ \(\bar{d}\) = \(\frac{\sum f_i d_i}{\sum f_i}\)
(c) पग-विचलन विपि । कभी-कभी कल्पित माध्य विधि में प्राप्त विचलनों di को वर्ग-माप h से भाग देते हैं तथा u_i प्राप्त करते हैं अर्थात् u_i = \(\frac{x_i-a}{h}\) तव माध्य (\(\bar{x}\)) = \(a+\left(\frac{\sum f_i u_i}{\sum f_i}\right) \times h\)

→ किसी वर्ग-अंतराल का मध्य बिंदु (वर्ग चिहून) उसकी उपरि और निचली वर्ग सीमाओं का औसत होता है। अर्थात

→ बहुलक : बहुलक (Mode) दिए हुए प्रेक्षणों में वह मान है जो सबसे अधिक बार आता है अर्थात उस प्रेक्षण का मान जिसकी वारंवारता अधिकतम है।

→ बहुसक वर्ग : एक वर्गीकृत वारंवारता बंटन में, वारंवारताओं को देखकर बहुलक ज्ञात करना संभव नहीं है। यहाँ, हम केवल वह वर्ग (class) ज्ञात कर सकते हैं जिसकी वारंवारता अधिकतम है। इस वर्ग को बहुतक वर्ग (modal class) कहते हैं।

→ वर्गीकृत जाँकड़ों का बहुतक निम्नलिखित सूत्र द्वारा ज्ञात किया जाता है-
बहुलक = \(l+\left(\frac{f_1-f_0}{2 f_1-f_0-f_2}\right) \times h\)
जहाँ l = बहुलक वर्ग की निम्न (निचली) सीमा
h = वर्ग अंतराल की माप (यह मानते हुए कि सभी अंतराल बराबर मापों के हैं)
f₁ = बहुलक वर्ग की वारंवारता
f₀ = बहुलक वर्ग से ठीक पहले वर्ग की बारंबारता तथा
f₂ = बहुलक वर्ग के ठीक बाद में आने वाले वर्ग की वारंवारता है।

→ संचवी बारंबारता : किसी पारंवारता चंटन में किसी वर्ग की संचयी वारंवारता उस वर्ग से पहले वाले सभी वर्गों की बारंबारताओं का योग होता है।

→ माध्यक माध्यक (median) बेटीय प्रवृत्ति का ऐसा मापक है, जो आंकड़ों में सबसे बीच के प्रेक्षण का मान देता है। अवर्गीकृत आँकड़ों का मायक ज्ञात करने के लिए, पहले हम प्रेक्षणों के मानों को आरोही क्रम में अवस्थित करते हैं। अब, यदि विषम है, तो माध्यक \(\left(\frac{n+1}{2}\right)\) प्रेक्षण का मान होता है, यदि n सम है, तो माध्यक \(\frac{n}{2}\) और \(\left(\frac{n}{2}+1\right)\) ये प्रेक्षणों के मानों का औसत (माध्य) होता है।

→ माध्यक वर्ग : हम दिए गए सभी वर्गों की संचयी बारंबारताएँ और \(\frac{n}{2}\) शास करते हैं। अब, हम वह वर्ग खोजते हैं जिसकी संचयी वारंवारता से अधिक और उसके निकटतम है। इस वर्ग को माध्यक वर्ग (median class) कहते हैं।

→ वर्गीकृत ओंकड़ों का माध्यक निम्नलिखित सूत्र द्वारा ज्ञात किया जाता है-
माध्यक = \(l+\left(\frac{\frac{n}{2}-c f}{f}\right) \times h\)
जहाँ l = माध्यक वर्ग की निम्न सीमा
n = प्रेक्षणों की संख्या
cf = माध्यक वर्ग से ठीक पहले वाले वर्ग की संचयी बारंबारता
f = माध्यक वर्ग की वारंवारता
h = वर्ग-माप (यह मानते हुए कि वर्ग-माप बराबर है)

→ तीनों केंद्रीय प्रवृत्ति के मापकों में संबंध : 3 माध्यक = बहुतक + 2 माध्य

→ संचयी वारंवारता बंटनों को आतेखीय रूप से संचयी बारंबारता वकों या से कम प्रकार के’ या ‘से अधिक प्रकार के तोरण द्वारा निरूपण।

→ वर्गीकृत ओंकड़ों का माध्यक इनके दोनों प्रकार के तोरणों के प्रतिच्छेद बिंदु से सैतिज अक्ष पर तंब डालकर संब और कैतिज अक्ष के प्रतिच्छेद बिंदु के संगत मान से प्राप्त हो जाता है।

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 2 बहुपद Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 2 बहुपद

Multiple Choice Questions With Answers:

प्रश्न 1.
निम्नलिखित प्रत्येक बहुपद में का गुणांक लिखिए।
(i) √2 + x – x²
(ii) 5x² + 3x + 2
हल :
(i) √2 + x – x² में x² का गुणांक = – 1
(ii) 5x² + 3x + 2 में x2 का गुणांक = 5.

प्रश्न 2.
बताइए कि निम्नलिखित दरुपदों में से कौन-कौन से बहुपद रैखिक हैं। कौन-कौन से द्विघाती हैं और कौन-कौन से त्रिघाती हैं-
(i) y² + 1
(ii) 5x³
(iii) y² + y + 5
(iv) √2 + x – x²
(v) u + 1
हल :
(i) बहुपद y² + 1 द्विघाती बहुपद है।
(ii) बहुपद 5x³ एक त्रिघाती बहुपद है।
(iii) बहुपद y² + y + 5 एक द्विघाती बहुपद है।
(iv) √2 + x – x² एक द्विघाती बहुपद है।
(v) बहुपद u + 1 एक रैखिक बहुपद है।

प्रश्न 3.
बताइए कि निम्नलिखित बहुपदों में से कौन-कौन से बहुपद एकपदी हैं, कौन-कौन से द्विपदी हैं और कौन-कौन से त्रिपदी हैं
(i) x⁴ + x + 5
(ii) 5y⁶ – 4y² – 6
(iii) x³ – 1
(iv) – 5x²
(v) u⁴
(vi) u⁴³ – u²
हल :
(i) बहुपद x⁴ + x + 5 एक त्रिपदी है।
(ii) बहुपद 5y⁶ – 4y – 6 एक त्रिपदी है।
(iii) बहुपद x³ – 1 एक द्विपदी है।
(iv) बहुपद – 5x² एक एकपदी है।
(v) बहुपद u⁴ एक एकपदी है।
(vi) बहुपद u⁴³ – u² एक द्विपदी है।

प्रश्न 4.
बहुपद p (x) = 4x⁴ + 5x³ – x² + 6 के लिए p (0), p (1) तथा p (2) का मान ज्ञात कीजिए।
हल :
यहाँ पर
p (x) = 4x⁴ + 5x³ – x² + 6
x = 0 रखने पर
p (0) = 4 (0)⁴ + 5 (0)³ – (0)² + 6
= 0 + 0 – 0 + 6
= 6

x = 1 रखने पर
p (1) = 4 (1)⁴ + 5 (1)³ – (1)² + 6
= 4 + 5 – 1 + 6
= 15 – 1 = 14

x = 2 रखने पर
p (2) = 4 (2)⁴ + 5 (2)³ – (2)² + 6
= 4 × 16 + 5 × 8 – 4 + 6
= 64 + 40 – 4 + 6
= 110 – 4 = 106

प्रश्न 5.
बहुपद p (x) = 2x + 1 का एक शून्यक ज्ञात कीजिए।
हल :
बहुपद का शून्यक ज्ञात करने के लिए आवश्यक है-
p (x) = 0
2x + 1 = 0
2x = 0 – 1
2x = -1
x = – \(\frac{1}{2}\)
अतः – \(\frac{1}{2}\) बहुपद 2x + 1 का एक शून्यक है।

प्रश्न 6.
3x² + x – 1 को x + 1 से भाग दीजिए।
हल :

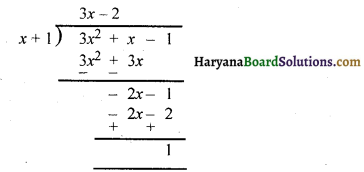
अतः भागफल = 3x – 2; शेषफल = 1

प्रश्न 7.
शेषफल ज्ञात करें जब बहुपद p (x) = 2x⁴ – 6x³ – 2x² – x + 2 को x + 2 से भाग किया जाता है।
हल :
यहाँ पर
p (x) = 2x⁴ – 6x³ – 2x² – x + 2
x + 2 का शून्यक -2 है।
∴ p(- 2) = 2(- 2)⁴ – 6 (- 2)³ – 2 (- 2)² – (- 2) + 2
= 2 (16) – 6 (- 8) – 2 (4) + 2 + 2
= 32 + 48 – 8 + 2 + 2 = 76
अतः p (x) को x + 2 से भाग देने पर शेषफल = 76.

प्रश्न 8.
यदि x – 1, 4x³ + 3x² – 4x + k का एक गुणनखंड हो, तो k का मान ज्ञात कीजिए।
हल :
क्योंकि x – 1, p (x) = 4x³ + 3x² – 4x + k का एक गुणनखंड है,
इसलिए
p(1) = 0 होगा।
p (1) = 4 (1)³ + 3 (1)² – 4 (1) + k
इसलिए 4 + 3 – 4 + k = 0
या k = 3.

प्रश्न 9.
x² + 14x + 45 का गुणनखंडन कीजिए।
हल:
x² + 14x + 45 = x² + 9x + 5x + 45
= x (x + 9) + 5 (x + 9)
= (x + 9) (x + 5).

प्रश्न 10.
द्विघात बहुपद 6x² + 5x – 6 के गुणनखण्ड ज्ञात कीजिए।
हल :
यहाँ पर
6x² + 5x – 6 = 6x² + 9x – 4x – 6
= 3x (2x + 3) – 2 (2x + 3)
= (2x + 3) (3x – 2)

प्रश्न 11.
x³ – 6x² + 11x – 6 का गुणनखंडन कीजिए।
हल :
माना
p(x) = x³ – 6x² + 11x – 6
यहाँ पर अचर पद – 6 है जिसके गुणनखंड ± 1, ± 2, ± 3, ± 6 हैं।
x = 1 रखने पर
p(1) = (1)³ – 6 (1)² + 11 (1) – 6
= 1 – 6 + 11 – 6
= 12 – 12 = 0
अतः x – 1, p (x) का एक गुणनखंड है।
अब

x³ – 6x² + 11x – 6 = (x – 1) (x² – 5x + 6)
= (x – 1) (x² – 3x – 2x + 6)
= (x – 1) [x (x – 3) – 2 (x – 3)]
= (x – 1) (x – 3)(x – 2)

प्रश्न 12.
सीधे गुणा किए बिना 102 × 103 का मान ज्ञात करें।
हल :
102 × 103 = (100 + 2) (100 +3)
= (100)² + (2 + 3) (100) + 2 × 3
= 10000 + 500 + 6 = 10506.

प्रश्न 13.
p⁴ – 625 का गुणनखंडन कीजिए।
हल:
p⁴ – 625 = (p²)² – (25)²
= (p² – 25) (p² + 25)
= [(p)² – (5)] (p² + 25)
= (p – 5) (p + 5) (p² + 25).

प्रश्न 14.
उपयुक्त सर्वसमिका का प्रयोग करके 105 × 106 का मान ज्ञात कीजिए।
हल :
105 × 106 = (100 + 5) (100 +6)
= (100)² + (5 + 6) × 100 + 5 × 6
= 10000 + 11 × 100 + 30
10000 + 1100 + 30
= 11130.

प्रश्न 15.
8x³ + y³ + 27z³ – 18xyz का गुणनखण्ड कीजिए।
हल :
हम जानते हैं कि a³ + b³ + c³ – 3abc = (a + b + c) (a² + b² + c² – ab – bc – ca)
8x³ + y³ + 27z³ – 18xyz = (2x)³ + (y)³ + (3z)³ – 3 (2x) (y) (z)
(2x + y + 3z) [(2x)² + (y)² + (3z)² – (2x) (y) – (y) (3z) – (3z) (2x)]
(2x + y + 3z) [4x² + y² + 9z² – 2xy – 3yz – 6zx]

Multiple Choice Questions With Answers:

प्रश्न 1.
बहुपद x⁵ – x⁴ + 3 की घात है-
(A) शून्य
(B) 3
(C) 4
(D) 5
उत्तर-
(D) 5

प्रश्न 2.
बहुपद 2 – x² – x³ + 2x⁸ की घात होगी-
(A) 2
(B) 3
(C) शून्य
(D) 8
उत्तर-
(D) 8

प्रश्न 3.
निम्नलिखित बीजीय व्यंजकों में कौन-सा एक बहुपद है ?
(A) x² + 5x + 6
(B) y + \(\frac{1}{2 y}\)
(C) 5t + 3
(D) \(\frac{1}{5 x+3}\)
उत्तर-
(A) x² + 5x + 6

प्रश्न 4.
निम्नलिखित वीजीय व्यंजकों में से कौन-सा व्यंजक बहुपद नहीं है ?
(A) x¹⁰ + 3x³ + 5x⁵⁰
(B) y² + √2
(C) 4y² – 3y + 7
(D) y + \(\frac{2}{2y}\)
उत्तर-
(D) y + \(\frac{2}{2y}\)

प्रश्न 5.
निम्नलिखित में से कौन-सा व्यंजक एक चर वाला है ?
(A) 4x² – 3x + 7
(B) x¹⁰ + y³ – t⁵
(C) 4x² – 3y + 7
(D) 4x² – 3y + 7z
उत्तर-
(A) 4x² – 3x + 7

प्रश्न 6.
निम्नलिखित में से कौन-सा व्यंजक दो चर वाला है ?
(A) 4x² – 3x + 7
(B) x¹⁰ + y³ – 150
(C) 4x² – 3y + 7
(D) 4x² – 3y + 7z
उत्तर-
(C) 4x² – 3y + 7.

प्रश्न 7.
\(\frac{\pi}{2}\) x² + x में :’ का गुणांक है-
(A) 1
(B) π
(C) \(\frac{1}{2}\)
(D) \(\frac{\pi}{2}\)
उत्तर-
(D) \(\frac{\pi}{2}\)

प्रश्न 8.
√2x – 1 में x² का गुणांक है-
(A) शून्य
(B) 1
(C) √2
(D) – 1
उत्तर-
(A) शून्य

प्रश्न 9.
निम्नलिखित बहुपदों में से कौन-सा बहुपद द्विघाती नहीं है ?
(A) x² + x
(B) x – x³
(C) y + y² + 4
(D) r²
उत्तर-
(B) x – x³

प्रश्न 10.
निम्नलिखित बहुपदों में से कौन-सा बहुपद रैखिक है ?
(A) x² + x
(B) y + 4
(C) 3t – t³
(D) 7
उत्तर-
(B) y + 4

प्रश्न 11.
निम्नलिखित बहुपदों में से कौन-सा बहुपद त्रिघाती है ?
(A) 1 + x
(B) y + y² + 4
(C) x – x³
(D) y² + y
उत्तर-
(C) x – x³

प्रश्न 12.
x = 1 पर बहुपद p(x) = 5x² – 3x + 7 का मान होगा-
(A) 8
(B) 15
(C) 9
(D) 1
उत्तर-
(C) 9

प्रश्न 13.
बहुपद p(x) = 2x + 1 का एक शून्यक होगा
(A) \(\frac{1}{2}\)
(B) – \(\frac{1}{2}\)
(C) 2
(D) – 2
उत्तर-
(B) – \(\frac{1}{2}\)

प्रश्न 14.
x = – 1 पर बहुपद 5x – 4x² + 3 का मान होगा-
(A) 6
(B) 4
(C) 6
(D) – 4
उत्तर-
(A) 6

प्रश्न 15.
बहुपद p(x) = (x – 1) (x + 1) के लिए p(0) का मान होगा-
(A) – 1
(B) 1
(C) 0
(D) 3
उत्तर-
(A) – 1

प्रश्न 16.
बहुपद p(y) = y² – y + 1 के लिए p(0) का मान होगा-
(A) 1
(B) – 1
(C) 2
(D) – 2
उत्तर-
(A)1

प्रश्न 17.
बहुपद p(x) = 2x + 5 का शून्यक होगा-
(A) \(\frac{5}{2}\)
(B) – \(\frac{5}{2}\)
(C) \(\frac{2}{5}\)
(D) – \(\frac{2}{5}\)
उत्तर-
(B) – \(\frac{5}{2}\)

प्रश्न 18.
बहुपद p(x) = cx + d; {c’ 0, c, d वास्तविक संख्याएँ हैं} में बहुपद का शून्यक होगा-
(A) \(\frac{d}{c}\)
(B) – \(\frac{d}{c}\)
(C) \(\frac{c}{d}\)
(D) – \(\frac{c}{d}\)
उत्तर-
(B) – \(\frac{d}{c}\)

प्रश्न 19.
बहुपद P(y) = 3y में बहुपद का शून्यक होगा-
(A) शून्य
(B) 1
(C) 3
(D) – 3
उत्तर-
(A) शून्य

प्रश्न 20.
3x² + x – 1 को x + 1 से भाग देने पर शेषफल प्राप्त होगा-
(A) 1
(B) – 1
(C) – 2
(D) 2
उत्तर-
(A) 1

प्रश्न 21.
3x⁴ + – 4x³ – 3x – 1 को x – 1 से भाग करने पर शेषफल प्राप्त होगा-
(A) 5
(B) – 5
(C) शून्य
(D) – 3
उत्तर-
(B) – 5

प्रश्न 22.
p(x) = x³ +3x² + 3x + 1 को x + π से भाग देने पर शेषफल प्राप्त होगा-
(A) – π³ + 3π² – 3π + 1
(B) π³ + 3π² – 3π + 1
(C) π³ + 3π² + 3π + 1
(D) – π³ – 3π² + 3π + 1
उत्तर-
(A) – π³ + 3π² – 3π + 1

प्रश्न 23.
x³ + 3x² + 3x + 1 को x + 1 से भाग देने पर शेषफल प्राप्त होगा-
(A) – 1
(B) 1
(C) शून्य
(D) 2
उत्तर-
(C) शून्य

प्रश्न 24.
p(x) = x³ – ax² + 6x – 4 को x – a से भाग देने पर शेषफल प्राप्त होगा-
(A) – 5a
(B) 5a
(C) 7a
(D) – 7a
उत्तर-
(B) 5a

प्रश्न 25.
p(y) = y³ + 3y² + 3y + 1 को y से भाग करने पर शेषफल प्राप्त होगा-
(A) शून्य
(B) – 1
(C) 1
(D) 2
उत्तर-
(C) 1.

प्रश्न 26.
यदि p(x) = x² + x + k का एक गुणनखंड (x-1) हो तो k का मान होगा-
(A) 2
(B) – 2
(C) 1
(D) – 1
उत्तर-
(B) – 2

प्रश्न 27.
y² – 5y + 6 का गुणनखंडन होगा-
(A) (y – 2) (y – 3)
(B) (y – 2) (y + 3)
(C) (y + 2) (y – 3)
(D) (y + 2) (y +3)
उत्तर-
(A) (y – 2) (y – 3)

प्रश्न 28.
2x² + 7x + 3 का गुणनखंडन होगा-
(A) (x – 3) (2x + 1)
(B) (x + 3) (2x + 1)
(C) (x + 3) (2x – 1)
(D) (x -3) (2x – 1)
उत्तर-
(B) (x + 3) (2x + 1)

प्रश्न 29.
उपयुक्त सर्वसमिका के उपयोग से (x + 4) (x + 10) का गुणनफल होगा-
(A) x² + 6x + 40
(B) x² + 14x + 40
(C) x² + 14x – 40
(D) x² + 14x – 40
उत्तर-
(B) x² + 14x + 40

प्रश्न 30.
उपयुक्त सर्वसमिका के उपयोग से (3x + 4) (3x – 5) का गुणनफल होगा-
(A) 9x² – 3x – 20
(B) 9x² + 3x + 20
(C) 9x² – 3x + 20
(D) 9x² + 3x – 20
उत्तर-
(A) 9x² – 3x – 20

प्रश्न 31.
104 × 96 का मान ज्ञात करने के लिए उपयुक्त है-
(A) (100 + 4) (90 + 6)
(B) (110 – 6) (90 + 6)
(C) (100 + 4) (100 – 4)
(D) (110 – 6) (100 – 4)
उत्तर-
(C) (100 + 4) (100 – 4)

प्रश्न 32.
(x + 3) (x + 3) = x² + ……………….. + 9 के रिक्त स्थान पर होगा-
(A) 2x
(B) 3x
(C) 6x
(D) 5x
उत्तर-
(C) 6x

प्रश्न 33.
(3 + 2x) (3 – 2x) का मान होगा-
(A) 9 + 4x²
(B) 9 – 4²
(C) 9 – 2x²
(D) 9 + 2x²
उत्तर-
(B) 9 – 4x²

प्रश्न 34.
9x² + 6xy + y² का गुणनखंडन होगा-
(A) (3x+ y) (3x + y)
(B) (3x – y) (3x – y)
(C) (3x + y) (3x–2)
(D) इनमें से कोई नहीं
उत्तर-
(A) (3x +y) (3x + y)

प्रश्न 35.
उपयुक्त सर्वसमिका का प्रयोग करके \(x^2-\frac{y^2}{100}\) का गुणनखंडन होगा
(A) \(\left(x-\frac{y}{10}\right)\left(x-\frac{y}{10}\right)\)
(B) \(\left(x+\frac{y}{10}\right)\left(x-\frac{y}{10}\right)\)
(C) \(\left(x+\frac{y}{10}\right)\left(x+\frac{y}{10}\right)\)
(D) इनमें से कोई नहीं
उत्तर-
(B) \(\left(x+\frac{y}{10}\right)\left(x-\frac{y}{10}\right)\)

प्रश्न 36.
उपयुक्त सर्वसमिका का प्रयोग करके 49a² + 70ab + 25b² का गुणनखंडन होगा-
(A) (7a + 5b) (7a + 5b)
(B) (7a-5b) (7a-5b)
(C) (7a + 5b) (7a-5b)
(D) इनमें से कोई नहीं
उत्तर-
(A) (7a + 5 b) (7a + 5b)

प्रश्न 37.
उपयुक्त सर्वसमिका का प्रयोग करके 4y² – 4y + 1 का गुणनखंडन होगा-
(A) (2y + 1) (2y + 1)
(B) (2y – 1) (2y – 1)
(C) (2y – 1) (2y + 1)
(D) इनमें से कोई नहीं
उत्तर-
(B) (2y – 1) (2y – 1)

प्रश्न 38.
(- 2x + 5y – 3z)² का प्रसारित रूप होगा-
(A) – 4x² + 25y² – 9z² – 20xy – 30yz + 12xz
(B) – 4x² + 25y² + 9z² + 20xy + 30yz + 12xz
(C) – 4x² + 25y² – 9z² + 20xy + 30yz + 12xz
(D) 4x² + 25y² + 922 – 20xy – 30yz + 12xz
उत्तर-
(D) 4x² + 25y² + 9z² – 20xy – 30yz + 12xz

प्रश्न 39.
(104) को सरल करने के लिए उपयुक्त सर्वसमिका है-
(A) (100 + 4)³
(B) (110 – 6)³
(C) (90 + 14)³
(D) (120 – 16)³
उत्तर-
(A) (100 + 4)³

प्रश्न 40.
(5p – 3q)³ का प्रसारित रूप होगा-
(A) 125p³ – 27q³ – 225pq² – 135pq²
(B) 125p³ — 27q³ – 225p²q + 135pq²
(C) 125p³ + 27q³ + 225p²q + 135pq²
(D) 125p³ – 27q³ + 225p²q + 135pq²
उत्तर-
(B) 125p³ — 27q³ – 225p²q + 135pq²

प्रश्न 41.
(2x + 1)³ का प्रसारित रूप होगा-
(A) 8x³ + 12x² + 6x + 1
(B) 8x³ + 12x² + 6x – 1
(C) 8x³ – 12x² + 6x – 1
(D) 8x³ – 12x² – 6x – 1
उत्तर-
(A) 8x³ + 12x² + 6x + 1

प्रश्न 42.
निम्नलिखित में से कौन-सी सर्वसमिका सत्य है ?
(A) x³ + y³ = (x + y) (x² + xy + y²)
(B) x³ + y³ = (x + y) (x² – xy + y²)
(C) x³ – y³ = (x – y) (x² – xy + y²)
(D) x³ – y³ = (x + y) (x² – xy + y²)
उत्तर-
(B) x³ + y³ = (x + y) (x² – xy + y²)

प्रश्न 43.
64m³ – 343n³ का गुणनखंडन करने पर प्राप्त होगा-
(A) (4m – 7n) (16m² + 49n² – 28mn)
(B) (4m + 7n) (16m² + 49n² – 28mn)
(C) (4m – 7n) (16m² + 49n² + 28mn)
(D) (4m + 7n) (16m² + 49n² + 28mn)
उत्तर-
(C) (4m – 7n) (16m² + 49n² + 28mn)

प्रश्न 44.
यदि x + y + z = 0 हो तो निम्नलिखित में से कौन-सा कथन सत्य है ?
(A) x³ – y³ – z³ = 3xyz
(B) x³ + y³ + z³ = 3xyz
(C) x³ – y³ + z³ = 3xyz
(D) x³ + y³ + z³ = – 3xyz
उत्तर-
(B) x³ + y³ + z³ = 3xyz

प्रश्न 45.
यदि किसी आयत का क्षेत्रफल 25a² – 35a + 12 हो तो उसकी लंबाई व चौड़ाई क्रमशः होगी-
(A) (5a – 3) व (5a – 4)
(B) (5a + 3) व (5a – 4)
(C) (5a + 3) व (5a + 4)
(D) (5a – 3) व (5a + 4)
उत्तर-
(A) (5a – 3) व (5a – 4)

प्रश्न 46.
यदि किसी घनाभ का आयतन 12ky² + 8ky – 206 हो तो उसकी संभावित विमाएँ होंगी-
(A) 4k, 3y – 5 व y – 1
(B) 4k, 3y + 5 व y – 1
(C) 4k, 3y + 5 व y + 1
(D) 4k, 3y – 5 व y + 1
उत्तर-
(B) 4k, 3y + 5 व y – 1

प्रश्न 47.
यदि किसी घनाभ का आयतन 3x² – 12x हो तो उसकी संभावित विमाएँ होंगी-
(A) 4, x और x + 3
(B) 3, x और x + 4
(C) 4, x और x – 3
(D) 3, x और x – 4
उत्तर-
(D) 3, x और x – 4

प्रश्न 48.
बहुपद 2 – x² – x³ + 5x⁷ की घात होगी-
(A) 2
(B) 3
(C) 7
(D) 5
उत्तर-
(C) 7