HBSE 10th Class Maths Notes Chapter 14 सांख्यिकी

Haryana State Board HBSE 10th Class Maths Notes Chapter 14 सांख्यिकी Notes.

Haryana Board 10th Class Maths Notes Chapter 14 सांख्यिकी

→ सांख्यिकी- सांख्यिकी वह विज्ञान है, जो संख्यात्मक आंकड़ों के संग्रह, प्रस्तुतीकरण एवं विश्लेषण की उपयोगी विधियों एवं तकनीकों का अध्ययन करती है तथा उन पर आधारित निष्कर्ष निकालती है।

→ सांख्यिकी आंकड़ों का निरूपण- साठिाकी आंकड़ों को निरूपित करने के लिए निम्नलिखित प्रकार के आलेखों या आरेखों का उपयोग किया जाता है-

• आयतचित्र,
• वारंवारता बहुभुज,
• वारंवारता बक,
• दंड आरेख,
• चित्रालेख,
• पाई चार्ट या वृत्तीय आरेख।

→ अवर्गीकृत आंकड़ों का माध्य (समांतर माण)-सांख्यिकी आंकड़ों का आदर्श मापक ‘माध्य’ होता है क्योंकि माध्य अथवा औसत ज्ञात करने के लिए सभी आंकड़ों को निरूपित किया जाता है। इसे \(\bar{x}\) द्वारा प्रकट किया जाता है तथा प्राप्त आंकड़ों का माध्य सभी प्रेक्षणों के योग को प्रेक्षणों की संख्या से भाग देकर ज्ञात किया जाता है।
यदि n प्रेक्षण x₁, x₂, x₃, …….., x_n हो तो,

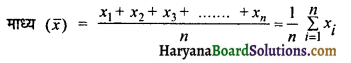
→ वर्गीकृत आंकड़ों के माध्य का परिकतन-इसकी निम्नलिखित दो विधियों हैं-
(a) प्रत्यक्ष विपि : यदि घर x के x₁, x₂, x₃, ………, x_n अलग-अलग मान हों तथा इनकी संगत वारंवारता f₁, f₂, f₃, …….., f_n हो तो,

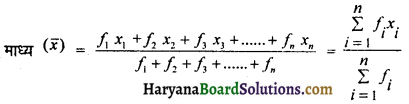
(b) कथित माध्य विधि : यदि बारंबारताएँ अधिक हों तो गणना कठिन हो जाती है और तब इस विधि का प्रयोग करते हैं। इस विधि में हम एक खेच्छ अचर मान ‘a’ को लेते हैं (ध्यान रहे कि ‘a’ का गान x का वह मान लेना चाहिए, जो बंटन के मध्य भाग में हो)। ‘a’ के मान को x_i में से घटाते जाते हैं। पटाने पर प्राप्त मान (x – a) को विषलन मान ‘d’ कहते हैं अर्थात d_i = x_i – a तो माध्य \(\bar{x}\) = a + \(\bar{d}\), जहाँ \(\bar{d}\) = \(\frac{\sum f_i d_i}{\sum f_i}\)
(c) पग-विचलन विपि । कभी-कभी कल्पित माध्य विधि में प्राप्त विचलनों di को वर्ग-माप h से भाग देते हैं तथा u_i प्राप्त करते हैं अर्थात् u_i = \(\frac{x_i-a}{h}\) तव माध्य (\(\bar{x}\)) = \(a+\left(\frac{\sum f_i u_i}{\sum f_i}\right) \times h\)

→ किसी वर्ग-अंतराल का मध्य बिंदु (वर्ग चिहून) उसकी उपरि और निचली वर्ग सीमाओं का औसत होता है। अर्थात

→ बहुलक : बहुलक (Mode) दिए हुए प्रेक्षणों में वह मान है जो सबसे अधिक बार आता है अर्थात उस प्रेक्षण का मान जिसकी वारंवारता अधिकतम है।

→ बहुसक वर्ग : एक वर्गीकृत वारंवारता बंटन में, वारंवारताओं को देखकर बहुलक ज्ञात करना संभव नहीं है। यहाँ, हम केवल वह वर्ग (class) ज्ञात कर सकते हैं जिसकी वारंवारता अधिकतम है। इस वर्ग को बहुतक वर्ग (modal class) कहते हैं।

→ वर्गीकृत जाँकड़ों का बहुतक निम्नलिखित सूत्र द्वारा ज्ञात किया जाता है-
बहुलक = \(l+\left(\frac{f_1-f_0}{2 f_1-f_0-f_2}\right) \times h\)
जहाँ l = बहुलक वर्ग की निम्न (निचली) सीमा
h = वर्ग अंतराल की माप (यह मानते हुए कि सभी अंतराल बराबर मापों के हैं)
f₁ = बहुलक वर्ग की वारंवारता
f₀ = बहुलक वर्ग से ठीक पहले वर्ग की बारंबारता तथा
f₂ = बहुलक वर्ग के ठीक बाद में आने वाले वर्ग की वारंवारता है।

→ संचवी बारंबारता : किसी पारंवारता चंटन में किसी वर्ग की संचयी वारंवारता उस वर्ग से पहले वाले सभी वर्गों की बारंबारताओं का योग होता है।

→ माध्यक माध्यक (median) बेटीय प्रवृत्ति का ऐसा मापक है, जो आंकड़ों में सबसे बीच के प्रेक्षण का मान देता है। अवर्गीकृत आँकड़ों का मायक ज्ञात करने के लिए, पहले हम प्रेक्षणों के मानों को आरोही क्रम में अवस्थित करते हैं। अब, यदि विषम है, तो माध्यक \(\left(\frac{n+1}{2}\right)\) प्रेक्षण का मान होता है, यदि n सम है, तो माध्यक \(\frac{n}{2}\) और \(\left(\frac{n}{2}+1\right)\) ये प्रेक्षणों के मानों का औसत (माध्य) होता है।

→ माध्यक वर्ग : हम दिए गए सभी वर्गों की संचयी बारंबारताएँ और \(\frac{n}{2}\) शास करते हैं। अब, हम वह वर्ग खोजते हैं जिसकी संचयी वारंवारता से अधिक और उसके निकटतम है। इस वर्ग को माध्यक वर्ग (median class) कहते हैं।

→ वर्गीकृत ओंकड़ों का माध्यक निम्नलिखित सूत्र द्वारा ज्ञात किया जाता है-
माध्यक = \(l+\left(\frac{\frac{n}{2}-c f}{f}\right) \times h\)
जहाँ l = माध्यक वर्ग की निम्न सीमा
n = प्रेक्षणों की संख्या
cf = माध्यक वर्ग से ठीक पहले वाले वर्ग की संचयी बारंबारता
f = माध्यक वर्ग की वारंवारता
h = वर्ग-माप (यह मानते हुए कि वर्ग-माप बराबर है)

→ तीनों केंद्रीय प्रवृत्ति के मापकों में संबंध : 3 माध्यक = बहुतक + 2 माध्य

→ संचयी वारंवारता बंटनों को आतेखीय रूप से संचयी बारंबारता वकों या से कम प्रकार के’ या ‘से अधिक प्रकार के तोरण द्वारा निरूपण।

→ वर्गीकृत ओंकड़ों का माध्यक इनके दोनों प्रकार के तोरणों के प्रतिच्छेद बिंदु से सैतिज अक्ष पर तंब डालकर संब और कैतिज अक्ष के प्रतिच्छेद बिंदु के संगत मान से प्राप्त हो जाता है।