Haryana State Board HBSE 9th Class Maths Important Questions Chapter 15 प्रायिकता Important Questions and Answers.
Haryana Board 9th Class Maths Important Questions Chapter 15 प्रायिकता
परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न:
प्रश्न 1.
टायर बनाने वाली एक कंपनी तय की गई उन दूरियों का एक रिकार्ड रखती थी, जिसके पहले टायर को बदल देने की आवश्यकता पड़ी। सारणी में 1000 स्थितियों के परिणाम दिखाए गए हैं।
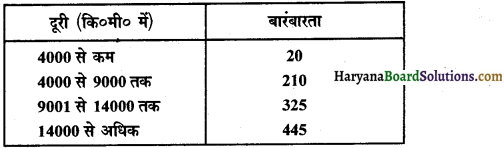
यदि आप इस कंपनी से एक टायर खरीदते हैं, तो इस बात की प्रायिकता क्या होगी कि
(i) 4000 कि०मी० की दूरी तय करने से पहले ही इसे बदलना आवश्यक होगा?
(ii) यह 9000 कि०मी० से भी अधिक दूरी तक चलेगा?
(iii) 4000 कि०मी० और 14000 कि०मी० के बीच की कोई दूरी तय करने के बाद इसे बदलना आवश्यक होगा?
हल :
संभाव्य परिणामों की कुल संख्या = 20 + 210 + 325 + 445 = 100
(i) उस टायर की बारंबारता, जिसे 4000 कि०मी० की दूरी तय करने से पहले बदलना आवश्यक हो, 20 है।
अतः, P (4000 कि०मी० की दूरी तय करने से पहले टायर बदलना आवश्यक हो)
= \(\frac{20}{1000}\) = 0.02
(ii) उस टायर की बारंबारता जो 9000 कि०मी० से भी अधिक दूरी तय करेगा = 325 + 445 = 770
अतः,P (टायर 9000 कि०मी० से भी अधिक दूरी तक चलेगा) = \(\frac{770}{1000}\) = 0.77
(iii) उस टायर की बारंबारता जिसे 4000 कि०मी० और 14000 कि०मी० के बीच की दूरी तय कर लेने के बाद बदलना आवश्यक होगा = 210 + 325 = 535
अतः, P (4000 कि०मी० और 14000 कि०मी० के बीच की कोई दूरी तय करने के बाद टायर को बदलना आवश्यक हो)
= \(\frac{535}{1000}\) = 0.535.
![]()
प्रश्न 2.
एक थैले में 3 लाल, 5 काली और 4 सफेद गेंदें हैं। थैले में से एक गेंद यादृच्छया निकाली गई। निकाली गई गेंद के
(i) सफेद?
(ii) लाल?
(iii) काली? होने की प्रायिकता क्या है?
हल :
(i) थैले में 4 सफेद गेंद हैं। तो सफेद गेंद निकलने की 4 संभावनाएं हैं और थैले में से एक गेंद की संभावित परिणाम की संभावना 12 है।
∴ P (सफेद गेंद निकालना) = \(\frac{4}{12}=\frac{1}{3}\)
(ii) P (लाल गेंद निकालना) = \(\frac{3}{12}=\frac{1}{4}\)
(iii) P (काली गेंद निकालना) = \(\frac{5}{12}\)
प्रश्न 3.
एक थैले में 3 लाल और 2 नीली गोलियां हैं। एक गोली यादृच्छया (at random) निकाली जाती है। नीली गोली के निकलने की प्रायिकता क्या है?
हल :
गोली को यादृच्छिक रूप से निकालने का अर्थ है कि परिणाम सम-संभावी हैं।
परिणामों की कुल संख्या = 3 + 2 = 5
चूंकि थैले में 2 नीली गोलियां हैं, अतः कुल 5 परिणाम में ।
से, अनुकूल परिणाम = 2
इसलिए, P (एक नीली गोली) = \(\frac{2}{5}\)
प्रश्न 4.
1 से 30 तक अंकित टिकटों को अच्छी तरह से मिलाकर एक बॉक्स में डाला जाता है तथा उसमें से एक टिकट निकाली जाती है। प्रायिकता (probability) ज्ञात कीजिए, जबकि टिकट पर अंकित अंक
(i) अभाज्य संख्या हो,
(ii) सम पूर्ण वर्ग हो,
(iii) 7 से भाज्य संख्या हो।
हल :
संभाव्य परिणामों की कुल संख्या = 30
(i) 1 से 30 तक अंकित टिकटों में अभाज्य संख्या वाले टिकट = 2, 3, 5, 7, 11, 13, 17, 19, 23, 29
अतः अनुकूल परिणामों की कुल संख्या = 10
∴ अभाज्य संख्या वाला टिकट निकलने की प्रायिकता = \(\frac{10}{30}=\frac{1}{3}\)
(ii) संपूर्ण वर्ग वाले टिकट = 4, 16
अतः अनुकूल परिणामों की संख्या = 2
∴ सम पूर्ण वर्ग वाले टिकट निकलने की प्रायिकता = \(\frac{2}{30}=\frac{1}{15}\)
(iii) 7 से भाज्य संख्या वाले टिकट = 7, 14, 21, 28
अतः अनुकूल परिणामों की संख्या = 4
∴ 7 से भाज्य संख्या वाले टिकट निकलने की प्रायिकता = \(\frac{4}{30}=\frac{2}{15}\)
![]()
प्रश्न 5.
रिक्त स्थानों की पूर्ति कीजिए :
(i) निश्चित घटना की प्रायिकता ___________ होती है।
(ii) असंभव घटना की प्रायिकता ___________ होती है।
(iii) किसी घटना (निश्चित और असंभव के अतिरिक्त) की प्रायिकता ___________ के बीच में होती है।
(iv) एक पासे को एक बार उछाला गया। अभाज्य संख्या प्राप्त होने की प्रायिकता ___________ है।
हल :
(i) 1
(ii) 0
(iii) 0 और 1
(iv) \(\frac{1}{2}\)
प्रश्न 6.
एक विद्यार्थी द्वारा मासिक यूनिट परीक्षा में प्राप्त किए गए अंकों का प्रतिशत नीचे दिया गया है-

इन आंकड़ों के आधार पर इस बात की प्रायिकता ज्ञात कीजिए कि एक यूनिट परीक्षा में वह विद्यार्थी 70% से अधिक अंक प्राप्त करता है।
हल :
यहाँ पर,
कुल संभाव्य परिणामों की संख्या = यूनिट (I + II + III + IV + V) = 5
70% से अधिक अंक प्राप्त करने के अनुकूल परिणामों की संख्या = यूनिट (II + III + V) = 3
∴ P (70% से अधिक प्राप्त करना) = \(\frac{3}{5}\) = 0.6
प्रश्न 7.
52 पत्तों की ताश की गड्डी से चिड़ी के बादशाह, बेगम और गुलाम को अलग करके शेष को अच्छी तरह से फेंट दिया गया है। शेष पत्तों में से एक पत्ता निकाला जाता है। निम्न की प्राप्ति की प्रायिकता ज्ञात कीजिए :
(i) पान
(ii) बादशाह।
हल :
(i) बादशाह, बेगम और गुलाम को अलग करके शेष बचे पत्तों की संख्या = 52 – 3 = 49 पत्ते
अब 49 पत्तों में 13 पान के पत्ते हैं।
अर्थात अनुकूल परिणामों की संख्या = 13
तथा संभाव्य परिणामों की कुल संख्या = 49
अब, P (पान) = अनुकूल परिणामों की संख्या / संभाव्य परिणामों की कुल संख्या
= \(\frac{13}{49}\)
(ii) 49 पत्तों में 3 बादशाह हैं क्योंकि 1 बादशाह को निकाल दिया गया है।
∴ अनुकूल परिणामों की संख्या = 3
अब, P (बादशाह) = अनुकूल परिणामों की संख्या / संभाव्य परिणामों की कुल संख्या
= \(\frac{3}{49}\)
![]()
Multiple Choice Questions with Answers:
प्रश्न 1.
किसी घटना के घटने की प्रायिकता होती है-
(A) 0 से 0.5 के बीच
(B) 0 से 1 के बीच
(C) 0 से 2 के बीच
(D) 0 से 5 के बीच
उत्तर-
(B) 0 से 1 के बीच
प्रश्न 2.
एक सिक्के को 1000 बार उछालने पर निम्नलिखित बारम्बारताएँ प्राप्त हुईं- चित – 455; पट – 545. इसमें पट प्राप्ति की प्रायिकता होगी-
(A) \(\frac{91}{200}\)
(B) \(\frac{1}{2}\)
(C) \(\frac{109}{200}\)
(D) 0
उत्तर-
(C) \(\frac{109}{200}\)
प्रश्न 3.
उपरोक्त प्रश्न नं० 2 में एक चित के आने की घटना की प्रायिकता है-
(A) 0.455
(B) 4.55
(C) 5.45
(D) 0.545
उत्तर-
(A) 0.455
![]()
प्रश्न 4.
दो सिक्कों को एक साथ 500 वार उछालने पर हमें प्राप्त होता है। दो चितः 105 बार; एक चित :275 वार; कोई भी चित नहीं-120 बार। इसमें एक चित के आने की घटना की प्रायिकता है-
(A) 0.275
(B) 2.75
(C) 0.55
(D) 0.21
उत्तर-
(C) 0.55
प्रश्न 5.
उपरोक्त प्रश्न नं0 4 में दो चित के आने की घटना की प्रायिकता है-
(A) 0.21
(B) 0.105
(C) 0.55
(D) 0.24
उत्तर-
(A) 0.21
प्रश्न 6.
उपरोक्त प्रश्न नं० 4 में कोई भी चित नहीं आने की घटना की प्रायिकता है-
(A) 0.21
(B) 0.12
(C) 0.55
(D) 0.24
उत्तर-
(D) 0.24
![]()
प्रश्न 7.
एक क्रिकेट मैच में एक महिला बल्लेबाज खेली गई 30 गेंदों में 6 बार चौका मारती है, चौका मारे जाने की प्रायिकता
(A) \(\frac{4}{5}\)
(B) \(\frac{3}{5}\)
(C) \(\frac{1}{5}\)
(D) \(\frac{2}{5}\)
उत्तर-
(C) \(\frac{1}{5}\)
प्रश्न 8.
एक क्रिकेट मैच में, एक महिला बल्लेबाज खेली गई 30 गेदों में 6 बार चौका मारती है। चौका न मारे जाने की प्रायिकता होगी-
(A) \(\frac{4}{5}\)
(B) \(\frac{3}{5}\)
(C) \(\frac{1}{5}\)
(D) \(\frac{2}{5}\)
उत्तर-
(A) \(\frac{4}{5}\)
प्रश्न 9.
तीन सिक्कों को एक साथ 200 बार उछाला गया है तथा इनमें विभिन्न परिणामों की बारम्बारताएँ हैं :

28 यदि तीनों सिक्कों को पुनः एक साथ उछाला जाए, तो दो चित के आने की प्रायिकता होगी
(A) \(\frac{23}{200}\)
(B) \(\frac{9}{25}\)
(C) \(\frac{77}{200}\)
(D) \(\frac{7}{50}\)
उत्तर-
(B) \(\frac{9}{25}\)
![]()
प्रश्न 10.
एक थैले में 3 लाल, 5 काली और 4 सफेद गेंदें हैं। थैले में से एक गेंद यदृच्छया निकाली गई। निकाली गई गेंद के सफेद होने की प्रायिकता होगी-
(A) \(\frac{5}{12}\)
(B) \(\frac{1}{4}\)
(C) \(\frac{1}{3}\)
(D) \(\frac{1}{2}\)
उत्तर-
(C) \(\frac{1}{3}\)
प्रश्न 11.
एक थैले में 3 लाल, 5 काली और 4 सफेद गेंदें हैं। थैले में से एक गेंद यदृच्छया निकाली गई। निकाली गई गेंद के लाल होने की प्रायिकता होगी-
(A) \(\frac{1}{5}\)
(B) \(\frac{3}{5}\)
(C) शून्य
(D) \(\frac{2}{5}\)
उत्तर-
(B) \(\frac{3}{5}\)
प्रश्न 12.
एक थैले में 3 लाल और 2 नीली गोलियां हैं। एक गोली यदृच्छया (at random) निकाली जाती है। नीली गोली के निकलने की प्रायिकता होगी
(A) \(\frac{1}{5}\)
(B) \(\frac{3}{5}\)
(C) शून्य
(D) \(\frac{2}{5}\)
उत्तर-
(D) \(\frac{2}{5}\)
![]()
प्रश्न 13.
सारणी-
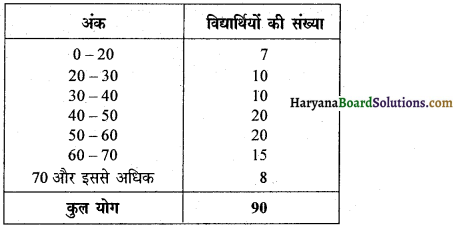
इस सारणी में एक विद्यार्थी द्वारा 20 से कम अंक प्राप्त करने की प्रायिकता होगी
(A) \(\frac{7}{90}\)
(B) \(\frac{17}{90}\)
(C) \(\frac{7}{10}\)
(D) \(\frac{27}{90}\)
उत्तर-
(A) \(\frac{7}{90}\)
प्रश्न 14.
प्रश्न नं0 13 की सारणी के अनुसार एक विद्यार्थी द्वारा 60 या उससे अधिक अंक प्राप्त करने की प्रायिकता होगी
(A) \(\frac{15}{90}\)
(B) \(\frac{23}{90}\)
(C) \(\frac{8}{90}\)
(D) \(\frac{67}{90}\)
उत्तर-
(B) \(\frac{23}{90}\)
प्रश्न 15.
प्रश्न नं० 13 की सारणी के अनुसार एक विद्यार्थी द्वारा 70 या उससे अधिक अंक प्राप्त करने की प्रायिकता होगी-
(A) \(\frac{15}{90}\)
(B) \(\frac{23}{90}\)
(C) \(\frac{8}{90}\)
(D) \(\frac{82}{90}\)
उत्तर-
(C) \(\frac{8}{90}\)
![]()
प्रश्न 16.
प्रश्न नं० 13 की सारणी के अनुसार एक विद्यार्थी द्वारा 30 से कम अंक प्राप्त करने की प्रायिकता होगी-
(A) \(\frac{7}{90}\)
(B) \(\frac{10}{90}\)
(C) \(\frac{3}{90}\)
(D) \(\frac{17}{90}\)
उत्तर-
(D) \(\frac{17}{90}\)
प्रश्न 17.
सांख्यिकी के बारे में विद्यार्थियों का मत जानने के लिए 200 विद्यार्थियों का सर्वेक्षण किया गया। प्राप्त आंकड़ों को नीचे दी गई सारणी में लिख लिया गया है-

प्रायिकता ज्ञात कीजिए कि यदृच्छया चुना गया विद्यार्थी सांख्यिकी पसंद करता है
(A) \(\frac{27}{40}\)
(B) \(\frac{13}{40}\)
(C) 1
(D) शून्य
उत्तर-
(A) \(\frac{27}{40}\)
प्रश्न 18.
अच्छी प्रकार से फेंटी गई, 52 पत्तों की ताश की गड्डी में से एक पत्ता खींचा गया है। एक इक्के की प्राप्ति की प्रायिकता होगी-
(A) \(\frac{1}{52}\)
(B) \(\frac{2}{26}\)
(C) \(\frac{1}{13}\)
(D) \(\frac{3}{52}\)
उत्तर-
(C) \(\frac{1}{13}\)
![]()
प्रश्न 19.
एक मौसम केंद्र के रिकॉर्ड को देखने से पता चलता है कि पिछले 250 क्रमागत दिनों में किए गए मौसम पूर्वानुमानों में से 175 बार उसके पूर्वानुमान सही रहे हैं। एक दिए हुए दिन पर पूर्वानुमान के सही होने की प्रायिकता होगी-
(A) 0.3
(B) 0.7
(C) 0.5
(D) 0.4
उत्तर-
(B) 0.7
प्रश्न 20.
एक विद्यार्थी द्वारा मासिक यूनिट परीक्षा में प्राप्त किए गए अंकों का प्रतिशत नीचे दिया गया है-
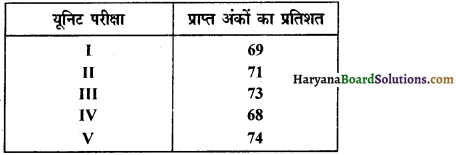
इन आंकड़ों के आधार पर इस बात की प्रायिकता क्या होगी कि एक यूनिट परीक्षा में वह विद्यार्थी 70% से अधिक अंक प्राप्त करता है-
(A) 0.6
(B) 0.4
(C) 0.5
(D) 0.2
उत्तर-
(A) 0.6
प्रश्न 21.
निश्चित घटना की प्रायिकता _____________ होती है।
(A) शून्य
(B) शून्य से 1 के बीच
(C) \(\frac{1}{2}\)
(D) 1
उत्तर-
(D) 1
![]()
प्रश्न 22.
असम्भव घटना की प्रायिकता _____________ होती है।
(A) एक
(B) \(\frac{1}{2}\)
(C) शून्य
(D) \(\frac{3}{2}\)
उत्तर-
(C) शून्य
प्रश्न 23.
एक पासे को एक बार उछाला गया। अभाज्य संख्या प्राप्त होने की प्रायिकता होगी
(A) \(\frac{1}{2}\)
(B) \(\frac{1}{3}\)
(C) \(\frac{2}{3}\)
(D) \(\frac{1}{6}\)
उत्तर-
(A) \(\frac{1}{2}\)
प्रश्न 24.
1 से 30 तक अंकित टिकटों को अच्छी तरह से मिलाकर एक बॉक्स में डाला जाता है तथा उसमें से एक टिकट निकाली जाती है। निकाली गई टिकट पर अंकित अंक 7 से भाज्य संख्या होने की प्रायिकता होगी-
(A) \(\frac{1}{30}\)
(B) \(\frac{1}{15}\)
(C) \(\frac{2}{15}\)
(D) \(\frac{1}{10}\)
उत्तर-
(C) \(\frac{2}{15}\)
![]()
प्रश्न 25.
आटे की उन ग्यारह थैलियों में, जिन पर 5 कि०ग्रा० अंकित है, वास्तव में आटे के निम्नलिखित भार (कि०ग्रा० में) हैं:
4.97 5.05 5.08 5.03 5.00 5.06 5.08 4.98 5.04 5.07 5.00
यादृच्छया चुनी गई एक थैली में 5 कि०ग्रा० से अधिक आटा होने की प्रायिकता होगी-
(A) \(\frac{7}{11}\)
(B) \(\frac{6}{11}\)
(C) \(\frac{5}{11}\)
(D) \(\frac{10}{11}\)
उत्तर-
(A) \(\frac{7}{11}\)
प्रश्न 26.
एक सिक्के को एक बार उछालने पर पट प्राप्त करने की प्रायिकता होती है-
(A) \(\frac{1}{2}\)
(B) \(\frac{1}{3}\)
(C) \(\frac{2}{3}\)
(D) \(\frac{1}{6}\)
उत्तर-
(A) \(\frac{1}{2}\)