Haryana State Board HBSE 10th Class Maths Notes Chapter 7 Coordinate Geometry Notes.
Haryana Board 10th Class Maths Notes Chapter 7 Coordinate Geometry
Introduction
We have studied in previous classes that how to locate the position of a point in co-ordinate plane of two dimensions in terms of two co-ordinates. The distance of a point from the y-axis is called its x-co-ordinate or abscissa. The distance of a point from the x-axis is called its y co-ordinate or ordinate. The coordiantes of a point on the x-axis are of the form (x, 0), and of a point on the y-axis are of the form (0, y).
In is chapter, we shall extend our knowledge by learning how to find the distance between the two points whose co-ordinates are given, and to find the area of the triangle formed by three given points. We shall also learn about how to find the co-ordinates of the point which divides a line segment joining two given points in a given ratio.
1. Plane-It is a flat surface, which extends indefinitely in all directions. The surface of a sheet of paper, the surface of a smooth green board, the surface of a smooth table top are some examples of a plane.
2. Co-ordinate axes-To locate the position of a point in a plane, two mutually perpendicular lines are drawn. One of them is horizontal known as x-axis and other is vertical known as y-axis. These axes are combindely called co-ordinate axes.
3. Origin-The point of intersection of two Axes is called origin.
4. Quadrants-The axes divide a plane into four parts called quadrants.
5. Collinear points-If three or more pointa lie on the same line, they are called collinear points. Otherwise, they are called non-collinear points.
![]()
Distance Formula
a1 = a = 0
Let P (x1, y1) and Q(x2, y2) be the given points in the plane. Draw PS ⊥ x-axis, QT ⊥ x-axis and PR ⊥ QT from P, Q and P respectively. Then
OS = x1, OT = x2, PS = y1, QT = y2
PR = ST = OT – OS = x2 – x1 and QR = QT – RT = y2 – y1
ΔQRP is a right angled triangle, right angled at R.
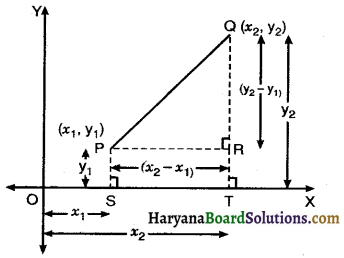
∴ PQ2 = PR2 + QR2 [By Pythagoras theorem]
PQ2 = (x2 – x1)2 + (y2 – y1)2
PQ = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)
Hence, distance between any two points
\(=\sqrt{\begin{array}{r}
(\text { difference of abscissa })^2+ \\
\text { (difference of ordinates) }^2
\end{array}}\)
It is called the distance formula.
Remark: (i) The distance of a point P(x, y) from the origin O(0, 0) is given by
OP = \(\sqrt{(x-0)^2+(y-0)^2}=\sqrt{x^2+y^2}\)

(ii) If three points A, B and C are collinear then AB + BC = AC.
(iii) Properties of different types of quadrilaterals
(a) Square : In a square, all sides and diagonals are equal
(b) Rectangle : In a rectangle opposite sides and diagoals are equal.
(c) Parallelogram : In a parallelogram opposite sides are equal.
(d) Paralleogram but not a rectangle : In this case opposite sides are equal but diagonals are not equal
(e) Rhombus but not a square : In this case all sides are equal, but diagonals are not equal.
Section Formula
By section formula we find out the coordinates of the point which divides the line segment joining the two given points in a given ratio internally.
Let P(x, y) be the point dividing the line segment joining the points. A(x1, y1) and B(x2, y2) internally in the ratio m1 : m2.
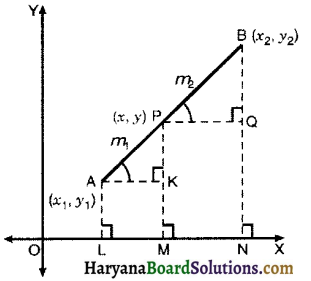
Draw AL ⊥ OX; PM ⊥ OX, BN ⊥ OX, Also draw AK ⊥ PM and PQ ⊥ BN. Then, OL = x1, OM = x, AL = y1, PM = y and BN = y2. ON = x2.
AK = LM = OM – OL = x – x1
PQ = MN = ON – OM
= x2 – x
PK = PM – KM = y – y1
BQ = BN – QN = y2 – y
In right ΔAKP and ΔPQB.
∠AKP = ∠PQB (Each is 90°)
∠AKP = ∠BPQ (Corresponding ∠s)
ΔAKP ~ ΔPQB [By AA similarity criterion]


Remarks: (1) If P is the mid point of AB then m1 : m2 = 1 : 1.
Then co-ordinates of P are
\(\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\)
(2) If the ratio in which P divides AB is k : 1. Then the coordiantes of the point P are
\(\left(\frac{k x_2+x_1}{k+1}, \frac{k y_2+y_1}{k+1}\right)\)
![]()
Co-ordinates of the Centroid of a Triangle
Let A(x1, y1), B(x2, y2) and C(x3, y3) be the vertices of a given ΔABC. Let D be the mid point of BC. Let G(x, y) be centroid of the triangle as shown in figure.
Co-ordinates of the point D are \(\left(\frac{x_2+x_3}{2}, \frac{y_2+y_3}{2}\right)\)
Since centroid divides each median in the ratio 2 : 1.
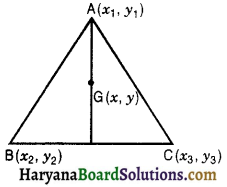
∴ G divides AD in the ratio 2 : 1
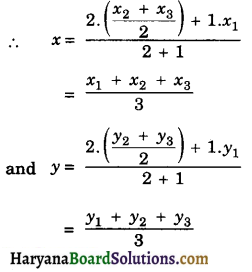
Hence, the coordinates of the centroid of the triangle are \(\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right)\)
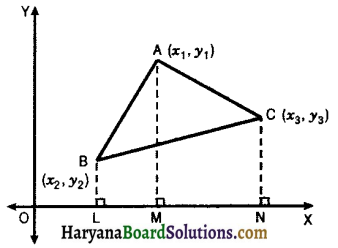
Area of Triangle
Let A(x1, y1) B(x2, y2) and C(x3, y3) be the vertices of the given ΔABC. Draw BL, AM and CN perpendicular to the x-axis.
Then, LM = (x1 – x2), LN = (x3 – x2)
MN = (x3 – x1)
Now, Area of ΔABC = ar(Trap BLMA) + ar(Trap AMNC) – ar(Trap BLNC)
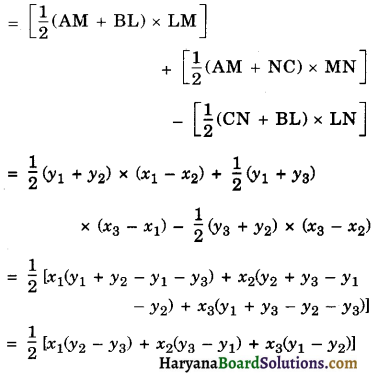
Since, the area is never negative, we have
Area (ΔABC) = \(\frac{1}{2}\)[(x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
![]()
Condition for the collinearity of three points
If three points A (x1, y1), B (x2, y2) and C(x3, y3) are collinear.
Then Area of ΔABC = 0
⇒ \(\frac{1}{2}\)[x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)
⇒ x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)
= 0
Remark : To find the area of a polygon we divide it in triangles and take numerical value of the area of each of the triangles.