Haryana State Board HBSE 10th Class Maths Notes Chapter 8 Introduction to Trigonometry Notes.
Haryana Board 10th Class Maths Notes Chapter 8 Introduction to Trigonometry
Introduction
In our daily life we measure the distances or heights by using some mathematical techniques which come under a branch of mathematics called trigonometry The word trigonometry is derived from the Greek words tri means three), gon (means sides), metron (means measure). Thus, trigonometry is the study of relationship between the sides and angles of a triangle Early even today trigonometrical technique used to find out the distances of the stars and planets from the Earth by astronomers. It is also used in Engineering and Physical science. In the present chapter, we shall study some ratios of the sides of a right triangle with respect to its acute angles, called trignometric ratios of the angle or briefly T-ratios. We shall also calculate the values of the trigonometric ratios for some specific angles, define them for angles 0° and 90° and establish some identities involving these ratios called trigonometric identities.
1. Trigonometry: Trigonometry is the study of relationship between the sides and angles of a triangle.
2. Trigonometric Ratios: The trigonometric ratios of an acute angle in a right triangle express the relationship between the angle and the length of its sides.
3. Trigonometrie Identity: An equation involving trigonometrie ration of an angle is cnlled a trigonometric identity, if it is true for all values of the angles involved.
4. sin θ: sin θ is the abbreviation used for sine of angle θ.
5. cos θ: cos θ is the abbreviation used for cosine of angle θ.
6. tan θ: tan θ is the abbreviation used for tangent of angle θ.
7. cosec θ: cosec θ is the abbreviation used for cosecant of angle θ.
8. sec θ: sec θ is the abbreviation used for secant of angle θ.
9. cot θ: cot θ is the abbreviation used for cotangent of angle θ.
10. Complementary angles: Two angles having sum 90° are called complementary angles.
![]()
Trigonometric Ratios
We shall define the trigonometric ratios for an acute angle of a right angled triangle. Let us take a right triangle ABC right angled at B.
Here, ∠CAB and ∠ACB both are acute angles.
The side BC which is opposite to the ∠A we call it the opposite side to ∠A and side AB which is adjacent to ∠A is called adjacent side to ∠A and AC is the hypotenuse of right triangle.
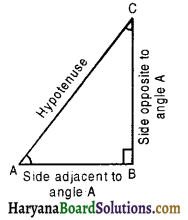
There are six trigonometric ratios of ∠A in right triangle ABC which are defined as follows:
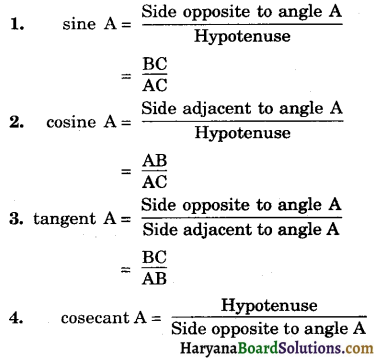

The ratios defined above are generally written in short form as sin A, cos A, tan A, cosec A, sec A and cot A respectively and ratios cosec A, sec A, and cot A are respectively the reciprocals of the ratios sin A, cos A and tan A.
Note: Position of the sides changes when we consider ∠C in place of ∠A as follows:

1. sine C = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
2. consine C = \(\frac{\mathrm{BC}}{\mathrm{AC}}\)
3. tangent C = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
4. cosecant C = \(\frac{\mathrm{AC}}{\mathrm{AB}}\)
5. secant C = \(\frac{\mathrm{AC}}{\mathrm{BC}}\)
6. cotangent C = \(\frac{\mathrm{BC}}{\mathrm{AB}}\)
So, the trigonometric ratios of an acute angle in a right triangle express the relationship between the angles and lengths of its sides.
Remark:
(1) sin A is not the product of ‘sin’ and A. The symbol ‘sin’ separated from the angle A has no meaning. Similarly, cos A is not the Product of cos’and A. Similar interpretations follows for other trigonometric ratios also.
(2) Since the hypotenuse is the longest side in a right triangle, the value of sin A or cos A is always less than 1 (or in particular, equal to 1).
(3) The values of cosec A and sec A cannot be smaller than 1.
![]()
(a) Relationship between the trignometric ratios of an angle:
Consider a right triangle ABC in which ∠B = 90° and ∠A = θ
Then, tan θ = \(\frac{\mathrm{BC}}{\mathrm{AB}}\)
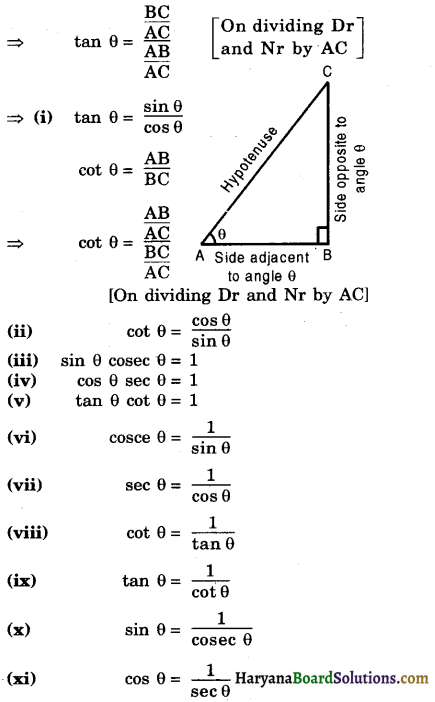
Trigonometric Ratios of Some Specific Angles
In this section, we will find the values of the trigonometric ratio of 30°, 45°, 60°, 90° and 0°.
(a) Trigonometric Ratios of 30° and 60°
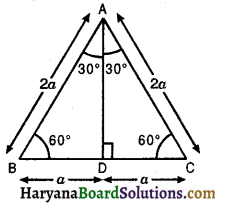
Consider an equilateral ΔABC with each side of length 2a. We know that each angle of an equilateral triangle is 60°. Therefore, ∠A = ∠B = ∠C = 60°. Draw AD ⊥ BC.
We know that in equilateral Δ, the perpendicular from vertex on the base, bisects the bruse and also the vertical angle.
∴ D is the midpoint of BC
⇒ BD = DC = a.
Also, AD is the bisector of ∠A,
∴ ∠BAD = ∠CAD = \(\frac{60^{\circ}}{2}\) = 30°
Now, in right ΔADB,
AB2 = BD2 + AD2
[By Pythagoras theorem]
(2a)2 = a2 + AD2
4a2 = a2 + AD2
AD2 = 4a2 – a2 = 3a2
AD = \(\sqrt{3}\)a
Trigonometric Ratios of 30°
In right ΔADB, we have
Base (AD) = \(\sqrt{3}\)a, Perpendicular (BD) = a, Hypotenuse (AB) = 2a and ∠BAD = 30°.

Trigonometric Ratios of 60°
In right ΔABD, we have
Base (BD) = a, Perpendicular (AD) = \(\sqrt{3}\)a, Hypotenuse (AB) = 2a and ∠ABD = 60°.

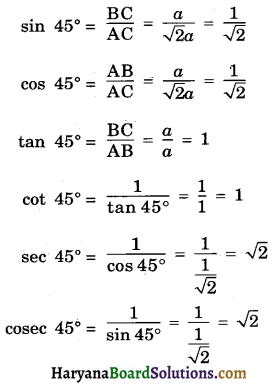
(b) Trigonometric Ratios of 45°
Consider a right triangle ABC, right angled at B such that ∠A = 45°.
∵ ∠A + ∠B + ∠C = 180°
[sum of ∠s of a triangle]
⇒ 45° + 90° + ∠C = 180°
⇒ ∠C + 135° = 180°
⇒ ∠C = 180° – 135°
= 45°
∴ ∠A = ∠C
⇒ AB = BC
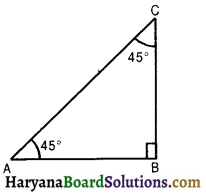
Let AB = BC = a. Then,
AC2 = AB2 + BC2
[By Pythagoras theorem]
AC2 = a2 + a2
AC2 = 2a2
AC = \(\sqrt{2}\)a
Now, in right ΔABC, we have
∠A = 45°, Base (AB) = a, Perpendicular (BC) = a, Hypotenuse (AC) = \(\sqrt{2}\)a.
(c) Trigonometric Ratios of 0° and 90°
Let ∠BAC = θ be an acute angle and let P be a point on its side AB. Draw PM ⊥ AC.
It is evidence from ΔPMA, that as becomes smaller and smaller, line segment PM also becomes smaller and smaller, and finally when θ becomes 0°, the point P will coincide with M. Consequently, we have,
PM = 0, AP = AM


(Not defined)
From ΔPMA, it is evident that as θ increases, the line segment AM becomes smaller and smaller and finally when θ becomes 90°, the point M will coincide A. Consequently, we have
AM = 0, AP = PM

Table of Values of Trigonometric ratios of 0°, 30°, 45°, 60° and 90°
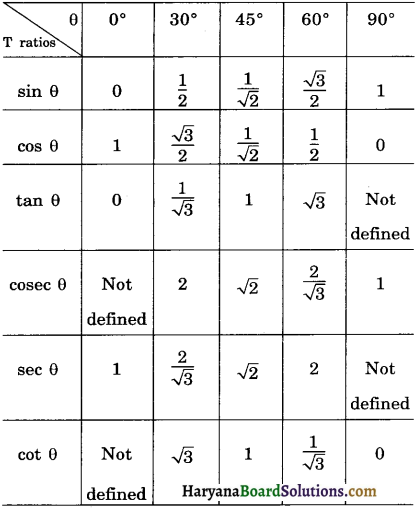
![]()
Trigonometric Ratios of Complementary Angles
Complementary Angles: Two angles are said to be complementary, if their sum is 90°.
Thus, θ and (90° – θ) are complementary angles.
Trigonometric Ratios of Complementary Angles:
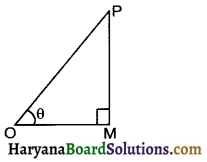
Consider a ΔOMP such that ∠M = 90°, ∠POM = 0.
Then, ∠OPM = (90° – θ) is its o complementary angle.
For the reference angle θ, we have
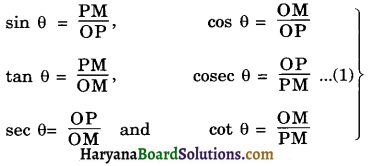
For the reference angle (90° – θ), we have
Base = PM, Perpendicular = OM and Hypotenuse = OP.

From (1) and (2), we get
sin (90° – θ) = cos θ
cos (90° – θ) = sin θ
tan (90° – θ) = cot θ
cosec (90° – θ) = sec θ
sec (90° – θ) = cosec θ
cot (90° – θ) = tan θ
Trigonometric Identities
An equation involving trigonometric ratios of an angle is called a trigonometric identity, if it is true for all values of the angles involved.
Fundamental Trigonometric Identities
1. sin2 θ + cos2 θ = 1
2. sec2 θ = 1 + tan2 θ
3. cosec2 θ = 1 + cot2 θ
In right ΔABC, right angled at B, we have
BC2 + AB2 = AC2 ……(1) [By Pythagoras theorem]
1. Dividing each term of (1) by AC2, we get
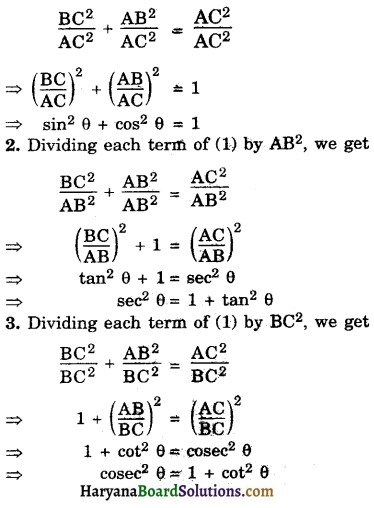
These fundamental identities can be expressed in the following forms:
(i) sin2 θ = 1 – cos2 θ
or sin θ = \(\sqrt{\left(1-\cos ^2 \theta\right)}\)
(ii) cos2 θ = 1 – sin2 θ
or cos θ = \(\sqrt{\left(1-\sin ^2 \theta\right)}\)
(iii) sec2 θ – tan2 θ = 1
(iv) tan2 θ = sec2 θ – 1
or tan θ = \(\sqrt{\sec ^2 \theta-1}\)
(v) cosec2 θ – cot2 θ = 1
(vi) cot2 θ = cosec2 θ – 1
or cot θ = ![]()