HBSE 8th Class Science Solutions Chapter 4 पदार्थ: धातु और अधातु
Haryana State Board HBSE 8th Class Science Solutions Chapter 4 पदार्थ: धातु और अधातु Textbook Exercise Questions and Answers.
Haryana Board 8th Class Science Solutions Chapter 4 पदार्थ: धातु और अधातु
HBSE 8th Class Science पदार्थ: धातु और अधातु InText Questions and Answers
पहेली बूझो
(पृष्ठ संख्या – 47)
प्रश्न 1.
क्या कॉपर में भी जंग लगता है? मैंने कॉपर के बर्तनों की सतह पर हरा पदार्थ जमा हुआ देखा है ?
उत्तर:
जब कॉपर के बर्तन को लम्बे समय तक नम वायु में खुला रखा जाता है तो उस पर एक हल्की हरी परत जम जाती है। यह हरा पदार्थ कॉपर हाइड्रॉक्साइड [Cu(OH)2] और कॉपर कार्बोनेट [CuCO3] का मिश्रण होता है। अभिक्रिया निम्नलिखित है –
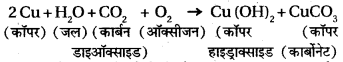
(पृष्ठ संख्या – 52)
प्रश्न 2.
मैंने सुना है पौधों में मैग्नीशियम पाया जाता है। यह उनमें किस रूप में पाया जाता है?
उत्तर :
पौधों में मैग्नीशियम, मैग्नीशियम ऑक्साइड के रूप में पाया जाता है। प्रश्न 3. डॉक्टर ने मेरे शरीर में आयरन की कमी बताई है। मेरे शरीर में आयरन कहाँ है ? (पृष्ठ संख्या-52) उत्तर : आयरन, शरीर के रक्त में पाया जाता है । मानव शरीर का अधिकांश आयरन लाल रक्त कोशिकाओं में पाया जाता है।
![]()
HBSE 8th Class Science संश्लेषित रेशे और प्लास्टिक Textbook Questions and Answers
प्रश्न 1.
निम्नलिखित में से किसको पीटकर पतली चादरों में परिवर्तित किया जा सकता है ?
(क) जिंक
(ख) फॉस्फोरस
(ग) सल्फर
(घ) ऑक्सीजन।
उत्तरः
(क) जिंक ।
प्रश्न 2.
निम्नलिखित में से कौन-सा कथन सही है ?
(क) सभी धातुएँ तन्य होती हैं।
(ख) सभी अधातुएँ तन्य होती हैं।
(ग) सामान्यतः धातुएँ तन्य होती हैं।
(घ) कुछ अधातुएँ तन्य होती हैं।
उत्तर :
(ग) सामान्यतः धातुएँ तन्य होती हैं।
प्रश्न 3.
रिक्त स्थानों की पूर्ति कीजिए –
(क) फॉस्फोरस बहुत …………………… अधातु है।
(ख) धातुएँ ऊष्मा और …………………… की …………………… होती हैं।
(ग) आयरन, कॉपर की अपेक्षा …………………… अभिक्रियाशील है।
(घ) धातुएँ, अम्लों से अभिक्रिया कर …………………… गैस बनाती हैं।
उत्तर:
(क) अभिक्रियाशील
(ख) विद्युत, सुचालक
(ग) अधिक
(घ) हाइड्रोजन ।
![]()
प्रश्न 4.
यदि कथन सही है तो ‘T’ और यदि गलत है तो कोष्ठक में ‘F’ लिखिए-
(क) सामान्यतः अधातु अम्लों से अभिक्रिया करते हैं।
(ख) सोडियम बहुत अभिक्रियाशील धातु है।
(ग) कॉपर, जिंक सल्फेट के विलयन से जिंक विस्थापित करता है।
(घ) कोयले को खींचकर तारें प्राप्त की जा सकती हैं।
उत्तर:
(क) सामान्यतः अधातु अम्लों से अभिक्रिया करते हैं। (F)
(ख) सोडियम बहुत अभिक्रियाशील धातु है। (T)
(ग) कॉपर, जिंक सल्फेट के विलयन से जिंक विस्थापित करता है। (F)
(घ) कोयले को खींचकर तारें प्राप्त की जा सकती हैं। (F)
प्रश्न 5.
नीचे दी गई सारणी में गुणों की सूची दी गई है । इन गुणों के आधार पर धातुओं और अधातुओं में अन्तर कीजिए
उत्तर:
| क्र. गुण | धातु | अधातु |
| 1. दिखावट | चमकीली | विभिन्न रंगों में |
| 2. कठोरता | कक्ष ताप पर ठोस और कठोर | कक्ष ताप पर ठोस, तरल और गैस तथा भुरभुरी |
| 3. आघातवर्धनीयता | आघातवर्धनीय होती हैं। पीटकर शीटें बनाई जा सकती हैं | भगुर होती है, चोट मारने पर टूट जाती है |
| 4. तन्यता | खींचकर तार बनाया जा सकता है। | यह अतन्य होती हैं। |
| 5. ऊष्माचालन | उपस्थिति | अनुपस्थित |
| 6. विद्युतचालन | विद्युत चालक होती हैं। | ग्रेफाइट को छोड़कर सभी कुचालक होती हैं। |
प्रश्न 6.
निम्नलिखित के लिए कारण दीजिए –
(क) ऐलुमिनियम की पन्नी का उपयोग खाद्य सामग्री को लपेटने में किया जाता है।
(ख) निमज्जन छड़ें (इमरशन रॉड) धात्विक पदार्थों से निर्मित होती हैं।
(ग) कॉपर, जिंक को उसके लवण के विलयन से = विस्थापित नहीं कर सकता ।
(घ) सोडियम और पोटैशियम को मिट्टी के तेल में रखा जाता है।
उत्तर:
(क) अन्य धातुओं की अपेक्षा धातुएँ अधिक आघातवर्धनीय होती हैं । इसलिए ऐलुमिनियम की पतली चादरें (शीट) बनाई जा सकती हैं । साथ ही एल्युमिनियम संक्षारण विरोधी धातु भी है। इस कारण ऐलुमिनियम की पन्नी का प्रयोग खाद्य सामग्री लपेटने में किया जाता है।
(ख) धातुएँ ऊष्मा और विद्युत दोनों की सुचालक होती हैं। इसलिए निमन्जन छड़ें धातुओं की बनाई जाती हैं।
(ग) कॉपर, जिंक से कम सक्रिय होता है और सिर्फ अधिक अभिक्रियाशील ही कम अभिक्रियाशील को विस्थापित कर सकता है। इसलिए उसे विस्थापित नहीं कर सकता ।
(घ) सोडियम और पोटैशियम दोनों अधिक क्रियाशील धातुएँ हैं । ये वातावरण और जल के साथ काफी तीव्रता से क्रिया करती हैं और जल उठती हैं । इसलिए वायु तथा नमी से अलग रखने के लिए इन्हें मिट्टी के तेल में रखा जाता है।
![]()
प्रश्न 7.
क्या आप नींबू के अचार को ऐलुमिनियम के पात्र में रख सकते हैं । स्पष्ट करिए ।
उत्तर:
नहीं । नींबू के अचार में सिट्रिक अम्ल होता है, जिससे इसकी प्रकृति अम्लीय होती है । अम्लीय पदार्थ ऐलुमिनियम पात्रों में संचित नहीं किए जाते, क्योंकि अम्ल और ऐलुमिनियम अभिक्रिया करके विषैला पदार्थ बनाते हैं, जो स्वास्थ्य विरोधी होते हैं।
प्रश्न 8.
नीचे दी गई सारणी के कॉलम ‘I’ में कुछ पदार्थ दिये गये हैं । कॉलम II’ में उनके कुछ उपयोग दिये गये हैं। कॉलम ‘I’ के पदार्थ का कॉलम ‘II’ से सही मिलान करिए –
| कॉलम – I | कॉलम – II |
| 1. गोल्ड | 1. थर्मामीटर |
| 2. आयरन | 2. बिजली के तार |
| 3. ऐलुमिनियम | 3. खाद्य सामग्री लपेटना |
| 4. कार्बन | 4. आभूषण |
| 5.कॉपर | 5. मशीनें |
| 6. मर्करी | 6. ईधन |
उत्तर:
| कॉलम – I | कॉलम – II |
| 1. गोल्ड | 4. आभूषण |
| 2. आयरन | 5. मशीनें |
| 3. ऐलुमिनियम | 3. खाद्य सामग्री लपेटना |
| 4. कार्बन | 6. ईधन |
| 5.कॉपर | 2. बिजली के तार |
| 6. मर्करी | 1. थर्मामीटर |
प्रश्न 9.
क्या होता है जब –
(क) तनु सल्फ्यूरिक अम्ल कॉपर प्लेट पर डाला जाता है?
(ख) लोहे की कील, कॉपर सल्फेट के विलयन में रखी जाती है? संबंधित अभिक्रियाओं के शब्द समीकरण लिखिए।
उत्तर:
(क) जब तनु सल्फ्यूरिक अम्ल कॉपर प्लेट पर डाला जाता है तो कॉपर सल्फेट जल तथा सल्फर डाइ ऑक्साइड उत्पन्न होती है ।
Cu + 2H2SO4 → CusO4+ 2H2O↑+SO2
(ख) आयरन, कॉपर सल्फेट विलयन से कॉपर को विस्थापित कर देता है. यह आयरन सल्फेट तथा कॉपर बनाता है।
CuSO4 + Fe → FeSO4+Cu
प्रश्न 10.
सलोनी ने लकड़ी के कोयले का जलता हुआ टुकड़ा लिया और उससे उत्सर्जित होने वाली गैस को एक परखनली में इकट्ठा किया –
(क) वह गैस की प्रकृति कैसे ज्ञात करेगी ?
(ख) इस प्रक्रम में होने वाली सभी अभिक्रियाओं के शब्द समीकरण लिखिए।
उत्तर:
(क) गैस की प्रकृति लाइम जल (चूने का पानी) या जलती हुई माचिस की तीली से ज्ञात की जा सकती है । चूने का पानी दूधिया हो जायेगा या माचिस की तीली बुझ जाएगी।
(ख) C + O2(g) → CO2(g)
कार्बन ऑक्सीजन कार्बन डाई ऑक्साइड
![]()
प्रश्न 11.
एक दिन रीता अपनी माँ के साथ आभूषण विक्रेता की दुकान पर गई । उसकी माँ ने सुनार को पॉलिश करने हेतु सोने के पुराने आभूषण दिए । अगले दिन जब वे आभूषण वापस लाईं तो उन्होंने पाया कि उनका भार कुछ कम हो गया है । क्या आप भार में कमी का कारण बता सकते हैं ?
उत्तर:
सुनार आभूषण साफ करने के लिए एक्वारीजिया (Aquaregia) नामक’ विलयन का उपयोग करते हैं क्योंकि सोना इस विलयन में घुल जाता है, इसलिए सोने के भार में कमी आ जाती है । एक्वारीजिया हाइड्रोक्लोरिक अम्ल (HCl) के तीन भाग तथा नाइट्रिक अम्ल (HNO3) के एक भाग को मिलाकर बनाया जाता है ।
HBSE 8th Class Science संश्लेषित रेशे और प्लास्टिक Important Questions and Answers
बहुविकल्पीय प्रश्न
1. कॉपर के बर्तन पर जमने वाली हरी पर्त होती है?
(अ) कॉपर हाइड्रॉक्साइड
(ब) कॉपर कार्बोनेट
(स) कॉपर हाइड्रॉक्साइड एवं कॉपर कार्बोनेट का मिश्रण
(द) इनमें से कोई नहीं ।
उत्तर:
(स) कॉपर हाइड्रॉक्साइड एवं कॉपर कार्बोनेट का मिश्रण
2. जो धातु ध्वनियाँ उत्पन्न करते हैं, उन्हें कहते हैं
(अ) गाने वाली धातु
(ब) ध्वनि स्रोत
(स) ध्वानिक
(द) इनमे से कोई नहीं ।
उत्तर:
(स) ध्वानिक
3. ऐसी धातु जो कमरे के तापमान पर द्रव है-
(अ) पोटैशियम
(ब) लोहा
(से) सोडियम
(द) पारा (मर्करी) ।
उत्तर:
(द) पारा (मर्करी) ।
4. निम्न में आघातवर्धनीय नहीं है
(अ) लोहा
(ब) ताँबा
(स) सोना
(द) कोयला।
उत्तर:
(द) कोयला।
5. वह अधातु जो वायु में खुला रखने पर आग पकड़ लेती है, वह है –
(अ) सोडियम
(ब) पोटैशियम
(स) जिंक
(द) फॉस्फोरस।
उत्तर:
(द) फॉस्फोरस।
![]()
रिक्त स्थान पूर्ति
(क) धातुओं का गुण जिसके कारण उन्हें पीटकर शीट में …………………. परिवर्तित किया जा सकता है, …………………. कहलाता है।
(ख) अधातु ऊष्मा तथा विद्युत के …………………. हैं।
(ग) सल्फ्यूरस अम्ल नीले लिटमस पत्र को …………………. कर देता है।
(घ) जिंक, कॉपर और आयरन से …………………. अभिक्रियाशील है।
उत्तर:
(क) आघातवर्धनीयता
(ख) कुचालक
(ग) लाल
(घ) अधिक।
सुमेलन
| कॉलम – I | कॉलम – II |
| (i) जिंक सल्फेट | (क) Cu(OH)2 |
| (ii) कॉपर सल्फेट | (ख) FeSO4 |
| (iii) आयरन सल्फेट | (ग) ZnSO4 |
| (iv) कॉपर हाइड्राक्साइड | (घ) CuSO4 |
उत्तर:
| कॉलम – I | कॉलम – II |
| (i) जिंक सल्फेट | (ग) ZnSO4 |
| (ii) कॉपर सल्फेट | (घ) CuSO4 |
| (iii) आयरन सल्फेट | (ख) FeSO4 |
| (iv) कॉपर हाइड्राक्साइड | (क) Cu(OH)2 |
![]()
सत्य / असत्य कथन
(क) धातुओं का वह गुण जिससे उन्हें खींचकर तारों में परिवर्तित किया जा सकता है, तन्यता कहलाता है।
(ख) ऐलुमिनियम एक अधातु है।
(ग) फॉस्फोरस एक अधातु है।
(घ) अधातुओं के ऑक्साइड अम्लीय प्रकृति के होते
उत्तर:
(क) सत्य
(ख) असत्य
(ग) सत्य
(घ) सत्य।
अति लघु उत्तरीय प्रश्न
प्रश्न 1.
आघातवर्धनीयता से आप क्या समझते हैं ?
उत्तर:
धातुओं का वह गुण जिसके कारण उन्हें पीटकर चादरें (शीटें) बनाई जाती हैं, आघातवर्धनीयता कहलाती है।
प्रश्न 2.
तन्यता की परिभाषा लिखिए।
उत्तर:
धातुओं का वह गुण जिसके कारण उनके तार खींचे जा सकते हैं, तन्यता कहलाती है।
प्रश्न 3.
किन धातुओं से विद्युत तार बनाये जाते हैं?
उत्तर:
कॉपर (तांबा), ऐलुमिनियम ।
प्रश्न 4.
आभूषण बनाने में स्वर्ण (गोल्ड) को वरीयता क्यों दी जाती है ?
उत्तर:
स्वर्ण (गोल्ड) मुलायम होने के कारण आसानी से सांचे में ढाला जा सकता है ।
प्रश्न 5.
धातुओं का प्रयोग मशीनें बनाने में क्यों होता है?
उत्तर:
धातुएँ कठोर होती हैं और अधिक तापमान पर अपना अस्तित्व बनाये रखती हैं।
![]()
प्रश्न 6.
धातुओं को लोहार किस प्रकार ढालता है?
उत्तर
लोहार धातुओं को अपनी भट्टी में रक्ततप्त गर्म करके हथौड़े से प्रहार कर ढालता है।
प्रश्न 7.
वो ऐसी धातुएँ जिन्हें चाकू से सरलतापूर्वक काटा जा सकता है, उन्हें लिखिए
उत्तर;
(i) पोटैशियम
(ii) सोडियम
प्रश्न 8.
धातुएँ आभूषणों में क्यों उपयोगी होती हैं?
उत्तर:
धात्विक चमक के गुण के कारण ।
प्रश्न 9.
थर्मामीटर में कौन-सी धातु का प्रयोग होता है?
उत्तर:
मरकरी (पारा) ।
प्रश्न 10.
सल्फ्यूरस अम्ल का लिटमस पत्र पर क्या प्रभाव पड़ता है?
उत्तर:
सल्फ्यूरस अम्ल नीले लिटमस पत्र को लाल कर देता है।
प्रश्न 11.
फॉस्फोरस को वायु में खुला रखने पर इस पर क्या प्रभाव पड़ता है?
उत्तर;
फॉस्फोरस को वायु में खुला रखने पर यह आग पकड़ लेता है।
प्रश्न 12.
धातु की सोडियम हाइड्रॉक्साइड से अभिक्रिया करने पर कौन सी गैस उत्पन्न होती है?
उत्तर:
हाइड्रोजन गैस।
![]()
प्रश्न 13.
ताँबे की छीलन को आयरन सल्फेट विलयन में डालने पर क्या होता है?
उत्तर:
कोई अभिक्रिया नहीं होती क्योंकि ताँबा आयरन की अपेक्षा कम अभिक्रियाशील होता है।
प्रश्न 14.
एक लोहे की कील को जिंक सल्फेट के विलयन में डालने पर क्या होता है? ।
उत्तर:
कोई क्रिया नहीं होती।।
प्रश्न 15.
आयरन की जंग के विलयन का लिटमस पत्र पर क्या प्रभाव पड़ता है? इस विलयन की प्रकृति बताइए।
उत्तर:
आयरन की जंग की विलयन लाल लिटमस पत्र को नीला कर देता है अर्थात आयरन की जंग (जलीय आयरन आक्साइड) का विलयन क्षारीय प्रकृति का है।
प्रश्न 16.
जल को शुद्ध करने में किस अधातु का प्रयोग किया जाता है?
उत्तर:
अजान ।
![]()
लघु उत्तरीय प्रश्न
प्रश्न 1.
धातु एवं अधातु शब्दों को परिभाषित कीजिए।
उत्तर:
धातु : वे पदार्थ जो कठोर, आघातवर्ध्य, तन्य, व विद्युत के सुचालक होते हैं. धात कहलाते हैं। जैसे – आयरन, कॉपर, ताँबा आदि ।
अधातु : वे पदार्थ जो दिखने में मलिन एवं नरम होते हैं तथा हथौड़े के प्रहार से टूटकर चूरा हो जाते हैं तथा ऊष्मा व विद्युत के कुचालक होते हैं, अधातु कहलाते हैं। जैसे – कोयला, सल्फर, ऑक्सीजन, फॉस्फोरस आदि ।
प्रश्न 2.
विभिन्न पदार्थों की आधातवर्धनीयता निर्धारित कीजिए- लोहे की कील, कोयले का टुकड़ा, ऐलुमिनियम की तार एवं पेंसिल लेड। (क्रियाकलाप)
उत्तर:
(i) लोहे की कील को हथौड़े से पीटने पर वह चपटी हो गयी, अर्थात् यह आघातवर्धनीयता है।
(ii) कोयले के टुकड़े को हथौड़े से पीटने पर इसके टुकड़े – हो गये अर्थात् यह आघातवर्धनीयता नहीं है।
(iii) ऐलुमिनियम के तार को हथौड़े से पीटने पर यह चपटा . हो गया अर्थात् यह आघातवर्धनीयता है।
(iv) पेंसिल लेड को हथौड़े से पीटने पर इसके टुकड़े हो गये अर्थात् यह आघातवर्धनीयता नहीं हैं।
प्रश्न 3.
निम्नलिखित पदार्थों की विद्युत चालकता बताइएलोहे की छड़/कील, गंधक, कोयला एवं ताँबे के तार (क्रियाकलाप)
उत्तर:
| पदार्थ | सुचालक/कुचालक |
| लोहे की छड़/कील | सुचालक |
| गंधक | कुचालक |
| कोयला | कुचालक |
| ताँबे की तार | कुचालक |
प्रश्न 4.
धातुएँ ध्वानिक होती हैं। इसे स्पष्ट कीजिए।
उत्तर:
धातुओं को जब कठोर सतह से टकराया जाता है तो एक निनाद ध्वनि उत्पन्न होती है, जैसे दो बर्तनों को बजाने पर ध्वनि उत्पन्न होती है । अतः धातु गायन ध्वानियाँ उत्पन्न करते हैं । इसी कारण से धातुओं को ध्वानिक कहते हैं।
प्रश्न 5.
चांदी के आभूषण कुछ समय बाद काले क्यों हो जाते हैं ? जबकि चाँदी ऑक्सीजन के साथ आसानी से अभिक्रिया नहीं करती।।
उत्तर:
चाँदी ऑक्सीजन के साथ अभिक्रिया नहीं करती, परन्तु यह वायु में उपस्थित सल्फर यौगिकों से अभिक्रिया करके सिल्वर सल्फाइड की काली परत बनाती है । इसी कारण चांदी से निर्मित आभूषण कुछ समय बाद काले पड़ने लगते हैं।
![]()
प्रश्न 6.
सल्फर व ऑक्सीजन की अभिक्रिया के बारे में बताइए। (क्रियाकलाप)
उत्तर:
सल्फर एवं ऑक्सीजन की अभिक्रिया होने पर सल्फर डाईऑक्साइड गैस बनती है । जब सल्फर डाई ऑक्साइड को जल में विलेय करते हैं तो सल्फ्यूरस अम्ल प्राप्त होता है, अभिक्रिया निम्नवत् है –
सल्फर डाईऑक्साइड (SO2) + जल (H2O) → सल्फ्यूरस अम्ल (H2SO3)
सल्फ्यूरस अम्ल नीले लिटमस पत्र को लाल कर देता है । सामान्यत: अधातुओं के ऑक्साइड अम्लीय प्रकृति के होते हैं।
प्रश्न 7.
क्या धातु एवं अधातु जल के साथ क्रिया करते हैं ? स्पष्ट कीजिए। उत्तर-धातुओं की जल के साथ क्रिया-कुछ धातु जैसे-सोडियम जल के साथ तीव्र अभिक्रिया करते हैं जिससे सोडियम ऑक्साइड बनता है, किन्तु अधिकतर धातुओं की जल के साथ क्रिया नहीं होती है । आयरन जल के साथ बहुत धीमी क्रिया करता है । अधातुओं की जल से क्रिया- सामान्य रूप से जल व अधातु की अभिक्रिया नहीं होती है इसीलिए कुछ अधातु जो वायु में सक्रिय हो जाती हैं, उन्हें जल में रखा जाता है। जैसे – फॉस्फोरस एक अत्यन्त सक्रिय अधातु है जिसे जल में रखा जाता है।
प्रश्न 8.
धातुओं व अम्लों की अभिक्रिया किस प्रकार होती है ?
उत्तर:
धातुएँ सामान्यतया अम्लों के साथ अभिक्रिया करके हाइड्रोजन गैस उत्पन्न करती हैं । इसके परीक्षण के लिए यदि इस गैस को जलाया जाता है तो यह पॉप ध्वनि के साथ जलती है। सामान्यतया अधातुओं की अम्लों के साथ अभिक्रिया नहीं होती है । धातुओं के साथ अम्ल निम्न प्रकार अभिक्रिया करते हैं –
![]()
प्रश्न 9.
सोडियम धातु जल से किस प्रकार अभिक्रिया करता है? इसके विलयन का लिटमस पत्र पर क्या प्रभाव पड़ता है। इस विलयन की प्रकृति बताइए। (क्रियाकलाप)
उत्तर- सोडियम अत्यधिक क्रियाशील धातु है, यह जल के साथ क्रिया करके ऊष्मा उत्पन्न करता है एवं सोडियम ऑक्साइड बनाता है। इसका विलयन लाल लिटमस पत्र को नौला कर देता है। यह विलयन क्षारीय होता है।
प्रश्न 10.
किसी धातु जैसे ऐलुमिनियम के टुकड़े को सोडियम हाइड्रॉक्साइड के विलयन में डालने पर कौन-सी गैस उत्पन्न होती है? इसका निर्धारण हम किस प्रकार कर सकते है? (क्रियाकलाप)
उत्तर:
इस अभिक्रिया में हाइड्रोजन गैस उत्पन्न होती है। इसका निर्धारण हम परखनली के मुँह के निकट एक जलती हुई माचिस की तीली ले जाकर करते है, जिसकी पॉप ध्वनि उत्पन्न होती है। यह ध्वनि हाइड्रोजन गैस की उपस्थिति दर्शाती है।
![]()
प्रश्न 11.
यदि कॉपर सल्फेट के विलयन में जिंक का टुकड़ा छड़ डाला जाए, तो क्या होगा?
उत्तर:
जिंक कॉपर की अपेक्षा अधिक अभिक्रियाशील होने के कारण कॉपर को उसके लवणीय विलयन में से विस्थापित कर देता है।
Zn + CuSO4 → ZnSO4 + Cu
प्रश्न 12.
अधातुएँ किस उपयोग में आती हैं ?
उत्तर:
अधातुओं के कुछ उपयोग-
1. अधातुएँ जल शुद्धिकरण में प्रयोग होती हैं ।
2. अधातुएँ औषधि निर्माण में प्रयुक्त होती हैं ।
3. अधातुएँ पटाखे आदि बनाने में प्रयुक्त होती हैं ।
4. अधातुओं का प्रयोग उर्वरकों में भी होता है, जो पौधों की वृद्धि में सहायक हैं।
प्रश्न 13.
धातुओं के प्रमुख उपयोग लिखिए ।
उत्तर:
धातुओं के प्रमुख उपयोग निम्नवत् हैं –
1. धातुओं का उपयोग मशीनों, कारों, रेलगाड़ियों आदि में किया जाता है ।
2. इनका उपयोग बॉयलर में किया जाता है।
3. उपग्रह निर्माण में इनका उपयोग होता है ।
4. औद्योगिक साजो सामान, खाना बनाने के पात्रों में इनका उपयोग किया जाता है।
प्रश्न 14.
यदि कॉपर सल्फेट के विलयन में एक लोहे की कील डाली जाए तो क्या होगा?
उत्तर:
लोहा (Fe) कॉपर की अपेक्षा अधिक अभिक्रिया होने के कारण कॉपर को उसके लवणीय विलयन से विस्थापित कर देता है एवं विलयन का रंग लाल हो जाता है।
Fe + CuSO → FeSO4 + Cu
प्रश्न 15.
यदि जिंक सल्फेट के विलयन में ताँबे की कील डाली जाए, तो क्या होगा?
उत्तर:
ताँबा (Cu) जिंक की अपेक्षा कम अभिक्रियाशील होता है अत: इसमें कोई क्रिया नहीं होती।
![]()
दीर्घ उत्तरीय प्रश्न
प्रश्न 1.
धातुओं एवं अधातुओं में अन्तर स्पष्ट कीजिए।
उत्तर:
धातु एवं अधातु में अन्तर-
| धातुएँ | अधातुएँ |
| 1. धातुएँ ऊष्मा एवं विद्युत की सुचालक होती हैं। | 1. अधातुएँ ऊष्मा एवं विद्युत की कुचालक होती हैं (ग्रेफाइट को छोड़कर) |
| 2. धातुएँ चमकदार होती हैं एवं उन पर पॉलिश की जा सकती है। | 2. अधातुएँ सामान्यत: चमकदार नहीं होतीं एवं उन पर पॉलिश नहीं की जा सकती । |
| 3. धातुओं के गलनांक एवं क्वथनांक सामान्यत: निम्न होते हैं। | 3. अधातुओं के गलनांक एवं क्वथनांक अपेक्षाकृत उच्च होते हैं। |
| 4. धातुएँ आघातवर्धनीय तथा तन्य होती हैं। | 4. अधातुएँ आघातवर्धनीय एवं तन्य नहीं होती हैं। |
| 5. धातुएँ क्षारीय ऑक्साइड बनाती हैं। | 5. अधातुएँ अम्लीय या उदासीन ऑक्साइड बनाती हैं। |
| 6. धातुएँ ठोस होती है। (मर्करी को छोड़कर, मर्करी एक द्रव धातु है) | 6. अधातुएँ ठोस, द्रव एवं गैस हो सकती हैं। |
प्रश्न 2.
धातुओं एवं अम्लों की अभिक्रियाएँ कैसे होती हैं, समझाइए।
उत्तर:
सक्रिय धातुएँ जैसे जिक, मैग्नीशियम, लोहा आदि अभिक्रियाशील श्रृंखला में हाइड्रोजन से ऊपर स्थित हैं, तनु हाइड्रोक्लोरिक और सल्फ्यूरिक अम्ल जैसे खनिज अम्लों से अभिक्रिया करके हाइड्रोजन का विस्थापन करती हैं –
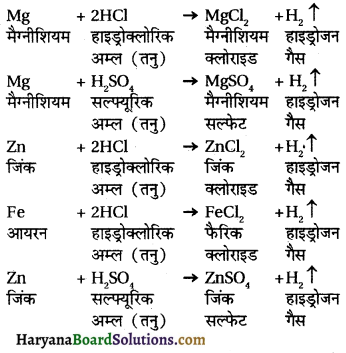
ऐसी धातुएँ जो हाइड्रोजन के नीचे स्थित हैं, तनु खनिज अम्लों के साथ हाइड्रोजन का विस्थापन नहीं करतीं । उदाहरणार्थ : कॉपर तनु HCl के साथ कोई भी अभिक्रिया नहीं करता ।
![]()
प्रश्न 3.
निम्नलिखित थातु एवं अधातु तनु Hcl एवं तनु H2SO, से सामान्य ताप पर एवं गर्म करने पर अभिक्रिया करते हैं अथवा नहीं, बताइए।
उत्तर:
धातु और अधातुओं की अम्लों से अभिक्रिया निम्न प्रकार होती है-
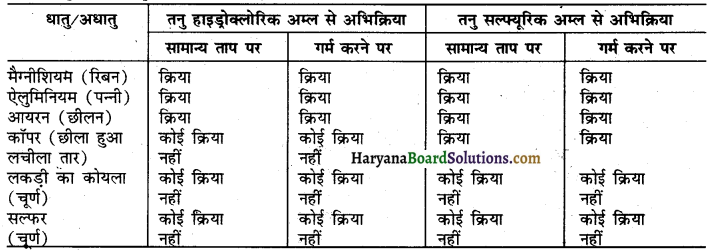
अधातु सामान्यत: अम्लों से अभिक्रिया नहीं करते, परन्तु धातु अम्लों से अभिक्रिया करते हैं, और हाइड्रोजन गैस उत्पन्न करते हैं, जो ‘पॉप’ ध्वनि के साथ जलती है । कॉपर तनु हाइड्रोक्लोरिक अम्ल से गर्म करने पर भी अभिक्रिया नहीं करता । परन्तु यह सल्फ्यूरिक अम्ल से अभिक्रिया कर लेता है।
पदार्थ: धातु और अधातु Class 8 HBSE Notes in Hindi
→ आघातवर्धनीयता (Malleability) :- धातुओं का वह गुण जिसके कारण उन्हें पीटकर शीट (चादर) में परिवर्तित किया जा सके ।
→ चालकता (Cunductance) :- धातुओं का वह गुण जिसके द्वारा ऊष्मा या विद्युत का चालन हो सके ।
→ तन्यता (Ductility) :- धातुओं का वह गुण जिससे उन्हें खींचकर तारों में परिवर्तित किया जा सके ।
→ ध्वानिक (Sonorus) :- धातुओं का वह गुण जिससे वे टकराने पर ध्वनि उत्पन्न करते हैं ।
→ चमकीलापन (Lustre) :- पदार्थों में चमकती सतह का गुण ।
→ धातु (Metal) :- वे पदार्थ जो ऊष्मां और विद्युत के सुचालक हैं, धातु कहलाते हैं।
→ अधातु (Non-metal) :- वे पदार्थ जो ऊष्मा और विद्युत के कुचालक हैं, अधातु कहलाते हैं।
→ अम्लीय ऑक्साइड (Acidic oxide) :- अधातुओं के ऑक्साइड, जिन्हें जल में घोलकर अम्ल बनाते हैं।
→ क्षारीय ऑक्साइड (Basic oxide) :- धातुओं के ऑक्साइड, जिन्हें जल में घोलकर क्षार बनाते हैं।
HBSE 8th Class Science Solutions Chapter 4 पदार्थ: धातु और अधातु Read More »