HBSE 8th Class Maths Solutions Chapter 6 वर्ग और वर्गमूल Ex 6.4

Haryana State Board HBSE 8th Class Maths Solutions Chapter 6 वर्ग और वर्गमूल Ex 6.4 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 6 वर्ग और वर्गमूल Ex 6.4

प्रश्न 1.
निम्नलिखित संख्याओं का वर्गमूल, भाग विधि से ज्ञात कीजिए
(i) 2304
(ii) 4489
(iii) 3481
(iv) 529
(v) 3249
(vi) 1369
(vii) 5776
(viii) 7921
(ix) 576
(x) 1024
(xi) 3136
(xii) 900
हल:
भाग विधि द्वारा संख्याओं का वर्गमूल ज्ञात करना|

(i) 2304 ⇒

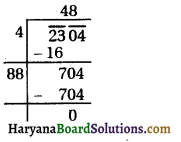
∴ √2304 = 48

(ii) 4489

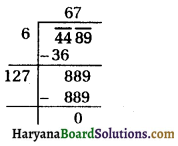
∴ √4489 = 67

(iii) 3481

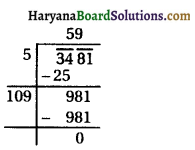
∴ √3481 = 59

(iv) 529

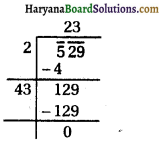
∴ √529 = 23

(v) 3249

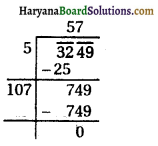
∴ √3249 = 57

(vi) 1369

∴ √1369 = 37

(vii) 5776

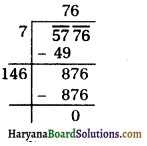
∴ √5776 = 76

(viii) 7921

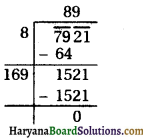
∴ √7921 = 89

(ix) 576

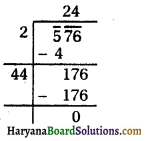
∴ √576 = 24

(x) 1024

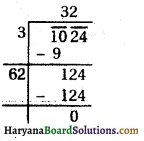
∴ √1024 = 32

(xi) 3136

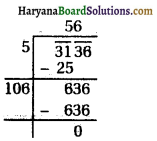
∴ √3136 = 56

(xii) 900

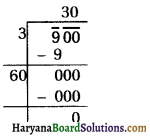
∴ √900 = 30

प्रश्न 2.
निम्नलिखित संख्याओं में से प्रत्येक के वर्गमूल के अंक ज्ञात कीजिए । (बिना गणना के)।
(i) 64
(ii) 144
(iii) 4489
(iv) 27225
(v) 390625
हल:
(i) 64 – संख्या में बार लगाने पर \(\overline{64}\) – (1 बार)
इस संख्या में 1 बार है, अत: वर्गमूल 1 अक का होगा ।

(ii) 144 – संख्या में बार लगाने पर \(\overline{1}\) \( \overline{44}\) – (2 बार)
इस संख्या में 2 बार हैं, अतः वर्गमूल 2 अंक का होगा ।

(iii)4489 – संख्या में बार लगाने पर \(\overline{44}\) \(\overline{89}\) – (2 बार)
अत: वर्गमूल 2 अंक का होगा ।

(iv) 27225 – संख्या में बार लगाने पर \(\overline{2}\) \(\overline{72} \) \(\overline{25}\) – (3 बार)
अत: वर्गमूल 3 अंक का होगा ।

(v) 390625-संख्या में बार लगाने पर \(\overline{39}\) \( \overline{06}\) \(\overline{25}\) – (3 बार)
अत: वर्गमूल 3 अंक का होगा ।

प्रश्न 3.
निम्नलिखित देशमलव संख्याओं के वर्गमूल ज्ञात कीजिए
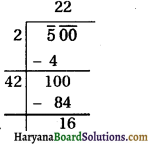
(i) 2.56
(ii) 7.29
(iii) 51.84
(iv) 42.25
(v) 31.36
हल:
(i) 2.56

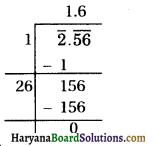
∴ √2.56 = 1.6

(ii) 7.29

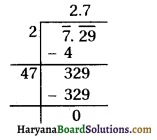
∴ √7.29 = 2.7

(iii) 51.84

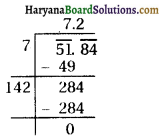
∴ √51.84 = 7.2

(iv) 42.25

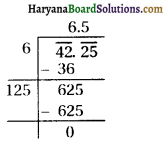
∴ √42.25 = 6.5

(v) 31.36

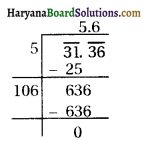
∴ √31.36 = 5.6

प्रश्न 4.
निम्नलिखित संख्याओं में से प्रत्येक में न्यूनतम संख्या क्या घटाई जाये कि एक पूर्ण वर्ग संख्या प्राप्त हो जाये । इस प्रकार प्राप्त पूर्ण वर्ग संख्याओं का वर्गमूल भी ज्ञात कीजिए।
(i) 402
(ii) 1989
(iii) 3250
(iv) 825
(v) 4000
हल :
(i) 402 का वर्गमूल ज्ञात करने पर हमें 2 शेषफल प्राप्त होता है।

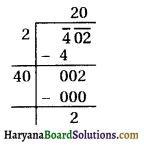
इसलिए (20)², 402 से 2 कम है।
यदि, संख्या से शेषफल (2) घटा की देते हैं, तो हमें पूर्ण वर्ग संख्या प्राप्त होती है।
∴ 402 – 2 = 400
∴ √400 = 20

(ii) 1989

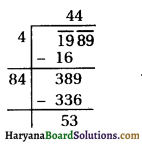
वर्गमूल ज्ञात करने पर-
53 शेषफल प्राप्त होता है।
अत: संख्या में से 53 घटायें,
तो एक पूर्ण वर्ग संख्या प्राप्त होगी ।
अत: 1989 – 53 = 1936
∴ √1936 = 44

(iii) 3250

वर्गमूल ज्ञात करने पर 1 शेषफल प्राप्त होता है।
अत: संख्या में से 1 घटायें,
तो एक पूर्ण वर्ग संख्या प्राप्त होगी ।
अत: 3250 – 1 = 3249
∴ √3249 = 55

(iv) 825

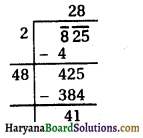
वर्गमूल ज्ञात करने पर 41 शेषफल प्राप्त होता है।
अत: संख्या में से 41 घटायें,
तो एक पूर्ण वर्ग संख्या प्राप्त होगी ।
अत: 825 – 41 = 784
∴ √784 = 28

(v) 4000

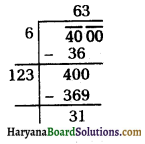
वर्गमूल ज्ञात करने पर 31 शेषफल प्राप्त होता है।
अत: संख्या में से 31 घटायें,
तो एक पूर्ण वर्ग संख्या प्राप्त होगी ।
अत: 4000 – 31 = 3969
∴ √3969 = 63

प्रश्न 5.
निम्नलिखित संख्याओं में से प्रत्येक में कम से कम कितना जोड़ा जाये कि एक पूर्ण वर्ग संख्या प्राप्त हो जाये । इस प्रकार प्राप्त पूर्ण वर्ग संख्याओं का वर्गमूल भी ज्ञात कीजिए।
(i) 525
(ii) 1750
(iii) 252
(iv) 1825
(v) 6412
हल :
(i) 525
525 का वर्गमूल ज्ञात करने पर शेषफल पर हम देखते हैं कि
(22)² < 525 < (23)².

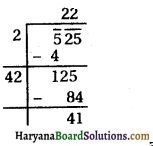
अतः, पूर्ण वर्ग बनाने के लिये कम से कम जोड़ी जाने वाली संख्या = (23)² -525
अत: अभीष्ट संख्या = 529 – 525 = 4
अतः प्राप्त पूर्ण वर्ग संख्या = 525 + 4 = 529
तथा, √1529 = 23

(ii) 1750
1750 का वर्गमूल ज्ञात करने पर यहाँ हम देखते हैं कि
(41)² < 1750 < (42)²

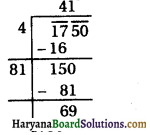
अतः पूर्ण वर्ग बनाने के लिए कम से कम जोड़ी जाने वाली संख्या = (42)²
= 1764 – 1750
= 14
अतः प्राप्त पूर्ण वर्ग संख्या = 1750 + 14 = 1764
तथा, √1764 = 42

(iii) 252
252 का वर्गमूल ज्ञात करने पर यहाँ पर हम देखते हैं कि
(15)² < 252 < (16)²

अतः पूर्ण वर्ग बनाने के लिए कम से कम जोड़ी जाने वाली संख्या = (16)² – 252
अत: अभीष्ट संख्या = (16)² – 252
= 256 – 252
= 4

अतः प्राप्त पूर्ण वर्ग संख्या = 252 +4
= 256
तथा, √256 = 16

(iv) 1825
1825 का वर्गमूल ज्ञात करने पर यहाँ पर हम देखते हैं कि
(42)² < 1825 < (43)²

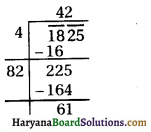
अतः पूर्ण वर्ग बनाने के लिए कम से कम जोड़ी जाने वाली संख्या = (43)² – 1825
अतः अभीष्ट संख्या = (43)² – 1825
= 1849 -1825 = 24
अतः प्राप्त पूर्ण वर्ग संख्या = 1825 + 24
= 1849
तथा, √1849 = 43

(v) 6412
80 यहाँ पर हम देखते हैं कि (80)² < 6412 < (81)²

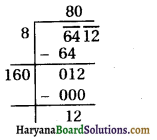
अत: पूर्ण वर्ग बनाने के लिए कम से कम जोड़ी जाने वाली संख्या = (81)² – 6412
= 6561 – 6412
= 149
अतः प्राप्त पूर्ण वर्ग संख्या = 6412 + 149
= 6561
तथा, √16561 = 81

प्रश्न 6.
किसी वर्ग की भुजा की लम्बाई ज्ञात करो जिसका क्षेत्रफल 441 m² है।।
हल:

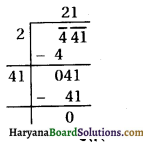
वर्ग का क्षेत्रफल = 441 m²
वर्ग की भुजा = √वर्ग का क्षेत्रफल
∴ भुजा = √441 – 21
∴ भुजा = 21 m

प्रश्न 7.
किसी समकोण त्रिभुज ABC में, ∠B = 90°.
(a) यदि AB = 6cm, BC = 8cm है, तो AC ज्ञात कीजिए।
(b) यदि, AC= 13 cm, BC = 5 cm है, तो AB ज्ञात कीजिए।
हल :

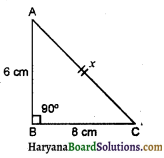
(a) AB = 6cm
BC = 8cm
AC = ? (x) माना
पाइथागोरस प्रमय स-
∴ AC² = AB² + BC²
x² = 6² + 8²
x² = 36 + 64
x² = 100
x = \(\sqrt {100}\) = 10 cm
∴ AC = 10 cm

(b) AC = 13 cm
BC = 5 cm
AB = ? (x) माना ।

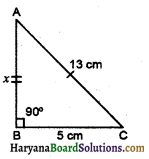
पाइथागोरस प्रमेय से
∴ AB² = AC² – BC²
x² = (13)² – (5)²
x² 169 – 25
x² 169 – 25
x² = 144
∴ x = \(\sqrt {144}\) = 12 cm
अत: AB = 12 cm

प्रश्न 8.
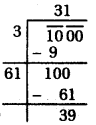
एक माली के पास 1000 पौधे हैं। इन पौधों को वह इस प्रकार लगाना चाहता है कि पंक्तियों की संख्या और कॉलम की संख्या समान रहे । इसके लिए कम से कम पौधों की संख्या ज्ञात कीजिए, जिसकी उसे आवश्यकता हो ।
हलः
माना, पंक्तियों की संख्या = x
कॉलम की संख्या = x

तब, कुल पौधों की संख्या = x × x
अब, x × x = 1000
x² = 1000
x = \(\sqrt {1000}\)
वर्गमूल करने पर 39 शेष आता है । अत: संख्या 1000 पूर्ण वर्ग नहीं है।
अतः (31)² < 1000 < (32)²
अतः कम से कम और पौधे चाहिए
= (32)² – 1000
= 1024 – 1000
= 24
अतः कम से कम 24 और पौधों की आवश्यकता होगी।

प्रश्न 9.
एक विद्यालय में 500 विद्यार्थी हैं, पी.टी. के अभ्यास के लिए इन्हें इस तरह से खड़ा किया गया कि पंक्तियों की संख्या कॉलम की संख्या के समान रहे। . इस व्यवस्था को बनाने में कितने विद्यार्थियों को बाहर जाना होगा?
हल:
माना पंक्तियों की संख्या = x
तथा कॉलम की संख्या = x

तब कुल विद्यार्थियों की संख्या = x × x
अतः x × x = 500
x² = 500
x = \(\sqrt {500 }\)
अत: वर्गमूल करने पर शेषफल 16 प्राप्त होता है ।
अत: इस व्यवस्था को बनाने के लिए 16 विद्यार्थी अतिरिक्त हैं।
अत: 16 विद्यार्थियों को बाहर जाना होगा।