Haryana State Board HBSE 9th Class Maths Solutions Chapter 9 Areas of Parallelograms and Triangles Ex 9.2 Textbook Exercise Questions and Answers.
Haryana Board 9th Class Maths Solutions Chapter 9 Areas of Parallelograms and Triangles Exercise 9.2
Question 1.
In figure 9.15, ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.

Solution:
In a parallelogram ABCD,
we have
AB = 16 cm, AE = 8 cm and CF = 10 cm
We know that
Area of parallelogram = base × height
= CD × AE
= AB × AE (∵ AB and CD are opposite sides of parallelogram or ||gm)
= 16 × 8
= 128 cm2
Again,
area of parallelogram = base × height
⇒ 128 = AD × CF [∵ AD is base and CF it’s corresponding height]
⇒ 128 = AD × 10
⇒ AD = \(\frac{128}{10}\) = 12.8 cm
Hence AD = 12.8 cm.
![]()
Question 2.
If E, F, G and H are respectively the mid points of the sides of a parallelogram ABCD, show that ar (EFGH) = \(\frac{1}{2}\)ar (ABCD).
Solution:
Join HF.
Since H and F are the mid points of AD and BC respectively.
AH = \(\frac{1}{2}\)AD and BF = \(\frac{1}{2}\)BC
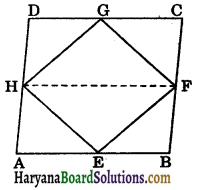
Now AD || BC and AD = BC
(opposite sides of ||gm)
⇒ AD || BC and \(\frac{1}{2}\)AD = \(\frac{1}{2}\)BC
⇒ AH || BF and AH = BF
⇒ ABFH is a parallelogram.
Since triangle EFH and parallelogram ABFH are on the same base FH and between the same parallels HF and AB.
∴ ar (ΔEFH) = \(\frac{1}{2}\)ar (||gm ABFH) ……(i)
Similarly, triangle GHF parallelogram CDHF are on the same base HF and between the same parallels CD and HF.
∴ ar (ΔGHF) = \(\frac{1}{2}\)ar (||gm CDHF) …….(ii)
Adding (i) and (ii), we get
ar (ΔEFH) + ar (ΔGHF) = \(\frac{1}{2}\)ar (||gm ABFH) + \(\frac{1}{2}\)ar (||gm CDHF)
⇒ ar (EFGH) = \(\frac{1}{2}\)[ar (||gr ABFH) + ar (||gm CDHF)
⇒ ar(EFGH) = \(\frac{1}{2}\)ar(||gm ABCD)
Hence, ar (EFGH) = \(\frac{1}{2}\)ar(ABCD). Proved
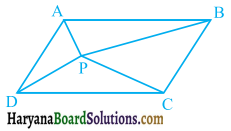
Question 3.
P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (APB) = ar (BQC).
Solution:
Since triangle APB and parallelogram ABCD are on the same base AB and between same parallels AB and CD.

∴ ar (ΔAPB) = \(\frac{1}{2}\)ar (||gm ABCD)
(By corollary)…(i)
Similarly, triangle BQC and parallelogram ABCD are on the same base BC and between same parallels BC and AD.
∴ ar (ΔBQC) = \(\frac{1}{2}\)ar(Ilgm ABCD) …..(ii)
From (1) and (2), we get
ar (ΔAPB) = ar (ΔBQC).
Hence proved
![]()
Question 4.
In figure 9.16, P is a point in the interior of a parallelogram ABCD. Show that:
(i) ar (APB) + ar (PCD) = \(\frac{1}{2}\)ar (ABCD)
(ii) ar (APD) + ar (PBC) = ar (APB) + ar (PCD).
Solution:
Through F draw a line EF parallel to AB.
(i) EF || AB
CD || AB (opposite sides of parallelogram)
∴ EF || CD
∴ ABFE and EFCD are two parallelograms.
Since, triangle APB and parallelogram ABFE are on the same base AB and between the same parallels AB and EF.
∴ ar (APB) = \(\frac{1}{2}\)ar (ABFE) …(i)
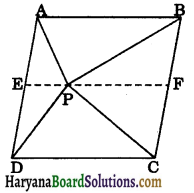
Similarly, triangle PCD and parallelogram EFCD are on the same base CD and between the same parallels CD and EF.
∴ ar(PCD) = \(\frac{1}{2}\)ar (EFCD) …..(ii)
Adding (i) and (ii), we get
ar (APB)+ ar (PCD) = \(\frac{1}{2}\)ar (ABFE) + \(\frac{1}{2}\)ar (EFCD)
⇒ ar (APB) + ar (PCD) = \(\frac{1}{2}\)[ar (ABFE) + ar (EFCD)]
⇒ ar (APB) + ar (PCD) = \(\frac{1}{2}\)ar (ABCD)…(iii)
(ii) From (iii), we have
ar (APB) + ar (CPD) = \(\frac{1}{2}\)ar (ABCD)
Similarly, we can prove that
ar (APD) + ar (PBC) = \(\frac{1}{2}\)ar (ABCD) …..(iv)
From (iii) and (iv), we get
ar (APD) + ar (PBC) = \(\frac{1}{2}\)ar (APB) + ar (PCD).
Hence proved
Question 5.
In figure 9.17, PQRS and ABRS are parallelograms and X is any point on side BR. Show that:
(i) ar (PQRS) = ar (ABRS)
(ii) ar (AXS) = \(\frac{1}{2}\)ar (PQRS).
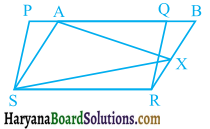
Solution:
(i) Since parallelograms PQRS and ABRS are on the same base SR and between the same parallels PB and SR.
∴ ar (PQRS) = ar (ABRS)
(ii) Since triangle AXS and parallelogram ABRS are on the same base AS and between the same parallels AS and BR.
∴ ar (AXS) = \(\frac{1}{2}\)ar (ABRS) …(i)
and ar (PQRS) = ar (ABRS)
(as proved above) …(ii)
From (i) and (ii), we get
ar (AXS) = \(\frac{1}{2}\)ar (PQRS).
Hence proved
![]()
Question 6.
A farmer was having a field in the form of a parallelogram PQRS. She took any point A on RS and joined it to points P and Q. In how many parts the fields is divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it.
Solution:
AP and AQ divide the parallelogram PQRS in three parts shape of each part is triangle.
Since triangle APQ and parallelogram PQRS are on the same base PQ and between the same parallels PQ and SR.
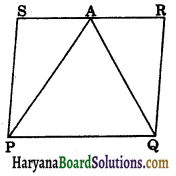
∴ ar(ΔAPQ) = \(\frac{1}{2}\)ar (||gm PQRS) …….(i)
Now
ar (ΔPAS) + ar (ΔQAR) = ar (||gm PQRS) – ar (ΔAPQ)
⇒ ar (ΔPAS) + ar (ΔQAR) = ar (||gm PQRS) – \(\frac{1}{2}\)ar(||gm PQRS) [Using (i)]
⇒ ar (ΔPAS) + ar (ΔQAR)= \(\frac{1}{2}\)ar (||gm PQRS) …(ii)
From (i) and (ii), we get
ar (ΔPAS) + ar (ΔQAR) = ar (ΔAPQ)
So, the farmer should sow wheat in ΔAPQ and pulses in triangles PAS and QAR or pulses in ΔAPQ and wheat in triangles PAS and QAR.