Haryana State Board HBSE 9th Class Maths Solutions Chapter 7 त्रिभुज Ex 7.4 Textbook Exercise Questions and Answers.
Haryana Board 9th Class Maths Solutions Chapter 7 त्रिभुज Exercise 7.4
प्रश्न 1.
दर्शाइए कि समकोण त्रिभुज में कर्ण सबसे लंबी भुजा होती है।
हल :
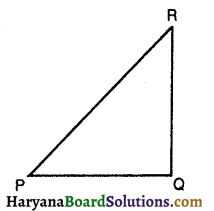
माना ΔPQR एक समकोण त्रिभुज है जिसमें,
∠PQR = 90°
हम जानते हैं कि ΔPQR में,
∠PQR + ∠QRP + ∠RPQ = 180°
या 90° + ∠QRP + ∠RPQ = 180°
या ∠QRP + ∠RPQ = 180° – 90° = 90°
⇒ ∠QRP = ∠RPQ = न्यून कोण
अतः ∠QRP < 90° तथा ∠RPQ < 90°
इस प्रकार ΔPQR में ∠PQR सबसे बड़ा कोण है तथा सबसे बड़े कोण के सामने की भुजा सबसे बड़ी होती है।
∴ PR सबसे बड़ी भुजा है।
अतः समकोण त्रिभुज में कर्ण सबसे लंबी भुजा होती है। [इति सिद्धम]
![]()
प्रश्न 2.
आकृति में, ΔABC की भुजाओं AB और AC को क्रमशः बिंदुओं Pऔर Q तक बढ़ाया गया है। साथ ही, ∠PRC < ∠QCB है। दर्शाइए कि AC > AB है।
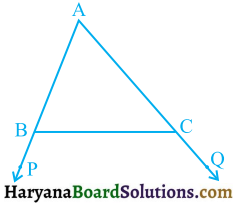
हल :
यहाँ पर दिया गया है,
∠PBC < ∠QCB या – ∠PBC > – ∠QCB
या 180° – ∠PBC > 180° – ∠QCB
या ∠ABC > ∠ACB
या AC > AB [∵ बड़े कोण की सम्मुख भुजा बड़ी होती है।] [इति सिद्धम]
प्रश्न 3.
आकृति में, ∠B < ∠A और ∠C < ∠D है। दर्शाइए कि AD < BC है।
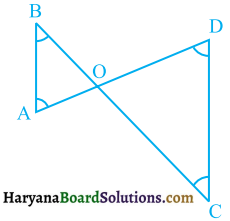
हल :
यहाँ पर दिया गया है,
∠B < ∠A और ∠C < ∠D
⇒ AO < BO तथा OD < OC [∵ बड़े कोण की सम्मुख भुजा बड़ी होती है]
दोनों को जोड़ने पर,
AO + OD < BO + OC
⇒ AD < BC [इति सिद्धम]
![]()
प्रश्न 4.
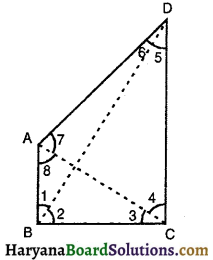
AB और CD क्रमशः एक चतुर्भुज ABCD की सबसे छोटी और सबसे बड़ी भुजाएं हैं (देखिए आकृति)। दर्शाइए कि ∠A > ∠C और ∠B > ∠D है।
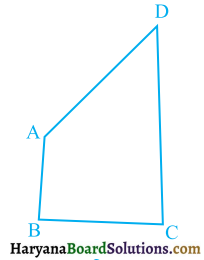
हल :
यहाँ पर, ABCD एक चतुर्भुज है, जिसमें AB सबसे छोटी भुजा है और CD सबसे बड़ी भुजा है।
AC तथा BD को मिलाया।
क्योंकि AB, चतुर्भुज ABCD की सबसे छोटी भुजा है।
∴ ΔABC में, BC > AB
∠8 > ∠3 ………..(i)
[∵ बड़ी भुजा के सामने का कोण बड़ा होता है]
इसी प्रकार CD चतुर्भुज ABCD की सबसे बड़ी भुजा है।
∴ ΔACD में,
CD > AD
∠7 > ∠4 …..(ii) [∵ बड़ी भुजा के सामने का कोण बड़ा होता है]
समीकरण (i) व (ii) से,
∠8 + ∠7 > ∠3 + ∠4
या ∠A > ∠C [इति सिद्धम]
अब ΔABD में,
AD > AB [∵ AB सबसे छोटी भुजा है]
या ∠1 > ∠6 ….(iii)
ΔBDC में,
CD > BC [∵ CD सबसे बड़ी भुजा है]
∴ ∠2 > ∠5 ……..(iv)
समीकरण (iii) व (iv) से
∠1 + ∠2 > ∠5 + ∠6
या ∠B > ∠D [इति सिद्धम]
प्रश्न 5.
आकृति में, PR > PQ है और PS कोण OPR को समद्विभाजित करता है। सिद्ध कीजिए कि ∠PSR > ∠PSQहै।
हल :
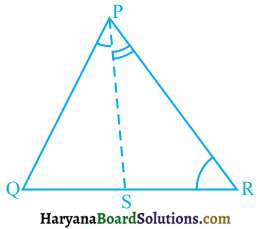
यहाँ पर ΔPQR में, PR > PQ [दिया है]
⇒ ∠PQR > ∠PRQ [∵ बड़ी भुजा के सामने का कोण बड़ा होता है]
दोनों ओर ∠1 जोड़ने पर,
∠PQR + ∠1 > ∠PRQ + ∠1
या ∠PQR + ∠1 > ∠PRQ + ∠2 ……..(i)
[∵ PS, ∠P का कोण समद्विभाजक है, ∴ ∠1 = ∠2]
अब ΔPQS में,
∠PQR + ∠1 + ∠PSQ = 180°
∠PQR + ∠1 = 180° – ∠PSQ …(ii)
इसी प्रकार ΔPSR में, ∠PRQ + ∠2 = 180° – ∠PSR ……(iii)
समीकरण (i), (ii) व (iii) से,
∴ 180° – ∠PSQ > 180° – ∠PSR
या – ∠PSQ > -∠PSR
या ∠PSQ < ∠PSR अर्थात ∠PSR > ∠PSQ [इति सिद्धम]
![]()
प्रश्न 6.
दर्शाइए कि एक रेखा पर एक दिए हुए बिंदु से, जो उस रेखा पर स्थित नहीं है, जितने रेखाखंड खींचे जा सकते हैं, उनमें लंब रेखाखंड सबसे छोटा होता है।
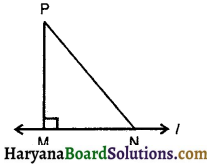
हल :
माना P कोई एक बिंदु है, जो रेखा l पर नहीं है,
तथा PM ⊥ l,M के अतिरिक्त रेखा l पर N कोई बिंदु है।
अब ΔPMN में,
∠M = 90°
⇒ ∠N < 90° [∵ ∠MPN + ∠PNM = 90° ⇒ ∠N < 90°]
या ∠N < ∠M
या PM < PN [∵ बड़े कोण के सामने की भुजा बड़ी होती है]
अतः P से l तक रेखाखंडों में से PM लंब सबसे छोटा रेखाखंड है। [इति सिद्धम]