HBSE 9th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.9

Haryana State Board HBSE 9th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.9 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Exercise 13.9

प्रश्न 1.
एक लकड़ी के बुकशेल्फ (book-shell) की बाहरी विमाएं निम्न हैं : ऊंचाई = 110 सें०मी०, गहराई = 25 सें०मी०, चौड़ाई = 85 सें०मी० (देखिए आकृति)। प्रत्येक स्थान पर तख्तों की मोटाई 5 सें०मी० है। इसके बाहरी फलकों पर पालिश कराई जाती है और आंतरिक फलकों पर पेंट किया जाना है। यदि पालिश कराने की दर 20 पैसे प्रति सें०मी० है और पेंट कराने की दर 10 पैसे प्रति सें०मी० है, तो इस बुक-शैल्फ पर पालिश और पेंट कराने का कुल व्यय ज्ञात कीजिए।

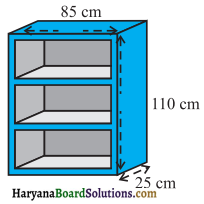
हल :
यहां पर, पॉलिश वाले तल का क्षेत्रफल = (110 × 85 + 2 × 85 × 25 + 2 × 25 × 110 + 4 × 75 × 5 + 2 × 110 × 5) सें०मी०²
= (9350 + 4250 + 5500 + 1500 + 1100) सें०मी०²
= 21700 सें०मी०²
इस पर पॉलिश कराने का खर्च = 21700 × \(\frac{20}{100}\) = ₹ 4340
पेंट वाले तल का क्षेत्रफल = (6 × 75 × 20 + 2 × 90 × 20 + 75 × 90) सें०मी०²
= (9000 + 3600 + 6750) सें०मी०² = 19350 सें०मी०²
इस पर पेंट कराने का खर्च = 19350 × \(\frac{10}{100}\) = ₹ 1935
पॉलिश व पेंट कराने का कुल खर्च = 4340 + 1935 = ₹ 6275 उत्तर

प्रश्न 2.
किसी घर के कंपाउंड के सामने की दीवार को 21 सें०मी० व्यास वाले लकड़ी के गोलों को छोटे आधारों पर टिका कर सजाया जाता है, जैसा कि आकृति में दिखाया गया है। इस प्रकार के आठ गोलों का प्रयोग इस कार्य के लिए किया जाना है और इन गोलों को चांदी वाले रंग में पेंट करवाना है। प्रत्येक आधार 1.5 सें०मी० त्रिज्या और ऊंचाई 7 सें०मी० का एक बेलन है तथा इन्हें काले रंग से पेंट करवाना है। यदि चांदी के रंग के पेंट करवाने की दर 25 पैसे प्रति से०मी० है तथा काले रंग के पेंट करवाने की दर 5 पैसे प्रति सें०मी० हो, तो पेंट करवाने का कुल व्यय ज्ञात कीजिए।

हल :
माना
लकड़ी के गोले का व्यास (d) = 21 सें०मी०
लकड़ी के गोले की त्रिज्या = \(\frac{21}{2}\) सें०मी०
∴ गोले का पृष्ठीय क्षेत्रफल = 4πr2
= \(4 \times \frac{22}{7} \times \frac{21}{2} \times \frac{21}{2}\) = 1386 सें०मी०²
गोले के जितने तल पर चांदी वाला रंग होगा = \(\left[1386-\frac{22}{7} \times \frac{3}{2} \times \frac{3}{2}\right]\) सें०मी०²
= \(\left[1386-\frac{99}{14}\right]\) सें०मी०²
= [1386 – 7.07] सें०मी०²
= 1378.93 सें०मी०²
8 गोलों में जितने तल पर चांदी वाला रंग होगा = 1378.93 × 8 सें०मी०² = 11031.44 सें०मी०²
चांदी का पेंट करने की दर = 25 पैसे प्रति सें०मी०²
∴ चांदी वाले रंग पर व्यय = \(\frac{11031.44 \times 25}{100}\)
= ₹ 2757.86
बेलन की त्रिज्या (r) = 1.5 = \(\frac{15}{10}=\frac{3}{2}\) सें०मी०
बेलन की ऊंचाई (h) = 7 सें०मी०
बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πrh
= \(2 \times \frac{22}{7} \times \frac{3}{2} \times 7\) = 66 सें०मी०²
8 बेलनों का वक्र पृष्ठीय क्षेत्रफल = 66 × 8 = 528 सें०मी०²
काले रंग का पेंट करवाने की दर = 5 पैसे प्रति सें०मी०²
बेलनों पर काला रंग कराने पर व्यय = \(\frac{528 \times 5}{100}\) = ₹ 26.40
दोनों रंगों के पेंट पर कुल व्यय = 2757.86 + 26.40
= ₹ 2784.26 उत्तर

प्रश्न 3.
एक गोले के व्यास में 25% की कमी हो जाती है। उसका वक्र पृष्ठीय क्षेत्रफल कितने प्रतिशत कम हो गया है?
हल :
माना,
गोले का पहला व्यास = 2x मी०
गोले की पहली त्रिज्या = x मी०
गोले का पहला पृष्ठीय क्षेत्रफल = 4πr² = 4πx² मी०²
25% कमी करने के पश्चात्