Haryana State Board HBSE 9th Class Maths Notes Chapter 8 चतुर्भुज Notes.
Haryana Board 9th Class Maths Notes Chapter 8 चतुर्भुज
→ चार रेखाखंडों से बनी बंद आकृति को चतुर्भुज कहते हैं। एक चतुर्भुज की चार भुजाएं, चार कोण व चार शीर्ष होते हैं।
→ चतुर्भुज के कोणों का योग 360° होता है।
→ प्रत्येक समांतर चतुर्भुज का एक विकर्ण उसे दो सर्वागसम त्रिभुजों में विभाजित करता है।
→ किसी समांतर चतुर्भुज में,
- सम्मुख भुजाएं बराबर होती हैं।
- सम्मुख कोण बराबर होते हैं।
- विकर्ण परस्पर समद्विभाजित करते हैं।
→ एक चतुर्भुज समांतर चतुर्भुज होता है, यदि-
- सम्मुख भुजाएं बराबर हों।
- सम्मुख कोण बराबर हों।
- विकर्ण परस्पर समद्विभाजित करते हों ।
- सम्मुख भुजाओं का एक युग्म बराबर और समांतर हो ।
![]()
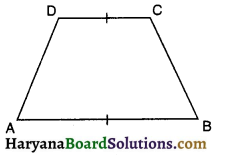
→ यदि चतुर्भुज ABCD की सम्मुख भुजाओं AB और CD का एक युग्म समांतर हो तो उसे समलंब कहते हैं।
→ आयत के विकर्ण परस्पर समद्विभाजित करते हैं और बराबर होते हैं। आयत का प्रत्येक कोण 90° का होता है।
→ समचतुर्भुज के विकर्ण परस्पर समकोण पर समद्विभाजित करते हैं। इसकी सभी भुजाएं समान होती हैं।
→ वर्ग के विकर्ण परस्पर समकोण पर समद्विभाजित करते हैं और बराबर होते हैं। वर्ग का प्रत्येक कोण 90° का होता है तथा सभी भुजाएं समान होती हैं।
→ किसी त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिंदुओं को मिलाने वाला रेखाखंड तीसरी भुजा के समांतर और उसका आधा होता है।
→ किसी त्रिभुज की एक भुजा के मध्य-बिंदु से दूसरी भुजा के समांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है।
→ किसी चतुर्भुज की भुजाओं के मध्य-बिंदुओं को एक क्रम से मिलाने वाले रेखाखंडों द्वारा बना चतुर्भुज एक समांतर चतुर्भुज होता है।