Haryana State Board HBSE 9th Class Maths Notes Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Notes.
Haryana Board 9th Class Maths Notes Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल
→ एक आकृति का क्षेत्रफल उस आकृति द्वारा घेरे गए तल के भाग से संबद्ध ( किसी मात्रक में) एक संख्या होती है।
→ दो सर्वांगसम आकृतियों के क्षेत्रफल बराबर होते हैं, परन्तु इसका विलोम आवश्यक रूप से सत्य नहीं है।
→ समांतर चतुर्भुज का क्षेत्रफल = आधार × संगत शीर्षलंब
→ दो आकृतियां एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित कही जाती हैं, यदि उनमें एक उभयनिष्ठ आधार (एक भुजा) हो तथा उभयनिष्ठ आधार के सम्मुख प्रत्येक आकृति के शीर्ष (का शीर्ष) उस आधार के समांतर किसी रेखा पर स्थित हों।
→ एक ही आधार वाले और एक ही समांतर रेखाओं के बीच स्थित समांतर चतुर्भुज क्षेत्रफल में बराबर होते हैं।
→ एक ही आधार वाले और बराबर क्षेत्रफलों वाले समांतर चतुर्भुज एक ही समांतर रेखाओं के बीच स्थित होते हैं।
→ यदि एक त्रिभुज और एक समांतर चतुर्भुज एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित हों, तो त्रिभुज का क्षेत्रफल समांतर चतुर्भुज के क्षेत्रफल का आधा होता है।
![]()
→ एक ही आधार (या बराबर आधारों) वाले और एक ही समांतर रेखाओं के बीच स्थित त्रिभुज क्षेत्रफल में बराबर होते हैं।
→ त्रिभुज का क्षेत्रफल उसके आधार और संगत शीर्षलंब के गुणनफल का आधा होता है।
→ एक ही आधार वाले और बराबर क्षेत्रफलों वाले त्रिभुज एक ही समांतर रेखाओं के बीच स्थित होते हैं।
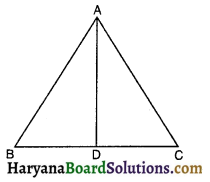
→ त्रिभुज की एक माध्यिका उसे बराबर क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करती है।
अर्थात ar (ΔABD) = ar (ΔACD)