Haryana State Board HBSE 9th Class Maths Important Questions Chapter 8 Quadrilaterals Important Questions and Answers.
Haryana Board 9th Class Maths Important Questions Chapter 8 Quadrilaterals
Very Short Answer Type Questions
Question 1.
In the figure 8.54, ABCD is a parallelogram. Find the measure of x.
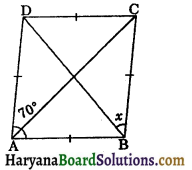
Solution:
Since ABCD is a parallelogram.
∴ ∠C = ∠A ⇒ ∠C = 70°
In ΔCBD, we have
BC = CD
⇒ ∠CDB = ∠CBD, (angles opposite to equal sides are equal)
⇒ ∠CBD = x
and ∠CDB + ∠CBD + ∠C = 180°
(sum of interior angles of a triangle = 180°)
⇒ x + x + 70° = 180°
⇒ 2x = 180° – 70°
⇒ 2x = 110°
⇒ x = \(\frac{110^{\circ}}{2}\) = 55°
Hence,measure of x = 55°.
Question 2.
In the figure 8.55, P, Q and R are the mid points of AB, BC and CA respectively. If PQ = 2.5 cm, QR = 3.0 cm and PR = 3.5 cm, calculate AB, BC and CA.
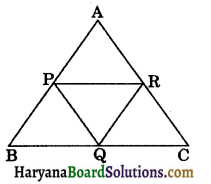
Solution:
Since, P and R are the mid points of AB and AC respectively.
∴ PR = \(\frac{1}{2}\)BC (By theorem 8.9)
⇒ 3.5 = \(\frac{1}{2}\)BC
⇒ BC = 3.5 × 2 = 7 cm
Again, Q and R are the mid points of BC and AC respectively.
∴ QR = \(\frac{1}{2}\)AB,
⇒ 3.0 = \(\frac{1}{2}\)AB
⇒ AB = 3 × 2 = 6 cm
and similarly, P and Q are the mid points of AB and BC respectively.
∴ PQ = \(\frac{1}{2}\)AC
⇒ 2.5 = \(\frac{1}{2}\)AC
⇒ AC = 2.5 × 2 = 5 cm
Hence, AB = 6 cm, BC = 7 cm and AC = 5 cm.
![]()
Question 3.
In a parallelogram ABCD, K is the mid point of side CD and DM is drawn parallel to BK, which meets CB produced at M and cut side AB at L. Prove that:
(i) AD = \(\frac{1}{2}\)CM
(ii) DM = 2BK.
Solution:
(i) In ΔCDM, K is the mid point of CD.
and BK || DM, (Given)
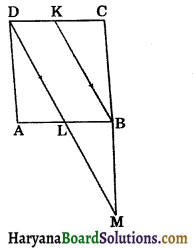
B is the mid point of CM. [By theorem 8.10]
⇒ CM = 2BC …..(i)
Since, ABCD is a parallelogram.
∴ AD = BC …..(ii)
(Opposite sides of parallelogram)
From (i) and (ii), we get
CM = 2AD
AD = \(\frac{1}{2}\)CM
Hence proved
(ii) In ΔMCD, B and K are respectively the mid points of CM and CD
∴ BK = \(\frac{1}{2}\)DM
⇒ DM = 2BK. Hence proved
Short Answer Type Questions
Question 1.
In the figure 8.57, ABC is a right angled triangle, D is the mid point of AC and E is the point on AB such that DE || BC. If AE = 6 cm and area of ΔADE = 22.5 cm2. Find the area of a ΔABC.
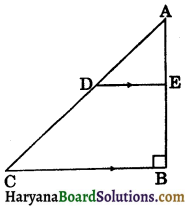
Solution:
Since,
DE || BC
∴ ∠AED = ∠ABC = 90°
Area of right ΔADE = \(\frac{1}{2}\)DE × AE
⇒ 22.5 = \(\frac{1}{2}\)DE × 6, [∵ ar ΔADE = 22.5 cm2 and AE = 6 cm]
⇒ \(\frac{22.5 \times 2}{6}\) = DE
⇒ DE = \(\frac{15}{2}\) = 7.5 cm
Since, D is the mid point of AC and DE || BC.
∴ E is the mid point of AB. [By theorem 8.10]
⇒ AB = 2 × AE = 2 × 6 = 12 cm
Since, D and E are mid points of AC and AB respectively.
∴ BC = 2 × DE
= 2 × 7.5 = 15 cm
Now, area of right
ΔABC = \(\frac{1}{2}\)BC × AB
= \(\frac{1}{2}\) × 15 × 12
= 90 cm2
Hence,
Area of ΔABC = 90 cm2.
![]()
Question 2.
ABCD is a trapezium in which AB || CD. P and Q are mid points of AD and BC respectively such that PQ || CD. If AB = 8 cm and CD = 10 cm, find the length of PQ.
Solution:
Join AC intersects PQ at R.
In ΔADC,
P is the mid point of AD and PR || CD.
[∵ PQ || CD]
∴ R is the mid point of AC.
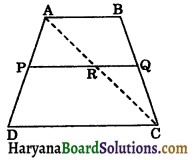
Thus, P and R are the mid points of AD and AC respectively.
∴ PR = \(\frac{1}{2}\)CD,
⇒ PR = \(\frac{1}{2}\) × 10
⇒ PR = 5 cm ……(1)
Since, AB || CD and PQ || CD, (Given)
Therefore, AB || PQ
⇒ AB || QR
In ΔCAB, QR || AB and R is the mid point of AC.
∴ Q is the mid point of BC.
⇒ QR = \(\frac{1}{2}\)AB,
⇒ QR = \(\frac{1}{2}\) × 8
⇒ QR = 4 cm ……(ii)
Adding (i) and (ii), we get
PR + QR = 5 + 4 ⇒ PQ = 9 cm
Hence, PQ = 9 cm.
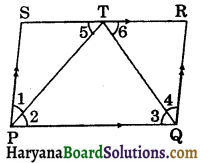
Question 3.
In the figure 8.59, PQRS is a parallelogram. Bisector of ∠P and ∠Q meets SR in T. Prove that PQ = 2QR.
Solution:
Since ABCD is a parallelogram.
∴ PQ || SR and PT intersects them.
⇒ ∠5 = ∠2, …..(i)
(Alternate interior angles)
∠1 = ∠2 …..(ii)
[PT is the bisector of ZP]
From (i) and (ii), we get
∠1 = ∠5
⇒ PS = ST ……(iii)
(Sides opposite to equal angles are equal)
Similarly, we can prove that
QR = TR ……(iv)
Adding (iii) and (iv), we get
PS + QR = ST + TR
⇒ QR + QR = SR, [∵ PS = QR]
⇒ 2QR = PQ, [∵ SR = PQ]
⇒ PQ = 2QR. Hence proved
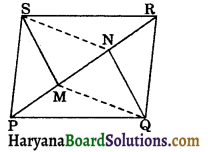
Question 4.
In the figure 8.60, PQRS is a parallelogram in which line segments SM and QN trisects the diagonal PR. Prove that:
(i) SM || QN and SM = QN,
(ii) SMQN is a parallelogram.
Solution:
(i) Since SM and QN trisects the diagonal PR.
∴ PM = MN = NR
⇒ PM = NR
⇒ PM + MN = NR + MN
(Adding MN on both sides)
⇒ PN = MR ……(i)
Now, PQRS is a parallelogram.
∴ PQ || RS and PR intersects them.
∠QPR = ∠SRP,
(Alternate interior angles)
⇒ ∠QPN = ∠SRM …..(ii)
In ΔPQN and ΔRSM, we have
PQ = RS, (Opposite sides of a parallelogram)
∠QPN = ∠SRM, [From (ii)]
and PN = MR [From (i)]
∴ ΔPQN = ΔRSM,
[By SAS congruence rule]
⇒ QN = SM, (CPCT)
and ∠PNQ = ∠RMS, (CPCT)
But these are alternate interior angles.
∴ QN || SM
Hence, SM || QN and SM = QN.
(ii) Since, SM || QN and SM = QN Proved
∴ SMQN is a parallelogram. Hence proved
![]()
Question 5.
ABCD is a parallelogram in which P and Q are points on the sides AB and CD such that PB = DQ. Prove that OP = OQ.
Solution:
Since, ABCD is a parallelogram.
∴ AB || CD and AC intersects them.
∴ ∠DCA = ∠BAC
(alternate interior angles)
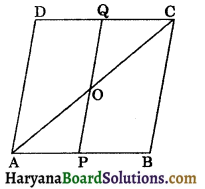
⇒ ∠QCO = ∠PAO …..(i)
and AB = CD, (opposite sides of a parallelogram)
⇒ AB – PB = CD – DQ
[∵ it is given that PB = DQ]
⇒ AP = CQ,
Now, in ΔAOP and ΔCOQ, we have
∠PAO = ∠QCO, [from (i)]
∠AOP = ∠COQ, (Vertically opposite angles)
and AP = CQ, [From (ii)]
ΔAOP ≅ ΔCOQ,
[By AAS congruence rule]
⇒ OP = OQ, [By CPCT]
Hence proved
Question 6.
In the figure 8.62, ABCD is a parallelogram. AB is produced to E such that BE = AB. EF meets CB produced at F and parallel to AC. Prove that:
(i) AFEC is a parallelogram.
(ii) AF = EC.
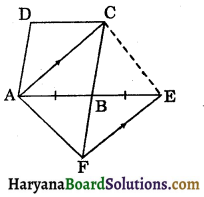
Solution:
(i) Since AC || FE and CF intersects them.
∴ ∠ACF = ∠EFC, (Alternate interior angles)
⇒ ∠ACB = ∠EFB ……(i)
Now, in ΔABC and ΔEBF, we have
∠ABC = ∠EBF, (Vertically opposite angles)
∠ACB = ∠EFB, [From (i)]
and AB = BE, (Given)
∴ ΔABC ≅ ΔEBF, (By AAS congruence rule)
⇒ AC = EF, (CPCT)
Now, AC = EF
and AC || EF, (Given)
∴ AFEC is a parallelolgram.
(ii) Since AFEC is a paralleogram.
∴ AF = EC, (Opposite sides of a parallelogram)
Hence proved
Question 7.
The figure ABCD is a trapezium in which AB || CD. P and Q are the mid points of diagonals BD and AC respectively. BQ joined and produced meets CD at R. Prove that:
(i) PQ || CD
(ii) PQ = \(\frac{1}{2}\)(CD – AB).
OR
Prove that the line joining the mid points of the diagonals of a trapezium is parallel to the parallel sides of the trapezium. [NCERTExemplar Problems]

Solution:
In ΔBAQ and ΔRCQ, we have
AQ = QC, (∵ Q is the mid point of AC)
∠BAQ = ∠RCQ, [∵ AB || CD and AC intersects them)
and ∠AQB = ∠CQR, (vertically opposite angles)
ΔBAQ ≅ ΔRCQ, [by AAS congruence rule]
⇒ BQ = RQ and AB = CR, (CPCT) …(i)
(i) In ΔBRD, P and Q are the mid points of BD and BR respectively.
∴ PQ || DR ⇒ PQ || CD.
⇒ PQ || AB and AB || CD (given)
(ii) In ΔBRD, P and Q are the mid points of BD and BR respectively.
∴ PQ = \(\frac{1}{2}\)DR, (by theorem 8.9)
⇒ PQ = \(\frac{1}{2}\)(CD – CR)
PQ = \(\frac{1}{2}\)(CD – AB), [from (i), CR = AB]
Hence proved
![]()
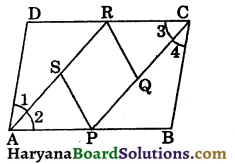
Question 8.
In the figure 8.64, ABCD is a parallelogram in which BD is a diagonal. P, Q and R are the mid points of BD, BC and CD respectively. If ΔPQR is an equilateral triangle, then prove that parallelogram ABCD is a rhombus not a square.
Solution:
In ΔDBC, R and P are the mid points of CD and BD respectively.
RP || BC and RP = \(\frac{1}{2}\)BC, (By theorem 8.9)
RP || CQ and RP =CQ,
[∵ Q is the mid point of BC]
∴ PQCR is parallelogram. [by theorem 8.8]
Since ΔPQR is an equilateral triangle.
∴ RP = PQ and ∠P = 60° …(i)
Thus, adjacent sides of a parallelogram are equal.
Therefore, PQCR is a rhombus.
∴ PQ = CQ = CR = PR
Now, CR = CQ
⇒ 2CR = 2CQ
⇒ CD = BC,
[∵ Q and R are the mid points of BC and CD respectively]
Thus, adjacent sides of a parallelogram ABCD are equal.
Therefore, ABCD is a rhombus.
But ∠P= 60° ⇒ ∠C = 60° [∵ ∠P = ∠C]
∴ ABCD is a rhombus not a square.
Long Answer Type Questions
Question 1.
ABCD is a quadrilateral in which AD = BC. E, F, G and H are the mid points of AB, BD, CD and AC respectively. Prove that EFGH is a rhombus.
Solution:
In ΔDCB, G and Fare mid points of CD and BD respectively.
∴ GF || BC
and GF = \(\frac{1}{2}\)BC ……(i)
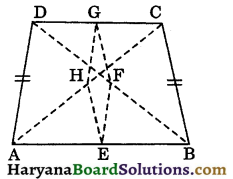
In ΔACB, H and E are mid points of AC and AB respectively.
∴ HE || BC
and HE = \(\frac{1}{2}\)BC ……(ii)
From (i) and (ii), we get
HE || GF
and HE = GF = \(\frac{1}{2}\)BC … (iii)
∴ EFGH is a parallelogram. (by theorem 8.8)
Similarly, in ΔBAD, E and F are mid points of AB and BD respectively.
∴ EF ||AD
and EF = \(\frac{1}{2}\)AD …(iv)
In ΔCAD, G and H are mid points of CD and AC respectively.
∴ HG || AD
and HG = \(\frac{1}{2}\)AD …(v)
From (iv) and (v), we get
HG = EF = \(\frac{1}{2}\)AD …(vi)
But, AD = BC (given) …(vii)
From (iii), (vi) and (vii), we get
HE = EF = GF = HG
Thus, in a parallelogram EFGH,
HE = EF = GF = HG.
Therefore, EFGH is a rhombus.
Hence proved
![]()
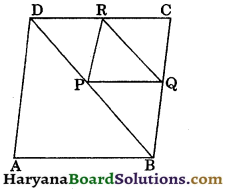
Question 2.
P and R are the mid points of opposite sides AB and CD of a parallelogram ABCD respectively. AR and CP are joined and if S and Q are mid points of AR and CP respectively. Prove that PQRS is a parallelogram.
Solution:
Since ABCD is a parallelogram.
∴ AB = CD, (opposite sides of a parallelogram)
⇒ \(\frac{1}{2}\)AB = \(\frac{1}{2}\)CD,
⇒ PB = DR and AP = CR …(i)
[∵ P and R are the mid points of AB and CD]
In ΔARD and ΔCPB, we have
DR = PB, (as proved above)
AD = BC,
(opposite sides of a parallelogram)
and ∠D = ∠B (opposite angles of a parallelogram)
∴ ΔARD ≅ ΔCPB, (by SAS congruence rule)
⇒ AR = CP, (CPCT)
\(\frac{1}{2}\)AR = \(\frac{1}{2}\)CP
⇒ RS = PQ
[∵ S and Q are mid points of AR and CP respectively]
and ∠1 = ∠4, (CPCT) … (iii)
Now, AR = CP, (as proved above)
⇒ AR – RS = CP – PQ,
[∵ RS = PQ, from (ii)]
⇒ AS = CQ ……(iv)
⇒ ∠A = ∠C, (opposite angles of parallelogram)
⇒ ∠A – ∠1 = ∠C – ∠1
⇒ ∠A – ∠1 = ∠C – ∠4,
[from (iii), ∠1 = ∠4]
⇒ ∠2 = ∠3 …(v)
Now, in ΔASP and ΔCQR, we have
AS = CQ, [from (iv)]
∠2 = ∠3, [from (v)]
and AP = CR, [from (i)]
∴ ΔASP ≅ ΔCQR, (by SAS congruence rule)
⇒ SP= QR, (CPCT) … (vi)
Thus, from (ii) and (vi), we get
RS = PQ and SP = QR
Hence, PQRS is a parallelogram. Proved
Question 3.
The figure 8.67, represents a trapezium ABCD in which AB || CD and AD = BC. Prove that:
(i) ∠DAB = ∠CBA
(ii) diagonal AC = diagonal BD,
(iii) OA = OB and OC = OD.
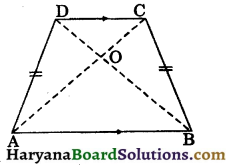
Solution:
Given : A trapezium ABCD in which AB || CD and AD = BC.
To prove : (i) ∠DAB = ∠CBA,
(ii) diagonal AC = diagonal BD,
(iii) OA = OB and OC = OD.
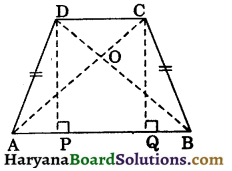
Construction : Draw DP ⊥ AB and CQ ⊥ AB.
Proof: (i) Since DP ⊥ AB and CQ ⊥ AB.
∴ DP || CQ
and PQ || CD, (∵ AB || CD)
∴ PQCD is a parallelogram.
⇒ DP = CQ ……(i)
(opposite sides of a parallelogram)
In ΔAPD and ΔBQC, we have
∠APD = ∠BQC, (Each = 90°)
Hyp. AD = Hyp. BC, (given)
and DP = CQ, [from (i)]
∴ ΔAPD ≅ ΔBQC,
[by RHS congruence rule]
⇒ ∠DAP = ∠CBQ, (CPCT)
⇒ ∠DAB = ∠CBA …(ii)
(ii) In ΔDAB and ΔCBA, we have
AD = BC, (given)
∠DAB = ∠CBA, [from (ii)]
and AB = AB, (common)
∴ ΔDAB ≅ ΔCBA,
(by SAS congruence rule)
⇒ BD = AC, (CPCT)
and ∠ADB = ∠BCA, (CPCT)
⇒ ∠ADO = ∠BCO …(iii)
(iii) In ΔAOD and ΔBOC, we have
⇒ ∠AOD = ∠BOC, (vertically opposite angles)
∠ADO = ∠BCO, [From (iii)]
and AD = BC, (given)
∴ ΔAOD ≅ ΔBOC, (by AAS congrunce rule)
⇒ OA = OB and OD = OC, (CPCT)
Hence proved
![]()
Question 4.
If through the middle point of the base of a triangle, a straight line is drawn parallel to one of the sides, prove that its intercepts on the internal and external bisectors of the vertical angle is equal to the other side.
Solution:
Given : P is the mid point of side BC of ΔABC. RK is drawn parallel to AB through P, such that RK is the intercept between AK and AR, the internal and external bisectors at ∠A.
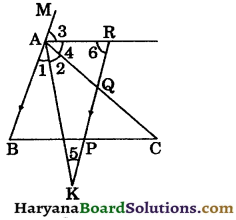
To prove: RK = AC.
Proof : ∵ AB || RK and transversal AK intersects them.
∠1 = ∠5 …..(i) (alternate interior angles)
and ∠1 = ∠2 …(ii)
AK bisects ∠A
From (i) and (ii), we get
∠2 = ∠5
⇒ AQ = KQ, ……..(iii)
(sides opposite to equal angles are equal)
∵ AR intersects parallel lines AB and RK.
∴ ∠3 = ∠6, …(iv)
(alternate interior angles)
and ∠3 = ∠4, …(v)
(AR bisects ∠MAC)
From (iv) and (v), we get
∠4 = ∠6
⇒ AQ = RQ ……(vi)
From (iii) and (vi), we get
AQ = KQ = RQ
⇒ AQ = \(\frac{1}{2}\)(KQ + RQ)
⇒ AQ = \(\frac{1}{2}\)RK ..(vii)
In ΔABC, PQ || AB and P is the mid point of BC.
∴ Q is the mid point of AC. (By theorem 8·10)
⇒ AQ = \(\frac{1}{2}\)AC …(viii)
From (vii) and (viii), we get
\(\frac{1}{2}\)RK = \(\frac{1}{2}\)AC
⇒ RK = AC. Hence proved
Question 5.
In the figure 8.70, AD = \(\frac{1}{2}\)AB, P is the mid point of AB, S is the mid point of DQ and PQ || BR. Prove that:
(i) AS || BR
(ii) QR = \(\frac{1}{3}\)DR.
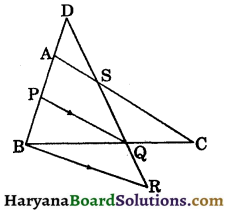
Solution:
(i) ∵ AD = \(\frac{1}{2}\)AB
AP = PB, (∵ P is the mid point of AB)
∴ AD = AP = PB …..(i)
In ΔDPQ, A is the mid point of DP and S is the mid point of DQ.
∴ AS || PQ
But BR || PQ (given)
∴ AS || BR
Now, AS || PQ || BR and a transversal BD making equal intercepts i.e., AP = PB.
Therefore, other transversal DR will also make equal intercepts i.e.,
SQ = QR …..(ii)
But, DS = SQ, …..(iii) (∵ S is the mid point of DQ)
From (ii) and (iii), we get
DS = SQ = QR
Now, DR = DS + SQ + QR
⇒ DR = QR + QR + QR
⇒ DR = 3QR
⇒ QR = \(\frac{1}{3}\)DR. Hence proved
![]()
Question 6.
Show that quadrilateral formed by joining the mid points of the sides of a square, is also a square. [NCERT Exemplar Problems]
Solution:
Given : A square ABCD in which P, Q, R and S are the mid points of sides AB, BC, CD and DA respectively. PQ, QR, RS and SP are joined
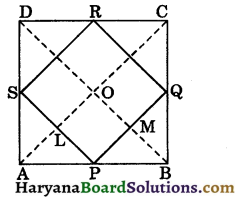
To prove : PQRS is a square.
Construction : Join AC and BD.
Proof: In ΔDAC, S and R are the mid points of AD and CD respectively.
∴ SR || AC and SR = \(\frac{1}{2}\)AC, …..(i)
In ΔBAC, P and Q are the mid points of AB and BC respectively.
∴ PQ || AC and PQ = \(\frac{1}{2}\)AC…(ii)
From (i) and (ii), we get
PQ || SR and PQ = SR
∴ PQRS is a parallelogram.
In ΔPBQ and ΔRCQ, we have
PB = CR,
[∵ AB = CD ⇒ \(\frac{1}{2}\)AB = \(\frac{1}{2}\)CD]
BQ = CQ, (∵ Q is the mid point of BC)
and ∠PBQ = ∠RCQ, (Each = 90°)
∴ ΔPBQ ≅ ΔRCQ, (By SAS congruence rule)
⇒ PQ = RQ (CPCT)
But, PQ = SR
(Opposite sides of parallelogram)
and SP = RQ
∴ PQ = RQ = SR = SP
Now, PQ || AC and PS || BD
PM || OL ⇒ LP || OM
∴ OLPM is a parallelogram.
∠LPM = ∠MOL …(iii)
(Opposite angles of parallelogram)
Since, diagonals of square bisect each other at 90°.
∠AOB = 90°
⇒ ∠MOL = 90° ……(iv)
From (iii) and (iv), we get
∠LPM = 90°
Thus, in a parallelogram PQRS,
PQ = QR = RS = SP
and ∠P = 90°
Hence, PQRS is a square.
Question 7.
In the figure 8.72, sides BC and DA of a quadrilateral produced respectively to M and N such that bisectors of ∠A and ∠C meets respectively M and N. Prove that:
∠M + ∠N = \(\frac{1}{2}\)(∠A + ∠C).
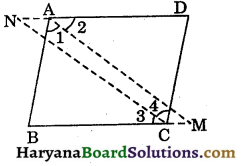
Solution:
In ΔABM, we have
∠1 + ∠B + ∠M = 180°,
[∵ Sum of interior angles of a triangle = 180°]
⇒ \(\frac{1}{2}\)∠A + ∠B + ∠M = 180° …….(i)
[∵ AM is the bisector of ∠A]
In ΔCND, we have
∠4 + ∠D + ∠N = 180°
⇒ \(\frac{1}{2}\)∠C + ∠D + ∠N = 180° …(ii)
[∵ CN is the bisector of ∠C]
Adding (i) and (ii), we get
\(\frac{1}{2}\)∠A + ∠B + ∠M + \(\frac{1}{2}\)∠C + ∠D + ∠N = 180° + 180°
⇒ \(\frac{1}{2}\)∠A + ∠C + ∠B + ∠D + ∠M + ∠N = 360° ….(ii)
But, ∠A + ∠B + ∠C + ∠D = 360°,
[∵ Sum of angles of a quadi. = 360°] …(iv)
From (iii) and (iv), we get
\(\frac{1}{2}\)∠A + \(\frac{1}{2}\)∠C + ∠B + ∠D + ∠M + ∠N = ∠A + ∠B + ∠C + ∠D
⇒ ∠M + ∠N = ∠A + ∠C – \(\frac{1}{2}\)∠A – \(\frac{1}{2}\)∠C
⇒ ∠M + ∠N = \(\frac{1}{2}\)∠A + \(\frac{1}{2}\)∠C
∠M + ∠N = \(\frac{1}{2}\)(∠A + ∠C).
Hence proved
![]()
Question 8.
ABCD is a parallelogram in which Pis the mid point of AB and DP bisects 2D. Prove that:
(i) BC = PB.
(ii) PC bisects ∠C.
(iii) ∠DPC = 90°.
Solution:
(i) Since ABCD is a parallelogram.
∴ AB || CD and DP intersects them.

⇒ ∠CDP = ∠APD …..(i) (Alternate interior angles)
and ∠CDP = ∠ADP, … (ii)
[∵ DP is the bisector of ∠D]
From (i) and (ii), we get
∠APD = ∠ADP
⇒ AD = AP …(iii)
(Sides opposite to equal angles are equal)
In parallelogram ABCD, we have
AD = BC, …(iv)
(∵ Opposite sides of parallelogram)
and AP = PB, …(v)
(∵ P is the mid point of AB)
From (iii), (iv) and (v), we get
BC = PB. Hence proved
(ii) ∵ BC = PB
⇒ ∠CPB = ∠PCB …….(vi)
(Angles opposite to equal sides are equal)
and ∠CPB = ∠DCP, …(vii)
(Alternate interior angles)
From (vi) and (vii), we get
∠DCP = ∠PCB
Hence, PC bisects ZC. Hence proved
(iii) AD || BC and CD intersects them.
∴ ∠C + ∠D = 180°,
(Sum of co-interior angles is 180°)
⇒ \(\frac{1}{2}\)∠C + \(\frac{1}{2}\)∠D = \(\frac{180^{\circ}}{2}\)
⇒ ∠DCP + ∠CDP = 90° ….(viii)
[∵ PD and CP are bisectors of ∠D and ∠C respectively]
Now in ΔDPC, we have
ΔDCP + ΔCDP + ΔDPC = 180°
[∵ Sum of interior angles of a triangle = 180°]
⇒ 90° + ∠DPC = 180° [Using (viii)]
⇒ ∠DPC = 180° – 90° = 90°.
Hence proved
Question 9.
ABCD is a rhombus. PABQ is a straight line such that PA = AB = BQ. Prove that PD and QC when produced meet at right angle.
Solution:
Let PD and QC when produced meet at point R.
Since, ABCD is a rhombus.
AB = BC = CD = AD …(i) (Sides of a rhombus)
and PA = AB = BQ(Given) …(ii)
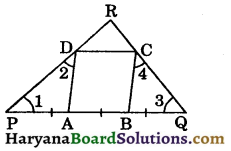
From (i) and (ii), we get
PA = AD
⇒ ∠1 = ∠2 …..(iii)
(Angles opposite to equal sides)
and BQ = BC
⇒ ∠3 = ∠4 …(iv)
In ΔPAD, we have
Ext. ∠DAB = ∠1 + ∠2,
[∵ Ext. angle is equal to sum of its opp. interior angles]
⇒ ∠DAB = ∠1 + ∠1 = 2∠1 …(v)
Similarly,
Ext. ∠CBA = ∠3 + ∠4
⇒ ∠CBA = ∠3 + ∠3 = 2∠3 …(vi)
Adding (v) and (vi), we get
∠DAB + ∠CBA = 2∠1 + 2∠3
= 2(∠1 + ∠3) …(vii)
Now, ABCD is a rhombus.
∴ AD || BC and AB intersects them.
⇒ ∠DAB + ∠CBA = 180° …..(viii)
[Sum of co-interior angles is 180°]
From (vii) and (viii), we get
2(∠1 + ∠3) = 180°
⇒ ∠1 + ∠3 = \(\frac{180^{\circ}}{2}\) = 90° …(ix)
In ΔPQR, we have
∠1 + ∠3 + ∠R = 180°, (∵ Sum of interior angles of a triangle is 180°)
⇒ 90° + ∠R = 180°, [Using (ix)]
⇒ ∠R = 180° – 90°
⇒ ∠R = 90°
Hence, PD and QC when produced meet at right angle. Proved
![]()
Question 10.
In the figure 8.75, ABCD is a square in which P, Q and R are the mid points of sides AB, BC and CD respectively. Prove that :
(i) ∠PQR = 90°,
(ii) if a line is drawn through P and parallel to QR bisects AD.

Solution:
(i) Join BD. Since ABCD is a square
∴ AB = BC
⇒ \(\frac{1}{2}\)AB = \(\frac{1}{2}\)BC
⇒ PB = BQ,
[∵ P is the mid point of AB and Q is the mid point of BC]
⇒ ∠1 = ∠2 ……(i)
[Angles opposite to equal sides are equal]
Similarly, ∠3 = ∠4 ……(ii)
In ΔPBQ,
∠1 + ∠2 + ∠B = 180°, (∵ Sum of interior angles of a triangle = 180°)
⇒ ∠1 + ∠2 + 90° = 180°,
(∵ Each angle of a square is 90°)
⇒ ∠1 + ∠2 = 180° – 90° = 90°…(iii)
Similarly, ∠3 + ∠4 = 90° …(iv)
Adding (iii) and (iv), we get
∠1 + ∠2 + ∠3 + ∠4 = 90° + 90°
⇒ ∠2 + ∠2 + ∠3 + ∠3 = 180°
⇒ 2(∠2+ ∠3) = 180°
⇒ ∠2+ ∠3 = \(\frac{180^{\circ}}{2}\) = 90° …….(v)
But, ∠2 + ∠3 + ∠PQR = 180°, (linear pair)
⇒ 90° + ∠PQR = 180°, [using (v)]
⇒ ∠PQR = 90°.
(ii) In ΔCBD, Q and R are the mid points of BC and CD respectively.
∴ QR || BD,
and QR || PS, (given)
∴ PS || BD
In ΔADB, PS || BD and P is the mid point of AB.
∴ S is the mid point of AD.
Hence, PS bisects AD. Proved
Multiple Choice Questions
Choose the correct option in each of the following:
Question 1.
Three angles of a quadrilateral are 70°, 85° and 90°. It’s fourth angle is :
(a) 90°
(b) 115°
(c) 100°
(d) 85°
Answer:
(b) 115°
Question 2.
The angles of quadrilateral are in the ratio 1 : 2 : 3 : 4. The greatest of these angles is :
(a) 120°
(b) 140°
(c) 144°
(d) 108°
Answer:
(c) 144°
![]()
Question 3.
If two adjacent sides of a parallelogram are equal, then it is a :
(a) rectangle
(b) square
(c) kite
(d) rhombus
Answer:
(d) rhombus
Question 4.
If diagonals of a parallelogram are equal, then it is a :
(a) square only
(b) rectangle only
(c) rhombus only
(d) both (a) and (b)
Answer:
(d) both (a) and (b)
Question 5.
D and E are the mid points of the sides AB and AC respectively of ΔABC. DE is produced to F. To prove that CF is equal and parallel to DA, we need an additional information which is : [NCERT Exemplar Problems]
(a) ∠DAE = ∠EFC
(b) AE = EF
(c) DE = EF
(d) ∠ADE = ∠ECF
Answer:
(c) DE = EF
Question 6.
If diagonals of a quadrilateral bisect each other at right angles, then it is :
(a) parallelogram
(b) square
(c) rectangle
(d) kite
Answer:
(b) square
Question 7.
In a square ABCD, the diagonals bisect at O, then ΔAOB is :
(a) an isosceles but not a right angled triangle
(b) an isosceles right angled triangle
(c) an equilateral triangle
(d) a right angled but not an isosceles triangle.
Answer:
(b) an isosceles right angled triangle
![]()
Question 8.
A quadrilateral is a rectangle but not a square when :
(a) it’s diagonals do not bisect each other
(b) it’s diagonals are not equal
(c) it’s diagonals are not perpendicular
(d) all angles are not equal.
Answer:
(c) it’s diagonals are not perpendicular
Question 9.
The bisectors of any two adjacent angles of a parallelogram intersect at :
(a) 90°
(b) 45°
(c) 80°
(d) 100°
Answer:
(a) 90°
Question 10.
The bisectors of the angles of a parallelogram enclose a :
(a) rectangle
(b) parallelogram
(c) kite
(d) both (a) and (b)
Answer:
(a) rectangle