Haryana State Board HBSE 9th Class Maths Important Questions Chapter 6 Lines and Angles Important Questions and Answers.
Haryana Board 9th Class Maths Important Questions Chapter 6 Lines and Angles
Very Short Answer Type Questions
Question 1.
Find the complement of the following angles :
(i) 64° 23′ 35″
(ii) 28° 25′ 48″.
Solution :
We can write,
90° = 89° 59′ 60″
(i) Complement of 64° 23′ 35″ = An angle of (90° – 64° 23′ 35″) = An angle of 25° 36′ 25″.
(ii) Complement of 28° 25′ 48″ = An angle of (90°- 28 °25′ 48″) = An angle of 61° 34′ 12″.
![]()
Question 2.
Find the measures of suppliment of the following angles :
(i) 115° 35′ 42″
(ii) 85° 15′ 59″.
Solution :
We can write,
180° = 179° 59′ 60″
(i) Supplement of 115° 35′ 42″ = An angle of (180° – 115°35′ 42″) = An angle of 64° 24′ 18″.
(ii) Suppliment of 85° 15′ 59″ = An angle of (180° – 85° 15′ 59”) = An angle of 94° 44′ 01″.
Question 3.
Find the measure of an angle which is 34° more than its complement.
Solution :
Let the complement of an angle be x° then
measure of an angle = (x + 34)°
We know that,
sum of an angle and its complement = 90°
∴ x° + (x + 34)° = 90°
⇒ 2x° + 34° = 90°
⇒ 2x° = 90° – 34°
⇒ 2x° = 56°
⇒ x° = \(\frac {56°}{2}\) = 28°
Hence,measure of an angle
= 28° + 34° = 62°.
Question 4.
Find the measure of an angle which is 26° less than its supplement.
Solution :
Let the supplement of an angle be x°
Then measure of an angle = (x – 26)°
We know that,
Sum of an angle and its supplement = 180°
∴ x° + (x – 26)° = 180°
⇒ 2x° – 26° = 180°
⇒ 2x° = 180° + 26°
⇒ 2x° = 206°
⇒ x° = \(\frac {206°}{2}\) = 103°
Hence measure of an angle = 103° – 26° = 77°.
Question 5.
Find the angle, which is 18° less than five times its complement.
Solution :
Let the complement angle be x°
Five times of complement angle = 5x°
Then angle = (5x – 18)°
We know that, Sum of an angle and its complement = 90°
∴ (5x – 18)° + x° = 90°
⇒ 6x° – 18° = 90°
⇒ 6x° = 90° + 18°
⇒ 6x° = 108°
⇒ x° = \(\frac {108°}{6}\) = 18°
Hence,measure of angle
= 5 × 18° – 18°
= 90° – 18° = 72°.
![]()
Question 6.
Find the angle, which is four times its supplement
Solution :
Let the supplement angle be x°.
Then angle = 4x°
We know that, Sum of an angle and its suppliment = 180°
∴ 4x° + x° = 180°
⇒ 5x° = 180°
⇒ x° = \(\frac {180°}{5}\) = 18°
Hence,measure of the angle
= 4 × 36° = 144°.
Question 7.
Find the measure of an angle whose supplement is three times of its complement.
Solution :
Let the angle be x°, then Supplement of an angle = (180 – x)°
Compliment of an angle = (90 – x)°
According to question,
(180 – x)° = 3(90 – x)°
⇒ 180° – x° = 270° – 3x°
⇒ – x° + 8x° = 270° – 180°
⇒ 2x° = 90°
⇒ x° = \(\frac {90°}{2}\) = 45°
Hence, the measure of the angle = 45°
Question 8.
Find the measure of an angle, if five times its complement is equal to two times of its supplement.
Solution :
Let the angle be x°, then
Complement of an angle = (90 – x)°
Supplement of an angle = (180 – x)°
According to question,
5(90 – x)° = 2(180 – x)°
⇒ 450° – 5x° = 360° – 2x°
⇒ – 5x° + 2x° = 360° – 450°.
⇒ – 3x° = – 90°
⇒ x° = \(\frac {-90°}{- 3}\) = 30°
Hence the measure of the angle = 30°.
Short Answer Type Questions
Question 1.
One of two complementary angles is seven-eighth as large as the other. How many degree are in each angle?
Solution :
Let the other complementary angle be x°.
One complimentary angle = \(\frac {7}{8}\)x°
We know that, Sum of two complementary angles = 90°

Hence, other complementary angle = 48° and one complementary angle = \(\frac {7}{8}\) × 48° = 42°.
![]()
Question 2.
In the figure, AC and BC are opposite rays. If 2x – 3y = 60°, then find the values of x and y.
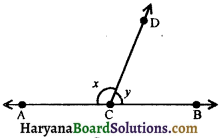
Solution :
Since, AC and BC are opposite rays. Therefore, ∠ACD + ∠BCD = 180°,
(Linear pair axiom)
⇒ x + y = 180° …(i)
2x – 3y = 60° (Given) …(ii)
Multiplying equation (i) by 3 and adding equation (i) and (ii), we get
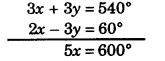
⇒ x = \(\frac {600°}{5}\) = 120°
Substituting the value of x in the equation (i), we get
120° + y = 180°
⇒ y = 180° – 120° = 60°
Hence, x = 120° and y = 60°
Question 3.
In figure, BCA is a line. Find the value of x.

Solution :
Since, BCA is a line. Therefore ∠BCD + ∠ACD = 180°,
(Linear pair axiom)
⇒ ∠BCD + ∠DCE + ∠ACE = 180°,
[∵ ∠ACD = ∠DCE + ∠ACE]
⇒ 2x° + (2x° + 30)° + x° = 180°
⇒ 5x° + 30° = 180°
⇒ 5x° = 180° – 30°
⇒ 5x° = 150°
⇒ x° = \(\frac {150°}{5}\) = 30°
Hence, x° = 30°
Question 4.
In figure, PQR is a line. If a : b : c = 2 : 3 : 5, find the values of a, b and c.
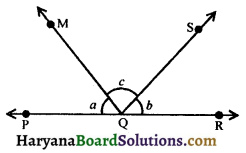
Solution :
Since, PQR is a line. Therefore ∠PQM + ∠RQM = 180°, (Linear pair axiom)
⇒ ∠PQM + ∠MQS + ∠RQS = 180°,
[∵ ∠RQM = ∠MQS + ∠RQS]
⇒ a + c + b = 180°
But a : b : c = 2 : 3 : 5
Sum of ratios = 2 + 3 + 5 = 10
∴ a = \(\frac {2}{10}\) × 180° = 36°
b = \(\frac {3}{10}\) × 180° = 54°
and c = \(\frac {5}{10}\) × 180° = 90°
Hence, a = 36°, b = 54 and c = 90°.
![]()
Question 5.
In figure, three straight lines AB, CD and EF intersect at a point o forming the angles as shown. Find the values of x, y, z and r.
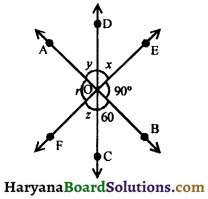
Solution:
y = 60°, (Vertically opposite angles)
r = 90° (Vertically opposite angles)
Since, AOB is a line.
∠AOE + ∠BOE = 180°
(Linear pair axiom)
⇒ ∠AOD + ∠DOE + ∠BOE = 180°
⇒ y + x + 90° = 180°
⇒ 60° + x + 90° = 180°
⇒ x + 150° = 180°
⇒ x = 180° – 150°= 30°
z = x
(Vertically opposite angles)
⇒ z = 30°
Hence,
x = 30°, y = 60°,
z = 30°, r = 90°.
Question 6.
In the figure , AB || CD, PQ || AX and ∠BAC = 70°, find ∠DPQ
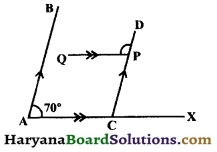
Solution :
∵ AB || CD and AX is a transversal
∴ ∠BAC + ∠ACD = 180°,
(Sum of a pair of allied angles is 180°)
⇒ 70° + ∠ACD = 180°,(∵ ∠BAC = 70°)
⇒ ∠ACD = 180° – 70°
⇒ ∠ACD = 110°
Now PQ || AX and CD is a transversal.
∠DPQ = ∠ACD, (Corresponding angles axiom)
⇒ ∠DPQ = 110°
Hence, ∠DPQ = 110°
Question 7.
In the figure, AB || CD aud m || n, find the value of x.
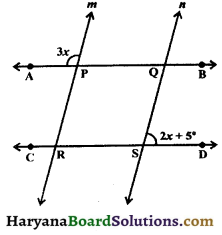
Solution :
∠QPR = 3x,
(Vertically opposite angles)
∵ AB || CD and line m is a transversal.
∴ ∠QPR + ∠PRS = 180°,
(A pair of allied angles is supplementary)
⇒ 3x + ∠PRS = 180°
⇒ ∠PRS = 180° – 3x ……(i)
Now, m || n and line CD is a transversal.
∠PRS = ∠QSD,
(Corresponding angles axiom)
⇒ 180° – 3x = 2x + 5°, [From (i), ∠PRS = 180° – 3x and ∠QSD = 2x + 5°]
⇒ 180° – 5° = 2x + 3x
⇒ 175° = 5x
⇒ \(\frac {175°}{5}\) = x
⇒ x = 35°
Hence, x = 35°
Question 8.
In the figure, AB || CD, find the value of x.

Solution :
From E, draw EF || AB || CD.
Now, AB || EF and AE is the transversal.
∴ ∠BAE + ∠AEF = 180°
(A pair of allied angles are supplementary)
⇒ 110° + ∠AEC + ∠CEF = 180°
⇒ 110° + 25° + ∠CEF = 180°
⇒ 135° + ∠CEF = 180°
⇒ ∠CEF = 180° – 135°
⇒ ∠CEF = 45°
Again CD || EF and CE is the transversal.
∴ ∠DCE + ∠CEF = 180°,
(A pair of allied angles is supplementary)
⇒ x + 45° = 180°
⇒ x = 180° – 45°
⇒ x = 135°
Hence, x = 135°
![]()
Question 9.
In the figure, AB || DE and x = y, prove that BC || EF.
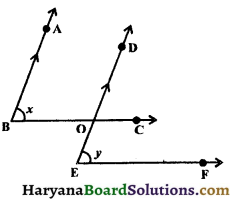
Solution :
Since AB || DE and BC is the transversal.
Therefore, ∠DOC = ∠ABC,
(Corresponding angles axiom)
⇒ ∠DOC = x
But x = y, (Given)
∴ ∠DOC = y
Thus, a pair of corresponding angles ∠DOC and y are equal. By converse of corresponding axiom, we have BC || EF. Hence proved
Question 10.
In the given figure, AB || CD, PQ || BC, ∠BAC = 52° and ∠DRS = 43°. Find the value of x.
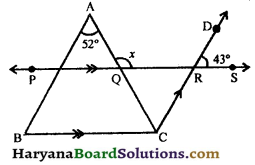
Solution :
Since, AB || CD and AC is the transversal.
∴ ∠ACD = ∠BAC,
(Alternate interior angles)
⇒ ∠ACD = 52°
⇒ ∠QCR = 52°,
(∵ ∠ACD = ∠QCR) …(i)
∠QRC = ∠DRS,
(Vertically opposite angles)
⇒ ∠QRC = 43° …….(ii)
In ΔCQR, we have
∠AQR = ∠QCR + ∠QRC,
⇒ x = 52° + 43°, [From (i) and (ii), ∠QCR = 52° and ∠QRC = 43°)
⇒ x = 95°
Hence, x = 95°
Question 11.
The sides BC, CA and AB of a triangle ABC are produced in order, forming exterior angles ∠ACD, ∠BAE and ∠CBF. Show that ∠ACD + ∠BAE + ∠CBF = 360°
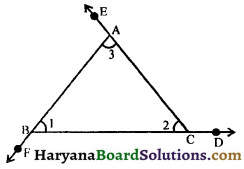
Solution :
In ΔABC, we have
∠ACD = ∠1 + ∠3 ………….(i)
∠BAE = ∠1 + ∠2 ………….(ii)
∠CBF = ∠2 + ∠3 ………….(iii)
Adding (i), (ii) and (iii), we get
∠ACD + ∠BAE + ∠CBF = ∠1 + ∠3 + ∠1 + ∠2 + ∠2 + ∠3
⇒ ∠ACD + ∠BAE + ∠CBF = 2∠1 + 2∠2 + 2∠3
⇒ ∠ACD + ∠BAE + ∠CBF = 2(∠1 + ∠2 + ∠3)
But ∠1 + ∠2 + ∠3 = 180°,
(Sum of the angles of a triangle = 180°)
∴ ∠ACD + ∠BAE + ∠CBF = 2 × 180°
⇒ ∠ACD + ∠BAE + ∠CBF = 360°
Hence proved
Question 12.
In the given figure, show that ∠A + ∠B + ∠C + ∠P + ∠Q + ∠R = 360°.
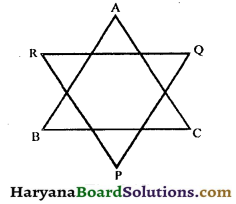
Solution :
In ΔABC, we have
∠A + ∠B + ∠C= 180°,
(Sum of angles of a triangle = 180°) …(i)
In ΔPQR, we have
∠P + ∠Q + ∠R = 180°,
(Sum of angles of a triangle = 180°) …(ii)
Adding (i) and (ii), we get
∠A + ∠B + ∠C + ∠P + ∠Q + ∠R = 180° + 180°
⇒ ∠A + ∠B + ∠C + ∠P + ∠Q + ∠R = 360°
Hence proved
![]()
Question 13.
ABC is a triangle in which ∠A = 66°, the internal bisectors of ∠B and ∠C intersect at O. Find the measure of ∠BOC.
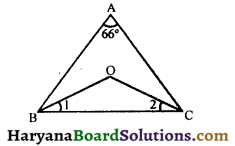
Solution :
In a triangle ΔABC, we have
∠A + ∠B + ∠C = 180°,
(Sum of angles of a triangle = 180°)
⇒ 66° + ∠B + ∠C = 180°
⇒ ∠B + ∠C = 180° – 66° = 114°
⇒ \(\frac {1}{2}\)∠B + \(\frac {1}{2}\)∠C = \(\frac {114°}{2}\) = 57°
⇒ ∠1 + ∠2 = 57° …….(i)
[∵ BO and CO are bisectors of ∠B and ∠C respectively]
Now, in ΔBOC, we have
∠1 + ∠2 + ∠BOC = 180°,
(Sum of angles of a triangle = 180°)
⇒ 57° + ∠BOC = 180°, [using (i)]
⇒ ∠BOC = 180° – 57°
⇒ ∠BOC = 123°
Hence, ∠BOC = 123°
Question 14.
The sum of two angles of a triangle is equal to its third angle. Prove that triangle is right-angled.
Solution :
Let the smaller angles be A and C and greater angle be B. According to question,
∠B = ∠A + ∠C ……..(i)
But, ∠A + ∠B + ∠C = 180°,
(∵ Sum of angles of a triangle = 180°)
(∠A + ∠C) + ∠B = 180°
⇒ ∠B + ∠B = 180°, [Using (i)]
⇒ 2∠B = 180°
⇒ ∠B = \(\frac {180°}{2}\)
⇒ ∠B = 90°
Hence, triangle ABC is right angled.
Proved
Question 15.
In the given figure, ∠P = ∠Q and ∠1 = ∠2. Prove that RT || PQ.
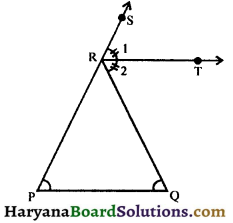
Solution :
In ΔRPQ, we have
∠SRQ = ∠P + ∠Q
⇒ ∠1 + ∠2 = ∠Q + ∠Q
(∵ It is given ∠P = ∠Q)
⇒ ∠2 + ∠2 = 2∠Q
(∵ It is given ∠1 = ∠2)
⇒ 2∠2 = 2∠Q
⇒ ∠2 = ∠Q
Thus, a pair of alternate interior angles 2 and Q are equal, then
RT || PQ. Hence proved
![]()
Question 16.
In figure, p || t and m || n. If ∠1 = 75°, prove that ∠2 = ∠1 + \(\frac {1}{3}\) of a right angle.
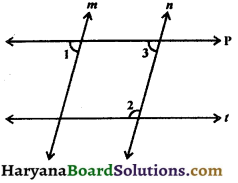
Solution :
∵ m || n and line p is a transversal
∴ ∠3 = ∠1
(Corresponding angles)
⇒ ∠3 = 75° (∴ ∠1 = 75°)
Now p || t and line n is a transversal.
∴ ∠2 + ∠3 = 180° (A pair of allied angles is supplementary)
⇒ ∠2 + 75° = 180°
⇒ ∠2 = 180° – 75°
⇒ ∠2 = 105°
⇒ ∠2 = 75° + 30°
⇒ ∠2 = ∠1 + \(\frac {1}{3}\) × 90°
(∵ ∠1 = 75°)
⇒ ∠2 = ∠1 + \(\frac {1}{3}\) of a right angle.
Hence proved
Long Answer Type Questions
Question 1.
In the figure, OP and OQ are respectively bisectors of angles ∠BOD and ∠AOC. Show that the rays OP and OQ are in the same straight line.
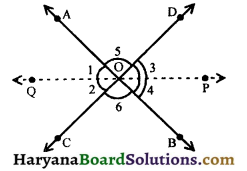
Solution :
∠1 + ∠2 + ∠6 + ∠4 + ∠3 + ∠5 = 360° …….(i)
(Sum of angles at a point = 360°)
∵ ray OP is the bisertor of ∠BOD.
∴ ∠3 = ∠4 …….(ii)
∵ ray OQ is the bisector of ∠AOC.
∴ ∠1 = ∠2 …….(iii)
∠5 = ∠6, (Vertically opposite angles) …(iv)
From (i), (ii), (iii) and (iv), we get
∠2 + ∠2 + ∠6 + ∠4 + ∠4 + ∠6 = 360°
⇒ 2∠2 + 2∠6 + 2∠4 = 360°
⇒ 2(∠2 + ∠6 + ∠4) = 360°
⇒ ∠2 + ∠6 + ∠4 = \(\frac {360°}{2}\) = 180°
⇒ ∠POQ = 180°
Hence, OP and OQ are in the same straight line.
Hence Proved
Question 2.
In the figure, AB || CD, find the value of x.
Solution :
Draw a line EF parallel to AB.
∵ AB || EF and a transversal PQ cuts them at P and Q respectively.
∴ ∠APQ + ∠EQP = 180°,
(∵ Sum of a pair of allied angles is 180°)
⇒ 40° + ∠EQP = 180°, (∵ ∠APQ = 40°)
⇒ ∠EQP = 180° – 40°
⇒ ∠EQP = 140° …….(i)
∴ AB || EF, (By construction)
and AB || CD, (Given)
∴ EF || CD, (By theorem 6.6)
∠EQR = ∠QRD,
(Alternate interior angles)
⇒ ∠EQR = 120°,
(∵ ∠QRD = 120°) …(ii)
Adding (i) and (ii), we get
∠EQP + ∠EQR = 140° + 120°
⇒ Reflex angle PQR = 260°
⇒ x = 260°
Hence, x= 260°.
![]()
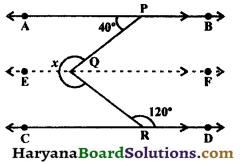
Question 3.
In the given figure :
(i) If x = 70°, find y and z.
(ii) If 3x = 2y, find x.
(iii) If z = 2(x + 15), find y.

Solution :
(i) ∵ CD || EF and CE is a transversal.
∴ x + z = 180° (Sum of a pair of allied angles is 180°)
⇒ 70° + z = 180°, (∵ x = 70°)
⇒ z = 180° – 70°
⇒ z = 110°
∵ AB || CD and AC is a transversal.
∴ y = z,
(Corresponding angles axiom)
⇒ y = 110°
Hence y = 110° and z = 110°.
(ii) 3x = 2y, (Given)
⇒ \(\frac {3}{2}\)x = y …….(i)
∵ AB || EF and AE is a transversal.
∴ x + y = 180° (Sum of a pair of allied angles is 180°)
⇒ x + \(\frac {3}{2}\)x = 180°
[From (i), y = \(\frac {3}{2}\)x]
⇒ \(\frac{2 x+3 x}{2}\) = 180°
⇒ 5x = 2 × 180°
⇒ x = \(\frac {360°}{5}\)
⇒ x = 72°
Hence, x = 72°.
(iii) ∵ CD || EF and CE is a transversal.
∴ x + z = 180°, (Sum of a pair of allied angle is 180°)
⇒ x + 2(z + 15) = 180,[∵ z = 2(x + 15°)
⇒ x + 2x + 30° = 180°
⇒ 3x + 30° = 180°
⇒ 3x = 180° – 30° = 150°
⇒ x = \(\frac {150°}{3}\) = 50°
Now,
z = 2(x + 15°)
⇒ z = 2(50° + 15°)
[Put x = 50°]
⇒ z = 2 × 65°
⇒ z = 130°
Now, y = z,
(Corresponding angles)
⇒ y = 130°
Hence, y = 130°
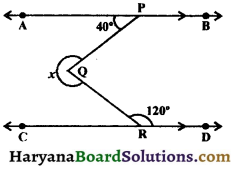
Question 4.
In the figure, PQ || RS, find the value of x.

Solution :
Through T draw LTM || PQ || RS.
∵ LT || PQ and PT is the transversal.
∴ ∠LTP = ∠TPQ,
(Alternate interior angles)
⇒ ∠LTP = 55° ……..(i)
and TM || RS and TR is the transversal.
∴ ∠MTR + ∠TRS = 180°,
(A pair of allied angles is supplementary)
⇒ ∠MTR + 115° = 180°
⇒ ∠MTR = 180° – 115°
⇒ ∠MTR = 65° ……..(ii)

Now LTM is a line.
∴ ∠LTP + ∠PTR + ∠MTR = 180°
(Straight line)
⇒ 55° + x + 65° = 180°. [From (i) and (ii), ∠LTP = 55° and ∠MTR = 65°]
⇒ 120° + x = 180°
⇒ x = 180° – 120°
⇒ x = 60°
Hence, x = 60°.
![]()
Question 5.
In the figure, AB || CD, find the values of x, y and z.
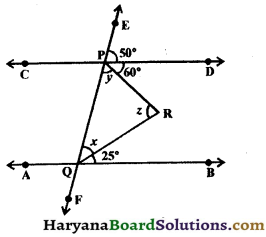
Solution :
∵ AB || CD and EF is the transversal
∴ ∠PQB = ∠EPD,
(Corresponding angles)
⇒ x + 25° = 50°
⇒ x = 50° – 25° = 25° and ∠DPQ + ∠PQB = 180°,
(A pair of allied angles is supplementary)
⇒ (y + 60°) + (x + 25°) = 180°
⇒ y + 60° + 25° + 25° = 180° (∵ x = 25°)
⇒ y + 110°= 180°
⇒ y = 180° – 110°
⇒ y = 70°
In the triangle ΔPQR, Sum of the angles of a triangle is 180°
∴ x + y + z = 180°
⇒ 25° + 70° + z = 180°
⇒ 95° + z = 180°
⇒ z = 180° – 95°
⇒ z = 85°
Hence,
x = 25°, y = 70° and z = 85°
Question 6.
In the given figure, if ΔABC right angled at B, then show that ∠x = ∠y.
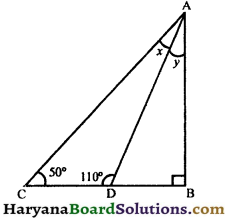
Solution :
Since, CDB is a straight line.
∠ADC + ∠ADB= 180°,(Linear pair axiom)
⇒ 110° + ∠ADB = 180°
⇒ ∠ADB = 180° – 110°
⇒ ∠ADB = 70°
In ΔABD, we have
∠ADC = ∠DAB + ∠ABD,
⇒ 110° = ∠y + 90°
⇒ 110° – 90° = ∠y
⇒ ∠y = 20° ………..(i)
Again in ΔADC, we have
∠ADB = ∠ACD + ∠DAC,
(By theorem 6.8)
⇒ 70° = 50° + ∠x
⇒ 70° – 50° = ∠x
⇒ ∠x = 20° ………..(ii)
From (i) and (ii), we get
∠x = ∠y. Hence proved
Question 7.
In the figure 6.110, AB || CD and EF is a transversal. Prove that bisectors of interior angles on the same side of transversal EF intersect at right angle. [NCERT Exemplar Problems]
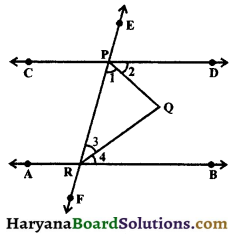
Solution :
Since AB || CD and EF is the transversal.
∠DPR + ∠PRB = 180°, (A pair of interior angles of the same side of transversal is supplementary) …(i)
⇒ ∠1 + ∠2 + ∠3 + ∠4 = 180°
But
∠1 = ∠2, (∵ PQ is the bisector of ∠DPR) …(ii) and
∠3 = ∠4, (∵ RQ is the bisector of ∠PRB) …(iii)
From (i), (ii) and (iii), we get
∠1 + ∠1 + ∠3 + ∠3 = 180°
⇒ 2∠1 + 2∠3 = 180°
⇒ 2(∠1 + ∠3) = 180°
⇒ ∠1 + ∠3 = 90° ……..(iv)
In the ΔPQR, Sum of the angles of a triangle is 180°,
∴ ∠1 + ∠3 + ∠PQR = 180°
⇒ 90° + ∠PQR = 180°,
[From (iv), ∠1 + ∠3 = 90°]
⇒ ∠PQR = 180° – 90°
⇒ ∠PQR = 90°
⇒ ∠PQR = a right angle
Hence, bisectors of interior angles on the same side of the transversal EF intersect at right angle.
Hence Proved
![]()
Question 8.
In the given figure, AD || BC, if y0 = \(\frac {3}{4}\)x0 and x0 = \(\frac {4}{5}\)z0, find the values of x0, y0, z0 and k0.
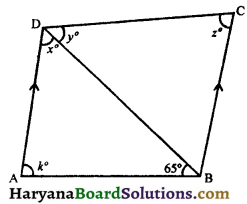
Solution :
Since, AD || BC and BD is the transversal.
∴ ∠DBC = ∠ADB,
(Alternate interior angles)
⇒ ∠DBC = x0
In ΔBDC, we have
x° + y° + z° = 180°, (Sum of angles of a triangle = 180°)

Now in ΔDAB,
∠DAB + ∠ADB + ∠ABD = 180°,
(Sum of angles of a triangle = 180°)
⇒ k° + x° + 65° = 180°
⇒ k° + 60° + 65° = 180° (∵ x = 60°)
⇒ k° + 125° = 180°
⇒ k° = 180° – 125°
⇒ k° = 55°
Hence,
x° = 60°, y° = 45°, z° = 75° and k° = 55°
Question 9.
The side BC of a tr iangle ΔABC is produced to D. The bisector of ∠A meets BC at M (see in figure). Prove that ∠ABC + ∠ACD = 2∠AMC.
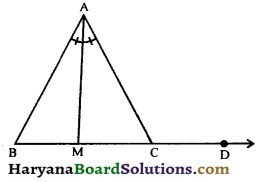
Solution :
In ΔABC, we have
∠ACD = ∠ABC + ∠BAC,
(By theorem 6.8) …(i)
But AM is the bisector of ∠BAC. (Given)
∴ ∠BAM = ∠CAM
or ∠BAC = 2∠BAM
Putting the value of ∠BAC in (i), we get
∠ACD = ∠ABC + 2∠BAM … (ii)
Again, in ΔABM, we have
∠AMC = ∠ABC + ∠BAM
⇒ 2∠AMC = 2∠ABC + 2∠BAM ……(iii)
Subtracting (ii) from (iii), we get
2∠AMC – ∠ACD = ∠ABC
⇒ 2∠AMC = ∠ABC + ∠ACD
⇒ ∠ABC + ∠ACD = 2∠AMC. Hence proved
Question 10.
If two parallel lines are intersected by a transversal, prove that the bisectors of the two pairs of interior angles enclose a rectangle.

Solution :
Given : Two parallel lines AB and CD are intersected by a transversal EF at P and R respectively. PQ, RS, PS and RQ are the bisectors of the two pairs of interior angles.
To prove: PQRS is a rectangle.
Proof : ∠BPR = ∠PRC,
(A pair of alternate interior angles)
⇒ \(\frac {1}{2}\)∠BPR = \(\frac {1}{2}\)∠PRC
⇒ ∠QPR = ∠PRS
[∵ PQ and RS are bisectors of ∠BPR and ∠PRC
∴ ∠QPR = \(\frac {1}{2}\)∠BPR and ∠PRS = \(\frac {1}{2}\)∠PRC]
But these are alternate interior angles.
PQ || SR, (By theorem 6.3)
Similarly, SP || RQ
∴ PQRS is a parallelogram.
Now, ∠BPR + ∠PRD = 180°,
(Sum of a pair of allied angles = 180°)
⇒ \(\frac {1}{2}\)∠BPR + \(\frac {1}{2}\)∠PRD = \(\frac {180°}{2}\)
⇒ \(\frac {1}{2}\)∠BPR + \(\frac {1}{2}\)∠PRD = 90°
⇒ ∠QPR + ∠QRP = 90° ,
[∵ PQ and RQ are the bisectors of ∠BPR and ∠PRD respectively]
Now in ΔPQR,
∠QPR + ∠PQR + ∠QRP = 180°,
(Sum of angles of a triangle is 180°)
⇒ ∠PQR + 90° = 180°, [Using (i)]
⇒ ∠PQR = 180° – 90° = 90°
In a parallelogram PQRS, ∠PQR = 90°
Hence, PQRS is a rectangle. Hence Proved
![]()
Question 11.
In the given figure, AB = AC in ΔABC. From B, BP is drawn such that BP = BC. From P, a line PQ is drawn parallel to BC to meet AB at Q. If exterior ∠RAB = 124°, find ∠BPQ.

Solution :
In ΔABC, we have
AB = AC
⇒ ∠ACB = ∠ABC, (The angles opposite to equal sides of a triangle are equal)
∠RAB = ∠ACB + ∠ABC, (By theorem 6.8)
⇒ 124° = ∠ABC + ∠ABC [∵ ∠ACB = ∠ABC]
⇒ 124° = 2∠ABC
⇒ \(\frac {124°}{2}\) = ∠ABC
⇒ ∠ABC = 62°
∴ ∠ACB = ∠ABC = 62°
Now in ΔBPC, we have
BP = BC, (Given)
∠BPC = ∠PCB, (The angles opposite to equal sides of a triangle are equal)
⇒ ∠BPC = ∠PCB = 62°, (∵ ∠PCB = ∠ACB)
In ΔBPC, we have
∠BPC + ∠PCB + ∠PBC = 180°,
(Sum of angles of a triangle = 180°)
⇒ 62° + 62° + ∠PBC = 180°
⇒ 124° + ∠PBC = 180°
⇒ ∠PBC = 180° – 124°
⇒ ∠PBC = 56°
Since, PQ || BC (Given)
∴ ∠BPQ = ∠PBC (A pair of alternate interior angles are equal)
⇒ ∠BPQ = 56°
Hence, ∠BPQ = 56°
Question 12.
In figure, ∠B > ∠C and L is a point on BC such that AL is the bisector of ∠BAC. If AM ⊥ BC, prove that ∠LAM = \(\frac {1}{2}\)(∠B – ∠C). [NCERT Exemplar Problems]

Solution :
Given : In ΔABC, AL is the bisector of ∠BAC and AM ⊥ BC.
To prove : ∠LAM = \(\frac {1}{2}\)(∠B – ∠C).
Proof : Since AL is the bisector of ∠BAC.
∴ ∠BAL = ∠CAL
⇒ ∠1 + ∠2 = ∠3 ………….(i)
In ΔAMB, ∠AMB = 90°, [∵ AM ⊥ BC]
∴ ∠ABM + ∠AMB + ∠1 = 180°,
(∵ Sum of angles of a triangle = 180°)
⇒ ∠ABM + 90° + ∠1 = 180°
⇒ ∠ABM = 180° – 90° – ∠1
⇒ ∠ABM = 90° – ∠1 ……..(ii)
Again in ΔAMC, we have
∠ACM + ∠AMC + ∠2 + ∠3 = 180°,
(∵ Sum of angles of a triangle = 180°)
⇒ ∠ACM + 90° + ∠2 + ∠3 = 180°
⇒ ∠ACM = 180° – 90° – ∠2 – ∠3
⇒ ∠ACM = 90° – ∠2 – ∠3 …….(iii)
Subtracting (iii) from (ii), we get
∠ABM – ∠ACM = 90° – ∠1 – 90° + ∠2 + ∠3
⇒ ∠B – ∠C = ∠2 + ∠3 – ∠1
⇒ ∠B – ∠C = ∠2 + (∠1 + ∠2) – ∠1,
[From (i), ∠3 = ∠1 + ∠2]
⇒ ∠B – ∠C = 2∠2
⇒ ∠2 = \(\frac {1}{2}\)(∠B – ∠C)
⇒ ∠LAM = \(\frac {1}{2}\)(∠B – ∠C).
Hence proved.
Question 13.
In figure, P and Q are two plane mirrors perpendicular to each other. Show that incident ray AB is parallel to the reflected ray CD.
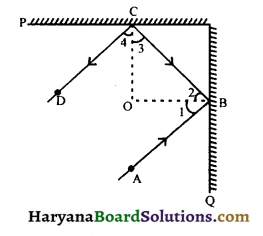
Solution :
∵ Angle of incidence = Angle of reflection
∴ ∠1 = ∠2 and ∠3 = ∠4
∴ ∠ABC = ∠1 + ∠2
= ∠2 + ∠2 = 2∠2 …(i)
and ∠DCB = ∠3 + ∠4 = ∠3 + ∠3
= 2∠3 …(ii)
Since, the two mirrors are perpendicular, the rays perpendicular to them are also perpendicular.
i.e., BO ⊥ OC or ∠BOC = 90°
In ΔBOC, we have
∠2 + ∠3 + ∠BOC= 180°,
(Sum of angles of a triangle = 180°)
⇒ ∠2 + ∠3 + 90° = 180°
⇒ ∠2 + ∠3 = 180° – 90°
⇒ ∠2 + ∠3 = 90°
⇒ 2∠2 + 2∠3 = 180°
⇒ ∠ABC + ∠DCB = 180°, [Using (i) and (ii)]
Thus, sum of a pair of co-interior angles ∠ABC and ∠DCB is 180°.
By theorem 6.5, we have
AB || CD. Hence proved
Multiple Choice Questions
Choose the correct alternative each of the following :
Question 1.
If two angles are supplementary of each other, then each angle is :
(a) a right angle
(b) an acute angle
(c) an obtuse angle
(d) a straight angle
Solution :
(a) a right angle
![]()
Question 2.
The complement of 47° 32′ 45″ is:
(a) 43° 28′ 15″
(b) 43° 27′ 15″
(c) 42° 27′ 15″
(d) 43° 27′ 15″
Solution :
(c) 42° 27′ 15″
Question 3.
The supplement of 75° 30′ 50″ is :
(a) 14° 29′ 10″
(b) 15° 30′ 10″
(c) 105° 30′ 10″
(d) 104° 29′ 10″
Solution :
(d) 104° 29′ 10″
Question 4.
The angles a triangle are in the ratio 5 : 3 : 7 The triangle is: [NCERT Exemplar Problems]
(a) an acute angled triangle
(b) an obtused angled triangle
(c) a right triangle
(d) an isosceles triangle
Solution :
(a) an acute angled triangle
Question 5.
If angles of a triangle are in the ratio 1 : 2 : 3, then the smallest angle of the triangle is :
(a) 60°
(b) 30°
(c) 90°
(d) 50°
Solution :
(b) 30°
Question 6.
If one angle of a triangle is equal to the sum of the other two angles, then triangle is : [NCERT Exemplar Problems]
(a) a right angled triangle
(b) acute angled triangle
(c) obtuse angled triangle
(d) equilateral triangle
Solution :
(a) a right angled triangle
Question 7.
If one of the angles of a triangle is 130°, then the angle between the bisectors of the other two angles can be : [NCERT Exemplar Problems]
(a) 50°
(b) 65°
(c) 145°
(d) 155°
Solution :
(d) 155°
Question 8.
In ΔPQR, side QR is produced to S such that ∠PRS = 110, if ∠P = ∠Q, then ∠Q is equal to :
(a) 70°
(b) 55°
(c) 50°
(d) 45°
Solution :
(b) 55°
![]()
Question 9.
In the figure, ∠x + ∠y + ∠z is equal to :
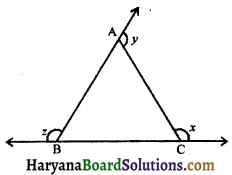
(a) 180°
(b) 90°
(c) 360°
(d) 270°
Solution :
(c) 360°
Question 10.
In the figure, ∠A + ∠B + ∠C + ∠P + ∠Q + ∠R is equal to :
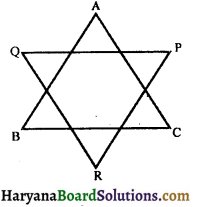
(a) 180°
(b) 270°
(c) 90°
(d) 360°
Solution :
(d) 360°