Haryana State Board HBSE 9th Class Maths Important Questions Chapter 9 Areas of Parallelograms and Triangles Important Questions and Answers.
Haryana Board 9th Class Maths Important Questions Chapter 9 Areas of Parallelograms and Triangles
Very Short Answer Type Questions
Question 1.
In the given figure ABCD is a quadrilateral and AC is one of its diagonal. Show that ABCD is a parallelogram and finds its area.
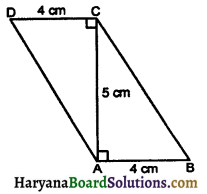
Solution:
We have,
∠ACD = ∠CAB (each angle = 90°)
But these are alternate interior angles.
∴ AB || CD
and AB = CD = 4 cm
∴ ABCD is a parallelogram.
Area of parallelogram ABCD = base × height
= AB × AC
= 4 × 5
= 20 cm2
Hence,
ar (||gm ABCD) = 20 cm2.
Question 2.
In the given figure, ABCD and QPCD are rectangle and parallelogram respectively. If area of ΔQPD is 35 cm2, then find the area of rectangle ABCD.
Solution:
Since rectangle ABCD and parallelogram QPCD are on the same base CD and between the same parallels CD and BQ.
∴ ar (rectangle ABCD) = ar(||gm QPCD)…(i)
[since rectangle is also a parallelogram]
Now, ΔQPD and parallelogram QPCD are on the same base QP and between the same parallels QP and CD.
ar (ΔQPD) = \(\frac{1}{2}\)ar (||gm QPCD) …..(ii)
From (i) and (ii), we get
ar (ΔQPD) = \(\frac{1}{2}\)ar (rectangle ABCD) [Using (i)]
⇒ 35 = \(\frac{1}{2}\)ar (rectangle ABCD),
[It is given that ar (AQPD) = 35 cm2]
⇒ 70 = ar (rectangle ABCD)
Hence,
ar (rectangle ABCD)= 70 cm2.
![]()
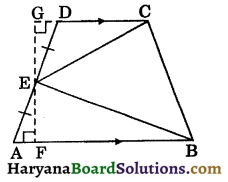
Question 3.
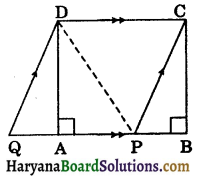
In the given figure, triangles DAC and BAC are on same base AC. If vertex B and D are on opposite side of AC such that area of ΔDAC is equal to area of ΔBAC. Prove that OD = OB.
Solution:
Draw BM ⊥ AC and DN ⊥ AC.
ar (ΔDAC) = ar (ΔBAC), (given)
⇒ \(\frac{1}{2}\)AC × DN = \(\frac{1}{2}\)AC × BM
⇒ DN = BM ……(i)
In ΔDNO and ΔBMO, we have
∠DNO = ∠BMO,
(by construction each = 90°)
∠DON = ∠BOM
(vertically opposite angles)
DN = BM (as proved above)
∴ ΔDNO ≅ ΔBMO,
(By AAS congruence rule)
⇒ OD = OB (CPCT) Hence proved
Question 4.
In a rhombus ABCD, AC and BD are its diagonals. Show that area of ABCD is equal to \(\frac{1}{2}\)(AC × BD)
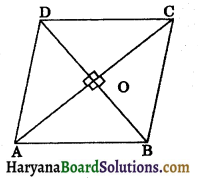
Solution:
Given: A rhombus ABCD whose diagonals AC and BD intersect at O.
To prove : ar (rhombus ABCD) = \(\frac{1}{2}\)(AC × BD).
Proof : Since diagonals of rhombus bisect each other at right angles.
∴ AO ⊥ BD and OC ⊥ BD
Now
⇒ ar (rhombus ABCD) = ar (ΔDAB) + ar (ΔBCD)
⇒ ar (rhombus ABCD) = \(\frac{1}{2}\)(BD × AO) + (BD × OC)
⇒ ar (rhombus ABCD) = \(\frac{1}{2}\)(AO + OC)
⇒ ar (rhombus ABCD) = \(\frac{1}{2}\)(BD × AC)
⇒ ar (rhombus ABCD) = \(\frac{1}{2}\)(AC × BD).
Hence proved
Question 5.
In the given figure, AD is the median of ΔABC and DE is the median of ΔABD. Show that:
ar (ΔABC) = 4 × ar(ΔBED).
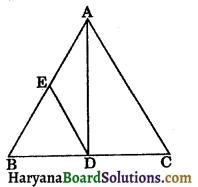
Solution:
Since AD is the median of AABC.
∴ ar (ΔABD) = ar (ΔACD)
[∵ a median divides the triangle into two triangles of equal areas]
⇒ ar (ΔABD)= \(\frac{1}{2}\)ar (ΔABC) …(i)
Again, DE is the median of ΔABD.
∴ ar (ΔBED) = \(\frac{1}{2}\)ar (ΔABD)
⇒ ar (ΔBED) = \(\frac{1}{2} \cdot \frac{1}{2}\)ar(ΔABC) [using (i)]
⇒ ar (ΔBED) = \(\frac{1}{4}\)ar (ΔABC)
⇒ ar (ΔABC) = 4 ar (ΔBED).
Hence proved
![]()
Question 6.
In fig. 9.78 BD || CA, E is the mid point of CA and BD = \(\frac{1}{2}\)CA. Prove that ar (ABC) = 2 ar (DBC)
Solution:
Join DE. Since, BD = CE and BD || CE. Therefore, BCED is a parallelogram.
∴ Triangles DBC and EBC are on the same base BC and between the same prallels BC and DE.
∴ ar (DBC) = ar (EBC) …(i)
In ΔABC, BE is the median and we know that a median divides the triangles into two triangles of equal areas.
∴ ar (EBC) = \(\frac{1}{2}\)ar (ABC)
⇒ ar (ABC) = 2 ar (EBC)
⇒ ar (ABC) = 2 ar (DBC) [Using (i)]
Hence, ar (ABC) = 2 ar (DBC). Proved
Short Answer Type Questions
Question 1.
In the given figure, ABCD and ABFE are parallelogram on the same base AB. Prove that :
(i) ar (ΔADB) + ar (ΔBFA) = ar (llgm ABFE)
(ii) If area of ||gm ABCD is 72 cm2
Find the area of ΔBFA.
Solution:
(i) Since parallelograms ABCD and ABFE are on the same base AB and between the same parallels AB and CE.
∴ ar (||gm ABCD) = ar (||gm ABFE) …(i)
ΔBFA and parallelogram ABFE are on the same base AB between the same parallels AB and FE.
∴ ar (ΔBFA) = \(\frac{1}{2}\)ar (||gm ABFE) …(ii)
ΔADB and parallelogram ABCD are on the same base AB and between the same parallels AB and CD.
∴ ar (ΔADB) = \(\frac{1}{2}\)ar (||gm ABCD) ….(iii)
Adding (ii) and (iii), we get
ar (ΔBFA) + ar (ΔADB) = \(\frac{1}{2}\)ar (||gm ABFE) + \(\frac{1}{2}\)ar (ABCD)
⇒ ar (ΔADB) + ar (ΔBFA) = \(\frac{1}{2}\)ar (||gm ABFE) + ar (||gm ABFE),
[∵ From (i) ar (||gm ABCD) = ar (||gm ABFE)
∴ \(\frac{1}{2}\)ar (||gm ABCD) = \(\frac{1}{2}\)ar (||gm ABFE)]
⇒ ar (ΔADB) + ar (ΔBFA) = ar (||gm ABFE). Hence proved
(ii) From (i) and (ii), we get
ar (ΔBFA) = \(\frac{1}{2}\)ar (||gm ABCD)
⇒ ar (ΔBFA) = \(\frac{1}{2}\) × 72,
It is given that
ar (||gm ABCD = 72 cm2)
⇒ ar (ΔBFA) = 36 cm2
Hence ar (ΔBFA) = 36 cm2.
![]()
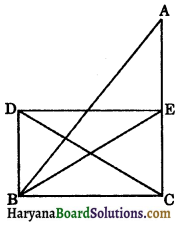
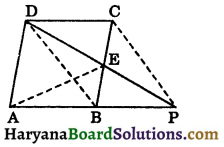
Question 2.
ABCD is a parallelogram in which BC is produced to E such that CE = BC (see fig 9.80). AE intersects CD at F. If ar(DFB)= 3 cm2, find the area of the parallelogram ABCD. [NCERT Exemplar Problems]
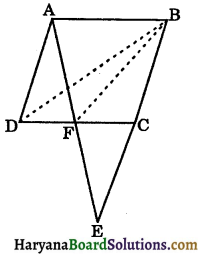
Solution:
In ΔEAB
Since, FC || AB (∵ CD || AB) and C is the mid point of BE. Therefore, F is the mid point of CD
∴ BF is the median in ΔBCD.
Since, we know that a median divides a
triangle into two triangles of equal areas.
∴ ar(CFB) = ar (DFB)
Now ar (BCD) = ar (CFB) + ar (DFB)
⇒ ar (BCD) = 2 ar (DFB)
⇒ ar (BCD) = 2 × 3 = 6 cm2
Since, BD is a diagonal of parallelogram ABCD and we know that a diagonal divides the parallelogram into two triangles of equal areas.
∴ ar (||gm ABCD) = 2 × ar (BCD)
= 2 × 6 = 12 cm2
Hence,
ar (||gm ABCD)= 12 cm2.
Question 3.
In the given figure PQR is a triangle in which PM divides QR in the ratio a : b.
Show that ar(ΔPQM)/ar(ΔPRM) = a/b.
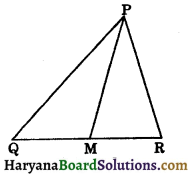
Solution:
Given : In ΔABC, PM divides QR in the ratio a : b.
To prove ar(ΔPQM)/ar(ΔPRM) = a/b
Construction : Draw PN ⊥ QR.
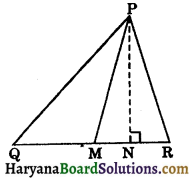
Proof : Since QM : MR = a : b
⇒ \(\frac{Q M}{M R}=\frac{a}{b}\) …..(i)
Area of ΔPQM = \(\frac{1}{2}\)QM × PN …..(ii)
and Area of ΔPRM = \(\frac{1}{2}\)MR × PN …..(iii)
Dividing (ii) by (iii), we get

Question 4.
In the given figure, AC is the diagonal of quadrilateral ABCD and DE is drawn parallel to AC, which meets BA produced at point E such that ED = AC. Prove that ar (ΔCBE) = ar (quad. ABCD)

Solution:
Since
ED || AC and ED = AC
∴ ACDE is a parallelogram.
Since ΔACD and parallelogram ACDE are on the same base AC and between the same parallels AC and DE.
∴ ar (ΔACD) = \(\frac{1}{2}\)ar (||gm ACDE) ……(i)
Similarly, ΔACE and parallelogram ACDE are on the same base AC and between the same parallels AC and DE.
∴ ar (ΔACE) = \(\frac{1}{2}\)ar (||gm ACDE) ……(ii)
From (i) and (ii), we get
ar (ΔACE) = ar (ΔACD)
⇒ ar(ΔACE) + ar(ΔABC) = ar(ΔACD) + ar(ΔABC)
[Adding ar (SABC) on both sides]
⇒ ar (ΔCBE) = ar (quadrilateral ABCD).
Hence proved
![]()
Question 5.
In the figure AB || CD || EF, BC || AE and CE || BF. Prove that ar (CEFH) = ar (ABCD).
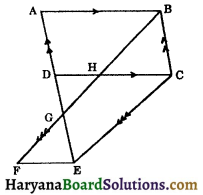
Solution:
Since,
AB || CD and AD || BC [∵ AE || BC]
∴ ABCD is a parallelogram.
Now CD || EF and CE || BF
⇒ HC || EF and CE || HF
∴ CEFH is a parallelogram.
Again,
AE || BC and CD || EF
⇒ GE || BC and HC || FE
∴ GECB is a parallelogram.
Now parallelogram GECB and ABCD are on the same base BC and between the same parallels AE and BC.
∴ ar (||gm GECB) = ar (||gm ABCD) …(i)
Parallelograms GECB and CEFH are on the same base CE and between the same parallels CE and BF.
∴ ar (||gm GECB)= ar (||gm CEFH) …(ii)
From (i) and (ii), we get
ar (||gm CEFH) = ar (||gm ABCD). Hence proved
Question 6.
In the given figure, D is a point on the side BC of ΔABC such that BD : CD = 2 : 3. Show that:
ar (ΔACD) = \(\frac{3}{5}\)ar (ΔABC).
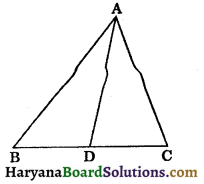
Solution:
Draw AE ⊥ BC
In ΔABC, we have
BD : CD = 2 : 3
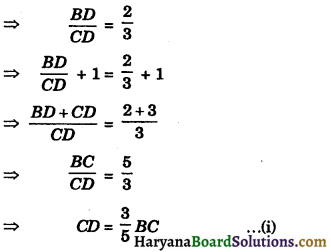
Now ar (ΔABC) = \(\frac{1}{2}\) × BC × AE ……(i)
and ar (ΔACD) = \(\frac{1}{2}\) × CD × AE
⇒ ar (ΔACD) = \(\frac{1}{2}\) × \(\frac{3}{5}\) × BC × AE
[From (1), CD = \(\frac{3}{5}\)BC]
⇒ ar (ΔACD) = \(\frac{3}{5}\)(\(\frac{1}{2}\) × BC × AE)
⇒ ar (ΔACD) = \(\frac{3}{5}\)ar (ΔABC) [using (ii)]
Hence proved
![]()
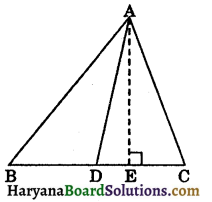
Question 7.
The medians AD and BE of a triangle ABC intersect at G. Prove that :
ar (ΔABG) = ar (quad. GECD).
Solution:
Since D and E are the mid points of BC and AC respectively.
∴ DE || AB
Now, ΔABE and ΔABD are on the same base AB and between the same parallels AB and ED.
∴ ar (ΔABE) = ar (ΔABD) …(i) (By theorem 9.2)
In a triangle ABC, BE is the median and we know that a median divides the triangle into, two triangles of equal areas.
∴ ar (ΔABE) = ar (ΔCBE) …(ii)
From (i) and (ii), we get
ar (ΔABD) = ar (ΔCBE)
⇒ ar (ΔABD) – ar (ΔGBD) = ar (ΔCBE) – ar (ΔGBD)
⇒ ar (ΔABG) = ar (quad. GECD). Hence proved
Question 8.
In the figure AB || CQ and CS || AT. Prove that:
(i) ar (ΔAPQ) = ar (ΔCPB)
(ii) ar (ΔACR) = ar (ΔSRT)
(iii) ar (quad. BCRQ) = ar (ΔSRT).

Solution:
(i) Since, ΔABQ and ΔBAC are on the same base AB and between the same parallels AB and CQ.
∴ ar (ΔABQ) = ar (ΔBAC) (By theorem 9.2)
⇒ ar(ΔABQ) – ar(ΔABP) = ar(ΔBAC) – ar(ΔABP)
⇒ ar (ΔAPQ) = ar (ΔCPB) …(i)
(ii) Since, ΔACT and ΔAST are on same base AT and between the same parallels AT and CS.
∴ ar (ΔACT) = ar (ΔAST)
⇒ ar(ΔACT) – ar (ΔART) = ar(ΔAST) – ar(ΔART)
⇒ ar (ΔACR) = ar (ΔSRT)
(iii) ar (ΔACR) = ar (ΔSRT)
⇒ ar (ΔAPQ) + ar (quad. PQRC) = ar (ΔSRT)
⇒ ar (ΔCPB) + ar (quad. PQRC) = ar (ΔSRT) [using (i)]
⇒ ar (quad. BCRQ) = ar (ΔSRT). Hence proved
Question 9.
In the given figure, D is the mid point of side AB of the SABC, E is any point on BC such that DE || FC. Prove that FE bisects the ΔABC.
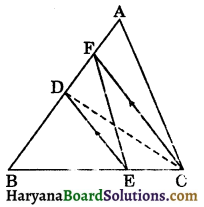
Solution:
Given: D is the mid point of the side AB of ΔABC. E is the point on BC such that DE || FC.
To prove : FE bisects ΔABC.
Construction : Join CD.
Proof : Since ΔFCD and ΔFCE are on the same base FC and between the same parallels FC and DE.
∴ ar (ΔFCD) = ar (ΔFCE)
⇒ ar (ΔFCD) + ar (ΔACF) = ar (ΔFCE) + ar (ΔACF)
⇒ ar (ΔACD) = ar (quad. AFEC) …(i)
In ΔABC, CD is the median.
ar (ΔACD) = \(\frac{1}{2}\)ar (ΔABC) …(ii)
From (i) and (ii), we get
ar (ΔACD) = ar (quad. AFEC) = \(\frac{1}{2}\)ar (ΔABC).
Hence, FE bisects ΔABC. Hence proved
![]()
Question 10.
Through the vertex A of a parallelogram ABCD, line AEF is drawn to meet BC at E and DC produced at F. Show that the triangles BEF and DCE are equal in area.
Solution:
Given: In a||gm ABCD, through vertex A, a straight line AEF is drawn to meet BC at E and DC produced at F.
To prove : ar (ΔBEF) = ar (ΔDCE).
Construction : Join BD.
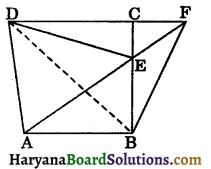
Proof: Since ΔABF and ||gm ABCD are on the same base AB and between the same parallels AB and DF.
∴ ar (ΔABF) = \(\frac{1}{2}\)ar (||gm ABCD ……(i)
Diagonal BD divides parallelogram ABCD into two triangles of equal area.
∴ ar (ΔBCD) = ar (||gm ABCD) ……(ii)
From (i) and (ii), we get
ar (ΔABF) = ar (ΔBCD) …(iii)
Now, ΔABE and ΔDBE are on the same base BE and between the same parallels BE and AD.
∴ ar (ΔABE) = ar (ΔDBE) ……(iv)
Subtracting (iv) from (iii), we get
ar (ΔABF) – ar (ΔABE) = ar (ΔBCD) – ar (ΔDBE)
⇒ ar (ΔBEF) = ar (ΔDCE). Hence proved
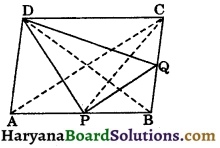
Question 11.
In the given figure, ABCD is a parallelogram. P is any point on AB. CB and DP are produced to meet Q. Prove that:
(i) ar (ΔCPQ) = ar (ΔBDQ)
(ii) If P is the mid point of AB, then prove that:
ar (ΔPBC) + ar (ΔPBD) = \(\frac{1}{2}\)ar (||gm ABCD).

Solution:
(i) Since ΔPBC and ΔPBD are on the same base PB and between the same parallels PB and CD.
∴ ar(ΔPBC) = ar (ΔPBD) ……(i)
⇒ ar (ΔPBC) + ar (ΔPBQ) = ar (ΔPBD) + ar (ΔPBQ)
⇒ ar (ΔCPQ) = ar (ΔBDQ).
(ii) ∵ Diagonal BD divides parallelogram ABCD into two triangles of equal areas.
∴ ar (ΔBAD) = \(\frac{1}{2}\)ar (||gm ABCD) …….(ii)
In ΔBAD, DP is the median.
∴ ar (ΔPBD) = \(\frac{1}{2}\)ar (ΔBAD)
⇒ ar (ΔPBD) = \(\frac{1}{2}\) · \(\frac{1}{2}\)ar (||gm ABCD) [using (ii)]
⇒ ar (ΔPBD) = \(\frac{1}{4}\)ar (||gm ABCD) ……(iii)
From (i) and (iii), we get
ar (ΔPBC) = ar (ΔPBD) = \(\frac{1}{4}\)ar (||gm ABCD)
Now, ar (ΔPBC) + ar (ΔPBD) = \(\frac{1}{4}\)ar (||gm ABCD + \(\frac{1}{4}\)ar (||gm ABCD)
⇒ ar (ΔPBC) + ar (ΔPBD) = \(\frac{1}{2}\)ar (||gm ABCD). Hence proved
Long Answer Type Questions
Question 1.
If the area of an equilateral triangle is equal to the area of a square, prove that the perimeter of the equilateral triangle is greater than the perimeter of the square.
Solution:
Let the side of the equilateral triangle be x units and side of the square be y units.
∴ Area of equilateral triangle = \(\frac{\sqrt{3}}{4} x^2\) square units
and area of a square = y2 square units
According to question,
Area of equilateral triangle = Area of a square

Therefore, perimeter of an equilateral triangle is greater than perimeter of a square.
Hence proved
![]()
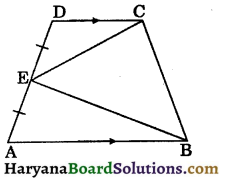
Question 2.
In the given figure, D and E are respectively the mid points of the sides AB and AC of a ΔABC. If XY || BC and BEX and CDY are straight lines, prove that:
(i) ar (ΔADY) = ar (ΔAEX)
(ii) ar (ΔACY) = ar (ΔBX).
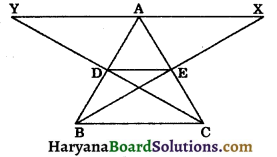
Solution:
Since D and E are the respectively mid points of the sides AB and AC.
Therefore, DE || BC
⇒ BC || DE || XY
(i) In ΔAEX and ΔCEB, we have
∠AEX = ∠CEB (vertically opposite angles)
∠AXE = ∠CBE
[∵ XY || BC ⇒ alternate interior angle AXE and CBE are equal]
and AE = EC
[∵ E is the mid point of AC]
∴ ΔAEX ≅ ΔCEB
(By AAS congruence rule)
⇒ ar (ΔAEX) = ar (ΔCEB) …(i)
Similarly, ΔADY ≅ ΔBDC
⇒ ar (ΔADY) = ar (ΔBDC) …(ii)
But ΔBDC and ΔCEB are on the same base BC and between the same parallels DE and BC.
∴ ar(ΔBDC) = ar (ΔCEB) …(iii)
From (i), (ii) and (iii), we get
ar (ΔADY) = ar (ΔAEX) …(iv)
(ii) Now, ΔDEB and ΔEDC are on the same base DE and between the same parallels DE and BC.
∴ ar (ΔDEB) = ar (ΔEDC)
⇒ ar (ΔDEB) + ar (ΔADE) = ar (ΔEDC) + ar (ΔADE)
⇒ ar (ΔABE) = ar (ΔACD)
⇒ ar (ΔACD) = ar (ΔABE) …..(v)
Adding (iv) and (v), we get
ar (ΔADY) + ar (ΔACD) = ar (ΔAEX) + ar (ΔABE)
⇒ ar (ΔACY) = ar (ΔABX). Hence proved
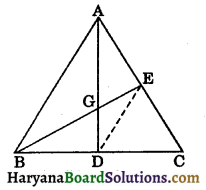
Question 3.
In the figure, ABC is a triangle in which E and D are the points on AC such that AE = ED = CD. EF drawn parallel to AB and FD is joined. If AF and BE intersect at G, then prove that:
(i) ar (ΔAEG) = ar (ΔBFG)
(ii) ar (ΔAFD) = ar (quad. BEDF)
(iii) ar (ΔAFC) = 3 ar (ΔFED).
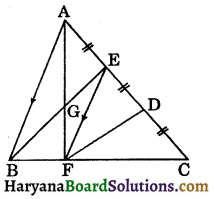
Solution:
(i) ΔABE and ΔABF are on the same base AB and between the same parallels AB and EF.
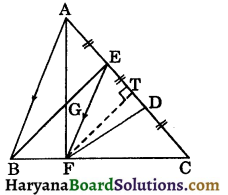
ar (ΔABE) = ar (ΔABF)
ar (ΔABE) – ar (ΔABG) = ar (ΔABF) – ar (ΔABG)
⇒ ar(ΔAEG) = ar (ΔBFG)
(ii) ar (ΔAEG) = ar (ΔBFG) (as proved above)
⇒ ar (ΔAEG) + ar (quad. GEDF) = ar (ΔBFG) + ar (quad. GEDF)
[Adding ar (quad. GEDF) on both sides]
⇒ ar (ΔAFD) = ar (quad. BEDF)
(iii) Draw FT ⊥ AC
Let AE = ED = CD = x
ar (ΔAEF) = \(\frac{1}{2}\)AE × FT
⇒ ar (ΔAEF) = \(\frac{1}{2}\) × x × FT ……(i)
Similarly,
ar (ΔFED) = \(\frac{1}{2}\) × x × FT …(ii)
and ar (ΔCDF) = \(\frac{1}{2}\) × x × FT …(iii)
From (i), (ii) and (iii), we get
ar (ΔAEF) = ar (ΔCDF) = ar (ΔFED) ……(iv)
Now, ar (ΔAFC) = ar (ΔAEF) + ar (ΔFED) + ar (ΔCDF)
⇒ ar (ΔAFC) = ar (ΔFED)+ ar (ΔFED) + ar (ΔFED) [using (iv)]
⇒ ar (ΔAFC)= 3 ar (ΔFED). Hence proved
![]()
Question 4.
In a parallelogram ABCD, the side AB is produced to point P such that BP = AB. A line DP intersects BC at E. Prove that:
(i) BPCD is a parallelogram
(ii) ar (ΔCEP) = \(\frac{1}{2}\)ar (ΔAED).
Solution:
(i) Since ABCD is a parallelogram.
∴ AB || CD
⇒ BP || CD [∵ AB = BP]
and AB = CD
AB = BP (given)
∴ BP = CD
Thus, BP = CD and BP || CD
⇒ BPCD is a parallelogram.
(ii) Since, BPCD is a parallelogram and BC and DP are its diagonals.
We know that in a parallelogram a diagonal divides the parallelogram into two triangles of equal areas.
∴ ar (ΔCBP) = ar (ΔCBD)
⇒ ar (ΔCBP) = \(\frac{1}{2}\)ar (||gm BPCD)…(i)
We know that diagonals of a parallelogram bisect each other.
∴ E is the mid point of BC.
⇒ ar (ΔCEP) = ar (ΔBEP)
[a median divides the triangle into two triangles of equal areas]
⇒ ar (ΔCEP) = \(\frac{1}{2}\)ar (ΔCBP) …(ii)
From (i) and (ii), we get
ar (ΔCEP) = \(\frac{1}{2} \cdot \frac{1}{2}\)ar (||gm BPCD)
⇒ ar (ΔCEP) = \(\frac{1}{4}\)ar (||gm BPCD) …(ii)
Parallelograms ABCD and BPCD are on the same base CD and between the same parallels CD and AP.
∴ ar (||gm ABCD) = ar (||gm BPCD) …(iv)
From (iii) and (iv), we get
ar (ΔCEP) = \(\frac{1}{4}\)ar (||gm ABCD)
4 ar (ΔCEP) = ar (||gm ABCD) …(v)
Now, ΔAED and parallelogram ABCD are on the same base AD and between the same paralles AD and BC.
∴ ar (ΔAED) = \(\frac{1}{2}\)ar (||gm ABCD)
⇒ 2 ar (ΔAED) = ar (||gm ABCD) …(vi)
From (v) and (vi), we get
4 ar (ΔCEP) = 2 ar (ΔAED)
⇒ ar (ΔCEP) = \(\frac{2}{4}\)ar (ΔAED)
⇒ ar (ΔCEP) = \(\frac{1}{2}\)ar (ΔAED). Hence proved
Question 5.
P and Q are respectively the mid points of the sides AB and BC of a parallelogram ABCD. Prove that ar (ΔDPQ) = \(\frac{3}{8}\)ar (||gm ABCD).
Solution:
Given : P and Q are respectively the mid points of the side AB and BC of a parallelogram ABCD.
To prove : ar (ΔDPQ) = \(\frac{3}{8}\)ar (||gm ABCD).
Construction : Join AC, BD and CP.
Proof : Since in ΔABC, P is the mid point of AB.
∴ CP is the median of ΔABC.
We know that a median divides the triangle into two triangles of equal areas.
∴ ar (ΔPBC) = \(\frac{1}{2}\)ar (ΔABC) …(i)
In ΔPBC, Q is the mid point of BC.
∴ PQ is the median of ΔPBC.
∴ ar (ΔPBQ) = \(\frac{1}{2}\)ar (ΔPBC)
⇒ 2 ar (ΔPBQ) = ar (ΔPBC) …….(ii)
From (i) and (ii), we get
2 ar (ΔPBQ) = \(\frac{1}{2}\)ar (ΔABC)
⇒ 4 ar (ΔPBQ) = ar (ΔABC) …….(iii)
Since, a diagonal divides the parallelogram into two triangles of equal area.
∴ ar (ΔABC) = \(\frac{1}{2}\)ar (||gm ABCD)..(iv)
From (iii) and (iv), we get
4 ar (ΔPBQ) = \(\frac{1}{2}\)ar (||gm ABCD)
⇒ ar (ΔPBQ) = \(\frac{1}{8}\)ar (||gm ABCD)…(v)
Since, diagonal BD divides parallelogram ABCD into two triangles of equal area.
∴ ar (ΔDAB) = \(\frac{1}{2}\)ar (||gm ABCD)..(vi)
In ΔDAB, DP is the median.
∴ ar (ΔDAP) = \(\frac{1}{2}\)ar (ΔDAB) …(vii)
From (vi) and (vii), we get
ar (ΔDAP) = \(\frac{1}{2} \cdot \frac{1}{2}\)ar (||gm ABCD)
ar (ΔDAP) = \(\frac{1}{4}\)ar (||gm ABCD) …..(8)
Similarly,
ar (ΔDCQ) = \(\frac{1}{4}\)ar (||gm ABCD) …..(9)
Now, ar (ΔDPQ) = ar (||gm ABCD) – [ar (ΔDAP) + ar (ΔDCQ) + ar (ΔPBQ)]
⇒ ar (ΔDPQ) = ar (||gm ABCD)

Question 6.
In the given figure, ABCD is a trapezium in which E is the mid point of AD. If E is joined to vertices B and C, prove that :
ar (ΔABE) + ar (ΔCDE) = \(\frac{1}{2}\)ar (trap. ABCD).
Solution:
Draw EF ⊥ AB and produced to opposite of EF meets CD produced at G.
Since, AB || CG
∴ ∠DGE = ∠AFE = 90° (alternate interior angles)
In ΔAFE and ΔDGE, we have
∠AFE = ∠DGE (Each = 90°)
∠AEF = ∠DEG (vertically opposite angles)
and AE = ED (∵ E is the mid point of AD)
∴ ΔAFE ≅ ΔDGE (By AAS congruence rule)
⇒ EF = EG (CPCT) ……(i)
Now, ar (ΔABE) = \(\frac{1}{2}\)AB × EF …(ii)
and ar (ΔCDE) = \(\frac{1}{2}\)CD × GE …(iii)
Adding (ii) and (iii), we get
ar (ΔABE) + ar (ΔCDE) = \(\frac{1}{2}\)AB × EF + \(\frac{1}{2}\)CD × GE
⇒ ar (ΔABE) + ar (ΔCDE) = \(\frac{1}{2}\)(AB × EF + CD × EF) [using (1)]
⇒ ar (ΔABE) + ar (ΔCDE) = \(\frac{1}{2}\)(AB + CD) × EF
⇒ ar (ΔABE) + ar (ΔCDE) = \(\frac{1}{2} \cdot \frac{1}{2}\)(AB + CD) × 2EF
⇒ ar (ΔABE) + ar (ΔCDE) = \(\frac{1}{2} \cdot \frac{1}{2}\)(AB + CD) × GF
⇒ ar (ΔABE) + ar (ΔCDE) = \(\frac{1}{2}\)ar (trap. ABCD).
Hence proved
![]()
Question 7.
In a triangle ABC, if the medians AD, BE and CF intersect at G. Show that:
ar (ΔABG) = ar (ΔACG) = ar (ΔBCG)
= \(\frac{1}{3}\)ar (ΔABC).
Solution:
Given : In a triangle ABC, medians AD, BE and CF intersect at G.
To prove: ar (ΔABG) = ar (ΔACG) = ar (ΔBCG)
= \(\frac{1}{3}\)ar (ΔABC).
Proof : We know that the median of a triangle divides it into two triangles of equal areas.
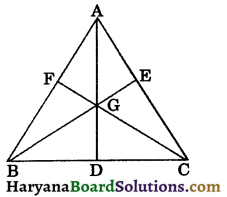
In ΔABC, AD is the median.
∴ ar (ΔABD) = ar (ΔACD) ….(i)
In ΔGBC, GD is the median.
∴ ar(ΔGBD) = ar (ΔGCD) …(ii)
Subtracting (ii) from (i), we get
ar (ΔABD) – ar (ΔGBD) = ar (ΔACD) – ar (ΔGCD)
⇒ ar (ΔABG) = ar (ΔACG) … (iii)
Similarly,
ar (ΔABG) = ar (ΔBCG) …(iv)
From (iii) and (iv), we get
ar (ΔABG) = ar (ΔACG) = ar (ΔBCG) …(v)
Now, ar(ΔABC) = ar (ΔABG) + ar (ΔACG) + ar (ΔBCG)
⇒ ar (ABC) = ar (ΔABG) + ar (ΔABG) + ar (ΔABG) [using (v)]
⇒ ar (ΔABC) = 3 ar (ΔABG)
⇒ ar(ΔABG) = \(\frac{1}{3}\)ar (ΔABC) …(vi)
From (v) and (vi), we get
ar (ΔABG) = ar (ΔACG)
= ar (ΔBCG)
= \(\frac{1}{3}\)ar (ΔABC). Hence proved
Question 8.
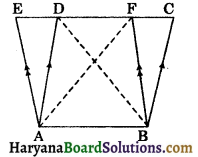
In the given figure, ABCD is a trapezium in which AB || CD, AB = 40 cm and CD = 30 cm. If M and N are respectively the mid points of AD and BC, prove that:
(i) MNCD is a trapezium
(ii) ar (trap. ABNM) = \(\frac{15}{13}\) ar(trap. MNCD).
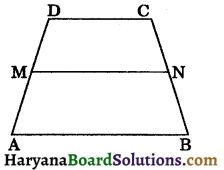
Solution:
(i) Join DN and produce it to meet AB produced at O.
In ΔDCN and ΔOBN, we have
∠DCN = ∠OBN (∵ CD || OA)
CN = BN
(∵ N is the mid point of BC)
and ∠CND = ∠BNO (vertically opp. angles)
∴ ΔDCN ≅ ΔOBN (By ASA congruence rule)
⇒ CD = OB (CPCT) …(i)
and DN = ON (CPCT)
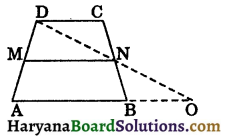
⇒ N is the mid point of OD.
In ΔAOD, M is the mid point of AD and N is the mid point of OD.
∴ MN || AO and MN = \(\frac{1}{2}\)AO
⇒ MN = \(\frac{1}{2}\)(AB + BO)
⇒ MN = \(\frac{1}{2}\)(AB + CD)
[From (i), OB = CD]
⇒ MN = \(\frac{1}{2}\)(40 + 30) = \(\frac{1}{2}\) × 70 = 35 cm
Now, MN || AO and CD || AB (given)
⇒ MN || AB and CD || AB
⇒ MN || CD
⇒ MNCD is a trapezium.
(ii) Since, M and N are respectively the mid points of AD and BC.
Therefore trapeziums MNCD and ABNM have the same height, say h cm.
ar (trap. ABNM) = \(\frac{1}{2}\)(AB + MN) × h
⇒ ar (trap. ABNM = \(\frac{1}{2}\)(40 + 35) × h = \(\frac{75}{2}\) × h ….(ii)
and ar (trap. MNCD) = \(\frac{1}{2}\)(MN + CD) × h
⇒ ar (trap. MNCD)= \(\frac{1}{2}\)(35 + 30) × h = \(\frac{65}{2}\) × h …..(iii)
Dividing (ii) by (iii), we get

Question 9.
ABCD is a trapezium in which AB || CD and E is the mid point of BC. Prove that:
ar (ΔAED) = \(\frac{1}{2}\)ar (trap. ABCD).

Solution:
Given : AB || CD and E is the mid point of BC.
To prove : ar (ΔAED) = \(\frac{1}{2}\)ar (trap. ABCD).
Construction : Join AC and BD.
Proof: ΔACD and ΔBCD are on the same base CD and between the same parallels AB and CD.
∴ ar (ΔACD) = ar (ΔBCD) …(i)
In ΔABC, AE is the median.
∴ ar (ΔAEB) = \(\frac{1}{2}\)ar (ΔABC) …(ii)
In ΔBCD, DE is the median.
∴ ar (ΔDEC) = \(\frac{1}{2}\)ar (ΔBCD) …….(iii)
Adding (ii) and (iii), we get
ar (ΔAEB) + ar (ΔDEC) = \(\frac{1}{2}\)ar (ΔABC) + \(\frac{1}{2}\)ar (ΔBCD)
⇒ ar (ΔAEB) + ar (ΔDEC) = \(\frac{1}{2}\)[ar (ΔABC) + ar (ΔBCD)]
⇒ ar (ΔAEB) + ar (ΔDEC) = \(\frac{1}{2}\)[ar (ABC) + ar (ΔACD)] [using (i)]
⇒ ar (ΔAEB) + ar (ΔDEC) = \(\frac{1}{2}\)ar (trap.ABCD) …..(iv)
Now,
ar (trap. ABCD) = ar (ΔAEB) + ar (ΔAED) + ar (ΔDEC)
⇒ ar (trap. ABCD) = ar (ΔAEB) + ar (ΔDEC) + ar (ΔAED)
⇒ ar (trap. ABCD) = \(\frac{1}{2}\)ar (trap. ABCD) + ar (ΔAED)
⇒ ar (ΔAED) = ar (trap. ABCD) – \(\frac{1}{2}\)ar (trap. ABCD)
⇒ ar (ΔAED) = \(\frac{1}{2}\)ar (trap. ABCD). Hence proved
![]()
Question 10.
ABCD is a parallelogram in which P is a point on AB such that AP : PB = 2 : 1 and Q is a point on BC such that BQ : QC = 2 : 1 and R is a point on CD such that CR : DR = 2 : 1. Prove that :
(i) ar (trap. APRD) = ar (trap. PBCR)
(ii) ar (ΔPBR) = \(\frac{1}{6}\)ar (||gm ABCD)
(iii) ar (ΔRCQ) = \(\frac{1}{2}\)ar (ΔRQB)
(iv) 2 ar (ΔPBR) = 3 ar (ΔRCQ).
Solution:
Draw
BM ⊥ CD and DN ⊥ AB
AP : PB = 2 : 1 and CR : DR = 2 : 1
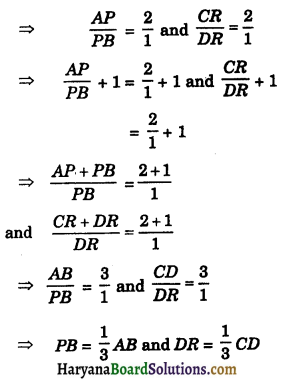
AP = AB – PB
and CR = CD – DR
⇒ AP = AB – \(\frac{1}{3}\)AB
and CR = CD – \(\frac{1}{3}\)CD
⇒ AP = \(\frac{2}{3}\)AB and CR = \(\frac{2}{3}\) CD
Similarly, CQ = \(\frac{1}{3}\)BC and BQ = \(\frac{2}{3}\)BC
(i) Area of trap. APRD = \(\frac{1}{2}\)(AP + DR) × DN
= \(\frac{1}{2}\left(\frac{2}{3} A B+\frac{1}{3} C D\right) \times D N\)
= \(\frac{1}{2}\left(\frac{2}{3} A B+\frac{1}{3} A B\right) \times D N\)
= \(\frac{1}{2}\)AB × DN

Hence,
ar (trap. APRD) = \(\frac{1}{2}\)AB × DN …(i)
Similarly,area of trap.

Since, perpendiculars BM and DN are between the parallel sides AB and CD.
∴ BM = DN ……(iii)
From (i), (ii) and (iii), we get
ar (trap. APRD) = ar (trap. PBCR)
(ii) ar (ΔPBR) = \(\frac{1}{2}\)PB × DN
⇒ ar (ΔPBR) = \(\frac{1}{2} \times \frac{1}{3}\)AB × DN
ar (ΔPBR) = \(\frac{1}{6}\)AB × DN
ar (ΔPBR) = \(\frac{1}{6}\)ar (||gm ABCD)
[∵ ar (||gm ABCD) = AB × DN]
(iii) Draw RO ⊥ BC
ar (ΔRCQ) = \(\frac{1}{2}\)CQ × RO
⇒ ar (ΔRCQ) = \(\frac{1}{2} \times \frac{1}{3}\)BC × RO
⇒ ar (ΔRCQ) = \(\frac{1}{6}\)BC × RO
⇒ 6 ar (ΔRCQ) = BC × RO …(iv)
and ar (ΔRQB) = \(\frac{1}{2}\) × BQ × RO
⇒ ar (ΔRQB) = \(\frac{1}{2} \times \frac{2}{3}\) BC × RO
⇒ 3 ar (ΔRQB) = BC × RO …(v)
From (iv) and (v), we get
6 ar (ΔRCQ) = 3 ar (ΔRQB)
⇒ ar (ΔRCQ) = \(\frac{3}{6}\)ar (ΔRQB)
⇒ ar (ARCQ) = \(\frac{1}{2}\)ar (ΔRQB)
(iv) ar (ΔRCB) = \(\frac{1}{2}\)CR × BM
⇒ ar (ΔRCB) = \(\frac{1}{2} \times \frac{2}{3}\)CD × BM
⇒ ar (ΔRCB) = \(\frac{1}{3}\)CD × BM …(vi)
Again, ar (ARCB) = \(\frac{1}{2}\)BC × RO ……(vii)
From (vi) and (vii), we get
\(\frac{1}{2}\)BC × RO = \(\frac{1}{3}\)CD × BM
⇒ RO = \(\frac{2}{3} \times \frac{C D \times B M}{B C}\)
Putting the value of RO in (iv), we get
ar (ΔRCQ) = \(\frac{1}{6} B C \times \frac{2}{3} \frac{C D \times B M}{B C}\)
⇒ ar (ΔRCQ) = \(\frac{1}{9}\)CD × BM
⇒ 9 ar (ΔRCQ) = CD × BM ……(viii)
From IInd part, we have
ar (ΔPBR) = \(\frac{1}{6}\)AB × DN
⇒ 6 ar (ΔPBR) = CD × BM ……(ix)
[∵ From (iii), BM = DN and AB = CD]
From (viii) and (ix), we get
6 ar (ΔPBR) = 9 ar (ΔRCQ)
⇒ ar (ΔPBR)= \(\frac{9}{6}\)ar (ΔRCQ)
⇒ ar (ΔPBR) = \(\frac{3}{2}\)ar (ΔRCQ)
⇒ 2 ar (ΔPBR) = 3 ar (ΔRCQ). Hence proved
![]()
Multiple Choice Questions
Choose the correct option in each of the following:
Question 1.
Out of the following given figures, which are on the same base and between the same parallels :
Answer:

Question 2.
In the given figure, ABCD is a trapezium in which AB || CD such that AB = a cm and CD = b cm. If F and E are the mid points of BC and AD respectively, then ar(ABFE)/ar(EFCD) is equal to: [NCERT Exemplar Problems]
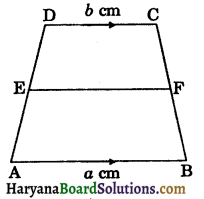
(a) \(\frac{a}{b}\)
(b) \(\frac{(3 a+b)}{(a+3 b)}\)
(c) \(\frac{(a+3 b)}{(3 a+b)}\)
(d) \(\frac{(2 a+b)}{(3 a+b)}\)
Answer:
(b) \(\frac{(3 a+b)}{(a+3 b)}\)
![]()
Question 3.
In the given figure, ARCD is a square, if diagonals AC and BD intersect at O and AO = 4 cm, then the area of square ABCD is :
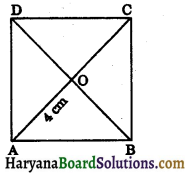
(a) 32 cm2
(b) 64 cm2
(c) 16 cm2
(d) 20 cm2
Answer:
(a) 32 cm2
Question 4.
In the given figure, ABCD is a rhombus. If OD = 3 cm and area of rhombus ABCD = 24 cm2, then length of diagonal AC is :

(a) 6 cm
(b) 8 cm
(c) 16 cm
(d) 10 cm
Answer:
(b) 8 cm
Question 5.
If two parallelograms are on the same base and between the same parallels. The ratio of their areas is : [NCERT Exemplar Problems]
(a) 1 : 3
(b) 1 : 2
(c) 1 : 1
(d) 2 : 1
Answer:
(c) 1 : 1
Question 6.
If a triangle and a parallelogram have a same base and are between the same parallels, then ratio of areas of parallelograms to the triangle is : [NCERT Exemplar Problems]
(a) 1 : 4
(b) 4 : 1
(c) 1 : 2
(d) 2 : 1
Answer:
(d) 2 : 1
Question 7.
If medians of a triangle ABC intersect at G, then ratio of ar (ΔBCG) : ar (ΔABC) is :
(a) 1 : 3
(b) 3 : 1
(c) 1 : 2
(d) 2 : 1
Answer:
(a) 1 : 3
![]()
Question 8.
The area of a parallelogram ABCD is 36 cm2, then area of figure obtained by joining the mid points of the sides of parallelogram ABCD is :
(a) 36 cm2
(b) 18 cm2
(c) 20 cm2
(d) 24 cm2
Answer:
(b) 18 cm2
Question 9.
If diagonal AC divides the quadrilateral ABCD into two triangles of equal area, then ABCD is a: [NCERT Exemplar Problems]
(a) rhombus
(b) parallelogram
(c) rectangle
(d) need not be any of (a), (b) or (c)
Answer:
(d) need not be any of (a), (b) or (c)
Question 10.
ΔΑΒC and ΔΑΡQ are two equilateral traingles such that P is the mid point of AB, then ratio of ar (ΔAPQ) : (ΔABC) is:
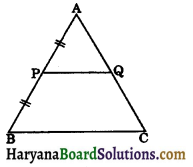
(a) 1 : 2
(b) 1 : 4
(c) 3 : 4
(d) 4 : 1
Answer:
(b) 1 : 4