HBSE 10th Class Maths Important Questions Chapter 10 Circles

Haryana State Board HBSE 10th Class Maths Important Questions Chapter 10 Circles Important Questions and Answers.

Haryana Board 10th Class Maths Important Questions Chapter 10 Circles

Short / Long Answer Type Questions

Question 1.
Two concetric circles of raddi a and b (a > b) are given. Find the length of chord of the larger circle which touches the smaller circle.
Solution :
Let two concetric circles of centre O with raddi a and b (a > b)
AO = OB = a and OM = b
OM ⊥ AB (By theorem 10.1)

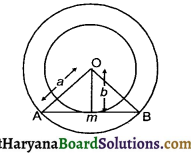
In right triangle AMO, we have
AO² = AM² + OM²
(By Pythagoras theorem)
⇒ a² = AM² + b²
⇒ AM² = a² – b²
⇒ AM = \(\sqrt{a^2-b^2}\) units
we know that perpendicular drawn from centre to chord bisect the chord
∴ AM = MB
AB = 2 × AM
= 2 × \(\sqrt{a^2-b^2}\) units
Hence, length of chord of larger circle
= 2\(\sqrt{a^2-b^2}\) units

Question 2.
How many tangents can be drawn on the circle of radius 5 cm from a point lying outside the circle at distance 9 cm from the centre.
Solution :
Draw a circle of radius 5 cm with centre O. Let P be the point outside 9 cm from the centre O.

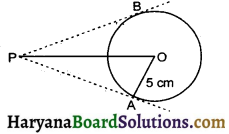
From external point P, we can draw two tangents PA and PB only.

Question 3.
In the given figure, two circles touch each other at the point C. Prove that common tangent to the circles at C, bisects the common tangents at P and Q.

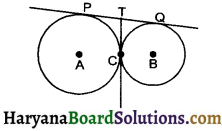
Solution :
PT and CT are tangents at circle with centre A from external point T
∴ PT = CT …… (1) [by theorem 10.2]
Similarly
QT = CT ……… (2)
From equ. (1) and (2)
PT = QT
Now, PQ = PT + QT
⇒ PQ = 2 PT
⇒ PT = QT = \(\frac {1}{2}\)PQ
Hence, common tangent CT bisects the common tangents at P and Q. Hence proved

Question 4.
In the given figure ΔABC is circumscribing a circle, the length of BC is ….. cm.

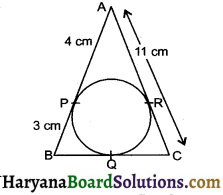
Solution :
BQ = BP = 3 cm
[by theorem 10.2]
AR = AP = 4 cm
[by theorem 10.2]
Now,
CR = AC – AR
= 11 – 4 = 7
CR = QC
⇒ QC = 7 cm
BC = BQ + QC
= 3 + 7 = 10 cm

Question 5.
In the given figure, PQ and PR are tangents to the circle with centre O such that ∠QPR = 50°, then find ∠OQR.

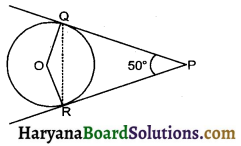
Solution :
Join QR
PQ = PR by theorem 10.2]
⇒ ∠PQR = ∠PRQ [Angles Opp. to equal sides are equal] … (1)
In ΔPQR, we have
∠PQR + ∠PRO + ∠QPR = 180°
⇒ ∠PQR + ∠PRO + 50° = 180° [using equ. (1)]
⇒ 2∠PQR = 180° – 50°
⇒ ∠PQR = \(\frac {130°}{2}\)
⇒ ∠PQR = 65°
Now, OQ ⊥ PQ
[By theorem 10.1]
⇒ ∠PRO = 90°
⇒ ∠OQR = ∠PQO – ∠PQR
= 90° – 65° = 25°
Hence, ∠OQR = 25°

Question 6.
In the given figure PQ is a chord of length 6 cm of the circle of radius 6 cm. TP and TQ are tangents to the circle at points P and Q respectively. Find the ∠PTQ.

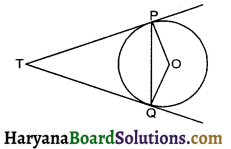
Solution :
Here PQ = 6 cm
PO = OQ = 6 cm
[equal raddi]
∴ PO = OQ = PQ
⇒ POQ is a equilateral triangle
∠POQ = 60°
Now, OP ⊥ PT and OQ ⊥ TQ
[By theorem 10.1]
In quadrilateral POQT, we have
∠POQ + ∠OPT + ∠PTQ + ∠OQT = 360°
⇒ 60° + 90° + ∠PTQ + 90° = 360°
⇒ 240° + ∠PTQ = 360°
⇒ ∠PTQ = 360° – 240°
⇒ ∠PTQ = 120°

Question 7.
In the figure, AB and CD are common tangents to two circles of unequal raddi. Prove that AB = CD.

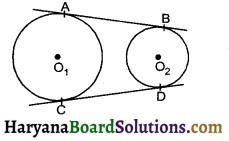
Solution :
Produced AB and CD to meet at P
Now, PA = PC
(By theorem 10.2) …. (1)

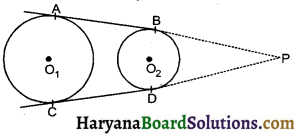
PB = PD
(By theorem 10.2) … (2)
Subtracting equ. (2) from equ. (1), we get
PA – PB = PC – PD
⇒ AB = CD Hence proved

Question 8.
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q.

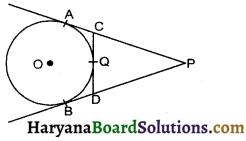
If PA = 12 cm, QC = DQ = 3 cm, then find PC + PD.
Solution :
AC = CQ
(By theorem 10.2) ……. (1)
BD = DQ
(By theorem 10.2) …….(2)
But CQ = DQ …….(3)
By equ. (1). (2) and (3), we get
AC = BD ……….(4)
Now,
AP = PB
(by theorem 10.2)
⇒ CP + AC = PD + BD
⇒ CP + AC = PD + AC
[using equ. (4)]
⇒ CP = PD
CP = AP – AC = 12 – CQ [∴ CQ = AC]
⇒ CP = 12 – 3 = 9 cm
[CQ = DQ = 3 cm]
∴ DP = CP = 9 cm
PC + PD = 9 + 9 = 18 cm

Question 9.
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively of lengths 6 cm and 9 cm. If the area of ΔABC is 54 cm², then find the lengths of sides AB and AC.

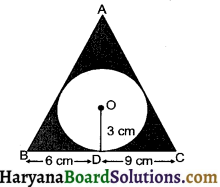
Solution :
Join OA, OB and OC
Draw OE ⊥ AC and OF ⊥ AB
Area of ΔABC = 54 cm² (given)
⇒ ar (ΔBOC) + ar (ΔAOC) + ar (ΔAOB) = 54
⇒ \(\frac {1}{2}\)BC × OD + \(\frac {1}{2}\)AC × OE + \(\frac {1}{2}\)AB × OF = 54
⇒ \(\frac {1}{2}\)[BC × 3 + AC × 3 + AB × 3] = 54
⇒ \(\frac {1}{2}\)[BC + AC + AB] = 54
⇒ AB + BC + AC = \(\frac{54 \times 2}{3}\)
⇒ AB + BC + AC = 36 cm ……….(1)
AF = AE [by theorem 10.2]
Let AF = AE = x cm
BD = BF and CD = CE [by theorem 10.2]
⇒ BF = 6 cm and CE = 9 cm

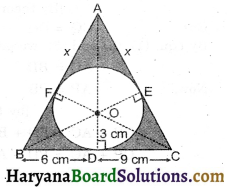
Now AB + BC + AC = 36
⇒ AF + BF + BD + CD + CE + AE = 36
⇒ x + 6 + 6 + 6 + 9 + 9 + 1 = 36
⇒ 2x + 30 = 36
⇒ 2x = 6
⇒ x = 3
∴ AB = 6 + 3 = 9 cm, AC = 9 + 3 = 12 cm.

Question 10.
Prove that the parallelogram circular scribing a circle is rhombus.
Solution :
Let ABCD be a parallelogram
∴ AB = CD and AD = BC
we know that length of tangents drawn to a circle from an exterior point are equal in length.
AP = AS …(1)
PB = BQ …(2)
CR = CQ …(3)
DR = DS ……(4)

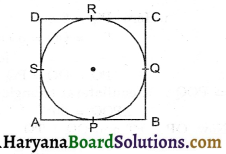
Adding equations (1), (2), (3) and (4), we get
AP + PB + CR + DR = AS + BQ + CQ + DS
⇒ AB + CD = AD + BC
⇒ AB+ AB = BC + BC
⇒ 2 AB = 2 BC
⇒ AB = BC
since, in a parallelogram ABCD adjacent sides AB and BC are equal.
So, ABCD is a rhombus.

Fill in the Blanks

Question 1.
Tangent is perpendicular to the …….. through the point of contact.
Solution :
radius

Question 2.
Only …….. tangents can be drawn to a circle from an external point.
Solution :
two

Question 3.
Lengths of tangents from an external point to a circle are ……..
Solution :
equal

Question 4.
The line containing the radius through the point of contact is also sometimes called the …….. to the circle at the point.
Solution :
normal

Question 5.
Circles having the same …….. are called concentric circles.
Solution :
centre

Question 6.
The word ……. to circle has been deribed from the latin word “……..”
Solution :
tangent

Question 7.
The point at which the tangent line meets the circles is called the ……..
Solution :
point of contact

Multiple Choice Questions

Choose the correct answer each of the following :

Question 1.
In the adjoining figure, if PA and PB are tangents to the circle with centre such that ∠APB = 50°, then ∠OAB is equal to :

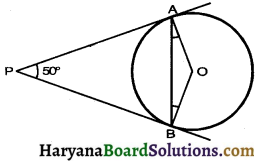
(a) 25°
(b) 30°
(c) 40°
(d) 50°
Solution :
From figure
∠1 + ∠P = 180°

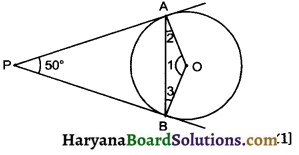
[Opposite angles of cyclic ∠1]
⇒ ∠1 + 50° = 180°
⇒ ∠1 = 180° – 50° = 130°
In ΔOAB,
OA = OB (radius)
⇒ ∠2 = ∠3 (Isosceles Δprop)
∠2 + ∠3 + ∠AOB = 180°
(Angle sum property of Δ)
⇒ ∠2 + ∠2 + 130° = 180°
⇒ 2∠2 = 180° – 130° = 50°
⇒ ∠2 = ∠OAB = \(\frac {50°}{2}\) = 25°
Hence correct choice is (a).

Question 2.
In the adjoining figure, if AP = 4 cm, CR = 5 cm and BQ = 6 cm the perimeter of ΔABC is:

(a) 15 cm
(b) 30 cm
(c) 25 cm
(d) 20 cm
Solution :
From Fig. BQ = BP = 6 cm
CQ = CR = 5 cm
PA = AR = 4 cm
The perimeter of ΔABC = BQ + CQ + CR + AR + AP + BP
= 60 + 5 + 5 + 4 + 4 + 6
= 30 cm
Hence correct choice is (b).

Question 3.
In the adjoining figure, if ∠AOB = 125°, then ∠COD is equal to :
(a) 62.5°
(b) 45°
(c) 35°
(d) 55°

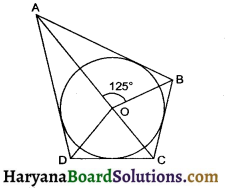
Solution :
From fig. ∠AOB + ∠COD = 180°
125° + ∠COD = 180°
⇒ ∠COD = 180° – 125°
= 55°
Hence correct choice is (d).

Question 4.
In the adjoining figure, AT is a tangent to the circle with centre O such that OT = 4 cm and ∠OTA = 30°. Then AT is equal to :
(a) 4 cm
(b) 2 cm
(c) 2\(\sqrt{3}\) cm
(d) 4\(\sqrt{3}\) cm

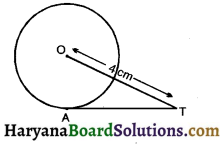
Solution :
∠OAT = 90° (Angle between radius and tangent)
Cos 30° = \(\frac {AT}{OT}\)

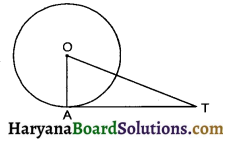
\(\frac{\sqrt{3}}{2}\) = \(\frac {AT}{OT}\)
⇒ AT = 2\(\sqrt{3}\)cm
Hence correct choice is (c).

Question 5.
In the given figure QR is a common tangent to the given circle, which touch externally at P. If QP = 3.8 cm, the length of QR is :
(a) 38 cm
(b) 7.6 cm
(c) 5 cm
(d) 1.9 cm

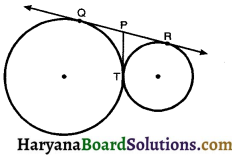
Solution :
From Fig QP = PT = PR = 3.8 cm
So, QR = QP + PR
= 3.8 + 3.8
= 7.6 cm
Hence correct choice is (b).

Question 6.
In the given figure, if ∠APO = 40°. Then ∠AOB is :
(a) 100°
(b) 80°
(c) 50°
(d) 40°

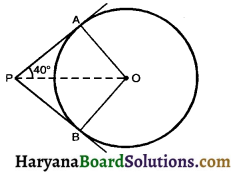
Solution :
Given ∠APO = 40°
and ∠OAP = 90°
(radius is ⊥ to tangent)
∴ In ΔPAQ
∠AOP = 180 – (40 + 90)
= 50°
∴ ∠AOB = 2 × ∠AOP
= 2 × 50°
= 100°
So correct choice is (a)

Question 7.
In the adjoining figure, if PQR is the tangent to a circle at Q whose centre is O, AB is a chord parallel to PR and ∠BQR = 70°, then ∠AQB is equal to
(a) 20°
(b) 40°
(c) 35°
(d) 45°

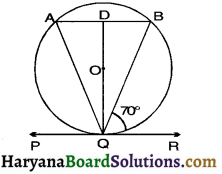
Solution :
∠DQR = 90°
(Angle between radius and tangent)
∠BQD = ∠DQR – ∠BQR
= 90° – 70°
= 20°
Similarly ∠AQD = 20
∠AQB = 20° + 20°
So correct choice is (b).

Question 8.
If two tangents inclined at an angle 60° are drawn to a circle of radius 3 cm then length of each tangent is equal to :
(a) \(\frac {3}{2}\)\(\sqrt{3}\) cm
(b) 6 cm
(c) 3 cm
(d) 3\(\sqrt{3}\) cm
Solution :
∠OBA = 90°
(Angle between radius and tangent)
In right ΔOBA
Tan 30° = \(\frac {OB}{AB}\)
\(\frac{1}{\sqrt{3}}\) = \(\frac {3}{AB}\)

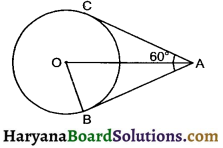
AB = 3\(\sqrt{3}\)
∴ AC = AB = 3\(\sqrt{3}\) (tangents from same external point)
So correct choice is (d).