HBSE 9th Class Maths Important Questions Chapter 12 हीरोन सूत्र

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 12 हीरोन सूत्र Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 12 हीरोन सूत्र

परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न:

प्रश्न 1.
उस त्रिभुज का क्षेत्रफल ज्ञात करें जिसकी भुजाएँ 40 m, 24 m व 32 m हों।
हल :
यहाँ पर
a = 40 m, b = 24 m, c= 32 m
∴ s = \(\frac{a+b+c}{2}=\frac{40+24+32}{2}=\frac{96}{2}\) = 48 m.
हीरोन के सूत्र द्वारा
त्रिभुज का क्षेत्रफल = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{48(48-40)(48-24)(48-32)}\) m²
= \(\sqrt{48 \times 8 \times 24 \times 16}\) m²
= \(\sqrt{6 \times 8 \times 8 \times 6 \times 4 \times 4 \times 2 \times 2}\) m²
= 6 × 8 × 4 × 2 = 384 m²

प्रश्न 2.
10 cm भुजा वाले समबाहु त्रिभुज का क्षेत्रफल ज्ञात करें।
हल :
यहाँ पर
a = 10 cm, b = 10 cm, c = 10 cm
∴ s = \(\frac{a+b+c}{2}=\frac{10+10+10}{2}=\frac{30}{2}\) = 15 cm
हीरोन के सूत्र द्वारा
त्रिभुज का क्षेत्रफल = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{15(15-10)(15-10)(15-10)}\) cm²
= \(\sqrt{15 \times 5 \times 5 \times 5}\) cm²
= \(\sqrt{3 \times 5 \times 5 \times 5 \times 5}\) cm²
= 5 × 5 × √3 cm² = 25√3 cm²

प्रश्न 3.
एक त्रिभुजाकार पार्क ABC की भुजाएँ 120 m, 80 m और 50 m हैं (देखिए आकृति)। एक मालिन धनिया को इसके चारों ओर एक बाड़ लगानी है और इसके अंदर घास उगानी है। उसे कितने क्षेत्रफल में घास उगानी है ? एक ओर 3m चौड़े एक फाटक के लिए स्थान छोड़ते हुए इसके चारों ओर ₹ 20 प्रति मीटर की दर से काँटेदार बाड़ लगाने का व्यय भी ज्ञात कीजिए।
हल :
यहाँ पर
a = 120m, b = 80 m, c = 50 m

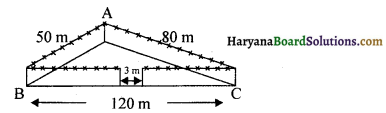
s = \(\frac{a+b+c}{2}=\frac{120+80+50}{2} \mathrm{~m}=\frac{250}{2} \mathrm{~m}\)
= 125 m
घास उगाने के लिए उपलब्ध क्षेत्रफल = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{125(125-120)(125-80)(125-50)}\) m²
= \(\sqrt{125 \times 5 \times 45 \times 75}\) m²
= \(\sqrt{5 \times 5 \times 5 \times 5 \times 3 \times 3 \times 5 \times 3 \times 5 \times 5}\) m²
= 5 × 5 × 5 × 3 \(\sqrt{3 \times 5}\) m²
= 375√15 m²
पार्क का परिमाप = a + b + c = 120 + 80 + 50 = 250 m
बाड़ लगाने के लिए आवश्यक तार की लंबाई = परिमाप – फाटक की लंबाई
= 250 m – 3 m
= 247 m
अतः बाड़ लगाने के लिए कुल व्यय = 20 × 247 = ₹ 4940.

प्रश्न 4.
किसी त्रिभुज की भुजाओं का अनुपात 3 : 5 : 7 है। उसका परिमाप 300 cm है। त्रिभुज का क्षेत्रफल ज्ञात करें।
हल :
यहाँ पर त्रिभुज की भुजाओं का अनुपातa : b : c= 3 : 5 : 7
अनुपाती योग = 3 + 5 + 7 = 15
a = \(\frac{3}{15}\) × 300 = 60 cm
b = \(\frac{5}{15}\) × 300 = 100 cm
c = \(\frac{7}{15}\) × 300 = 140 cm
s = \(\frac{a+b+c}{2}=\frac{300}{2}\) = 150 cm
अतः हीरोन के सूत्र द्वारा
त्रिभुज का क्षेत्रफल = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{150(150-60)(150-100)(150-140)}\) cm²
= \(\sqrt{150 \times 90 \times 50 \times 10}\) cm²
= \(\sqrt{2 \times 3 \times 5 \times 5 \times 2 \times 3 \times 3 \times 5 \times 2 \times 5 \times 5 \times 2 \times 5}\) cm²
= 2 × 2 × 3 × 5 × 5 × 5 × √3 = 1500√3 cm²

प्रश्न 5.
कमला के पास 240 m, 200 m और 360 m भुजाओं वाला एक त्रिभुजाकार खेत है, जहाँ वह गेहूँ उगाना चाहती है। इसी खेत से संलग्न 240 m,320 m और 400 m भुजाओं वाला एक अन्य खेत है, जहाँ वह आलू और प्याज उगाना चाहती है (देखिए आकृति)। उसने इस खेत की सबसे लंबी भुजा के मध्य-बिंदु को सम्मुख शीर्ष से जोड़कर उसे दो भागों में विभाजित कर दिया। इनमें से एक भाग में उसने आलू उगाए और दूसरे भाग में प्याज उगाए। गेहूँ, आलू और प्याज के लिए कितने-कितने क्षेत्रफलों (हेक्टेयर में) का प्रयोग किया गया है ? (1 हेक्टेयर = 10000 m² है)
हल :

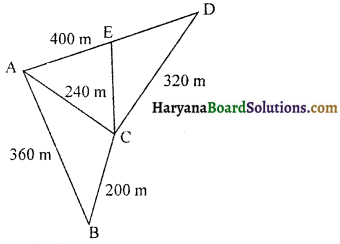
माना ABC वह खेत है, जहाँ गेहूँ उगाया गया है।
साथ ही, ACD वह खेत है जिसकी भुजा AD के मध्य-बिंदु E को C से जोड़कर इस खेत को दो भागों में विभाजित करती है।
∆ABC के लिए
a = 200 m, b = 240 m, c = 360 m
अतः s = \(\frac{a+b+c}{2}=\frac{200+240+360}{2} \mathrm{~m}\) = 400 m
इसलिए गेहूँ उगाने के लिए क्षेत्रफल = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{400(400-200)(400-240)(400-360)}\) m²
= \(\sqrt{400 \times 200 \times 160 \times 40}\) m²
= 16000 √2 m²
= 1.6 × √2
= 1.6 × 1.41 हेक्टेयर
= 2.26 हेक्टेयर (लगभग)

अब, ∆ACD के लिए =
a = 240 m, b = 320m, c = 400 m
s = \(\frac{a+b+c}{2}=\frac{240+320+400}{2} \mathrm{~m}\) = 480 m

अतः ∆ACD का क्षेत्रफल = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{480(480-240)(480-320)(480-400)}\) m²
= \(\sqrt{480 \times 240 \times 160 \times 80}\) m²
= 38400 m² = 3.84 हेक्टेयर
अतः आलू उगाने के लिए क्षेत्रफल = प्याज उगाने के लिए क्षेत्रफल
= \(\frac{3.84}{2}\) = 1.92 हेक्टेयर

प्रश्न 6.
चतुर्भुज ABCD का क्षेत्रफल ज्ञात करें जिसमें विकर्ण AC की लंबाई 10 cm तथा Ba D से AC पर खींचे गए लंबों की लंबाइयाँ क्रमशः 7 cm तथा 5 cm हैं।
हल :

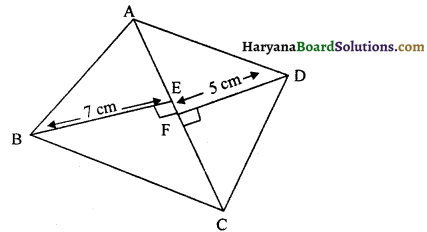
आकृति अनुसार,
AC = 10 cm
BE = 7 cm
DF = 5 cm
चतुर्भुज ABCD का क्षेत्रफल = (∆ABC + ∆ACD) का क्षेत्रफल
= \(\frac{1}{2}\) × AC × BE + \(\frac{1}{2}\) × AC × DF
= [\(\frac{1}{2}\) × 10 × 7 + \(\frac{1}{2}\) × 10 × 5] cm²
= (35 + 25) cm² = 60 cm²

प्रश्न 7.
चतुर्भुज ABCD का क्षेत्रफल ज्ञात करें जिसकी भुजाओं की लंबाई क्रमशः 6 cm, 8 cm, 7 cm व 9 cm हो। पहली दो भुजाओं के बीच का कोण समकोण है।
हल :
माना चतुर्भुज ABCD में

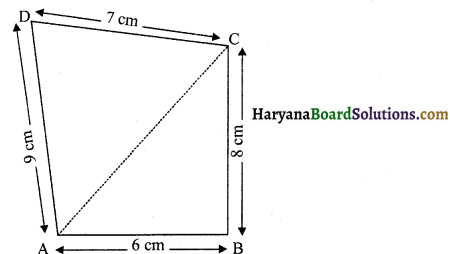
AB = 6 cm, BC = 8 cm, CD = 7 cm व DA = 9 cm
∠B = 90°
समकोण ∆ABC में
AC = \(\sqrt{\mathrm{AB}^2+\mathrm{BC} \mathrm{C}^2}\)
= \(\sqrt{(6)^2+(8)^2}=\sqrt{36+64}=\sqrt{100}\) = 10 cm

समकोण ∆ABC का क्षेत्रफल = \(\frac{1}{2}\) × AB × BC
= \(\frac{1}{2}\) × 6 × 8 cm² = 24 cm²
∆ADC के लिए a = 7 cm, b = 9 cm, c = 10 cm
s = \(\frac{a+b+c}{2}=\frac{7+9+10}{2} \mathrm{~cm}=\frac{26}{2}\) = 13 cm

हीरोन सूत्र से
∆ADC का क्षेत्रफल = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{13(13-7)(13-9)(13-10)}\) cm²
= \(\sqrt{13 \times 6 \times 4 \times 3}\) cm²
= \(\sqrt{13 \times 2 \times 3 \times 2 \times 2 \times 3}\) cm²
= 2 × 3 × 26 cm²
= 6√26 cm²

चतुर्भुज ABCD का क्षेत्रफल = (∆ABC + ∆ADC) का क्षेत्रफल
= (24 + 6√26) cm²

प्रश्न 8.
एक समचतुर्भुज का परिमाप 24 cm है। इसके एक विकर्ण का माप 8 cm है। समचतुर्भुज का क्षेत्रफल ज्ञात करें।
हल :
माना ABCD एक समचतुर्भुज है जिसमें विकर्ण
AC = 8 cm
समचतुर्भुज की प्रत्येक भुजा = \(\frac{24}{4}\) = 6 cm

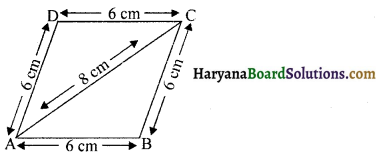
∆ABC के लिए
a = 6 cm, b = 6 cm, c = 8 cm
s = \(\frac{a+b+c}{2}=\frac{6+6+8}{2}=\frac{20}{2}\) = 10 cm
हीरोन सूत्र से
∆ABC का क्षेत्रफल = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{10(10-6)(10-6)(10-8)}\)
= \(\sqrt{10 \times 4 \times 4 \times 2}\) = 8√5 cm²
चतुर्भुज ABCD का क्षेत्रफल = 2 × ∆ABC का क्षेत्रफल
= 2 × 8√5 cm²
= 16√5 cm²

Multiple Choice Questions with Answers:

प्रश्न 1.
एक त्रिभुज जिसका आधार 12 cm तथा ऊँचाई 5 cm हो, तो उसका क्षेत्रफल होगा-
(A) 60 cm²
(B) 30 cm²
(C) 30 m²
(D) 60 m²
उत्तर-
(B) 30 cm²

प्रश्न 2.
10 cm भुजा वाली समबाहु त्रिभुज का क्षेत्रफल होगा-
(A) 25√2 cm²
(B) 25√5 cm²
(C) 50√3 cm²
(D) 50√2 cm²
उत्तर-
(B) 25√3 cm²

प्रश्न 3.
असमान भुजा 8 cm और बराबर भुजाएँ 5 cm वाले समद्विबाहु त्रिभुज का क्षेत्रफल क्या होगा ?
(A) 12 cm²
(B) 12 m²
(C) 12 cm
(D) 12 m
उत्तर-
(A) 12 cm²

प्रश्न 4.
एक यातायात संकेत बोर्ड पर ‘आगे स्कूल है’ लिखा है और यह भुजा ‘a’ वाले एक समबाहु त्रिभुज के आकार का है। हीरोन के सूत्र का प्रयोग करके इस बोर्ड का क्षेत्रफल होगा
(A) \(\frac{\sqrt{3}}{4}\) a
(B) \(\frac{\sqrt{3}}{4}\) a²
(C) \(\frac{\sqrt{3}}{2}\) a
(D) \(\frac{\sqrt{3}}{2}\) a²
उत्तर-
(B) \(\frac{\sqrt{3}}{4}\) a²

प्रश्न 5.
ABCD एक चतुर्भुज है तथा BD इसके विकर्णों में से एक है जैसा कि आकृति में दर्शाया गया है। इसका क्षेत्रफल होगा-

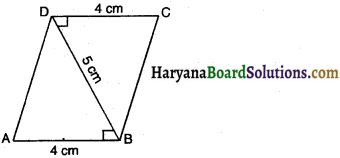
(A) 20 cm²
(B) 15 cm²
(C) 10 cm²
(D) 40 cm²
उत्तर-
(A) 20 cm²

प्रश्न 6.
उस त्रिभुज का क्षेत्रफल क्या होगा जिसकी दो भुजाएँ 18 m और 10 m हैं तथा परिमाप 42 m है ?
(A) 21√11 cm
(B) 21√11 cm²
(C) 21√11 cm³
(D) 21√11 m²
उत्तर-
(D) 21√11 m²

प्रश्न 7.
एक त्रिभुज की भुजाओं का अनुपात 12 : 17 : 25 है और उसका परिमाप 540 cm है। इसकी सबसे बड़ी भुजा की लंबाई होगी-
(A) 120 cm
(B) 170 cm
(C) 250 cm
(D) 540 cm
उत्तर-
(C) 250 cm

प्रश्न 8.
एक समबाहु त्रिभुज जिसका परिमाप 180 cm है, इसका क्षेत्रफल होगा-
(A) 900√3 cm
(B) 900√3 cm²
(C) 90√3 m
(D) 90√3 m²
उत्तर-
(B) 900√3 cm²

प्रश्न 9.
एक त्रिभुज की भुजाओं का अनुपात 12 : 17 : 25 है और उसका परिमाप 540 cm है। इस त्रिभुज का क्षेत्रफल होगा-
(A) 9000 cm²
(B) 9000 m²
(C) 9000 cm³
(D) 9000 m³
उत्तर-
(A) 9000 cm²

प्रश्न 10.
एक समद्विबाहु त्रिभुज का परिमाप 30 cm है और उसकी बराबर भुजाएँ 12 cm लंबाई की हैं। इस त्रिभुज का क्षेत्रफल होगा-
(A) 9√15 cm³
(B) 9√15 m³
(C) 9√15 cm²
(D) 9√15 m²
उत्तर-
(C) 9√15 cm²

प्रश्न 11.
समांतर चतुर्भुज ABCD में, AB = 12 cm है। भुजाओं AB तथा AD के संगत शीर्षलंब क्रमशः 6 cm और 8 cm हैं जैसा कि संलग्न आकृति में दर्शाया गया है। AD का मान होगा-

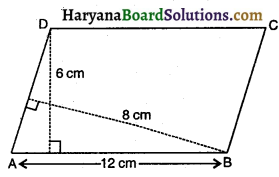
(A) 4.5 cm
(B) 9 cm
(C) 13.5cm
(D) 18 cm
उत्तर-
(B) 9 cm

प्रश्न 12.
आकृति में ∠ACO = 90°, AC = BC, OA = 12 cm तथा OC = 6.5 cm है। ∆AOB का क्षेत्रफल होगा जबकि AC =10 cm हो-

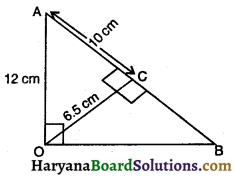
(A) 30 cm
(B) 60 cm²
(C) 65 cm²
(D) 70 cm²
उत्तर-
(C) 65 cm²

प्रश्न 13.
सानिया के पास एक खेत है, जो एक समचतुर्भुज के आकार का है। वह अपनी एक पुत्री और एक पुत्र से यह चाहती थी कि वे इस खेत पर काम करके अलग-अलग फसलों (या उपजों) का उत्पादन करें। उसने इस खेत को दो बराबर भागों में विभाजित कर दिया। यदि इस खेत का परिमाप 400 m है और एक विकर्ण 160 m है, तो प्रत्येक को खेती के लिए कितना क्षेत्रफल प्राप्त होगा ?
(A) 4800 m²
(B) 9600 m²
(C) 4800 m
(D) 9600 m
उत्तर-
(A) 4800 m²

प्रश्न 14.
एक पार्क चतुर्भुज PQRS के आकार का है, जिसमें ZR = 90%, PQ= 9 m, QR = 12 m, RS = 5 m और PS = 8 m है। इस पार्क का क्षेत्रफल होगा-
(A) 65.5 m²
(B) 65.5 cm²
(C) 65.5 m
(D) 65.5 cm
उत्तर-
(A) 65.5 m²

प्रश्न 15.
एक चतुर्भुज ABCD का क्षेत्रफल क्या होगा, जिसमें AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm और AC = 5 cm है ?
(A) 15.2 m²
(B) 15.2 cm²
(C) 15.2 m
(D) 15.2 cm
उत्तर-
(B) 15.2 cm²

प्रश्न 16.
एक त्रिभुज और एक समांतर चतुर्भुज का एक ही आधार है और क्षेत्रफल भी एक ही है। यदि त्रिभुज की भुजाएँ 26 cm, 28 cm और 30 cm हैं तथा समांतर चतुर्भुज 28 cm के आधार पर स्थित है, तो उसकी संगत ऊँचाई होगी-
(A) 12 cm
(B) 12 cm²
(C) 12 m
(D) 12 m²
उत्तर-
(A) 12 cm

प्रश्न 17.
किसी समलंब का क्षेत्रफल ज्ञात करने का सूत्र होता है-
(A) समांतर भुजाओं का योग × उनके बीच की दूरी
(B) असमांतर भुजाओं का योग × उनके बीच की दूरी
(C) \(\frac{1}{2}\) × समांतर भुजाओं का योग × उनके बीच
(D) असमांतर भुजाओं का योग × उनके बीच की दूरी की दूरी
उत्तर-
(C) \(\frac{1}{2}\) × समांतर भुजाओं का योग × उनके बीच की दूरी

प्रश्न 18.
6 cm, 8 cm तथा 10 cm भुजाओं वाली त्रिभुज का क्षेत्रफल होगा-
(A) 18 cm²
(B) 22 cm²
(C) 24 cm²
(D) 12 cm²
उत्तर-
(C) 24 cm²

प्रश्न 19.
एक समकोण त्रिभुज जिसमें समकोण बनाने वाली भुजाओं की लंबाई 5 cm तथा 12 cm है। इसका क्षेत्रफल होगा-
(A) 30 cm²
(B) 60 cm²
(C) 90 cm²
(D) 75 cm²
उत्तर-
(A) 30 cm²

प्रश्न 20.
समांतर चतुर्भुज के क्षेत्रफल का सूत्र होता है-
(A) \(\frac{1}{2}\) × आधार × ऊँचाई
(B) आधार × ऊँचाई
(C) 2 × आधार × ऊँचाई
(D) 3 × आधार × ऊँचाई
उत्तर-
(B) आधार × ऊँचाई

प्रश्न 21.
एक समचतुर्भुजाकार घास के खेत में 18 गायों के चरने के लिए घास है। यदि इस’ समचतुर्भुज की प्रत्येक भुजा 30 m है और बड़ा विकर्ण 48 m है, तो प्रत्येक गाय को चरने के लिए इस घास के खेत का कितना क्षेत्रफल प्राप्त होगा ?
(A) 48 m²
(B) 48 m
(C) 48 cm²
(D) 48 cm
उत्तर-
(A) 48 m²

प्रश्न 22.
दो विभिन्न रंगों के कपड़ों के 10 त्रिभुजाकार टुकड़ों को सीकर एक छाता बनाया गया है जैसाकि आकृति में दिखाया गया है। प्रत्येक टुकड़े के माप 20 cm, 50 cm और 50 cm हैं। छाते में प्रत्येक रंग का कितना कपड़ा लगा है ?

(A) 200√6 cm²
(B) 2000√6 cm²
(C) 1000√6 cm²
(D) 400√6 cm²
उत्तर-
(C) 1000√6 cm²

प्रश्न 23.
एक पतंग तीन भिन्न-भिन्न शेडों (shades) के कागजों से बनी है। इन्हें आकृति में I, II और III से दर्शाया गया है। पतंग का ऊपरी भाग 32 cm विकर्ण का एक वर्ग है और निचला भाग 6 cm, 6 cm और 8 cm भुजाओं का एक समद्विबाहु त्रिभुज है। ज्ञात कीजिए शेड III में कितना कागज प्रयुक्त हुआ ?

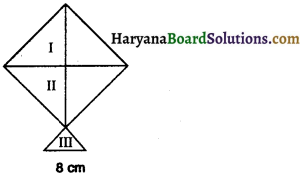
(A) 256 cm
(B) 256 cm²
(C) 17.92 cm
(D) 17.92 cm²
उत्तर-
(D)17.92 cm²

प्रश्न 24.
एक समद्विबाहु त्रिभुज का आधार 10 cm है तथा समान भुजाओं में से एक भुजा 13 cm है। हीरोन के सूत्र द्वारा इसका क्षेत्रफल होगा-
(A) 60 cm²
(B) 30 cm²
(C) 90 cm²
(D) 45 cm²
उत्तर-
(A) 60 cm²

प्रश्न 25.
एक समचतुर्भुज का परिमाप 24 cm है, उसके एक विकर्ण का माप 8 cm है। इसका क्षेत्रफल होगा-
(A) 8√5 cm²
(B) 12√5 cm²
(C) 16√5 cm²
(D) 24√5 cm²
उत्तर-
(C) 16√5 cm²

प्रश्न 26.
उस समद्विबाहु त्रिभुज की ऊँचाई क्या होगी जिसका आधार 30 cm और क्षेत्रफल 120 cm- हो ?
(A) 4 cm
(B) 8 cm
(C) 4 cm²
(D) 8 cm²
उत्तर-
(B) 8 cm

प्रश्न 27.
किसी समांतर चतुर्भुज की दो आसन्न भुजाओं की माप 5 cm और 3.5 cm हैं। उसके एक विकर्ण की माप 6.5 cm हो, तो समांतर चतुर्भुज का क्षेत्रफल होगा-
(A) 10√3 cm
(B) 10√3 m
(C) 10√3 cm²
(D) 10√3 m²
उत्तर-
(C) 10√3 cm²

प्रश्न 28.
यदि किसी त्रिभुज की भुजाओं को दुगुना कर दिया जाए तो उसका क्षेत्रफल कितने प्रतिशत बढ़ जाएगा ?
(A) 100%
(B) 200%
(C) 300%
(D) 400%
उत्तर-
(B) 200%

प्रश्न 29.
एक त्रिभुजाकार खेत की भुजाएँ 60 m, 80 m और 100 m हैं। ₹ 2.50 प्रति वर्ग मीटर की दर से इस खेत को जोतने पर कितना खर्च आएगा ?
(A) ₹ 60
(B) ₹ 600
(C) ₹ 5000
(D) ₹ 6000
उत्तर-
(D) ₹ 6000

प्रश्न 30.
किसी त्रिभुज का अर्ध-परिमाप क्या होगा यदि उसकी भुजाएँ 40 m, 24 m और 32 m हो?
(A) 3072 m
(B) 96 m
(C) 48 m²
(D) 48 m
उत्तर-
(D) 48 m

प्रश्न 31.
उस समांतर चतुर्भुज का क्षेत्रफल क्या होगा जिसकी दो आसन्न भुजाओं की लंबाई 5 cm तथा 6 cm है और एक विकर्ण की लंबाई 7 cm है ?
(A) 6√6 cm²
(B) 12√6 cm²
(C) 24√6 cm²
(D) 18√6 cm²
उत्तर-
(B) 12√6 cm²

प्रश्न 32.
एक खेत समलंब के आकार का है, जिसकी समांतर भुजाएँ 25 m और 10 m हैं। इसकी असमांतर भुजाएँ 14 m और 13 m हैं। इस खेत का क्षेत्रफल होगा-
(A) 196 m²
(B) 196 m³
(C) 196 m
(D) 196 cm²
उत्तर-
(A) 196 m²

प्रश्न 33.
किसी समांतर चतुर्भुज की दो आसन्न भुजाओं की लंबाइयाँ क्रमशः 51 cm और 37 cm हैं। इसका एक विकर्ण 20 cm हो, तो समांतर चतुर्भुज का क्षेत्रफल होगा-
(A) 306 cm²
(B) 612 cm²
(C) 612 m²
(D) 306 m²
उत्तर-
(B) 612 cm²

प्रश्न 34.
एक त्रिभुजाकार प्लेट की भुजाएँ 8 cm, 15 cm और 17 cm हैं। यदि इसका भार 96 ग्राम हो, तो प्लेट का प्रति वर्ग सें०मी० भार क्या होगा ?
(A) 16 gm
(B) 8 gm
(C) 1.6 gm
(D) 0.8 gm
उत्तर-
(C) 1.6 gm

प्रश्न 35.
एक त्रिभुज का परिमाप 270 m है तथा इसकी भुजाओं में अनुपात 12 : 17 : 25 है, तो इसकी सबसे छोटी भुजा होगी-
(A) 60 m
(B) 85 m
(C) 125 m
(D) 270 m
उत्तर-
(A) 60 m