Haryana State Board HBSE 10th Class Maths Important Questions Chapter 8 Introduction to Trigonometry Important Questions and Answers.
Haryana Board 10th Class Maths Important Questions Chapter 8 Introduction to Trigonometry
Short/Long Answer Type Questions
Question 1.
If tan2A = cot (A – 24°). Find A.
Solution :
We have,
tan 2A = coat (A – 24°)
tan 2A = tan (90° – (A – 24))
[∴ tan (90 – θ) = cotθ]
⇒ 2A = 90° – (A – 24°)
⇒ 2A = 90° – A + 24°
⇒ 2A + A = 114°
⇒ 3A = 114°
⇒ A = \(\frac {114}{3}\) = 38°
![]()
Question 2.
If cos3A = sin (A – 34°), where A is an acute angle, find the value of A.
Solution :
We have,
cos 3A = sin (A – 34°)
⇒ sin (90° – 3A) = sin (A – 34°)
[∴ sin (90 – θ) = cos θ]
⇒ 90° – 3A = A – 34°
⇒ 90° + 34° = A + 3A
⇒ 124° = 4A
⇒ A = \(\frac {124°}{4°}\)
⇒ A = 31° Hence proved
Question 3.
The value of (tan 1° tan 2° …. tan 89°) is equal to ?
Solution :
We have, tan 1° tan 2° tan 3° ….. tan 43° tan 44° tan 45° tan 46° tan 47° ….. tan 87° tan 88° tan 89° = tan 1° tan 2° tan 3° ….. tan 43° tan 44°
1. tan (90° – 44°) tan (90° – 43°) ….. tan (43° – 3°). tan (90° – 2°). tan (90° – 1°).
= tan 1° tan 2° tan 3° ….. tan 43° tan 44° : 1. cot 44° cot 43°….. cot 3° cot 2° cot 1
= tan 1° × \(\frac {1}{tan 1°}\) . tan 2° × \(\frac {1}{tan 2°}\) . tan 3° × \(\frac {1}{tan 3°}\) ……… tan 43° × \(\frac {1}{tan 43°}\) . tan 44° × \(\frac {1}{tan 44°}\) . 1
= 1 × 1 × 1 × 1 × 1 × 1 = 1
![]()
Question 4.
The value of (sin2θ + \(\frac{1}{1+\tan ^2 \theta}\)) = _____
Solution :
We have,
sin2θ + \(\frac{1}{1+\tan ^2 \theta}\) = sin2θ + \(\frac{1}{\sec ^2 \theta}\)
[∴ 1 + tan2θ = sec2θ)
= sin2θ + cos2θ
= 1 Hence proved
Question 5.
(1 + tan2θ) (1 – sinθ) (1 + sinθ)
Solution :
(1 + tan2θ) (1 – sinθ) (1 + sinθ)
= sec2θ (1 – sin2θ)
= sec2θ × cos2θ
= \(\frac{1}{\cos ^2 \theta}\) × cos2θ
= 1 Hence proved
Question 6.
Prove that : \(\frac{\tan A-\sin A}{\tan A+\tan A}=\frac{\sec A-1}{\sec A+1}\)
Solution :
We have,
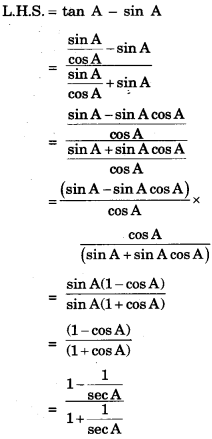

Question 7.
Prove the following identify, where the angles involved are acute angles for which the expression is defined.
\(\frac{1+\cot ^2 \mathrm{~A}}{1+\tan ^2 \mathrm{~A}}\) = (\(\frac{1-\cot A}{1-\tan A}\))2
Solution :
We have,
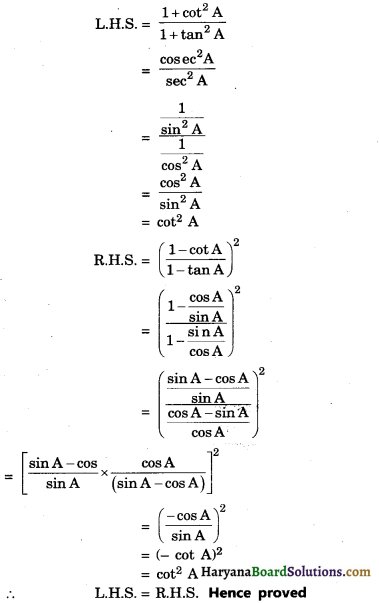
![]()
Question 8.
Prove that
![]()
Solution :

Question 9.
Prove that :
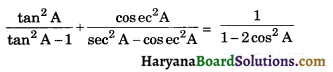
Solution :
We have
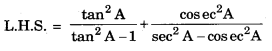
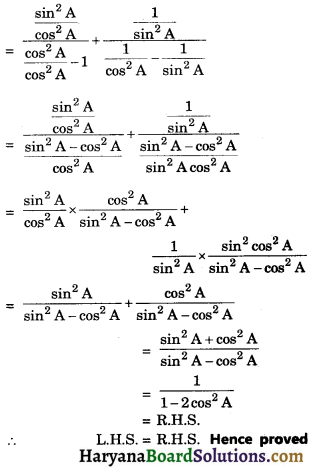
![]()
Question 10.
Prove that:
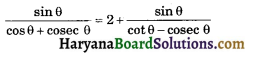
Solution :
We have,

= R.H.S
L.H.S. = R.H.S. Hence proved
Question 11.
Prove that:
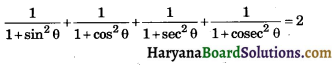
Solution :
We have,
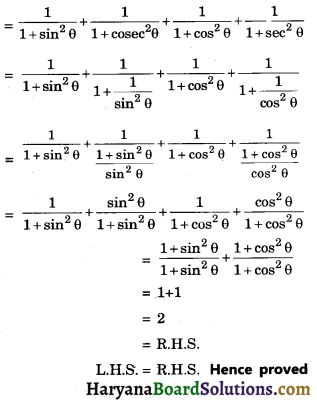
Question 12.
If sin θ + cos θ = \(\sqrt{3}\), then prove that tan θ + cot θ = 1
Solution :
We have,
sin θ + cos θ = \(\sqrt{3}\)
⇒ (sin θ + cos θ)2 = \(\sqrt{3}\)2
⇒ sin2θ + cos2θ + 2sin θ cos θ = 3
⇒ 1 + 2 sinθ cosθ = 3
⇒ sinθ cosθ = \(\frac {2}{2}\) = 1 ………..(1)
Now L.H.S. = tanθ + cotθ
= \(\frac{\sin \theta}{\cos \theta}+\frac{\cos \theta}{\sin \theta}\)
= \(\frac{\sin ^2 \theta+\cos ^2 \theta}{\sin \theta \cos \theta}\)
= \(\frac {1}{1}\)[using equ. (1)]
= 1 = R.H.S.
L.H.S. = R.H.S. Hence proved
![]()
Question 13.
If sin A + sinA2 = 1, then find the value of the expression cos2A + cost4A.
Solution :
We have, sin A + sin2A = 1
⇒ sin A = 1 – sin2A
⇒ sin A = cos2A
squaring both sides, we get
sin2A = cos4A
⇒ 1 – cos2A = cos4A
⇒ 1 = cos2A + cos4A
⇒ cos2A + cos4A = 1.
Hence proved
Fill in the Blanks
Question 1.
____ is the study of relationship between the sides and angles of a triangle.
Solution :
Trigonometry
Question 2.
An equation involving trignometric ratios of an angle is called a trignometeric.
Solution :
identity
![]()
Question 3.
The word is derived from the Greek words tri (means three), gon (means sides), metron (means measure).
Solution :
Trigonometry
Question 4.
In a right triangle, aide opposite to right angle is known as _______ .
Solution :
hypotenuse
Question 5.
cot θ is the abbrevation used for ________ of angle θ.
Solution :
cotangent
Question 6.
The ratio of the sides of a triangle with respect to its acute angle are called trigonometric ____ of the angle.
Solution :
ratios
![]()
Question 7.
If ΔABC is right, right angled at C, then value of cos (A + B) is ______.
Solution :
0 (zero).
Multiple Choice Questions
Question 1.
If cos A = \(\frac {12}{13}\), then cot A is :
(a) \(\frac {12}{5}\)
(b) \(\frac {13}{12}\)
(c) \(\frac {13}{5}\)
(d) \(\frac {5}{12}\)
Solution :
(a) \(\frac {12}{5}\)
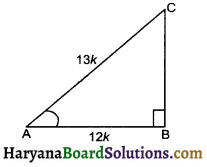
Let us draw the triangle ABC in which ∠B = 90°
Then cos A = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{12}{13}\)
Let AB = 12k and AC = 13k
where k is a positive integer
By using Pythagoars Theorem, we have
AC2 = AB2 + BC2
(13k)2 = (12k)2 + BC2
BC2 = (13k)2 – (12k)2
BC2 = 169k2 – 144k2
BC2 = 25k2
\(\sqrt{\mathrm{BC}^2}\) = 5k
cot A = \(\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{12 k}{5 k}=\frac{12}{5}\)
Question 2.
The rod AC of TV disc antena is fixed at right angles to wall AB and a rod CD is supporting the disc as shown in given figure. If AC = 1.5 cm long and CD = 3m, then sec θ + cosec θ is :
(a) \(\frac {41}{12}\)
(b) \(\frac {41}{13}\)
(c) \(\frac {26}{12}\)
(d) \(\frac {15}{41}\)
Solution :
(b) \(\frac {41}{13}\)
The rod AC of TV disc antena is fixed at right angles to wall AB and rod CD is supporting the disc as shown. In right triangle ACD, we have
CD2 = AD2 + AC2
[By Phythogoras Theorem]
⇒ 32 = AD2 + 1.52
⇒ 32 – (1.5)2 = AD2
⇒ AD2 = 9 – 2.25
⇒ AD2 = 6.75
⇒ AD = \(\sqrt{6.75}\)
⇒ AD = 2.6 om (approx)
⇒ sec θ + cosec θ = \(\frac{C D}{A D}+\frac{C D}{A C}\)
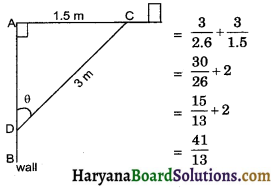
![]()
Question 3.
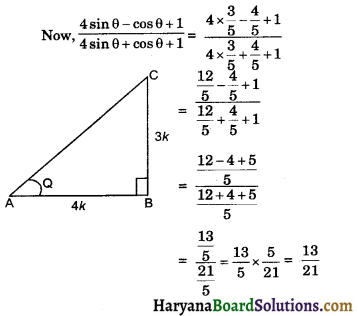
If 4 tan θ = 3, then [latex]\frac{4 \sin \theta-\cos \theta+1}{4 \sin \theta+\cos \theta+1}[/latex] is :
(a) \(\frac {13}{5}\)
(b) \(\frac {5}{21}\)
(c) \(\frac {13}{21}\)
(d) \(\frac {12}{13}\)
Solution :
(c) \(\frac {13}{21}\)
We have, 4 tan θ = 3
⇒ tan θ = \(\frac{3}{4}=\frac{\mathrm{BC}}{\mathrm{AB}}\)
consider a triangle ABC in which ∠B = 90°
Let BC be 3k and AB be 4k wherek is positive integer.
In right triangle ABC, we have
AC2 = AB2 + BC2
= (4k)2 + (BC)2
= 16k2 + 9k2
= 25k2
AC = \(\sqrt{25 k^2}\)
= 5k
sin θ = \(\frac{3 k}{5 k}=\frac{3}{5}\)
and cos θ = \(\frac{4 k}{5 k}=\frac{4}{5}\)
Question 4.
If sin (A + 2B) = \(\frac{\sqrt{3}}{2}\) and cos (A + 4B) = 0, A > B and A + 4B ≤ 90°, then A and B is :
(a) 30°, 45°
(b) 15°, 45°
(c) 60°, 15°
(d) 30°, 45°
Solution :
(d) 30°, 45°
We have,
sin (A + 2B) = \(\frac{\sqrt{3}}{2}\)
⇒ sin (A + 2B) = sin 60°
⇒ A + 2B = 60° ………(1)
And cos (A + 4B) = 0
⇒ Cos (A + 4B) = cos 90°
⇒ A + 4B = 90° ……(2)
Subtracting equation (2), from (1), we get

⇒ B = \(\frac{\sqrt{-30}}{-2}\) = 15°
Substituting the value of B in equ. (1), we get
A + 2 × 15 = 60°
⇒ A + 30° = 60°
⇒ A = 60 – 30 = 30°
Hence, A = 30° and B = 15°
![]()
Question 5.
The value of sin 23° cos 67° + cos 23° sin 67° is:
Solution :
We have, sin 23° cos 67° + cos 23° sin 67°
= sin 23° cos (90° – 23°) + cos23° sin (90° – 23°)
= sin 23° sin 23° + cos 23° cos 23°
= sin2 23° + cos223°
= 1 [sin2θ + cos2θ = 1]
Question 6.
The value of sin 32° cos 58° + cos 32° sin 58° is:
(a) 0
(b) 1
(c) 2
(d) 3
Solution :
(b) 1
We have sin 32° cos 58° + cos 32° sin 58°
= sin 32° cos (90° – 32°) + cos 32° sin (98° – 32°)
= sin 32° sin 32° + cos 32° cos 32°
= sin232° + cos2 32°
= 1 [∴ sin2θ + cos2θ = 1]
![]()
Question 7.
\(\frac{\cos 80^{\circ}}{\sin 10^{\circ}}\) + cos 59° cosec 31° = :
(a) 0
(b) 1
(c) 2
(d) 3
Solution :
(c) 2
We have, \(\frac{\cos 80^{\circ}}{\sin 10^{\circ}}\) + cos 59° cosec 31°
= \(\frac{\cos \left(90^{\circ}-10^{\circ}\right)}{\sin 10^{\circ}}\) + cos 59° cosec (90° – 5°)
= \(\frac{\sin 10^{\circ}}{\sin 10^{\circ}}\) + cos 59° sec 59°
= \(\frac{\sin 10^{\circ}}{\sin 10^{\circ}}+\frac{\cos 59^{\circ}}{\cos 59^{\circ}}\)
= 1 + 1 = 2