Haryana State Board HBSE 8th Class Maths Solutions Chapter 16 संख्याओं के साथ खेलना Intext Questions and Answers.
Haryana Board 8th Class Maths Solutions Chapter 16 संख्याओं के साथ खेलना Intext Questions
(प्रयास कीजिए – पृष्ठ 260)
प्रश्न 1.
निम्नलिखित संख्याओं को व्यापक रूप में लिखिए-
(i) 25
(ii) 73
(iii) 129
(iv) 302
हल:
(i) 25 = 20 + 5 = 10 × 2 + 1 × 5
(ii) 73 = 70 + 3 = 10 × 7 + 1 × 3
(iii) 129 = 100 + 20 +9 = 100 × 1 + 10 × 2 + 1 × 9
(iv) 302 = 300 + 00 + 2 = 100 × 3 + 10 × 0 + 1 × 2
प्रश्न 2.
निम्नलिखित को सामान्य रूप में लिखिए-
(i) 10 × 5 + 6
(ii) 100 × 7 + 10 × 1 + 8
(ii) 100a + 10c + b
हल:
(i) 10 × 5 + 6 = 50 + 6 = 56
(ii) 100 × 7 + 10 × 1 + 8 = 700 + 10 + 8 = 718
(iii) 100a + 10c + b = 110acb
![]()
(प्रयास कीजिए – पृष्ठ 261)
प्रश्न 1.
जाँच कीजिए कि यदि सुंदरम ने निम्नलिखित संख्याएँ चुनी होतीं, तो परिणाम क्या प्राप्त होते है-
1. 27
2. 39
3. 64
4. 17
हल:
1. माना कि सुंदरम संख्या 27 चुनता है। अतः उसे 27 कि उलटी संख्या 72 प्राप्त होती है, वह इन दोनों संख्याओं को जोड़कर 27 + 72 = 99 प्राप्त करता है।
अंत में वह इस संख्या को 11 द्वारा विभाजित करता है, 99 ÷ 11 = 9 भागफल प्राप्त होता है, जिसमें कुछ शेषफल नहीं बचता।
इस प्रकार, भागफल 9 चुनी गई संख्या के अंकों का योग = 2 +7 = 9 है।
2. माना सुंदरम 39 चुनता है। अत: उसे 39 की उलटी संख्या 93 प्राप्त होती है। वह इन दोनों संख्याओं को जोड़कर 39 + 93 = 132 प्राप्त करता है। अन्त में वह इस संख्या को 11 द्वारा विभाजित करके 132 ÷ 11 = 12 भागफल प्राप्त करता है तथा कोई शेषफल नहीं बचता है।
इस प्रकार, भागफलं 12 – चुनी गई संख्या के अंकों का योग (3 +9 = 12) हैं।
3. माना सुंदरम संख्या 64 चुनता है। अतः उसे 64 की उलटी संख्या 46 प्राप्त होती है। वह इन दोनों संख्याओं को जोड़कर 64+46 = 110 प्राप्त करता है। अन्त में वह इस संख्या को 11 द्वारा विभाजित करके 110 ÷ 11 = 10 भागफल तथा शेषफल शून्य प्राप्त करता है।
इस प्रकार, भागफल 10 चनी गई संख्या के अंकों का योग (6 + 4 = 10) है।
4. माना सुंदरम संख्या 17 चुनता है। अतः उसे 17 की उलटी संख्या 71 प्राप्त होती है। वह इन दोनों संख्याओं को जोड़कर 17 + 71 = 88 प्राप्त करता है। अन्त में वह इस संख्या को 11 से विभाजित करके 88 ÷ 11 = 8 भागफल प्राप्त करता है तथा शेषफल शून्य प्राप्त करता है।
इस प्रकार, भागफल 8 = चुनी गई संख्या के अंकों का योग (1 + 7 = 8) है।
(प्रयास कीजिए – पृष्ठ 261)
प्रश्न 1.
जांच कीजिए कि यदि सुंदरम ने अपने व मीनाक्षी के बीच खेलनी को जारी रखने के लिए निम्नलिखित संख्याएँ चुनी होती, तो क्या परिणाम प्राप्त होते-
1.17
2.21
3.98
4.37
हल:
1. माना कि सुंदरम संख्या 17 सोचता है। अतः उसकी गणनाएँ इस प्रकार होंगी-पहले उसे संख्या 71 प्राप्त होगी; इसके बाद 71 – 17 = 54 और अन्त में वह 54 ÷ 9 -6 भागफल प्राप्त करता है, जिसमें शेषफल शुन्य आता है। वह देखता है कि 6 = 7 – 1, अर्थात् वह संख्याओं के बीच अन्तर है।
2. माना कि सुंदरम संख्या 21 सोचता है। अतः उसकी गणनाएँ इस प्रकार होंगी-पहले उसे संख्या 12 प्राप्त होगी; इसके बाद 21 – 12 = 9; और अन्त में वह 9 ÷ 9 = 1 प्राप्त करता है, शेषफल शून्य आता है। वह देखता है कि 1 = 2 – 1 अर्थात् वह संख्याओं के बीच अन्तर है।
3. माना कि सुंदरम संख्या 96 सोचता है। अत: उसकी गणनाएँ इस प्रकार होंगी-पहले उसे संख्या 69 प्राप्त होगी; इसके बाद 96-69 3 273; और अन्त में वह 27 ÷ 9 = 3 भागफल प्राप्त करता है, शेषफल शून्य आता है। वह देखता है कि 3 = 9 – 6, अर्थात् वह संख्याओं के बीच अन्तर है।
4. माना कि सुंदरम संख्या 37 सोचता है। अत: उसकी गणनाएँ इस प्रकार होंगी-पहले उसे संख्या 73 प्राप्त होगी; इसके बाद 73 -37 = 36; और अन्त में वह 36 ÷ 9 = 4 भागफल, शेषफल शून्य प्राप्त करता है। वह देखता है कि 4 = 7 – 3, अर्थात् यह संख्याओं के बीच अन्तर है।
![]()
(प्रयास कीजिए – पृष्ठ 262)
प्रश्न 1.
जाँच कीजिए कि यदि मीनाक्षी ने निम्नलिखित संख्याएँ चुनी होती, तो परिणाम क्या प्राप्त होता? प्रत्येक स्थिति में, अन्त में प्राप्त हुए भागफल का एक रिकॉर्ड (record) रखिए।
1. 132
2.469
3.797
4. 901
हल:
1. मान कि मीनाक्षी 132 संख्या चुनती है, अतः उसे उलटी संख्या 231 प्राप्त होती है।
दोनों का अन्तर : 231 – 132 = 99
विभाजन : 99 ÷ 99 = 1, शेषफल कुछ नहीं।
अत: उसे भागफल 1 प्राप्त होता है, और वह देखती है कि 1 = 2 – 1, अर्थात् भागफल सैकड़े के अंक और इकाई के अंक के बीच का अन्तर है।
2. मान कि मीनाक्षी 469 संख्या चुनती है, अतः उसे उलटी संख्या 964 प्राप्त होती है।
दोनों का अन्तर : 964 – 469 = 495
विभाजन : 495 ÷ 99 = 5, शेषफल कुछ नहीं।
अत: उसे भागफल 1 प्राप्त होता है, और वह देखती है कि 5 = 9 – 4, अर्थात् भागफल सैकड़े के अंक और इकाई के अंक के बीच का अन्तर है।
3. मीनाक्षी संख्या 737 चुनती है, अत: उसे उलटी संख्या 737 प्राप्त होती है।
दोनों का अन्तर : 737 – 737 = 0
विभाजन : 0 ÷ 99 = 0; शेषफल कुछ नहीं।
अत: उसे भागफल 0 प्राप्त होता है, और वह देखती है कि 0 = 7 – 7, अर्थात् भागफल इकाई के अंक और सैकड़े के अंक के बीच का अन्तर है।
4. माना कि मीनाक्षी संख्या 901 चुनती है, अत: उसे उलटी संख्या 109 प्राप्त होती है।
दोनों का अन्तर : 901 – 109 = 792
विभाजन : 792 ÷ 99 = 8, शेषफल कुछ नहीं
अतः उसे भागफल 8 प्राप्त होता है, और वह देखती है कि 8-9-1 अर्थात् भागफल इकाई के अंक और सैकड़े के अंक के बीच का अन्तर है।
(प्रयास कीजिए – पृष्ठ 263)
प्रश्न 1.
जाँच कीजिए कि यदि संदरम ने निम्नलिखित संख्याएँ सोची होती, तो परिणाम क्या प्राप्त होता?
1. 417
2. 882
3. 117
4. 937
हल :
1. दी गई संख्या 417 है।
4, 1, 7 अंकों के प्रयोग द्वारा 3-अंकों की दो और संख्याएँ प्राप्त होती है- 741 और 174
इन संख्याओं को जोड़ने पर,

1332 को 37 से विभाजित करने पर,
1332 ÷ 37 = 36, शेषफल कुछ नहीं।
2. दी गई संख्या 632 है।
6, 3, 2 अंकों के प्रयोग द्वारा 3 अंकों की दो और संख्याएँ प्राप्त होती है- 263 और 326
इन संख्याओं को जोड़ने पर,

1221 को 37 से विभाजित करने पर,
1221 ÷ 37 = 33, शेषफल कुछ नहीं।
3. दी गई संख्या 117 है।
1, 1, 7 अंकों के प्रयोग द्वारा 3 अंकों की दो और संख्याएँ प्राप्त होती है- 711 और 171
इन संख्याओं को जोड़ने पर,
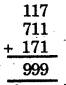
999 को 37 से विभाजित करने पर,
999 ÷ 37 = 27, शेषफल कुछ नहीं।
4. दी गई संख्या 937 है।
9, 3, 7 अंकों के प्रयोग द्वारा 3 अंकों की 2 और संख्याएँ प्राप्त होती है- 793 और 379
इन संख्याओं को जोड़ने पर,
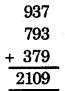
999 को 37 से विभाजित करने पर,
999 ÷ 37 = 27, शेषफल कुछ नहीं।
![]()
(इन्हें कीजिए – पृष्ठ 266)
प्रश्न 1.
दो अंकों की एक संख्या ab लिखिए तथा इसके अंकों को पलटने पर प्राप्त संख्या ba लिखिए। इनका योग ज्ञात कीजिए। मान लीजिए यह योग एक तीन अंकों की संख्या dad है।
अर्थात् ab + ba = dad
(10a + b) + (10b + a) = dad
11(a + b) = dad
योग (a + b) संख्या 18 से अधिक नहीं हो सकता (क्यों?)। क्या dad, 11 का एक गुणज है? क्या dad 198 से कम है? 198 तक तीन अंकों की ऐसी सभी संख्याएँ लिखिए, जो 11 की गुणज हैं। a और 6 के मान ज्ञात कीजिए।
हल :
दिया हैदो अंकों की संख्या ab है।
ab + ba = dad, ⇒ 11 (a + b) = dad __ यह योग तीन अंकों का है जिसमें इकाई का अंक = सैकड़े का अंक जहाँ dad 11 का एक गुणज है।
इसलिए dad का मान 11 का गुणन होगा अतः 198 तक तीन अंकों की सभी संख्याएँ निम्न होंगी-
11 × 10 = 110
11 × 11 = 121
11 × 12 = 132
11 × 13 = 143
11 × 14 = 154
11 × 15 = 164
11 × 16 = 176
11 × 17 = 187
11 × 18 = 198
इन संख्याओं में इकाई का अंक व सैकड़े का अंक समान वाली संख्या 121 है।
अतः dad = 121 होगा।
जिसमें d =1 तथा a = 2 है।
अब
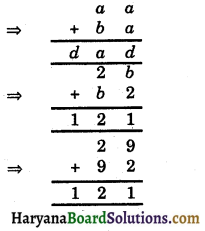
1 2 1 अत: b = 9 होगा।
a = 1, b = 9 तथा d = 1
अब (a + b) = (2 + 9) = 11 जो कि 18 से कम है।
(प्रयास कीजिए – पृष्ठ 268)
प्रश्न 1.
यदि विभाजन N + 5 से शेषफल 3 प्राप्त होता है, तो N की इकाई का अंक क्या हो सकता है?
हल:
संख्या N को 5 से भाग देने पर शेषफल = 3
इसलिए संख्या N होगी-
5 + 3 = 8,
10 + 3 = 13,
15 + 3 = 18,
20 + 35 23.
अत: संख्या N की ईकाई का अंक 3 या 8 होगा।
प्रश्न 2.
यदि विभाजन N +5 से शेषफल 1 प्राप्त होता है, तो Nकी इकाई का अंक क्या हो सकता है?
हल:
संख्या N को 5 से भाग देने पर शेषफल = 1
इसलिए संख्या N होगी-
5 + 1 = 6,
10 + 1 = 11,
15 + 1 = 16,
20 + 1 = 21
अत: संख्या N की ईकाई का अंक 1 या 6 होगा।
![]()
प्रश्न 3.
यदि विभाजन N+5 से शेषफल 4 प्राप्त होता है, तो N की इकाई का अंक क्या हो सकता है?
हल :
संख्या N को 5 से भाग देने पर शेषफल = 4
सख्या N होगा-
5 + 4 = 9,
10 + 4 = 14,
15 + 4 = 19,
20 + 4 = 24
अत: संख्या N की इकाई का अंक = 4 या 9 होगा।
(प्रयास कीजिए – पृष्ठ 268)
प्रश्न 1.
यदि विभाजन N +2 से शेषफल 1 प्राप्त होता है, तो N की इकाई का अंक क्या हो सकता है?
हल :
संख्या N को 2 से भाग देने पर शेषफल = 1
संख्या N होगी-
2 + 1 = 3,
4 + 1 = 5,
6 + 1 = 7,
8 + 1 = 9,
10 + 1 = 11,
इसलिए N इकाई का अंक विषम होगा। अत: N की इकाई का अंक 1,3,5,7 या 9 होगा)
प्रश्न 2.
यदि विभाजन N + 2 से शेष प्राप्त नहीं होता (अर्थात् शेषफल 0 है), तो N की इकाई का अंक क्या हो सकता है?
हल :
संख्या N + 2 से शेषफल = 1
संख्या को 2 से भाग देने पर शेषफल = 0
संख्या N होगी:
2 + 0 = 2,
2 + 2 = 4,
4 + 2 = 6,
6 + 2 = 8
8 + 2 = 10.
इसलिए N इकाई का अंक सम संख्या होगा। अतः इकाई का अंक 0, 2, 4, 6 या होगा।
![]()
प्रश्न 3.
मान लीजिए कि विभाजन N + 5 से शेषफल 4 और विभाजन N + 2 से शेषफल 1 प्राप्त होता है। की इकाई का अंक क्या होना चाहिए?
हल :
संख्या N + 5 से देने पर शेषफल = 4
अत: संख्या N होगी :
9, 14, 19, 24, 29, 34, 39,….
संख्या N को 2 से भाग देने पर शेषफल = 1
अत: संख्या N होगी:
3,5, 7, 11, 13, 15, 17, 19,…….(ii)
कथन (i) व (ii) से, दोनों कथनों में संख्या 9, 19,….
उभयनिष्ठ है, अतः संख्या N की इकाई का अंक 9 होगा।
(प्रयास कीजिए – पृष्ठ 270)
प्रश्न 1.
निम्नलिखित संख्याओं की 9 से विभाज्यता की जाँच कीजिए
1.108, 2.616, 3. 294, 4.482, 5.927
हल:
9 की भाजकता के नियम द्वारा यदि कोई संख्या 9 से विभाज्य होती है। तो उसके अंकों का योग 9 से विभाज्य होता है, अतः
1. दी गई संख्या = 108, इसके अंकों का योग = 1 + 0 + 8 = 9 है जो 9 से विभाज्य है, अतः 108 संख्या 9 से विभाज्य है।
2. दी गई संख्या = 616, इसके अंकों का योग = 6 + 1 + 6 = 13 है। यह 9 से अविभाज्य है। अतः,616 संख्या 9 से विभाज्य नहीं है।
3. दी गई संख्या = 294, इसके अंकों का योग = 2 + 9 + 4 = 15 है, जो 9 से अविभाज्य है। अत:, 294 संख्या 9 से विभाज्य नहीं है।
4. दी गई संख्या = 492, इसके अंकों का योग = 4 + 3 + 2 = 9, जो 9 से विभाज्य है। अत: 432 संख्या 9 से विभाज्य है।
5. दी गई संख्या = 927, इसके अंकों का योग = 9 + 2 + 7 = 18, जो 9 से विभाज्य है। अत: 927 संख्या 9 से विभाज्य है।
(प्रयास कीजिए – पृष्ठ 271)
प्रश्न 1.
निम्नलिखित संख्याओं की 3 से विभाज्यता की जाँच कीजिए
1.108, 2.816, 3.294, 4.492, 5.927
हल:
3 की भाजकता के नियम के द्वारा यदि कोई संख्या 3 से विभाज्य होती है, तो उसके अंकों का योग 3 से विभाज्य होता है। अतः
1. दी गई संख्या = 108 : इसके अंकों का योग = 1 + 0 + 8 = 9 है, जो 3 से विभाज्य है। अत: 108 संख्या 3 से विभाज्य है।
2. दी गई संख्या = 816 : इसके अंकों का योग = 8 + 1 + 6 = 13 है, जो 3 से अविभाज्य है। अत: 616 संख्या 3 से अविभाज्य है।
3. दी गई संख्या = 294 : इसके अंकों का योग = 2 + 9 + 4 = 15 है, जो 3 से विभाज्य है। अतः, 294 संख्या 3 से विभाज्य होती है।
4. दी गई संख्या = 432 : इसके अंकों का योग = 4 + 3 + 2 = 9 है, जो 3 से विभाज्य है। अत: 927 संख्या 3 से विभाज्य है।
5. दी गई संख्या = 927 : इसके अंकों का योग = 9 + 2 + 7 = 18 है, जो 3 से विभाज्य है। अत: 927 संख्या 3 से विभाज्य है।