Haryana State Board HBSE 6th Class Maths Solutions Chapter 11 बीजगणित Ex 11.2 Textbook Exercise Questions and Answers.
Haryana Board 6th Class Maths Solutions Chapter 11 बीजगणित Exercise 11.2
प्रश्न 1.
एक समबाहु त्रिभुज की भुजा को। से दर्शाया जाता है। इस समबाहु त्रिभुज के परिमाप को l का प्रयोग करते हुए व्यक्त कीजिए।
हल :
समबाहु त्रिभुज के परिमाप को P से व्यक्त करते हैं। एक समबाहु त्रिभुज की प्रत्येक भुजा l हो, तो
P = l + l + l = 3 × l = 3l उत्तर
प्रश्न 2.
एक सम षड्भुज (Regular hexagon) की एक भुजा को l से व्यक्त किया गया है (आकृति)। l का प्रयोग करते हुए, इस षड्भुज के परिमाप को.व्यक्त कीजिए। (संकेत : एक सम षड्भुज की सभी 6 भुजाएँ बराबर होती है और सभी कोण बराबर होते है।
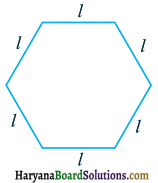
हल :
l भुजा वाले सम षड्भुज के परिमाप को P से व्यक्त करते हैं, तो P = l + l + l + l + l + l
= 6 × l = 6l अतः सम षड्भुज का परिमाप = 61 उत्तर
![]()
प्रश्न 3.
घन (Cube) एक त्रिविमीय (three dimensional) आकृति होती है, जैसे कि आकृति में दिखाया गया है। इसके 6 फलक होते हैं और ये सभी सर्वसम (identical) वर्ग होते हैं। घन के एक किनारे की लम्बाई l से दी जाती है। घन के किनारों की कुल लम्बाई के लिए एक सूत्र ज्ञात कीजिए।
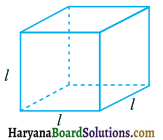
हल :
घन के सभी 12 किनारे समान होते हैं जिन्हें l द्वारा व्यक्त करें, तो इनकी कुल लम्बाई = 12 × l = 12l
अतः घन के किनारों की कुल लम्बाई = 12l उत्तर
प्रश्न 4.
वृत्त का एक व्यास वह रेखाखण्ड है जो वृत्त पर स्थित दो बिन्दुओं को जोड़ता है और उसके केन्द्र से होकर जाता है। संलग्न आकृति में, AB वृत्त का व्यास है और C उसका केन्द्र है। वृत्त के व्यास (d) को उसकी त्रिज्या (r) के पदों में व्यक्त कीजिए।
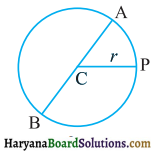
हल :
दी गई आकृति में,
वृत्त का व्यास AB = AC + CB
d = CP + CP
(∵ AC = CB = CP = त्रिज्या)
⇒ d = r + r
⇒ d = 2r उत्तर
![]()
प्रश्न 5.
तीन संख्याओं 14, 27 और 13 के योग पर विचार कीजिए। हम यह योग दो प्रकार से ज्ञात कर सकते हैं:
(a) हम पहले 14 और 27 को जोड़कर 41 प्राप्त कर सकते हैं और फिर 41 में 13 जोड़कर कुल योग 54 प्राप्त कर सकते हैं। या
(b) हम पहले 27 और 13 को जोड़कर 40 प्राप्त कर सकते हैं और फिर इसे 14 में जोड़कर कुल योग 54 प्राप्त कर सकते हैं। इस प्रकार (14 + 27) + 13 = 14 + (27 + 13) हुआ है।
ऐसा किन्हीं भी तीन संख्याओं के लिए किया जा सकता है। यह गुण संख्याओं के योग का साहचर्य (associative) गुण कहलाता है। इस गुण को जिसे हम पूर्ण संख्याओं के अध्याय में पढ़ चुके हैं, चर a, b और c का प्रयोग करते हुए, एक व्यापक रूप में व्यक्त कीजिए।
हल :
योग का साहचर्य गुण इस प्रकार हैं :
तीन चर a, b और c के लिए,
(a + b) + c = a + (b + c) उत्तर