HBSE 12th Class Physics Important Questions Chapter 12 परमाणु

Haryana State Board HBSE 12th Class Physics Important Questions Chapter 12 परमाणु Important Questions and Answers.

Haryana Board 12th Class Physics Important Questions Chapter 12 परमाणु

वस्तुनिष्ठ प्रश्न:

प्रश्न 1.
हाइड्रोजन परमाणु की लाइमैन श्रेणी की प्रथम रेखा की तरंगदैर्ध्य हाइड्रोजन समान आयन की बामर श्रेणी की द्वितीय रेखा की तरंगदैर्घ्य के बराबर है। हाइड्रोजन समान आयन का परमाणु क्रमांक 2 है:
(अ) 2
(ब) 3
(स) 4
(द) 1
उत्तर:
(अ) 2

प्रश्न 2.
उत्तेजित हाइड्रोजन परमाणु में यदि बोर के सिद्धान्त के अनुसार इलेक्ट्रॉन का कोणीय संवेग (2h/2π) हो तो उसकी ऊर्जा होगी:
(अ) – 3.4 ev
(ब) + 3.4 eV
(स) – 13.6 ev
(द) + 13.6 ev
उत्तर:
(अ) – 3.4 ev

प्रश्न 3.
हाइड्रोजन परमाणु में स्पेक्ट्रम में किस श्रेणी में रेखायें दृश्य भाग में मिलती हैं:
(अ) लाइमन
(ब) बामर
(स) पाश्चन
(द) ब्रेकेट
उत्तर:
(ब) बामर

प्रश्न 4.
प्रमुख क्वाण्टम संख्या 1 एवं बोर कक्षा की त्रिज्या rn में निम्न निर्भरता होती है:
(अ) rn α n^1/2
(ब) rn α n²
(स) rn α n^1/3
(द) rn α n
उत्तर:
(ब) rn α n²

प्रश्न 5.
हाइड्रोजन परमाणु में यदि इलेक्ट्रॉन तीसरी कक्षा से दूसरी कक्षा में संक्रमण करता है, तो उत्सर्जित हिरण की तरंगदैर्ध्य होगी:
(अ) \( \frac{5 R}{6}\)
(ब) \( \frac{R}{6}\)
(स) \( \frac{R}{36}\)
(द) \( \frac{5}{R}\)
उत्तर:
(स) \( \frac{R}{36}\)

प्रश्न 6.
लाइमैन तथा बामर श्रेणी की न्यूनतम तरंगदैर्घ्य का अनुपात होगा:
(अ) 1.25
(ब) 0.25
(स) 5
(द) 10
उत्तर:
(ब) 0.25

प्रश्न 7.
एक उत्तेजित हाइड्रोजन परमाणु में एक इलेक्ट्रॉन की ऊर्जा – 3.4 eV है। बोर के सिद्धान्त के अनुसार उसका कोणीय संवेग होगा:
(अ) \(\frac{h}{2 \pi}\)
(ब) \(\frac{2h}{2 \pi}\)
(स) \(\frac{3h}{2 \pi}\)
(द) \(\frac{4h}{2 \pi}\)
उत्तर:
(ब) \(\frac{2h}{2 \pi}\)

प्रश्न 8.
बोर के अनुसार केवल वे कक्ष स्थायी होती हैं जिनमें इलेक्ट्रॉन के कोणीय संवेग का मान होगा:
(अ)\(\frac{nh}{2 \pi}\)
(ब) \(\frac{nh}{\pi}\)
(स) \(\frac{2nh}{\pi}\)
(द) \(\frac{n}{2 \pi h}\)
उत्तर:
(अ)\(\frac{nh}{2 \pi}\)

प्रश्न 9.
हाइड्रोजन स्पेक्ट्रम में जब इलेक्ट्रॉन किसी बाह्य कक्ष से तीसरी कक्षा में संक्रमण करता है, तब स्पेक्ट्रम की श्रेणी होगी:
(अ) लाइमैन श्रेणी
(ब) बॉमर श्रेणी
(स) पाश्चन श्रेणी
(द) ब्रेकेट श्रेणी।
उत्तर:
(स) पाश्चन श्रेणी

प्रश्न 10.
यदि बोर के प्रथम कक्ष की त्रिज्या है तो दूसरे कक्ष की त्रिज्या होगी:
(अ) r/2
(ब) √2r
(स) 2r
(द) 4r
उत्तर:
(द) 4r

प्रश्न 11.
सोडियम की पीली रेखा की तरंगदैर्ध्य 5896 À है। इसकी तरंग संख्या होगी:
(अ) 50883 x 10¹⁰ प्रति सेकण्ड
(ब) 16961 प्रति सेमी.
(स) 17581 प्रति सेमी.
(द) 5.883 प्रति सेमी.
उत्तर:
(ब) 16961 प्रति सेमी.

प्रश्न 12.
हाइड्रोजन स्पेक्ट्रम की कौनसी श्रेणी पूर्ण तथा पराबैंगनी क्षेत्र में उपस्थित होती है:
(अ) लाइमन
(ब) बामर
(स) ब्रेकेट
(द) पाश्चन
उत्तर:
(अ) लाइमन

प्रश्न 13.
10 गुने आयनित सोडियम परमाणु की आयनन ऊर्जा होगी:
(अ) \(\frac{13.6}{11} \mathrm{eV}\)
(ब) \(\frac{13.6}{12} \mathrm{eV}\)
(स) 13.6 x (11)² ev
(द) 13.6 ev
उत्तर:
(स) 13.6 x (11)² ev

प्रश्न 14.
उत्सर्जित आवृत्ति का मान का संक्रमण होता है:
(अ) n = 5 से n = 3
(ब) n = 6 से n = 2
(स) n = 2 से n = 0
(द) n = 0 से n = 2
उत्तर:
(स) n = 2 से n = 0

प्रश्न 15.
बोहर कक्षा की त्रिज्या r पूर्णांक n तथा नियतांक K में सम्बन्ध:
(अ) r = n²K
(ब) r = nK
(स) r = n/k²
(द) r = n/K
उत्तर:
(अ) r = n²K

प्रश्न 16.
हाइड्रोजन परमाणु के प्रथम कक्षा की त्रिज्या 0.53 À है तो उसकी चतुर्थ कक्षा की त्रिज्या होगी:
(अ) 0.193 A°
(ब) 4.24 A°
(स) 2.12 A°
(द) 8.48 A°
उत्तर:
(द) 8.48 A°

प्रश्न 17.
हाइड्रोजन परमाणु में त्रिज्या की कक्षा में चक्कर काट रहे इलेक्ट्रॉन के लिए गतिज ऊर्जा होगी:
(अ) \(\frac{e^2}{2 r}\)
(ब) \(\frac{e^2}{r^2}\)
(स) \(\frac{e^2}{r}\)
(द) \(\frac{\mathrm{e}^2}{2 \mathrm{r}^2}\)
उत्तर:
(अ) \(\frac{e^2}{2 r}\)

प्रश्न 18.
एक उत्तेजित हाइड्रोजन परमाणु तरंगदैर्ध्य 2 के फोटोन को उत्सर्जित करने के पश्चात् मूल अवस्था में आ जाता है। उत्तेजित अवस्था की क्वाण्टम संख्या है-
(अ) \(\sqrt{\frac{\lambda R}{\lambda R-1}}\)
(ब) \(\sqrt{\frac{\lambda R-1}{\lambda R}}\)
(स) \(\sqrt{\lambda R-1}\)
(द) \(\sqrt{\frac{1}{\lambda R-1}}\)
उत्तर:
(अ) \(\sqrt{\frac{\lambda R}{\lambda R-1}}\)

प्रश्न 19.
यदि हाइड्रोजन परमाणु का आयनन विभव 13.6V है तो n = 3 पर इसकी लगभग ऊर्जा है:
(अ) – 1.14 ev
(ब) – 1.51 ev
(स) – 3.4 ev
(द) – 4.53 ev
उत्तर:
(ब) – 1.51 ev

प्रश्न 20.
बामर श्रेणी की प्रथम रेखा की तरंगदैर्घ्य 6563 À है लाइमन श्रेणी की प्रथम रेखा की तरंगदैर्घ्य होगी:
(अ) 1215.4 A°
(ब) 2500 A°
(स) 7500 A°
(द) 600 A°
उत्तर:
(अ) 1215.4 A°

प्रश्न 21.
बामर श्रेणी की सीमा 3646 A है। इस श्रेणी के प्रथम सदस्य की तरंगदैर्घ्य होगी:
(अ) 6563 A°
(स) 7200 A°
(ब) 3646 A°
(द) 1000 A°
उत्तर:
(अ) 6563 A°

प्रश्न 22.
किसी हाइड्रोजन परमाणु की nवीं कक्षा में ऊर्जा En है। एकल आयनित हीलियम परमाणु की ऊर्जा होगी:
(अ) 4 En
(ब) \(\frac{E_n}{4}\)
(स) 2 En
(द) \(\frac{E_n}{2}\)
उत्तर:
(अ) 4 En

प्रश्न 23.
हाइड्रोजन परमाणु के बोहर प्रतिरूप में इलेक्ट्रॉन की क्वान्टम में गतिज ऊर्जा तथा कुल ऊर्जा का अनुपात होगा:
(अ) 1
(ब) -1
(स) 2
(द) -2
उत्तर:
(ब) -1

प्रश्न 24.
हाइड्रोजन परमाणु में एक इलेक्ट्रॉन n = 4 ऊर्जा स्तर से n = 1 स्तर तक संक्रमण करता है। उत्सर्जित हो सकने वाले फोटॉनों की अधिकतम संख्या होगी:
(अ) 1
(ब) 2
(स) 3
(द) 6
उत्तर:
(द) 6

प्रश्न 25.
हाइड्रोजन स्पेक्ट्रम में चामर श्रेणी की अधिकतम तरंगदैर्घ्य का मान 6652 À है, इस श्रेणी की न्यूनतम तरंगदैर्ध्य है:
(अ) 304 Å
(ब) 3645 Å
(स) 1070 Å
(द) 10760 Å
उत्तर:
(ब) 3645 Å

प्रश्न 26.
बोर के सिद्धान्तानुसार इलेक्ट्रॉन की 1वीं कक्षा में कुल ऊर्जा होती है:
(अ) En = -13.6/n²ev
(ब) En = 13.6 n² eV
(स) 136 ev
(द) इनमें से कोई नहीं
उत्तर:
(अ) En = -13.6/n²ev

प्रश्न 27.
लाइमैन व बामर श्रेणी, हाइड्रोजन स्पेक्ट्रम में क्रमशः प्राप्त होती
(अ) पराबैंगनी व दृश्य क्षेत्र में
(ब) दृश्य व दृश्य क्षेत्र में
(स) पराबैंगनी व पराबैंगनी क्षेत्र में
(द) दोनों अवरक्त क्षेत्र में
उत्तर:
(अ) पराबैंगनी व दृश्य क्षेत्र में

प्रश्न 28.
जब बामर श्रेणी के लिए न्यूनतम और अधिकतम तरंगदैर्घ्य प्राप्त होते हैं, तब 12 के मान क्रमशः होंगे:
(अ) अनन्त व तीन
(ब) तीन व शून्य
(स) शून्य व तीन
(द) शून्य व शून्य
उत्तर:
(अ) अनन्त व तीन

प्रश्न 29.
रदरफोर्ड के कणों के प्रकीर्णन प्रयोग में धातुओं के पतली पन्नी से नाभिक का परमाणु क्रमांक बढ़ने पर प्रकीर्णन कोण का पथ होता है:
(अ) अपरिवर्तित रहता है
(ब) घटता है
(स) बढ़ता है
(द) इनमें से कोई नहीं
उत्तर:
(स) बढ़ता है

प्रश्न 30.
चिरसम्मत सिद्धान्त के अनुसार रदरफोर्ड मॉडल में इलेक्ट्रॉन
(अ) वृत्ताकार
(ब) सीधी रेखा में
(स) परवलय में
(द) सर्पिल वक्र में
उत्तर:
(द) सर्पिल वक्र में

प्रश्न 31.
H परमाणु में इलेक्ट्रॉन के प्रथम कक्ष की त्रिज्या A में होती है:
(अ) 0.529
(ब) 1.046
(स) 2.052
(द) 2.068
उत्तर:
(अ) 0.529

प्रश्न 32.
प्रकीर्णन प्रयोग में Q-कण कौनसे बल के कारण प्रकीर्णित होते हैं?
(अ) नाभिकीय बल
(ब) कूलॉम बल
(स) (अ) और (ब) दोनों
(द) गुरुत्वाकर्षण बल
उत्तर:
(ब) कूलॉम बल

प्रश्न 33.
यदि हाइड्रोजन परमाणु की मूल अवस्था में आयनन ऊर्जा 13.6 eV हो तो प्रथम उत्तेजित अवस्था की आयनन ऊर्जा होगी:
(अ) शून्य
(ब) 6.8 ev
(स) 10.2 ev
(द) 3.4 ev
उत्तर:
(द) 3.4 ev

प्रश्न 34.
निम्न में से कौन-सी एक बोहर मॉडल के अनुसार हाइड्रोजन परमाणु द्वारा उत्सर्जित फोटॉन की ऊर्जा सम्भव नहीं है?
(अ) 1.9 eV
(ब) 11.1 ev
(स) 13.6 ev
(द) 0.65 ev
उत्तर:
(ब) 11.1 ev

प्रश्न 35.
किसी अचल हाइड्रोजन परमाणु का एक इलेक्ट्रॉन पाँचवें ऊर्जा स्तर से न्यूनतम स्तर को गमन करता है, तो फोटॉन उत्सर्जन के परिणामस्वरूप परमाणु द्वारा प्राप्त वेग होगा:
(अ) \(\frac{24hR}{25m}\)
(ब) \(\frac{25hR}{24m}\)
(स) \(\frac{24hR}{24m}\)
(द) \(\frac{25hR}{25m}\)
उत्तर:
(अ) \(\frac{24hR}{25m}\)

अतिलघूत्तरात्मक प्रश्न:

प्रश्न 1.
परमाणु संरचना से सम्बन्धित रदरफोर्ड प्रयोग की कोई दो मुख्य कमियाँ लिखिए।
उत्तर:
(1) रेखीय वर्णक्रम की व्याख्या करने में असफल।
(2) परमाणु के स्थायित्व की व्याख्या करने में असफल। नोट – (अन्य उचित कमियाँ भी मान्य)

प्रश्न 2.
α कण प्रकीर्णन प्रयोग में स्वर्ण-पत्र ही क्यों प्रयुक्त किये गये?
उत्तर:
सोने का नाभिक भारी होने के कारण Q-कण का विक्षेप अधिक होता है तथा इसके अत्यधिक बारीक पत्र बनाये जा सकते हैं।

प्रश्न 3.
रदरफोर्ड के ca-प्रकीर्णन प्रयोग से प्राप्त दो मुख्य निष्कर्ष लिखिए।
उत्तर:
(i) परमाणु का अधिकांश द्रव्यमान तथा सम्पूर्ण आवेश परमाणु के अति सूक्ष्म स्थान में निहित है जिसे नाभिक कहते हैं।
(ii) नाभिक की त्रिज्या परमाणु की त्रिज्या का लगभग (1/ 10000) वाँ भाग है।

प्रश्न 4.
हाइड्रोजन परमाणु में बोर कक्षा की त्रिज्या का सूत्र लिखिए।
उत्तर:
rn = \(\frac{\epsilon_0 \mathrm{~h}^2}{\pi \mathrm{mZe}}\)
n2, जहाँ n = कक्षा की संख्या है और सभी शेष प्रतीकों के सामान्य अर्थ हैं।

प्रश्न 5.
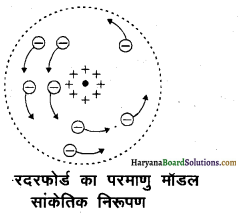
प्लम पुडिंग मॉडल किसे कहा गया था?
उत्तर:
जे. जे. टॉमसन के पहले परमाणु मॉडल को कहा गया था। इसके अनुसार परमाणु का धन आवेश परमाणु में पूर्णतया एकसमान रूप से वितरित है तथा ऋण आवेशित इलेक्ट्रॉन इसमें ठीक उसी प्रकार अंतःस्थापित है जैसे किसी तरबूज में बीज इस मॉडल को चित्रमय रूप में प्लम पुडिंग मॉडल कहा गया।

प्रश्न 6.
नाभिक किसे कहते हैं?
उत्तर:
किसी परमाणु का कुल धनावेश तथा अधिकांश द्रव्यमान एक सूक्ष्म आयतन में संकेन्द्रित होता है, जिसे नाभिक कहते हैं और इसके चारों ओर इलेक्ट्रॉन उसी प्रकार परिक्रमा करते हैं जैसे सूर्य के चारों ओर ग्रह परिक्रमा करते हैं।

प्रश्न 7.
बोर की आवृत्ति का सूत्र लिखिए
उत्तर:
बाह्य कक्षा से आन्तरिक कक्षा में किसी परमाणु में इलेक्ट्रॉन के कूदने से उत्सर्जित विकिरण की आवृत्ति E = hv = E2 – E1
यहाँ पर E = इलेक्ट्रॉन की आंतरिक कक्षा में कुल ऊर्जा और E = बाह्य कक्षा में इलेक्ट्रॉन की कुल ऊर्जा।

प्रश्न 8.
निकटतम पहुँच की दूरी को परिभाषित कीजिए।
उत्तर:
वह न्यूनतम दूरी जहाँ तक नाभिक की दिशा में सीधा गतिशील एक ऊर्जायुक्त a कण तब तक आ सके जब तक कि वह अपने पथ पर पुनः न लौट जाये, निकटतम पहुँच की दूरी कहलाती है।
F = \(\frac{1}{4 \pi \epsilon_0} \frac{(2 \mathrm{e})(\mathrm{Ze})}{\mathrm{r}^2}\)
जहाँ ऐल्फा कण की नाभिक से दूरी है।

प्रश्न 9.
संघट्ट प्राचल की परिभाषा दीजिए।
उत्तर:
a- कण के वेग सदिश की नाभिक से अभिलम्ब दूरी जब यह परमाणु से बहुत दूर है, को संघट्ट प्राचल कहते हैं। इसे b से प्रदर्शित करते हैं।

प्रश्न 10.
किसी परमाणु के इलेक्ट्रॉन के कोणीय संवेग के लिए बोर की क्वांटीकरण शर्त क्या है?
उत्तर:
mvr = \(\frac{\mathrm{nh}}{2 \pi}\) पूर्ण संख्या है।

प्रश्न 11.
निम्न घटना का कारण लिखिए अधिकांश -कण स्वर्ण पत्र के आर-पार बिना प्रभावित हुए सीधे ही निकल जाते हैं।
उत्तर:
क्योंकि परमाणु का अधिकांश भाग अन्दर से खोखला होता है।

प्रश्न 12.
a कणों के बड़े कोण से प्रकीर्णन के लिए परमाणु का नाभिक ही उत्तरदायी है, इलेक्ट्रॉन क्यों नहीं?
उत्तर:
इलेक्ट्रॉन Q-कण की तुलना में बहुत हल्का होता है इसलिए संवेग संरक्षण के सिद्धान्तानुसार वह Q-कण को बड़े कोण पर प्रकीर्णित नहीं कर सकता।

प्रश्न 13.
परमाणु की त्रिज्या तथा नाभिक की त्रिज्या की कोटि को लिखिए।
उत्तर:
क्रमशः 10^-10 m 10^-15 m

प्रश्न 14.
हाइड्रोजन परमाणु का व्यास लगभग कितना होगा?
उत्तर:
हाइड्रोजन परमाणु में एक प्रोटोन युक्त नाभिक केन्द्र में तथा एक इलेक्ट्रॉन 0.53 À त्रिज्या की कक्षा में गति करता है अतः परमाणु का व्यास 1.06 À के लगभग होगा।

प्रश्न 15
अवशोषण तथा उत्सर्जन संक्रमण से क्या तात्पर्य है?
उत्तर:
निम्नतम ऊर्जा स्तर से किसी भी उच्च ऊर्जा-स्तर में जाना अवशोषण संक्रमण तथा किसी उच्च ऊर्जा स्तर से किसी भी निम्न ऊर्जा स्तर में आना उत्सर्जन संक्रमण कहलाता है।

प्रश्न 16.
ऊर्जा स्तर क्या है? इसे कैसे प्रदर्शित करेंगे?
उत्तर:
किसी परमाणु की स्थायी कक्षा में इलेक्ट्रॉन की ऊर्जा को क्षैतिज रेखा से प्रदर्शित किया जा सकता है, जिसे ऊर्जा स्तर कहते हैं। इसे उचित ऊर्जा पैमाने के अनुसार क्षैतिज रेखा से प्रदर्शित कर सकते हैं।

प्रश्न 17.
हाइड्रोजन स्पेक्ट्रम की उस श्रेणी का नाम लिखिए जो कि पराबैंगनी दृश्य क्षेत्र में स्थित है।
उत्तर:
लाइमन श्रेणी।

प्रश्न 18.
हाइड्रोजन के रेखीय वर्णक्रम में पाई जाने वाली किन्हीं दो श्रेणियों के नाम लिखिए।
उत्तर:
लाइमन तथा बामर श्रेणी।

प्रश्न 19.
क्या कोई हाइड्रोजन परमाणु उस फोटॉन जिसकी ऊर्जा बंधन ऊर्जा से अधिक हो, अवशोषित कर सकता है?
उत्तर:
हाँ, परन्तु परमाणु आयनीकृत हो जायेगा।

प्रश्न 20.
हाइड्रोजन परमाणु की ब्रेकेट श्रेणी की रेखाओं का अनुभूतिमूलक व्यंजक लिखिए।
उत्तर:
V = RC \(\left(\frac{1}{4^2}-\frac{1}{n^2}\right)\) ; n = 5,6,7,

प्रश्न 21.
इलेक्ट्रॉन की कक्षाओं में कक्षा त्रिज्या तथा इलेक्ट्रॉन वेग में सम्बन्ध को लिखिए।
उत्तर:
r = \(\frac{e^2}{4 \pi \epsilon_0 m v^2}\)

प्रश्न 22.
हाइड्रोजन के परमाणु में इलेक्ट्रॉन की गतिज ऊर्जा (K) और स्थितिज ऊर्जा U के मान लिखिए।
उत्तर:
k = \(\frac{e^2}{8 \pi \epsilon_0 r}\) तथा \(\frac{-e^2}{4 \pi \epsilon_0 r}\)

प्रश्न 23.
इलेक्ट्रॉन की कुल ऊर्जा ऋणात्मक होती है। यह तथ्य क्या दर्शाता है? यदि धनात्मक होती तो यह क्या दर्शाता?
उत्तर:
इलेक्ट्रॉन की कुल ऊर्जा का मान E = K + U = \(\frac{-\mathrm{e}^2}{8 \pi \epsilon_0 \mathrm{r}}\)
यहाँ पर ऋणात्मक तथ्य यह दर्शाता है कि इलेक्ट्रॉन नाभिक से परिबद्ध है। यदि E का मान धनात्मक होता तो इलेक्ट्रॉन नाभिक के चारों ओर बन्द कक्ष में नहीं घूमता।

प्रश्न 24.
हाइड्रोजन के लिए स्पेक्ट्रम श्रेणी लाइमैन तथा पाश्चन के सूत्रों को लिखिए।
उत्तर:
लाइमैन श्रेणी \(\frac{1}{\lambda}\) = \(\frac{r1}{\lambda}\)
n = 2, 3, 4…..
पाश्चन श्रेणी \(\frac{1}{\lambda}\) = R
n = 4, 5, 6…..

प्रश्न 25.
बोर की कक्षा को ‘स्थायी कक्षा’ क्यों कहते हैं?
उत्तर:
ऐसी किसी कक्षा में चक्कर काटते हुए इलेक्ट्रॉन न तो ऊर्जा उत्सर्जित करता है और न ही अवशोषित। अतः इन कक्षाओं को ‘स्थायी कक्षा’ कहते हैं।

प्रश्न 26.
रदरफोर्ड के प्रयोग में नाभिक के द्रव्यमान का महत्व क्यों नहीं है?
उत्तर:
रदरफोर्ड के प्रकीर्णन प्रयोग में नाभिक का आवेश प्रकीर्णन का कारण है। नाभिक के आवेश का वैद्युत क्षेत्र प्रकीर्णन का कारण है। अतः नाभिक के द्रव्यमान से प्रकीर्णन स्वतंत्र हैं।

प्रश्न 27.
कोणीय संवेग की बोर के क्वांटमीकरण के प्रतिबंध का उल्लेख कीजिए। द्वितीय कक्षा में इलेक्ट्रॉन के लिए इसका क्या मान है?
उत्तर:
इसके अनुसार इलेक्ट्रॉन का कोणीय संवेग का
पूर्णांक गुणक है।
अर्थात् L=n. 2r 22 जहाँ n = 1, 2, 3,
द्वितीय क्रम की कक्षा के लिए n = 2,
∴ L = \(\frac{2 \mathrm{~h}}{2 \pi}\) = \(\frac{\mathrm{h}}{\pi}\) = \(\frac{6.63 \times 10^{-34}}{3.14}\)
= 2.11 × 10^-34

प्रश्न 28.
हाइड्रोजन परमाणु के उत्सर्जन स्पेक्ट्रम की विभिन्न श्रेणियों के नाम लिखिए। बताइए कि ये विद्युत चुम्बकीय स्पेक्ट्रम के किन-किन क्षेत्रों में पाई जाती हैं?
उत्तर:
लाइमैन श्रेणी- पराबैंगनी क्षेत्र में, बामर श्रेणी- दृश्य क्षेत्र में,
पाश्चन, ब्रेकेट तथा फुंट श्रेणी अवरक्त क्षेत्र में।

प्रश्न 29.
एक स्थायी कक्षा में घूमते इलेक्ट्रॉन की चाल मुख्य क्वांटम संख्या से कैसे संबंधित है?
उत्तर:
nth कक्षा में इलेक्ट्रॉन की चाल
अर्थात्
Vn = K.2πe²/nh से दिया जा 1

अर्थात् चाल मुख्य क्वांटम संख्या के व्युत्क्रमानुपाती है।

प्रश्न 30.
विभिन्न स्थायी कक्षाओं की त्रिज्यायें मुख्य क्वांटम संख्या से कैसे संबंधित हैं?
उत्तर:
हम जानते हैं:
अर्थात्
rn = \(\frac{n^2 h^2}{\mathrm{Ke}^2 4 \pi^2 \mathrm{~m}}\)
एक कक्षा की त्रिज्या मुख्य क्वांटम संख्या के वर्ग के अनुक्रमानुपाती

प्रश्न 31.
यदि एक इलेक्ट्रॉन की कुल ऊर्जा शून्य हो, तो आप क्या निष्कर्ष निकालते हैं?
उत्तर:
शून्य ऊर्जा का अर्थ है कि इलेक्ट्रॉन नाभिक से अनन्त दूरी पर है या यह केवल स्वतंत्र है।

प्रश्न 32.
कुछ कणों के 90° से अधिक कोण पर प्रकीर्णन से क्या निष्कर्ष प्राप्त करते हैं?
उत्तर:
(i) धनआवेशित a कणों के 90° से अधिक कोणों पर प्रकीर्णन के लिए आवश्यक है कि स्वर्ण पत्र के परमाणुओं में सूक्ष्म क्षेत्र में धनावेशित केन्द्रित है।
(ii) यह एक परमाणु के स्पेक्ट्रम को नहीं समझा सकता।

प्रश्न 33.
रिडबर्ग नियतांक R का मान ज्ञात करने का सूत्र लिखिए और इस नियतांक का मान कितना होता है?
उत्तर:
R = \(\frac{m e^4}{8 \in_0^2 h^3 c}\)
विभिन्न नियतांकों के मान प्रतिस्थापित करने पर R का मान होगा:
R = 1.03 x 10⁷ m^-1

प्रश्न 34.
परमाणु की सामान्य अवस्था के लिए क्वांटम संख्या n = 1 है आयनित अवस्था के लिए n का मान क्या है?
उत्तर:
n = ∞

प्रश्न 35.
उत्सर्जन स्पेक्ट्रम क्या है?
उत्तर:
जब किसी पदार्थ को गर्म किया जाता है तो उत्सर्जित प्रकाश से प्राप्त स्पेक्ट्रम को उत्सर्जन स्पेक्ट्रम कहते हैं।

प्रश्न 36.
रेखीय स्पेक्ट्रम पदार्थ की किस अवस्था में प्राप्त होता
उत्तर:
परमाण्वीय अवस्था में।

प्रश्न 37.
हाइड्रोजन स्पेक्ट्रम की कौन-सी श्रेणी पराबैंगनीं क्षेत्र में पड़ती है?
उत्तर:
लाइमैन श्रेणी

प्रश्न 38.
आयनन ऊर्जा को परिभाषित कीजिए। हाइड्रोजन परमाणु के लिए इसका मान क्या होता है?
उत्तर:
आयनन ऊर्जा- किसी परमाणु में इलेक्ट्रॉन को दी गई वह न्यूनतम ऊर्जा जिससे वह संक्रमण के द्वारा परमाणु से बाहर चला जाये, इस आवश्यक ऊर्जा को आयनन ऊर्जा कहते हैं। हाइड्रोजन परमाणु के आयनन ऊर्जा का मान 13.6 eV होता है।

प्रश्न 39.
हाइड्रोजन परमाणु के सबसे आन्तरिक कक्षा की त्रिज्या 5.3 x 10¹¹m है। द्वितीय उत्तेजित स्तर की कक्षा की त्रिज्या क्या है?
उत्तर:
हाइड्रोजन परमाणु की nवीं कक्षा की त्रिज्या
प्रश्नानुसार
rn = n²r₁
r1 = 5.3 x 10¹¹ m
∴ द्वितीय उत्तेजित स्तर के
लिए n = 3 होता है।
r3 = (3)2 × 5.3 x 10¹¹
यहाँ दिया गया है- n= 3
इसलिए
= 9 × 5.3 × 10¹¹
= 47.7 × 10¹¹ m

प्रश्न 40.
α-कण के बड़े कोण के प्रकीर्णन के लिए परमाणु का नाभिक ही उत्तरदायी है, इलेक्ट्रॉन क्यों नहीं?
उत्तर:
क्योंकि इलेक्ट्रॉन Q-कण की अपेक्षा बहुत हल्का होता है, इसलिए संवेग संरक्षण के सिद्धान्त के अनुसार यह a कण को बड़े कोण पर प्रकीर्णित नहीं कर सकता।

लघुत्तरात्मक प्रश्न:

प्रश्न 1.
α- प्रकीर्णन प्रयोग से गाइगर और उसके साथियों ने क्या प्रेक्षण किया?
उत्तर:
α- कण प्रकीर्णन प्रयोग से निम्न प्रेक्षण निकाले गये:
(i) अधिकांश a कण अविचलित सोने की पन्नी में से निकल जाते हैं।
(ii) कुछ a कण छोटे कोण पर निक्षेपित होते हैं।
(iii) कुछ a कण अधिक कोण ( > 90° ) पर विचलित होते हैं।
(iv) अत्यन्त अल्प मात्रा में Q-कण 180° से विक्षेपित होते हैं।
(v) पर्दे पर 6 कोण के अन्दर पहुँचने वाले प्रति एकांक क्षेत्रफल पर α- कणों की संख्या N(θ) = 1/sin⁴(θ/2) होती है।

प्रश्न 2.
किसी दिए हुए समयांतराल में विभिन्न कोणों पर प्रकीर्णित कुछ ऐल्फा- कणों की संख्या के प्रारूपिक आलेख को दर्शाइए।
उत्तर:

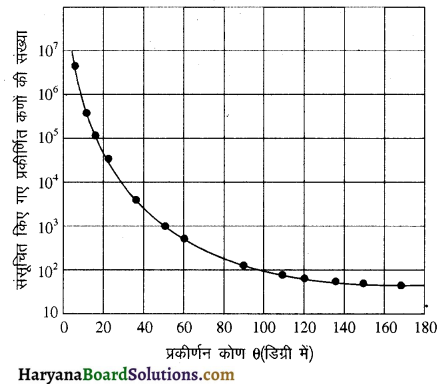
प्रश्न 3.
बोर परमाणु में इलेक्ट्रॉन की कुल ऊर्जा का ऋणात्मक होना क्या प्रकट करता है?
उत्तर:
इलेक्ट्रॉन की स्थितिज ऊर्जा ऋणात्मक तथा गतिज ऊर्जा धनात्मक होती है स्थितिज ऊर्जा गतिज ऊर्जा से अधिक होती है अतः कुल ऊर्जा ऋणात्मक होती है जो परमाणु के स्थायित्व को दर्शाती है तथा इससे इलेक्ट्रॉन बाहर निकालने के लिए बाहर से ऊर्जा देनी पड़ेगी।

प्रश्न 4.
स्वर्ण-पत्र पर आपतित कणों में से कुछ ऐसे भी हैं जो प्रकीर्णित होकर वापस अपने ही मार्ग पर लौट आते हैं। (कारण दीजिए)
उत्तर:
किसी भी परमाणु के भीतर एक अत्यन्त सूक्ष्म स्थान में धनावेश केन्द्रित रहता है जो a-कण पर इतना अधिक प्रतिकर्षण बल लगाता है कि a कण अपने ही मार्ग से वापस लौटता है।

प्रश्न 5.
पदार्थों के परमाण्वीय स्पेक्ट्रम की कुछ सुनिश्चित रेखायें ही प्राप्त होती हैं, क्यों?
उत्तर:
परमाणु की केवल सुनिश्चित तथा विविक्त ऊर्जा अवस्थायें ही होती हैं अतः परमाणु के संक्रमणों द्वारा उत्सर्जित विकिरणों की कुछ सुनिश्चित आवृत्तियाँ ही सम्भव हैं।

प्रश्न 6.
हाइड्रोजन परमाणु में इलेक्ट्रॉन की ऊर्जा निम्नांकित सूत्र से व्यक्त की जाती है
En = \(-\left(\frac{13.6 \mathrm{eV}}{\mathrm{n}^2}\right)\)
जहाँ n = 1, 2, 3,
इस सूत्र का प्रयोग करते हुए सिद्ध कीजिए कि-
(a) हाइड्रोजन परमाणु में इलेक्ट्रॉन की ऊर्जा – 6.8 eV नहीं हो सकती। (b) हाइड्रोजन परमाणु के स्पेक्ट्रम में संलग्न रेखाओं के बीच की दूरी n के बढ़ने के साथ-साथ घटती जाती है।
उत्तर:
सूत्र En = \(-\left(\frac{13.6 \mathrm{eV}}{\mathrm{n}^2}\right)\) में n = 1, 2, 3, …..∞
रखकर सरल करने पर,
E1 = \(-\left(\frac{13.6 \mathrm{eV}}{\mathrm{n}^2}\right)\) = -13.6eV
E2 = \(-\left(\frac{13.6}{2^2}\right)\)eV = \(\frac{-13.6}{4}\) = -3.4ev
E3 = \(-\left(\frac{13.6}{3^2}\right)\)ev = \(-\left(\frac{13.6}{9}\right)\) = -1.51ev
E4 = \(-\left(\frac{13.6}{3^4}\right)\) = \(-\left(\frac{13.6}{81}\right)\) = – 0.85ev
(a) अतः स्पष्ट है कि हाइड्रोजन परमाणु में इलेक्ट्रॉन की ऊर्जा – 6.8 eV नहीं हो सकती।
(b) यह भी स्पष्ट है कि n में वृद्धि के साथ दो संलग्न रेखाओं (ऊर्जा स्तरों) का ऊर्जा अन्तर घटता जाता है। अतः उनके बीच की दूरी भी घटती जाती है।

प्रश्न 7.
बोर के सिद्धान्त में कोणीय संवेग के क्वाण्टीकरण से सम्बन्धित परिकल्पना का उल्लेख कीजिये।
अथवा
हाइड्रोजन परमाणु में इलेक्ट्रॉन की कक्षीय गति के लिए बोर का क्वाण्टम प्रतिबन्ध बताइए।
उत्तर:
बोर की द्वितीय परिकल्पना – इलेक्ट्रॉन केवल उन्हीं कक्षाओं में घूम सकता है जिनमें इलेक्ट्रॉन का कोणीय संवेग
(L = mvr), का पूर्ण गुणक हो।
बोर की इस परिकल्पना के अनुसार
या
L = \(\frac{\mathrm{nh}}{2 \pi}\)
mvr = \(\frac{\mathrm{nh}}{2 \pi}\)
यहाँ पर 1 एक पूर्णांक है जिसके मान क्रमश: 1, 2, 3, हैं n को मुख्य क्वाण्टम संख्या एवं इस प्रतिबन्ध को बोर का क्वाण्टम प्रतिबन्ध कहते हैं। यह प्रतिबन्ध इलेक्ट्रॉन की गति को निश्चित सम्भव कक्षाओं में सीमित करता है। n को निर्धारित विभिन्न मान देने पर इलेक्ट्रॉन की विभिन्न त्रिज्या वाली स्थायी कक्षायें प्राप्त होती हैं।

प्रश्न 8.
रदरफोर्ड परमाणु प्रतिरूप के दोषों का उल्लेख कीजिये।
उत्तर:
रदरफोर्ड परमाणु प्रतिरूप की कमियाँ- रदरफोर्ड के परमाणु मॉडल में दो कमियाँ पायी गई-
(i) परमाणु के स्थायित्व के सम्बन्ध में नाभिक के चारों ओर घूमते इलेक्ट्रॉन में अभिकेन्द्र त्वरण होता है। विद्युत गति विज्ञान के अनुसार त्वरित आवेशित कण ऊर्जा उत्सर्जित करता है। अतः नाभिक के चारों ओर विभिन्न कक्षाओं में घूमते इलेक्ट्रॉनों से विद्युत चुम्बकीय तरंगें लगातार उत्सर्जित होनी चाहिये। इस प्रकार इलेक्ट्रॉन की ऊर्जा का हास होने के कारण उनके वृत्तीय पथ की त्रिज्या लगातार कम होती जानी चाहिये और अन्त में वे नाभिक में गिर जाने चाहिये। इस प्रकार परमाणु स्थायी (stable) ही नहीं रह सकता है।

(ii) रेखीय स्पेक्ट्रम की व्याख्या के सम्बन्ध में रदरफोर्ड मॉडल में इलेक्ट्रॉनों के वृत्तीय पथ की त्रिज्या के लगातार बदलते रहने से उनके घूमने की आवृत्ति भी बदलती रहेगी। इसके फलस्वरूप इलेक्ट्रॉन सभी आवृत्तियों की विद्युत चुम्बकीय तरंगें उत्सर्जित करेंगे अर्थात् इन तरंगों का स्पेक्ट्रम संतत (continuous) होगा, परन्तु वास्तव में परमाणुओं के स्पेक्ट्रम संतत न होकर रेखीय होते हैं अर्थात् उनमें बहुत-सी बारीक रेखायें होती हैं तथा प्रत्येक स्पेक्ट्रम रेखा की एक निश्चित आवृत्ति होती है अतः परमाणु से केवल कुछ निश्चित आवृत्तियों की ही तरंगें उत्सर्जित होनी चाहिये सभी आवृत्तियों की नहीं इस प्रकार रदरफोर्ड मॉडल रेखीय स्पेक्ट्रम की व्याख्या करने में असक्षम रहा।

प्रश्न 9.
हाइड्रोजन स्पेक्ट्रम में कौनसी श्रेणी दृश्य स्पेक्ट्रम क्षेत्र में होती है? इस श्रेणी की विभिन्न रेखाओं की तरंग संख्यायें ज्ञात करने के लिये सूत्र लिखिये।
उत्तर:
हाइड्रोजन स्पेक्ट्रम में बामर श्रेणी दृश्य स्पेक्ट्रम क्षेत्र में होती है। बामर श्रेणी, हाइड्रोजन परमाणु का इलेक्ट्रॉन जब किसी ऊँचे स्तरों n2 = 3, 4, 5….. से द्वितीय ऊर्जा स्तर n = 2 में संक्रमण करता है तो उत्सर्जित विकिरण की श्रृंखला को बामर श्रेणी कहते हैं।
\(\frac{1}{\lambda}\) = \(\mathrm{R}\left[\frac{1}{2^2}-\frac{1}{\mathrm{n}_2^2}\right]\)
जहाँ पर n 2 = 3, 4, 5 ……….. ∞ है इस श्रेणी की सबसे बड़ी तरंगदैर्ध्य 6563 Å तथा सबसे छोटी तरंगदैर्ध्य 3646 À है।

प्रश्न 10.
रदरफोर्ड के Q-कण के प्रयोग में यह देखने में आता है कि (i) अधिकतर a-कण लगभग बिना प्रकीर्णित हुए सीधे निकल जाते हैं, (ii) जबकि उनमें कुछ बड़ा कोण बनाते हुए प्रकीर्णित होते हैं तथा कुछ कण ऐसे भी हैं जो प्रकीर्णित होकर वापस अपने ही मार्ग पर लौट आते हैं। परमाणु की संरचना के विषय में इससे क्या सूचना प्राप्त होती है?
उत्तर:
(i) परमाणु के भीतर अधिकांश भाग खोखला है तथा
(ii) में धनावेश एक अत्यन्त सूक्ष्म स्थान (नाभिक) में संकेन्द्रित है।

प्रश्न 11.
एक α-कण V वोल्ट विभवान्तर से गुजरकर एक नाभिक से टकराता है। सिद्ध कीजिए कि यदि परमाणु संख्या Z हो, तो कण की नाभिक के पास पहुँचने की निकटतम दूरी 14.4 (Z/V) Å होगी।
(दिया है : 1/4r πE0 = 9.0 x 10⁹ न्यूटन मीटर / कूलॉम’; तथा e = 1.6 x 10^-19कूलॉम)
उत्तर:
α-कण की नाभिक के निकटतम पहुँचने की स्थिति में α-कण की गतिज ऊर्जा = α-कण नाभिक निकाय की वैद्युत
स्थितिज ऊर्जा
⇒ 2e x v = 1/4πE0(2e x Ze/r0)
⇒ 9 x 10⁹(2e x Ze/r0)
⇒ 2ev = \(\frac{2 \times 9 \times 10^9 \times \mathrm{Ze}^2}{\mathrm{r}_0}\)
⇒ r0 = \(\frac{9 \times 10^9 \mathrm{Ze}}{\mathrm{V}}\) मीटर
मान रखने पर
9 x 10⁹ 1.6 x 10^-19 मीटर
= 14.4 x 10¹⁰

प्रश्न 12.
किसी हाइड्रोजन परमाणु में प्रथम उत्तेजित स्तर तथा मूल स्तर के संगत कक्षाओं की त्रिज्याओं का अनुपात क्या होता है?
उत्तर;
हम जानते हैं rn α nⁿ
मूल स्तर के लिए n = 1 तथा प्रथम उत्तेजित स्तर के लिए n = 2 होता है।
प्रथम उत्तेजित स्तर की त्रिज्या (5) मूल स्तर की त्रिज्या (i)

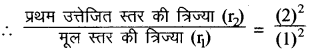
\(\frac{r_2}{r_1}\) = \(\frac{4}{1}\)
r2 : r1 = 4 : 1

प्रश्न 13.
क्या कारण है कि किसी परमाणु के अवशोषण संक्रमणों की संख्या उत्सर्जन संक्रमणों से कम होती है?
उत्तर:
इसका कारण है कि उत्सर्जन संक्रमण किसी भी उच्च ऊर्जा स्तर से प्रारम्भ होकर उससे किसी भी निम्न ऊर्जा स्तर पर समाप्त हो सकते हैं, जबकि अवशोषण संक्रमण सदैव मूल ऊर्जा स्तर से ही प्रारम्भ होकर किसी भी उच्च ऊर्जा स्तर पर समाप्त होते हैं।

प्रश्न 14.
हाइड्रोजन परमाणु में केवल एक ही इलेक्ट्रॉन है, परन्त उसके उत्सर्जन वर्णक्रम में कई रेखाएँ होती हैं। ऐसा कैसे होता है? कारण सहित समझाइए।
उत्तर:
प्रत्येक परमाणु के कुछ सुनिश्चित ऊर्जा स्तर होते हैं। सामान्य अवस्था में हाइड्रोजन परमाणु का इलेक्ट्रॉन निम्नतम ऊर्जा- स्तर में रहता है। जब परमाणु को बाहर से पर्याप्त ऊर्जा मिलती है तो इलेक्ट्रॉन निम्न ऊर्जा स्तर को छोड़कर किसी ऊँचे ऊर्जा स्तर में चला जाता है, अर्थात् उत्तेजित हो जाता है। लगभग 10 सेकण्ड में ही इलेक्ट्रॉन ऊँचे ऊर्जा स्तर को छोड़ देता है। अब यह सीधे निम्नतम ऊर्जा स्तर में भी लौट सकता है अथवा नीचे ऊर्जा स्तरों से होते हुए भी निम्नतम ऊर्जा स्तर में लौट सकता है। चूँकि किसी प्रकाश स्रोत (हाइड्रोजन लैम्प में असंख्य परमाणु हैं, अतः स्रोत में सभी सम्भव संक्रमण होने लगते हैं तथा स्पेक्ट्रम में अनेक रेखाएँ दिखाई पड़ती है।

प्रश्न 15.
सतत परास की आवृत्ति वाले फोटॉन विरलित (rarefied) हाइड्रोजन नमूने में से गुजारे जाते हैं। चित्र में तीन अवशोषित रेखाएँ दर्शाई गई हैं।

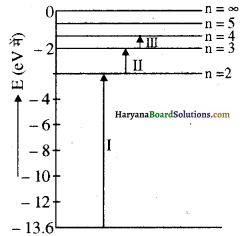
(i) ये रेखाएँ हाइड्रोजन स्पेक्ट्रम की किस श्रेणी से सम्बन्धित
(ii) इनमें से किसकी तरंगदैर्ध्य सबसे अधिक होगी?
उत्तर:
(i) I = लाइमैन श्रेणी II = बामर श्रेणी III = पाश्चन श्रेणी।
(ii) ∵ λ = hc/ΔΕ अधिकतम तरंगदैर्घ्य के लिए AE न्यूनतम होनी चाहिए। यह III रेखा के लिए है। अतः इसकी तरंगदैर्ध्य सबसे अधिक होगी।

प्रश्न 16.
H2 परमाणु में पहली बोहर कक्षा की त्रिज्या ro है। दूसरी कक्षा की त्रिज्या कितनी होगी? एकल आयनित हीलियम परमाणु की द्वितीय कक्षा की त्रिज्या कितनी होगी?
उत्तर:
H2 परमाणु के लिए r α n²; इसलिए इसकी दूसरी
कक्षा की त्रिज्या
r2 = 2²r1 = 2² x ro = 4ro
H2 सदृश परमाणु के लिए r α (n²/Z) तथा एकल आयनित हीलियम परमाणु के लिए Z = 2

= \(\frac{2^2 / 2}{2^2}\)
अतः एकल आयनित He परमाणु की द्वितीय कक्षा की त्रिज्या
= H2 परमाणु की द्वितीय कक्षा की त्रिज्या / 2
= 4r/2 = 2ro

प्रश्न 17.
हाइड्रोजन परमाणु को उत्तेजित करने वाले इलेक्ट्रॉन की न्यूनतम ऊर्जा कितनी हो कि हाइड्रोजन स्पेक्ट्रम में तीन स्पेक्ट्रमी रेखाएँ प्राप्त हों?
उत्तर:
हाइड्रोजन स्पेक्ट्रम तीन स्पेक्ट्रमी रेखाएँ प्राप्त करने के लिए आवश्यक है कि परमाणु को उत्तेजित करने वाले इलेक्ट्रॉन में इतनी ऊर्जा हो कि उसको n = 1 से n = 3 में उत्तेजित कर सकें जिससे तीन उत्सर्जन संक्रमण = (3 → 2, 3 → 1, 2 → 1) प्राप्त हो जायेंगे।
इस स्थिति में सूत्र En = ( 13.6/n 2 ) eV. से.
अतः
E1 = -(13.6/1²)ev = -13.6ev
E3 = -(13.6/3²)ev = -1.5ev
आवश्यक न्यूनतम ऊर्जा = E3 – E1
= – 1.5 eV – (- 13.6 eV)
= – 1.5 eV + 13.6 eV = 12.1 ev
यद्यपि परमाणु के अवशोषण स्पेक्ट्रम में तीन स्पेक्ट्रमी रेखाएँ : (1 → 2, 1 → 3, 1 → 4) प्राप्त करने के लिए अपेक्षाकृत अधिक ऊर्जा (E4 – E1) = 12.75 ev चाहिए।

प्रश्न 18.
बोर के सिद्धान्त की कमियों का उल्लेख कीजिये।
उत्तर:
बोर प्रतिरूप की कमियाँ
(1) बोर का सिद्धान्त एक इलेक्ट्रॉन वाले परमाणु, जैसे- हाइड्रोजन या आयनित हीलियम के लिये ही उपयुक्त है। इसके द्वारा अन्य परमाणुओं के स्पेक्ट्रम की व्याख्या नहीं की जा सकी।
(2) इस सिद्धान्त में नाभिक को स्थिर माना गया है, परन्तु यह तभी सम्भव है जब नाभिक का द्रव्यमान अनन्त हो।
(3) इसमें इलेक्ट्रॉन की कक्षायें वृत्ताकार मानी गयी हैं, जबकि यह अधिकतर दीर्घ वृत्ताकार होती हैं।
(4) इसके आधार पर स्पेक्ट्रमी रेखाओं की तीव्रता की व्याख्या नहीं की जा सकती है।
(5) कोणीय संवेग के क्वांटीकरण का कोई तर्कसंगत आधार नहीं दिया गया।
(6) इसके आधार पर स्पेक्ट्रमी रेखाओं की सूक्ष्म संरचना की व्याख्या नहीं की जा सकती।
(7) चुम्बकीय क्षेत्र प्रयुक्त करने पर स्पेक्ट्रमी रेखाओं में विपाटन (Splitting ) होता है, यह प्रभाव जेमान प्रभाव कहलाता है जिसकी व्याख्या बोर सिद्धान्त से नहीं हो सकी। इस तरह विद्युत क्षेत्र में स्पेक्ट्रमी रेखाओं का विपाटन प्रेक्षित होता है जिसे स्टार्क प्रभाव कहते हैं।

प्रश्न 19.
बोर के अभिगृहीतों के आधार पर हाइड्रोजन परमाणु की nवीं स्थाई कक्षा में इलेक्ट्रॉन के कक्षीय वेग के व्यंजक की व्युत्पत्ति कीजिए।
हाइड्रोजन परमाणु की निम्नतम अवस्था में ऊर्जा (-) Xev है। इस अवस्था में इलेक्ट्रॉन की गतिज ऊर्जा कितनी होगी?
उत्तर:
बोर की प्रथम परिकल्पना – परमाणु में इलेक्ट्रॉन नामिक के चारों ओर विभिन्न स्थायी वृत्ताकार कक्षों में घूमते हैं। इलेक्ट्रॉन एवं नाभिक के आवेश के बीच कार्य करने वाला कूलॉम बल, इलेक्ट्रॉन की वृत्तीय कक्षा में घूमने के लिये आवश्यक अभिकेन्द्रीय बल प्रदान करता है। अतः बोर की प्रथम परिकल्पना से

बोर की द्वितीय परिकल्पना: इलेक्ट्रॉन केवल उन्हीं कक्षाओं में घूम सकता है जिनमें इलेक्ट्रॉन का कोणीय संवेग ( L = mvr), h/2π का पूर्ण गुणक हो। बोर की इस परिकल्पना के अनुसार
L = nh/2π
या
mvr = n(h/2π) ….(2)
जहाँ h = प्लांक नियतांक तथा n = 1. 2. 3…. मुख्य क्वाण्टम
संख्यायें हैं।
समीकरण (1) से
mv²r = \(\frac{\mathrm{Ze}^2}{4 \pi \epsilon_0}\)
या mvrv = \(\frac{\mathrm{Ze}^2}{4 \pi \epsilon_0}\) ………(3)
समीकरण (2) से mvr का मान रखने पर

(जहाँ n = 1. 2. 3….. )
समीकरण (4) स्थायी कक्षाओं में इलेक्ट्रॉन के वेग का सामान्य व्यंजक है। इस सूत्र में e, E0 तथा h सार्वत्रिक नियतांक हैं। परमाणु
विशेष के लिये Z भी नियतांक है अतः v α 1/n
अर्थात् “स्थायी कक्षाओं में इलेक्ट्रॉन का वेग कक्षा की संख्या अर्थात् मुख्य क्वाण्टम संख्या के व्युत्क्रमानुपाती होता है। ” इलेक्ट्रॉन की गतिज ऊर्जा का मान
K =- (-) X ev
K = XeV

प्रश्न 20.
एक ऐल्फा कण, जिसकी गतिज ऊर्जा 4.5 Mev है, Z = 80 के किसी नाभिक से टकराता है, रुकता है और अपनी दिशा उत्क्रमित करता है, तो निकटतम उपगमन की दूरी निर्धारित कीजिए।
उत्तर:
माना निकटतम उपगमन की दूरी है।
था
K = 4.5Mev
= 4.5 x 10⁶ ev
Z = 80

आंकिक प्रश्न:

प्रश्न 1.
गांइगर मार्सडन प्रयोग में Z = 80 नाभिक से निकटतम पहुँच की दूरी ज्ञात कीजिए जब 8 Mev ऊर्जा का Q-कण उसकी ओर प्रेक्षित किया जाता है जो क्षणभर के लिए विरामावस्था में आने से पहले उसकी दिशा प्रतिलोम हो जाती है। जब Q-कण की गतिज ऊर्जा दुगुनी कर दी जाये तो निकटतम पहुँच की दूरी कैसे प्रभावित होगी?
उत्तर:
निकटतम पहुँच की दूरी का सूत्र
r0 = K2Ze²/Ek
दिया है:
z = 80, E = 8 Mev
= 8 × 106 × 1.6 x 10^-19 J
e = 1.6 x 10^-19 कूलॉम
मान रखने पर
ro = \(\frac{9 \times 10^9 \times 2 \times 80 \times\left(1.6 \times 10^{-19}\right)^2}{8 \times 10^6 \times 1.6 \times 10^{-19}}\)
= \(\frac{2304 \times 10^{-10}}{8 \times 10^6}\)
= 288 ×10^-16
जब
= 28.8 × 10^-15m
Ek = 2 × 8 MeV = 16 Mev
= 16 × 100 × 1.6 × 10^-16J
तब
= \(\frac{9 \times 10^9 \times 2 \times 80 \times\left(1.6 \times 10^{-19}\right)^2}{16 \times 10^6 \times 1.6 \times 10^{-19}}\)
= \(\frac{2304 \times 10^{-10}}{16 \times 10^6}\)
= 144 x 10^-16
= 14.4 × 10^-15m
यदि अल्फा कण की ऊर्जा दुगुनी कर दी जाये तो निकटतम पहुँच दूरी आधी हो जायेगी।

प्रश्न 2.
हाइड्रोजन परमाणु की प्रथम व द्वितीय बोर कक्षों की त्रिज्याएँ, वेग व ऊर्जा स्तरों की गणना कीजिए दिया है h = 6.6 x 10^-14 जूल- सेकण्ड;
इलेक्ट्रॉन का द्रव्यमान m = 9.1 x 10^-31 किलोग्रामः
e = 1.6 × 10^-19 कूलॉम;
Eo = 8.85 × 10^-12 कूलॉम / न्यूटन मीटर
उत्तर:
(i) कक्षा की त्रिज्या rn =\(\frac{\epsilon_0 n^2 h^2}{\pi m e^2}\)
अतः प्रथम कक्षा की त्रिज्या के लिए n = 1
∴ r1 = \(\frac{\epsilon_0 h^2}{\pi \mathrm{me}^2}\)
= \(\frac{8.85 \times 10^{-12} \times\left(6.6 \times 10^{-34}\right)^2}{3.14 \times 9.1 \times 10^{-31} \times\left(1.6 \times 10^{-19}\right)^2}\) मीटर
= 5.29 × 10^-11 मीटर
= 0.529 ऐंग्स्ट्रम
(ii) द्वितीय कक्षा n = 2 के लिए r2 = n2r1
= 4 × 0.529 Å = 2.116 ऐंग्स्ट्रम

(iii) यदि प्रथम कक्षा में वेग V1 है, तो
= \(\frac{\mathrm{e}^2}{2 \epsilon_{\mathrm{o}} \mathrm{nh}}\)
= \(\frac{\left(1.6 \times 10^{-16}\right)^2}{2 \times 8.85 \times 10^{-12} \times 6.6 \times 10^{-34}}\)
= 2.2 × 10⁶ मीटर/सेकण्ड

(iv) द्वितीय कक्षा में वेग V2
Vn = V1/n यहाँ n = 2
∴ V2 = \(\frac{\left(1.6 \times 10^{-16}\right)^2}{2 \times 8.85 \times 10^{-12} \times 6.6 \times 10^{-34}}\)
= 1.1 x 10⁶मीटर / सेकण्ड

(v) nवीं कक्षा की ऊर्जा En = \(\frac{-m e^4}{8 \epsilon_0^2 h^2 n^2}\)
n = 1 रखने पर प्रथम कक्षा ( मूल स्तर) की ऊर्जा
E1 = \(\frac{-m e^4}{8 \epsilon_0^2 h^2}\)
= \(\frac{9.1 \times 10^{-31} \times\left(1.6 \times 10^{-19}\right)^4}{8 \times\left(8.85 \times 10^{-12}\right)^2 \times\left(6.6 \times 10^{-34}\right)^2}\)
= – 2.179 × 10¹⁸ जूल
= \(\frac{-2.179 \times 10^{-18}}{1.6 \times 10^{-19}}\)
= – 13.6 इलेक्ट्रॉन वोल्ट

(vi) दूसरे कक्षा की ऊर्जा En = E1/n²
(यहाँ n = 2)
∴ E2 = -13.6eV/4 = -3.4
इलेक्ट्रॉन वोल्ट

प्रश्न 3.
एक परमाणु का ऊर्जा स्तर आरेख चित्र में प्रदर्शित किया गया है। संक्रमण B तथा D से प्राप्त फोटॉनों के तरंगदैर्ध्य ज्ञात कीजिये।

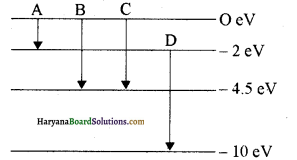
उत्तर:
संक्रमण B के लिए
E1 = – 4.5 eV तथा E2 = 0 ev
E = E2 – E1 = 0 + 4.5 = 4.5 ev
अतः उत्सर्जित स्पेक्ट्रमी रेखा ( फोटॉन की तरंगदैर्ध्य )
λ = hc/E
∴ λ = hc/4.5ev
मान रखने पर
λ = \(\frac{6.62 \times 10^{-34} \times 3 \times 10^8}{4.5 \times 1.6 \times 10^{-19}}\)
λ = \(\frac{6.62 \times 3 \times 10^{-34} \times 10^{27}}{4.5 \times 1.6}\)
= \(\frac{19.8 \times 10^{-7}}{7.2}\)
= 2.75 x 10⁷ m
= 2750 × 10^-10m = 2750 A
संक्रमण D के लिए
E1 = – 10 eV तथा E2 =- 2e V.
E = E2 – E से
= -2eV + 10 eV = 8 ev
अतः उत्सर्जित स्पेक्ट्रमी रेखा ( फोटॉन की तरंगदैर्ध्य )
∴ λ = hc/E = hc/8ev
मान रखने पर
λ = \(\frac{6.6 \times 10^{-34} \times 3 \times 10^8}{8 \times 1.6 \times 10^{-19}}\)
= 1.547 × 10⁷ m
= 1547 x 10^-10 m
= 1547 A

प्रश्न 4.
हाइड्रोजन परमाणु की प्रथम उत्तेजित अवस्था में ऊर्जा – 3.4 V है। मूल अवस्था प्राप्त करने पर उत्सर्जित फोटॉन का तरंगदैर्ध्य ज्ञात कीजिये उत्तेजित अवस्था में इलेक्ट्रॉन की स्थितिज एवं गतिज ऊर्जाओं की गणना भी कीजिये।
उत्तर:
n वीं कक्षा में इलेक्ट्रॉन की गतिज एवं स्थितिज ऊर्जायें क्रमशः हैं (H-परमाणु के लिये )
है।
गतिज ऊर्जा Kn = 13.6/n²ev
और स्थितिज ऊर्जा Un = -27.2/n² ev
n = 2, द्वितीय कक्षा जिसे हम प्रथम उत्तेजित अवस्था भी कहते
∴ n = 2 रखने पर K2 = 13.6/2²eV = 3.4ev
U2 = -27.2/2²ev = -6.8eV
हाइड्रोजन परमाणु के इलेक्ट्रॉन के प्रथम उत्तेजित अवस्था से मूल अवस्था में लौटने पर उसकी ऊर्जा में हुआ हास
13.6 + 3.4 = -10.2 ev
प्रश्नानुसार इसमें 3 तरंगदैर्घ्य का फोटॉन उत्सर्जित होता है।
hc/λ = 10.2 x 1.6 x 10^-19
λ = \(\frac{h c}{10.2 \times 1.6 \times 10^{-19}}\)
= \(\frac{6.62 \times 10^{-34} \times 3 \times 10^8}{10.2 \times 1.6 \times 10^{-19}}\)
= 1.217 x 10⁷ m
= 1217 A

प्रश्न 5.
(i) चित्रानुसार जब कोई इलेक्ट्रॉन ऊर्जा स्तर 2E से ऊर्जा स्तर E में संक्रमण करता है तो तरंगदैर्ध्य का फोटॉन उत्सर्जित होता है। यदि यह इलेक्ट्रॉन ऊर्जा स्तर स्तर E में संक्रमण करता है तो उत्सर्जित फोटॉन ज्ञात कीजिए।

(ii) हाइड्रोजन परमाणु के प्रथम कक्ष की त्रिज्या 0.53है तो इसके दूसरे कक्ष की त्रिज्या कितनी होगी?
उत्तर:

समीकरण (1) में समीकरण (2) का भाग देने पर
\(\frac{\lambda_1}{\lambda}\) = \(\frac{3 R}{4 E^2}\) \(\frac{25 \mathrm{E}^2}{9 R}\)
\(\frac{\lambda_1}{\lambda}\) = \(\frac{25}{12}\)
λ = \(\frac{25}{12}\)

(ii) सूत्र rn = 0.53n²/Z
हाइड्रोजन के लिए Z = 1
∴ rn = 0.53n² A
दूसरे कक्ष के लिए
n = 2
r2 = 0.53 × 2²
= 0.53 × 4
= 2.12A

प्रश्न 6.
किसी परमाणु में ऊर्जा स्तर A से C में संक्रमण से 1000 ऐंग्स्ट्रम तथा संक्रमण B से C में 5000 ऐंग्स्ट्रम तरंगदैर्ध्य के विकिरण उत्सर्जित होते हैं, ऊर्जा स्तर A से B में संक्रमण के लिए उत्सर्जित विकिरण की तरंगदैर्ध्य कितनी होगी?
उत्तर:
हम जानते हैं कि
\(E_{n_2}-E_{n_1}=\frac{h c}{\lambda}\)
प्रश्नानुसार
E_A – E_C = \(\frac{\mathrm{hc}}{\lambda}\) यहाँ λ₁ = 1000 Å
अतः
E_A – E_C = \(\frac{h c}{1000 Å}\) ……(1)
इसी प्रकार E_B – E_C = \(\frac{h c}{5000 Å}\) …..(2)
यदि A से B में संक्रमण से उत्सर्जित विकिरण (फोटॉन) की तरंगदैर्ध्य λ₃ हो तो
E_B – E_C = \(\frac{\mathrm{hc}}{\lambda_3}\) …….(3)
समीकरण (1) में से समीकरण (2) घटाने पर
E_A – E_C = \(\frac{h c}{1000 Å}\) – \(\frac{h c}{5000 Å}\)
= \(\mathrm{hc}\left[\frac{(5000-1000) Å}{1000 \times 5000 Å \times Å}\right]\) ……(4)
समीकरण (4) में समीकरण (3) से मान रखने पर
\(\frac{\mathrm{hc}}{\lambda_3}\) = \(\frac{h c 4000}{1000 \times 5000} \frac{1}{Å}\)
या
λ₃ = \(\frac{5000 Å}{4}\) = 1250 ऐंग्स्ट्रम

प्रश्न 7.
किसी तत्व का ऊर्जा स्तर आरेख नीचे चित्र में दिया गया है, आवश्यक गणना करके यह पहचानें कि कौनसा संक्रमण उत्सर्जन की स्पेक्ट्रमी रेखा का तरंगदैर्घ्य 102.7 nm के संगत है?

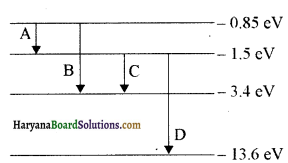
उत्तर:
संक्रमण A के लिए
E1 = – 1.5 eV और E2 = – 0.85 eV
∴ E = E2 – E1
= -0.85 (-1.5)
= – 0.85 + 1.5
E = 0.65 eV
= 0.65 x 1.6 x 10^-19 J
अतः उत्सर्जित स्पेक्ट्रमी रेखा की तरंगदैर्ध्य
λ = \(\frac{h c}{E}\) सूत्र से ज्ञात करेंगे
मान रखने पर
λ = \(\frac{6.62 \times 10^{-34} \times 3 \times 10^8}{0.65 \times 1.6 \times 10^{-19}}\)
= \(\frac{19.86 \times 10^{-7}}{1.04}\) = 19.1 × 10^-7
= 1910 nm
संक्रमण B के लिए
E1 = – 3.4 eV और E2 = – 0.85 ev
E = E2 – E1 = – 0.85 – (-3.4)
= – 0.85 + 3.4
E = 2.55 eV = 2.55 x 1.6 x 10^-19 J
अतः उत्सर्जित स्पेक्ट्रमी रेखा ( फोटॉन) की तरंगदैर्ध्य
λ = \(\frac{h c}{E}\) से ज्ञात करेंगे।
मान रखने पर
λ = \(\frac{6.62 \times 10^{-34} \times 3 \times 10^8}{2.55 \times 1.6 \times 10^{-19}}\)
19.86/4.08 x 10^-7m
= 4.87 × 10^-7m
= 487 nm
संक्रमण C के लिए
E1 = – 3.4 eV तथा E2 = -1.5 ev
E = E2 – E1 = – 1.5 – (-3.4)
= – 1.5 + 3.4
= 1.9 ev
अतः उत्सर्जित स्पेक्ट्रमी रेखा ( फोटॉन) की तरंगैदर्घ्य का सूत्र
λ = \(\frac{h c}{E}\) से ज्ञात करेंगे।
λ = \(\frac{6.62 \times 10^{-34} \times 3 \times 10^8}{1.9 \times 1.6 \times 10^{-19}}\) मीटर
= 19.86/3.04 ×10^-7 = 6.533 x 10^-7 m
= 653.3 nm
संक्रमण D के लिए
E1 = – 13.6 eV और E2 = -1.5 ev
E = E2 – E1
= – 1.5 (- 13.6)
= 1.5+ 13.6
E= 12.1 ev
अतः उत्सर्जित स्पेक्ट्रमी रेखा ( फोटॉन) की तरंगदैर्ध्य
λ = \(\frac{h c}{E}\) से ज्ञात करेंगे।
λ = \(\frac{h c}{E}\) = \(\frac{6.62 \times 10^{-34} \times 3 \times 10^8}{12.1 \times 1.6 \times 10^{-19}}m\)
λ = \(\frac{19.86}{13.6}\) x 10^-7m
= 1.026 × 10^-7 m
λ = 102.6nm
उपर्युक्त गणनाओं से यह ज्ञात होता है कि संक्रमण D से उत्सर्जित स्पेक्ट्रमी रेखा की तरंगदैर्घ्य 102.6nm के संगत है।

प्रश्न 8.
हाइड्रोजन परमाणु की मूल अवस्था में ऊर्जा -13.6 ev है, यदि एक इलेक्ट्रॉन ऊर्जा स्तर 0.85 ev से -3.4 eV ऊर्जा स्तर में संक्रमण करता है तो उत्सर्जित स्पेक्ट्रमी रेखा की तरंगदैर्ध्य ज्ञात कीजिए यह तरंगदैर्घ्य हाइड्रोजन स्पेक्ट्रम के किस श्रेणी में स्थित होती है?
उत्तर:
उत्सर्जित फोटॉन की ऊर्जा
E = – 0.85 – (-3.4) = 0.85 + 3.4
E = 2.55 ev
= 2.55 × 1.6 x 10^-19 J
उत्सर्जित स्पेक्ट्रमी रेखा ( फोटॉन) की तरंगदैर्घ्य
λ = hc/E से ज्ञात करेंगे।
= \(\frac{6.62 \times 10^{-34} \times 3 \times 10^8}{2.55 \times 1.6 \times 10^{-19}}\)
= \(\frac{19.86}{4.08}\) x 10^-7 m
= 4.8676 × 10^-7m
= 486.76nm
= 4867.6 A
यह तरंगदैर्घ्य हाइड्रोजन स्पेक्ट्रम के बामर श्रेणी में स्थित होती है।

प्रश्न 9.
हाइड्रोजन परमाणु की मूल अवस्था ऊर्जा 13.6ev है तो
(i) द्वितीय उत्तेजित अवस्था में इलेक्ट्रॉन की ऊर्जा क्या है?
(ii) यदि इलेक्ट्रॉन द्वितीय उत्तेजित अवस्था से मूल अवस्था में कूदता है तो उत्सर्जित स्पेक्ट्रमी रेखा के तरंगदैर्घ्य की गणना कीजिए।
उत्तर:
हाइड्रोजन परमाणु में nवीं कक्षा में इलेक्ट्रॉन की ऊर्जा होगी
En = \(\frac{-13.6}{n^2} e V\) …..(1)
(i) द्वितीय उत्तेजित अवस्था के लिए n = 3 लेने पर
∴ E3 = \(\frac{-13.6}{3^2} \mathrm{eV}\) = \(\frac{-13.6}{9}\) = -1.510V
(ii) द्वितीय उत्तेजित अवस्था (n = 3) से मूल अवस्था (n = 1) में इलेक्ट्रॉन के कूदने पर उत्सर्जित ऊर्जा
E = E3 – E1
= – 1.51 – (-13.6)
= – 1.51 + 13.6 = 12.09 ev
उत्सर्जित स्पेक्ट्रमी रेखा की तरंगदैर्घ्य का मान होगा
λ = \(\frac{h c}{E}\) = \(\frac{6.62 \times 10^{-34} \times 3 \times 10^8}{12.09 \times 1.6 \times 10^{-19}}\)
= \(\frac{19.86}{19.344}\)
= 1.027 × 10^-7m
= 102.7 nm = 1027 A

प्रश्न 10.
किसी परमाणु के ऊर्जा स्तर A, B व C की ऊर्जाएँ क्रमशः EA, EB, Ec हैं तथा EA < EB < EC हैं। यदि C से B में, B से A में तथा C से A में इलेक्ट्रॉन के संक्रमण से प्राप्त फोटॉनों की तरंगदैर्ध्य क्रमशः λ1, λ2 λ3 हैं, तो सिद्ध कीजिए कि λ3 = \(\frac{\lambda_1 \lambda_2}{\lambda_1+\lambda_2}\)
उत्तर:
हम जानते हैं कि
∆E = hv = \(\frac{\mathrm{hc}}{\lambda}\)
अतः EC – EB= \(\frac{h c}{\lambda_1}\) …..(1)
EB – EA = \(\frac{h c}{\lambda_2}\) …..(2)
तथा EC – EA = \(\frac{h c}{\lambda_3}\) …..(3)
समीकरण ( 1 ) एवं समीकरण (2) के योग से
EC – EA = hc(\(\frac{1}{\lambda_1}\) + \(\frac{1}{\lambda_2}\)) ……..(4)
समीकरण (3) व समीकरण (4) से
\(\frac{h c}{\lambda_3}\) = hc\([\frac{1}{\lambda_1}+\frac{1}{\lambda_2}]\)
या \(\frac{1}{\lambda_3}\) = \(\frac{1}{\lambda_1}\) + \(\frac{1}{\lambda_2}\)
अतः
λ3 = \(\frac{\lambda_1 \lambda_2}{\lambda_1+\lambda_2}\)
यही सिद्ध करना था।

प्रश्न 11.
हाइड्रोजन परमाणु की बामर श्रेणी की दूसरी रेखा की तरंगदैर्घ्य का मान 4861 ऐंग्स्ट्रम है। इस श्रेणी की चौथी रेखा के तरंगदैर्घ्य की गणना कीजिए।
उत्तर:
हाइड्रोज़न स्पेक्ट्रम की किसी भी रेखा के लिए n₂ = n₁+ P(P रेखा की संख्या है)। अतः इस श्रेणी की दूसरी रेखा के लिए n₂ = 2 + 2 = 4 तथा चौथी रेखा के लिए n₂= 2 + 4 = 6। इन रेखाओं की तरंगदैर्घ्य क्रमशः λ2 व λ4 हों तो
\(\frac{1}{\lambda_2}\) = R\(\frac{1}{2^2}-\frac{1}{4^2}\)
\(\frac{1}{\lambda_2}\) = \(\frac{3}{16} R\) …….(1)
\(\frac{1}{\lambda_4}\) = R\(\frac{1}{2^2}-\frac{1}{6^2}\)
इसी प्रकार \(\frac{1}{\lambda_4}\) = \(\frac{8R}{36}\) ………..(2)
समीकरण (1) में समीकरण (2) का भाग देने पर
\(\frac{\lambda_4}{\lambda_2}\) = \(\frac{3 R}{16}\) \(\frac{36}{8 R}\) = \(\frac{27}{32}\)
∴ λ₄ = \(\frac{27}{32}\) × λ₂
= \(\frac{27}{32}\) × 4861A = 41015A

प्रश्न 12.
एक हाइड्रोजन परमाणु प्रारम्भ में मूल अवस्था में एक फोटॉन अवशोषित करता है, जिससे वह n = 4 स्तर तक उत्तेजित होता है। फोटॉन की तरंगदैर्घ्य तथा आवृत्ति ज्ञात कीजिए।
उत्तर:
हम जानते हैं कि फोटॉन की तरंगदैर्घ्य
\(\frac{1}{\lambda}\) = R\(\frac{1}{n_1^2}-\frac{1}{n_2^2}\)
\(\frac{1}{\lambda}\) = 1.09 × 10⁷ \(\frac{1}{1_1^2}-\frac{1}{4_2^2}\)
\(\frac{1}{\lambda}\) = 1.09 × 10⁷ \(1-\frac{1}{16}\)
= \(\frac{15}{16}\) 1.09 × 10⁷m
था λ = = 980 × 10^-10m
था λ = 980 × 10^-10 = 980
इसलिए आवृत्ति
v = \(\frac{\mathbf{c}}{\lambda}\) = \(\frac{3 \times 10^8}{9.8 \times 10^{-8}}\)
= 3.06 × 10^-15 per second

प्रश्न 13.
यदि लाइमैन श्रेणी की प्रथम रेखा की तरंगदैर्घ्य 1216 है तो बामर व पाश्चन श्रेणी की प्रथम रेखा की तरंगदैर्घ्य ज्ञात कीजिए।
उत्तर:
लाइमैन श्रेणी की प्रथम रेखा की तरंगदैर्घ्य λ^L बामर श्रेणी की प्रथम रेखा की तरंगदैर्घ्य λ^B तथा पाश्चन श्रेणी की प्रथम रेखा की तरंगदैर्घ्य λ^p हो तो हम तरंगदैर्घ्य के समीकरण से जानते हैं

प्रश्न 14.
हाइड्रोजन परमाणु की मूल अवस्था की ऊर्जा -13.6eV है, इस अवस्था में इलेक्ट्रॉन की गतिज तथा स्थितिज ऊर्जायें क्या हैं?
उत्तर:
प्रश्नानुसार दिया है:
E1 = – 13.6ev
∵ E_k1 = \(\) तथा E1 = \(\)
∵E_k1 = -E1 = -(-13.6) = 13.6 ev
∵ E_k1 तथा E1 = \(\)
∵E_P1 = 2E1 = 2 × (-13.6) = -27.2ev
अतः मूल अवस्था में इलेक्ट्रॉन की गतिज ऊर्जा
E_k1 = 13.6ev
तथा स्थितिज ऊर्जा E_P1 = -27.2ev

प्रश्न 15.
हाइड्रोजन परमाणु की निम्नतम अवस्था मे ऊर्जा -13.6eV है। इस दशा में इलेक्ट्रॉन की गतिज़ ऊर्जा तथा स्थितिज ऊर्जा ज्ञात करें।
उत्तर:
यहाँ E1 = -13.6ev
इसलिये गतिज ऊर्जा k = -(E1) = -(-13.6ev)
k = 13.6ev
स्थितिज ऊर्जा U = 2E1 = 2 ×(-13.6ev)
= -27.2ev