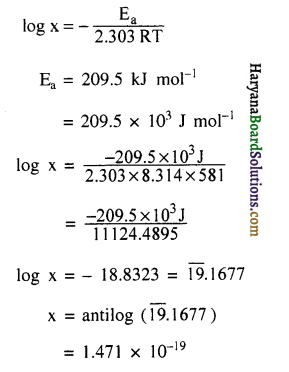HBSE 12th Class Chemistry Solutions Chapter 4 रासायनिक बलगतिकी

Haryana State Board HBSE 12th Class Chemistry Solutions Chapter 4 रासायनिक बलगतिकी Textbook Exercise Questions and Answers.

Haryana Board 12th Class Chemistry Solutions Chapter 4 रासायनिक बलगतिकी

प्रश्न 4.1.
निम्न अभिक्रियाओं के वेग व्यंजकों से इनकी अभिक्रिया कोटि तथा वेग स्थिरांकों की इकाइयाँ ज्ञात कीजिए-
(i) 3NO (g) → N₂O(g); वेग = k[NO]²
(ii) H₂O₂ (aq) + 3I^– (aq) + 2H⁺ → 2H₂O(I) + I^–₃; वेग = k[H₂O₂][I^–]
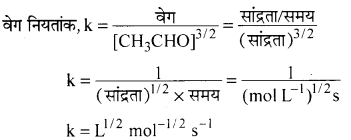
(iii) CH₃CHO (g) → CH₄ (g) + CO(g); वेग = k[H₂CHO]^3/2
(iv) C₂H₅Cl (g) → C₂H₄ (g) + HCl(g); वेग = k[C₂H₅Cl]
उत्तर:
(i) वेग = k[NO]²
अतः अभिक्रिया की कोटि = 2

अतः k की इकाई = L mol^-1 s^-1

(ii) वेग = k[H₂O₂][I^–]
अभिक्रिया की कोटि = 1 + 1 = 2

अतः K की इकाई = L mol^-1 s^-1

(iii) वेग = k [CH₃CHO]^3/2
अभिक्रिया की कोटि = 1.5

(iv) अभिक्रिया की कोटि = 1

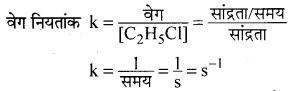
प्रश्न 4.2.
अभिक्रिया 2A + B → A₂B के लिए वेग = k[A][B]² यहाँ k का मान 2.0 × 10^-6 mol^-2 L²s^-1 है। प्रारंभिक वेग की गणना कीजिए; जब [A] = 0.1 mol L^-1 एवं [B] = 0.2 mol L^-1 हो तथा अभिक्रिया वेग की गणना कीजिए; जब [A] घटकर 0.06mol L ^-1 रह जाए।
उत्तर:
अभिक्रिया 2A + B A₂B के लिए प्रारंभिक वेग = k[A][B]²
k = 2.0 × 10^-6 mol^-2L²s^-1,
दिया है – [A] = 0.1 mol L^-1 तथा [B] = 0.2 mol L^-1
अतः प्रारंभिक वेग = 2.0 × 10^-6 × 0.1 × (0.2)²
= 2 × 10^-6 × 0.1 × 0.04
= 8 × 10^-9 mol L^-1s^-1
जब A की सांद्रता घटकर 0.06 mol L^-1 रह जाती है अर्थात् 0.1 मोल A में से 0.04 मोल क्रिया करता है तो अभिक्रिया की रससमीकरणमिति के अनुसार, 2A + B → A₂B
प्रारम्भिक सांद्रता 0.1 0.2
t समय पर सांद्रता (0.1 0.04) (0.2 – 9.02)
अतः [A] = 0.06M तथा [B] = 0.18 M
इस स्थिति में अभिक्रिया का वेग = k[A] [B]²
= 2 × 10^-6 × 0.06 × (0.18)²
वेग = 3.888 × 10⁹ = 3.89 × 10^-9 mol L^-1s^-1

प्रश्न 4.3.
प्लैटिनम सतह पर NH₃ का अपघटन शून्य कोटि की अभिक्रिया है । N₂ एवं H₂ के उत्पादन की दर क्या होगी जब k का मान 2.5 × 10^-4 mol L^-1s^-1 हो?
उत्तर:
अमोनिया के विघटन की अभिक्रिया निम्न प्रकार होती है- 2NH₃ → N₂ + 3H₂
अभिक्रिया का वेग = \(\frac{\mathrm{d}\left[\mathrm{N}_2\right]}{\mathrm{dt}}\) = k [सांद्रता]°
क्योंकि अभिक्रिया की कोटि = शून्य
अतः = \(\frac{\mathrm{d}\left[\mathrm{N}_2\right]}{\mathrm{dt}}\) = 2.5 × 10^-4 mol L^-1s^-1 × 1
अतः N₂ के बनने की दर
= \(\frac{\mathrm{d}\left[\mathrm{N}_2\right]}{\mathrm{dt}}\) = 2.5 × 10^-4 mol L^-1s^-1
तथा H₂ के बनने की दर
= \(\frac{\mathrm{d}\left[\mathrm{H}_2\right]}{\mathrm{dt}}\) = 3 × \(\frac{\mathrm{d}\left[\mathrm{N}_2\right]}{\mathrm{dt}}\)
=3 × 2.5 × 10^-4 mol L^-1s^-1
= 7.5 × 10^-4 mol L^-1s^-1

प्रश्न 4.4.
डाइमेथिल ईथर के अपघटन से CH₄, H₂ तथा CO बनते हैं। इस अभिक्रिया का वेग निम्न समीकरण द्वारा दिया जाता है-
वेग= k[CH₃OCH₃]^3/2
अभिक्रिया के वेग का अनुगमन बंद पात्र से बढ़ते दाब द्वारा किया जाता है, अतः वेग समीकरण को डाइमेथिल ईथर के आंशिक दाब के पद में भी दिया जा सकता है। अतः
वेग = \(\left(\mathrm{p}_{\mathrm{CH}_3 \mathrm{OCH}_3}\right)^{3 / 2}\) यदि दाब को bar में तथा समय को मिनट में मापा जाये तो अभिक्रिया के वेग एवं वेग स्थिरांक की इकाइयाँ क्या होंगी?
उत्तर:
डाइमेथिल ईथर के अपघटन की अभिक्रिया निम्न प्रकार होगी-
CH₃ – O – CH₃ → CH₄ + H₂ + CO
अभिक्रिया का वेग k = \(\left(\mathrm{p}_{\mathrm{CH}_3 \mathrm{O}-\mathrm{CH}_3}\right)^{3 / 2}\)
अतः वेग की इकाई = bar min^-1 या = bar s^-1
वेग स्थिरांक,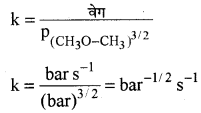
अतः वेग स्थिरांक की इकाई bar^-1/2 s^-1 होगी।

प्रश्न 4.5.
रासायनिक अभिक्रिया के वेग पर प्रभाव डालने वाले कारकों का उल्लेख कीजिए।
उत्तर:
रासायनिक अभिक्रिया के वेग को प्रभावित करने वाले मुख्य कारक निम्नलिखित हैं-
(i) अभिकारकों की प्रकृति
(ii) अभिकारकों की सांद्रता (गैसों के संदर्भ में दाब )
(iii) ताप
(iv) उत्प्रेरक ।

(i) अभिकारकों की सान्द्रता – द्रव्यअनुपाती क्रिया के नियम के अनुसार अभिकारकों की सान्द्रता बढ़ाने पर अभिक्रिया का वेग बढ़ता है। अभिक्रिया वेग को अभिकारकों की सान्द्रता के पदों में व्यक्त करना वेग नियम (Rate Law) या वेग व्यंजक या वेग समीकरण कहलाता है। गैसीय अभिक्रियाओं में दाब बढ़ाने पर अभिक्रिया का वेग उस दिशा में बढ़ता है जिस तरफ गैसीय अणुओं की संख्या कम होती है।

(ii) अभिकारकों की सांद्रता – अभिक्रिया मिश्रण का विलोडन करने पर अणुओं के मध्य समागम बढ़ता है जिससे अभिक्रिया का वेग बढ़ता है।

(iii) ताप – सामान्यतः ताप बढ़ाने पर अभिक्रिया का वेग बढ़ता है क्योंकि ताप बढ़ाने पर क्रियाकारकों की गतिज ऊर्जा बढ़ती है जिसके कारण ऊर्जित अणुओं की सान्द्रता बढ़ती है अतः प्रति सेकण्ड प्रभावी टक्करों की संख्या बढ़ती है। प्रयोगों से ज्ञात हुआ है कि 10°C ताप बढ़ाने पर अभिक्रिया का वेग 2 से 3 गुना हो जाता है। अभिक्रिया वेग पर ताप के प्रभाव की व्याख्या आरेनियस के सिद्धान्त से की जाती है, जिसका विस्तृत अध्ययन आगे खण्ड 4.5 में करेंगे।

(iv) उत्प्रेरक – उत्प्रेरक वे पदार्थ होते हैं जिनमें स्वयं में कोई स्थायी रासायनिक परिवर्तन के बिना, अभिक्रिया वेग को बढ़ाते हैं । वह पदार्थ जो अभिक्रिया के वेग को बढ़ा देता है लेकिन वह स्वतः रासायनिक रूप से अपरिवर्तित रहता है उसे उत्प्रेरक कहते हैं तथा इस क्रिया को उत्प्रेरण कहते हैं ।

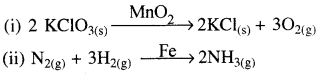
वे पदार्थ जो अभिक्रिया के वेग को कम करते हैं उन्हें निरोधक (Inhibitor) कहते हैं।

प्रश्न 4.6
किसी अभिक्रियक के लिए एक अभिक्रिया द्वितीय कोटि की है। अभिक्रिया का वेग कैसे प्रभावित होगा; यदि अभिक्रियक की सांद्रता-
(i) दुगुनी कर दी जाए
(ii) आधी कर दी जाए।
उत्तर:
किसी अभिक्रिया के लिए कोटि 2 है अतः अभिक्रिया का वेग = k [सांद्रता]²
(i) अभिक्रियक की सांद्रता दुगुनी करने पर,
वेग = k [2 सांद्रता]²
वेग = 4k [सांद्रता]²
अतः अभिक्रिया का वेग चार गुना हो जाता है।

(ii) अभिक्रियक (Reactant) की सांद्रता आधी कर दी जाए तो
वेग = k[\(\frac { 1 }{ 2 }\) – सांद्रता]²
वेग = \(\frac { 1 }{ 4 }\) [सांद्रता]²
अतः अभिक्रिया का वेग एक चौथाई अर्थात् \(\frac { 1 }{ 4 }\) गुना हो जाता है।

प्रश्न 4.7.
वेग स्थिरांक पर ताप का क्या प्रभाव पड़ता है? ताप के इस प्रभाव को मात्रात्मक रूप से कैसे प्रदर्शित कर सकते हैं?
उत्तर:
सामान्यतः ताप बढ़ाने पर अभिक्रिया का वेग बढ़ जाता है। अभिक्रिया का वेग, वेग स्थिरांक के रूप में व्यक्त किया जाता है। अतः ताप बढ़ाने पर वेग स्थिरांक का मान बढ़ जाता है।
किसी रासायनिक अभिक्रिया के ताप में 10°C की वृद्धि करने पर वेग स्थिरांक लगभग दुगुना हो जाता है।
अतः ताप गुणांक = \(\frac{k_{(t+10)}}{k_t} \approx 2\)
अभिक्रिया के वेग की ताप पर निर्भरता को आर्रेनिअस समीकरण से समझा सकते हैं।
k = Ae^-Ea/RT
यहाँ A आर्रेनिअस गुणक अथवा आवृत्ति गुणक है, इसे पूर्व – चरघातांकी गुणक भी कहते हैं। यह किसी विशिष्ट अभिक्रिया के लिए स्थिरांक होता है। यहाँ R गैस स्थिरांक है तथा E_a सक्रियण ऊर्जा है जिसे J mol^-1 में व्यक्त करते हैं।
अभिकारक तथा उत्पाद के मध्य सक्रियित संकुल बनता है जिसके बनने के लिए आवश्यक ऊर्जा को सक्रियण ऊर्जा (E_a) कहते हैं।

प्रश्न 4.8.
एक प्रथम कोटि की अभिक्रिया के निम्नलिखित आँकड़े प्राप्त हुए-

30 से 60 सेकंड समय अंतराल में औसत वेग की गणना कीजिए ।
उत्तर:
औसत वेग = (r_av) = – \(\frac{\Delta[\mathrm{R}]}{\Delta \mathrm{t}}\) = \(\frac{c_2-c_1}{\Delta t}\)
= – \(\frac{(0.17-0.31)}{60-30}\) = – \(\frac{(-0.14)}{30}\)
= 4.666 × 10^-3
= 4.67 × 10^-3 mol L^-1 s^-1

प्रश्न 4.9.
एक अभिक्रिया A के प्रति प्रथम तथा B के प्रति द्वितीय कोटि की है
(i) अवकल वेग समीकरण लिखिए।
(ii) B की सांद्रता तीन गुनी करने से वेग पर क्या प्रभाव पड़ेगा?
(iii) A तथा B दोनों की सांद्रता दुगुनी करने से वेग पर क्या प्रभाव पड़ेगा?
उत्तर:
यह अभिक्रिया A के प्रति प्रथम तथा B के प्रति द्वितीय कोटि की है अतः
(i) अवकल वेग समीकरण-
वेग = k [A]¹ [B]²
अतः अभिक्रिया की कुल कोटि = 1 + 2 = 3

(ii) B की सांद्रता तीन गुनी करने पर –
वेग = k[A]¹ [3B]²
|वेग = 9k[A]¹ [B]²
अतः अभिक्रिया का वेग 9 गुना हो जाता है।

(iii) A तथा B दोनों की सांद्रता दुगुनी करने पर –
वेग = k[A]¹ [B]²
वेग = k[2A]¹ [2B]²
वेग = 8k [A]¹ [B]²
अतः अभिक्रिया का वेग 8 गुना हो जाता है।

प्रश्न 4.10.
A और B के मध्य अभिक्रिया में A और B की विभिन्न प्रारंभिक सांद्रताओं के लिए प्रारंभिक वेग (r₀) नीचे दिए गए हैं।
A और B के प्रति अभिक्रिया की कोटि क्या है?

उत्तर:
माना कि A के संदर्भ में अभिक्रिया की कोटि = a तथा B के संदर्भ में अभिक्रिया की कोटि = b
अतः वेग = k[A]^a[B]^b
पाठ्यांक (Reading) (1) तथा (2) से
5.07 × 10^-5 = k [0.20]^a [0.30]^b …..(1)
5.07 × 10^-5 = k [0.20]^a [0.10]^b …..(2)
समीकरण (2) में समीकरण (1) का भाग देने पर,
\(\frac{5.07 \times 10^{-5}}{5.07 \times 10^{-5}}\) = \(\frac{\mathrm{k}[0.20]^a[0.10]^b}{\mathrm{k}[0.20]^{\mathrm{a}}[0.30]^{\mathrm{b}}}\)
या 1 = \(\left(\frac{0.10}{0.30}\right)^b\) या b = 0

पाठ्यांक (2) से,
वेग = 5.07 × 10^-5 = k [0.20]^a [0.10]^b
5.07 × 10^-5 = k [0.20]^a × 1 ….(3)
(∵ b = 0)

पाठ्यांक (3) से,
वेग = 1.43 × 10^-4 = k[0.40]^a [0.05]^b ….(4)
= k[0.40]^a × 1

समीकरण (4) को समीकरण (3) से भाग देने पर,
\(\frac{1.43 \times 10^{-4}}{5.07 \times 10^{-5}}\) = \(\frac{k[0.40]^a}{k[0.20]^a}\) = \(\left[\frac{0.4}{0.2}\right]^{\mathrm{a}}\) = (2)^a
(2)^a = 2.820
a log 2 = log 2.820
a = \(\frac{\log 2.820}{\log 2}\) = \(\frac{0.4490}{0.3010}\)
a = 1.49 = 1.5
अतः A के लिए अभिक्रिया की कोटि, 1.5 तथा B के लिए अभिक्रिया की कोटि शून्य है।

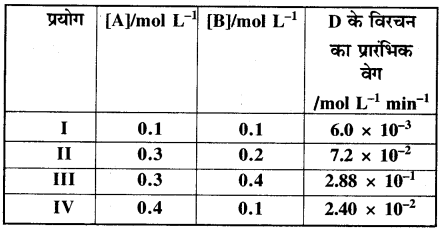
प्रश्न 4.11.
2A + B → C + D अभिक्रिया की बलगतिकी अध्ययन करने पर निम्नलिखित परिणाम प्राप्त हुए। अभिक्रिया के लिए वेग नियम तथा वेग स्थिरांक ज्ञात कीजिए ।

उत्तर:
अभिक्रिया 2A + B → C + D के लिए वेग व्यंजक-
वेग k[A]^a[B]^b
यहाँ a तथा b, A व B के संदर्भ में अभिक्रिया की कोटि है।
प्रयोग I तथा IV से-
वेग = 6.0 × 10^-3 = k[0.1]^a [0.1]^b ….(1)
2.4 × 10^-2 = k[0.4]^a [0.1]^b ….(2)
समीकरण ( 2 ) में समीकरण (1) का भाग देने पर,

\(\frac{2.4 \times 10^{-2}}{6.0 \times 10^{-3}}\) = \(\left(\frac{0.4}{0.1}\right)^{\mathrm{a}}\)
4 = 4^a अतः a = 1
प्रयोग II तथा III से-
वेग 7.2 × 10^-2 = k(0.3)^a (0.2)^b ….(3)
2.88 × 10^-1 = k(0.3)^a (0.4)^b ….(4)

समीकरण (4) में समीकरण (3) का भाग देने पर,
\(\frac{2.88 \times 10^{-1}}{7.2 \times 10^{-2}}\) = \(\frac{k(0.3)^l(0.4)^b}{k(0.3)^l(0.2)^b}\)
4 = (2)^b अतः b = 2
अतः a तथा b के मान से इस अभिक्रिया के लिए वेग नियम इस प्रकार लिखा जा सकता है-
a = 1 तथा b = 2

वेग नियम = k[A]¹[B]²
अतः अभिक्रिया की कोटि = 1 + 2 = 3
प्रयोग I के अनुसार,
वेग = 6 × 10^-3 = k[0.1]^a[0.1]^b, (a = 1, b = 2)

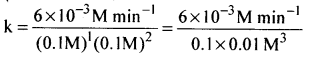
अतः वेग स्थिरांक k = 6.0 M^-2 min^-1

प्रश्न 4.12.
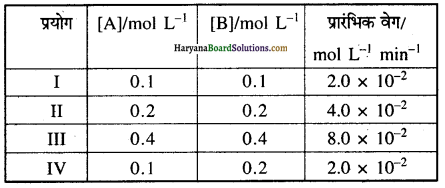
A तथा B के मध्य अभिक्रिया A के प्रति प्रथम तथा B के प्रति शून्य कोटि की है निम्न तालिका में रिक्त स्थान भरिए ।

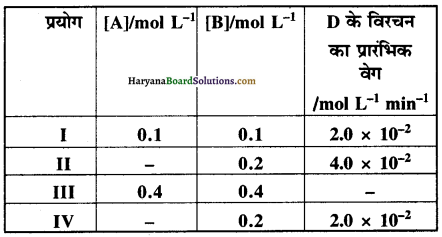
उत्तर:
A तथा B के मध्य अभिक्रिया में A के संदर्भ में अभिक्रिया प्रथम कोटि तथा B के संदर्भ में अभिक्रिया शून्य कोटि की है।
अतः इसके लिए वेग समीकरण
= k[A]¹ [B]⁰
= k[A]
(i) प्रयोग से.
वेग = 2.0 × 10^-2 = k[0.1]
अतः वेग नियतांक, k = \(\frac{2.0 \times 10^{-2}}{0.1}\) = 0.2 min^-1

(ii) प्रयोग II से,
वेग = k[A]

(iii) प्रयोग III से,
वेग = k[A]
= 0.2 × 0.4
= 0.08 M min^-1
= 8.0 × 10^-2 2M min^-1

(iv) प्रयोग IV से,
वेग = K[A]

अतः रिक्त स्थानों की पूर्ति के पश्चात् सम्पूर्ण तालिका निम्न प्रकार होगी-

प्रश्न 4.13.
नीचे दी गई प्रथम कोटि की अभिक्रियाओं के ar स्थिरांक से अर्धायु की गणना कीजिए-
(i) 200 s^-1
(ii) 2 min^-1
(iii) 4 year^-1
उत्तर:
प्रथम कोटि अभिक्रिया के लिए-
अर्धायु, t_1/2 = \(\frac { 0.693 }{ k }\)

(i) वेग नियतांक, k = 200s^-1
अतः t_1/2 = \(\frac { 0.693 }{ 200 }\) = 0.003465
= 3.465 × 10^-3 s
= 3.47 × 10^-3 s

(ii) k = 2 min^-1 तो t_1/2 = \(\frac { 0.693 }{ 2 }\)
= 0.3465 min
= 0.35 min

(iii) k = 4 year^-1 तो t_1/2 = \(\frac { 0.693 }{ 4 }\) = 0.1732 year
t_1/2 = 0.173 year

प्रश्न 4.14.
¹⁴C रेडियोएक्टिव क्षय की अर्धायु 5730 वर्ष है। एक पुरातत्व कलाकृति की लकड़ी में, जीवित वृक्ष की लकड़ी की तुलना में 80% ¹⁴C की मात्रा है। नमूने की आयु का परिकलन कीजिए ।
उत्तर:
अर्धायु, ^t1/2 = 5730 वर्ष
अतः वेग नियतांक (क्षयांक), k या λ = \(\frac{0.693}{t_{1 / 2}}\)
k = \(\frac{0.693}{5730}\)
k = 1.209 × 10^-4 वर्ष^-1
चूँकि रेडियोएक्टिव विघटन की अभिक्रिया प्रथम कोटि की होती है
अतः वेग नियतांक या क्षयांक
k = \(\frac{2.303}{t}\) log \(\frac{\left[R_0\right]}{[R]}\)
चूँकि 20% विघटन हो रहा है अतः t पर ¹⁴C है = 80%
[R₀] = 100 तथा [R] = 80
अतः t = \(\frac{2.303}{k}\) log \(\frac { 100 }{ 80 }\)
t = \(\frac{2.303}{1.209 \times 10^{-4}}\) log 1.25
t = \(\frac{2.303}{1.209 \times 10^{-4}}\) × (0.0969)
= 0.1845 × 10⁴ = 1845 वर्ष

प्रश्न 4.15.
गैस प्रावस्था में 318K पर N₂O₅ के अपघटन की [2N₂O₅ → 4NO₂+O₂] अभिक्रिया के आँकड़े आगे दिए गए हैं-

(i) [N₂O₅] एवं t के मध्य आलेख खींचिए ।
(ii) अभिक्रिया के लिए अर्धायु की गणना कीजिए ।
(iii) log [N₂O₅] एवं t के मध्य ग्राफ खींचिए ।
(iv) अभिक्रिया के लिए वेग नियम क्या है?
(v) वेग स्थिरांक की गणना कीजिए।
(vi) k की सहायता से अर्धायु की गणना कीजिए तथा इसकी तुलना (ii) से कीजिए ।
उत्तर:
(i) N₂O₅ की सांद्रता [N₂O₅] तथा t के मध्य ग्राफ खींचने पर निम्न प्रकार का ग्राफ प्राप्त होता है-

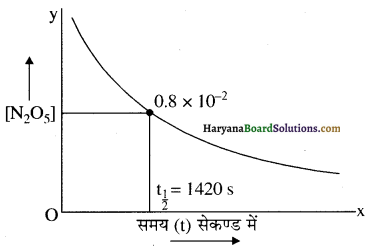
(ii) इस अभिक्रिया के लिए अर्धायु वह समय है जब N₂O₅ की सांद्रता 1.63 × 10^-2 M से आधी अर्थात् 0.815 × 10^-2 M हो जाए ग्राफ से 1420 वर्ष आता है अतः इस अभिक्रिया की अर्धायु 1420 वर्ष है।

(iii) log[N₂O₅] तथा t के मध्य ग्राफ खींचने के लिए पहले N₂O₅ के विभिन्न मानों का log लेते हैं जो निम्न प्रकार हैं-

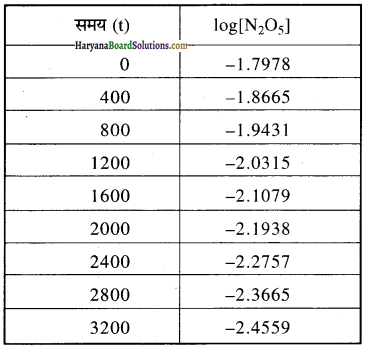
फिर, समय (t) तथा log [N₂O₅] के मध्य ग्राफ खींचते हैं जो निम्न प्रकार है-

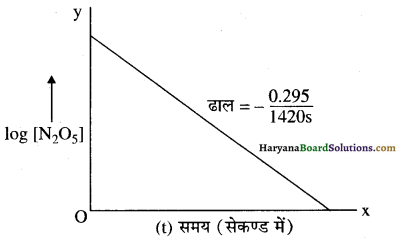
(iv) log [N₂O₅] तथा t के मध्य ग्राफ एक सीधी रेखा है अतः अभिक्रिया प्रथम कोटि की है इसलिए वेग नियम K[N₂O₅]

(v) ढाल = – \(\frac { k }{ 2.303 }\) = \(\frac { -0.295 }{ 1420s }\)
अतः वेग स्थिरांक, k = \(\frac{0.295 \times 2.303}{1420 \mathrm{~s}}\)
k = 4.784 × 10^-4s^-1
k =4.8×10^-4s^-1

(vi) अर्धायु, ^t1/2 = \(\frac { 0.693 }{ k }\) = \(\frac{0.693}{4.8 \times 10^{-4}}\)
^t1/2 = 0.1443 x 104 = 1443 s
यह अर्धायु, (ii) से प्राप्त अर्धायु के लगभग समान है।

प्रश्न 4.16.
प्रथम कोटि की अभिक्रिया के लिए वेग स्थिरांक 60 s^-1 है। अभिक्रियक को अपनी प्रारंभिक सांद्रता से 1/16 वाँ भाग रह जाने में कितना समय लगेगा?
उत्तर:
अभिक्रिया का वेग स्थिरांक = 60 s^-1
अभिकारक प्रारंभिक सांद्रता का 1/16 वाँ भाग रह रहा है अर्थात् इसका 5/16 भाग क्रिया कर रहा है।
प्रथम कोटि अभिक्रिया का वेग स्थिरांक,
k = \(\frac { 2.303 }{ t }\) log \(\frac{[\mathrm{R}]_0}{[\mathrm{R}]}\)
माना, [R₀] = 1 तो [R] = \(\frac { 1 }{ 16 }\)
अतः t = \(\frac { 2.303 }{ 60 }\) log\(\frac { 1 }{ 1/16 }\)
t = \(\frac { 2.303 }{ 60 }\) log\(\frac { 16 }{ 1 }\)
t = 0.03838 (1.2041)
t = 0.046s = 4.6 × 10^-2 सेकंड

प्रश्न 4.17.
नाभिकीय विस्फोट का 28.1 वर्ष अर्धायु वाला एक उत्पाद ⁹⁰Sr होता है। यदि कैल्सियम के स्थान पर 1 pg. Sr नवजात शिशु की अस्थियों में अवशोषित हो जाए और उपापचयन से ह्रास न हो तो इसकी 10 वर्ष एवं 60 वर्ष पश्चात् कितनी मात्रा रह जाएगी ?
उत्तर:
यहाँ नाभिकीय विखण्डन हो रहा है तथा नाभिकीय विखण्डन की सभी अभिक्रियाएँ प्रथम कोटि की होती हैं अतः
क्षयांक या वेग स्थिरांक, λ या k = \(\frac{0.693}{t_{1 / 2}}\)
k = \(\frac { 0.693 }{ 28.1 }\) = 0.02466 = 0.02467 वर्ष^-1

(i) 10 वर्ष बाद ⁹⁰Sr की बची हुई मात्रा –
k = \(\frac { 2.303 }{ t }\) log \(\frac{[\mathrm{R}]_0}{[\mathrm{R}]}\)
दिया गया है – [R]₀ = प्रारंभिक पदार्थ है- 1 μg = 1 × 10^-6 g
0.02467 = \(\frac { 2.303 }{ 10 }\) log\(\frac{\left[1 \times 10^{-6}\right]}{[\mathrm{R}]}\)
log \(\frac{1 \times 10^{-6}}{[\mathrm{R}]}\) = \(\frac{10 \times 0.02467}{2.303}\)
log \(\frac{1 \times 10^{-6}}{[\mathrm{R}]}\) = \(\frac{0.2467}{2.303}\) = 0.10707 = 0.1071
\(\frac{1 \times 10^{-6}}{[\mathrm{R}]}\) = Antilog 0.1071 = 1.279
\(\frac{1 \times 10^{-6}}{[R]}\) = 1.279
अतः [R] = \(\frac{1 \times 10^{-6}}{1.279}\) = 0.7818 × 10^-6 g
[R] = 0.7818 μg

(ii) 60 वर्ष पश्चात् ⁹⁰Sr की बची हुई मात्रा
k = \(\frac { 2.303 }{ t }\) log \(\frac{[\mathrm{R}]_0}{[\mathrm{R}]}\)
0.02467 = \(\frac { 2.303 }{ 60 }\) log\(\frac{1 \times 10^{-6}}{[\mathrm{R}]}\)
log\(\frac{1 \times 10^{-6}}{[\mathrm{R}]}\) = \(\frac{0.02467 \times 60}{2.303}\) = 0.6427
\(\frac{1 \times 10^{-6}}{[\mathrm{R}]}\) = Antilog 0.6427
\(\frac{1 \times 10^{-6}}{[\mathrm{R}]}\) = 4.392
[R] = \(\frac{1 \times 10^{-6}}{4.392}\) = 0.227 × 10^-6 g = 0.227 μg
अतः 10 वर्ष के बाद ⁹⁰Sr, 0.7818 μg बचेगा तथा 60 वर्ष के 0.227 μg बचेगा।

प्रश्न 4.18.
दर्शाइए कि प्रथम कोटि की अभिक्रिया में 99% अभिक्रिया पूर्ण होने में लगा समय 90% अभिक्रिया पूर्ण होने में लगने वाले समय से दुगुना होता है।
उत्तर:
किसी प्रथम कोटि अभिक्रिया के लिए समय,
t = \(\frac { 2.303 }{ 2 }\) log\(\frac{[\mathrm{R}]_0}{[\mathrm{R}]}\)
t समय बाद, R = 0.01 [R₀] क्योंकि 99% अभिक्रिया हो रही है। 99% अभिक्रिया पूर्ण होने में लगा समय-
t_0.99 = \(\frac { 2.303 }{ k }\) = log \(\frac{[\mathrm{R}]_0}{0.01[\mathrm{R}]_0}\) = \(\frac { 2.303 }{ k }\) log 10²
90% अभिक्रिया पूर्ण होने पर, [R] = 0.1 [R₀]
अतः 90% अभिक्रिया पूर्ण होने में लगा समय
t_0.90 = \(\frac { 2.303 }{ k }\) log \(\frac{[\mathrm{R}]_0}{0.1[\mathrm{R}]_0}\) = \(\frac { 2.303 }{ k }\) log 10
अतः \(\frac{\mathrm{t}_{0.99}}{\mathrm{t}_{0.90}}\) = \(\frac { 2.303 }{ k }\) log 10² × \(\frac { k }{ 2.303 }\) × \(\frac { l }{ log 10 }\)
\(\frac{\mathrm{t}_{0.99}}{\mathrm{t}_{0.90}}\) = \(\frac{\log 10^2}{\log 10}\) = \(\frac { 2 }{ 1 }\)
\(\frac{\mathrm{t}_{0.99}}{\mathrm{t}_{0.90}}\) = \(\frac { 2 }{ 1 }\)
इससे सिद्ध होता है कि प्रथम कोटि की अभिक्रिया में 99% अभिक्रिया पूर्ण होने में लगा समय, 90% अभिक्रिया पूर्ण होने में लगने वाले समय से दुगुना होता है।

प्रश्न 4.19.
एक प्रथम कोटि की अभिक्रिया 30% में वियोजन होने में 40 मिनट लगते हैं। t_1/2 की गणना कीजिए ।
उत्तर:
अभिक्रिया 30% हो रही है। अतः [R]₀ = 1 मानने पर,
[R] = 1 – 0.3 = 0.7 तथा t = 40 मिनट
अतः वेग स्थिरांक, k = \(\frac { 2.303 }{ t }\) log\(\frac{[\mathrm{R}]_0}{[\mathrm{R}]}\)
k = \(\frac { 2.303 }{ 40 }\) log\(\frac { 1 }{ 0.7 }\)
k = 0.05757 log\(\frac { 10 }{ 7 }\)
k = 0.05757 (log 10 – log 7)
k = 0.05757 (1 – 0.8451)
k = 0.05757 × (0.1549)
k = 8.917 × 10^-3 मिनट^-1
k = 8.92 × 10^-3 मिनट^-1
t_1/2 = \(\frac { 0.693 }{ k }\) = \(\frac{0.693}{8.92 \times 10^{-3}}\)
t_1/2 = 07769 × 10³ मिनट
t_1/2 = 77.7 मिनट

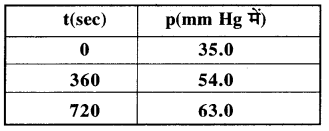
प्रश्न 4.20.
543K ताप पर एजो आइसोप्रोपेन के हेक्सेन तथा नाइट्रोजन में विघटन के निम्न आँकड़े प्राप्त हुए। वेग स्थिरांक की गणना कीजिए।

उत्तर:
एजोआइसोप्रोपेन का विघटन निम्न प्रकार होता है-
A → B + C
(CH₃)₂ CH – N = N – CH (CH₃)₂ N₂ + C₆H₁₄
माना t = 0 पर प्रारंभिक दाब = P_i
तथा t समय पर दाब में कमी = x atm

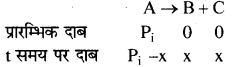
कुल दाब = P_t
अतः t समय पर कुल दाब P_t = ( P_i – x) + x + x
P_t = P_i + x या x = P_t – P_i
यह एक प्रथम कोटि अभिक्रिया है अतः
वेग स्थिरांक, k = \(\frac { 2.303 }{ t }\) log \(\frac{[\mathrm{R}]_0}{[\mathrm{R}]}\)
k = \(\frac{2.303}{t}\) log\(\frac{P_i}{P_i-x}\)
k = \(\frac{2.303}{t}\) log\(\frac{P_i}{P_i-\left(P_t-P_i\right)}\)
k = \(\frac{2.303}{t}\) log\(\frac{P_i}{2 P_i-P_t}\)
P_i = 35 mm Hg P_t = 54.0 mm Hg (t = 360 s पर)

मान रखने पर,
k = \(\frac { 2.303 }{ 100 }\) log\(\frac { 0.5 }{ 0.4 }\)
k = \(\frac { 2.303 }{ 100 }\) log\(\frac { 35 }{ 16 }\)
k = 0.006397 (log 2.1875)
k = 0.006397 × 0.3399
k = 2.17 × 10^-3 = 2.20 × 10^-3 s^-1

प्रश्न 4.21.
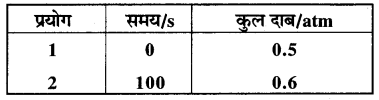
स्थिर आयतन पर SO₂Cl₂ के प्रथम कोटि के ताप अपघटन पर निम्न आँकड़े प्राप्त हुए-
SO₂Cl₂(g) → SO₂(g) + Cl₂(g)
अभिक्रिया वेग की गणना कीजिए जब कुल दाब 0.65 atm हो ।

उत्तर:
अभिक्रिया SO₂Cl₂(g) → SO_2(g) + Cl_(g) माना प्रारंभिक दाब = P_i तथा t समय पर दाब में कमी x atm प्रश्नानुसार-

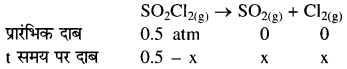
कुल दाब, P_t = 0.5 – x + x + x = 0.5 + x atm
t समय पर कुल दाब = 0.6 atm.
अतः 0.6 = 0.5 + x, x = 0.1 atm
इसलिए t समय (100 s) पर, SO₂Cl₂ का दाब
= 0.5 – x = 0.5 – 0.1 = 0.4 atm
यह एक प्रथम कोटि अभिक्रिया है अतः
k = \(\frac { 2.303 }{ t }\) log\(\frac{[\mathrm{R}]_0}{[\mathrm{R}]}\) के अनुसार
वेग स्थिरांक,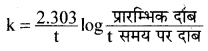
मान रखने पर,
k = \(\frac { 2.303 }{ 100 }\) log\(\frac { 0.5 }{ 0.4 }\)
k = 0.02303 log 1.25
k = 0.02303 × 0.0969
k = 2.23 × 10^-3 s^-1
कुल दाब = 0.65 atm पर अभिक्रिया का वेग-
कुल दाब 0.65 atm पर SO₂Cl₂ का आंशिक दाब, = 0.5 – x
चूँकि कुल दाब = 0.5 + x
अतः 0.65 = 0.5 + x
x = 0.65 – 0.5 = 0.15
अतः 0.5 – x 0.5 – 0.15 = 0.35
वेग = k (P_SO2Cl2)
वेग = 2.23 × 10^-3 × 0.35
वेग = 7.8 × 10^-4 atm s^-1

प्रश्न 4.22.
विभिन्न तापों पर N₂O₅ के अपघटन के लिए वेग स्थिरांक नीचे दिए गये हैं-

In k एवं 1/T के मध्य ग्राफ खींचिए तथा A एवं E_a की गणना कीजिए। 30°C तथा 50°C पर वेग स्थिरांक को प्रागुक्त (Predict) कीजिए।
उत्तर:
ln k तथा 1/T के मध्य ग्राफ बनाने के लिए सर्वप्रथम दिए गए मानों से निम्न प्रकार सारणी तैयार करते हैं-

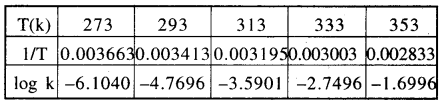
फिर log k तथा 1/T के मध्य ग्राफ खींचने पर निम्नलिखित प्रकार का ग्राफ प्राप्त होता है जो कि एक सीधी रेखा है।

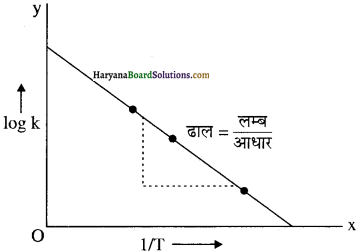
समीकरण, In k = – \(\frac{E_a}{\mathrm{RT}}\) + In A
या log k = – \(\frac{E_a}{\mathrm{2.303RT}}\) + log A के अनुसार इस ग्राफ काढाल
= – \(\frac{E_a}{\mathrm{2.303R}}\) होगा तथा अन्तःखण्ड = log A होगा।
ग्राफ से ढाल = –\(\frac { 2.4 }{ 0.00047 }\) = –\(\frac{\mathrm{E}_{\mathrm{a}}}{2.303 \mathrm{R}}\)
अतः सक्रियण ऊर्जा, E_a = \(\frac{2.4 \times 2.303 \times R}{0.00047}\)
E_a = \(\frac{2.4 \times 2.303 \times 8.314}{0.00047}\)
= 97772.64 J mol^-1
E_a = 97.772 kJ mol^-1
ग्राफ से अंतःखण्ड ज्ञात करके log A ज्ञात कर लेते हैं जिसका Antilog लेने पर A प्राप्त हो जाएगा जो कि लगभग 1.585 × 10⁶ टक्कर आता है।

ग्राफ से 30°C (303K) तथा 50°C (323K ) पर log K पर ज्ञात करके, Antilog लेने पर K के मान प्राप्त हो जाते हैं जो कि लगभग 6.31 × 10^-5 s^-1 (303K पर ) तथा 1.585 x 10^-3 s^-1 (323K पर) है।

प्रश्न 4.23
546 K ताप पर हाइड्रोकार्बन के अपघटन में वेग स्थिरांक 2.418 × 10^-5 s^-1 है। यदि सक्रियण ऊर्जा 179.9 kJ/mol हो तो पूर्व- घातांकी गुणन का मान क्या होगा?
उत्तर:
In k = –\(\frac{E_a}{R T}\) + In A
In A = In k + \(\frac{E_a}{R T}\)
दिया है : log A = log k + \(\frac{E_a}{2.303 \mathrm{RT}}\)
E_a = 179.9 kj/mol
= 179900 J mol^-1
k = 2.418 × 10^-5 s^-1
R = 8.314 Jk^-1 तथा T = 546k
मान रखने पर,
log A = log 2.418 × 10^-5 + \(\frac{179900}{2.303 \times 8.314 \times 546}\)
log A = log 10^-5 + log 2.418 + \(\frac { 179900 }{ 10,454.339 }\)
log A = – 5 log10 + 0.3834) + 17.208
log A = – 5 + 0.3834 + 17.21
log A = – 4.6166 + 17.21
log A = 12.5934
A = Antilog 12.5934
A = 3.921 × 10¹²
अतः पूर्व घातांकी गुणन, A = 3.9 × 10¹² s^-1

प्रश्न 4.24.
किसी अभिक्रिया A → उत्पाद के लिए k = 2.0 × 10^-2 s^-1 है। यदि A की प्रारंभिक सांद्रता 1.0 mol L^-1 हो तो 100s के पश्चात् इसकी सांद्रता क्या रह जाएगी ?
उत्तर:
दिए गए समीकरण के अनुसार अभिक्रिया प्रथम कोटि की है
अतः k = \(\frac { 2.303 }{ t }\) log\(\frac{[\mathrm{R}]_0}{[\mathrm{R}]}\)
k = 2.0 × 10^-2 s^-1, t = 100s,
[R]₀ = 1.0 mol L^-1, [R] = ?
मान रखने पर,
2.0 × 10^-2 = \(\frac { 2.303 }{ 100 }\) log\(\frac { 1 }{ [R] }\)
log\(\frac { 1 }{ [R] }\) = \(\frac{2 \times 10^{-2} \times 100}{2.303}\)
log\(\frac { 1 }{ [R] }\) = \(\frac { 2 }{ 2.303 }\) = 0.8684
\(\frac { 1 }{ [R] }\) = Antilog 0.8684
\(\frac { 1 }{ [R] }\) = 7.386
[R] = 7.386
[R] = \(\frac { 1 }{ 7.386 }\) = 0.135 M
अतः 100s के पश्चात् A की सांद्रता, 0.135M रह जायेगी ।

प्रश्न 4.25.
अम्लीय माध्यम में सूक्रोस का ग्लूकोस एवं फ्रक्टोज़ में विघटन प्रथम कोटि की अभिक्रिया है । इस अभिक्रिया की अर्धायु 3.0 घंटे है। 8 घंटे बाद नमूने में सूक्रोस का कितना अंश बचेगा ?
उत्तर:
C₁₂H₁₂O₁₁ + H₂O → C₆H₁₂O₆ + C₆H₁₂O₆
सूक्रोस (आधिक्य में) ग्लूकोस फ्रक्टोस
यह प्रथम कोटि अभिक्रिया है अतः इसके लिए अर्धायु
t_1/2 = \(\frac { 0.693 }{ k }\)
k = \(\frac{0.693}{t_{1 / 2}}\) = \(\frac{0.693}{3.0 \mathrm{hr}}\)
k = 0.231 hr^-1
माना सूक्रोस की प्रारंभिक सांद्रता [R]₀ = 1 mol
t = 8hr तथा k = 0.231 hr^-1
k = \(\frac { 2.303 }{ t }\) log\(\frac{[\mathrm{R}]_0}{[\mathrm{R}]}\)
0.231 = \(\frac { 2.303 }{ 8 }\) log\(\frac { 1}{ [R] }\)
log\(\frac { 1}{ [R] }\) = \(\frac{0.231 \times 8}{2.303}\) = \(\frac { 1.848 }{ 2.303 }\)
log\(\frac { 1}{ [R] }\) = 0.8024
log\(\frac { 1}{ [R] }\) = Antilog 0.8024
\(\frac { 1}{ [R] }\) = 6.345
R = \(\frac { 1}{ 6.345 }\) = 0.1576M
अतः 8 घंटे के बाद सूक्रोस का बचा अंश = 0.158 M

प्रश्न 4.26.
हाइड्रोकार्बन का विघटन निम्न समीकरण के अनुसार होता है। E_a की गणना कीजिए ।
k = (4.5 × 10¹¹ s^-1)e^-28000K/T
उत्तर:
आर्रेनिअस समीकरण के अनुसार
k = A·e ^{̄Ea / RT} ….(1)
दिया गया है, k = (4.5 × 10^-11s^-1)e^-28000K/T ….(2)
समीकरण (1) तथा (2) की तुलना करने पर,
– \(\frac{E_a}{R T}\) = \(\frac{-28000 K}{T}\)
या \(\frac{E_a}{R}\) = 28000K
E_a = R × 28000 K
E_a = 8.314 JK^-1 mol^-1 × 28,000 K
E_a = 232792 J mol^-1
अतः सक्रियण ऊर्जा E_a = 232.79 kJ mol^-1

प्रश्न 4.27.
H2O2 के प्रथम कोटि के विघटन को निम्न समीकरण द्वारा लिख सकते हैं-
log k = 14.34 – 1.25 × 10⁴ K/T
इस अभिक्रिया के लिए E_a की गणना कीजिए कितने ताप पर इस अभिक्रिया की अर्धायु 256 मिनट होगी?
उत्तर:
आरेंनिअस समीकरण के अनुसार-
k = Ae ^-E_a/RT
log लेने पर, log k = log A – \(\frac{E_a}{2.303 R T}\) ….(1)
दिया गया है- log k = 14.34 – 1.25 × 10⁴ K/T ….(2)
समीकरण (1) व (2) की तुलना करने पर,
\(\frac{E_a}{2.303 R}\) = 1.25 × 10⁴

E_a = 2.303 × R × 1.25 × 10⁴
E_a = 2.303 × 8.314 × 1.25 × 10⁴
E_a = 23.9339 × 10⁴ J mol^-1
E_a = 23.9339 J mol^-1
अतः सक्रियण ऊर्जा, E_a = 23.9339 kJ mol^-1
H₂O₂ का विघटन प्रथम कोटि अभिक्रिया है अतः
अर्घायु, t_1/2 = \(\frac{0.693}{k}\)
t_1/2 = 256 min = 256 × 60 s
k = \(\frac{0.693}{t_{1 / 2}}\) = \(\frac{0.693}{256 \times 60}\)
वेग स्थिरांक k = 4.51 × 10^-5 s^-1
दिया गया है : log k = 14.34 – 1.25 × 10⁴ K/T
मान रखने पर,

अतः 668.8K ताप पर अभिक्रिया की अर्धायु 256 मिनट होगी ।

प्रश्न 4.28.
10°C ताप पर A के उत्पाद में विघटन के लिए k का मान 4.5 × 10³s^-1 तथा सक्रियण ऊर्जा 60kJ mol^-1 है, किस ताप पर k का मान 1.5 × 10⁴s^-1 होगा?
उत्तर:

प्रश्न 4.29.
298K ताप पर प्रथम कोटि की अभिक्रिया के 10% पूर्ण होने का समय 308K ताप पर 25% अभिक्रिया पूर्ण होने में लगे समय के बराबर है। यदि A का मान 4 × 10¹⁰ s^-1 हो तो 318K ताप पर k तथा E_a की गणना कीजिए ।
उत्तर:
प्रथम कोटि अभिक्रिया के लिए

प्रश्न 4.30.
ताप में 293K से 313K तक वृद्धि करने पर किसी अभिक्रिया का वेग चार गुना हो जाता है । इस अभिक्रिया के लिए सक्रियण ऊर्जा की गणना यह मानते हुए कीजिए कि इसका मान ताप के साथ परिवर्तित नहीं होता ।
उत्तर:
आर्रेनिअस समीकरण से,

HBSE 12th Class Chemistry रासायनिक बलगतिकी Intext Questions

प्रश्न 4.1.
R → P, अभिक्रिया के लिए अभिकारक की सांद्रता 0.03M से 25 मिनट में परिवर्तित होकर 0.02M हो जाती है। औसत वेग की गणना सेकण्ड तथा मिनट दोनों इकाइयों में कीजिए।
उत्तर:
अभिक्रिया का औसत वेग = \(\frac{-\Delta[\mathrm{R}]}{\Delta \mathrm{t}}\)
∆R = [R₂] – [R₁] = 0.02M – 0.03M – 0.01M (a) ∆t = 25 मिनट
अतः औसत वेग = \(\frac{-(-0.01)}{25}=\frac{0.01}{25}\)
= 0.0004 M min^-1

(b) ∆t = 25 x 60 = 1500 सेकण्ड
अतः औसत वेग = \(\frac { 0.01 }{ 1500 }\) = 6.66 x 10^-6 ms^-1
= 6.66 x 10^-6 mol L^-1 s^-1

प्रश्न 4.2.
2A → उत्पाद, अभिक्रिया में A की सांद्रता 10 मिनट में 0.5mol L^-1 से घट कर 0.4mol L^-1 रह जाती है। इस समयांतराल के लिए अभिक्रिया वेग की गणना कीजिए।
उत्तर:
2A → उत्पाद के लिए
अभिक्रिया का वेग = – \(\frac{\mathrm{d}[\mathrm{A}]}{2 \mathrm{dt}}\)

A की सांद्रता में परिवर्तन = 0.4 – 0.5mol L^-1
d[A] = – 0.1mol L ^-1
dt = 10 मिनट
अतः अभिक्रिया का वेग = \(\frac{-(-0.1)}{2 \times 10}=\frac{0.1}{20}\)
अभिक्रिया का वेग = A के विलुप्त होने की दर
= 0.005 mol L^-1 min^-1

प्रश्न 4.3.
एक अभिक्रिया A + B → उत्पाद, के लिए वेग नियम r = k[A]^1/2[B]² से दिया गया है। अभिक्रिया की कोटि क्या है?
उत्तर:
वेग नियम r = k[A]^1/2[B]² के अनुसार अभिक्रिया की कोटि 2.5 है, क्योंकि अभिक्रिया के वेग नियम व्यंजक में सांद्रता के घातांकों का योग 2.5 है जो कि अभिक्रिया की कोटि होती है।

प्रश्न 4.4.
अणु X का Y में रूपांतरण द्वितीय कोटि की बलगतिकी के अनुरूप होता है। यदि X की सांद्रता तीन गुनी कर दी जाए तो Y के निर्माण होने के वेग पर क्या प्रभाव पड़ेगा?
उत्तर:
प्रश्नानुसार अभिक्रिया X → Y के लिए
अभिक्रिया का वेग = k [X]² … (1)
अतः अभिक्रिया की कोटि = 2
X की सांद्रता को तीन गुनी कर देने पर
अभिक्रिया का वेग = k [3X] ²
= k = 9[X]² … (2)
अतः अभिक्रिया का वेग 9 गुना हो जाता है।

प्रश्न 4.5.
एक प्रथम कोटि की अभिक्रिया का वेग स्थिरांक 1.15 x 10^-3s^-1 है। इस अभिक्रिया में अभिकारक की 5g मात्रा को घटकर 3g होने में कितना समय लगेगा?
उत्तर:
प्रथम कोटि अभिक्रिया के लिए
वेग स्थिरांक k = \(\frac{2.303}{\mathrm{t}} \log \frac{\left[\mathrm{R}_0\right]}{[\mathrm{R}]}\)
t = \(\frac{2.303}{k} \log \frac{\left[R_0\right]}{[\mathrm{R}]}\)
t = समय, k = वेग स्थिरांक = 1.15 x 10^-3s^-1
[R_o] = अभिकारक की प्रारंभिक सान्द्रता = 5 g
[R] = अभिकारक की t समय पर सांद्रता = 3 g
अतः t = \(\frac{2.303}{1.15 \times 10^{-3}} \log \frac{5}{3}\)
t = 2 × 10³ (log 5 – log 3 )
t = 2 × 10³ (0.6990 – 0.4771)
t = 2 × 10³ (0.2219)
t = 443.8
t = 444 s

प्रश्न 4.6.
SO₂Cl₂ को अपनी प्रारंभिक मात्रा से मात्रा में वियोजित होने में 60 मिनट का समय लगता है। यदि अभिक्रिया प्रथम कोटि की हो तो वेग स्थिरांक की गणना कीजिए।
उत्तर:
अभिक्रिया में प्रारंभिक मात्रा से आधी मात्रा वियोजित हो रही है-
अतः t = 60 मिनट = अर्ध आयुकाल
t_1/2 = \(\frac { 0.693 }{ k }\)
वेग स्थिरांक,
K = \(\frac{0.693}{\mathrm{t}_{1 / 2}}\)
t_1/2 = 60 x 60 = 3600 s
k = \(\frac { 0.693 }{ 3600 }\)
= 1.925 x 10^-4 s^-1

प्रश्न 4.7.
ताप का वेग स्थिरांक पर क्या प्रभाव होगा?
उत्तर:
सामान्यतः ताप बढ़ाने पर वेग स्थिरांक का मान बढ़ता है। यह पाया गया है कि किसी रासायनिक अभिक्रिया में 10°C ताप वृद्धि से वेग स्थिरांक लगभग दुगुना हो जाता है। लेकिन ऊष्माक्षेपी अभिक्रियाओं में ताप बढ़ाने पर वेग स्थिरांक का मान कम हो जाता है। ताप बढ़ाने पर अणुओं के मध्य प्रभावी टक्करें बढ़ती हैं जिससे अभिक्रिया का वेग भी बढ़ जाता है।

प्रश्न 4.8.
परमताप, 298 K में 10 K की वृद्धि होने पर रासायनिक अभिक्रिया का वेग दुगुना हो जाता है। इस अभिक्रिया के लिए E_a की गणना कीजिए।
उत्तर:

प्रश्न 4.9.
581K ताप पर अभिक्रिया 2HI(g) → H₂(g) + I₂(g) के लिए सक्रियण ऊर्जा का मान 209.5 kJ mol^-1 है। अणुओं के उस अंश की गणना कीजिए जिसकी ऊर्जा सक्रियण ऊर्जा के बराबर अथवा इससे अधिक है।
उत्तर:
अणुओं का वह अंश (x) जिसकी ऊर्जा सक्रियण ऊर्जा के बराबर अथवा इससे अधिक है = \(\mathrm{e}^{-\mathrm{E}_2 / R T}\) लोग (लघुगणक) लेने पर,