HBSE 11th Class Physics Solutions Chapter 9 ठोसों के यांत्रिक गुण

Haryana State Board HBSE 11th Class Physics Solutions Chapter 9 ठोसों के यांत्रिक गुण Textbook Exercise Questions and Answers.

Haryana Board 11th Class Physics Solutions Chapter 9 ठोसों के यांत्रिक गुण

प्रश्न 1.
4.7m लम्बे व 3.0 x 10^-5 m² अनुप्रस्थ काट के स्टील के तार तथा 3.5 m लम्बे व 4.0 x 10^-5 m² अनुप्रस्थ काट के ताँबे के तार पर दिए गए समान परिमाण के भारों को लटकाने पर उनकी लम्बाइयों में समान वृद्धि होती है। स्टील तथा ताँबे के यंग प्रत्यास्थता गुणांकों में क्या अनुपात है?
उत्तर:
यंग प्रत्यास्थता गुणांक
Y = \(\frac{\mathrm{F} / \mathrm{A}}{\Delta \mathrm{L} / \mathrm{L}}=\frac{\mathrm{FL}}{\mathrm{A} \Delta \mathrm{L}}\)
समान भार F तथा समान वृद्धि (∆L) के लिए
Y α \(\frac{\mathrm{L}}{\mathrm{A}}\)
अतः
\(\frac{\mathrm{Y}_s}{\mathrm{Y}_c}=\frac{\mathrm{L}_s}{\mathrm{~L}_c} \times \frac{\mathrm{A}_c}{\mathrm{~A}_s}\)
∵ L, = 4.7m, A = 3.0 x 10^-5 m²
L = 3.5m,
Ac = 4.0 x 10^-5 m²
∴ \(\frac{Y_s}{Y_c}=\frac{4 \cdot 7}{3 \cdot 5} \times \frac{4 \cdot 0 \times 10^{-5}}{3.0 \times 10^{-5}}=1.8\)
अत:
Ys : Yc = 1.8 : 1

प्रश्न 2.
चित्र में किसी दिए गए पदार्थ के लिए प्रतिबल विकृति वक्र दर्शाया गया है। इस पदार्थ के लिए (a) यंग प्रत्यास्थता गुणांक, तथा (b) सन्निकट पराभव सामर्थ्य क्या है?

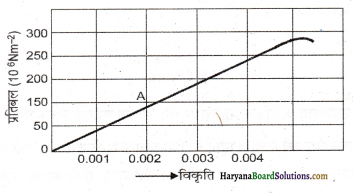
उत्तर:
(a) ग्राफ पर स्थित बिन्दु A पर,
i cy a = 150 x 10⁶ Nm²
तथा
विकृति e = 0.002
∴ यंग प्रत्यास्थता गुणांक Y = \(\frac{\sigma}{\varepsilon}\)
= \(\frac{150 \times 10^6 \mathrm{Nm}^{-2}}{0.002}\)
= 7.5 x 10 10¹⁰ Nm²

(b) पराभव सामर्थ्य = ग्राफ के उच्चतम बिन्दु के संगत
प्रतिबल = 300 × 10⁶ Nm² लगभग

प्रश्न 3.
दो पदार्थों A और B के लिए प्रतिबल – विकृति ग्राफ चित्र 9.20 में दर्शाए गए हैं।

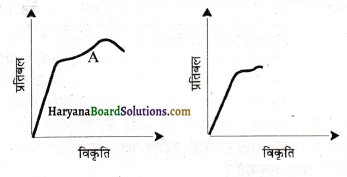
इन ग्राफों को एक ही पैमाना मानकर खींचा गया है।
(a) किस पदार्थ का यंग प्रत्यास्थता गुणांक अधिक है?
(b) दोनों पदार्थों में कौन अधिक मजबूत है?
उत्तर:
(a) ग्राफ A के सरल रेखीय भाग का ढाल, B की अपेक्षा अधिक है। चूँकि सरल रेखीय भाग का ढाल प्रतिबल/विकृति = Y को प्रकट करता है। अतः A का यंग प्रत्यास्थता गुणांक, B की अपेक्षा अधिक है।
(b) पदार्थ A अधिक मजबूत है क्योंकि इसका प्रत्यास्थता गुणांक पदार्थ B से अधिक है।

प्रश्न 4.
निम्नलिखित दो कथनों को ध्यान से पढ़िए और कारण सहित बताइए कि वे सत्य हैं या असत्य:
(a) इस्पात की अपेक्षा रबर का यंग प्रत्यास्थता गुणांक अधिक है;
(b) किसी कुण्डली का तनन उसके अपरूपण गुणांक से निर्धारित होता है।
उत्तर:
(a) माना स्टील व रबर के दो तार समान लम्बाई L व समान त्रिज्या r के हैं। माना इन पर Mg भार लटकाने से स्टील के तार में वृद्धि
ls व रबर की डोरी की लम्बाई में वृद्धि l_R है। यदि स्टील व रबर के यंग प्रत्यास्थता गुणांक क्रमश: Y_s व Y_pहैं, तो
\(\mathrm{Y}_{\mathrm{S}}=\frac{\mathrm{MgL}}{\pi r^2 l_{\mathrm{S}}}\)
तथा
\(\mathrm{Y}_{\mathrm{R}}=\frac{\mathrm{MgL}}{\pi r^2 l_{\mathrm{R}}}\)
\(\frac{\mathrm{Y}_{\mathrm{R}}}{\mathrm{Y}_{\mathrm{S}}}=\frac{\mathrm{MgL} / \pi r^2 l_{\mathrm{R}}}{\mathrm{MgL} / \pi r^2 l_{\mathrm{S}}}=\frac{l_{\mathrm{S}}}{l_{\mathrm{R}}}\)
चूँकि रबर की डोरी स्टील के तार के तुलना में समान भार के लिए लम्बाई में अधिक खिंचता है अर्थात् l_R > l_s अतः स्पष्ट है Y_s > Y_R अर्थात् रबर की अपेक्षा स्टील अधिक प्रत्यास्थ है अतः यह कथन असत्य है।
(b) सत्य; क्योंकि कुण्डली का तनन करने पर न तो लम्बाई में वृद्धि होती है और न ही आयतन में परिवर्तन होता है। चूँकि कुण्डली की आकृति में परिवर्तन होता है।

प्रश्न 5.
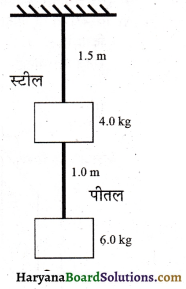
0.25cm व्यास के दो तार, जिनमें एक इस्पात का तथा दूसरा पीतल का है चित्र 9.21 के अनुसार भारित हैं। बिना भार लटकाये इस्पात तथा पीतल के तारों की लम्बाइयाँ क्रमश: 1.5m तथा 1.0m हैं। यदि इस्पात तथा पीतल के यंग प्रत्यास्थता गुणांक क्रमशः 2.0 x 10¹¹ Pa तथा 0.91 ×10¹¹ Pa हों, तो इस्पात तथा पीतल के तारों में विस्तार की गणना कीजिए।
उत्तर:
∴ इस्पात के तार के लिए
E = 1.5m,
M = (4.0 + 6.0)
= 10.0kg
r = \(\frac{0 \cdot 25}{2}\) Cm
= 0.125 × 10^-2m,
Y₁ = 2.0 × 10^-2 Pa
\(\mathrm{Y}=\frac{\mathrm{MgL}}{\pi r^2 \Delta \mathrm{L}}\)
\(\Delta \mathrm{L}_1=\frac{10.0 \times 9.8 \times 1.5}{3.14 \times\left(0.125 \times 10^{-2}\right)^2 \times 2.0 \times 10^{11}}\)
= 1.5 x 10^-4m
तथा पीतल के तार के लिए,
L = 10m, M = 6.0 kg,
Y₂ = 0.91 × 10¹¹Pa

= 1.3 × 10^-4 m

प्रश्न 6.
ऐलुमिनियम के किसी घन के किनारे 10 cm लम्बे हैं। इसकी एक फलक किसी ऊर्ध्वाधर दीवार से कसकर जुड़ी हुई है। इस के सम्मुख फलक से 100 kg का एक द्रव्यमान जोड़ दिया गया है। ऐलुमिनियम का अपरूपण गुणांक 25 GPa है। इस फलक का ऊर्ध्वाधर विस्थापन कितना होगा?
उत्तर:
दिया है : अपरूपण गुणांक η = 25 GPa
= 25 × 10⁹ Nm^-2
आरोपित बल का क्षेत्रफल
A = 10 cm x 10 cm
= 100 cm² = 100 × 10^-4m²
आरोपित बल F = 100 kg x 9.8N/kg = 980 N

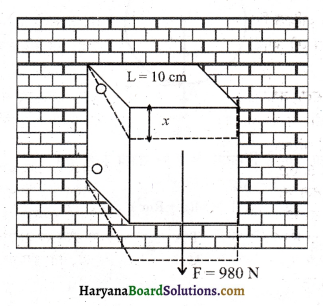
माना फलक का ऊर्ध्वं विस्थापन = ∆x
जबकि L = 10cm = 0.1m
∴ सूत्र η = \(\frac{(\mathrm{F} / \mathrm{A})}{(\Delta x / \mathrm{L})}\)
फलक का विस्थापन
\(\Delta x=\frac{\mathrm{FL}}{\eta \mathrm{A}}\)
= \(\frac{980 \times 0.1}{25 \times 10^9 \times 100 \times 10^{-4}}\)
= 3.92 × 10^-7m
= 4 x 10^-7 m

प्रश्न 7.
मृदु इस्पात के चार समरूप खोखले बेलनाकार स्तम्भ 50000 kg द्रव्यमान के किसी बड़े ढाँचे को आधार दिये हुए हैं। प्रत्येक स्तम्भ की भीतरी तथा बाहरी त्रिज्याएँ क्रमशः 30 तथा 60 cm हैं। भार वितरण को एकसमान मानते हुए प्रत्येक स्तम्भ की सम्पीडन विकृति की गणना कीजिए।
उत्तर:
ढाँचे का कुल भार F = 50000 kg x 9.8Nkg^-1
= 4.9 x 10⁵N
∵ ढाँचे का भार चारों स्तम्भों पर एकसमान पड़ता है अतः प्रत्येक
स्तम्भ पर पड़ने वाला भार
F₁ = \( \frac{F}{4}\)
= \(\frac{4.9 \times 10^5}{4}\)
= 1-225 × 10⁵ N
तथा प्रत्येक स्तम्भ का अनुप्रस्थ क्षेत्रफल
A = π
= 3.14[(0.6)² – (0.3)²]
= 0.8478 m² = 0.85m²
सूत्र \(\mathrm{Y}=\frac{\mathrm{FL}}{\mathrm{A \Delta L}}\) से,
सम्पीडन विकृति (% में) \(\frac{\Delta \mathrm{L}}{\mathrm{L}} \times 100=\frac{\mathrm{F}_1}{\mathrm{AY}} \times 100\)
= \(\frac{1.225 \times 10^5}{0.85 \times 2 \times 10^{11}} \times 100\)
[ ∵ Y = 2 × 10¹¹ Nm²]
सम्पीडन विकृति % = 7.2 x 10^-5 x 4
अतः सभी स्तंभों की संपीडन विकृति %
= 7.2 x 10^-5 x 4
= 2.88 x 10^-5 %

प्रश्न 8.
ताँबे का एक टुकड़ा, जिसका अनुप्रस्थ परिच्छेद 15.2 mm x 19.1 mm का है, 44500 N बल के तनाव से खींचा जाता है, जिससे केवल प्रत्यास्थ विरूपण उत्पन्न हो । उत्पन्न विकृति की गणना कीजिए।
उत्तर:
दिया है F = 44500N,
A = 15.2mm x 19.1mm
= 15.2 × 10^-3m × 19.1 × 10^-3 m
= 2.90 × 10^-4 m²
ताँबे के लिए Y = 1.1 × 10¹¹ Nm^-2,
विकृति = ?
सूत्र \(Y=\frac{(F / A)}{(\Delta L / L)}\)
∴ विकृति
= \(\frac{44500}{2.9 \times 10^{-4} \times 1 \cdot 1 \times 10^{11}}\)
= 0.00139
प्रतिशत विकृति \(\frac{\Delta \mathrm{L}}{\mathrm{L}}\) x 100
= 0.00139 x 100 = 0.139%

प्रश्न 9.
1.5 cm त्रिज्या का एक इस्पात का केबिल भार उठाने के लिए इस्तेमाल किया जाता है। यदि इस्पात के लिए अधिकतम अनुज्ञेय प्रतिबल 10⁸ Nm^-2 है तो उस अधिकतम भार की गणना कीजिए जिसे केबिल उठा सकता है।
उत्तर:
दिया है
अधिकतम अनुज्ञेय प्रतिबल = 10⁸ Nm^-2
त्रिज्या r = 1.5 cm
= 1.5 x 10^-2 m
लटकाया गया अधिकतम भार= ?
अधिकतम अनुज्ञेय प्रतिबल =
= अनुज्ञेय प्रतिबल x A
∴ अधिकतम भार (Mg)
= 10⁸ x πr²
= 10⁸ × 3.14 × (1-5 × 10^-2)²
= 7.07 × 10⁴ N

प्रश्न 10.
15 kg द्रव्यमान की एक दृढ़ पट्टी को तीन तारों, जिनमें प्रत्येक की लम्बाई 2 m है, से सममित लटकाया गया है। सिरों के दोनों तार ताँबे के हैं तथा बीच वाला लोहे का है। तारों के व्यासों के अनुपात निकालिए, प्रत्येक पर तनाव उतना ही रहना चाहिए।
उत्तर:
पट्टी, तारों से सममिति से लटकी है अतः प्रत्येक पट्टी के भार का एक तिहाई भार का वहन करेगा।
माना एक तार का व्यास D है, तब त्रिज्या r = \(\frac{\mathrm{D}}{2}\)

प्रश्न 11.
एक मीटर अतानित लम्बाई के इस्पात के तार के एक सिरे से 14.5 kg का द्रव्यमान बाँधकर उसे एक ऊर्ध्वाधर वृत्त में घुमाया जाता है, वृत्त की तली पर उसका कोणीय वेग 2 rev/s है। तार के अनुप्रस्थ परिच्छेद का क्षेत्रफल 0.065 cm² है। तार में विस्तार की गणना कीजिए जब द्रव्यमान अपने पथ के निम्नतम बिन्दु पर है।
उत्तर:
दिया है
M = 14.5 kg, L = 1 m
A = 0.065 cm² = 6.5 x 10^-6 m²
वृत्त की त्रिज्या R = 1m, AL = ?
ω = 2π x 2 = 4π rad/s; Y = 2 x 10¹¹ Nm^-2

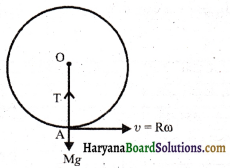
माना वृत्त के निम्नतम बिन्दु पर तनाव T है, तब
T – Mg = MRω²
या
T = M(g + Rω²)
परन्तु
\(\mathrm{Y}=\frac{\mathrm{T} / \mathrm{A}}{\Delta \mathrm{L} / \mathrm{L}}\) से,
तार में विस्तार

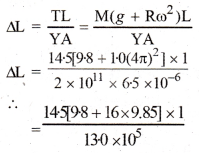
= 1.86 x 10^-3 मी = 0.186 सेमी

प्रश्न 12.
नीचे दिए गए आँकड़ों से जल के आयतन प्रत्यास्थता गुणांक की गणना कीजिए:
प्रारम्भिक आयतन 100.00 लीटर, दाब में वृद्धि 100.0atm (1 atm = 1.013 × 10⁵ Pa) अन्तिम आयतन 100.5 लीटर। नियत ताप पर जल तथा वायु के आयतन प्रत्यास्थता गुणांकों की तुलना कीजिए। सरल शब्दों में समझाइए कि यह अनुपात इतना अधिक क्यों है?
उत्तर:
दिया है:
∆P = 100 वायुमण्डलीय दाब
= 100 × 1.013 × 10⁵ Pa
= 1.013 × 10⁷ Pa
V₁ = 100 लीटर,
V₂ = 100.5 लीटर

आयतन में परिवर्तन ∆V = V₂ – V₁
= 100.5 – 100 = 0.5 लीटर
= 0.5 × 10^-3 m³
∴ जल का आयतन प्रत्यास्थता गुणांक
= \(\frac{\Delta \mathrm{P}}{\Delta \mathrm{V} / \mathrm{V}}=\frac{\mathrm{V} \Delta \mathrm{P}}{\Delta \mathrm{V}}\)
Bजल =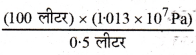
B. = 2.206 × 10⁹ Pa
तथा वायु का आयतन प्रत्यास्थता गुणांक
Bवायु = 1.0 × 10⁵ Nm²

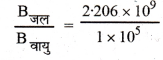
इतना अधिक अनुपात होने का कारण यह है कि गैसों में अन्तराष्विक बल, द्रवों की तुलना में नगण्य होते हैं।

प्रश्न 13.
जल का घनत्व उस गहराई पर जहाँ दाब 80.0 atm हो, कितना होगा? दिया गया है कि पृष्ठ पर जल का घनत्व 1.03 x 10³ kg m^-3, जल की सम्पीड्यता 45.8 x 10^-11 Pa^-1 (1 Pa = 1 Nm^-2)
उत्तर:
आयतन प्रत्यास्थता गुणांक B =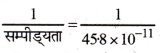
∴ B = 2.18 x 10⁹ Pa
माना जल का द्रव्यमान M, आयतन V तथा घनत्व p है, तब
द्रव्यमान = आयतन घनत्व
M= Vp = नियत
अवकलित करने पर, V∆p + p∆v = 0
अतः आयतन विकृति \(\frac{\Delta V}{V}=-\frac{\Delta \rho}{\rho}\) ….(1)
तथा आयतन प्रत्यास्थता गुणांक
\(\mathrm{B}=-\frac{\Delta \mathrm{P}}{\Delta \mathrm{V} / \mathrm{V}}\)
= \(\frac{\Delta \mathrm{V}}{\mathrm{V}}=-\frac{\Delta \mathrm{P}}{\mathrm{B}}\) ……….(2)
समी (1) व (2) से,
\(\frac{\Delta \rho}{\rho}=\frac{\Delta P}{B}\)
या
\(\Delta \rho=\frac{\Delta P \rho}{B}\)
∴ ∆p = दाब में परिवर्तन
= गहराई में दाब – सतह पर दाब
= 80 – 1
∆p = 79 वायुमण्डल
= 79 × 1.013 × 10⁵ Nm²
अतः
\(\Delta \rho=\frac{\left(79 \times 1.013 \times 10^5\right) \times 1.03 \times 10^3}{2.18 \times 10^9}\)
∆p = 4kgm^-3
= 0.004 x 10³ kg m^-3
∴ गहराई पर जल का घनत्व
p = p + ∆p
= 1.03 × 10³ + 0.004 × 10³
= 1.034 x 10³ kg m^-3

प्रश्न 14.
काँच के स्लैब पर 10 atm का जलीय दाब लगाने पर उसके आयतन के भिन्नात्मक अन्तर की गणना कीजिए।
उत्तर:
दिया है
∆p = 10 atm = 10 x 10⁵ Pa
काँच की आयतन प्रत्यास्थता B = 37 x 10⁹ Nm^-2
आयतन प्रत्यास्थता B = \(\frac{-\Delta \mathrm{P}}{\Delta \mathrm{V} / \mathrm{V}}\)
अतः
∴ स्लैब के आयतन में भिन्नात्मक अन्तर
\(\frac{\Delta \mathrm{V}}{\mathrm{V}}=\frac{10 \times 10^5}{37 \times 10^9}\) = 2.70 × 10^-5
अथवा
\(\frac{\Delta \mathrm{V}}{\mathrm{V}}\) × 100 = 2.7 × 10⁵ × 100%
= 0.0027%

प्रश्न 15.
ताँबे के एक ठोस घन का एक किनारा 10 cm का है। इस पर 7.0 x 10⁶ Pa का जलीय दाब लगाने पर इसके आयतन में संकुचन निकालिए।
उत्तर:
दिया है घन की भुजा a = 10 cm = 0.1m
∴ घन का आयतन V = a = (0.1)³ = 10³ m³
जलीय दाब P = 7 x 10⁶ Pa
तथा
ताँबे के लिए B = 140 x 10⁹ Pa
सूत्र
B = \(\frac{{ }^{\prime} \mathrm{P}}{\Delta \mathrm{V} / \mathrm{V}}\) से,
आयतन में संकुचन
∆v = \(\frac{\Delta \mathrm{PV}}{\mathrm{B}}=\frac{7 \times 10^6 \mathrm{~Pa} \times 10^{-3} \mathrm{~m}^3}{140 \times 10^9 \mathrm{~Pa}}\)
= 5 × 10⁸ m³
= 0.05 cm³

प्रश्न 16.
1 लीटर जल पर दाब में कितना अन्तर किया जाए कि वह 0.10% से सम्पीडित हो जाए?
उत्तर:
दिया है:
V = 1 लीटर,
B = 2.2 x 10⁹ Nm^-2
\(\frac{\Delta \mathrm{V}}{\mathrm{V}}\) x 100 = 0.10 या ∆V = \(\frac{0 \cdot 10}{100}\) × 1
= \(\frac{1}{1000}\) लीटर
∵ \(B=\frac{\Delta P}{\Delta V / V}\)
∴ \(\Delta P=B \frac{\Delta V}{V}\)
= 2.2 × 10⁹ × \(\frac{1}{1000}\)
∆P = 2.2 × 10⁶ Pa

अतिरिक्त अभ्यास

प्रश्न 17.
हीरे के एकल क्रिस्टलों से बनी निहाइयों जिनकी आकृति चित्र 9.24 में दिखाई गई है, का उपयोग अति उच्च दाब के अन्तर्गत द्रव्यों के व्यवहार की जाँच के लिए किया जाता है। निहाई के संकीर्ण सिरों पर सपाट फलकों का व्यास 0.50mm है। यदि निहाई के चौड़े सिरों पर 50000 N का बल लगाया गया हो तो उसकी नोंक पर दाब ज्ञात कीजिए।

उत्तर:
सपाट फलक की त्रिज्या
R = \(\frac{D}{2}=\frac{0.50}{2}\) = 0.25 mm
= 2.5 × 10^-4 m
∴ नोंक पर दाब P = \(\frac{F}{A}=\frac{F}{πr^2}=\frac{50000 \mathrm{~N}}{3.14 \times\left(2.5 \times 10^{-4}\right)^2}\)
= 2.55 × 10¹¹ Pa

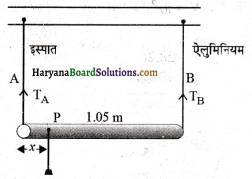
प्रश्न 18.
1.05m लम्बाई तथा नगण्य द्रव्यमान की एक छड़ को बराबर लम्बाई के दो तारों, एक इस्पात का (तार A) तथा दूसरा ऐल्युमिनियम का तार (तार B) द्वारा सिरों से लटका दिया गया है, जैसा कि निम्न चित्र में दिखाया गया है। A तथा B के तारों के अनुप्रस्थ परिच्छेद के क्षेत्रफल क्रमश: 1.0 mm और 2.0 mm हैं। छड़ के किस बिन्दु से एक द्रव्यमान m को लटका दिया जाए ताकि इस्पात तथा ऐलुमिनियम के तारों में
(a) समान प्रतिबल तथा
(b) समान विकृति उत्पन्न हो।

उत्तर:
तारों के अनुप्रस्थ काट के क्षेत्रफल
A_A = 1.0 mm² , A_B = 2.0 mm²
तथा Y_A = 2 × 10¹¹ Nm^-2,
Y_B = 0.7 × 10¹¹ Nm^-2
माना द्रव्यमान को तार A वाले सिरे से, x दूरी पर बिन्दु P से लटकाया गया है तब इसकी दूसरे सिरे से दूरी (1.05 – x ) m होगी।
माना इस भार के कारण तारों में T तथा T तनाव उत्पन्न होते हैं। तब P के परितः बलों के आघूर्णी का बीजीय योग साम्यावस्था में शून्य होना चाहिए, अतः
T_A . x = T_B(1.05 – x) …………(1)
\(\frac{\mathrm{T}_{\mathrm{A}}}{\mathrm{T}_{\mathrm{B}}}=\frac{1 \cdot 05-x}{x}\)

(a) तारों में समान प्रतिबल है अतः
\(\frac{\mathrm{T}_{\mathrm{A}}}{\mathrm{A}_{\mathrm{A}}}=\frac{\mathrm{T}_{\mathrm{B}}}{\mathrm{A}_{\mathrm{B}}}\)
\(\frac{\mathrm{T}_{\mathrm{A}}}{\mathrm{T}_{\mathrm{B}}}=\frac{\mathrm{A}_{\mathrm{A}}}{\mathrm{A}_{\mathrm{B}}}\) …………(2)
समीकरण (1) व (2) की तुलना करने पर
\(\frac{\mathrm{A}_{\mathrm{A}}}{\mathrm{A}_{\mathrm{B}}}=\frac{1 \cdot 05-x}{x}\)
\(\frac{1 \cdot 05-x}{x}=\frac{1 \mathrm{~mm}^2}{2 \mathrm{~mm}^2}\)
x = 2 ( 1.05 – x)
या x = 2.10 – 2x
3x = 2.10
x = 0.70 = 70 cm
अतः द्रव्यमान को तार A वाले सिरे से 70 cm की दूरी पर लटकाना चाहिए।

(b) सूत्र Y = \(\frac {FL}{A∆L}\) से, \(\frac { ∆L }{ L }\) = \(\frac {F}{AY}\)
दोनों तारों में समान विकृति उत्पन्न होती है
अतः
\(\frac{\mathrm{T}_{\mathrm{A}}}{\mathrm{A}_{\mathrm{A}} \mathrm{Y}_{\mathrm{A}}}=\frac{\mathrm{T}_{\mathrm{B}}}{\mathrm{A}_{\mathrm{B}} \mathrm{Y}_{\mathrm{B}}}\)
समी (1) में समी (3) से भाग देने पर,
A_AY_A x = (1.05 – x ) A_BY_B
या \(\frac{x}{1 \cdot 05-x}=\frac{\mathrm{A}_{\mathrm{B}}}{\mathrm{A}_{\mathrm{A}}} \times \frac{\mathrm{Y}_{\mathrm{B}}}{\mathrm{Y}_{\mathrm{A}}}\)
या \(\frac{x}{1.05-x}=\frac{2 \mathrm{~mm}^2}{1 \mathrm{~mm}^2} \times \frac{0.7 \times 10^{11} \mathrm{Nm}^{-2}}{2.0 \times 10^{11} \mathrm{Nm}^{-2}}\)
या \(\frac{x}{1 \cdot 05-x}=\frac{7}{10}\)
या 10x = 1.05 × 7 – 7x
या 17x = 7.35
⇒ x = \(\frac {7.35}{17}\) = 0.43m = 43 cm
अतः द्रव्यमान को तार A वाले सिरे से 43 cm की दूरी पर लटकाना चाहिए।

प्रश्न 19.
मृदु इस्पात के एक तार, जिसकी लम्बाई 1.0 m तथा अनुप्रस्थ परिच्छेद का क्षेत्रफल 0.50 × 10² cm² है, को दो खम्बों के बीच क्षैतिज दिशा में प्रत्यास्थ सीमा के अन्दर ही तनित किया जाता है। तार के मध्य बिन्दु से 100g का एक द्रव्यमान लटका दिया जाता है। मध्य- बिन्दु पर अवनमन की गणना कीजिए ।
उत्तर:

दिया है
L = 1m
A = 0.5 × 10² cm²
A = \(0.50 \times 10^{-2} \mathrm{~cm}^2=5 \times 10^{-7} \mathrm{~m}^2\)
m = 100gm = 0.1 kg
Y = 2 × 10¹¹ Nm^-2
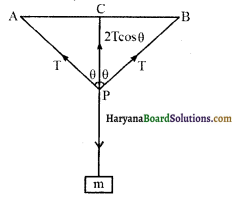
सन्तुलन की स्थिति में तार के दोनों भागों में तनाव समान होगा, जो कि T है तब,
2T cos θ = mg
(C तार का मध्य- बिन्दु है जो भार लटकाने पर P तक विस्थापित हो जाता है।)
तब
l =AC = BC = \(\frac {1}{2}\) = 0.5 m
माना अवनमन PC है, जो कि अत्यन्त कम है
AP = \(\sqrt{\mathrm{AC}^2+\mathrm{PC}^2}=\sqrt{l^2+x^2}\)
भाग AC की लम्बाई में वृद्धि

= 0.5 × 2.13 × 10^-6 m
∴ x = 0.01 m

प्रश्न 20.
धातु के दो पहियों के सिरों को चार रिवेट से आपस में जोड़ दिया गया है। प्रत्येक रिवेट का व्यास 6 mm है। यदि रिवेट पर अपरूपण प्रतिबल 6.9 x 10⁷ Pa से अधिक नहीं बढ़ना हो तो रिवेट की हुई पट्टी द्वारा आरोपित तनाव का अधिकतम मान कितना होगा? मान लीजिए कि प्रत्येक रिवेट एक चौथाई भार वहन करता है।
उत्तर:
प्रत्येक रिवेट पर अधिकतम प्रतिबल
S_max = 6.9 × 10⁷ Pa
रिवेट का अनुप्रस्थ क्षेत्रफल
A = πr²
= 3.14 × (3 × 10^-3 m)²
= 28.26 × 10^-6 m²
. प्रत्येक रिवेट पर अधिकतम तनाव बल
= S_max × अनुप्रस्थ क्षेत्रफल
= 6-9 × 10⁷ × 28.26 × 10^-6
= 1.95 × 10³ N
तथा रिवेट की गई पट्टी द्वारा आरोपित अधिकतम तनाव
= 4 × 1.95 × 10³
= 7.8 × 10³ N

प्रश्न 21.
प्रशांत महासागर में स्थित मैरिना खाई एक स्थान पर पानी की सतह से 11 km नीचे चली जाती है और उस खाई में नीचे तक 0.32 m³ आयतन का इस्पात का एक गोला गिराया जाता है तो गोले के आयतन में परिवर्तन की गणना करें। खाई के तल पर जल का दाब 1.1 x 10⁸ Pa है और इस्पात का आयतन गुणांक 160 GPaहै
उत्तर:
दाब में परिवर्तन ∆P तली पर जल का दाब
= 1.1 × 10⁸ Pa
गोले का आयतन V = 0.32m³,
इस्पात के लिए B = 160 GPa
= 160 × 10⁹ Pa
परिभाषा से, \(\mathrm{B}=-\frac{\Delta \mathrm{P}}{\Delta \mathrm{V} / \mathrm{V}}\)
अतः आयतन में कमी
\(\Delta V=\frac{\Delta P V}{B}\)
= \(\frac{1.1 \times 10^8 \mathrm{~Pa} \times 0.32 \mathrm{~m}^3}{160 \times 10^9 \mathrm{~Pa}}\)
= 2.2 × 10^-4 m³