HBSE 11th Class Physics Solutions Chapter 14 दोलन

Haryana State Board HBSE 11th Class Physics Solutions Chapter 14 दोलन Textbook Exercise Questions and Answers.

Haryana Board 11th Class Physics Solutions Chapter 14 दोलन

प्रश्न 1.
नीचे दिए गए उदाहरणों में कौन आवर्ती गति को निरूपित करता है?
(i) किसी तैराक द्वारा नदी के एक तट से दूसरे तट तक जाना और अपनी एक वापसी यात्रा पूरी करना।
(ii) किसी स्वतन्त्रतापूर्वक लटकाए गए दण्ड चुम्बक को उसकी N-S दिशा से विस्थापित कर छोड़ देना।
(iii) अपने द्रव्यमान केन्द्र के परितः घूर्णी गति करता कोई हाइड्रोजन परमाणु ।
(iv) किसी कमान से छोड़ा गया तीर
उत्तर :
(i) तैराक को नदी के एक तट से दूसरे तट तक प्रत्येक बार जाने-आने पर लगे समय अलग-अलग होंगे अतः यह आवर्ती गति नहीं होगी।
(ii) यह आवर्ती गति होगी। चूँकि स्वतन्त्रतापूर्वक लटकाया गया चुम्बक एक बार NS दिशा से विस्थापित करने के पश्चात् माध्य स्थिति के दोनों ओर दोलन करता है। अतः सरल आवर्त गति भी है। (iii) यह एक आवर्ती गति है क्योंकि गति स्वयं दोहराती है।
(iv) तीर कमान से छेड़ने के पश्चात् वह वापस प्रारम्भिक स्थिति में नहीं लौटता, अतः यह आवर्ती गति नहीं है।

प्रश्न 2.
नीचे दिए गए उदाहरणों में कौन (लगभग) सरल आवर्त गति को तथा कौन आवर्ती परन्तु सरल आवर्त गति निरूपित नहीं करते हैं?
(i) पृथ्वी की अपने अक्ष के परितः घूर्णन गति ।
(ii) किसी नली में दोलायमान पारे के स्तम्भ की गति ।
(iii) किसी चिकने वक्रीय कटोरे के भीतर एक बॉल बेयरिंग की गति जब उसे निम्नतम बिन्दु से कुछ ऊपर के बिन्दु से युक्त रूप से छोड़ा जाए।
(iv) किसी बहुपरमाणुक अणु की अपनी साम्यावस्था की स्थिति के परितः व्यापक कम्पन।
उत्तर :
(i) पृथ्वी की अपनी अक्ष के परितः गति आवर्त गति है, परन्तु सरल आवर्त नहीं।
(ii) U-नली में दोलायमान पारे के स्तम्भ की गति रेखीय सरल आवर्त गति है।
(iii) किसी चिकने चक्रीय कटोरे के भीतर बॉल बेयरिंग की गति सरल आवर्त गति है।
(iv) यह आवर्ती परन्तु सरल आवर्त गति को निरूपित नहीं करता है। किसी बहुपरमाणुक अणु की कई प्राकृतिक आवृत्तियाँ होती हैं। अतः व्यापक रूप में, इसका कम्पन विभिन्न आवृत्तियों की कई सरल आवर्त गतियों का अध्यारोपण होता है। यह अध्यारोपण आवर्ती तो होता है परन्तु सरल आवर्त गति से नहीं होता ।

प्रश्न 3.
चित्र में किसी कण की रैखिक गति के लिए चार xv आरेख दिए गए हैं। इनमें से कौन-सा आरेख आवर्ती गति का निरूपण करता है? उस गति का आवर्तकाल क्या है? (आवर्ती गति वाली गति का) ।

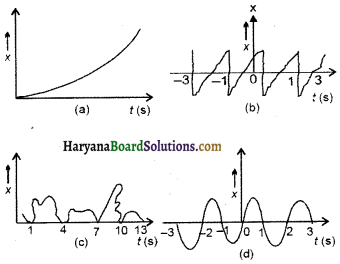
उत्तर :
(a) ग्राफ में कण अपनी गति की पुनरावृत्ति नहीं करता है, अतः यह गति आवर्त गति नहीं है। किसी गति के लिए आवर्ती होने के लिए केवल किसी एक स्थिति की पुनरावृत्ति होना ही पर्याप्त नहीं होता। एक आवर्तकाल की समस्त गति की क्रमागत पुनरावृत्ति होनी चाहिए।
(b) इसमें कण प्रत्येक 2 सेकण्ड के पश्चात् अपनी गति की पुनरावृत्ति करता है, अतः यह गति एक आवर्ती गति है, जिसका आवर्तकाल 25 है।
(c) इसमें कण पूरी गति को नहीं दोहराता, यह केवल एक स्थिति में ही (शून्य विस्थापन) अपनी गति को दोहराता है, जो आवर्ती गति के लिए पर्याप्त नहीं है, अतः यह एक आवर्ती गति नहीं है।
(d) कण प्रत्येक 2 सेकण्ड के पश्चात् अपनी प्रारम्भिक स्थिति को दोहराता है, अतः यह गति एक आवर्ती गति है।

प्रश्न 4.
नीचे दिए गए समय के फलनों में कौन (a) सरल आवर्त गति (b) आवर्ती परन्तु सरल आवर्त गति नहीं तथा (c) अनावर्ती गति का निरूपण करते हैं। प्रत्येक आवर्ती गति का आवर्तकाल ज्ञात कीजिए – (ω कोई धनात्मक अचर है।)
(a) sin ωt – cos ωt
(b) sin³ ωt
(c) 3 cos(\(\frac{π}{2}\) – 2ωt)
(d) cos ωt + cos 3 ωt + cos 5 ωf
(e) exp (- ω²t³)
(f) 1 + ωt + ω²t²
उत्तर :
सरल आवर्त गति हेतु त्वरण ∝ – विस्थापन
a ∝ -x
(a) दिया गया फलन
x = sin ωt – cos ωt
= √2(\(\sin ωt \cdot \frac{1}{\sqrt{2}}-\cos ωt \cdot \frac{1}{\sqrt{2}}\))
= √2(\(\sin ωt \cos \frac{\pi}{4}-\cos ωt \sin \frac{\pi}{4}\))
x = √2 sin(ωt – \(\frac{\pi}{4}\))
इससे स्पष्ट है कि यह फलन आयाम की सरल आवर्त गति को निरूपित करता है जिसका आवर्तकाल T = \(\frac{2π}{ω}\) है।

(b) फलन sin³ ωt आवर्त गति को निरूपित करता है इसका
आवर्तकाल T = \(\frac{2π}{ω}\) है, परन्तु यह सरल आवर्त गति निरूपित नहीं करता
( क्योंकि \(\overrightarrow{a}\) ≠ ω²x)

(c) 3 cos(\(\frac{π}{2}\) – 2ωt)
वेग v = \(\frac{dx}{dt}\) = 6ω sin(\(\frac{\pi}{4}\) – 2ωt)
तथा त्वरण a = \(\frac{dv}{dt}\)
= 12 ω² cos(\(\frac{\pi}{4}\) – 2ωt)
= -4ω²x
a = -(2ω)²x
अर्थात् a ∝ -x अतः यह एक सरल आवर्त गति है, इसका
आवर्तकाल T = \(\frac{2π}{2ω}=\frac{π}{ω}\)

(d) यह फलन भी आवर्त गति को निरूपित करता है जो कि सरल आवर्त गति नहीं है।
फलन cos ωt का आवर्तकाल T₁ = \(\frac{2π}{ω}\)
फलन cos 3ωt का आवर्तकाल T₂ = \(\frac{2π}{3ω}\)
फलन cos 5ωt का आवर्तकाल T₃ = \(\frac{2π}{5ω}\)
यहाँ T₁ = 3 T₂ तथा T₁ = 5 T₃
अर्थात् जहाँ T₁ समय पश्चात् प्रथम फलन की एक बार दूसरे की तीन बार तथा तीसरे की पाँच बार पुनरावृत्ति हो जाएगी।
अतः दिए गए फलन का आवर्तकाल T = T₁ = \(\frac{2π}{ω}\)

(e) फलन exp (- ω²t³), आवर्ती फलन नहीं है।

(f) 1 + ωt + ω²t² जब t → ∞ तब फलन f(t) → ∞
अतः यह आवर्ती फलन नहीं है।

प्रश्न 5.
कोई कण एक-दूसरे से 10 cm दूरी पर स्थित दो बिन्दुओं A तथा B के बीच रैखिक सरल आवर्त गति कर रहा है। A से B की ओर की दिशा को धनात्मक मानकर वेग, त्वरण तथा कण पर लगे बल के चिह्न ज्ञात कीजिए जबकि यह कण-
(a) A सिरे पर है,
(b) B सिरे पर है,
(c) A की ओर जाते हुए AB के मध्य बिन्दु पर है,
(d) A की ओर जाते हुए B से 2 cm दूर है,
(e) B की ओर जाते हुए A से 3 cm दूर है, तथा
(f) A की ओर जाते हुए B से 4 cm दूर है।

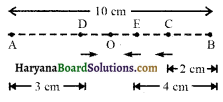
उत्तर :
स्पष्ट है कि बिन्दु A तथा B अधिकतम विस्थापन की स्थितियाँ हैं तथा इनका मध्य- बिन्दु 0 सरल आवर्त गति का केन्द्र है।
(a) A सिरे पर वेग शून्य है, त्वरण तथा बल दोनों धनात्मक हैं (दिशा A से O) अत:
उत्तर : 0, +, +
(b) B सिरे पर वेग शून्य हैं, त्वरण तथा बल दोनों ऋणात्मक हैं। (B से O की ओर)। अतः
उत्तर : 0, -, –
(c) AB के मध्य बिन्दु O पर A की ओर जाते हुए वेग (अधिकतम) ऋणात्मक है, त्वरण तथा बल शून्य है। अतः
उत्तर : -, 0, 0
(d) B से 2 cm दूर C बिन्दु पर, A की ओर जाते हुए वेग, त्वरण तथा बल सभी ऋणात्मक है। अतः
उत्तर : -, -, –
(e) A से 3 cm दूर D बिन्दु पर, B की ओर जाते हुए वेग, त्वरण तथा बल सभी धनात्मक हैं। अतः
उत्तर : +, +, +
(f) B से 4 cm दूर बिन्दु E पर, A की ओर जाते हुए, वेग, त्वरण तथा बल सभी ऋणात्मक है। अतः
उत्तर : -, -, –

प्रश्न 6.
किसी कण के त्वरण a और विस्थापन x के बीच निम्नलिखित में से किस संबंध में सरल आवर्त गति होती है?
(a) a = 0.7x
(b) a = – 200 x²
(c) a = – 10x
(d) a = 100 x³
उत्तर :
उपर्युक्त में से केवल सम्बन्ध (c) में a = – 10x, त्वरण विस्थापन के अनुक्रमानुपाती है तथा विस्थापन के विपरीत दिशाएँ हैं, अतः केवल यही सम्बन्ध सरल आवर्त गति को निरूपित करता है।

प्रश्न 7.
सरल आवर्त गति करते किसी कण की गति का वर्णन नीचे दिए गए विस्थापन फलन द्वारा किया जाता है,
x (t) = A cos (ωt + ϕ)
यदि कण की आरंभिक (0) स्थिति 1 cm तथा उसका आरंभिक वेग x cm s^-1 है, तो कण का आयाम तथा आरंभिक कला कोण क्या है ? कण की कोणीय आवृत्ति πs^-1 है। यदि सरल आवर्त गति का वर्णन करने के लिए कोज्या (cos) फलन के स्थान पर हम ज्या (sin) फलन चुनें, x = B sin (ωt+ α), तो उपर्युक्त आरंभिक प्रतिबन्धों में कण का आयाम तथा आरंभिक कला कोण क्या होगा ?
उत्तर ;
दिए गए समीकरण में
x (t) = A cos (ωt + ϕ) ………..(1)
वेग v (t) = \(\frac{dx(t)}{dt}\) = Aω sin (ωt + ϕ) ………(2)
प्रश्नानुसार, t = 0, x = 1 cm तथा v= π cm s^-1 तथा ω = π s^-1
समीकरण (l) में रखने पर, A cos ϕ = 1 ………….(3)
अब समीकरण (2) मैं t = 0 पर v = π cm s^-1, ω = π s^-1 रखने पर,
π = – A π sin ϕ
A sin ϕ = -1 ……….(4)
समी (4) को समी (3) से भाग देने पर,
tan ϕ = -1
ϕ = tan^-1(-1)
= \(\left(2 \pi-\frac{\pi}{4}\right)=\frac{7 \pi}{4}\)
समी (4) से, A = \(\frac{1}{\cos \phi}=\frac{1}{\cos \frac{7 \pi}{4}}\)
√2 = 1.41 cm
अत: आयाम = √2 cm तथा प्रारम्भिक कला = \(\frac{7 \pi}{4}\)
यदि सरल आवर्त गति का समीकरण
x=B sin (ωt + α) हो ………..(5)
तब वेग v = \(\frac{d x}{d t}=\mathrm{B} \omega \cos (\omega t+\alpha)\) ………….(6)
समीकरण (5) में t = 0 पर x = 1 cm रखने पर,
\(1=\mathrm{B} \sin \alpha \text { या } \mathrm{B}=\frac{1}{\sin \alpha}\) ………..(7)
समी (6) में t = 0 पर v = π cm s^-1, ω = π s^-1 रखने पर,
π = B π cos α ⇒ B cos α = 1
⇒ B = \(\frac{1}{cos α}\) ………….(8)
समीकरण (7) व (8) की तुलना करने पर,
\(\frac{1}{\sin \alpha}=\frac{1}{\cos \alpha}\)
या \(\sin \alpha=\cos \alpha \Rightarrow \alpha=\frac{\pi}{4}=45^{\circ}\)
∴ \(\mathrm{B}=\frac{1}{\sin \alpha}=\frac{1}{\sin 45^{\circ}}=\sqrt{2}\) cm
अतः आयाम = √2 cm तथा प्रारम्भिक कला कोण
=\(\frac{\pi}{4}\) = 45°

प्रश्न 8.
किसी कमानीदार तुला का पैमाना 0 से 50 kg तक अंकित है और पैमाने की लम्बाई 20 cm है। इस तुला से लटकाया गया कोई पिण्ड, जब विस्थापित करके मुक्त किया जाता है, 0.65 के आवर्तकाल से दोलन करता है। पिण्ड का भार कितना है?
हल :
दिया है, यदि m = 50 kg तब कमानी की लम्बाई में वृद्धि l = 20 cm
∴ mg = kl सूत्र से,
k = \(\frac{\mathrm{mg}}{0.2}=\frac{50 \times 9.8}{0.2} \mathrm{Nm}^{-1}\) = 2450 Nm^-1
यदि दोलन करने वाले पिण्ड का द्रव्यमान W’ है, तब
\(\mathrm{T}=2 \pi \sqrt{\frac{m^{\prime}}{k}} \Rightarrow m^{\prime}=\frac{k \mathrm{~T}^2}{4 \pi^2}\)
\(m^{\prime} =\frac{2450 \times(6 \cdot 0)^2}{4 \times(3 \cdot 14)^2}=22.36 \mathrm{~kg}\)
∴ पिण्ड का भार m’g = 22.36 98 = 219 N

प्रश्न 9.
1200 Nm कमानी स्थिरांक की कोई कमानी चित्र में दर्शाए अनुसार किसी क्षैतिज मेज से जुड़ी है। कमानी के मुक्त सिरे से 3 kg द्रव्यमान का कोई पिण्ड जुड़ा है। इस पिण्ड को एक ओर 2.0 दूरी तक खींच कर मुक्त किया जाता है,

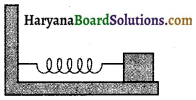
(i) पिण्ड के दोलन की आवृत्ति,
(ii) पिण्ड का अधिकतम त्वरण तथा
(iii) पिण्ड की अधिकतम चाल ज्ञात कीजिए।
हल :
दिया है, बल नियतांक k = 1200 Nm^-1, m = 3 kg
∵ पिण्ड को 2 cm तक खींचकर छोड़ा गया है
अतः पिण्ड के दोलनों का आयाम
a = 2 cm = 0.02m होगा
(i) दोलन आवृत्ति v = \(\frac{1}{2}\)
v = \(\frac{1}{T}=\frac{1}{2 \pi} \sqrt{\frac{k}{m}}\)
v = \(\frac{1}{2 \times 3.14} \sqrt{\frac{1200}{3}}\)
\(\frac{20}{6.28}\) = 3.18 ≈ 3.2 s^-1

(ii) सरल आवर्त गति का कोणीय वेग
ω = 2πv
= 2 π × 3.2
= 20 rad s^-1
अधिकतम त्वरण α = ω²a = (20)² × 0.02
= 8 ms²

(iii) पिण्ड की अधिकतम चाल
u_max = aω = 0.02 × 20 = 0.4 ms^-1

प्रश्न 10.
प्रश्न 9 में मान लीजिए जब कमानी अतानित अवस्था में है, तब पिण्ड की स्थिति है तथा बाएँ से दाएँ की दिशा अक्ष की धनात्मक दिशा है। दोलन करते पिण्ड के विस्थापन x को समय के फलन के रूप में दर्शाइए, जबकि विराम घड़ी को आरम्भ (४0) करते समय पिण्ड,
(a) अपनी माध्य स्थिति,
(b) अधिकतम तानित स्थिति, तथा
(c) अधिकतम सम्पीडन की स्थिति पर है।
सरल आवर्त गति के लिए ये फलन एक-दूसरे से आवृत्ति में, आयाम में अथवा आरंभिक कला में किस रूप में भिन्न हैं?
हल :
(a) माना कण का विस्थापन समीकरण
x = a cos (ωt – ϕ) ……….(1)
t = 0, x = 0 व a = 2.0 cm रखने पर,
0 = 2.0 cos ϕ
⇒ cos ϕ = 0 = cos \(\frac{π}{2}\)
⇒ ϕ = cos \(\frac{π}{2}\)
अतः x = 2 cos (ωt – \(\frac{π}{2}\))
= 2.0 sin ωt
परन्तु प्रश्न 9 से, ω = 20 rad s^-1
अत : x = 2 sin 20 t

(b) अधिकतम तानित स्थिति में t = 0 पर x = 2 cm (अधिकतम)
अत: t = 0, x = 2 cm तथा a = cm समीकरण (1) में रखने पर,
2 = 2 cos ϕ
⇒ cos ϕ =1
cos ϕ =cos θ = 1
⇒ ϕ = θ
अतः अभीष्ट समीकरण x = 2 cos ωt
x = 2 cos 20 t
(ω = 20 rad s^-1)

(c) अधिकतम सम्पीडन की स्थिति में
x = -a = -2.0 cm होगा
∴ t = 0, x = 2 cm तथा a = 2 cm समी. (i) में रखने पर,
– 2 = 2 cos ϕ
⇒ cos ϕ = -1
∴ ϕ = π
अतः अभीष्ट समीकरण x = 2 cos (ωt – π)
x = -2 cos ωt
∴ x = 2 cos 20 t
यहाँ x cm में है। इन फलनों के न तो आयाम में कोई अन्तर है और न ही आवृत्ति में कोई अन्तर है इनकी प्रारंभिक कलाओं में अन्तर है।

प्रश्न 11.
चित्र में दिए गए दो आरेख दो वर्तुल गतियों के तदनुरूपी हैं। प्रत्येक आरेख पर वृत्त की त्रिज्या, परिक्रमण काल, आरंभिक स्थिति और परिक्रमण की दिशा दर्शायी गई है। प्रत्येक प्रकरण में, परिक्रमण करते कण के त्रिज्य सदिश के अक्ष पर प्रक्षेप की तदनुरूपी सरल आवर्त गति ज्ञात कीजिए।

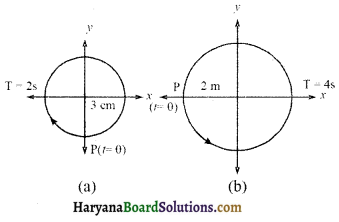
हल :
त्रिज्य सदिश के x- अक्ष पर प्रक्षेप के लिए समीकरण निम्नवत् है-
x = a cos (ωt + ϕ) ………….(1)
(a) यहाँ a → त्रिज्य सदिश का अधिकतम प्रक्षेप 3 cm,
आवर्तकाल T = 2 sec
तथा कोणीय आवृत्ति ω = \(\frac{2 \pi}{\mathrm{T}}=\frac{2 \pi}{2}=\pi \mathrm{rad} \mathrm{s}^{-1}\)
∵ कण दक्षिणावर्त (clockwise) चल रहा है अत: प्रारम्भिक कला
ϕ = +\(\frac{π}{2}\)
∴ समीकरण (1) से,
x = 3 cos(πt + \(\frac{π}{2}\))
या x = sin πt (x cm)

(b) यहाँ a = 2m, T = 4 sec
कोणीय आवृत्ति, ω = \(\frac{2 \pi}{\mathrm{T}}=\frac{2 \pi}{2}=\frac{\pi}{2} \mathrm{rad} \mathrm{s}^{-1}\)
∵ कण वामावर्त (anticlockwise) चल रहा है, 10 पर x प्रक्षेप बायीं ओर किनारे पर है,
ϕ = +π
समी (1) से x = 2 cos (\(\frac{π}{2}\)t – π)
या x = 2 cos \(\frac{π}{2}\)t (x मीटर में है)

प्रश्न 12.
नीचे दी गई प्रत्येक सरल आवर्त गति के लिए तदनुरूपी निर्देश वृत्त का आरेख खींचिए घूर्णी कण की आरंभिक (20) स्थिति, वृत्त की त्रिज्या तथा कोणीय कला दर्शाइए। सुगमता के लिए प्रत्येक प्रकार में परिक्रमण की दिशा वामावर्त लीजिए। (x को cm में तथा को में लीजिए ।)
(a) x = – 2 sin (3t + π /3)
(b) x = cos (π /6 – t)
(c) x = 3 sin (2πt + π /4)
(d) x = 2 cos π t.
हल :
(a)

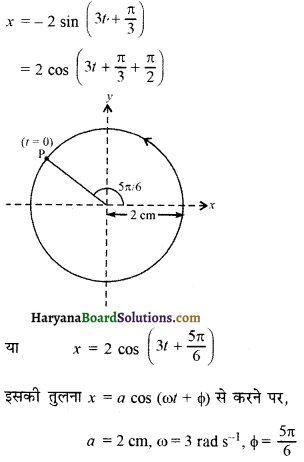
(b)

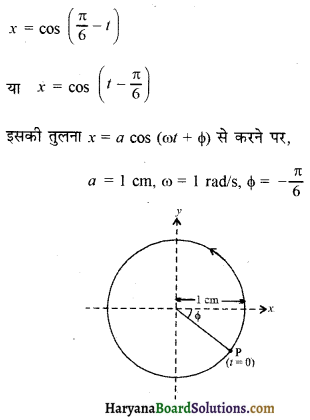
(c)

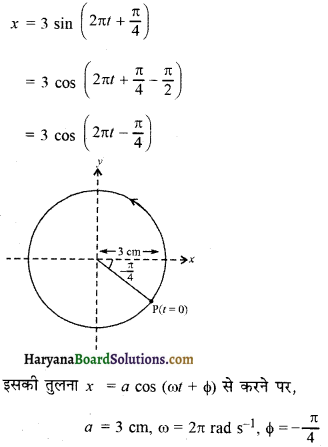
(d) x = 2 cos π t.

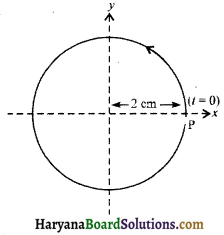
इसकी तुलना समीकरण x = a cos (ωt + ϕ) से करने पर,
a = 2 cm, ω = π rad s^-1 ,ϕ = 0

प्रश्न 13.
चित्र (a) में बल स्थिरांक की किसी कमानी के एक सिरे को किसी दृढ़ आधार से जकड़ा तथा दूसरे मुक्त सिरे से एक द्रव्यमान 1 जुड़ा दर्शाया गया है कमानी के मुक्त सिरे पर बल आरोपित करने से कमानी तन जाती है। चित्र (b) में उसी कमानी के दोनों मुक्त सिरों से द्रव्यमान 18 जुड़ा दर्शाया गया है। कमानी के दोनों सिरों को चित्र में समान बल द्वारा तानित किया गया है।

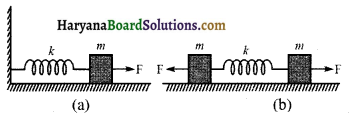
(i) दोनों प्रकरणों में कमानी का अधिकतम विस्तार क्या है?
(ii) यदि (a) तथा (b) के सभी द्रव्यमानों को मुक्त छोड़ दिया जाए, तो प्रत्येक प्रकरण में दोलन का आवर्तकाल ज्ञात कीजिए।
हल :
(i) माना कमानी का अधिकतम विस्तार x_max है, तब चित्र (a)
में, F = k x_max
∴ अधिकतम विस्तार x_max = \(\frac{F}{k}\)
तथा चित्र (b) में कमानी किसी स्थिर वस्तु से सम्बद्ध नहीं है अतः दूसरे पिण्ड पर लगे बल का कार्य केवल कमानी को स्थिर रखना है, अतः विस्तार अभी भी मात्र एक ही बल के कारण होगा।
∴ F = -k x_max से,
अधिकतम विस्थापन x_max = \(\frac{F}{k}\)

(ii) चित्र (a) में –
माना कि पिण्ड को खींचकर छोड़ने पर वापसी की गति करता पिण्ड किसी क्षण साम्यावस्था से दूरी पर है, तब कमानी में प्रत्यानयन बल F = -kx होगा।
यदि पिण्ड का त्वरण a है, तो F = ma
∴ ma = – kx_max
=> a = -(\(\frac{k}{m}\)) x
स्पष्ट है कि पिण्ड की गति सरल आवर्त गति है।
इस समीकरण से, \(\frac{x}{a}=\frac{m}{k}\)
∴ पिण्ड के दोलनों का आवर्तकाल

चित्र (b) में –
जब दोनों द्रव्यमानों को छोड़ दिया जाता है तो द्रव्यमान केन्द्र की प्रमेय से प्रत्येक (समान) द्रव्यमान उसी मात्रा में विपरीत दिशा में विस्थापित हो जाता है, अतः कमानी का कुल विस्तार = 2x
प्रत्येक द्रव्यमान पर प्रत्यानयन बल F = -k.2x
प्रत्येक द्रव्यमान की गति का समीकरण है-
ma = k. (2x)
या a = -(\(\frac{2k}{m}\))x
∴ पिण्ड की गति सरल आवर्त गति है।
\(\frac{x}{a}=\frac{m}{2k}\) (आंकिक रूप से)

प्रश्न 14.
किसी रेलगाड़ी के इंजन के सिलेण्डर हेड में पिस्टन का स्ट्रोक (आयाम का दो गुना) 1.0m का है। यदि पिस्टन 200 rad/min की कोणीय आवृत्ति से सरल आवर्त गति करता है, तो उसकी अधिकतम चाल कितनी है?
हल :
दिया है, स्ट्रोक की लम्बाई = 1.0m
यदि सरल आवर्त गति का आयाम R है, तब
2A = 1.0
या A = 0.5 मीटर
तथा कोणीय आवृत्ति ω = 200 rad/min
= \(\frac{200}{60}\) rad s^-1
∴ ω = \(\frac{10}{3}\) rad s^-1
अतः पिस्टन की अधिकतम चाल
u_max = Aω
= 0.5 × \(\frac{10}{3}\)
= \(\frac{5}{3}\) m/s

प्रश्न 15.
चन्द्रमा के पृष्ठ पर गुरुत्वीय त्वरण 1.7 ms है। यदि किसी सरल लोलक का पृथ्वी के पृष्ठ पर आवर्तकाल 3.55 है, तो उसका चन्द्रमा के पृष्ठ पर आवर्तकाल कितना होगा?
(पृथ्वी के पृष्ठ पर g = 9.8ms^-2)
हल :
सरल लोलक का आवर्तकाल T = 2π \(\sqrt{\frac{l}{g}}\)
l के निश्चित मान के लिए T ∝ \(\frac{1}{\sqrt{g}}\)
यदि चन्द्रमा तथा पृथ्वी के पृष्ठ पर गुरुत्वीय त्वरण g_m तथा g_e हाँ तथा संगत आवर्तकाल क्रमश: T_m व T_e हों, तो

प्रश्न 16.
नीचे दिए गए प्रश्नों के उत्तर दीजिए-
(a) किसी कण की सरल आवर्त गति के आवर्तकाल का मान उस कण के द्रव्यमान तथा बल- स्थिरांक पर निर्भर करता है : T = 2π\(\sqrt{\frac{m}{k}}\) । कोई सरल लोलक सन्निकट सरल आवर्त गति करता है, तब फिर किसी लोलक का आवर्तकाल लोलक के द्रव्यमान पर निर्भर क्यों नहीं करता ?
(b) किसी सरल लोलक की गति छोटे कोण के सभी दोलनों के लिए सन्निकट सरल आवर्त गति होती है। बड़े कोण के दोलनों के लिए एक अधिक गूढ़ विश्लेषण यह दर्शाता है कि T का मान 2π\(\sqrt{\frac{m}{k}}\) से अधिक होता है। इस परिणाम को समझने के लिए किसी गुणात्मक कारण का चिन्तन कीजिए।
(c) कोई व्यक्ति कलाई घड़ी बाँधे किसी मीनार की चोटी से गिरता है। क्या मुक्त रूप से गिरते समय उसकी घड़ी यथार्थ समय बताती है?
(d) गुरुत्व बल के अन्तर्गत मुक्त रूप से गिरते किसी केबिन में लगे सरल लोलक के दोलन की आवृत्ति क्या होती है?
उत्तर :
(a) सरल लोलक के लिए
F = \(-\frac{mg}{l}\) y = -ky
∴ k = \(\frac{mg}{l}\)
सरल लोलक का आवर्तकाल
T = \(2 \pi \sqrt{\frac{m}{k}}=2 \pi \sqrt{\frac{m}{\left(\frac{m g}{\dot{l}}\right)}}=2 \pi \sqrt{\left(\frac{l}{g}\right)}\)
इसलिए किसी लोलक का आवर्तकाल, लोलक के द्रव्यमान पर निर्भर नहीं करता है।

(b) सरल लोलक के लिए प्रत्यानयन बल
F = -mg sin θ
यदि छोटा है, तो sin θ ≈ θ ≈ \(\frac{x}{l}\)
∴ F = -(\(\frac{mg}{l}\))x
या F ∝ -x
अर्थात् यह गति सरल आवर्त होगी तथा आवर्तकाल T = 2π\(\sqrt{\frac{l}{g}}\) होगा। यदि θ छोटा नहीं है तो हम sin θ ≈ θ नहीं ले पाएँगे तब गति सरल आवर्त गति नहीं रहेगी। अतः आवर्तकाल T = 2π\(\sqrt{\frac{l}{g}}\) से बड़ा होगा।
θ के बड़े कोणों के लिए, हम F = -mg sin θ लेंगे, जो कि निश्चय ही mg होता है क्योंकि 6 के बड़े मानों के लिए sin θ < θ होता है। इसलिए बड़े 8 के लिए 8 का प्रभावित मान g sin θ हो जाता है। स्पष्टत: g sine<g.

(c) कलाई घड़ी की कार्यविधि स्प्रिंग क्रिया पर आधारित है, अतः आवर्तकाल T = 2π\(\sqrt{\frac{m}{k}}\) के मान पर निर्भर नहीं करता, अत: मुक्त रूप से गिरते समय कलाई घड़ी यथार्थ समय बताती है।

(d) मुक्त रूप से गिरते केबिन में गुरुत्वीय त्वरण का प्रभावी मान शून्य होता है अतः उसमें लगे सरल लोलक की आवृत्ति
f = \(\frac{1}{\mathrm{~T}}=\frac{1}{2 \pi} \sqrt{\frac{g}{l}}\) शून्य है।

प्रश्न 17.
किसी कार की छत से / लम्बाई का कोई सरल लोलक, जिसके लोलक का द्रव्यमान है, लटकाया गया है। कार R त्रिज्या की वृत्तीय पथ पर एकसमान चाल से गतिमान है। यदि लोलक त्रिज्य दिशा में अपनी साम्यावस्था की स्थिति के इधर-उधर छोटे दोलन करता है तो इसका आवर्तकाल क्या होगा ?
उत्तर :
कार के मोड़ पर मुड़ते समय उसकी गति में \(\frac{v^2}{R}\) अभिकेन्द्रीय त्वरण होता है। इस प्रकार कार एक अजड़त्वीय निर्देश तन्त्र है।

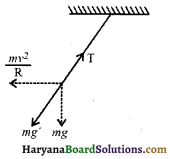
गोलक पर एक छद्म बल \(\frac{mv^2}{R}\) वृत्तीय पथ के बाहर की ओर लगेगा जिसके कारण लोलक ऊर्ध्वाधर रहने के स्थान पर थोड़ा तिरछा हो जाएगा। इस समय गोलक पर दो बल क्रमशः भार mg तथा अपकेन्द्रीय बल \(\frac{mv^2}{R}\)

यदि गोलक के लिए 8 का प्रभावी मान है तो गोलक पर प्रभावी g बल mg होगा जो कि उक्त दो बलों का परिणामी है।

प्रश्न 18.
आधार क्षेत्रफल A तथा ऊँचाई के एक कॉर्क का बेलनाकार टुकड़ा 1 घनत्व के किसी द्रव में तैर रहा है। कॉर्क को थोड़ा नीचे दबाकर स्वतन्त्र छोड़ देते हैं। यह दर्शाइए कि कॉर्क ऊपर-नीचे सरल आवर्त दोलन करता है जिसका आवर्तकाल \(2 \pi \sqrt{h \rho / \rho_1 g}\) है।
यहाँ कॉर्क का घनत्व है (द्रव की श्यानता के कारण अवमन्दन को नगण्य मानिए)।
उत्तर :
माना कॉर्क के टुकड़े का द्रव्यमान है। माना साम्यावस्था मैं इसकी l लम्बाई द्रव में डूबी है। अतः तैरने के सिद्धान्त से, कॉर्क के डूबे भाग द्वारा हटाए गए द्रव का भार कॉर्क के भार के बराबर होगा,
अतः Vρ₁.g = mg [∵ द्रव्यमान आयतन × घनत्व ]
जहाँ V डूबे भाग द्वारा हटाए गए द्रव का आयतन है।
यदि कॉर्क का अनुप्रस्थ क्षेत्रफल A है, तो V = Al
∴ (A) ρ₁.g = mg अथवा Aρ₁.l = m

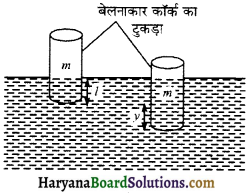
माना किसी क्षण कॉर्क को द्रव में नीचे दबाने पर किसी क्षण साम्यावस्था से नीचे की और विस्थापन है, इस स्थिति में, इसकी लम्बाई के द्वारा हटाए गए द्रव का उत्क्षेप बेलनाकार बर्तन को प्रत्यानयन बल F प्रदान करेगा।
अतः F =- Ay ρ₁g
∴ a = \(\frac{\mathrm{F}}{m}=\frac{-\mathrm{Ay} \rho_1 g}{m}\) ………..(1)
कॉर्क के टुकड़े की ऊँचाई 1⁄2 व घनत्व है अतः
m = Aρh
अतः त्वरण a = \(\frac{-\mathrm{Ay} \rho_1 g}{Aρh}\) = \(-\left(\frac{\rho_1 g}{h \rho}\right) y\) …………..(2)
∵ \(\frac{\rho_1 g}{h \rho}\) एक नियतांक है अतः a ∝ -y
इस प्रकार कॉर्क के टुकड़े का त्वरण a. विस्थापन के अनुक्रमानुपाती एवं विपरीत दिशा में है, अत: कॉर्क के टुकड़े की गति सरल आवर्त गति है।
समीकरण (2) से,

प्रश्न 19.
पारे से भरी किसी नली का एक सिरा किसी चूषण पम्प से जुड़ा है, तथा दूसरा सिरा वायुमण्डल में खुला छोड़ दिया गया है। दोनों स्तम्भों में कुछ दाबान्तर बनाए रखा जाता है। यह बताइए कि जब चूषण पम्प को हटा देते हैं, तब नली में पारे का स्तम्भ सरल आवर्त गति करता है।
उत्तर :
चूषण पम्प के न जुड़ा होने पर समान होंगे। यह साम्यावस्था की स्थिति है वाली नली में पारे का तल ऊपर उठ जाता दोनों नलियों में पारे के तल चूषण पम्प लगाने पर पम्प है तथा पम्प हटाते ही पारा साम्यावस्था को प्राप्त करने का प्रयास करता है।
माना पम्प हटाने पर किसी क्षण दूसरी नली में पारे का तल साम्यावस्था से y दूरी नीचे है तो दूसरी ओर यह y दूरी ऊपर होगा।

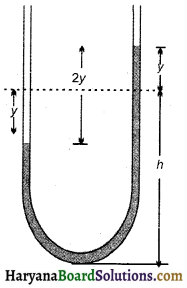
यदि नली की एकांक लम्बाई में भरे पारे का द्रव्यमान in है तो पम्प वाली नली में चढ़े अतिरिक्त पारे के स्तम्भ का भार 2 mg होगा, यह भार ही द्रव को दूसरी ओर धकेलता है।
अतः प्रत्यानयन बल F = -2mgy
ऋण चिह्न बताता है कि यह बल विस्थापन y के विपरीत दिशा में है ।
माना साम्यावस्था में दोनों नलियों में पारे के स्तम्भ की ऊँचाई है, तब नलियों में भरे पारे का कुल द्रव्यमान M = 2mh होगा।
यदि पारे के स्तम्भ का त्वरण हो, तब F = Ma
– 2mgy = 2hma
त्वरण a = -(\(\frac{g}{h}\)) y
अत: a ∝ -y
अतः पारे के स्तम्भ की गति सरल आवर्त गति है।

अतिरिक्त अभ्यास

प्रश्न 20.
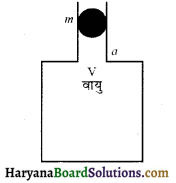
चित्र में दर्शाए अनुसार v आयतन के किसी वायु कक्ष की ग्रीवा (गर्दन) की अनुप्रस्थ काट का क्षेत्रफल A है। इस ग्रीवा में द्रव्यमान की कोई गोली बिना किसी घर्षण के ऊपर-नीचे गति कर सकती है। यह दर्शाइए कि जब गोली को थोड़ा नीचे दबाकर मुक्त छोड़ देते हैं, तो वह सरल आवर्त गति करती है। दाब आयतन विचरण को समतापी मानकर दोलनों के आवर्तकाल का व्यंजक ज्ञात कीजिए।

उत्तर :
जब गोली को थोड़ा नीचे दबाकर छोड़ते हैं तो गोली अपनी साम्यावस्था के ऊपर-नीचे सरल रेखीय दोलन करने लगती है।
माना किसी क्षण गोली का साम्यावस्था से नीचे की ओर विस्थापन x है। माना इस स्थिति में कक्ष में भरी वायु का आयतन V घटकर (V – ∆V) हो जाता है तथा दाब P से बढ़कर (P – ∆P) हो जाता है। समतापी परिवर्तन में, बॉयल के नियम से,
PV = (P+ ∆P) (V- ∆V)
या PV = PV + ∆PV – P∆V – ∆P∆V
∆P∆V अत्यन्त सूक्ष्म राशि है, अतः इसे नगण्य मानने पर,
∆PV = P∆V
∴ P = \(\frac{∆P}{∆V/V}\)
∵ E_T = P = वायु की समतापी प्रत्यास्थता
E_T = \(\frac{∆P}{∆V/V}\) ⇒ ∆P = E_T\(\frac{∆V}{V}\)
या अभिलम्ब प्रतिबल = \(\frac{F}{A}\) = E_T\(\frac{∆V}{V}\)
जहाँ F वायु द्वारा गोली पर आरोपित बल है तथा A ग्रीवा का अनुप्रस्थ क्षेत्रफल है।
ग्रीवा में गोली का नीचे की ओर विस्थापन है अतः वायु x आयतन में कमी ∆V = Ax होगी।
अतः \(\frac{F}{A}\) = E_T\(\frac{∆V}{V}\)
या F = (\(\frac{E_T A^2}{V}\)) x
गोली पर वायु द्वारा लगाया गया यह बल बाहर की ओर (साम्यावस्था की ओर) लगता है, अतः यह बल गोली में विस्थापन के विपरीत है अर्थात् यह एक प्रत्यानयन बल है।
यदि गोली का त्वरण a है तो F = ma से,
ma = (\(\frac{E_T A^2}{V}\)) x
a = (\(\frac{E_T A^2}{Vm}\)) x
ऋण चिह्न प्रदर्शित करता है कि त्वरण विस्थापन के विपरीत है।
अतः त्वरण ∝ विस्थापन (-x)
अतः गोली की गति सरल आवर्त गति है।

प्रश्न 21.
आप किसी 3000 kg द्रव्यमान के स्वचालित वाहन पर सवार हैं। यह मानिए कि आप इस वाहन की निलम्बन प्रणाली के दोलनी अभिलक्षणों का परीक्षण कर रहे हैं जब समस्त वाहन इस पर रखा जाता है, तब निलम्बन 15 cm अतानित होता है। साथ ही एक पूर्ण दोलन की अवधि में दोलन के आयाम में 50% घटोत्तरी हो जाती है। निम्नलिखित के मानों का आकलन कीजिए-
(a) कमानी स्थिरांक, तथा
(b) कमानी तथा एक पहिए के प्रघात अवशोषक तन्त्र के लिए अवमन्दन स्थिरांक 61
यह मानिए कि प्रत्येक पहिया 750 kg द्रव्यमान वहन करता है।
हल :
चारों कमानियों द्वारा साधित कुल भार = Mg
अतः l कमानी द्वारा साधित भार = \(\frac{Mg}{4}\)
यदि स्प्रिंग नियतांक तथा झुकाव x हो, तो
\(\frac{Mg}{4}\) = kx
तब k = \(\frac{Mg}{4x}\) = \(\frac{3000 × 10}{4 × 0.15}\)
= 5 × 10⁴ Nm^-1

(b) माना प्रारम्भ में दोलनों का आयाम A है, तब समय बाद अवमन्दन के कारण नया आयाम A_t = A₀e^-bt/2m होगा।
प्रश्नानुसार, एक दोलन में t = T तथा A_t = \(\frac{A_0}{2}\)

प्रश्न 22.
यह दर्शाइए कि रैखिक सरल आवर्त गति करते किसी कण के लिए दोलन की किसी अवधि की औसत गतिज ऊर्जा उसी अवधि की औसत स्थितिज ऊर्जा के समान होती है।
उत्तर :
माना द्रव्यमान का कोई कण कोणीय आवृत्ति से सरल आवर्त गति कर रहा है, जिसका आयाम A हैं।
माना गति अधिकतम विस्थापन की स्थिति से प्रारम्भ होती है तब t समय में कण का विस्थापन
x= A cos ωt
इस स्थिति में कण की गतिज ऊर्जा K = \(\frac{1}{2}\) mu²

प्रश्न 23.
10 kg द्रव्यमान की कोई वृत्तीय चक्रिका अपने केन्द्र से जुड़े किसी तार से लटकी है। चक्रिका को घूर्णन देकर तार में ऐंठन उत्पन्न करके मुक्त कर दिया जाता है। मरोड़ी दोलन का आवर्तकाल 1.5s है। चक्रिका की त्रिज्या 15 cm है। तार का मरोड़ी कमानी नियतांक ज्ञात कीजिए। मरोड़ी कमानी नियतांक α सम्बन्ध J = -αθ द्वारा परिभाषित किया जाता है, यहाँ प्रत्यानयन बल युग्म है तथा θ ऐंठन कोण है।
उत्तर :
चक्रिका का अपने केन्द्र से गुजरने वाले तथा तल के लम्बवत् अक्ष के परितः जड़त्व आघूर्ण

प्रश्न 24.
कोई वस्तु 5 cm के आयाम तथा 0.2 सेकण्ड की आवृत्ति से सरल आवर्त गति करती है। वस्तु का त्वरण तथा वेग ज्ञात कीजिए जब कि वस्तु का विस्थापन (a) 5 cm (b) 3 cm (c) 0cm हो।
उत्तर :
दिया है: A = 5 cm = 0.05m. T = 0.25
∴ ω = \($\frac{2 \pi}{T}=\frac{2 \pi}{0.2}$\) = 10 π rad s^-1

(a) जब विस्थापन = 5 cm = a अर्थात् अधिकतम विस्थापन है, तब
त्वरण
a = -ω²x = -(10π)² × 0.05m = 5π² ms^-2
तथा इस क्षण वेग u = ω\(\sqrt{R^2 – x^2}\) = 0

(b) जब विस्थापन x = 3 cm = 0.03m, तब
त्वरण a = -ω²x = -(10π)² × 0.03 = -3π² ms^-2
तथा वेग u = ω\(\sqrt{R^2 – x^2}\)
∴ u = 10π \(\sqrt{(0.05)^2 – (0.03)^2}\)
= 10π × 0.04 = 0.4π ms^-1

(c) जब विस्थापन x = 0 है, तो
त्वरण a = -ω²x = 0
तथा वेग u = ω\(\sqrt{R^2 – x^2}\)
= 10π \(\sqrt{(0.05)^2 – 0^2}\)
∴ u = 0.5π ms^-1

प्रश्न 25.
किसी कमानी से लटका एक पिण्ड एक क्षैतिज तल में कोणीय वेग से घर्षण या अवमंदन रहित दोलन कर सकता है। इसे जब दूरी तक खींचते हैं और खींचकर छोड़ देते हैं तो यह सन्तुलन केन्द्र से समय t = 0 पर, v₀ वेग से गुजरता है। प्राचल ω, x₀ तथा v₀ के पदों में परिणामी दोलन का आयाम ज्ञात करिए।
(संकेत: समीकरण x = a cos (ωt + θ) से प्रारम्भ कीजिए। ध्यान रहे कि प्रारंभिक वेग ऋणात्मक है।)
उत्तर :
माना सरल आवर्त गति का समीकरण
x = R cos (ωt + θ) …(1)
तब वेग u = \(\frac{d x}{d t}\)
⇒ u = \(-\omega \mathrm{R} \sin (\omega t+\theta)\) ………….(2)
∴ समय t = 0 पर x = x⁰ अतः समी (1) से,
x⁰ = R cos
तथा t = 0 पर v = v⁰ अतः समी (2) से,
\(\frac{-v_0}{\omega}=\mathrm{R} \sin \theta\)
समी (3) व (4) के वर्गों का योग करने पर,
\(x_0^2+\frac{v_0^2}{\omega^2}=\mathrm{R}^2\left(\cos ^2 \theta+\sin ^2 \theta\right)=\mathrm{R}^2\)
अतः आयाम \(\mathrm{R}=\sqrt{x_0^2+\frac{v_0^2}{\theta^2}}\)