HBSE 11th Class Physics Important Questions Chapter 7 कणों के निकाय तथा घूर्णी गति

Haryana State Board HBSE 11th Class Physics Important Questions Chapter 7 कणों के निकाय तथा घूर्णी गति Important Questions and Answers.

Haryana Board 11th Class Physics Important Questions Chapter 7 कणों के निकाय तथा घूर्णी गति

बहुविकल्पीय प्रश्न (Multiple Choice Questions)

प्रश्न 1.
द्रव्यमान केन्द्र की गति का मुख्य कारण है-
(a) पारस्परिक बल
(b) नाभिकीय बल
(c) बाह्य बल
(d) इनमें से कोई नहीं
उत्तर:
(c) बाह्य बल

प्रश्न 2.
एक तार जिकसी लम्बाई L तथा द्रव्यमान M है, को वृत्ताकार छल्ले में मोड़ा जाता है। इसका जड़त्व आघूर्ण केन्द्र से गुजरने वाली तथा तल के लम्बवत् अक्ष के परित: है-
(a) \(\frac{ML²}{8π²}\)
(b) 8π² ML²
(c) \(\frac{ML²}{4π²}\)
(d) π² ML²
उत्तर:
(c) \(\frac{ML²}{4π²}\)

प्रश्न 3.
द्रव्यमान केन्द्र वह बिन्दु है जिसके सापेक्ष किसी पिण्ड के लिए निम्न राशि का मान शून्य होता है-
(a) कोणीय आघूर्ण
(b) बलाघूर्ण
(c) द्रव्यमान आघूर्ण
(d) भार
उत्तर:
(c) द्रव्यमान आघूर्ण

प्रश्न 4.
द्रव्यमान केन्द्र हमेशा वह बिन्दु है-
(a) जो पिण्ड का ज्यामितीय केन्द्र है
(b) जहाँ से सभी कणों की दूरी समान है।
(c) जहाँ पिण्ड का सम्पूर्ण द्रव्यमान केन्द्रित माना जा सके
(d) जो निर्देश तन्त्र का मूल बिन्दु है।
उत्तर:
(c) जहाँ पिण्ड का सम्पूर्ण द्रव्यमान केन्द्रित माना जा सके

प्रश्न 5.
यदि HCI अणु में H की द्रव्यमान केन्द्र से दूरी हो तो CI35 की दूरी होगी-
(a) 35x
(b) x
(c) \(\frac{36x}{35}\)
(d) \(\frac{x}{35}\)
उत्तर:
(d) \(\frac{x}{35}\)

प्रश्न 6.
बाह्य बल की अनुपस्थिति में द्रव्यमान केन्द्र से सम्बद्ध राशि नियत रहती है-
(a) वेग
(b) त्वरण
(c) स्थिति
(d) इनमें से कोई नहीं
उत्तर:
(a) वेग

प्रश्न 7.
एक घूमती हुई चकती की त्रिज्या यकायक आधी कर दी जाये परन्तु द्रव्यमान स्थिर रहे तो उसका कोणीय वेग हो जायेगा-
(a) दोगुना
(b) आधा
(c) चार गुना
(d) अपरिवर्तित
उत्तर:
(c) चार गुना

प्रश्न 8.
कोणीय संवेग का 2 घटक रैखिक संवेग के घटकों रूप में निम्न है-
(a) L_z =xp_y – yP_x
(b) L_z = yp_y – xP_x
(c) L_z = yP_x – xP_y
(d) L_z =xp_x – yp_z
उत्तर:
(a) L_z =xp_y – yP_x

प्रश्न 9.
ग्रहों की परिभ्रमण गति में नियत रहता है-
(a) गुरुत्वीय बल
(b) अभिकेन्द्र बल
(c) कोणीय संवेग
(d) कोणीय त्वरण
उत्तर:
(c) कोणीय संवेग

प्रश्न 10.
घूर्णन गति में किया गया कार्य होता है-
(a) \(\vec{\tau} \cdot \vec{\alpha}\)
(b) \(\vec{\tau} \cdot \vec{\theta}\)
(c) \(\vec{\tau} \cdot \vec{\omega}\)
(d) \(\vec{L} \cdot \vec{\theta}\)
उत्तर:
(b) \(\vec{\tau} \cdot \vec{\theta}\)

प्रश्न 11.
केन्द्रीय बल क्षेत्र में नियत रहता है-
(a) रैखिक संवेग
(b) कोणीय संवेग
(c) गतिज ऊर्जा
(d) स्थितिज ऊर्जा
उत्तर:
(b) कोणीय संवेग

प्रश्न 12.
दो बिन्दु द्रव्यमान क्रमश: m₁,m₂ अपने परस्पर गुरुत्वीय आकर्षण बल के प्रभाव में गति करते हैं। यदि कोई अन्य बल नहीं लग रहा हो तो संरक्षित रहेगा-
(a) केवल रैखिक संवेग
(b) केवल कोणीय संवेग
(c) दोनों रैखिक एवं कोणीय संवेग
(d) उपर्युक्त में से कोई नहीं।
उत्तर:
(c) दोनों रैखिक एवं कोणीय संवेग

प्रश्न 13.
यदि दो द्रव्यमान m₁ तथा m₂ की द्रव्यमान केन्द्र से दूरी क्रमशः r₁ तथा r₂ हो तो का मान होगा-
(a) m₁ / m₂
(b) (m₁ / m₂)²
(c) m₂ / m₁
(d) (m₂ / m₁)²
उत्तर:
(c) m₂ / m₁

प्रश्न 14.
दो कण जिनके द्रव्यमान 10 तथा 30 किलोग्राम हैं और इनके स्थिति सदिश क्रमश: \((\hat{i}+\hat{j}+\hat{k})\) तथा \((-\hat{i}-\hat{j}-\hat{k})\) है तो निकाय का द्रव्यमान केन्द्र होगा-
(a) \(– \frac{(\hat{i}+\hat{j}+\hat{k})}{2}\)
(b) \(\frac{(\hat{i}+\hat{j}+\hat{k})}{2}\)
(c) \(– \frac{(\hat{i}+\hat{j}+\hat{k})}{4}\)
(d) \(\frac{(\hat{i}+\hat{j}+\hat{k})}{4}\)
उत्तर:
(a) \(– \frac{(\hat{i}+\hat{j}+\hat{k})}{2}\)

प्रश्न 15.
एक समान वर्गाकार प्लेट ABCD के दो किनारों B व C पर एक-एक किग्रा के पिण्ड रखे हैं। एक तीसरे 2 किग्रा द्रव्यमान के पिण्ड को प्लेट पर कहाँ रखें कि प्लेट का द्रव्यमान केन्द्र वर्ग के केन्द्र 0 पर ही रहे?

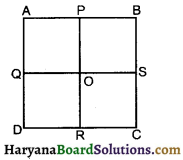
(a) P
(b) 2
(c) R
(d) s
उत्तर:
(b) 2

प्रश्न 16.
जूल सेकण्ड मात्रक है-
(a) शक्ति का
(b) कोणीय संवेग का
(c) बल आघूर्ण का
(d) रैखिक संवेग का
उत्तर:
(b) कोणीय संवेग का

प्रश्न 17.
डिस्क की स्वयं की अक्ष के प्रति घूर्णन त्रिज्या है-
(a) R / 2
(b) R / √2
(c) R
(d) R√2
उत्तर:
(b) R / √2

प्रश्न 18.
लम्बाई तथा द्रव्यमान के एक पतले तार को अर्धवृतत के रूप में मोड़ा गया है। उसके स्वतन्त्र किनारों को मिलाने वाली रेखा के सापेक्ष जड़त्व आघूर्ण होगा-
(a) \(\frac{m l^2}{2 \pi^2}\)
(b) \(\frac{m l^2}{2}\)
(c) \(\frac{m l^2}{\pi^2}\)
(d) ml²
उत्तर:
(a) \(\frac{m l^2}{2 \pi^2}\)

प्रश्न 19.
एक छल्ला किसी नत तल पर प्रथम बार बिना लुढ़के खिसकता है तथा दूसरी बार बिना खिसके लुढ़कता है तो दोनों परिस्थितियों में उत्पन्न त्वण का अनुपात है-
(a) 1 : 1
(b) 2 : 1
(c) 1 : 2
(d) 4 : 1
उत्तर:
(b) 2 : 1

प्रश्न 20.
एक पतला खोखला बेलन जिसका व्यास 0.3 मीटर है, 2 मीटर ऊँचे नत तल पर विरामावस्था से लुढ़कता है पैदे पर पहुँचने पर उसका रेखीय वेग होगा-
(a) 2g
(b) √2g
(c) g/2
(d) \(\frac{3g}{10}\)
उत्तर:
(b) √2g

प्रश्न 21.
बाह्य बल की अनुपस्थिति में द्रव्यमान केन्द्र का वेग-
(a) शून्य है
(b) नियत रहेगा
(c) बढ़ेगा
(d) छटेगा।
उत्तर:
(b) नियत रहेगा

प्रश्न 22.
किसी पदार्थ के गोले के लिए उसके व्यास के जड़त्व आघूर्ण / का मान उसकी त्रिज्या R की किस घात के समानुपाती है?
(a) R²
(b) R²
(c) R⁴
(d) R²
उत्तर:
(b) R²

प्रश्न 23.
किसी ठोस गोले का व्यास के सापेक्ष जड़त्व आघूर्ण का मान I है तो गोले का उसकी स्पर्श रेखा के सापेक्ष जड़त्व आघूर्ण होगा-
(a) \(\frac{7}{2}\)I
(b) \(\frac{5}{2}\)I
(c) \(\frac{2}{5}\)I
(d) \(\frac{1}{2}\)I
उत्तर:
(a) \(\frac{7}{2}\)I

प्रश्न 24.
1 मीटर व 5 मीटर त्रिज्या की दो वलय एक नत तल पर एक साथ बिना फिसले प्रारम्भ करते हैं। पृथ्वी तल पर कौन-सी वलय पहले पहुंचेगी?
(a) बड़ी वलय
(b) छोटी वलय
(c) दोनों एक साथ
(d) कुछ नहीं कहा जा सकता।
उत्तर:
(c) दोनों एक साथ

अति लघु उत्तरीय प्रश्न (Very Short Answer Questions)

प्रश्न 1.
दृढ़ पिण्ड की साम्यावस्था के लिए प्रतिबन्ध लिखिए।
उत्तर:
ΣF = 0 तथा Στ = 0

प्रश्न 2.
द्विपरमाणुक अणु के जड़त्व आघूर्ण के लिए व्यंजक लिखिए।
उत्तर:
I = \(\frac{m_1m_2}{m_1+m_2}\)r² जहाँ दोनों परमाणुओं के मध्य दूरी।

प्रश्न 3.
क्या किसी पिण्ड की घूर्णन त्रिज्या अचर राशि है?
उत्तर:
नहीं; घूर्णन अक्ष बदलने पर जड़त्व आघूर्ण एवं घूर्णन त्रिज्या दोनों के मान बदल जाते हैं।

प्रश्न 4.
धनात्मक आघूर्ण व ऋणात्मक आघूर्ण से क्या अभिप्राय है?
उत्तर:
यदि बल की प्रवृत्ति पिण्ड को वामावर्त (Anticlockwise) दिशा में घुमाने की है तो उसका बल आघूर्ण धनात्मक आघूर्ण कहलाता है। इसके विपरीत पिण्ड को दक्षिणावर्त (clockwise) दिशा में घुमाने की प्रवृत्ति रखने वाले बल का आघूर्ण ऋणात्मक आघूर्ण कहलाता है।

प्रश्न 5.
किसी गोले को पिघलाकर उसे चकती का स्वरूप प्रदान कर दिया जाता है तो उसके जड़त्व आघूर्ण पर क्या प्रभाव पड़ेगा?
उत्तर:
चकती का जड़त्व आघूर्ण गोले के जड़त्व आघूर्ण से अधिक होगा।

प्रश्न 6.
क्या द्रव्यमान केन्द्र व गुरुत्व केन्द्र सम्पाती होते हैं?
उत्तर:
समरूप द्रव्यमान घनत्व वाली वस्तुओं में उक्त दोनों केन्द्र सम्पाती होते हैं।

प्रश्न 7.
पेंचकस का हत्या चौड़ा क्यों बनाया जाता है?
उत्तर:
पेंचकस के हत्थे पर अंगूठे एवं उँगलियों की सहायता से बलयुग्म लगाकर उसे घूर्णन गति प्रदान की जाती है और बलयुग्म का आघूर्ण τ = F × r
अतः r के मान को बढ़ाने के लिए पेंचकस का हत्था चौड़ा लिया जाता है ताकि कम बल (F) लगाने पर भी अधिक बलयुग्म का आघूर्ण (τ) प्राप्त हो सके और पेंच को आसानी से खोला या कसा जा सके।

प्रश्न 8.
किसी दृढ़ पिण्ड के समस्त कणों के कोणीय वेग एक समान होते हैं या भिन्न-भिन्न?
उत्तर:
दृढ़ पिण्ड के सभी कणों के कोणीय वेग समान होते हैं।

प्रश्न 9.
समान द्रव्यमान त्रिज्या तथा आकृति की खोखली तथा ठोस वस्तुओं में किसका जड़त्व अधिक होगा?
उत्तर:
खोखली वस्तुओं का जड़त्व अधिक होता है ।

प्रश्न 10.
क्या घर्षण रहित नत तल पर कोई वस्तु लोटनी गति कर सकती है?
उत्तर:
नहीं; वह फिसल जायेगी।

प्रश्न 11.
किसी पिण्ड के कोणीय संवेग J, जड़त्व आघूर्ण एवं कोणीय वेग 00 में क्या सम्बन्ध होता है?
उत्तर:
J = I.ω ।

प्रश्न 12.
किसी पिण्ड का जड़त्व आघूर्ण किन कारकों पर निर्भर करता है?
उत्तर:
(i) घूर्णन अक्ष की स्थिति पर
(ii) घूर्णन अक्ष के सापेक्ष पिण्ड के द्रव्यमान वितरण पर ।

प्रश्न 13.
क्या यह आवश्यक है कि द्रव्यमान केन्द्र पर द्रव्यमान उपस्थित हो?
उत्तर:
नहीं। उदाहरण के लिए वलय का द्रव्यमान केन्द्र उसके केन्द्र पर होता है जहाँ द्रव्यमान नहीं होता है।

प्रश्न 14.
क्या द्रव्यमान केन्द्र एक वास्तविकता है?
उत्तर:
नहीं, यह केवल एक गणितीय अवधारणा है।

प्रश्न 15.
क्या रेखीय गति में वस्तु में कोणीय संवेग हो सकता है?
उत्तर:
हाँ।

प्रश्न 16.
यदि पृथ्वी की त्रिज्या कम हो जाये तो दिन की लम्बाई में क्या प्रभाव होगा?
उत्तर:
पृथ्वी की त्रिज्या कम होने पर जड़त्व आघूर्ण (I) कम हो जायेगा। फलस्वरूप कोणीय संवेग संरक्षण के सिद्धान्त के अनुसार (I.ω = नियतांक) उसका कोणीय वेग ω का मान बढ़ेगा और ω का मान बढ़ने से (ω = \(\frac{2π}{T}\)) आवर्तकाल T का मान कम होगा। परिणामस्वरूप दिन की लम्बाई घट जायेगी।

प्रश्न 17.
किस अक्ष के सापेक्ष जड़त्व आघूर्ण न्यूनतम होता है?
उत्तर:
द्रव्यमान केन्द्र से गुजरने वाली अक्ष के सापेक्ष जड़त्व आघूर्ण न्यूनतम होता है।

प्रश्न 18.
एक व्यक्ति घूर्णन कर रही मेज पर अपनी भुजाएं फैलाये हुए बैठा है। यदि वह भुजाएं सिकोड़ ले तो क्या होगा?
उत्तर:
भुजाएं सिकोड़ने पर उसका जड़त्व आघूर्ण कम होने से उसका कोणीय वेग बढ़ जायेगा।

प्रश्न 19.
एक पतली छड़ का द्रव्यमान M एवं इसकी लम्बाई L है तो छड़ के सिरे से छड़ के लम्बवत् गुजरने वाली अक्ष के सापेक्ष उसका जड़त्व आघूर्ण क्या होगा?
उत्तर:
I = \(\frac{ML^{2}}{3}\)

प्रश्न 20.
गतिशील वाहनों के पहिए बीच में खोखले एवं परिधि पर मोटे बनाये जाते हैं क्यों?
उत्तर:
ऐसा करने से पहिए का जड़त्व आघूर्ण बढ़ जाता है और वह गति पालक चक्र (Flywheel) की भाँति कार्य करने लगता है। फलस्वरूप इंजन बन्द कर देने पर भी वाहन अचानक नहीं रुकता है।

प्रश्न 21.
क्या पिण्ड के जड़त्व आघूर्ण का मान उसके कोणीय वेग पर निर्भर करता है?
उत्तर:
नहीं।

प्रश्न 22.
M द्रव्यमान तथा / लम्बाई के एक खोखले बेलन की आंतरिक तथा बाह्य त्रिज्याएं क्रमश: R1 व R2 हैं। इसके केन्द्र से होकर जाने वाली तथा बेलन के लम्बवत् अक्ष के सापेक्ष जड़त्व आघूर्ण कितना होता है?
उत्तर:
\(I=M\left[\frac{l^2}{12}+\frac{R_1^2+R_2^2}{4}\right]\)

प्रश्न 23.
कोणीय संवेग में परिवर्तन की दर किस भौतिक राशि को प्रदर्शित करती है?
उत्तर:
बल आघूर्ण को = \(\left[\tau=\frac{\Delta J}{\Delta t}\right]\)

प्रश्न 24.
बलयुग्म किस प्रकार की गति उत्पन्न करता है?
उत्तर:
केवल घूर्णन गति उत्पन्न करता है।

प्रश्न 25.
साइकिल के पहिए तानेंदार (spokes) क्यों बनाये जाते हैं?
उत्तर:
जड़त्व आघूर्ण बढ़ाने के लिए साइकिल के पहिए तानेदार बनाये जाते हैं।

प्रश्न 26.
जब कोई वस्तु क्षैतिज से θ कोण पर झुके तल पर फिसलती है तो उसका त्वरण क्या होता है?
उत्तर:
g sin θ

प्रश्न 27.
समान कोणीय वेग से घूर्णन कर रहे एक वृत्ताकार प्लेटफार्म के किनारे के निकट एक व्यक्ति बैठा है। यदि वह अचानक प्लेटफार्म के केन्द्र की ओर चलना प्रारम्भ करता है तो प्लेटफार्म के कोणीय वेग पर क्या प्रभाव पड़ेगा?
उत्तर:
केन्द्र की ओर व्यक्ति के चलने पर कुल जड़त्व आघूर्ण कम होगा फलस्वरूप कोणीय संरक्षण के सिद्धान्त से कोणीय वेग बढ़ जायेगा।

प्रश्न 28.
विलगित निकाय क्या होता है?
उत्तर:
वह निकाय जिस पर कोई बाह्य बल न लग रहा हो, विलगित निकाय कहलाता है।

प्रश्न 29.
यदि दो विभिन्न द्रव्यमान के तरबूज एक पुल से एक साथ ऊर्ध्वाधर नीचे की ओर गिराये जायें तो तरबूजों के द्रव्यमान केन्द्र का त्वरण क्या होगा?
उत्तर:
दोनों तरबूजों के द्रव्यमान केन्द्र का त्वरण g होगा।

प्रश्न 30.
एक त्रिभुजाकार पटल के द्रव्यमान केन्द्र की स्थिति क्या होगी?
उत्तर:
त्रिभुजाकार पटल की तीनों मध्यिकाओं का कटान बिन्दु ही पटल का द्रव्यमान केन्द्र होगा।

प्रश्न 31.
एक आयताकार पटल का द्रव्यमान M, लम्बाई l व चौड़ाई b है तो उसके तल के लम्बवत् तथा उसके द्रव्यमान केन्द्र से गुजरने वाली अक्ष के परित: उसका जड़त्व लिखिए ।
उत्तर:
\(I=M\left[\frac{l^2+b^2}{12}\right]\)

प्रश्न 32.
ठोस गोले का उसके किसी व्यास के सापेक्ष जड़त्व आघूर्ण क्या होगा?
उत्तर:
I = \(\frac{2}{5}\) MR²,
जहाँ M = गोले का द्रव्यमान
R = गोले की त्रिज्या

प्रश्न 33.
किसी वलय का उसके व्यास के सापेक्ष जड़त्व आपूर्ण क्या होगा?
उत्तर:
I = \(\frac{1}{2}\) MR²
जहाँ M= वलय का जड़त्व आघूर्ण;
R = वलय की त्रिज्या

प्रश्न 34.
रेखीय गति में बल = द्रव्यमान × त्वरण होता है। इससे संगत घूर्णन गति का व्यंजक लिखिये।
उत्तर:
बल आघूर्ण = जड़त्व आघूर्ण × कोणीय त्वरण

प्रश्न 35.
पेन का ढक्कन दो अंगुलियों की सहायता से आसानी से खुल जाता है परन्तु एक अंगुली से नहीं, क्यों?
उत्तर:
पेन का ढक्कन खोलने के लिए बलयुग्म की आवश्यकता होती है जो दो अंगुलियों द्वारा ही सम्भव हो पाता है।

लघु उत्तरीय प्रश्न (Short Answer Questions)

प्रश्न 1.
धातु की दो वृत्ताकार चकतियाँ A व B के द्रव्यमान व मोटाई समान हैं। 4 का घनत्व B के घनत्व का दो गुना है। चकती व B का इनके अक्षों के प्रति जड़त्व आघूर्णो का अनुपात क्या होगा ?
उत्तर:
चकती का जड़त्व आघूर्ण I = \(\frac{1}{2}\) Mr²

प्रश्न 2.
जब ठोस गोला किसी नत तल पर लुढ़कता है तो घूर्णन ऊर्जा कुल ऊर्जा का कितना प्रतिशत होगी?
उत्तर:

प्रश्न 3.
तीन वलय जिनमें प्रत्येक का द्रव्यमान M एवं त्रिज्या है, त्रिभुजाकार आकृति में व्यवस्थित है। इस निकाय का YY” अक्ष के सापेक्ष जड़त्व आघूर्ण ज्ञात कीजिए।

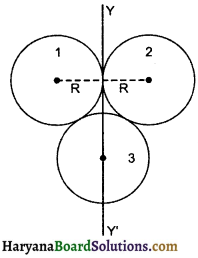
उत्तर:
वलय का उसकी अक्ष के सापेक्ष जड़त्व आघूर्ण = MR²
वलय का व्यास के सापेक्ष जड़त्व आघूर्ण
I_d = \(\frac{1}{2}\) MR²
अतः व्यास के समान्तर स्पर्शरेखीय अक्ष के परितः जड़त्व आघूर्ण
I_T = \(\frac{3}{2}\) MR²
अतः पूरे निकाय का YY’ अक्ष के सापेक्ष जड़त्व आघूर्ण
I_YY’ = I₁ + I₂ + I₃
= \(\frac{3}{2}\) MR² + \(\frac{3}{2}\) MR² + \(\frac{1}{2}\) MR²
या I_YY’ = \(\frac{7}{2}\) MR²

प्रश्न 4.
एक सीढ़ी दीवार के सहारे तिरछी लगी है। यदि वह फिसले तो उसका तात्क्षणिक घूर्णन केन्द्र कहाँ होगा?
उत्तर:
ऊपरी सिरे के स्पर्श बिन्दु पर दीवार के लम्बवत् तथा नीचे के स्पर्श बिन्दु पर जमीन के लम्ब के कटान बिन्दु पर होगा।

प्रश्न 5.
द्रव्यमान m का एक कण v वेग से X-दिशा में गतिशील है। जब वह बिन्दु (x,y,z) पर स्थित होता है तो उस पर मूल बिन्दु के परितः कण के कोणीय संवेग के घटक ज्ञात कीजिए।
उत्तर:
कण X- अक्ष के अनुदिश गतिशील है अतः उसका रेखीय संवेग

प्रश्न 6.
समान पदार्थ के गोलों के लिए जड़त्व आघूर्ण तथा त्रिज्या का क्या सम्बन्ध है?
उत्तर:
ठोस गोले का जड़त्व आघूर्ण
I = \(\frac{2}{5}\) MR²
∵ M = \(\frac{4}{3}\) πR³ . ρ
∴ I = \(\frac{2}{5}\) × \(\frac{4}{3}\) πR³ . ρ . R²
= \(\frac{8}{15}\) πρR⁵
∴ I ∝ R⁵ (क्योंकि \(\frac{8πρ}{15}\) = नियतांक)

प्रश्न 7.
एक वलय का उसकी अक्ष के सापेक्ष जड़त्व आघूर्ण मात्रक है। वलय का उसके तल में स्थित परितः अक्ष (अर्थात् वलय के तल में स्पशरिखीय अक्ष) के सापेक्ष जड़त्व आघूर्ण ज्ञात कीजिए।
उत्तर;
दिया है MR² = 8 मात्रक
∴ वलय के तल में स्थित स्पर्शरेखीय अक्ष के सापेक्ष वलय का जड़त्व आघूर्ण समान्तर अक्षों की प्रमेव से-
I = I_CM + MR² = I_d + MR² = \(\frac{1}{2}\)MR² + MR²
I = \(\frac{3}{2}\) MR²
= \(\frac{3}{2}\) × 8 = 12 मात्रक
या I = 12 मात्रक

प्रश्न 8.
समान द्रव्यमान के ठोस गोले भिन्न-भिन्न पदार्थों के बनाये जाते हैं। गोलों के जड़त्व आघूर्ण का उनके घनत्व d के साथ क्या सम्बन्ध होगा?
उत्तर;
ठोस गोले का जड़त्व आघूर्ण I = \(\frac{1}{2}\)MR²

प्रश्न 9.
यदि एक ठोस गोला जिसका द्रव्यमान M है, ऊर्ध्वाधर दिशा में एक नत तल पर से hm नीचे लुढ़ककर आ जाता है। गोले का वेग ज्ञात कीजिए।
उत्तर:
नत तल पर लुढ़कने पर प्राप्त वेग,

प्रश्न 10.
हेलिकॉप्टर में दो नोदक (Propellers) क्यों काम में लाये जाते हैं?
उत्तर:
हेलिकॉप्टर में केवल एक नोदक लगाने पर कोणीय संवेग संरक्षण के नियमानुसार हेलिकॉप्टर स्वयं नोदक के घूर्णन के विपरीत दिशा में घूम जायेगा। फलस्वरूप वह ऊपर नहीं उठ पायेगा। इस समस्या के निदान के लिए दो नोदक प्रयोग में लाये जाते हैं।

प्रश्न 11.
मोम की एक चकती को पिघलाकर ठोस गोले के रूप में डाल दिया जाता है। केन्द्र से गुजरने वाली उभयनिष्ठ अक्ष के प्रति जड़त्व आघूर्ण पर क्या प्रभाव पड़ेगा?
उत्तर:
चकती को पिघलाकर गोले के रूप में डाल देने उसकी त्रिज्या (R) का मान काफी कम हो जायेगा अतः गोले का जड़त्व आघूर्ण (\(\frac{2}{5}\)MR₁²) चकती के जड़त्व आघूर्ण (\(\frac{1}{2}\)MR²) से काफी कम हो जायेगा।

प्रश्न 12.
मूल बिन्दु से (\((2 \hat{i}-4 \hat{j}+2 \hat{k})\))m दूरी पर एक बिन्दु पर बल \((3 \hat{i}+2 \hat{j}-4 \hat{k})\) N कार्य कर रहा है। बल आघूर्ण का परिमाण ज्ञात कीजिए।
उत्तर:

प्रश्न 13.
समान द्रव्यमान के एवं समान त्रिज्या के एक ठोस व खोखले गोले को एक साथ समान कोणीय वेग से घुमाया जाता है तो कौन सा गोला पहले रुकेगा?
उत्तर:
ठोस गोला क्योंकि इसका जड़त्व आघूर्ण कम है अतः यह समान घूर्णन गति का विरोध कम करेगा।

प्रश्न 14.
m₁, m₂ तथा m₃ द्रव्यमानों के तीन कण एक समबाहु त्रिभुज के तीन शीर्षो पर स्थित हैं। त्रिभुज की प्रत्येक भुजा की लम्बाई a हो, तो इस निकाय का जड़त्व आघूर्ण त्रिभुज की m₁ द्रव्यमान से गुजरने वाली माध्यिका के परितः ज्ञात कीजिए।
उत्तर:
द्रव्यमानों एवं माध्यिका की व्यवस्था संलग्न चित्र में प्रदर्शित है।

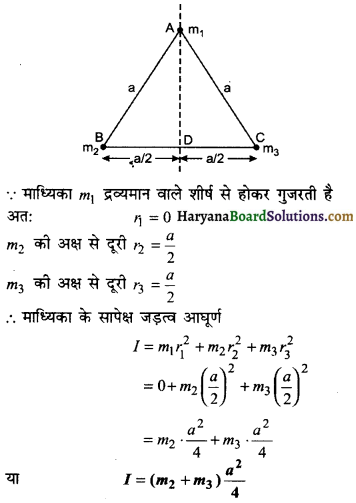
प्रश्न 15.
द्रव्यमान m व त्रिज्या r की एक ठोस चकती क्षैतिज तल पर कोणीय चाल ω से लुढ़क रही है। मूल बिन्दु O के परितः चकती का कोणीय संवेग ज्ञात कीजिए।

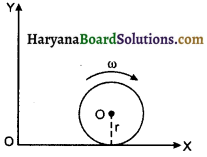
उत्तर:
OX अक्ष के सापेक्ष चकती का जड़त्व आघूर्ण
I = I_CM + Mr² = \(\frac{1}{2}\)Mr² + Mr²
या I = \(\frac{3}{2}\) Mr²
∴ चकती का कोणीय संवेग,
J = I.ω = \(\frac{3}{2}\) Mr².ω

प्रश्न 16.
समान द्रव्यमान तथा समान मोटाई की दो कतियाँ A व B भिन्न धातुओं की बनी हैं जिनके घनत्व ρ_A व ρ_B (ρ_A > ρ_B) हैं। यदि उनके वृत्ताकार तलों के लम्बवत् तथा गुरुत्वीय केन्द्रों से पारित अक्षों के परितः जड़त्व आघूर्ण I_A व I_B हों तो I_A व I_B में कौन बड़ा होगा?
उत्तर:
चकती का उसकी अक्ष के सापेक्ष जड़त्व आघूर्ण I = \(\frac{3}{2}\) MR²
यदि चकतियों की मोटाई t हो तो चकती का द्रव्यमान
M = आयतन × घनत्व = πR².t.ρ

प्रश्न 17.
यदि ध्रुवों पर जमी हुई बर्फ पिघल जाये तो दिन-रात, की अवधि पर क्या प्रभाव सम्भव है?
उत्तर:
ध्रुवों पर दिन रात की अवधि पृथ्वी के अपनी अक्ष के परितः घूर्णन गति पर निर्भर करती है। यदि ध्रुवों की बर्फ पिघल जाये तो यह पृथ्वी की सतह पर फैल जायेगी जिससे पृथ्वी का द्रव्यमान विस्तार बढ़ने से जड़त्व आघूर्ण बढ़ जायेगा और जड़त्व आघूर्ण बढ़ जाने पर कोणीय वेग घट जायेगा। अत: सूत्र (ω = \(\frac{2π}{T}\)) के अनुसार ω घटने से T (दिन-रात की अवधि) का मान बढ़ जायेगा अर्थात् दिन-रात की अवधि बढ़ जायेगी।

प्रश्न 18.
न्यूटन का गति विषयक नियम निकाय के अलग-अलग कणों के लिए लागू है, फिर भी निकाय की गति को न्यूटन के नियम द्वारा वर्णित किया जा सकता है। समझाइये।
उत्तर:
निकाय का सम्पूर्ण द्रव्यमान निकाय के द्रव्यमान केन्द्र पर संकेन्द्रित माना जा सकता है तथा सभी बाह्य बल भी द्रव्यमान केन्द्र पर लगे माने जा सकते हैं। तब न्यूटन के नियम के अन्तर्गत द्रव्यमान केन्द्र की गति निकाय की गति को व्यक्त करेगी।

प्रश्न 19.
एक बिल्ली गिरने पर अपने पैरों पर सुरक्षित उत्तर जाती है। क्यों?
उत्तर:
कोणीय संवेग संरक्षण के अनुसार,
Iω = नियतांक ⇒ ω ∝ \(\frac{1}{I}\)
जब बिल्ली नीचे गिरती है तो यह अपनी पूँछ एवं शरीर को तान लेती है जिससे बिल्ली का जड़त्व आघूर्ण बढ़ जाता है और फलस्वरूप उसका कोणीय वेग घट जाता है। इस प्रकार बिल्ली गिरने पर अपने पैरों पर सुरक्षित उतर जाती है।

प्रश्न 20.
गुरुत्व केन्द्र एवं द्रव्यमान केन्द्र में अन्तर स्पष्ट कीजिए। क्या ये पिण्ड में एक ही बिन्दु पर होते हैं?
उत्तर:
\(\vec{r}_{C M}=\frac{\Sigma m_i \overrightarrow{r_i}}{\Sigma m_i}\) तथा \(\overrightarrow{r_{C G}}=\frac{\Sigma m_i g_i \overrightarrow{r_i}}{\Sigma m_i g_i}\)
अतः एक समान गुरुत्व केन्द्र में अर्थात् पिण्ड का आकार पृथ्वी की तुलना में बहुत छोटा होने पर, इसके प्रत्येक कण पर का मान समान होने से दोनों द्रव्यमान केन्द्र व गुरुत्व केन्द्र सम्पाती होंगे।

प्रश्न 21.
घूर्णन गति करने वाली दो वस्तुओं 4 तथा B के जड़त्व आघूर्ण I_A व I_B हैं। यदि इनके कोणीय संवेग बराबर हों, तो किसकी गतिज ऊर्जा अधिक होगी? दिया है- I_A > I_B
उत्तर;
दिया है: J_A = J_B

प्रश्न 22.
छोटी डोरी से एक पत्थर के टुकड़े को बाँधकर घुमाना आसान होता है जबकि बड़ी डोरी से बाँधकर इसे घुमाना कठिन है, क्यों?
उत्तर:
पत्थर का जड़त्व आघूर्ण I = mr²
यदि डोरी छोटी है, तो वृत्त की त्रिज्या (r) कम होगी अतः जड़त्व आघूर्ण कम होगा। इसके विपरीत डोरी बड़ी होने पर जड़त्व आघूर्ण अधिक होगा। घूर्णन गति के समीकरण τ = Iα के अनुसार समान कोणीय त्वरण उत्पन्न करने के लिए छोटी डोरी की स्थिति में कम व बड़ी डोरी की स्थिति में अधिक बल-आघूर्ण लगाना पड़ेगा। अतः छोटी डोरी से पत्थर को बाँधकर घुमाना आसान है।

प्रश्न 23.
चक्रवात में चक्करदार वायु के झोंके के अक्ष के निकट की परतों का वेग बहुत अधिक होता है। समझाइये क्यों?
उत्तर:
चक्रवात में वायु की आन्तरिक परतें अक्ष के बहुत निकट होती हैं जिससे वायु के कणों का जड़त्व आघूर्ण बहुत कम हो जाता है अतः कोणीय संवेग संरक्षण के सिद्धान्त से इन आन्तरिक परतों का कोणीय वेग बहुत अधिक हो जाता है।

दीर्घ उत्तरीय प्रश्न (Long Answer Questions)

प्रश्न 1.
दृढ़ पिण्ड से क्या अभिप्राय है? इसकी स्थानान्तरीय एवं घूर्णन गतियों की व्याख्या कीजिए।
उत्तर:
दृढ पिण्ड (Rigid Body) :
“वे पिण्ड जिनकी आकृति बाह्य बल लगाने पर भी अपरिवर्तित रहती है अर्थात् जिनके कणों की आन्तरिक दूरियाँ अपरिवर्तित रहती हैं, दृढ़ पिण्ड कहलाते हैं।”
प्रकृति में कोई वस्तु पूर्णतः दृढ़ पिण्ड नहीं होती है क्योंकि उच्च दाब या बल लगाकर वस्तु में विकृति उत्पन्न की जा सकती है। अतः ऐसी वस्तुओं का अध्ययन करने के लिए आदर्श दृढ़ पिण्ड की कल्पना करते हैं जिसमें विकृतियाँ नगण्य रहती हैं। दृढ पिण्ड की गति में स्थानान्तरीय गति (Translational motion) तथा घूर्णन गति (Rotational motion) सम्मिलित होती है। यदि दृढ पिण्ड उससे गुजरने वाली स्थिर अक्ष के प्रति घूर्णन करती है, तो उसे पिण्ड की शुद्ध घूर्णन गति (Pure-rotational motion) कहते हैं तथा अक्ष घूर्णन अक्ष (axis of rotation) कहलाती है, उदाहरण के लिए छत से लटके पंखे की गति शुद्ध घूर्णन गति होती है। परन्तु कुछ स्थितियों में दृढ़ पिण्ड की गति के दौरान घूर्णन अक्ष स्थिर नहीं रहती है। इस स्थिति में पिण्ड में घूर्णन गति के साथ-साथ स्थानान्तरीय गति भी होती है। यदि गति के दौरान दृढ़ पिण्ड के कण परस्पर समान्तर पथ में गति करते हैं, तो वह स्थानान्तरीय गति कहलाती है । उदाहरण के लिए किसी पिण्ड का किसी तल पर फिसलना व्यक्ति का किसी तल पर चलना आदि।

जब गति के दौरान दृढ़ पिण्ड के कण घूर्णन अक्ष के सापेक्ष अपनी स्थिति परिवर्तित करते हैं तो वह गति घूर्णन एवं स्थानान्तरीय गतियों का मिश्रण होती है।

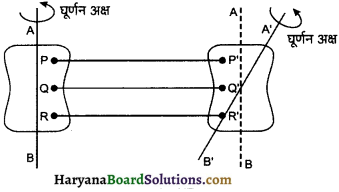
दौरान दृढ पिण्ड का प्रत्येक कण घूर्णन अक्ष के परितः वृत्ताकार गति करता है। गति के दौरान घूर्णन अक्ष स्थिर या अपनी दिशा परिवर्तित कर सकती है। अतः “यदि दृढ़ पिण्ड का प्रत्येक बिन्दु वृत्ताकार पथ में गति करता हो तथा प्रत्येक वृत्त का केन्द्र एक उभयनिष्ठ रेखा पर स्थित हो, तो उस गति को शुद्ध घूर्णन गति कहते हैं तथा रेखा को घूर्णन-अक्ष कहते हैं।”

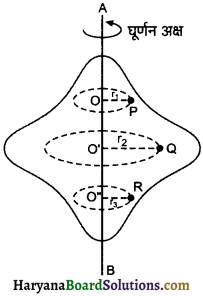
चित्र में पिण्ड की घूर्णन गति को दर्शाया गया है। चित्र में पिण्ड के तीन कण P, Q R दिखाये गये हैं जो घूर्णन अक्ष AB से क्रमशः r₁, r₂ व r₃ दूरियों पर स्थित हैं। पिण्ड की घूर्णन गति के दौरान इन कणों के वृत्तीय पथों की त्रिज्याएं क्रमशः r₁, r₂ व r₃ होगी और इन पथों के केन्द्र O, O’ और O” उभयनिष्ठ अक्ष AB पर होंगे। इन सभी कणों के कोणीय वेग एवं आवर्तकाल समान होंगे।

कुछ विशेष स्थितियों में दृढ़ पिण्ड के घूर्णन अक्ष की स्थिति में परिवर्तन होता रहता है परन्तु उसमें कोई स्थानान्तरण नहीं होता है। उदाहरण के लिए घूमते हुए लट्टू की गति। इस गति को शुद्ध पुरस्सरण गति (Pure Precessional motion) कहते हैं।

प्रश्न 2.
द्रव्यमान केन्द्र से क्या अभिप्राय है? इसके कार्तीय घटकों के लिए व्यंजक प्राप्त कीजिए।
उत्तर:
द्रव्यमान केन्द्र (Centre of Mass) :
दृढ़ पिण्डों की जटिल गतियों, जिनमें वह स्थानान्तरीय गति के साथ-साथ घूर्णन गति भी करता है, को समझना गणितीय रूप से अत्यधिक कठिन होता है। इस प्रकार की गतियों को समझने के लिए यदि हम पिण्ड के एक विशेष बिन्दु पर ध्यान रखें तो गति का विश्लेषण करना अत्यधिक सरल हो जाता है। इस विशेष बिन्दु को द्रव्यमान केन्द्र कहते हैं। द्रव्यमान केन्द्र को निम्न प्रकार परिभाषित करते हैं-
“किसी दृढ़ पिण्ड अर्थात् कणों के निकाय का द्रव्यमान केन्द्र वह बिन्दु है जो इस प्रकार गति करता है कि मानों निकाय का समस्त द्रव्यमान वहाँ पर केन्द्रित हो और समस्त बाह्य बल इसी बिन्दु पर कार्यरत् हों।” उदाहरण के लिए ठोस गोले का केन्द्र ही द्रव्यमान केन्द्र होता है। सामान्यत: नियमित आकार के पिण्डों का द्रव्यमान केन्द्र उनका ज्यामितीय केन्द्र होता है।

दो कणों के निकाय का द्रव्यमान केन्द्र (Centre of Mass of a System of Two Particles) :
माना किसी निकाय में दो कण हैं जिनके द्रव्यमान क्रमशः m₁ व m₂ हैं तथा निर्देश बिन्दु O से जिनके स्थिति सदिश \(\overrightarrow{r_1}\) व \(\overrightarrow{r_2}\) हैं एवं इन कणों का आपस में तथा बाह्म वातावरण से सम्बन्ध है। इनके द्रव्यमान केन्द्र (C.M.) का स्थिति सदिश,

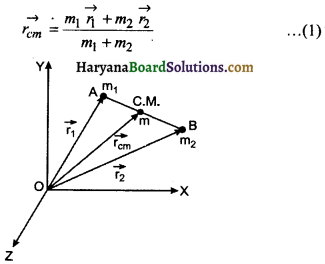
उपपत्ति (Proof):
माना इन कणों पर कार्य करने वाले बाह्य बल क्रमश: \(\vec{F}_{1 \mathrm{ext}}\) व \(\overrightarrow{F_{2 \mathrm{ext}}}\) तथा आन्तरिक बल क्रमश: \(\overrightarrow{F_{12}}\) व \(\overrightarrow{F_{21}}\) हैं। अतः कण A पर नेट बल,

माना किसी क्षण पर द्रव्यमान केन्द्र के स्थिति सदिश, वेग तथा त्वरण क्रमशः \(\overrightarrow{r_{c m}} ; \overrightarrow{v_{c m}}\) एवं \(\overrightarrow{a_{c m}}\) हैं।
निकाय का कुल द्रव्यमान M = (m₁ + m₂)
∵ द्रव्यमान केन्द्र की अभिधारणा से कुल बाह्य बल \(\vec{F}=\vec{F}_{1 \mathrm{ext}}+\vec{F}_{2 \mathrm{ext}}\) द्रव्यमान केन्द्र पर कार्य करता है तथा कुल द्रव्यमान भी द्रव्यमान केन्द्र पर केन्द्रित माना जाता है। अत: न्यूटन के गति के द्वितीय नियम से

प्रश्न 3.
सतत् पिण्ड के द्रव्यमान केन्द्र के लिए सूत्र प्राप्त कीजिए।
उत्तर:
दो कणों के निकाय का द्रव्यमान केन्द्र (Centre of Mass of a System of Two Particles) :
माना किसी निकाय में दो कण हैं जिनके द्रव्यमान क्रमशः m₁ व m₂ हैं तथा निर्देश बिन्दु O से जिनके स्थिति सदिश \(\overrightarrow{r_1}\) व \(\overrightarrow{r_2}\) हैं एवं इन कणों का आपस में तथा बाह्म वातावरण से सम्बन्ध है। इनके द्रव्यमान केन्द्र (C.M.) का स्थिति सदिश,

उपपत्ति (Proof):
माना इन कणों पर कार्य करने वाले बाह्य बल क्रमश: \(\vec{F}_{1 \mathrm{ext}}\) व \(\overrightarrow{F_{2 \mathrm{ext}}}\) तथा आन्तरिक बल क्रमश: \(\overrightarrow{F_{12}}\) व \(\overrightarrow{F_{21}}\) हैं। अतः कण A पर नेट बल,

माना किसी क्षण पर द्रव्यमान केन्द्र के स्थिति सदिश, वेग तथा त्वरण क्रमशः \(\overrightarrow{r_{c m}} ; \overrightarrow{v_{c m}}\) एवं \(\overrightarrow{a_{c m}}\) हैं।
निकाय का कुल द्रव्यमान M = (m₁ + m₂)
∵ द्रव्यमान केन्द्र की अभिधारणा से कुल बाह्य बल \(\vec{F}=\vec{F}_{1 \mathrm{ext}}+\vec{F}_{2 \mathrm{ext}}\) द्रव्यमान केन्द्र पर कार्य करता है तथा कुल द्रव्यमान भी द्रव्यमान केन्द्र पर केन्द्रित माना जाता है। अत: न्यूटन के गति के द्वितीय नियम से

प्रश्न 4.
सिद्ध कीजिए कि जब किसी तन्त्र पर बाह्य बल शून्य होता है तो उसका द्रव्यमान केन्द्र नियत वेग से गति करता है।
उत्तर:
द्रव्यमान केन्द्र का रेखीय संवेग (Linear Momentum of Centre of Mass) :
माना कि एक निकाय n कणों से मिलकर बना है, जिसके कणों का द्रव्यमान क्रमशः \(m_1, m_2, m_3 \ldots . m_n\) तथा वेग क्रमशः \(v_1, v_2, v_3 \ldots . v_n\) है इसलिए इस निकाय का संवेग
\(\vec{p}=m \overrightarrow{v_1}+m \overrightarrow{v_2}+m \overrightarrow{v_3}+\ldots \ldots . .+m_n \overrightarrow{v_n}\)
लेकिन हम जानते हैं
\(\overrightarrow{v_cm}=\frac{1}{2}(m \overrightarrow{v_1}+m \overrightarrow{v_2}+m \overrightarrow{v_3}+\ldots \ldots . .+m_n \overrightarrow{v_n})\)
\(\vec{p}=M \vec{v_cm}\) ………….(1)
अर्थात् कणों के निकाय का कुल रेखीय संवेग, निकाय के कुल द्रव्यमान तथा द्रव्यमान केन्द्र के वेग के गुणनफल के बराबर होता है।
समी० (1) का समय t के सापेक्ष अवकलन करने पर

अर्थात् जब किसी निकाय पर आरोपित बाह्य बलों का योग शून्य होता है तब उस निकाय का कुल रेखीय संवेग नियत अर्थात् संरक्षित रहता है। यह किसी निकाय के द्रव्यमान केन्द्र का रेखीय संरक्षण नियम कहलाता है।
∴ \(\frac{d \vec{p}}{d t}=0\) होने पर
\(\frac{d}{d t}\left(M v_{c m}\right)=0\)
v _cm= नियतांक ………….(4)
या \(m_A \overrightarrow{a_A}+m_B \overrightarrow{a_B}=0\)
यहाँ \(\overrightarrow{a_A}[latex] व [latex]\overrightarrow{a_B}\) क्रमश: A व B की गतियों में त्वरणों का मान है। यदि \(\overrightarrow{F_{A B}}\) एवं \(\overrightarrow{F_{B A}}\) क्रमशः A व B पर B व A के कारण लगने वाले आन्तरिक बल हैं, तो-
\(\overrightarrow{F_{A B}}+\overrightarrow{F_{B A}}=0\)
या \(\overrightarrow{F_{A B}}=-\overrightarrow{F_{B A}}\)
यह न्यूटन का क्रिया एवं प्रतिक्रिया का नियम है।

प्रश्न 5.
बल आघूर्ण की परिभाषा दीजिए एवं इसके लिए सूत्र प्राप्त कीजिए तथा दैनिक जीवन में बल आघूर्ण के उपयोग समझाइये।
उत्तर:
बल आघूर्ण (Torque) tau :
“घूर्णन गति में दिये गये घूर्णन अक्ष के सापेक्ष किसी कण पर कार्यरत् बल का आघूर्ण ही बल आघूर्ण कहलाता है।’ इसे \(\vec{\tau}\) (tau) से व्यक्त करते हैं।

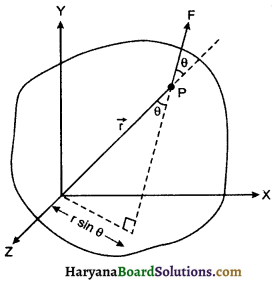
चित्र में एक कण P पर बल \(\vec{F}\) आरोपित है। जिससे वह O से गुजरने वाले घूर्णन अक्ष के सापेक्ष घूर्णन गति करता है।
बल आघूर्ण = बल × बल की घूर्णन अक्ष से लम्बवत् दूरी
τ = F(OM)
= F r sin θ
τ = r F sin θ
सदिश गुणन के रूप में \(\vec{\tau}=\vec{r} \times \vec{F}\)
यहाँ पर \theta, \(\vec{r}\) और \(\vec{F}\) के मध्य कोण है। बल आघूर्ण की दिशा \(\vec{r}\) तथा \(\vec{F}\) के तल के लम्बवत् दक्षिणावर्ती पेंच नियम से ज्ञात करते हैं। चित्र में \(\vec{r}\) व \(\vec{F}\) X-Y तल में है अतः बल आघूर्ण Z अक्ष की धन दिशा में होगा।
बल आघूर्ण का मात्रक-न्यूटन-मीटर होता है तथा इसका विमीय सूत्र \(\left[\mathrm{M}^1 \mathrm{~L}^2 \mathrm{~T}^{-2}\right]\) होता है।

प्रश्न 6.
कोणीय वेग एवं कोणीय त्वरण की परिभाषा दीजिए तथा घूर्णन गति के समीकरणों की उपपत्ति दीजिए।
उत्तर:
कोणीय वेग (Angular Velocity) :
“समय के साथ कोणीय विस्थापन के परिवर्तन की दर को कोणीय वेग कहते हैं।” इसे ω से व्यक्त करते हैं। यह सदिश राशि है। यह एक अक्षीय सदिश है जिसकी दिशा पिण्ड की घूर्णन अक्ष के अनुदिश होती है। यदि दृढ़ पिण्ड वामावर्त (anti clockwise) दिशा में घूर्णन करता है, तो उसका कोणीय वेग घूर्णन अक्ष के अनुदिश पिण्ड के तल से बाहर की ओर होगा। अर्थात् यदि पिण्ड X-Y तल में वामावर्त (anti clockwise) दिशा में घूर्णन गति करता है तो कोणीय वेग +z दिशा में होगा। इसी प्रकार यदि पिण्ड दक्षिणावर्त (clockwise) दिशा में घूर्णन करता है तो कोणीय वेग -z दिशा के अनुदिश होगा।

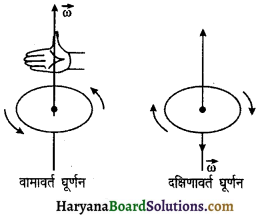
कोणीय वेग की दिशा को दाहिने हाथ के नियम से व्यक्त किया जाता है जैसा कि चित्र में प्रदर्शित किया गया है। कोणीय वेग की दिशा को ज्ञात करने के लिए दाहिने हाथ से घूर्णन अक्ष को इस पकड़े जाने की कल्पना करें कि अंगूठा अक्ष के समान्तर रहे तो यदि उँगलियों के घुमाव से पिण्ड के घूर्णन की दिशा व्यक्त होती है तो अँगूठे द्वारा कोणीय वेग की दिशा व्यक्त होगी। कोणीय वेग को rad.s^-1 में मापा जाता है।
यदि समयान्तर ∆t = (t₂ – t₁ ) में कोणीय विस्थापन ∆θ = (θ₂ – θ₁ ) हो तो औसत कोणीय वेग
\(\omega_{a v}=\vec{\omega}=\frac{\Delta \theta}{\Delta t}=\frac{\left(\theta_2-\theta_1\right)}{\left(t_2-t_1\right)}\)
यदि ∆t का मान अत्यल्प हो अर्थात् ∆t → 0 तो पिण्ड के कोणीय वेग का तात्क्षणिक मान (Instantaneous Values of Angular Velocity) निम्न प्रकार व्यक्त होगा-
\(\omega=\lim _{\Delta t \rightarrow 0} \frac{\Delta \theta}{\Delta t}=\frac{d \theta}{d t}\) ………..(2)
\(\omega=\frac{d \theta}{d t}\)
इसी तात्क्षणिक कोणीय वेग को ‘कोणीय वेग’ के नाम से जाना जाता है। कोणीय वेग धनात्मक एवं ऋणात्मक हो सकता है लेकिन कोणीय चाल सदैव धनात्मक होती है।

कोणीय त्वरण (Angular Acceleration) :
जब किसी पिण्ड के कोणीय वेग का मान परिवर्तित होता है तो उसमें कोणीय त्वरण होता है। उदाहरण के लिए जब हम साइकिल चलाते हैं या उसको रोकते हैं तो दोनों स्थितियों में उसके कोणीय वेग में परिवर्तन होता है अर्थात् साइकिल पहियों में कोणीय त्वरण होता है। अतः “पिण्ड के कोणीय वेग में परिवर्तन की दर को कोणीय त्वरण कहते हैं।” इसे द्वारा प्रदर्शित करते हैं और यह एक सदिश राशि है और इसका मात्रक rad.s^-2 होता है।
माना t₂ एवं t₁ क्षण पर दृढ पिण्ड के कोणीय वेग ω₁ व ω₂ हैं।
अतः पिण्ड का औसत कोणीय त्वरण
\(\alpha_{a v}=\bar{\alpha}=\frac{\omega_2-\omega_1}{t_2-t_1}=\frac{\Delta \omega}{\Delta t}\) ……(1)
कोणीय त्वरण की दिशा को दाँये हाथ के नियम से ज्ञात किया जा सकता है। α की दिशा पिण्ड के कोणीय वेग में वृद्धि की दिशा में होगी। अर्थात् यदि ω₂ > ω₁ तो कोणीय वेग में वृद्धि होने पर α का मान धनात्मक होगा एवं ω₂ < ω₁ होने पर कोणीय वेग में कमी होगी और फलस्वरूप α का मान ऋणात्मक होगा। अतः धनात्मक α त्वरण की दिशा कोणीय वेग ω की दिशा में एवं ऋणात्मक α की दिशा कोणीय वेग की विपरीत दिशा में होगी।
यदि ∆t का मान अत्यल्प हो अर्थात् ∆t → 0 तो पिण्ड के कोणीय त्वरण को तात्क्षणिक कोणीय त्वरण या केवल कोणीय त्वरण के नाम से जाना जाता है।

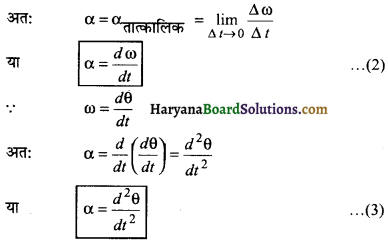
प्रश्न 7.
निम्नलिखित राशियों में सम्बन्ध स्थापित कीजिए-
(i) रेखीय वेग, कोणीय वेग तथा त्रिज्या में।
(ii) रेखीय त्वरण एवं कोणीय त्वरण में ।
उत्तर:
रेखीय वेग तथा कोणीय वेग में संबंध (Relation between Linear Velocity and Angular Velocity) :
जब कोई दृढ़ पिण्ड अपनी स्थिर अक्ष के परितः घूर्णन करता है तो उसका प्रत्येक कण विभिन्न त्रिज्याओं के वृत्तीय पथों पर गति करता है। सभी पथों के केन्द्र घूर्णन अक्ष पर होते हैं और सभी का कोणीय वेग समान होता है लेकिन उनकी चाल घूर्णन अक्ष से उनकी दूरी अर्थात् उनके वृत्तीय पथों की त्रिज्या पर निर्भर करती है। दूरी बढ़ने पर चाल बढ़ जाती है। शुद्ध घूर्णी गति में कण की चाल का मान उसके कोणीय वेग के अनुक्रमानुपाती होता है। संलग्न चित्र (7.18) में दृढ़ पिण्ड का कण P त्रिज्या r के वृत्तीय पथ में घूर्णन गति कर रहा है। यदि किसी क्षण उसका कोणीय विस्थापन θ rad. हो तो, चाप PP’ की लम्बाई s निम्न प्रकार व्यक्त कर सकते हैं।

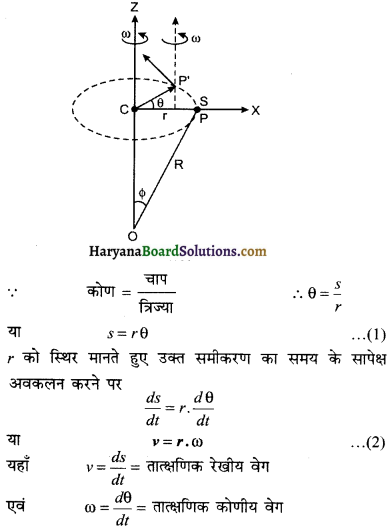
शुद्ध घूर्णी गति में सभी कणों के लिए कोणीय वेग ω समान होता है अत: समी० (2) से स्पष्ट है कि घूर्णन अक्ष से दूरी (r) बढ़ने पर रेखीय वेग (v) उतना ही अधिक बढ़ जायेगा।
उक्त सम्बन्ध [समी० (2)] को सदिश गुणनफल में निरूपित करने के लिए माना कण P का t = 0 पर स्थिति सदिश \(\vec{R}=\overrightarrow{O P}\) है। अत: चित्र से-
\(\frac{r}{R}=\sin \phi \quad \text { या } \quad r=R \sin \phi\)
अत: समी० (2) से
\(v=\omega \cdot R \sin \phi\)
चूँकि \(\omega R \sin \phi\) कोणीय वेग ω के तल के लम्बवत् है, अत: उक्त समी० (2) को सदिश गुणनफल के रूप में निम्न प्रकार व्यक्त कर सकते हैं।
\(\vec{v}=\vec{\omega} \times \overrightarrow{\boldsymbol{R}}\)
यहाँ यह ध्यान देने योग्य कि \(\phi=\frac{\pi}{2} \mathrm{rad}\) की स्थिति में R का मान वृत्तीय पथ की त्रिज्या r के तुल्य होगा।

रेखीय त्वरण एवं कोणीय त्वरण में सम्बन्ध (Relation between Linear Acceleration and Angular Acceleration):
जब कोई कण वृत्तीय पथ पर नियत कोणीय वेग से गति करता है, तो उस पर केवल त्रिज्य त्वरण \(\vec{a}_{\mathrm{rad}}\) ही कार्य करता है, लेकिन कण की चाल (v) भी बदलती है, तो उसमें \(\vec{a}_{\mathrm{rad}}\) के साथ-साथ स्पर्श रेखीय त्वरण \(\vec{a}_{\mathrm{tan}}\) भी होता है। इन्हीं दोनों त्वरणों का परिणामी कण का त्वरण \(\overrightarrow{a_R}\) होता है। इन दोनों घटकों एवं परिणामी त्वरण \(\left(\overrightarrow{a_R}\right)\) को संलग्न चित्र 7.19 में दिखाया गया है। स्पर्श रेखीय त्वरण \(\left(\vec{a}_{\text {tan }}\right)\) की दिशा कण के रेखीय वेग \(\vec{v}\) की दिशा में होती है, क्योंकि इस त्वरण की उत्पत्ति रेखीय वेग \(\vec{v}\) के परिमाण में परिवर्तन से ही होती है। अत:
\(a_{\mathrm{tan}}=\frac{d v}{d t}=r \cdot \frac{d \omega}{d t}=r \cdot \alpha\)

यहाँ \(\alpha=\frac{d \omega}{d t}\) कण का कोणीय त्वरण है। कण के त्रिज्य त्वरण \(\left(a_{\mathrm{rad}}\right)\) का मान कण के रेखीय वेग की दिशा में परिवर्तन से सम्बन्धित होता है। अत:

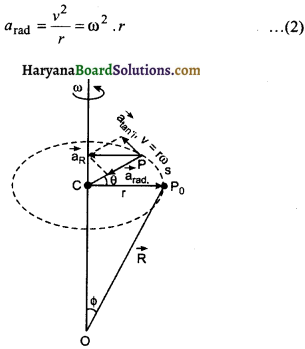
कण के रेखीय त्वरण व कोणीय त्वरण के सम्बन्ध को सदिश रूप में निम्न प्रकार व्यक्त करते हैं।
यदि कण का स्थिति सदिश \(\vec{R}\) हो तो चित्र से,
r =R sin ϕ
a_tan =αR sin ϕ
या \(\overrightarrow{a_{\tan }} \propto R \sin \hat{n}\)

जहाँ \(\hat{n}\) घूर्णन तल के लम्बवत् दिशा में एकांक सदिश को व्यक्त करता है। अत:

\(\vec{a}_{\mathrm{tan}}=\vec{a}=\vec{\alpha} \times \vec{R}\) ………………..(3)
यदि \(\phi=\frac{\pi}{2} \mathrm{rad} तो R \sin \phi=r\)
अतः a = α . r
यदि घूर्णन अक्ष स्थिर है तो कण के ω व α के मान स्थिर रहेंगे। कण पर परिणामी त्वरण
\(a_R=\sqrt{a_{\mathrm{rad}}^2+a_{\mathrm{tan}}^2} \text { क्योंकि } \vec{a}_{\mathrm{rad}} \perp \vec{a}_{\mathrm{tan}}\)

प्रश्न 8.
जड़त्व आघूर्ण की परिभाषा दीजिए एवं दैनिक जीवन में इसके महत्व की विवेचना कीजिए।
उत्तर:
जड़त्व आघूर्ण (Moment of Inertia):
न्यूटन के प्रथम नियम के अनुसार बाह्य बल की अनुपस्थिति में वस्तुएँ अपनी अवस्था परिवर्तन का विरोध करती हैं अर्थात् यदि वस्तु विरामावस्था में है, तो वह गति में आने का विरोध करती हैं और यदि गतिशील हैं तो उसी दिशा में उसी वेग से चलती रहना चाहती है और वेग तथा वेग की दिशा में परिवर्तन का विरोध करती है। वस्तुओं के इस गुण को जड़त्व (Inertia) कहते हैं जो कि पदार्थ का मूल गुण है। इसीलिए न्यूटन के प्रथम नियम को जड़त्व का नियम भी कहते हैं।

इसी प्रकार यदि कोई वस्तु किसी अक्ष के परितः घूर्णन के लिए स्वतन्त्र हैं तो बाह्य बल आघूर्ण की अनुपस्थिति में वह अपनी अवस्था परिवर्तन का विरोध करती है अर्थात् यदि विरामावस्था में है तो घूर्णन गति करने का विरोध करती है और यदि घूर्णन कर रही है तो कोणीय वेग में ‘ परिवर्तन का विरोध करती है। किसी अक्ष के परितः वस्तुओं के इस गुण को घूर्णन जड़त्व या ‘जड़त्व आघूर्ण (Moment of Inertia) कहते हैं। इसे प्रायः I से व्यक्त करते है “पिण्ड के किसी कण का घूर्णन अक्ष के परित: जड़त्व आघूर्ण उस कण के द्रव्यमान तथा उसकी घूर्णन अक्ष से दूरी के वर्ग के गुनणनफल के बराबर होता है।” अर्थात्
I = mr²
I का मात्रक = kg.m²
तथा I का विमीय सूत्र = [M¹L²T⁰] …(1)

1. कणों के निकाय का जड़त्व आघूर्ण (Moment of Inertia of a System of Particles ) :
माना M द्रव्यमान का कोई दृढ पिण्ड (कणों का निकाय) चित्र में प्रदर्शित एक बिन्दु O से गुजरने वाली ऊर्ध्वाधर अक्ष के परितः घूर्णन के लिए स्वतन्त्र है और पिण्ड का इसी अक्ष के परितः जड़त्व आघूर्ण ज्ञात करना है। माना पिण्ड विभिन्न द्रव्यमानों m₁, m₂, m₃ …………., m_n के n कणों से मिलकर बना है और घूर्णन अक्ष से इन कणों की दूरियाँ क्रमश: r₁, r₂, r₃ …………., r_n हैं। इन सभी कणों के जड़त्व आघूर्णो का योग पूरे पिण्ड का जड़त्व आघूर्ण प्रदान करेगा अर्थात्

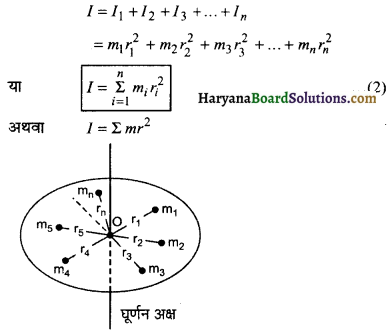
2. सतत् द्रव्यमान वितरण वाले पिण्ड या निकाय का जड़त्व आघूर्ण (Moment of Inertia of a Block of Homogeneous Mass Distribution ) :
यदि किसी पिण्ड में कणों की संख्या अत्यधिक व अति पास-पास स्थित हो जैसे- बेलन, चकती, गोला, मीटर स्केल आदि तो ऐसे पिण्डों को या निकाय को सतत् द्रव्यमान वितरण वाले निकाय के रूप में जाना जाता है। इन पिण्डों के जड़त्व आघूर्ण ज्ञात करने के लिए समाकलन (Integration) विधि का उपयोग करते हैं।
माना dm द्रव्यमान का एक अल्पांश घूर्णन अक्ष से r दूरी पर स्थित है तो इस अल्पांश का जड़त्व आघूर्ण
dI = dm.r² …..(3)
अतः पूरे पिण्ड का जड़त्व आघूर्ण उचित सीमाओं के अन्तर्गत समी० (3) का समाकलन ज्ञात करके ज्ञात करते हैं, अर्थात्
I = \(\int r^2 \cdot d m\) ………….(4)

जड़त्व आघूर्ण का भौतिक महत्व (Physical Significance of Moment of Inertia):
जब किसी वस्तु पर कोई बाह्य बल लगाया जाता है, तो यदि वह विरामावस्था में है अथवा सीधी रेखा में किसी वेग से गतिशील है, अपनी अवस्था परिवर्तन का विरोध करती है। वस्तुओं या पिण्डों के इस गुण को ‘जड़त्व’ कहते हैं। किसी पिण्ड का द्रव्यमान जितना अधिक होता है, उसकी अवस्था परिवर्तन हेतु उतने ही अधिक बल की आवश्यकता होती है अतः किसी पिण्ड का द्रव्यमान ही उसके जड़त्व की माप है।

ठीक इसी प्रकार किसी पिण्ड को जो विरामावस्था में है, किसी अक्ष के परितः घुमाने के लिए अथवा घूर्णन गति कर रहे पिण्ड के कोणीय वेग में परिवर्तन के लिए उस पर बल आघूर्ण लगाने की आवश्यकता होती है। पिण्ड के इस गुण को ‘जड़त्व आघूर्ण’ कहते हैं। पिण्ड का जड़त्व आघूर्ण जितना अधिक होता है, उसकी अवस्था परिवर्तन ( घूर्णन गति में) के लिए उतने ही अधिक बल आघूर्ण की आवश्यकता होती है।

उक्त विवेचना से स्पष्ट है कि “रेखीय गति में जो भूमिका द्रव्यमान की होती है, वही भूमिका घूर्णन गति में जड़त्व आघूर्ण की होती है। इसी प्रकार जो भूमिका रेखीय गति में बल की होती है वही भूमिका घूर्णन गति में बल आघूर्ण की होती है।”

जड़त्व तथा जड़त्व आघूर्ण में अन्तर (Difference between Inertia and Moment of Inertia):
पिण्ड का जड़त्व आघूर्ण केवल पिण्ड के द्रव्यमान पर निर्भर करता है परन्तु पिण्ड का जड़त्व आघूर्ण पिण्ड के द्रव्यमान पर तो निर्भर करता ही है, साथ ही साथ पिण्ड की घूर्णन अक्ष से दूरी पर भी निर्भर करता है अर्थात् पूरे पिण्ड का जड़त्व आघूर्ण इस तथ्य पर निर्भर करता है कि पूरे पिण्ड के द्रव्यमान का घूर्णन अक्ष के परितः वितरण कैसा है। पिण्ड के द्रव्यमान का जितना अधिक भाग घूर्णन अक्ष से दूर होगा, पिण्ड का जड़त्व आघूर्ण उतना ही अधिक होगा।

जड़त्व आघूर्ण का दैनिक जीवन में महत्व :
(Importance of Moment of Inertia in Daily Life)
हमारे दैनिक जीवन में जड़त्व आघूर्ण की अहम् भूमिका है। स्कूटर, मोटर साइकिल, साइकिल, रिक्शा, ताँगा तथा बैलगाड़ी इत्यादि में पहिए का जड़त्व आघूर्ण बढ़ाने के लिए पदार्थ की अधिकतम मात्रा परिधि पर रखने का प्रयास किया जाता है परिधि का घेरा तानों द्वारा घूर्णन अक्ष से जुड़ा होता है। ऐसा करने से पहिये में ‘गतिपालक चक्र’ (Fly wheel) का गुण उत्पन्न हो जाता है अर्थात् साइकिल के पैडल चलाना बन्द कर देने पर भी साइकिल कुछ दूरी तक चलती रहती है।

जड़त्व आघूर्ण का व्यावहारिक एवं अच्छा उपयोग ऑटोमोबाइल क्षेत्र में होता है। ऑटोमोबाइल इंजन जो घूर्णी गति पैदा करता है, इसमें बहुत अधिक जड़त्व आघूर्ण वाली एक चकती लगी रहती हैं जिसे गतिपालक चक्र कहते हैं। जब शैफ्ट को घुमाने वाले बल आघूर्ण का मान घटता या बढ़ता है, तो गतिपालक चक्र अपने अधिक जड़त्व आघूर्ण के कारण लगभग एक समान चाल से घूमता रहता है जिससे झटके वाली स्थिति से बच जाते हैं।

बच्चों के खिलौने के मोटर के नीचे भी एक छोटा सा गतिपालक चक्र लगा रहता है। इसे जमीन से रगड़ कर घुमाकर छोड़ देते हैं। जड़त्व आघूर्ण के कारण मोटर कुछ देर तक चलती रहती है।

प्रश्न 9.
बल आघूर्ण एवं जड़त्व में सम्बन्ध स्थापित कीजिए और इसकी सहायता से जड़त्व आघूर्ण की परिभाषा कीजिए।
उत्तर:
बल आघूर्ण, जड़त्व आघूर्ण एवं कोणीय त्वरण में सम्बन्ध (Relation between Torque, Moment of Inertia and Angular Acceleration) :
किसी घूर्णन अक्ष के सापेक्ष किसी बल का आघूर्ण बल एवं घूर्णन अक्ष से बल की क्रिया रेखा की लम्बवत् दूरी के गुणनफल से प्राप्त होता है; अर्थात्
बल आघूर्ण = बल × घूर्णन अक्ष से बल की क्रिया रेखा की लम्बवत् दूरी

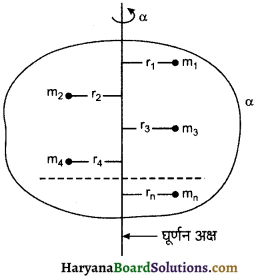
या τ = F × r
∵ F = ma एवं a = r.a
जहाँ a रेखीय त्वरण एवं α कोणीय त्वरण है।
τ = ma × r = m × r α × r
या τ = mr²α
यदि पिण्ड बड़ा है तो उसे अनेक छोटे-छोटे द्रव्यमान कणों से मिलकर बना हुआ मान सकते हैं जिनके द्रव्यमान क्रमश: \(m_1, m_2, \ldots, m_n\) हैं। सभी कणों का कोणीय त्वरण पिण्ड के कोणीय त्वरण α के बराबर होगा। इन सभी कणों पर लगने वाले बल आघूर्णों का योग पूरे पिण्ड का बल आघूर्ण प्रदान करेगा। अत:

उक्त समीकरण में यदि α = 1 rad.s^-2 तो τ = I “अर्थात् किसी पिण्ड का जड़त्व आघूर्ण उस बल आघूर्ण के तुल्य है जो पिण्ड में एकांक कोणीय त्वरण उत्पन्न कर दे।”

प्रश्न 10.
घूर्णन ऊर्जा के लिए व्यंजक प्राप्त कीजिए एवं इसकी सहायता से जड़त्व आघूर्ण की परिभाषा कीजिए।
उत्तर:
घूर्णन गतिज ऊर्जा (Rotational Kinetic Energy):
घूर्णन गति में किसी कण की गतिज ऊर्जा ही घूर्णन गतिज ऊर्जा कहलाती है। इसे E_R से व्यक्त करते हैं। यदि m द्रव्यमान का कण घूर्णन अक्ष के परितः r त्रिज्या के वृत्तीय मार्ग पर v चाल से घूर्णन गति करता है तो उसकी घूर्णन गतिज ऊर्जा

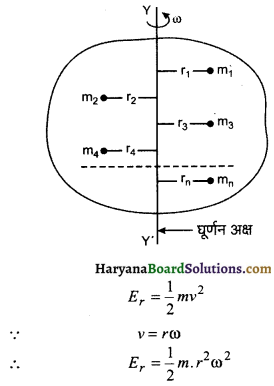
यदि पिण्ड बड़ा है तो उसे अनेक छोटे-छोटे द्रव्यमान कणों से मिलकर बना हुआ मान सकते हैं। इन कणों के द्रव्यमान क्रमशः \(m_1, m_2, m_3, \ldots, m_n\) एवं घूर्णन अक्ष से इनकी दूरियाँ क्रमश: \(r_1, r_2, r_3, \ldots, r_n\) हैं। चूँकि पूरा पिण्ड ω कोणीय वेग से घूर्णन गति करता है, अत: सभी कणों का कोणीय वेग ω होगा। सभी कणों की घूर्णन गतिज ऊर्जाओं का योग पूरे पिण्ड की घूर्णन गतिज ऊर्जा प्रदान करेगा; अर्थात्

जहाँ I = Σmr² = पिण्ड का जड़त्व आघूर्ण
समी० (1) एक समान घूर्णन गति में घूर्णन ऊर्जा का सूत्र है। स्पष्ट है कि जिस प्रकार किसी पिण्ड की रेखीय गतिज ऊर्जा (\(\frac{1}{2} m v^2\)) पिण्ड के द्रव्यमान m तथा रेखीय वेग के वर्ग v² के गुणनफल की आधी होती है; उसी प्रकार घूर्णन गतिज ऊर्जा (\(\frac{1}{2} I \omega^2\)) पिण्ड के जड़त्व आघूर्ण I एवं कोणीय वेग के वर्ग ω² के गुणनफल की आधी होती है।
समी० (1) में यदि ω = 1 rad.s^-1
तो I = 2 E_r
अर्थात् “किसी घूर्णन अक्ष के सापेक्ष किसी पिण्ड का जड़त्त आघूर्ण उसकी घूर्णन ऊर्जा के दोगुने के तुल्य है जो पिण्ड में एकांक कोणीय वेग की अवस्था में होती है।”
यदि कोई पिण्ड अपनी अक्ष पर घूमने के साथ-साथ सरल रेखा में भी गतिमान हो (जैसे चलते हुए वाहनों के पहिए) तो उसकी कुल गतिज ऊर्जा उसकी घूर्णन गतिज ऊर्जा एवं रेखीय गतिज ऊर्जा के योग के बराबर होगी। अर्थात्
\(E_{\text {total }}=E_K+E_R[latex]
या [latex]E_{\text {total }}=\frac{1}{2} m v^2+\frac{1}{2} I \omega^2\) ………..(2)

प्रश्न 11.
सिद्ध कीजिए
उत्तर:
द्रव्यमान केन्द्र की गति (Motion of Centre of Mass) :
माना एक निकाय n कणों से मिलकर बना है, जिसके द्रव्यमान \(m_1, m_2, m_3 \ldots . m_n\) हैं तथा स्थिति सदिश \(\overrightarrow{r_1}, \overrightarrow{r_2}, \vec{r}_3, \ldots . \vec{r}_n\) हैं। द्रव्यमान केन्द्र की परिभाषा के अनुसार इस निकाय के द्रव्यमान केन्द्र की स्थिति

न्यूटन के द्वितीय नियम से, पहले कण पर बल \(\vec{F}_1=m_1 \vec{a}_1\) तथा द्वितीय कण पर बल \(\overrightarrow{F_2}=m_2 \overrightarrow{a_2}\) तथा इसी प्रकार अन्य सभी कणों के लिए बल लेते हैं। अत:
\(M \overrightarrow{a c m}_{c m}=\vec{F}_1+\vec{F}_2+\ldots . \vec{F}_n=\sum_{i=1}^n \vec{F}_i\)
सभी कणों पर लगने वाले बाह्य बलों का योग \(\vec{F}=\sum_{i=1}^n \vec{F}_i\) है। कणों के मध्य लाने वाले आन्तरिक बल, बराबर तथा विपरीत युग्म में होते हैं। अत: वे परस्पर निरस्त हो जाते हैं। इस प्रकार
\(M \overrightarrow{a_{c m}}=\vec{F}=\overrightarrow{F_{\mathrm{ext}}}\)
अत: निकाय का द्रव्यमान तथा द्रव्यमान केन्द्र के त्वरण का गुणनफल निकाय पर आरोपित बाह्म बलों के सदिश योग के बराबर होता है।

प्रश्न 12.
दिखाइये कि क्षैतिज से 8 कोण पर झुके तल पर बिना फिसले लुढ़कने वाले पिण्ड के द्रव्यमान केन्द्र का त्वरण निम्न सम्बन्ध द्वारा दिया जाता है-
\(a=\frac{g \sin \theta}{1+\frac{K^2}{R^2}}\)
जहाँ गुरुत्वीय त्वरण; K पिण्ड की घूर्णन त्रिज्या एवं R त्रिज्या है।
उत्तर:
नत तल पर लोटनी गति (Rolling Motion on Inclined Plane):
जब आनत तल पर कोई पिण्ड बिना फिसले लुढ़कता है तो पिण्ड की इस गति को लोटनी गति कहते हैं। इस गति में पिण्ड अपने द्रव्यमान केन्द्र के परित: अक्ष के सापेक्ष घूर्णन गति करती है तथा साथ ही वस्तु का द्रव्यमान केन्द्र भी आगे बढ़ता है। इस प्रकार लोटनी गति में स्थानान्तरीय एवं घूर्णन गति दोनों प्रकार की गति होती है। नत तल पर जब वस्तु नीचे की ओर लोटनी गति करती है तो पिण्ड की स्थितिज ऊर्जा कम होती है और गतिज ऊर्जा बढ़ती है।

माना एक नत तल θ° के कोण पर झुका है और तल के शीर्ष की ऊँचाई h है। शीर्ष से कोई पिण्ड स्वतन्त्रतापूर्वक नत तल पर छोड़ दिया जाता है तो लोटनी गति करते हुए नीचे आती है। तल के आधार पर पहुँचने पर पिण्ड की सम्पूर्ण स्थितिज ऊर्जा (M g h), पिण्ड की गतिज ऊर्जा \(\left(\frac{1}{2} M v^2\right)\) एवं घूर्णन ऊर्जा \(\left(\frac{1}{2} I \omega^2\right)\) में बदल जाती है। अत:

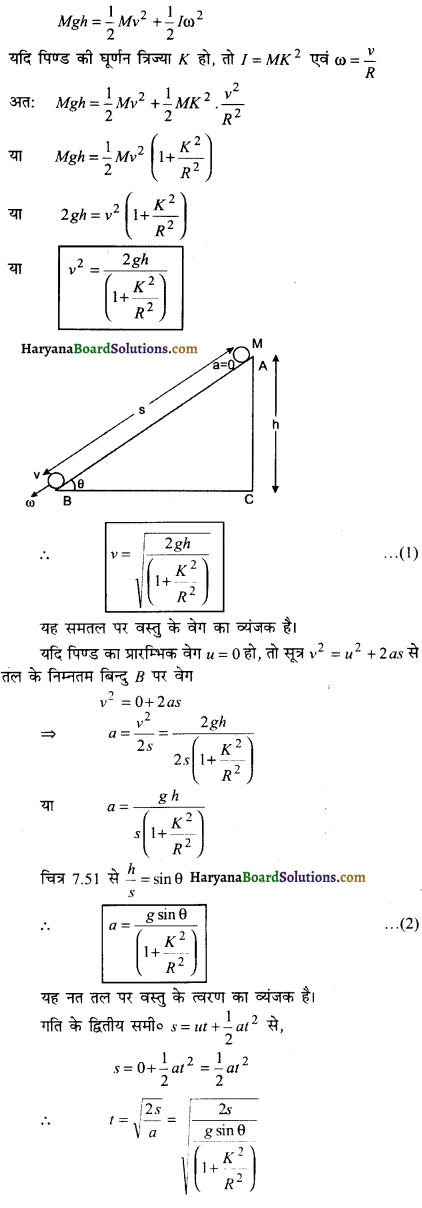
प्रश्न 13.
कोणीय संवेग संरक्षण का सिद्धान्त उदाहरण सहित समझाइये।
उत्तर:
कोणीय संवेग संरक्षण का नियम (Law of Conservation of Angular Momentum):
जब कोई पिण्ड एक बाह्य बल आघूर्ण के अन्तर्गत किसी अक्ष के सापेक्ष घूर्णन गति करता है तो पिण्ड के कोणीय संवेग परिवर्तन की दर उस पर लगने वाले बल आघूर्ण के बराबर होती है। अर्थात्
\(\vec{\tau}=\frac{d \vec{J}}{d t}\)
\(\text { यदि } \vec{\tau}=0 \text { तो } \frac{d \vec{J}}{d t}=0\)
\(\text { या } \vec{J}\text { नियतांक }\)
\(\text { या } J=I \omega\text { नियतांक }\)
अर्थात् “बाह्य बल आघूर्ण की अनुपस्थिति में कण या पिण्ड का कुल कोणीय संवेग नियत रहता है। यही कोणीय संवेग संरक्षण का नियम है।”
बाह्य बल आघूर्ण की अनुपस्थिति में यदि घूर्णन गति के दौरान किसी पिण्ड का जड़त्व आघूर्ण I₁ से बदलकर I₁ कर दिया जाये तो माना उसका कोणीय वेग ω₁ से ω₂ में बदल जाता है। अतः कोणीय संवेग संरक्षण के सिद्धान्त से,
I₁ω₁ = I₂ω₂ …………(1)

प्रश्न 14.
दृढ़ पिण्डों के संतुलन की व्याख्या कीजिए।
उत्तर:
दृढ़ पिण्डों का संतुलन (Equilibrium of Rigid Bodies):
किसी पिण्ड पर आरोपित बल के कारण स्थानान्तरीय गति उत्पन्न होती है जिसके कारण पिण्ड के रेखीय संवेग में परिवर्तन होता है। रेखीय संवेग में परिवर्तन की दर आरोपित बल के बराबर होती है। ठीक उसी प्रकार यदि पिण्ड पर बल आघूर्ण क्रिया करता है तो पिण्ड घूर्णन गति करता है, जिसके कारण पिण्ड के कोणीय संवेग में परिवर्तन होता है और कोणीय संवेग में परिवर्तन की दर आरोपित बल आघूर्ण के बराबर होती है।

यदि बाह्म बल का मान शून्य हो जाये तो रेखीय संवेग नियत हो जाता है और यदि बल आघूर्ण शून्य हो जाये तो कोणीय संवेग का मान नियत हो जाता है। अत: स्पष्ट है बाह्य बल एवं बल आघूर्ण दोनों शून्य होने पर पिण्ड का रेखीय त्वरण एवं कोणीय त्वरण दोनों शून्य हो जाते हैं।
” किसी दृढ़ पिण्ड को यांत्रिक संतुलन की अवस्था में तब कहा जाता है जब इसके रेखीय व कोणीय दोनों प्रकार के संवेग समय के साथ न बदलें।” अर्थात् पिण्ड में न तो रेखीय त्वरण हो और न ही कोणीय त्वरण हो। इस प्रकार किसी पिण्ड के यांत्रिक संतुलन के लिए-
(i) पिण्ड पर लगने वाले सभी बलों का सदिश योग शून्य होना चाहिए, अर्थात्
\(\vec{F}_1+\vec{F}_2+\ldots+\vec{F}_n=\sum_{i=1}^n F_i=0\) …………(1)
यदि पिण्ड पर लगने वाला कुल बल शून्य होगा तो उस पिण्ड के रेखीय संवेग में समय के साथ परिवर्तन नहीं होगा। समी० (1) को पिण्ड के स्थानान्तरीय संतुलन की शर्त कहते हैं।
समी० (1) को x, y व z घटकों के रूप में निम्न प्रकार लिख सकते
हैं-
\(\sum_{i=1}^n \vec{F}_{i x}=0 ; \sum_{i=1}^n \vec{F}_{i y}=0 ; \sum_{i=1}^n \vec{F}_{i z}=0\) ……….(2)

यहाँ F_ix, F_iy व F_iz बल F_i के क्रमशः X, Y व Z दिशाओं में घटक हैं।

(ii) दृढ़ पिण्ड पर लगने वाले बल आघूर्णों का सदिश योग शून्य होना चाहिए, अर्थात्
\(\overrightarrow{\tau_1}+\overrightarrow{\tau_2}+\overrightarrow{\tau_3}+\ldots+\overrightarrow{\tau_n}=\sum_{i=1}^n \overrightarrow{\tau_i}=0\) ………..(3)
यदि पिण्ड पर आरोपित कुल बल आघूर्ण शून्य है तो उसका कुल कोणीय संवेग समय के साथ नहीं बदलेगा। समीकरण (3) को पिण्ड के घूर्णी संतुलन की शर्त है। समी० (3) निम्न तीन समीकरणों के तुल्य हैं-
\(\sum_{i=1}^n \overrightarrow{\tau_{i x}}=0 ; \sum_{i=1}^n \overrightarrow{\tau_{i y}}=0 ; \sum_{i=1}^n \overrightarrow{\tau_{i z}}=0\)

जहाँ, τ_ix, τ_iy व τ_iz क्रमशः X, Y व Z दिशाओं में τ_i के घटक हैं। समीकरण (2) व (4) किसी दृढ़ पिण्ड के यांत्रिक संतुलन के लिए आवश्यक छः ऐसी शर्तें बताते हैं जो एक-दूसरे पर निर्भर नहीं करती हैं।

यदि किसी पिण्ड पर लगने वाले बल एक तल में हों तो पिण्ड के यांत्रिक संतुलन के लिए केवल तीनों शर्तों का पूर्ण होना आवश्यक होगा। इनमें से दो शर्तें स्थानान्तरीय संतुलन के संगत होंगी जिनके अनुसार सभी बलों के इस तल स्वच्छ चुनी गईं दो परस्पर लम्बवत् अक्षों के अनुदिश अवयवों का सदिश योग अलग-अलग शून्य होगा। तीसरी शर्त घूर्णी संतुलन के संगत है। बलों के तल के अभिलम्बवत् अक्ष के अनुदिश बल आघूर्णों का सदिश योग शून्य होगा।

एक पिण्ड आंशिक संतुलन में तभी हो सकता है अर्थात् दृढ़ पिण्ड स्थानान्तरीय संतुलन में तो हो, परन्तु घूर्णी संतुलन में न हो या फिर घूर्णी संतुलन में तो हो परन्तु स्थानान्तरीय संतुलन में न हो।

सुमेलन सम्बन्धित प्रश्न
(Matrix Matching Type Questions)

प्रश्न 1.
पृथ्वी की त्रिज्या व द्रव्यमान M है। यदि पृथ्वी की त्रिज्या सिकुड़कर आधी हो जाये जबकि उसका द्रव्यमान परिवर्तित न हो तो स्तम्भ को स्तम्भ ।। से सुमेलित कीजिए ।

स्तम्भ – I	स्तम्भ – II
(A) पृथ्वी का कोणीय वेग	(P) दो गुना हो जायेगा
(B) पृथ्वी के अपनी अक्ष के परितः घूर्णन का परिक्रमण काल	(Q) चार गुना हो जायेगा
(C) पृथ्वी की घूर्णन गतिज ऊर्जा	(R) नियत रहेगा
	(S) कोई नहीं

उत्तर:

स्तम्भ – I	स्तम्भ – II
(A) पृथ्वी का कोणीय वेग	(R) नियत रहेगा
(B) पृथ्वी के अपनी अक्ष के परितः घूर्णन का परिक्रमण काल	(S) कोई नहीं
(C) पृथ्वी की घूर्णन गतिज ऊर्जा	(Q) चार गुना हो जायेगा

प्रश्न 2.
सूची (A) तथा सूची (B) को सुमेलित कीजिए ।

स्तम्भ – I	स्तम्भ – II
(A) वृत्ताकार वलय ( इसके केन्द्र से गुजरने वाली एवं इसके तल के लम्बवत् अक्ष)	(P) \(I=\frac{2}{5} M R^2\)
(B) वृत्ताकार डिस्क (ज्यामितीय अक्ष)	(Q) \(I=\frac{2}{3} M R^2\)
(C) ठोस गोला (व्यास)	(R) \(I=\frac{1}{2} M R^2\)
(D) खोखला गोला (व्यास)	(S) \(I=M R^2\)

उत्तर:

स्तम्भ – I	स्तम्भ – II
(A) वृत्ताकार वलय ( इसके केन्द्र से गुजरने वाली एवं इसके तल के लम्बवत् अक्ष)	(S) \(I=M R^2\)
(B) वृत्ताकार डिस्क (ज्यामितीय अक्ष)	(R) \(I=\frac{1}{2} M R^2\)
(C) ठोस गोला (व्यास)	(P) \(I=\frac{2}{5} M R^2\)
(D) खोखला गोला (व्यास)	(Q) \(I=\frac{2}{3} M R^2\)

आंकिक प्रश्न (Numerical Questions )

द्रव्यमान केन्द्र पर आधारित प्रश्न
प्रश्न 1.
1 kg तथा 3 kg के दो कण क्रमश: \((2 \hat{i}+3 \hat{j})\) तथा \((3 \hat{i}-4 \hat{j})\) ms^-1 के वेग से गतिमान हैं। द्रव्यमान केन्द्र का वेग बताइये।
उत्तर:
\(\frac{1}{4}(11 \hat{i}-9 \hat{j})\)

प्रश्न 2.
तीन बिन्दु द्रव्यमान m₁ = 1kg, m₂ = 2 kg एवं m₃ = 3 kg एक समबाहु त्रिभुज के तीनों शीर्षो पर स्थित हैं। त्रिभुज की प्रत्येक भुजा की लम्बाई ० है द्रव्यमान केन्द्र की स्थिति के सापेक्ष
उत्तर:
\(-\left(\frac{7}{12} a, \frac{3 \sqrt{3}}{12} a, 0\right)\)

प्रश्न 3.
दो कणों के एक निकाय में, कणों के द्रव्यमान क्रमशः 2 व 5 kg हैं। इनकी स्थितियाँ t = 0 पर क्रमश: \((4 \hat{i}+3 \hat{j})\) तथा \((6 \hat{i}-3 \hat{j}+7 \hat{k})\) m हैं तथा उनके वेग क्रमशः \((10 \hat{i}-6 \hat{k})\) तथा \((3 \hat{i}+6 \hat{j})\) ms^-1 है। इस कण तन्त्र के द्रव्यमान केन्द्र का वेग ज्ञात कीजिए | समय t = 0 तथा t = 4 पर द्रव्यमान केन्द्र की स्थितियाँ क्या होंगी?
उत्तर:
\(v_{C M}=\frac{1}{7}(35 \hat{i}+30 \hat{j}-12 \hat{k}) \mathrm{ms}^{-1}\)
\(t=0 \text { पर } \overrightarrow{r_{C M}}=\frac{1}{7}(38 \hat{i}-29 \hat{j}+35 \hat{k}) \mathrm{m}\)
\(t=4 \text { पर } \overrightarrow{r_{C M}}=\frac{1}{7}(178 \hat{i}+91 \hat{j}-13 \hat{k}) \mathrm{m}\)

बल आघूर्ण, कोणीय संवेग तथा घूर्णन गति के नियमों पर आधारित प्रश्न

प्रश्न 4.
m द्रव्यमान का एक कण वेग से क्षैतिज से 6 कोण पर फेंका जाता है जब कण महत्तम ऊँचाई पर पहुँचता हैं तब प्रक्षेपण बिन्दु के परितः कोणीय संवेग ज्ञात कीजिए।
उत्तर-
\(\frac{m v^3 \sin ^2 \theta \cos \theta}{2 g}\)

प्रश्न 5.
0.05 kg.m² जड़त्व आघूर्ण वाला एक गतिमान पहिया 10 चक्कर / मिनट से अपने अक्ष के परितः घूर्णन कर रहा है। उसको 5 गुना तेजी से घुमाने के लिए और कितना कार्य करना पड़ेगा?
उत्तर:
0.6573 J

प्रश्न 6.
20 kg द्रव्यमान का एक पिण्ड 0.20m व्यास के वृत्ताकार पथ पर 3 सेकण्ड में 100 चक्कर की दर से घूम रहा है। ज्ञात कीजिए – (i) पिण्ड की घूर्णन गतिज ऊर्जा, (ii) पिण्ड का कोणीय संवेग, r = 9.86
उत्तर:
(i) 4.382×10³ J
(ii) 41.87 J.s.

प्रश्न 7.
किसी वलय (ring) का जड़त्व आघूर्ण 0.40 kg.m² है। यदि यह प्रति मिनट 2100 चक्कर लगा रही हो तो इसे 2s में रोकने के लिए कितने बल आघूर्ण की आवश्यकता होगी?
उत्तर:
44 N.m

प्रश्न 8.
एक व्यक्ति अपने हाथों में 10-10 kg के गोले लेकर 2s में 1 चक्कर लगाने वाली घूमती मेज पर खड़ा है। उसकी भुजाएं फैली हैं तथा प्रत्येक गोला घूर्णन अक्ष से 3 m दूर है। यदि वह व्यक्ति गोलों को दूर फेंक दे तो मेज का नया कोणीय वेग क्या होगा? व्यक्ति सहित मेज का जड़त्व आघूर्ण 15 kg.m² है।
उत्तर:
6.5 चक्कर / सेकण्ड

प्रश्न 9.
5 × 10 kg.m^-4 जड़त्व आघूर्ण की एक चकती अपनी अक्ष के परितः 40 चक्कर / मिनट लगा रही है। यदि 0.02 Kg की मोम की एक गोली अक्ष से 0.08m की दूरी पर धीरे से गिरा दी जाती है। तो अब वह कितने चक्कर प्रति मिनट करेगी?
उत्तर:
31.85 चक्कर / मिनट

प्रश्न 10.
25 cm त्रिज्या तथा 5000 g द्रव्यमान का ऊर्ध्वाधर ठोस पहिया अपनी क्षैतिज धुरी पर घूमने के लिए स्वतन्त्र है। पहिए पर एक डोरी लिपटी है। डोरी को 2 N के बल से 55 तक खींचा जाता है। गणना कीजिए कि पहिया किस कोणीय वेग से घूमने लगेगा? (धुरी घर्षण रहित है।)
उत्तर:
16 rad.s^-1

संतुलन पर आधारित

प्रश्न 11.
समान घनत्व की एक मीटर लम्बी छड़ 40 cm के निशान पर कीलकित की जाती है। 10g द्रव्यमान एक ब्लॉक 10 cm के चिन्ह पर लटकाया जाता है। यदि छड़ सन्तुलित अवस्था में हो तो उसका द्रव्यमान ज्ञात कीजिए।

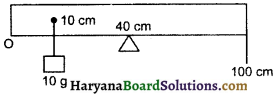
उत्तर:
30 g

प्रश्न 12.
एक छड़ जिसका भार W है, दो समान्तर क्षुरधारों A व B पर आधारित है, क्षैतिज स्थिति में संतुलित है। क्षुरधारों के बीच की दूरी d है। छड़ का द्रव्यमान केन्द्र क्षुरधार A से x दूरी पर है। बिन्दु A व B पर अभिलम्ब प्रतिक्रियाएं ज्ञात कीजिए।
उत्तर:
\(R_A=\frac{W(d-x)}{d} ; R_B=\frac{W \cdot x}{d}\)

जड़त्व आघूर्ण, घूर्णन गतिज ऊर्जा तथा संरक्षण के नियमों पर आधारित

प्रश्न 13.
लकड़ी के हल्के मीटर पैमाने 18 पर 200 g व 300 g के भार क्रमश: 20 cm व 70 cm के चिन्हों पर रखे हैं। इस निकाय का जड़त्व आघूर्ण (i) 0cm; (ii) 50 cm (iii) 100 cm वाले चिन्हों से गुजरने वाली तथा मीटर पैमाने के लम्बवत् अक्षों के परितः ज्ञात
कीजिए।

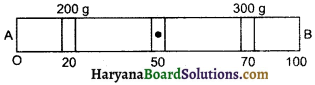
उत्तर:
(i) 15.5 × 10⁵ g.cm²;
(ii) 3 × 10⁵ g.cm²;
(iii) 5.9 × 10⁵ g.cm²

प्रश्न 14.
एक वृत्ताकार चकती जिसका द्रव्यमान 49 kg तथा त्रिज्या 50 cm है, अपनी अक्ष के परितः 120 घूर्णन / मिनट की दर से घुमायी जाती है। चकती की गतिज ऊर्जा की गणना कीजिए।
उत्तर:
484J

प्रश्न 15.
एक मीटर लम्बी एक पतली छड़ पर पाँच बिन्दुवत् कण जिनमें प्रत्येक का द्रव्यमान 1 kg है, समान दूरी पर क्रमश: A, B, C, D और E पर चित्र के अनुसार स्थित हैं। छड़ का द्रव्यमान 0.5 है जो केन्द्रीय बिन्दु पर केन्द्रित माना गया है। इस निकाय का जड़त्व आघूर्ण से पारित एवं छड़ के लम्बवत् अक्ष के सापेक्ष ज्ञात कीजिए।
उत्तर:
2 kg.m²

प्रश्न 16.
यदि पृथ्वी अचानक सिकुड़ जाती है जिससे इसकी त्रिज्या पूर्व त्रिज्या की एक तिहाई रह जाये तो अब दिन कितना छोटा हो जायेगा? यह मान लीजिए कि द्रव्यमान अपरिवर्तित रहता है।
उत्तर:
21 घंटे 20 मिनट

प्रश्न 17.
एक पुच्छल तारें की सूर्य से अधिकतम एवं न्यूनतम दूरी क्रमश: 1.4 × 10¹² m एवं 7 × 10¹⁰ m है। यदि सूर्य के निकटतम इसका वेग 6 × 10⁴ ms^-1 है तो दूरस्थ स्थिति में इसका वेग ज्ञात कीजिए। पुच्छल तारे का पथ वृत्ताकार माना गया है।
उत्तर:
3 × 10³ ms^-1

प्रश्न 18.
एक 500 kg द्रव्यमान एवं 1 m त्रिज्या वाला गतिपालक चक्र 500 घूर्णन प्रति मिनट की दर से घूम रहा है। यह मानते हुए कि उसका सम्पूर्ण द्रव्यमान इसकी परिधि पर रहा है, निम्नलिखित की गणना कीजिए।
(i) कोणीय वेग (ii) जड़त्व आघूर्ण (iii) घूर्णन ऊर्जा ।
उत्तर:
(i) 52.33 rad.s^-1
(ii) 500 kg.m²;
(iii) 6.85 × 10⁵ J

लोटनी गति पर आधारित

प्रश्न 19.
10 kg द्रव्यमान तथा 20 cm त्रिज्या का एक गोला 5 mis के रेखीय वेग से एक क्षैतिज पर बिना फिसले लुढ़क रहा है। इसकी कुल गतिज ऊर्जा ज्ञात कीजिए।
उत्तर;
175 J

प्रश्न 20.
एक वृत्ताकार चकती का द्रव्यमान 0.05 kg तथा त्रिज्या 0.01 m है। यह क्षैतिज तल पर 0.05 ms^-1 के वेग से लुढ़कता है। कुल गतिज ऊर्जा की गणना कीजिए।
उत्तर:
9.4 × 10^-5 J