HBSE 11th Class Physics Important Questions Chapter 10 तरलों के यांत्रिकी गुण

Haryana State Board HBSE 11th Class Physics Important Questions Chapter 10 तरलों के यांत्रिकी गुण Important Questions and Answers.

Haryana Board 11th Class Physics Important Questions Chapter 10 तरलों के यांत्रिकी गुण

वस्तुनिष्ठ प्रश्न (Multiple Choice Questions)

प्रश्न 1.
कौन-सा कथन अशुद्ध है-
(a) द्रव के ऊपरी मुक्त तल पर द्रव का दाब शून्य होता है।
(b) किसी बर्तन में भरे द्रव का दाब सभी बिन्दुओं पर समान रहता है।
(c) किसी क्षैतिज तल में द्रव का दाब सभी बिन्दुओं पर समान रहता है।
(d) किसी तल पर द्रव का दाब क्षेत्रफल पर निर्भर नहीं करता है।
उत्तर:
(b) किसी बर्तन में भरे द्रव का दाब सभी बिन्दुओं पर समान रहता है।

प्रश्न 2.
द्रव दाब निर्भर करता है-
(a) केवल गहराई पर
(b) केवल घनत्व पर
(c) केवल गुरुत्वीय त्वरण पर
(d) गहराई, घनत्व तथा गुरुत्वीय त्वरण तीनों पर।
उत्तर:
(d) गहराई, घनत्व तथा गुरुत्वीय त्वरण तीनों पर।

प्रश्न 3.
किसी बाह्य बल के कार्य न करने पर एक छोटी बूँद की आकृति निर्धारित होती है-
(a) द्रव के पृष्ठ तनाव से
(b) द्रव के घनत्व से
(c) द्रव की श्यानता से
(d) वायु के ताप से केवल ।
उत्तर:
(a) द्रव के पृष्ठ तनाव से

प्रश्न 4.
द्रव का पृष्ठ तनाव-
(a) क्षेत्रफल के साथ बढ़ता है
(b) क्षेत्रफल के साथ घटता है
(c) ताप के साथ बढ़ता है
(d) ताप के साथ घटता है।
उत्तर:
(d) ताप के साथ घटता है।

प्रश्न 5.
जल की बड़ी बूँद को छोटी-छोटी बूंदों में फुहारने की क्रिया में-
(a) ताप बढ़ता है
(b) ताप घटता है
(c) पृष्ठीय ऊर्जा घटती है
(d) इनमें से कोई नहीं।
उत्तर:
(b) ताप घटता है

प्रश्न 6.
पेन्ट गन आधारित है-
(a) बरनौली के सिद्धान्त पर
(b) बॉयल के नियम पर
(c) आर्किमिडीज के सिद्धान्त पर
(d) न्यूटन के नियमों पर ।
उत्तर:
(a) बरनौली के सिद्धान्त पर

प्रश्न 7.
सीसे की गोली किसी श्यान द्रव में मुक्त रूप से गिर रही है। गोली का वेग-
(a) बढ़ जाता है
(b) घट जाता है
(c) सदैव समान रहता है
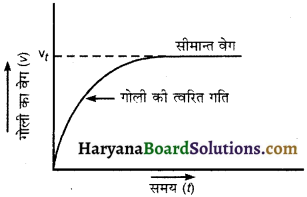
(d) बढ़ता है फिर गोली एक निश्चित वेग से गिरती रहती है।
उत्तर:
(d) बढ़ता है फिर गोली एक निश्चित वेग से गिरती रहती है।

प्रश्न 8.
त्रिज्या की एक छोटी गोली द्रव में गिर रही है। इसका सीमान्त वेग अनुक्रमानुपाती है-
(a) 1/r²
(b) 1/r
(c) r²
(d) r
उत्तर:
(c) r²

प्रश्न 9.
ताप बढ़ने पर गैस की श्यानता-
(a) बढ़ती हैं
(b) घटती है
(c) अपरिवर्तित रहती है
(d) इनमें से कोई नहीं।
उत्तर:
(a) बढ़ती हैं

प्रश्न 10.
बरनौली प्रमेय आधारित है-
(a) संवेग संरक्षण पर
(b) ऊर्जा संरक्षण पर
(c) द्रव्यमान संरक्षण पर
(d) इनमें से किसी पर नहीं।
उत्तर:
(b) ऊर्जा संरक्षण पर

प्रश्न 11.
किसी असमान त्रिज्या वाली नली में जल बह रहा है नली के प्रविष्टि तथा निकासी सिरों पर त्रिज्याओं का अनुपात 5:7 है। नली में प्रविष्ट करने वाले तथा बाहर निकलने वाले जल के वेगों का अनुपात होगा-
(a) 25 : 49
(b) 125 : 343
(c) 49 : 25
(d) 1 : 1.
उत्तर:
(c) 49 : 25

प्रश्न 12.
श्यान द्रव में सीमान्त वेग से गिरने वाले पिण्ड का त्वरण है-
(a) शून्य
(b) g
(c) g से अधिक
(d) g से कम।
उत्तर:
(a) शून्य

प्रश्न 13.
असमान अनुप्रस्थ परिच्छेद के क्षैतिज पाइप में जल बह रहा है। पाइप में संकरे स्थान पर होगा-
(a) वेग अधिक दाब अधिक
(b) वेग कम दाब अधिक
(c) वेग अधिक दाब कम
(d) वेग कम दाब कम ।
उत्तर:
(c) वेग अधिक दाब कम

प्रश्न 14.
दो गोलों की त्रिज्याओं का अनुपात 1:2 है। वे एक श्यान दव में नीचे गिर रहे हैं। इनके सीमान्त वेगों का अनुपात होगा-
(a) 1 : 2
(b) 2 : 1
(c) 1 : 4
(d) 4 : 1.
उत्तर:
(c) 1 : 4

प्रश्न 15.
जल से भरे बर्तन में मुक्त तल से 3-2 मीटर गहराई पर एक छिद्र हो, तो जल का बहिःस्राव वेग है। यदि गुरुत्वीय त्वरण 10 ms^-2 होगा-
(a) 5.7 m/s
(b) 7.5 m/s
(c) 8 m/s
(d) 32 m/s.
उत्तर:
(c) 8 m/s

प्रश्न 16.
मोम युक्त केशनली को जल में डुबाने पर उसमें जल-
(a) ऊपर चढ़ेगा
(b) नीचे गिरेगा
(c) ऊपर चढ़कर फब्बारों के रूप में गिरेगा
(d) पहले चढ़ेगा फिर गिरेगा ।
उत्तर:
(b) नीचे गिरेगा

प्रश्न 17.
एक द्रव ठोस की सतह को नहीं भिगोएगा, यदि स्पर्श कोण है-
(a) 0°
(b) अधिक कोण
(c) 450
(d) 60°
उत्तर:
(b) अधिक कोण

प्रश्न 18.
किसी केशिका में चड़े हुए पानी की ऊँचाई होगी-
(a) 4°C पर अधिकतम
(b) 2°C पर अधिकतम
(c) 4°C पर न्यनतम
(d) 0°C पर न्यूनतम ।
उत्तर:
(c) 4°C पर न्यनतम

प्रश्न 19.
पृष्ठ तनाव के कारण गोलाकार मुड़े हुए पृष्ठ के भीतर दाब आधिक्य होता है-
(a) \(\frac{2T}{r}\)
(b) \(\frac{T}{2r}\)
(c) \(\frac{T}{r_1}+\frac{T}{r_2}\)
(d) \(\frac{T}{r_1}-\frac{T}{r_2}\)
उत्तर:
(c) \(\frac{T}{r_1}+\frac{T}{r_2}\)

प्रश्न 20.
जब पानी की सतह पर तेल डाल दिया जाये तो मच्छर प्रजनन नहीं कर सकते, क्योंकि-
(a) उन्हें ऑक्सीजन नहीं मिलती है
(b) पृष्ठ तनाव कम हो जाता है।
(c) श्यानता बढ़ जाती है
(d) उपर्युक्त में से कोई नहीं।
उत्तर:
(b) पृष्ठ तनाव कम हो जाता है।

प्रश्न 21.
ताप कम करने पर पृष्ठ तनाव होता है-
(a) बढ़ता है
(b) कम होता है
(c) अपरिवर्तित रहता है
(d) इनमें से कोई नहीं।
उत्तर:
(a) बढ़ता है

प्रश्न 22.
रेनॉल्ड्स संख्या का विमीय सूत्र है-
(a) [M⁰L⁰T⁰]
(b) [M^-1L⁰T¹]
(c) [ML⁰T⁰]
(d) [MLT^-2]
उत्तर:
(a) [M⁰L⁰T⁰]

प्रश्न 23.
वायु में अधिक ऊँचाई से जल की बूंद गिरती है। यदि बूँद h ऊँचाई से गिरे तो सीमान्त वेग है-
(a) h के समानुपाती
(b) √h के समानुपाती
(c) \(\frac{1}{h}\) के समानुपाती
(d) h पर निर्भर नहीं करता।
उत्तर:
(d) h पर निर्भर नहीं करता।

प्रश्न 24.
पृथ्वी पर एक केश नली में द्रव स्तम्भ की ऊँचाई h है। चन्द्रमा पर जहाँ गुरुत्वीय त्वरण पृथ्वी का है, यह ऊँचाई है-
(a) \(\frac{h}{6}\)
(b) 6 h
(c) h
(d) शून्य ।
उत्तर:
(b) 6 h

प्रश्न 25.
क्रान्तिक ताप पर पृष्ठ तनाव हो जाता है-
(a) अनन्त
(b) शून्य
(c) ऋणात्मक एवं निश्चित
(d) धनात्मक एवं निश्चित ।
उत्तर:
(b) शून्य

प्रश्न 26.
ताप बढ़ने पर द्रवों तथा गैंसों में श्यानता-
(a) दोनों में बढ़ती है
(b) दोनों में घटती है
(c) द्रवों में बढ़ती है तथा गैसों में घटती है।
(d) द्रवों में घटती है तथा गैसों में बढ़ती है।
उत्तर:
(d) द्रवों में घटती है तथा गैसों में बढ़ती है।

प्रश्न 27.
यदि एक काँच की छड़ को पारे में डुबोकर निकालें तो पारा छड़ से नहीं चिपकता है, क्योंकि-
(a) स्पर्श कोण बहुत छोटा होता है
(b) ससंजक बल अधिक है
(c) आसंजक बल अधिक है।
(d) पारे का घनत्व अधिक है।
उत्तर:
(b) ससंजक बल अधिक है

प्रश्न 28.
पृष्ठ तनाव के कारण बेलनाकार मुड़े हुए पृष्ठ के भीतर दाब आधिक्य होता है-
(a) \(\frac{2T}{r}\)
(b) \(\frac{T}{r}\)
(c) \(2T {\frac{T}{r_1}+\frac{T}{r_2}}\)
(d) \(4T {\frac{T}{r_1}-\frac{T}{r_2}}\)
उत्तर:
(b) \(\frac{T}{r}\)

प्रश्न 29.
चॉक द्वारा श्यामपट्ट पर लिखना किस गुण के कारण सम्भव है-
(a) ससंजक बल
(b) आसंजक बल
(c) पृष्ठ तनाव
(d) श्यानता।
उत्तर:
(b) आसंजक बल

प्रश्न 30.
बैरोमीटर को पहाड़ से खान में ले जाने पर पारे का तल-
(a) गिरेगा
(b) ऊपर उठेगा
(c) उतना ही रहेगा
(d) इनमें से कोई नहीं।
उत्तर:
(b) ऊपर उठेगा

प्रश्न 31.
वायुमण्डलीय दाब में अचानक कमी का संकेत मिलता
(a) तूफान
(b) वर्षा
(c) साफ मौसम
(d) शीत लहर
उत्तर:
(a) तूफान

प्रश्न 32.
संकीर्ण नली के लिये रेनॉल्ड्स संख्या का मान होता है-
(a) 10
(b) 100
(c) 1000
(d) 10000.
उत्तर:
(c) 1000

प्रश्न 33.
एक नली में दाब P पर प्रवाहित जल की दर Q है। यदि नली की त्रिज्या पहले से आधी कर दी जाये तथा दाब को 2P कर दिया जाये तो प्रवाह दर होगी-
(a) 4Q
(b) \(\frac{Q^2}{4}\)
(c) \(\frac{Q}{4}\)
(d) \(\frac{Q}{8}\)
उत्तर:
(d) \(\frac{Q}{8}\)

अतिलघु उत्तरीय प्रश्न (Very Short Answer Questions)

प्रश्न 1.
वायुमण्डलीय दाब के अचानक कम हो जाने पर क्या सूचना प्राप्त होती है ?
उत्तर:
तूफान आने की सूचना प्राप्त होती है।

प्रश्न 2.
सूटकेस के हत्थे चौड़े क्यों बनाए जाते हैं ?
उत्तर: हत्थे चौड़े बनाने से क्षेत्रफल बढ़ जाता है जिससे दाव घट जाता है। यदि ऐसा न किया जाए तो हत्थे हाथ पर अधिक दबाव डालेंगे |

प्रश्न 3.
स्वस्थ मनुष्य का प्रकुंचन रक्त दाब कितना होता है ?
उत्तर:
स्वस्थ मनुष्य का प्रकुंचन रक्त दाब 120mm ऊँचाई वाले पारे के स्तम्भ के दाब के बराबर (120 टॉर) होता है।

प्रश्न 4.
क्या बहते हुए द्रव में दो धारा रेखाएँ एक-दूसरे को काट सकती हैं ?
उत्तर:
नहीं, दो धारा रेखाएँ एक-दूसरे को काटेंगी तो कटान बिन्दु पर द्रव के वेग की दो दिशाएँ होंगी जो कि असम्भव है।

प्रश्न 5.
द्रवों तथा गैसों की श्यानता पर ताप का क्या प्रभाव पड़ता है ?
उत्तर:
द्रवों की श्यानता ताप बढ़ाने पर घटती है जबकि गैसों की श्यानता ताप के बढ़ने पर बढ़ जाती है।

प्रश्न 6.
क्रिकेट तथा टेनिस के खेल में चक्रण करती हुई गेंद अपने मार्ग से घूम जाती है। इसकी व्याख्या किस सिद्धान्त या प्रमेव के आधार पर की जा सकती है ?
उत्तर:
क्रिकेट तथा टेनिस के खेल में चक्रण करती हुई गेंद के अपने मार्ग से घूम जाने की व्याख्या बरनौली प्रमेय के आधार पर की जा सकती है।

प्रश्न 7.
जल, वायु, रक्त तथा शहद को श्यानता के बढ़ते क्रम में लिखिए।
उत्तर:
वायु, जल, रक्त, शहद।

प्रश्न 8.
वर्षा की छोटी बूँदें जमीन पर नियत वेग से पहुँचती हैं, अथवा नियत त्वरण से।
उत्तर:
वायुमण्डल की श्यानता के कारण वर्षा की छोटी बूँदें नियत वेग से गिरती हैं।

प्रश्न 9.
नली में प्रवाहित द्रव की कौन-सी पर्त का वेग सबसे अधिक होता है ?
उत्तर:
नली के अक्ष पर स्थित पर्त का वेग सबसे अधिक होता है।

प्रश्न 10.
किस द्रव में पिण्ड का सीमान्त वेग कम होगा-जल में या ग्लिसरीन में ?
उत्तर:
ग्लिसरीन में, क्योंकि ग्लिसरीन की श्यानता अधिक होती है।

प्रश्न 11.
क्या बरनौली की प्रमेय विक्षुब्ध प्रवाह के लिए भी सत्य है ?
उत्तर:
नहीं, वरनौली की प्रमेय केवल धारा रेखीय प्रवाह के लिए ही सत्य है।

प्रश्न 12.
यदि टंकी में ताजे जल के स्थान पर मिट्टी का तेल भर दें तो क्या मिट्टी के तेल का बाहर निकलने का वेग बदल जायेगा ?
उत्तर:
नहीं, क्योंकि बहिःस्राव वेग द्रव के घनत्व पर निर्भर नहीं करता।

प्रश्न 13.
यदि हम धागे की रील के छेद में ऊपर से फूँक मारें तो उसके निचले सिरे पर रखा गत्ते का टुकड़ा नीचे नहीं गिरता, क्या कारण है ?
उत्तर:
रील व गत्ते के टुकड़े के बीच वायु वेग अधिक हो जाने से दाब वायुमण्डलीय दाब से कम हो जाता है।

प्रश्न 14.
जल के पृष्ठ तनाव को कैसे कम कर सकते हैं ?
उत्तर:
गर्म करके, तेल अथवा साबुन का घोल डालकर ।

प्रश्न 15.
कपड़े पर मोम रगड़ देने पर कपड़ा ‘वाटर प्रूफ’ हो जाता है, क्यों ?
उत्तर:
कपड़े के धागों में बनी केशनलियाँ समाप्त हो जाती हैं।

प्रश्न 16.
थर्मामीटर की नली (काँच) में पारे का भरना कठिन होता है, क्यों ?
उत्तर:
पारे तथा काँच का स्पर्श कोण अधिककोण है, अतः जब थर्मामीटर की नली के एक सिरे को पारे में डुबोते हैं तो उसमें पारे का तल नीचे गिरता है।

प्रश्न 17.
क्या वर्षा की सभी बूँदें (बड़ी और छोटी) एक ही अन्तिम वेग से पृथ्वी पर पहुँचती हैं ?
उत्तर:
नहीं, चूँकि v_t ∝ r², अतः बड़ी बूंद का अन्तिम वेग अधिक होता है।

प्रश्न 18.
समान आकार की लोहे की गेंद और टेनिस की गेंद एक ऊँची मीनार की चोटी से गिराई जाती हैं वायु का अक्षेप तथा श्यानता को ध्यान में रखते हुए यह बताइए कि कौन सी गेंद पृथ्वी पर पहले पहुँचेगी ?
उत्तर:
पहले लोहे की गेंद पहुँचेगी।

प्रश्न 19.
एक बर्तन की तली में एक क्षैतिज केशनली जुड़ी है जिससे प्रति सेकण्ड प्रवाहित द्रव का आयतन Q है। अब यदि इस केशनली के साथ एक अन्य समान लम्बाई व समान त्रिज्या की केशनली को श्रेणीक्रम में जोड़ दिया जाये तो द्रव की प्रवाह दर क्या होगी ?
उत्तर:
\(Q=\frac{πpr^4}{8ηl}\), अत: लम्बाई दुगनी होने पर प्रवाह दर आधी अर्थात् \(\frac{Q}{2}\) रह जायेगी।

प्रश्न 20.
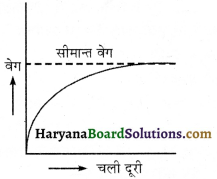
एक छोटी ठोस गोल गेंद किसी श्यान द्रव में छोड़ी जाती है। द्रव में इसके गमन के लिए वेग तथा चली दूरी में अनुमानित ग्राफ खींचिए ।
उत्तर:
वेग तथा चली दूरी के बीच ग्राफ चित्र के अनुसार होगा।

प्रश्न 21.
पॉस्कल नियम के दो अनुप्रयोग लिखिये ।
उत्तर:
द्रवचालिक ब्रेक, द्रवचालित लिफ्ट

प्रश्न 22.
जल के पृष्ठ तनाव को कैसे कम कर सकते हैं ?
उत्तर:
गर्म करके, तेल अथवा साबुन का घोल डालकर ।

प्रश्न 23.
खेतों में बरसात के तुरन्त बाद जुताई कर दी जाती है, क्यों ?
उत्तर:
जुताई करने से मिट्टी में बनी केशनलियों टूट जाती हैं, जिससे मिट्टी के अन्दर का पानी ऊपर चढ़कर वाष्पित नहीं हो पाता है।

प्रश्न 24.
गर्म सूप ठण्डे सूप की अपेक्षा स्वादिष्ट क्यों लगता है ?
उत्तर:
गर्म सूप का पृष्ठ तनाव कम होने से वह जीभ के अधिक पृष्ठ क्षेत्रफल पर फैल जाता है और स्वादिष्ट लगता है।

प्रश्न 25.
तापवृद्धि से स्पर्श कोण के मान पर क्या प्रभाव पड़ता है ?
उत्तर:
स्पर्श कोण कम हो जाता है।

प्रश्न 26.
क्षैतिज नली के लिए बर्नूली सिद्धान्त क्या है ?
उत्तर:
(P₁ – P₂) = \(\frac{1}{2}\) ρ(v₂² – v₁²)

प्रश्न 27.
जल का पृष्ठ तनाव किस ताप पर अधिक होगा ?
उत्तर:
4°C पर ।

प्रश्न 28.
किस पदार्थ की केशनली में जल का नवचन्द्रक समतल होगा ?
उत्तर:
चाँदी की केशनली में।

प्रश्न 29.
पृष्ठ तनाव व पृष्ठ ऊर्जा में क्या सम्बन्ध है ?
उत्तर:
W = T.∆A

प्रश्न 30.
द्रव का पृष्ठ तनाव किस ताप पर शून्य हो जायेगा ?
उत्तर:
क्रान्तिक ताप पर ।

प्रश्न 31.
पृष्ठ तनाव की व्याख्या किन बलों के आधार पर करते
उत्तर:
अंतराणविक बलों के आधार पर।

प्रश्न 32.
फाउन्टेन पेन से अखबार के कागज की लिखावट अस्पष्ट हो जाती है क्या कारण है ?
उत्तर:
अखबार के कागज की केशनलियों से स्याही फैल जाती है।

प्रश्न 33.
श्यानता का CGS मात्रक लिखिए।
उत्तर:
प्वाइज या डाइन- से / सेमी²

प्रश्न 34.
रेनॉल्डस संख्या से क्या तात्पर्य है ?
उत्तर:
यह शुद्ध संख्या है जो पाइप में तरल के प्रवाह की प्रकृति को बताती है।

प्रश्न 35.
पृष्ठ तनाव के लिए उत्तरदायी बल कौन-सा है ?
उत्तर:
ससंजक बल ।

प्रश्न 36.
गर्मियों में सूती कपड़े अधिक आरामदायक होते हैं ?
उत्तर:
सूती कपड़ों में धागों के मध्य केशनलियाँ होती हैं जिनसे पसीना उनमें प्रवेश कर जाता है और वाष्प बनकर उड़ जाता है अतः शरीर को ठण्डक का अनुभव होता है।

प्रश्न 37.
द्रव में हवा का बुलबुला ऊपर क्यों उठता है ?
उत्तर:
क्योंकि हवा के बुलबुले का सीमान्त वेग ऋणात्मक होता है अतः वह ऊपर उठता है।

प्रश्न 38.
बहते हुए द्रव के वेग शीर्ष एवं दाब शीर्ष के सूत्र लिखिए।
उत्तर:
वेग शीर्ष- \(\frac{v^2}{2g}\)
दाब शीर्ष – \(\frac{ρ}{ρg}\)

प्रश्न 39.
भारहीनता की स्थिति में यदि केशनली को पानी में डुबोया जाये तो क्या होगा ?
उत्तर:
भारहीनता की स्थिति में द्रव नली की पूरी लम्बाई तक चढ़ जायेगा।

प्रश्न 40.
एक सुई साफ पानी में तैरती है, लेकिन साबुन के पानी में ‘डूब जाती है। क्यों ?
उत्तर:
साफ पानी का पृष्ठ तनाव साबुन मिले पानी से अधिक होता है, अतः साफ पानी का पृष्ठ तनाव सुई के भार को सन्तुलित कर सकता है।

प्रश्न 41.
किसी बेलनाकार नली में बहते हुए द्रव में किस पर्त का वेग सर्वाधिक होता है ?
उत्तर:
नली की अक्ष के अनुदिश पर्त का।

प्रश्न 42.
केशनली में पारा भरना कठिन क्यों है ?
उत्तर:
काँच के लिए पारे का स्पर्श कोण 135° है अतः यह केशनली में अवनमन दिखाता है।

प्रश्न 43.
यदि टंकी में ताजे जल के स्थान पर समुद्री जल भर दें तो क्या छिद्र से निकलने वाले जल का वेग बदल जाएगा ?
उत्तर:
नहीं, बहिस्राव वेग घनत्व पर निर्भर नहीं करता।

लघुत्तरीय प्रश्न (Very Short Answer Questions)

प्रश्न 1.
लालटेन की बत्ती में मिट्टी का तेल बराबर कैसे चढ़ता रहता है ?
उत्तर:
लालटेन की बत्ती के धागों के बीच में असंख्य केशनलियाँ होती हैं। जब मिट्टी के तेल में डुबोया जाता है तो मिट्टी का तेल इन केशनलियों में से ऊपर चढ़ जाता है।

प्रश्न 2.
दाबमापी में पारे का उपयोग क्यों किया जाता है ?
उत्तर:
इसके निम्न कारण हैं-
(1) पारा केशनली की दीवारों से चिपकता नहीं है।
(2) पारे का घनत्व अधिक होने के कारण प्रयुक्त केशनली की लम्बाई कम होती है।
(3) पारे का वाष्प दाब कम होता है।

प्रश्न 3.
समुद्र की लहरों को शान्त करने के लिए लहरों पर तेल डाल देते हैं, क्यों ?.
उत्तर:
तेल डाल देने पर तेज हवा तेल को जल के पृष्ठ पर हवा की दिशा में दूर तक फैला देती है, बिना तेल वाले जल का पृष्ठ तनाव तेल वाले जल से अधिक होता है, अतः बिना तेल वाला जल, तेल वाले जल को वायु की विपरीत दिशा में खींचता है, जिससे समुद्र की लहरें शान्त हो जाती हैं।

प्रश्न 4.
वायुयान लगभग 10 km की ऊंचाई पर ही उड़ाये जाते हैं जबकि इतनी ऊँचाई तक ले जाने में काफी ईंधन (Fuel) खर्च होता है, क्यों ?
उत्तर:
10 km से कम ऊँचाई पर वायुमण्डल सघन है, इसलिए 10 km से कम ऊँचाई पर वायु की श्यानता प्रभावी होती है। वायु की श्यानता के कारण वायुयान पर पीछे की ओर एक श्यान बल लगेगा, जो वायुवान के वेग के अनुक्रमानुपाती होगा। वायुयान का वेग अधिक होने के कारण श्यान बल भी अधिक होगा। इससे वायुवान गर्म हो जायेगा तथा ईंधन भी अधिक खर्च होगा, यही कारण है कि वायुयान 10 km से कम ऊँचाई पर नहीं उड़ाये जाते ।

प्रश्न 5.
एक असमान परिच्छेद वाले क्षैतिज पाइप में जल बह रहा है। जल का किसी बिन्दु P पर वेग एक अन्य बिन्दु Q पर जल के वेग का चार गुना है। बिन्दु P पर पाइप का व्यास बिन्दु Q के सापेक्ष कितना होगा ?
उत्तर:
सातत्य समीकरण से,
A₁v₁ = A₂v₂
πr₁².v₁ = πr₂².v₂
या \(\frac{\mathrm{D}_1^2}{4} \cdot v_1=\frac{\mathrm{D}_2^2}{4} \cdot v_2\)
या \(\mathrm{D}_1^2 \cdot 4 v_2=\mathrm{D}_2^2 v_2\)
या \(2 \mathrm{D}_1=\mathrm{D}_2 \Rightarrow \mathrm{D}_1=\mathrm{D}_2 / 2\)
अतः व्यास आधा होगा।

प्रश्न 6.
बरसात के बाद किसान भूमि की जुताई करते हैं, क्या कारण है ?
उत्तर:
खेत की जुताई कर देने से मिट्टी में बनी केशनलियाँ टूट जाती हैं, फलस्वरूप नीचे का जल पौधों के काम आता है। जुताई न करने पर मिट्टी में बनी केशनलियों में चढ़कर जल भूमि की सतह पर ऊपर आ जायेगा तथा वाष्प बन कर उड़ जायेगा।

प्रश्न 7.
यदि किसी द्रव व ठोस के बीच स्पर्श कोण 90° से कम हो तो क्या वह द्रव ठोस को भिगोयेगा ? उस ठोस से बनी केशनली में इसका पृष्ठ कैसा होगा ? क्या वह केशनली में चढ़ेगा ?
उत्तर:
भिगोयेगा, अवतल चढ़ेगा।

प्रश्न 8.
किसी ठोस के पृष्ठ और द्रव के बीच ‘स्पर्श कोण’ की परिभाषा लिखिए।
उत्तर:
स्पर्श कोण – “द्रव व ठोस के किसी स्पर्श विन्दु से द्रव के तल पर खींची गई स्पर्श रेखा तथा ठोस के तल पर द्रव के अन्दर की ओर खींची गई स्पर्श रेखा के बीच बने कोण को उस द्रव एवं ठोस के लिए स्पर्श कोण कहते हैं।

प्रश्न 9.
तेल में छोड़ी गई पानी की बूंद क्यों सिकुड़ जाती है?
उत्तर:
जल के अणुओं के बीच ससंजक बल, जल व तेल के अणुओं के बीच आसंजक बल की तुलना में अधिक शक्तिशाली होता है जब जल की बूँद तेल की सतह पर डाली जाती है तो जल के अणु ससंजक बलों के कारण परस्पर चिपके रहकर गोल आकृति ग्रहण किए रहते हैं तथा सतह पर नहीं फैलते हैं।

प्रश्न 10.
पृष्ठ तनाव को प्रभावित करने वाले कारक लिखिए।
उत्तर:
पृष्ठ तनाव को प्रभावित करने वाले कारक (Factors Affecting Surface Tension):

• ताप का प्रभाव (Effect of temperature): ताप बढ़ने पर पृष्ठ तनाव रेखीय रूप से घटता है।
  लेकिन पिघले ताँबे तथा कैडमियम के लिए ताप बढ़ाने पर पृष्ठ तनाव बढ़ता है।
• संदूषण पर (On Contamination): जल की सतह पर मिट्टी के कण या चिकनाई युक्त पदार्थ उपस्थित होने पर जल का पृष्ठ तनाव घट जाता है।
• विद्युतीकरण पर (On electrification): विद्युतीकरण के कारण द्रव का पृष्ठ तनाव घट जाता है क्योंकि इसके कारण द्रव के मुक्त पृष्ठ के लम्बवत् बाहर की तरफ बल लगता है।
• विलेय पदार्थ का प्रभाव (Effect of solute): सामान्यतः किसी द्रव में विलेय पदार्थ घुला हो तो उसका पृष्ठ तनाव कम हो जाता है। जल में साबुन या फीनॉल डालने पर उसका पृष्ठ तनाव घट जाता है, परन्तु यदि विलेय पदार्थ बहुत घुलनशील है तो द्रव का पृष्ठ तनाव बढ़ जाता है।

प्रश्न 11.
चक्रण गति करती हुई गेंद के पथ में परिवर्तन का कारण समझाइए है ?
उत्तर:
मैगनस प्रभाव (Magnus Effect):
टेनिस या क्रिकेट के खिलाड़ी जब गेंद को स्पिन (spin) करते हुए फेंकते हैं तो गेंद वायु में एक सरल रेखा पर न चलकर एक वक्राकार पथ पर चलती है जिसे गेंद का स्विंग (swing) करना कहते हैं। इसका कारण यह है कि जब गेंद स्पिन करती है तो उसके साथ-साथ उसके चारों ओर की वायु भी v वेग से घूमती है । स्पिन करती हुई गेंद जब आगे बढ़ती है तो गेंद के आगे की वायु गेंद द्वारा छोड़े गए खाली स्थान को भरने के लिए u वेग से पीछे की ओर दौड़ती है। गेंद के ऊपर वायु की धारा रेखाओं की दिशा गेंद की स्पिन गति के विपरीत है, अतः गेंद के ऊपर वायु का परिणामी वेग (u – v) हो जाता है। गेंद के नीचे वायु की धारा रेखाओं की दिशा गेंद की स्पिन गति की दिशा में है, अतः गेंद के नीचे वायु का परिणामी वेग (u + v) हो जाता है ।

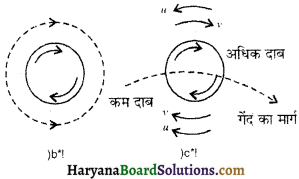
इस प्रकार गेंद के ऊपर वायु का वेग घट जाता है तथा नीचे बढ़ जाता है, अतः बर्नूली की प्रमेय के अनुसार गेंद के ऊपर वायुदाब अधिक तथा गेंद के नीचे वायुदाब कम हो जाता है। इस दाबान्तर के कारण गेंद सरल रेखा में न चलकर नीचे की ओर झुकते हुए वक्राकार पथ पर चलती है, इसे मैगनस प्रभाव कहते हैं।

प्रश्न 12.
जल की छोटी बूँदें फुहारने से ठण्डक क्यों उत्पन्न होती
उत्तर:
पृष्ठ तनाव पर आधारित दैनिक घटनाएँ (Events in Daily Life Based on Surface Tension):
(i) सीसे के छर्रे बनाना-सीसे के गोल छर्रे बनाने के लिए पिघलते हुए सीसे को धीरे: धीरे ऊँचाई से पानी पर गिराते हैं। पृष्ठ तनाव के कारण गिरते समय पिघला हुआ सीसा न्यूनतम पृष्ठ क्षेत्रफल घेरता हुआ गोलीय आकृति धारण कर लेता है तथा पानी में पहुँचने पर ठोस बन जाता है। इस प्रकार सीसे के छोटे-छोटे गोल छर्डे बन जाते हैं। छर्रा जितना अधिक बड़ा होगा, गुरुत्व बल उतना ही अधिक प्रभावी होगा तथा छर्रा भी उतना ही अधिक चपटा हो जायेगा।

(ii) जल की अपेक्षा साबुन के घोल के अधिक बड़े बुलबुले बनाए जा सकते हैं: साबुन के घोल का पृष्ठ तनाव शुद्ध जल की अपेक्षा कम होता है। पृष्ठ तनाव कम होने का अर्थ है कि द्रव के पृष्ठ की न्यूनतम क्षेत्रफल घेरने की प्रवृत्ति कम हो जाती है, अतः साबुन के घोल के अधिक बड़े बुलबुले बनाए जा सकते हैं जबकि जल के बड़े बुलबुले अधिक पृष्ठ तनाव के कारण टूट जाते हैं।

(iii) साबुन मिले हुए गरम जल से शुद्ध जल की अपेक्षा कपड़ों की धुलाई अधिक साफ होती है: साबुन के घोल का पृष्ठ तनाव शुद्ध जल की अपेक्षा काफी कम होता है, अतः साबुन के घोल की एक बूँद शुद्ध जल की एक बूँद की अपेक्षा कपड़े के अधिक क्षेत्रफल को भिगोती है।
इस प्रकार साबुन का घोल कपड़े के बारीक छिद्रों में घुसकर, वहाँ जमे मैल को अपने साथ चिपकाकर बाहर निकाल लाता है (क्योंकि घोल व मैल के बीच आसंजक बल का मान, घोल के अपने ससंजक बल के मान से अधिक होता है); यदि घोल को गरम कर दिया जाए तो उसका पृष्ठ तनाव और भी कम हो जाता है। इस प्रकार साबुन मिले हुए गरम जल से शुद्ध जल की अपेक्षा कपड़ों की धुलाई अधिक साफ होती है।

(iv) काँच की नली के सिरों का गर्म होने पर गोल हो जाना: जब काँच की एक नली को बर्नर की ज्वाला में गर्म करते हैं तो काँच पिघलकर द्रव बन जाता है। इस द्रव का पृष्ठ कम-से-कम क्षेत्रफल घेरने का प्रयत्न करता है। चूँकि दिए हुए आयतन के लिए गोले का क्षेत्रफल न्यूनतम होता है, अतः पिघला हुआ काँच गोले की आकृति लेने का प्रयत्न करता है जिससे नली के सिरे गोल हो जाते हैं।

(v) फुहारने से ठण्डक उत्पन्न होती है: जब किसी द्रव को फुहारा जाता है तो उसकी असंख्य छोटी-छोटी बूँदें बन जाती हैं। जिससे द्रव का पृष्ठीय क्षेत्रफल बहुत बढ़ जाता है। इस प्रक्रिया में द्रव के भीतर के अणु ऊपर उठकर बूँदों के पृष्ठ पर पहुँचते हैं जिसके लिए उन्हें ससंजक बल के विरुद्ध कार्य करना पड़ता है। इससे द्रव की आन्तरिक ऊर्जा कम हो जाती है और बूँदों का ताप गिर जाता है।

प्रश्न 13.
यदि कोई वस्तु असमरूपी होती है तो वस्तु तरल में घूमने क्यों लग जाती है ?
उत्तर:
यह इसलिए होता है क्योंकि गुरुत्व केन्द्र, उत्प्लावन केन्द्र के सम्पाती नहीं होता है। इस कारण वस्तु का भार तथा द्रव का उत्प्लावक बल एक बल युग्म का निर्माण करते हैं। इस बल युग्म का आघूर्ण ही वस्तु को घूर्णन गति कराने के लिए उत्तरदायी है।

प्रश्न 14.
दोनों सिरों पर खुली केशनली को जल में डुबाने पर केशनली में जल कुछ ऊपर तक क्यों चढ़ जाता है ?
उत्तर:
केशनली के भीतर, अवतल जल पृष्ठ के नीचे दाब, पृष्ठ के ऊपर वाले दाब से 2T / R कम होता है,
अतः केशनली के बाहर जल का आधिक्य दाब, केशनली में अतिरिक्त जल भेजकर जल को कुछ ऊपर तक चढ़ा देता है।

प्रश्न 15.
वह कपास जिसमें चर्बी तथा चिकनाई अलग कर दी जाती है, अधिक जल अवशोषित करती है, क्यों ?
उत्तर:
जब कपास को जल में डुबाते हैं तो उसमें बनी केशिकाओं में पृष्ठ तनाव के कारण जल चढ़ता है जिसकी ऊँचाई पृष्ठ तनाव पर निर्भर करती है। चिकनी कपास के सम्पर्क में जल का पृष्ठ तनाव घट जाता है जिससे जल कम ऊपर चढ़ता है।

प्रश्न 16.
भारहीनता की अवस्था में (जैसे कृत्रिम उपग्रह में) यदि किसी केशनली को जल में डुबोया जाये तो उसमें जल का चढ़ना सामान्य अवस्था में जल के चढ़ने से किस प्रकार भिन्न होगा ?
उत्तर:
सामान्य अवस्था में पृष्ठ तनाव का बल (जिसके कारण जल केशनली में चढ़ता है) जब नली में चढ़े जल-स्तम्भ के भार के बराबर हो जाता है तो जल का चढ़ना रुक जाता है। भारहीनता की अवस्था में (g = 0) नली में चढ़ने वाले जल-स्तम्भ का प्रभावी भार शून्य होगा। अतः जल केशनली के दूसरे सिरे पर पहुँच जायेगा चाहे केशनली कितनी ही लम्बी क्यों न हो ?

प्रश्न 17.
गर्म सूप ठण्डे सूप की अपेक्षा अधिक स्वादिष्ट लगता है, क्यों ?
उत्तर:
द्रव का ताप बढ़ने पर पृष्ठ तनाव कम हो जाता है जिस कारण गर्म सूप का पृष्ठ तनाव ठण्डे सूप की अपेक्षा कम हो जाता है पृष्ठ तनाव कम होने के कारण द्रव का क्षेत्रफल अधिक हो जाता है जिससे गर्म सूप जीभ के अधिक क्षेत्रफल में फैल जाता है और अधिक स्वादिष्ट लगता है।

प्रश्न 18.
आकाश में बादल तैरते क्यों दिखाई देते हैं ?
उत्तर:
जब वायु में उपस्थित जल की वाप्य धूल, धुएँ आदि के कणों पर संघनित होती है तो प्रारम्भ में बहुत छोटी बूँदें बनती हैं। जब ये बूँदें नीचे गिरती हैं तो वायु द्वारा इन पर ऊपर की ओर श्यान बल लगाया जाता है, अतः कुछ समय बाद ये बूँदें सीमान्त वेग से नीचे गिरने लगती हैं। चूँकि बूँदें बहुत ही छोटी होती हैं, अतः इनका सीमान्त वेग बहुत कम होता है। जिससे ये नीचे गिरने की बजाय आकाश में तैरती प्रतीत होती हैं, ऐसी अवस्था में इन्हें ‘बादल’ (clouds) कहते हैं।

प्रश्न 19.
फब्बारे के ऊपर हल्की गेंद क्यों टिकी रहती है ? नीचे क्यों नहीं गिर जाती ?
उत्तर:
गेंद फब्बारे की जल धारा पर ऊपर-नीचे नाचती रहती है, जल धारा से अलग होकर गिरती नहीं है, क्योंकि बरनौली प्रमेय के अनुसार जल फुहार का वेग अधिक होने के कारण वहाँ दाब कम रहता है, अतः जब भी गेंद जल धारा से बाहर आने की कोशिश करती है तो के दाब से जल धारा के भीतर कम दाब की ओर पुनः खिंच जाती है।

प्रश्न 20.
आँधी में टीन की छतें क्यों उड़ जाती हैं ?
उत्तर:
आँधी में टीन की ऊपरी सतह पर से वायु का वेग अधिक होने के कारण बरनौली प्रमेय के अनुसार वायु की गतिज ऊर्जा बढ़ जाने से इसकी सतह पर वायु दाब टीन की निचली सतह पर वायु दाब की तुलना में कम हो जाता है। अतः टीन की नीचे की सतह के अधिक दाब के कारण टीन की छतें आँधी में उड़ जाती हैं।

प्रश्न 21.
वर्षां की बूंदें अन्त में नियत वेग से क्यों गिरती हैं ?
उत्तर:
जब वर्षा की बूँदें अपने भार के कारण पृथ्वी की ओर गिरती हैं तो वायु की श्यानता इनके गिरने का विरोध करती है। गुरुत्व के कारण जैसे-जैसे बूँदों के नीचे गिरने का वेग बढ़ता है, स्टोक्स के नियमानुसार वैसे-वैसे इसके विरुद्ध वायु का श्यान बल भी बढ़ता जाता है। एक विशेष स्थिति में विरोधी श्वान बल नीचे की ओर कार्य करने वाले प्रभावी गुरुत्व बल के बराबर हो जाता है। इस दशा में अन्त में बूँदें एक निश्चित सीमान्त वेग से गिरती हैं।

प्रश्न 22.
गहरा जल सदैव शान्त बहता है, कारण बताइए।
उत्तर:
बरनौली प्रमेय के अनुसार किसी द्रव के क्षैतिज प्रवाह के लिए P+ +2pv2 = नियतांक; अत: गहरे जल का दाब (P) अधिक होने से वेग ” का मान कम होता है।

प्रश्न 23.
जल की एक बड़ी बूँद को अनेक छोटी-छोटी बूँदों में विभाजित करने पर पृष्ठीय ऊर्जा में क्या परिवर्तन होगा ?
उत्तर:
एक बड़ी बूँद को अनेक छोटी बूंदों में विभाजित करने पर, जल का मुक्त पृष्ठ क्षेत्रफल बढ़ेगा। अतः पृष्ठीय ऊर्जा भी बढ़ेगी।

प्रश्न 24.
वर्षा की बूँदे अनन्त से नियत वेग से क्यों गिरती है ?
उत्तर:
जब बूँद वायु में नीचे गिरती है तो उस पर 40 लगने वाले बल चित्र में दर्शाए हैं। इन बलों में दो बल नियत रहते हैं- (i) बूँद का भार mg एवं बूँद पर ऊपर उछाल U; लेकिन स्टोक्स बल F = 6πnrv का मान बूँद का वेग बढ़ने के साथ बढ़ता हैं एक स्थिति ऐसी आती है जब बूंद का भार ऊपर की ओर लगने वाले बलों के योग के बराबर हो जाता है तो परिणामी बल शून्य हो जाने के कारण बूँद नियत वेग से गिरने लगती है।

प्रश्न 25.
हिमखण्ड जल पर क्यों तैरता है ?
उत्तर:
हिमखण्ड का घनत्व जल के घनत्व से कम होता है, जिससे हिमखण्ड के आयतन के बराबर जल का mig उत्क्षेप-बल हिमखण्ड के भार से अधिक हो जाता है और हिमखण्ड जल पर तैरता रहता है। तैरते समय हिमखण्ड का केवल उतना आयतन ही जल में डूबता है, जितने आयतन के द्वारा हटाये गये जल का भार हिमखण्ड के भार के बराबर होता है।

प्रश्न 26.
काँच की छड़ के सिरे को उच्च ताप पर गर्म करने पर सिरा गोल क्यों हो जाता है ?
उत्तर:
जब काँच को गर्म करते हैं तो वह पिघलकर द्रव बन जाता है। इस द्रव का पृष्ठ कम-से-कम क्षेत्रफल घेरने का प्रयत्न करता है। हम जानते हैं कि दिये हुए आयतन के लिये गोले के पृष्ठ का क्षेत्रफल सबसे कम होता है। अतः पिघला हुआ काँच गोले का रूप लेने का प्रयत्न करता है जिससे कि नली के किनारे गोल हो जाते हैं।

प्रश्न 27.
चिपकन रहित खाना पकाने के लिए बर्तन पर टेफ्लॉन की परत क्यों चढ़ाई जाती है ?
उत्तर:
बर्तनों पर टेफ्लॉन की परत चढ़ाई जाती है, क्योंकि टेफ्लॉन की परत तथा तेल आदि के बीच का स्पर्श कोण 90° से अधिक होता है। इसके कारण वर्तन चिपकन रहित हो जाता है।

प्रश्न 28.
पास-पास लटकी दो हल्की गेंदों के मध्य फूँक मारने पर वे एक-दूसरे की ओर आकर्षित होती हैं क्यों ?
उत्तर:
फूँक मारने पर गेंदों के बीच का वायु वेग बढ़ जाता है, अतः बरनौली के प्रमेय से इसका दाब कम हो जाता है। इसीलिए गेंद परस्परं आकर्षण बल का अनुभव करती है।

प्रश्न 29.
भारी वाहनों के पहियों के टायर अधिक चौड़े क्यों बनाये जाते हैं ?
उत्तर:
भारी वाहनों के पहियों के टायर चौड़े होने से सड़क अथवा जमीन पर लगने वाला दाब कम हो जाता है क्योंकि वाहन का भार अधिक क्षेत्रफल पर लगता है। इसलिये वाहन के पहिये सड़क पर भैंसने से बच जाते हैं।

प्रश्न 30.
धमनियों में बनूंली सिद्धान्त से रक्त के प्रवाहको समझने में किस प्रकार सहायता मिलती है ?
उत्तर:
धमनी की भीतरी दीवार पर प्लाक (Plaque) का जमाव होने के कारण धमनी भीतर से संकीर्ण हो जाती है इन संकरी धमनियों से रक्त प्रवाहित कराने के लिए हृदय की गतिविधि पर अधिक बोझ पड़ जाता है। इस क्षेत्र में रक्त के प्रवाह की चाल बढ़ जाती है और आन्तरिक दाब घट जाता है। बाहरी दाब के कारण धमनी दब जाती है। हृदय इस धमनी को खोलने के लिए रक्त को धक्का देता है। जैसे ही रक्त इसे खोलकर बाहर की ओर तीव्र गति से प्रवाहित होता है, आंतरिक दाब पुनः गिर जाता है और धमनी पुनः दब जाती है, इससे हार्ट अटैक हो सकता है।

प्रश्न 31.
चाय की केतली के ढ़क्कन में सुराख होता है, क्यों ?
उत्तर:
चाय की केतली के दक्कन में सुराख न होने पर चाय से भरी केतली के अन्दर का दाब वायुमण्डलीय दाब से कम होगा। स्पष्ट है, केतली को टेढ़ा करने पर उसकी टोंटी से चाय सरलता से नहीं निकलेगी क्योंकि बाहर का दाब केतली के अन्दर के दाब से अधिक होगा।

प्रश्न 32.
धारा रेखीय प्रवाह तथा विक्षुब्ध प्रवाह में अन्तर बताइये।
उत्तर:
धारा रेखीय प्रवाह व विक्षुब्ध प्रवाह में निम्नलिखित अन्तर हैं-

धारा रेखीय प्रवाह	विक्षुब्ध प्रवाह
(1) यह द्रव का व्यवस्थित और नियमित रूप से प्रवाह है।	यह द्रव का अव्यवस्थित व अनियमित प्रवाह है।
(2) धारा रेखीय प्रवाह में द्रव का वेग क्रांतिक वेग से कम होता है।	इस प्रवाह में द्रव का वेग क्रान्तिक वेग से अधिक होता है।
(3) इस प्रवाह में द्रव के अन्दर भंवर धाराएँ उत्पन्न नहीं होती है।	इस प्रवाह में द्रव के अन्दर भंवर धाराएँ उत्पन्न होती हैं।
(4) किसी बिन्दु से गुजरने वाले कणों के वेग की दिशा नियत रहती है।	इस प्रवाह में किसी बिन्दु से गुजरने वाले कणों के वेग की दिशा परिवर्तित होती रहती है।

दीर्घ उत्तरीय प्रश्न (Long Answer Questions)

प्रश्न 1.
बर्नूली प्रमेय का कथन लिखते हुए इसे सिद्ध कीजिए।
उत्तर:
बर्नूली का सिद्धान्त (Bernoulli’s Theorem)
बर्नूली के सिद्धान्त के अनुसार, “जब कोई आदर्श द्रव (अश्यान एवं असंपीड्य) धारा रेखीय प्रवाह में बहता है तो प्रवाह के प्रत्येक स्थान पर द्रव की सम्पूर्ण ऊर्जा नियत रहती है अर्थात् द्वव की गतिज ऊर्जा, स्थितिज ऊर्जा तथा दाब ऊर्जा का योग नियत रहता है।” अर्थात्
दाब ऊर्जा + गतिज ऊर्जा + स्थितिज ऊर्जा = नियतांक
अतः एकांक आयतन के लिए,
P + \(\frac{1}{2}\)ρv² + ρgh = नियतांक
अथवा एकांक द्रव्यमान के लिए
\(\frac{{P}}{\rho}+\frac{1}{2} v^2+g h\) = नियतांक
अथवा
\(\frac{{P}}{\rho g}+\frac{v^2}{2 g}+h\) = नियतांक
जहाँ \(\frac{{P}}{\rho g}\) दाब शीर्ष, \(\frac{v^2}{2 g}\) वेग शीर्ष व h गुरुत्वीय शीर्ष है।

उपपत्ति (Derivation)
माना असमान परिच्छेद के क्षैतिज पाइप में एक आदर्श तरल का धारा रेखीय प्रवाह हो रहा है। पाइप के दो स्थानों {X} व {Y} पर पाइप का परिच्छेद क्षेत्रफल क्रमशः A₁ व A₂ है और इन स्थानों पर द्रव के वेग क्रमशः v₁ व v₂ हैं और इन स्थानों के गुरुत्वीय तल क्रमशः h₁ व h₂ हैं।

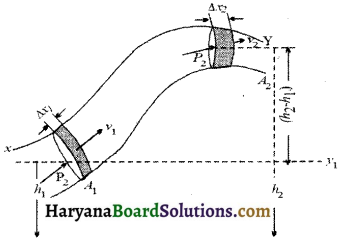
यदि एकांक समय में प्रवाहित द्रव का द्रव्यमान m हो तो अविरतता के सिद्धान्त से-
m = A₁v₁ρ = A₂v₂ρ
\(\frac{m}{ρ}\) = A₁v₁ = A₂v₂ …………..(11)
अतः विस्थापित द्रव पर किया गया कुल कार्य
\({W}={W}_1+{W}_2={P}_1 {~A}_1 v_1-{P}_2 {~A}_2 v_2\)
\({~W}=\frac{{P}_1 m}{\rho}-\frac{{P}_2 m}{\rho}\)

इस प्रकार बर्नूली के सिद्धान्त में ऊर्जा संरक्षण के नियम का उपयोग किया गया और यह माना गया है कि घर्षण के कारण कोई ऊर्जा क्षति नहीं होती। परन्तु वास्तव में, जब तरल प्रवाह करता है तो आन्तरिक घर्षण के कारण कुछ ऊर्जा की हानि हो जाती है। इसी व्युत्पत्ति तरल की विभिन्न परतों के भिन्न-भिन्न वेगों के कारण होती है। यह सतें एक-दूसरे पर घर्षण बल लगाती हैं और परिणामस्वरूप ऊर्जा का ह्रस होता है। अतः बर्नूली का समीकरण शून्य श्यानता पर लागू होता है। बर्नूली प्रमेय पर एक और प्रतिबन्ध है कि यह असंपीड्य तरलों पर ही लागू होता है, क्योंकि तरलों की प्रत्यास्थ ऊर्जा को नहीं लिया गया है। अस्थिर अथवा विक्षोभ प्रवाह में भी बर्नूली समीकरण काम नहीं आता क्योंकि इसमें वेग तथा दाब समय में लगातार अस्थिर रहते हैं।

प्रश्न 2.
किसी टंकी में पानी के धरातल से मीटर नीचे छिद्र से बहिःस्राव वेग का सूत्र व्युत्पन्न कीजिए। टॉरिसेली सिद्धान्त को भी समझाइये।
उत्तर:
टॉरिसेली प्रमेय : बहिःस्राव वेग (Torricelli’s Theorem : Velocity of Efflux) :
कथन (Statement): इसके अनुसार द्रव से भरे किसी टैंक में किसी गहराई पर बने छिद्र से निकलने वाले द्रव का वेग अर्थात् बहिःस्त्राव वेग उस वेंग के बराबर होता है जो द्रव अपने स्वतन्त्र तल से छिद्र तक स्वतन्त्रतापूर्वक गिरने में प्राप्त कर लेता है। इसे बर्नूली-प्रमेय के आधार पर सिद्ध किया जा सकता है।

उपपत्ति (Proof): चित्र में एक बर्तन दर्शाया गया है जिसमें H ऊँचाई तक कोई द्रव भरा है। इसका घनत्व माना ρ है। बर्तन में द्रव के स्वतन्त्र तल से h गहराई पर एक छिद्र A है। माना A से निकलने वाले द्रव का बहि:स्राव वेग v है। द्रव के स्वतन्त्र तल पर गतिज ऊर्जा शून्य है, केवल स्थितिज ऊर्जा है। परन्तु A से निकलने वाले द्रव में स्थितिज

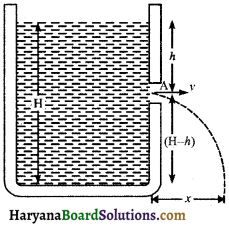
तथा गतिज दोनों ही प्रकार की ऊर्जाएँ हैं। द्रव के स्वतन्त्र तल तथा छ्दिध्र से बाहर निकलते द्रव जैट दोनों पर वायुमण्डलीय दांब P होगा। माना छिद्र से निकलने वाले द्रव का बहिःसाव वेग v है। बर्नूली प्रमेय के अनुसार, द्रव के स्वतन्त्र तल पर तथा छिद्र के प्रत्येक बिन्दु पर दाब तथा द्रव के एकांक आयतन की कुल ऊर्जा का योग बराबर होना चाहिए। अतः
\({P}+0+\rho g {H}={P}+\frac{1}{2} \rho v^2+\rho g({H}-h)\)
अथवा \(\frac{1}{2} \rho v^2=\rho g h\) अथवा \(v=\sqrt{(2 g h)}\)
इस सूत्र की स्थापना सर्वप्रथम सन् 1644 ई. में टॉरिसली ने की थी।

द्रव की परास (Range of Liquid): छिद्र से निकलने वाले द्रव द्वारा तय की गयी क्षैतिज दूरी को द्रव की परास कहते हैं।”
छिद्र से निकलने वाले द्रव का वेग क्षैतिज होता है जबकि वह (H-h) ऊर्ध्व ऊँचाई गुरुत्वीय त्वरण के अन्तर्गत गिरता है, अतः द्रव का मार्ग परवलयाकार हो जाता है।
माना (H-h) ऊँचाई तय करने में द्रव को लगा समय t हो तो u = 0, a = +g तथा s = H – h
s = ut + \(\frac{1}{2}\)at²
(H – h) = 0 + \(\frac{1}{2}\)gt²
\(t=\sqrt{\frac{2(H-h)}{g}}\) …………..(2)
चूँकि क्षैतिज दिशा में कोई बल कार्य नहीं करता है अतः उसका क्षैतिज वेग v ही रहता है।
अतः
R = v.t
= \(\sqrt{2 g h} \cdot \sqrt{\frac{2({H}-h)}{g}}\)
= \(2 \sqrt{h({H}-h)}\) ………..(3)
अतः इस सूत्र द्वारा स्पष्ट होता है कि h तथा (H-h) को आपस में बदल देने पर द्रव की परास में कोई परिवर्तन नहीं होता है। इसलिए क्षैतिज परास R समान रहता है।
अधिकतम परास के लिए,

प्रश्न 3.
बेन्चयूरी प्रवाह मापी द्वारा नली में प्रति सेकण्ड बहने वाले द्रव की मात्रा के लिए सूत्र स्थापित कीजिए।
उत्तर:
(ii) वैंटुरीमापी (Venturimeter):
यह बर्नूली प्रमेय पर आधारित वह युक्ति है, जिसकी सहायता से किसी नली में बहने वाले द्रव के प्रवाह की दर ज्ञात की जा सकती है।

उपकरण का वर्णन-इसमें एक क्षैतिज नली RST होती है जिसका बीच का भाग (S) संकरा है। R व S भागों पर दो ऊर्ध्वाधर नलियाँ E तथा F जुड़ी रहती हैं। दोनों ऊर्ध्वाधर नलियाँ R व S स्थानों पर द्रव दाब नापने के लिए काम में लायी जाती हैं। इसे वैंटुरीमीटर कहते हैं। इसे उस नली के साथ जोड़ देते हैं, जिससे द्रव दाब की गणना करनी है।

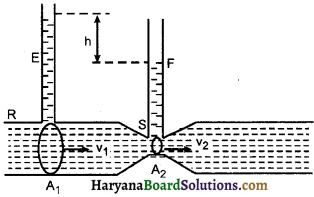
कार्यविधि (Working): जब द्रव नली RST में प्रवाह करता है तो अविरतता के सिद्धान्त से नली के चौड़े भाग {R} की अपेक्षा संकरे भाग (S) पर वेग अधिक होता है, अतः बरनौली प्रमेय से चौड़े भाग की अपेक्षा संकरे भाग ({S}) पर दाब कम होता है। इस दाबान्तर को नलियों {E} तथा {F} में चढ़े द्रव के अन्तर को पढ़कर ज्ञात किया जा सकता है।
माना नली में आदर्श द्रव का प्रवाह धारा रेखीय है, नली के {R} से {S} स्थानों पर क्रमशः नली के परिच्छेद क्षेत्रफल A₁ व A₂ हैं, द्रव के प्रवाह वेग v₁ व v₂ तथा दाब P₁ व P₂ हैं।
चूँकि नली क्षैतिज है, अतः बर्नूली प्रमेय से,

इस प्रकार द्रव के प्रवाह की दर ज्ञात की जाती है।
इस सिद्धान्त पर मोटर वाहनों में काबुरिटर में नोजल काम करती है जिसमें तीव्र गति से वायु प्रवाहित होती है। संकरी गर्दन पर दाब कम होता है इसलिए पेट्रोल भीतर की ओर चैम्बर में चूस लिया जाता है ताकि दहन के लिए वायु तथा ईंधन का सही मिश्रण प्राप्त हो सके।

प्रश्न 4.
केशिकत्व क्या है ? केशनली में चढ़े जल स्तम्भ की ऊँचाई के लिए सूत्र प्रतिपादित कीजिए ।
उत्तर:
केशनली में द्रव के उन्नयन के लिए सूत्र (Formula For Capillary Rise of Liquid):
माना ρ घनत्व का कोई द्रव r त्रिज्या की केशनली में भरा है, जैसा कि चित्र में दर्शाया गया है। द्रव का पृष्ठ तनाव T है। नली के अन्दर द्रव के वक्र तल की त्रिज्या R व स्पर्श कोण θ है। चढ़े हुए द्रव स्तम्भ की ऊँचाई h है। द्रव स्तम्भ के दाब में कमी \(\frac{2T}{R}\) है, अत:
द्रव स्तम्भ का दाब = दाब आधिक्य

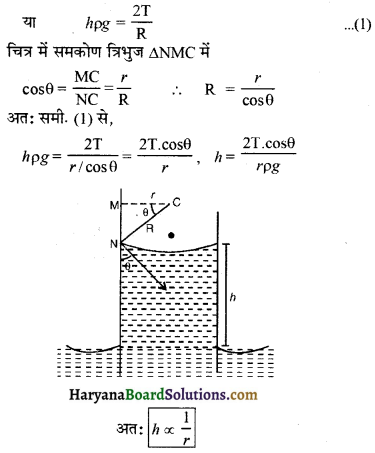
स्पष्ट है कि r का मान जितना कम होगा अर्थात् नली जितनी संकीर्ण होगा, h का मान उतना ही अधिक होगा अर्थात् केशनली में द्रव का उन्नयन उतना ही अधिक होगा।

प्रश्न 5.
आन्तरिक बलों के आधार पर पृष्ठ तनाव की व्याख्या कीजिए ।
उत्तर:
पृष्ठ तनाव की आण्विक बलों के आधार पर व्याख्या (Explanation of Surface Tension Based on Molecular Forces);
लाप्लास (Laplace) ने पृष्ठ तनाव को अन्तराण्विक बलों के आधार पर समझाया। हम पढ़ चुके हैं कि जब अणुओं के बीच की दूरी आण्विक परास (≈ 10^-9. मीटर) से अधिक होती है तो उनके बीच लगने वाला ससंजक बल नगण्य होता है तथा जब अणुओं के बीच की दूरी आण्विक परास से कम होती है तो उनके बीच ससंजक बल कार्य करता है। किसी अणु को केन्द्र मानकर आण्विक परास की त्रिज्या के बराबर खींचा गया गोला, ‘आण्विक सक्रियता का गोला’ कहलाता है।

चित्र में बर्तन में भरे किसी द्रव में तीन अणु A, B व C दिखाए गए हैं। इन अणुओं के चारों ओर आण्विक सक्रियता के गोले खींचे गए हैं। अणु A पूर्णतः द्रव के अन्दर, अणु B द्रव के पृष्ठ के ठीक नीचे तथा अणु C द्रव के पृष्ठ पर स्थित है।

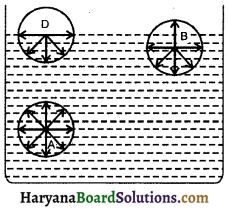
अणु A के आण्विक सक्रियता का गोला पूर्णतः द्रव के भीतर है, अतः यह अणु अपने चारों ओर के अणुओं द्वारा सभी दिशाओं में समान बल से आकर्षित होता है। इस प्रकार इस अणु पर परिणामी ससंजक बल का मान शून्य होता है। अणु B के आण्विक सक्रियता के गोले का कुछ भाग द्रव के पृष्ठ के बाहर है। इस स्थिति में इस अणु के नीचे स्थित अणुओं की संख्या, ऊपर स्थित अणुओं की संख्या से अधिक होती है जिससे यह अणु नीचे की ओर अधिक आकर्षित होता है, अतः अणु B पर द्रव के भीतर की ओर परिणामी बल कार्य करता है। अणु C के आण्विक सक्रियता के गोले का आधा भाग द्रव के पृष्ठ के बाहर तथा आधा भाग द्रव के अन्दर है, इस गोले के निचले अर्धभाग में ही द्रव के अणु हैं, अतः अणु C पर एक परिणामी ससंजक बल द्रव के पृष्ठ के लम्बवत् नीचे की ओर कार्य करता है जिसका मान अधिकतम होता है (पृष्ठ के द्रव वाष्प के अणुओं के कारण आकर्षण बल को नगण्य माना जा सकता है।)

इस प्रकार द्रव के पृष्ठ पर स्थित प्रत्येक अणु पर नीचे की ओर अधिकतम आकर्षण बल कार्य करता है। द्रव के पृष्ठ नीचे जाने पर इस आकर्षण बल का मान कम हो जाता है। द्रव के पृष्ठ से आण्विक परास की दूरी से अधिक दूरी पर इस परिणामी बल का मान शून्य हो जाता है। अतः द्रव के स्वतन्त्र पृष्ठ से आण्विक परास ( 10 m ) की गहराई तक द्रव का भाग पृष्ठीय झिल्ली (surface film) कहलाता है। पृष्ठीय झिल्ली में स्थित सभी अणु द्रव के अन्दर की ओर आकर्षण बल का अनुभव करते हैं।

जब किसी अणु को द्रव के अन्दर से पृष्ठीय झिल्ली में लाया जाता है, तो द्रव के अन्दर की ओर लगने वाले आकर्षण बल के विरुद्ध कार्य करना पड़ता है। यह कार्य अणु में स्थितिज ऊर्जा के रूप में संचित हो जाता है। स्पष्ट है कि पृष्ठीय झिल्ली में स्थित अणुओं की स्थितिज ऊर्जा द्रव के भीतर स्थित अणुओं की स्थितिज ऊर्जा से अधिक होती है। इस प्रकार द्रव के स्वतन्त्र पृष्ठ पर स्थित अणुओं की स्थितिज ऊर्जा अधिकतम होती है। यदि स्वतन्त्र पृष्ठ का क्षेत्रफल अधिक है तो उसमें स्थित अणुओं की संख्या भी अधिक होगी, अतः उसकी स्थितिज ऊर्जा भी अधिक होगी, परन्तु हम जानते हैं कि कोई भी निकाय (system) उस समय स्थायी साम्यावस्था में होता है जब उसकी स्थितिज ऊर्जा न्यूनतम होती है, अतः द्रव के पृष्ठ पर स्थित अणुओं की स्थितिज ऊर्जा न्यूनतम होने के लिए पृष्ठ का क्षेत्रफल कम-से-कम होना चाहिए। इस प्रकार द्रव का स्वतन्त्र पृष्ठ एक तनी हुई झिल्ली की भाँति कार्य करता है। द्रव की इस प्रवृत्ति को पृष्ठ तनाव कहते हैं।

प्रश्न 6.
एक अनन्त विस्तार के श्यान द्रव में गिर रहे गोले के लिए अन्तिम वेग का सूत्र प्रतिपादित कीजिए।
उत्तर:
सीमान्त वेग (Terminal Velocity):
जब कोई गोलाकार वस्तु किसी श्यान माध्यम में स्वतन्त्रतापूर्वक गिरने दी जाती है तो वस्तु का वेग उसके भार (W) के कारण पहले बढ़ता है लेकिन वेग बढ़ने के साथ-साथ माध्यम द्वारा उस पर आरोपित घर्षण बल भी बढ़ता है जो गति के विपरीत दिशा में कार्य करता है। वस्तु के घर्षण बल का कारण यह है कि वस्तु के सम्पर्क में आने वाली परत वस्तु के साथ गति करना चाहती है अबकि दूर की अन्य परतें स्थिर रहती हैं। द्रव की परतों में इस आपेक्षिक गति के कारण परतों के मध्य आन्तरिक घर्षण बल उत्पन्न हो जाता है। यही श्यान बल होता है। एक स्थिति ऐसी आती है जब वस्तु का भार उस पर ऊपर की ओर लगने वाले उत्प्लावन बल एवं स्टोक्स बल के योग के बराबर हो जाता है तो वस्तु पर परिणामी बल शून्य हो जाता है और वह नियत वेग से गिरने लगती है। इसी नियत वेग को ‘सीमान्ते वेग’ या ‘ चरम वेग’ या ‘अधिकतम वेग’ या ‘अन्तिम वेग’ कहते हैं।

सीमान्त वेग के लिए सूत्र-माना r त्रिज्या एवं ρ घनत्व की एक गोलाकार वस्तु σ घनत्व एवं η श्यानता गुणांक वाले द्रव में स्वतन्त्रतापूर्वक गिर रही है। वस्तु पर लगने वाले बर्लों को चित्र में दिखाया गया है। इन बलों में केवल स्टोक्स बल वस्तु के वेग पर निर्भर करता है। अतः चरम वेग (v_t) की अवस्था में,

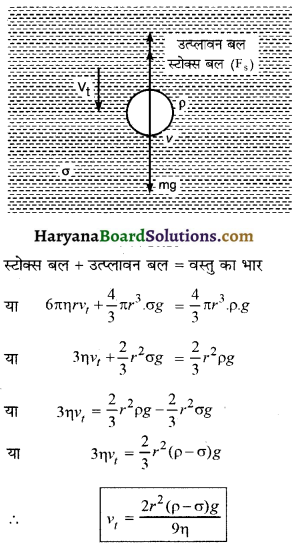
स्पष्ट है कि गोली का सीमान्त वेग (v_t), गोली की त्रिज्या (r), गोली के घनत्व (ρ), माध्यम के घनत्व (σ) तथा माध्यम की श्यानता (η) पर निर्भर करता है।
यदि द्रव में गिरती हुई वस्तु के वेग एवं समय के मध्य ग्राफ खींचा जाये तो ग्राफ की भाँति मिलेगा।

प्रश्न 7.
कोशिका उन्नयन विधि द्वारा पृष्ठ तनाव ज्ञात करने की विधि का वर्णन कीजिए।
उत्तर:
कोशिका उन्नयन विधि द्वारा जल का पृष्ठ तनाव ज्ञात करना
(Determination Of Surface Tensionof Liquid By Capillary Rise Method):
आवश्यक उपकरण-द्रत्र भरा बीकर, स्टैण्ड, एक समान व्यास की साफ केशनली तथा चल सूक्ष्मदर्शी।
आवश्यक सूत्र-द्रव का पृष्ठ तनाव \(\mathrm{T}=\frac{r h \rho g}{\cos \theta}\)
जहाँ r → केशनली की त्रिज्या
h → केशनली में चढ़े स्तम्भ की ऊँचाई
ρ → द्रव का घनत्व, g → गुरुत्वीय त्वरण
θ → स्पर्श कोण
प्रयोग विधि-प्रयोग के लिए काँच की केशनली को तनु नाइट्रिक अम्ल एवं कॉस्टिक सोडा के विलयन से साफ करके शुद्ध जल से धोकर सुखा लेते हैं। अब इस स्वच्छ नली को एक स्टैण्ड की सहायता से जल

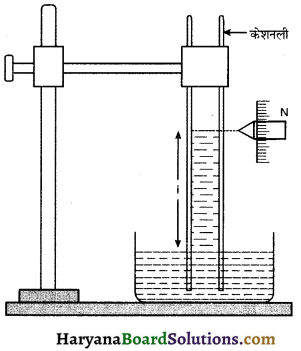
से भरे बीकर में इस प्रकार डुबोया जाता है कि केशनली ऊर्ध्वाधर रहे । ऐसा करने पर केशनली में पृष्ठ तनाव के कारण (केशिकत्व) द्रव चढ़ने लगता है। जिस समय द्रव का चढ़ना बन्द हो जाए, केशनली में द्रव स्तम्भ की ऊँचाई चलायमान सूक्ष्मदर्शी की सहायता से नाप ली जाती है। नली की त्रिज्या भी सूक्ष्मदर्शी की सहायता से व्यास ज्ञात करके ज्ञात करते हैं। अब सूत्र में h व r के मान रखकर द्रव का पृष्ठ ज्ञात कर लेते हैं।

प्रायोगिक सावधानियाँ:

• केशनली, बीकर, पैमाना सब बिल्कुल साफ होने चाहिए। जल भी स्वच्छ होना चाहिए। आसुत जल (distilled water) का प्रयोग नहीं करना चाहिए क्योंकि इसमें कुछ-न-कुछ चिकनाई अवश्य मिली रहती है। थोड़ी-सी धूल अथवा चिकनाई पृष्ठ तनाव के मान को काफी बदल देती है।
• केशनली की आन्तरिक त्रिज्या उसी स्थान पर नापनी चाहिए जहाँ तक द्रव नली में चढ़ा था। इसके लिए नली को उसी स्थान पर तोड़ लेना चाहिए।
• प्रयोग में समस्त द्रव के ताप को अवश्य लिखना चाहिए क्योंकि पृष्ठ तनाव पर ताप का प्रभाव पड़ता है।
• केशनली एकदम ऊर्ध्वाधर होनी चाहिए जिससे द्रव (पानी) के स्तम्भ की ऊँचाई ठीक-ठीक नापी जा सके।

प्रश्न 8.
किसी द्रव का क्षेत्रफल बढ़ाने में आवश्यक कार्य का पृष्ठ तनाव से सम्बन्ध स्थापित कीजिए।
उत्तर:
पृष्ठ तनाव तथा पृष्ठीय ऊर्जा में सम्बन्ध (Relation between Surface Tension and Surface Energy):
माना PQRS एक तार का आयताकार छल्ला है, जिसकी भुजा QR अपने सम्पर्क वाली भुजाओं पर गति करने के लिए स्वतन्त्र है। यदि इस छल्ले में किसी द्रव की कोई फिल्म बनायी जाये तो पृष्ठ तनाव के कारण फिल्म के प्रत्येक भुजा पर अन्दर की ओर बल आरोपित करेगी। भुजा Q, R की लम्बाई यदि $l$ हो तो इस भुजा पर F = 2T. l बल लगेगा। चूँकि फिल्म में दो पृष्ठ होते हैं। अतः तार की प्रति एकांक लम्बाई पर दोनों पृष्ठ एक ही दिशा में T पृष्ठ तनाव बल लगायेंगी। इस प्रकार प्रति एकांक लम्बाई पर 2T बल लगेगा। इस बल F के प्रभाव में भुजा QR अन्दर की ओर गति करने लगेगी। अतः इसे अपने स्थान पर बनाये रखने के लिए इस पर बाहर की ओर इतना ही बल F’ लगाना होगा।

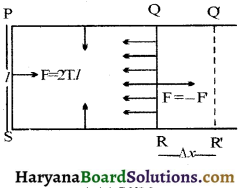
यदि F’ को थोड़ा बढ़ाकर QR भुजा को ∆x विस्थापन देकर Q’R’ स्थिति में पहुँचा दे तो इस क्रिया में पृष्ठ तनाव बल के विरुद्ध कृत कार्य

W =F . ∆x = 2T.l.∆x
W = F.2l.x
W = T.∆A
जहाँ ∆A = 2.l.∆x क्षेत्रफल में प्रभावी वृद्धि
यही कार्य बढ़े हुए पृष्ठ की पृष्ठीय ऊर्जा के रूप में संचित हो जायेगा। अतः पृष्ठीय ऊर्जा
E_s = T.∆A
यदि ∆A =1 m² तो E_s = T
“अर्थात् किसी द्रव के एकांक क्षेत्र की पृष्ठीय ऊर्जा उसके पृष्ठ तनाव के तुल्य होती है।”
\(\mathrm{T}=\frac{\mathrm{E}_s}{\Delta \mathrm{A}}=\frac{\mathrm{W}}{\Delta \mathrm{A}}\)

T का मात्रक- जूल / मी²
T का विमीय सूत्र- [M¹L⁰T^-2]

प्रश्न 9.
पॉस्कल का नियम लिखिये और इसका सत्यापन कीजिये। इसके आधार पर कार्य करने वाले दो उपकरणों का नाम लिखिये । और उनका वर्णन कीजिये।
उत्तर:
पास्कल का नियम (Pascal’s Law)
इस नियम के अनुसार, “यदि गुरुत्व के प्रभाव को नगण्य मान लें तो किसी द्रव के किसी भाग पर लगाया गया दाब बिना क्षय हुए सम्पूर्ण द्रव में सभी दिशाओं में समान रूप से संचरित हो जाता है। इसे द्रव के दाब का संचरण नियम भी कहते हैं।”

नोट-इस नियम का प्रतिपादन करने वाले वैज्ञानिक ब्लेज पास्कल थे। ब्लेज पास्कल के नाम पर इस नियम को जाना जाता है पास्कल के सम्मान में दाब का S.I. मात्रक ‘पास्कल’ (P_a) लिया जाता है।

व्युत्पत्ति (Derivation): चित्र में विराम स्थिति के किसी तरल के भीतर कोई अवयव दिखाया गया है यह ABC-DEF एक समकोण प्रिज्म के रूप में है। इस अवयव पर आरोपित बल शेष तरल के कारण हैं। तरल के कारण बल पृष्ठों के अभिलम्बवत् कार्य करते हैं। अवयव के फलकों BEFC, ADFC तथा ADEB पर बल क्रमशः F_a, F_b, F_c तथा दाब क्रमशः P_a, P_b, P_c हैं तथा इन फलकों के क्षेत्रफल क्रमशः A_a, A_b व A_c हैं।

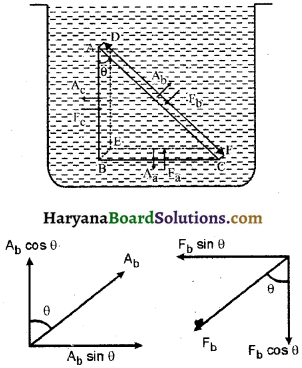
चित्र में प्रदर्शित अवयव (ABC-DEF) अत्यन्त छोटा है ताकि गुरुत्व के प्रभाव की उपेक्षा की जा सके, लेकिन स्पष्टता के दृष्टिकोण से इसे बड़ा दिखाया गया है।
साम्यावस्था में बलों में निम्न सम्बन्ध होंगे-
F_b sin θ = F_c; F_b cos θ = F_a
तथा ज्यामिति से,
A_b sin θ = A_c; A_b cos θ = A_a
अतः भाग देने पर
\(\frac{F_b}{A_b}=\frac{F_c}{A_c}\) तथा \(\frac{F_b}{A_b}=\frac{F_a}{A_a}\)
या P_a = P_c तथा P_b = P_a
या P_a = P_b = P_c
अतः विरामावस्था में द्रव के अन्दर सभी दिशाओं में दाब समान रूप से कार्य करता है। यही पास्कल का नियम है।

प्रश्न 10.
द्रव के भीतर स्थित किसी बिन्दु पर दाब के व्यंजक को ज्ञात कीजिये और सिद्ध कीजिये कि P ∝ h होता है यदि द्रव के मुक्त पृष्ठ पर वायुमण्डलीय दाब Po हो तो द्रव के मुक्त पृष्ठ से / गहराई पर कुल दाब ज्ञात कीजिये।
उत्तर:
दाब (Pressure):
किसी क्षेत्रफल पर लगने वाले बल का प्रभाव क्षेत्रफल पर निर्भर करता है। क्षेत्रफल बदल जाने पर बल का प्रभाव भिन्न हो जाता है। उदाहरण के लिए यदि सुई पर थोड़ा भी बल लगाया जाये तो वह हमारी त्वचा में धँस जाती है जबकि चम्मच पर अधिक बल लगाने पर भी वह त्वचा में नर्ही धँसती है। इन दोनों घटनाओं में अन्तर क्षेत्रफल के कारण है। सुई की नोंक का सम्पर्क क्षेत्रफल अति अल्प जबकि चम्मच का सम्पर्क क्षेत्रफल अधिक होता है। स्पष्ट है क्षेत्रफल बढ़ाने पर बल का प्रभाव कम हो जाता है।

इन अनुभवों से स्पष्ट है कि बल के साथ-साथ वह क्षेत्रफल भी महत्त्वपूर्ण होता है जिस पर बल कार्य करता है। जब कोई पिण्ड किसी तरल में डूबा रहता है तो तरल द्वारा इस पिण्ड पर उसके पृष्ठ के लम्बवत् बल आरोपित किया जाता है। “एकांक क्षेत्रफल पर आरोपित बल को दाब कहते हैं।” यदि पृष्ठ का क्षेत्रफल A एवं इस पर आरोपित अभिलम्बवत् बल F हो तो दाब
\(P=\frac{F}{A}\).
सैद्धान्तिक रूप में पिण्ड के क्षेत्रफल को अत्यन्त सूक्ष्म ले सकते है। तब
\(\mathrm{P}=\lim _{\Delta \mathrm{A} \rightarrow 0} \frac{\Delta \mathrm{F}}{\Delta \mathrm{A}}=\frac{d \mathrm{~F}}{d \mathrm{~A}}\)
यदि समान परिमाण का बल भिन्न-भिन्न क्षेत्रफलों के पृष्ठ पर आरोपित किया जाये तो कम क्षेत्रफल वाले पृष्ठ पर कार्यरत दाब अधिक होगा। दाब एक अदिश राशि है।
मात्रक एवं विमीय सूत्र
मात्रक- MKS मात्रक न्यूटन / मी² \left(N-m^-2) या पॉस्कल CGS मात्रक- डाइन/सेमी²
दाब के अन्य मात्रक-
(i) वायुमण्डलीय दाब: 76 सेमी पारा स्तम्भ का दाबं 1 वायुमण्डलीय दाब (1 atm दाब) कहलाता है।
1 वायुमण्डलीय दाब = 0.76 × 13.6 × 10³ × 9.8
& =1.013 × 10⁵ N-m^-2

(ii) बार-मौसम विज्ञान में दाब को बार या मिलीबार में व्यक्त
1 बार (bar)=10⁵ Pa
विमीय सूत्र – [M¹L^-1T^-2]

प्रश्न 11.
पानी की बड़ी बूँद को छोटी बूंदों में फुहारने पर पृष्ठ ऊर्जा में वृद्धि ज्ञात कीजिए।
उत्तर:
जल की एक बड़ी बूँद को m छोटी बूँदों में फुहारने पर पृष्ठीय ऊर्जा में वृद्धि (Increase in Surface Energy on Spraying a Big Water Drop):
पानी की बड़ी बूँद को छोटी बूँदों में फुहारने पर पृष्ठ क्षेत्रफल का मान बढ़ता है, अतः पृष्ठ ऊर्जा में वृद्धि होती है। लेकिन इस कार्य में आन्तरिक ऊर्जा में कमी होती है। अतः ताप गिरने से ठण्डक उत्पन्न होती है जिसे हम दैनिक जीवन में फब्वारे के नीचे नहते समय अनुभव करते हैं।
माना R त्रिज्या की एक बड़ी बूँद है जिसे r त्रिज्या की n छोटी समान बूँदों में फुहारा जाता है। इस क्रिया में आयतन नियत रहता है। अत:
बड़ी बूँद का आयतन = n × छोटी बूँदों का आयतन

प्रश्न 12.
गोलीय बूंद के लिए दाब आधिक्य P_ex = \(\frac{2T}{R}\) का व्यंजक प्राप्त कीजिए।
उत्तर:
पृष्ठीय ऊर्जा (Surface Energy):
यदि किसी द्रव के पृष्ठ का क्षेत्रफल बढ़ाया जाये तो कुछ अणु द्रव के अन्दर से द्रव के पृष्ठ पर आ जाते हैं। इन अणुओं को द्रव के पृष्ठ के ठीक नीचें वाले अणुओं के आकर्षण बल के विरुद्ध कार्य करना पड़ता है। यही कार्य नये पृष्ठ में स्थितिज ऊर्जा के रूप में संचित हो जाता है। इस प्रकार द्रव के पृष्ठ पर स्थित अणुओं के पास कुछ अतिरिक्त ऊर्जा को ही पृष्ठ ऊर्जा कहते हैं।

आंकिक प्रश्न

प्रश्न 1.
एक व्यक्ति का भार 60 kg है तथा उसके प्रत्येक पैर का क्षेत्रफल 30 cm है। बताइए व्यक्ति द्वारा पृथ्वी पर कितना दाब डाला जायेगा यदि (i) वह एक पैर पर खड़ा है, (ii) दोनों पैरों पर खड़ा है।
उत्तर:
(i) 19.6 × 10⁴ N/m²
(ii) 9.8 × 10⁴ N/m²

प्रश्न 2.
एक बेलनाकार जार के अनुप्रस्थ काट का क्षेत्रफल 50 cm² है। यह 20 cm ऊँचाई तक जल से भरा हुआ है। इसके पिस्टन का द्रव्यमान नगण्य है। जब इसके पिस्टन पर 1 kg द्रव्यमान रखा जाता है तो जार की तली में दाब की गणना कीजिए। वायुमण्डलीय दाब को नगण्य मानिए।
उत्तर:
3.92 × 10³ N/m²

आर्किमिडीज के सिद्धान्त पर आधारित

प्रश्न 3.
एक ठोस गेंद जिसका घनत्व जल के घनत्व का आधा है, 19.6m की ऊँचाई से गुरुत्वीय क्षेत्र में स्वतन्त्रता पूर्वक गिरकर जल के अन्दर प्रवेश करती है गेंद जल में कितनी गहराई तक जायेगी ? जल की सतह पर फिर दुबारा आने में इसे कितना समय लगेगा ? (g = 9.8 m/sec²) जल की श्यानता तथा वायु के अवरोध को नगण्य मान लीजिए।
उत्तर:
19.6 m, 4 sec

प्रश्न 4.
समुद्र में एक हिम शैल स्थित है, (i) जल की सतह के नीचे हिम शैल का प्रभाग ज्ञात कीजिए, (ii) जल की सतह के ऊपर हिम शैल का प्रभाग ज्ञात कीजिए। दिया है, बर्फ का घनत्व = 917 kg/m³ और समुद्री जल का घनत्व 1.024 × 103 kg/m³
उत्तर:
(i) 89.7% (ii) 10.3%

प्रश्न 5.
अन्दर से खोखली एक ताँबे की गेंद का वायु में धार 264 ग्राम तथा जल में डुबाने पर भार 221 ग्राम है यदि ताँबे का घनत्व 8.8 ग्राम / सेमी हो, तो गेंद के खोखले भाग का आयतन ज्ञात कीजिए।
उत्तर:
13 सेमी³

श्यानता पर आधारित

प्रश्न 6.
10 cm × 10 cm की एक समतल प्लेट तथा बड़ी प्लेट के बीच 1 mm मोटी ग्लिसरीन की तह है। यदि ग्लिसरीन का श्यानता गुणांक 1.0 kg/m sec हो, तो प्लेट को 10 cm/sec के वेग से चलाने के लिए कितना बल चाहिए।
उत्तर:
1.0 न्यूटन

प्रश्न 7.
100 cm² क्षेत्रफल की एक समतल प्लेट तथा एक बड़ी प्लेट के बीच ग्लिसरीन की 1.0mm मोटी तह है, यदि ग्लिसरीन का श्यानता गुणांक 1.0 kg/m sec हो, तो प्लेट को 7.0 cm/sec के वेग से चलाने के लिए कितना बल चाहिए।
उत्तर:
0.70 न्यूटन

प्रश्न 8.
5 cm² क्षेत्रफल की एक चौरस प्लेट तथा एक बड़ी प्लेट के बीच ग्लिसरीन की 1 mm मोटी पर्त है यदि ग्लिसरीन का n = 10 प्वॉइज हो तो प्लेट को 7 cm/see के वेग से चलाने के लिए कितना बल चाहिए ?
उत्तर:
0.035 न्यूटन

प्रश्न 9.
पानी की दो समान्तर परतों में आपेक्षिक वेग 18.0 cms^-1 है। यदि परतों के बीच की लम्बवत् दूरी 0.1 cm हो तो वेग प्रवणता ज्ञात कीजिए।
उत्तर:
180 s^-1

सीमान्त वेग पर आधारित

प्रश्न 10.
जल की एक बूँद का व्यास 0.003 mm है। यह वायु से गिर रही है, बूंद का सीमान्त वेग ज्ञात कीजिए।
वायु का श्यानता गुणांक 1.8 × 10^-5 kg/m see वायु का घनत्व उपेक्षणीय है।
उत्तर:
2.72 × 10 m/sec

प्रश्न 11.
यदि बूँद का अन्तिम वेग 12 cm/sec हो तो वायु में गिरती हुई पानी की बूंदों की त्रिज्या ज्ञात कीजिए, वायु की श्यानता 1.8× 10^-4 वॉइज है तथा वायु का घनत्व 1.21 × 10^-3 ग्राम / सेमी है।
उत्तर:
3.15 × 10³ cm

प्रश्न 12.
समान त्रिज्या की दो बूँदें वायु में गिर रही हैं। उनके क्रान्तिक वेग 10 cm/sec हैं। यदि बूँदें संयुक्त हो जाए तो क्रान्तिक वेग ज्ञात कीजिए।
उत्तर:
15.9 cm / sec

प्रश्न 13.
तेल की एक बूंद का वायु में सीमान्त वेग 5.0 × 10^-4 m/sec है। बूँद की त्रिज्या क्या है ? यदि ऐसी ही दो बूँदें परस्पर मिल जायें तो परिणामी बूँद का सीमान्त वेग कितना होगा ? तेल का श्यानता गुणांक 1.8 × 10^-3 kg/m-sec तथा घनत्व 9 × 10² kg/m² है। वायु का घनत्व तेल के सापेक्ष नगण्य है तथा (2)^2/3 = 1.59, g = 9.8 m/sec²
उत्तर:
2.14 × 10^-5m, 7.95 × 10^-4 m / sec

अविरतता के समीकरण पर आधारित

प्रश्न 14.
8 × 10^-3 m आन्तरिक व्यास वाली एक टोंटी से पानी सततः 4 × 10^-1 m/sec के प्रारम्भिक वेग से बह रहा है। टोंटी के नीचे 2 × 10^-1 m की दूरी पर पानी की धारा के व्यास की गणना कीजिए।
उत्तर:
3.56 × 10 m

प्रश्न 15.
हौज पाइप जिसका आन्तरिक व्यास 2.1 cm है, से जल 1.1m/sec की चाल से प्रवाहित हो रहा है नोजल का व्यास क्या होना चाहिए यदि इससे जल 4 m/sec की चाल से निकल रहा है ?
उत्तर:
1.1 cm

प्रश्न 16.
एक क्षैतिज पाइप लाइन के अनुप्रस्थ काट का क्षेत्रफल असमान है। इसमें जल 0.2m³/sec की दर से प्रवाहित हो रहा है उस बिन्दु पर जल के वेग की गणना कीजिए जहाँ पाइप के अनुप्रस्थ काट का क्षेत्रफल 0.02 m² हो ।
उत्तर:
10 m/sec

बरनौली के प्रमेय तथा इसके अनुप्रयोगों (वेन्दुरीमीटर तथा बहिःस्राव वेग) पर आधारित

प्रश्न 17.
4 × 10⁴ न्यूटन /मी दाब का जल 2 मीटर / सेकण्ड वेग से 0.02 मीटर² अनुप्रस्थ-परिच्छेद के पाइप से प्रवाहित होता है जिसका अनुप्रस्थ परिच्छेद घटकर 0.01 मी हो जाता है। पाइप के छोटे अनुप्रस्थ- परिच्छेद में कितना दाब है ?
उत्तर:
3.4 × 10⁴ न्यूटन / मी²

प्रश्न 18.
हृदय से रुधिर को सिरे के शीर्ष (ऊर्ध्वाधर दूरी = 50 cm) तक पहुँचाने के लिए आवश्यक न्यूनतम दाब की गणना कीजिए। रुधिर का घनत्व 1.04 ग्रा. सेमी^-3 है। घर्षण नगण्य है।
उत्तर:
5.096 × 10⁴ डाइन / सेमी²

प्रश्न 19.
एक क्षैतिज पाइप जिसमें जल बह रहा है, उसके दो बिन्दुओं पर जल के दावों का अन्तर 1.4 cm पारे के स्तम्भ के बराबर है, यदि असमान परिच्छेद के कारण अधिक परिच्छेद वाले बिन्दु पर जल की चाल 60 cm/sec है, तो दूसरे बिन्दु पर जल की चाल की गणना कीजिए पारे का घनत्व 13.6 × 10 kg/m. तथा g = 9.8N/kg.
उत्तर:
2.02 m/sec

प्रश्न 20.
एक क्षैतिज नली के दो बिन्दुओं A व B पर अनुप्रस्थ क्षेत्रफल भिन्न-भिन्न हैं। A पर व्यास 4 cm तथा B पर 2 cm है। A तथा B पर दो मैनोमीटर भुजाएँ लगी हैं। जब 0.8 ग्राम / सेमी घनत्व का द्रव नली में से होकर बहता है तो मैनोमीटर की भुजाओं के बीच दावान्तर 8 cm है। नली में बहने वाले द्रव के प्रवाह की दर की गणना कीजिए। (g = 980 cm/sec²)
उत्तर:
406 cm³/sec

प्रश्न 21.
एक क्षैतिज सिरिंज में, जमीन से 1.25m की ऊँचाई पर, जल भरा है। प्लंजर का व्यास 8 mm एवं नोजिल का व्यास 2 mm है। प्लंजर को एक नियत चाल 0.25 m/sec से दबाया जाता है। जमीन पर सिरिंज से निकलने वाली जल धारा का क्षैतिज परास ज्ञात कीजिए। (g = 10 m/sec²)
उत्तर:
2m

प्रश्न 22.
35m ऊँचाई तक भरे जल की एक टंकी में जल पृष्ठ से 7m नीचे टंकी की दीवार में 1 cm त्रिज्या का एक छेद है। ज्ञात कीजिए – (i) बहि:स्राव वेग, (ii) छेद से जल प्रवाह की दर, (iii) जल का परास, (iv) जल पृष्ठ से वह गहराई जहाँ टंकी में छेद करने पर परास का मान वही हो जो 7m गहराई पर है, (v) वह गहराई जहाँ छेद पर परास का मान अधिकतम हो, (vi) अधिकतम परास ।
उत्तर:
(i) 11.7m/sec.
(ii) 3.67 10m / sec
(iii) 28 m.
(iv) 28 m
(v) 17.5 m
(vi) 35 m

प्वाइजली सूत्र पर आधारित

प्रश्न 23.
एक केशिकानली का व्यास 1 mm व लम्बाई 15 cm है। इसे एक क्षैतिज विधि से किसी पात्र से जोड़ दिया जाता है जो ऐल्कोहॉल से भरा हुआ है जिसका घनत्व 0.8 ग्राम/सेमी³ है। केशिकानली के केन्द्र की गहराई ऐल्कोहॉल के मुक्त पृष्ठ से 25 cm नीचे है। यदि ऐल्कोहॉल की श्यानता 0.12 प्वॉइज हो तो 5 min में बहने वाले द्रव की मात्रा ज्ञात कीजिए।
उत्तर:
6,408 ग्राम

पृष्ठ तनाव तथा पृष्ठीय ऊर्जा पर आधारित

प्रश्न 24.
एक पतला तार 3.0 cm व्यास की रिंग के रूप में मोड़ा गया है। इस रिंग को साबुन के घोल में क्षैतिज स्थिति में रखकर, धीरे-धीरे ऊपर उठाया जाता है रिंग व घोल के बीच बनी फिल्म को तोड़ने के लिए कितना उपरिमुखी (upward) बल चाहिए ? साबुन के घोल का पृष्ठ तनाव = 3.0 × 10^-2 N/m
उत्तर:
5.652 × 10^-3 N

प्रश्न 25.
जल की R त्रिज्या की एक बड़ी बूँद को 8000 समान आयतन की छोटी बूँदों में विभाजित करने में 5.582 πR² जूल कार्य करना पड़ता है जल का पृष्ठ तनाव ज्ञात कीजिए
उत्तर:
7.3 × 10^-2 N/m

प्रश्न 26.
दो सीधे 10 cm लम्बाई वाले समान्तर तारों के बीच जो 0.5 cm दूर हैं, जल की एक फिल्म बनाई जाती है। यदि तारों के बीच की दूरी 1 mm बढ़ाई जाये, तो कितना कार्य करना पड़ेगा ? जल का पृष्ठ तनाव 72 × 10^-3 N/m
उत्तर:
1.44 × 10^-5 जूल

प्रश्न 27.
जल की 1000 छोटी बूँदों को जिनमें से प्रत्येक की त्रिज्या 10^-7 m है, आपस में मिलाकर एक बुड़ी बूँद बनाने पर मुक्त ऊर्जा ज्ञात कीजिए। जल का पृष्ठ तनाव 7 × 10^-2 N/m.
उत्तर:
7,92 × 10^-12 Joule

दाब आधिक्य तथा केशिकत्व पर आधारित

प्रश्न 28.
साबुन के दो बुलबुलों की त्रिज्याएँ क्रमश: 0.5 cm व 1.0 cm है। इनके अन्दर दाबों का अन्तर 14 N/m² है। साबुन के घोल का पृष्ठ तनाव ज्ञात कीजिए।
उत्तर:
0.035 N/m

प्रश्न 29.
1 mm व्यास की काँच की केशनली पारा भरे बीकर में ऊर्ध्वाधर खड़ी की जाती है। केशनली का निचला सिरा बीकर में पारे के पृष्ठ से 1 coin नीचे है। केशनली के निचले सिरे पर वायु का अर्द्धगोलीय बुलबुला . बनाने के लिए केशनली में वायु का गेज दाब क्या होना चाहिए ? पारे का पृष्ठ तनाव (0.465 N/m, तथा बुलबुले का व्यास केशनली के व्यास के बराबर मान लें।
उत्तर:
3193 N/m²

प्रश्न 30.
पारे के एक बैरोमीटर की नली का व्यास 3 mm है। पृष्ठ तनाव के कारण पाठ में क्या त्रुटि आयेगी ? स्पर्श कोण = 135° पारे का घनत्व = 13.5 × 10³ kg/m³ H T = 465 × 10^-3 N/m.
उत्तर:
3.3 mm गिर जायेगा

प्रश्न 31.
एक U-नली की दोनों ऊर्ध्वाधर नलियों के व्यास क्रमश: 5.0 mm तथा 2.0 mm है। इसमें जल भरा है, नलियों में जल स्तम्भ की ऊँचाइयों में कितना अन्तर है ? जल का पृष्ठ तनाव = 7.3 × 10^-2 N/ml
उत्तर:
8.94 mm

प्रश्न 32.
एक केशनली की लम्बाई 0.10 m है, जब इसे ऊर्ध्वाधर स्थिति में जल में रखा जाता है तो जल 0.06 m ऊँचाई तक चढ़ जाता है। यदि केशनली को ऊर्ध्वाधर स्थिति में 30° पर झुका दिया जाये तो केशनली में जल-स्तम्भ की लम्बाई क्या होगी ? यदि केशनली को बीचों-बीच से काट दिया जाये, तो केशनली में जल के पृष्ठ की स्थिति क्या होगी ? क्या जल फब्बारे के रूप में निकलने लगेगा ?
उत्तर:
6.94 cm, 0.05 m, जल पृष्ठ की वक्रता कम हो जायेगी।