HBSE 10th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल और आयतन Ex 13.3

Haryana State Board HBSE 10th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल और आयतन Ex 13.3 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल और आयतन Exercise 13.3

(जब तक अन्यथा न कहा जाए, π = \(\frac{22}{7}\) लीजिए।)

प्रश्न 1.
त्रिज्या 4.2 cm वाले धातु के एक गोले को पिघलाकर त्रिज्या 6 cm वाले एक बेलन के रूप में ढाला जाता है। बेलन की ऊँचाई ज्ञात कीजिए।
हल :
यहाँ पर,
धातु के गोले की त्रिज्या (r) = 4.2 cm
धातु के गोले का आयतन = ³
= \(\frac{4}{3}\) π(4.2)³ cm³
धातु के गोले को पिघलाकर बने बेलन की त्रिज्या (R)= 6 cm
माना
धातु के गोले को पिघलाकर बने बेलन की ऊँचाई = H cm
धातु के गोले को पिघलाकर बने बेलन का आयतन = πR²H cm³
= π(6)²H cm³
= 36 π H cm³\(\frac{4}{3}\) πr
प्रश्नानुसार
36 π H = \(\frac{4}{3}\) π (4.2)³
H = \(\frac{4}{3} \times \frac{1}{36}\) × 4.2 × 4.2 × 4.2
= 2.744 cm = 2.74 cm
अतः धातु के गोले को पिघलाकर बने बेलन की ऊँचाई = 2.74 cm

प्रश्न 2.
क्रमशः 6 cm, 8 cm और 10 cm त्रिज्याओं वाले धातु के तीन ठोस गोलों को पिघलाकर एक बड़ा ठोस गोला बनाया जाता है। इस गोले की त्रिज्या ज्ञात कीजिए।
हल :
यहाँ पर, पहले ठोस गोले की त्रिज्या (r₁) = 6 cm
दूसरे ठोस गोले की त्रिज्या (r₂) = 8 cm
तीसरे ठोस गोले की त्रिज्या (r₃) = 10 cm
माना तीनों ठोस गोलों को पिघलाकर
बने बड़े ठोस गोले की त्रिज्या = R cm
बड़े ठोस गोले का आयतन = (पहले + दूसरे + तीसरे) ठोस गोलों का आयतन
प्रश्नानुसार
बड़े ठोस गोले का आयतन = (पहले + दूसरे + तीसरे) ठोस गोलों का आयतन

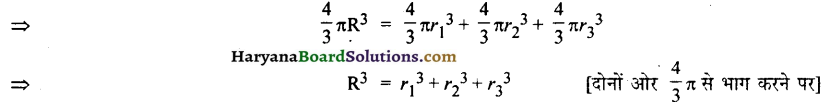
R³ = (6)³ + (8)³ + (10)³
= 216 + 512 + 1000 = 1728 = (12)³
R³ = 12
अतः तीनों ठोस गोलों को पिघलाकर बने बड़े ठोस गोले की त्रिज्या= 12 cm

प्रश्न 3.
व्यास 7 m वाला 20 m गहरा एक कुआँ खोदा जाता है और खोदने से निकली हुई मिट्टी को समान रूप से फैलाकर 22 m × 14 m वाला एक चबूतरा बनाया गया है। इस चबूतरे की ऊँचाई ज्ञात कीजिए।
हल :
यहाँ पर, बेलनाकार कुएँ का व्यास = 7 m
बेलनाकार कुएँ की त्रिज्या (r) = \(\frac{7}{2}\)
बेलनाकार कुएँ की गहराई (h) = 20 m
बेलनाकार कुएँ को खोदकर निकाली गई मिट्टी का आयतन = πr²h
= \(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\) × 20m³
= 770 m³
मिट्टी से बनने वाले चबूतरे का क्षेत्रफल = 22 × 14 m²
= 308 m²
मिट्टी का आयतन अतः मिट्टी से बनने वाले चबूतरे की ऊँचाई = चबतरे का क्षेत्रफल

प्रश्न 4.
व्यास 3 m का एक कुआँ 14 m की गहराई तक खोदा जाता है। इससे निकली हुई मिट्टी को कुएँ के चारों ओर 4m चौड़ी एक वृत्ताकार वलय (ring) बनाते हुए, समान रूप से फैलाकर एक प्रकार का बाँध बनाया जाता है। इस बाँध की ऊँचाई ज्ञात कीजिए।
हल :

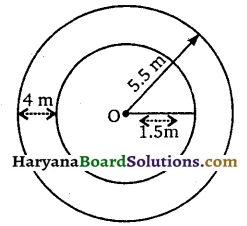
यहाँ पर, बेलनाकार कुएँ का व्यास = 3 m
बेलनाकार कुएँ की त्रिज्या (r) = \(\frac{3}{2}\) m
बेलनाकार कुएँ की गहराई (h) = 14 m
बेलनाकार कुएँ को खोदकर निकाली गई
मिट्टी का आयतन = πr²h
= \(\frac{22}{7} \times \frac{3}{2} \times \frac{3}{2}\) × 14 m³
= 99 m³
कुएँ की त्रिज्या (r) = 1.5 m
वृत्ताकार वलय (बांध) की चौड़ाई = 4.0 m
वृत्ताकार वलय की बाहरी त्रिज्या (R) = (1.5 +4) m = 5.5 m
अब वृत्ताकार वलय (बाँध) का क्षेत्रफल = बाहरी क्षेत्रफल – आंतरिक क्षेत्रफल
= πR² – πr² = π [(5.5)² – (1.5)²] m²
= \(\frac{22}{7}\) × 28 m² = 88 m²

प्रश्न 5.
व्यास 12 cm और ऊँचाई 15 cm वाले एक लंब वृत्तीय बेलन के आकार का बर्तन आइसक्रीम से पूरा भरा हुआ है। इस आइसक्रीम को ऊँचाई 12 cm और व्यास 6 cm वाले शंकुओं में भरा जाना है, जिनका ऊपरी सिरा अर्धगोलाकार होगा। उन शंकुओं की संख्या ज्ञात कीजिए जो इस आइसक्रीम से भरे जा सकते हैं।
हल :
यहाँ पर,
आइसक्रीम के लिए बेलनाकार बर्तन का व्यास = 12 cm
आइसक्रीम के लिए बेलनाकार बर्तन की त्रिज्या (R) = \(\frac{12}{2}\) cm = 6 cm
आइसक्रीम के लिए बेलनाकार बर्तन की ऊँचाई (H) = 15 cm
आइसक्रीम के लिए बेलनाकार बर्तन का आयतन = πR²H
= π (6)² × 15 cm³
= 540 π cm³
शंक्वाकार बर्तन का व्यास = 6 cm
शंक्वाकार वर्तन की त्रिज्या (7) = \(\frac{6}{2}\) cm = 3 cm
शंक्वाकार बर्तन की ऊँचाई (h) = 12 cm
शंक्वाकार बर्तन का आयतन = \(\frac{1}{3}\) πr²h
= [atex]\frac{1}{3}[/latex] × π(3)² × 12 cm³
= 36 π cm³ .
शंकु के ऊपर अर्धगोलाकार आइसक्रीम का आयतन = \(\frac{2}{3}\)πr³
= \(\frac{2}{3}\)π(3)³ = 18πcm³
प्रत्येक शंकु में आइसक्रीम का आयतन = (36 π + 18 π) cm³

प्रश्न 6.
विमाओं 5.5 cm × 10 cm × 3.5 cm वाला एक घनाभ बनाने के लिए 1.75 cm व्यास और 2 mm मोटाई वाले कितने चाँदी के सिक्कों को पिघलाना पड़ेगा?
हल :
यहाँ पर, वांछित घनाभ का आयतन = 5.5 × 10 × 3.5 cm³
= 192.5 cm³
चाँदी के प्रत्येक सिक्के का व्यास = 1.75 cm
चाँदी के प्रत्येक सिक्के की त्रिज्या (7) = \(\frac{1.75}{2}=\frac{175}{200}=\frac{7}{8}\) cm
चाँदी के प्रत्येक सिक्के की ऊँचाई (h) = 2 mm = \(\frac{2}{10}\) cm = \(\frac{1}{5}\) cm
चाँदी के प्रत्येक सिक्के का आयतन = πr²h
= \(\frac{22}{7} \times \frac{7}{8} \times \frac{7}{8} \times \frac{1}{5} \mathrm{~cm}^{3}=\frac{77}{160} \mathrm{~cm}^{3}\)
अतः घनाभ बनाने के लिए आवश्यक

प्रश्न 7.
32 cm ऊँची और आधार त्रिज्या 18 cm वाली एक बेलनाकार बाल्टी रेत से भरी हुई है। इस बाल्टी को भूमि पर खाली किया जाता है और इस रेत की एक शंक्वाकार ढेरी बनाई जाती है। यदि शंक्वाकार ढेरी की ऊँचाई 24 cm है, तो इस ढेरी की त्रिज्या और तिर्यक ऊँचाई ज्ञात कीजिए।
हल :
यहाँ पर, दी गई बेलनाकार बाल्टी के आधार की त्रिज्या (R) = 18 cm
दी गई बेलनाकार बाल्टी की ऊँचाई (H) = 32 cm
दी गई बेलनाकार बाल्टी के रेत का आयतन = πR²H
= π(18)² (32) cm³
माना बाल्टी को खाली करने से बनी
शंक्वाकार रेत की ढेरी की त्रिज्या = r cm
व बाल्टी को खाली करने से बनी
शंक्वाकार रेत की ढेरी की ऊँचाई (h) = 24 cm
बाल्टी को खाली करने से बनी शंक्वाकार रेत की ढेरी का आयतन = \(\frac{1}{3}\)πr²h

प्रश्न 8.
6 m चौड़ी और 1.5m गहरी एक नहर में पानी 10 km/h की चाल से बह रहा है। 30 मिनट में, यह नहर कितने क्षेत्रफल की सिंचाई कर पाएगी, जबकि सिंचाई के लिए 8 cm गहरे पानी की आवश्यकता होती है।
हल :
यहाँ पर,
नहर में पानी की चाल (l) = 10 km/h = \(\frac{10 \times 1000}{60}\) m/min = \(\frac{500}{3}\) m/min
नहर की चौड़ाई (b) = 6 m
नहर की गहराई (h) = 1.5 m
30 मिनट में नहर से निकले पानी का आयतन = [atex]\frac{500}{3}[/latex] × 30 × 6 × 1.5 m³
= 45000 m³
सिंचाई वाले क्षेत्र में पानी की ऊँचाई = 8 cm = \(\frac{8}{100}\) m

= 562500 m²

प्रश्न 9.
एक किसान अपने खेत में बनी 10 m व्यास वाली और 2 m गहरी एक बेलनाकार टंकी को आंतरिक व्यास 20 cm वाले एक पाइप द्वारा एक नहर से जोड़ता है। यदि पाइप में पानी 3 km/h की चाल से बह रहा है, तो कितने समय बाद टंकी पूरी भर जाएगी?
हल :
यहाँ पर,
दी गई बेलनाकार टंकी का व्यास = 10 m
दी गई बेलनाकार टंकी की त्रिज्या (R) = \(\frac{10}{2}\) m = 5m
दी गई बेलनाकार टंकी की गहराई (H) = 2 m
दी गई बेलनाकार टंकी का आयतन = πR²H
= π (5)² (2) m³
= 50 π m³
पाइप से निकलने वाले पानी की चाल = 3 km/h
= \(\frac{3 \times 1000}{60}\) = 50 m/min
60 माना पाइप द्वारा बेलनाकार टंकी को
भरने में लगा समय = t min
दिए गए पाइप का आंतरिक व्यास = 20 cm = \(\frac{20}{100} m=\frac{1}{5} m\)
दिए गए पाइप की आंतरिक त्रिज्या (r) = \(\frac{1}{10}\) m
अतः दिए गए पाइप से t min निकलने वाले
पानी का आयतन = π\(\left(\frac{1}{10}\right)^{2}\)(50 t) m³
= \(\frac{\pi}{2}\)t m³
प्रश्नानुसार \(\frac{\pi}{2}\) t = 50 π
t = 50 × 2 = 100
अतः पाइप द्वारा बेलनाकार टंकी को भरने में लगा समय = 100 मिनट