HBSE 10th Class Maths Solutions Chapter 1 Real Numbers Ex 1.1

Haryana State Board HBSE 10th Class Maths Solutions Chapter 1 Real Numbers Ex 1.1 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 1 Real Numbers Exercise 1.1

Question 1.
Use Euclid’s division algorithm to find the HCF of :
(i) 135 and 225
(ii) 196 and 38220
(iii) 867 and 255
Solution :
(i) 225 > 135 By Euclid’s division lemma,
225 = 135 × 1 + 90
Since remainder 90 ≠ 0

So, we consider divisor 135 and remainder 90 and apply Euclid’s division lemma.
135 = 90 × 1 + 45

Now, we consider new divisor 90 and new remainder 45 and apply Euclid’s division lemma.
90 = 45 × 2 + 0

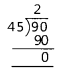
Since, the remainder at this stage is zero and divisor is 45.
Therefore, HCF of 135 and 225 is 45.

(ii) 38220 > 196
By Euclid’s division lemma, 38220 = 196 × 195 + 0

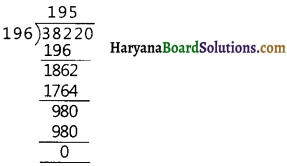
Since, at this stage remainder is zero and divisor is 196.
Hence, from calculation of right side division we find, HCF of 196 and 38220 is 196.

(iii) 867 > 255
By Euclid’s division lemma, 867 = 255 × 3 + 102

Since, remainder 102 ≠ 0
So, we consider divisor 255 and remaihder 102 and apply the Euclid’s division lemma.
255= 102 × 2 + 51

Now we consider new divisor 102 and new remainder 51 and apply Euclid’s division lemma.
102 = 51 × 2 + 0

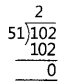
Since, the remainder at this stage is zero and divisor is 51.
Hence, HCF of 867 and 255 is 51.

Question 2.
Show that any positive odd integer is of the form 6q + 1 or 6q + 3 or 617 + 5, where q is some integer.
Solution :
Let a be any given positive integer and b = 6.
Then by Euclid’s division algorithm there exists integers q and r such that
a = 6q + r where 0 ≤ r < 6
r = 0, 1, 2, 3, 4, 5
For r = 0, a = 6q + 0 = 6q = 2(3q)
For r = 1, a = 6q + 1
For r = 2, a = 6q + 2 = 2(3q + 1)
For r = 3, a = 6q + 3
For r = 4, a = 6g + 4 = 2(3g + 2)
For r = 5, a = 6q + 5
a = 6q, 6q + 2 and 6 32
By Euclid’s division lemma,
616 = 32 × 19 + 8.

Since, remainder 8 ≠ 0.
So, we consider divisor 32 and remainder 8 and apply Euclid’s division lemma.
32 = 8 × 4 + 0

Since, the remainder at this stage is zero and divisor is 8.
Therefore, HCF of 616 and 32 is 8. Hence, the maximum number of column = 8.

Question 4.
Use Euclid’s division lemma to show that the square of any positive integer is either of the form 3m or 3m + 1 for some integer m.
[Hint – Let x be any positive integer then it is of the form 3q, 3q + 1 or 3q + 2. Now square each of these and show that they can be written in the form 3 m or 3m + 1.]
Solution :
Let x be any given positive integer and 6 = 3. Then by Euclid’s division algorithm there exists positive integers q and r such that :
x = 3q + r, where 0 ≤ r < 3
x = 3q, 3q + 1 or 3q +.2.
So, we have the following cases :
Case I : When x = 3q
x² = 9q² = 3 (3q²) [Squaring on both sides]
x² = 3m, where m = 3q²

Case II: When x = 3q + 1
= (3q + 1)² [Squaring on both sides]
= x² = 9q² + 6q + 1
= 3(3q² + 2q) + 1
= 3m + 1, where m = 3q² + 2q

Case III: When x = 3q + 2
x² = (3q + 2)² [Squaring on both sides]
= 9q² + 12q + 4
= 9q² + 12q + 3 + 1
= 3 (3q² + 4q + 1) + 1
= 3m+ 1, where m = 3q² + 4q + 1
Hence, square of any positive integer is either of the form 3m or 3m + 1 for some integer m.

Question 5.
Use Euclid’s division lemma to show that the cube of any positive integer is of the form 9m, 9m + 1 or 9m + 8.
Solution:
Let x be positive integer and by applying Eucids division lemma it is of the form 3q or 3q + 1 or 3q + 2.
So, we have the following cases :
Case I: When x = 3q.
x³ = (3q)³ = 27q³ [Cube on both sides]
= 9(3q³)
= 9m, where m = 3q³

Case II: When x = 3q + 1
x³ = (3q + 1)³ (Cube on both sides]
= 27q³ + 27q² + 9q + 1
= 9 (3q³ + 3q² + q) + 1
= 9m + 1, where m = 3q³ + 3q² + q

Case III: When x = 3q + 2
[Cube on both sides]
x³ = (3q + 2)³
= 27q³ + 54q² + 36q + 8
= 9q(3q² + 6q + 4) + 8
= 9m + 8
where m = q(3q² + 6q + 4
Hence, x³ is either of the forms 9m, 9m + 1, 9m + 8.