HBSE 10th Class Maths Important Questions Chapter 6 Triangles

Haryana State Board HBSE 10th Class Maths Important Questions Chapter 6 Triangles Important Questions and Answers.

Haryana Board 10th Class Maths Important Questions Chapter 6 Triangles

Short/Long Answer Type Questions

Question 1.
In the adjoining figure, DE || BC, find the length of side AD, given that AE = 1.8 cm, BD = 7.2 cm and CE = 5.4 cm.

Solution :
We have
AE = 1.8 cm, BD = 7.2 cm, CE = 5.4 cm and DE || BC
∴ \(\frac{\mathrm{AD}}{\mathrm{BD}}=\frac{\mathrm{AE}}{\mathrm{CE}}\)
[By theorem 6.1 (BPT)]
⇒ \(\frac{\mathrm{AD}}{\mathrm{7.2}}=\frac{\mathrm{1.8}}{\mathrm{5.4}}\)
⇒ AD = \(\frac{7.2 \times 1.8}{5.4}\)
⇒ AD = \(\frac{7.2 \times 1.8}{54}\) = 2.4 cm

Question 2.
In the given fig. ∠D = ∠E and \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\) prove that ΔBAC is an isosceles triangle.

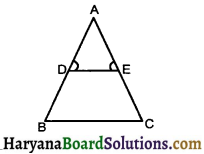
Solution :
We have, In triangle ABC,
\(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
⇒ DE || BC (By converse of BPT)
DE || BC and AD is a transversal line
∠D = ∠B (Corresponding angles) … (1)
DE || BC and AC is a transversal line, So, ∠E = ∠C (Corresponding angles) …(2)
But ∠D = ∠E ……(3)
From equ. (1), (2) and (3) we get
∠B = ∠C
⇒ AB = AC [Sides opp. to equal angles are equal]
Hence Proved.

Question 3.
In the adjoining figure, DE || AC and DC || AP. Prove that \(\frac{\mathrm{BE}}{\mathrm{EC}}=\frac{\mathrm{BC}}{\mathrm{CP}}\)

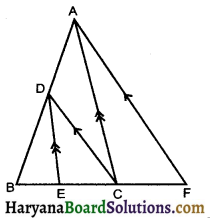
Solution :
In ΔABP, we have DC || AP
∴ \(\frac{\mathrm{AD}}{\mathrm{BD}}=\frac{\mathrm{BC}}{\mathrm{CP}}\) …….(1)
[By BPT]
Again, In ΔABC, we have
DE || AC
∴ \(\frac{\mathrm{AD}}{\mathrm{BD}}=\frac{\mathrm{BE}}{\mathrm{EC}}\) ……….(2)
From equation (1) and (2), we get
∴ \(\frac{\mathrm{AD}}{\mathrm{BD}}=\frac{\mathrm{BE}}{\mathrm{EC}}\)
Hence Proved.

Question 4.
In the adjoining figure, if ΔABC ~ ΔDEF and their sides of length (in cm) are marked along them, then find the lengths of the sides of each triangle.

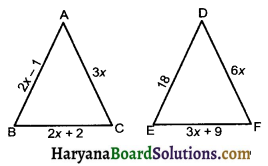
Solution :
We have, ΔABC ~ ΔDEF

⇒ 2x – 1 = \(\frac {18}{2}\) and 4x + 4 = 3x + 9
⇒ 2x = 9 + 1 and 4x – 3x = 9 – 4
⇒ 2x = 10 and x = 5
⇒ x = 5 and x = 5
Substituting the value of x in the length of sides of two triangles, we get
AB = 2x – 1 = 5 × 2 – 1 = 9 cm
BC = 2x + 2 = 5 × 2 + 2 = 12 cm
AC = 3x = 5 × 3 = 15 cm
DE = 18, EF = 3x + 9
= 3 × 5 + 9 = 24 cm
And DF = 6 × x = 6 × 5 = 30 cm
Hence, sides of ΔABC are 9cm, 12 cm, 15 cm, and sides of ΔDEF are 18 cm, 24 cm and 30 cm.

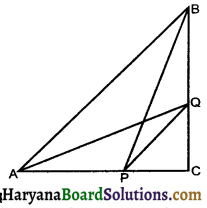
Question 5.
In similar triangle ABC and PQR, AD and PM are the medians respectvely, prove that \(\frac{\mathrm{AD}}{\mathrm{PM}}=\frac{\mathrm{AB}}{\mathrm{PQ}}\)

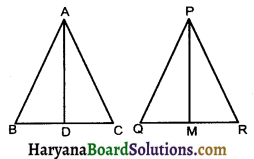
Solution :
Given : AD and PM are medians of ΔABC and ΔPQR and ΔABC ~ ΔPQR.
To prove : \(\frac{\mathrm{AD}}{\mathrm{PM}}=\frac{\mathrm{AB}}{\mathrm{PQ}}\)
Proof : ΔABC ~ ΔPQR
∴ ∠B = ∠Q
(Corresponding ∠S of similar triangles)….(1)

and ∠B = ∠Q [proved above] …………..(1)
From (1), ∠2, ΔABC ~ ΔPQM [By SAS similarity criterian]
⇒ \(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{AD}}{\mathrm{QM}}\)
[Corrosponding sides of similar triangles]

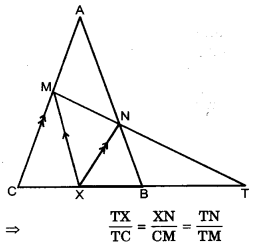
Question 6.
X is a point on side BC of ΔABC, XM and XN are drawn parallel to AB and AC respectively meeting AB in N and AC in M. MN produced meets CB produced at T. Prove that TX² = TB × TC
Solution :
In ΔTCM, XN||CM
∴ ΔTXN ~ ΔTCM

Question 7.
Given ΔABC ~ ΔPQR, if \(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{1}}{\mathrm{3}}\) then \(\frac{a r(\triangle \mathrm{ABC})}{a r(\Delta \mathrm{PQR})}\) = …………..
Solution :
Since ΔABC ~ ΔPQR

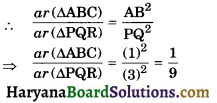
Question 8.
ΔABC and ΔBDE are two equilateral triangle such that D is the mid point of BC. Ratio of the areas of triangles ABC and BDE is …………………

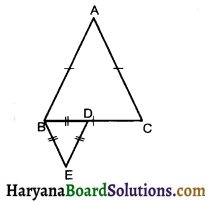
Solution :
Let each side of equilateral ABC be 2x units then BD = \(\frac {2x}{2}\) [D is the mid point of BC]
⇒ BD = x units
Each of anlge ΔABC is 60° (equilateral Δ)
Each angle of ΔBDE is 60° (equilateral Δ)
ΔABC ~ ΔBDE (By AAA similarity criterian)

Question 9.
The area of two similar triangles are in the ratio 16 : 18. Find the ratio of its sides.
Solution :
Let ΔABC ~ ΔPQR

Question 10.
If the ratio of corresponding medians of two similar triangles are 9 : 16, then find the ratio of their area.
Solution :
We have,
Ratio of corresponding medians of two similar triangles = 9 : 16
We know that, Ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medi
= 81 : 256

Question 11.
If ΔABC – ΔDEF in which AB = 1.6 cm and DE = 2.4 cm. Find the ratio of areas of ΔABC and ΔDEF.
Solution :
∵ ΔABC ~ ΔDEF

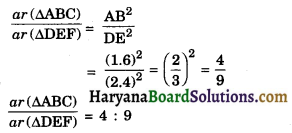
Question 12.


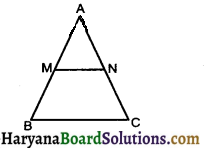
Solution :
We have, In ΔABC, MN || BC
∴ ΔAMN ~ ΔABC

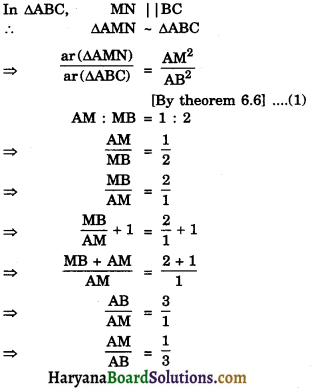
Substituting the value of \(\frac {AM}{AB}\) in the equation (1), we get

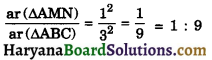
Question 13.
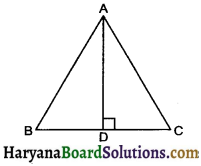
In the given figure, ∠ACB = 90° and CD ⊥ AB. Prove that CD² = BD × AD.

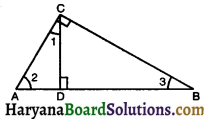
Solution :
Given : A ΔABC i. which ∠ACB = 90° and CD ⊥ AB
To prove : CD² = BD × AD
Proof: In Right ΔADC,
∠1 + ∠2 + ∠ADC = 180°
⇒ ∠1 + ∠2 + 90° = 180°
⇒ ∠1 + ∠2 = 180° – 90°
⇒ ∠1 + ∠2 = 90° …………..(1)
Similary in right ΔACB,
∠2 + ∠3 = 90° ……….(2)
From (1) and (2), we get
∠1 + ∠2 = ∠2 + ∠3
⇒ ∠1 = ∠3.
In ΔADC and ∠CDB
∠1 = ∠3 (proved above)
∠ADC = ∠CDB (each = 90°)
∴ ΔADC ~ ΔCDB
[By AA similarity criterion]
∴ \(\frac{\mathrm{AD}}{\mathrm{CD}}=\frac{\mathrm{CD}}{\mathrm{BD}}\)
⇒ CD² = BD × AD
Hence Proved

Question 14.
ΔABC is a right triangle in which ∠C = 90° and CD ⊥ AB. If BC = a, CA = b, ABC and CD = p, then prove that :
(i) cp = ab
(ii) \(\frac{1}{\mathrm{p}^2}=\frac{1}{\mathrm{a}^2}+\frac{1}{\mathrm{~b}^2}\)
Solution :
(i) Area of right ΔABC
= \(\frac {1}{2}\) base × height
= \(\frac {1}{2}\) a × b
= \(\frac {1}{2}\) ab …(1)

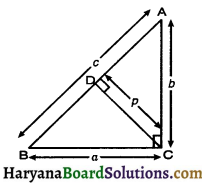
Again, Area of right ΔABC
= \(\frac {1}{2}\) × base × height
= \(\frac {1}{2}\) × c × p
= \(\frac {1}{2}\) × cp …(2)
From (1) and (2), we get
\(\frac {1}{2}\)ab = \(\frac {1}{2}\)cp
⇒ ab = cp
Hence Proved

(ii) In right ΔACB,
AB² = BC² + AC²
⇒ c² = a² + b² ……………(3)

Hence Proved

Question 15.
If P and Q are points on sides CA and CB respectively of ΔABC, right angled at C. Prove that (AQ² + BP²) – (AB² + PQ²)
Solution :
Given: A right triangle ABC in which ∠C = 90°, P and Q are points on sides CA and CB respectively.
Construction: Join AQ, BP and PQ.

To prove : AQ² + BP² = AB² + PQ²
Proof : In right ΔACQ. we have
AQ² = AC² + QC² ……………(1)
In right ΔBPC, we have
BP² = CP² + BC² ………………(2)
Adding equ. (1) and (2), we get
AQ² + BP² = AC² + QC² + CP² + BC²
= (AC² + BC²) + (CP² + QC²)
= AB² + PQ²
[∵ AC² + BC² = AC² and CP² + QC² = PQ²]

Fill in the Blanks

Question 1.
If the basector of an angle of a triangle ………….. the opposite side then triangle is an equilateral triangle.
Solution :
bisects

Question 2.
Thales theorem is also known as basic ………
Solution :
proportionality

Question 3.
All equilateral triangles are …………
Solution :
similar

Question 4.
Phythagoras theorem is sometimes also referred to as the ……………. theorem.
Solution :
Baudhayan

Question 5.
If a line divides any two sides of a triangle in the same ………… then line is parallel to the third side.
Solution :
ratio

Question 6.
If corresponding angles of two triangles are equal, then they are known as ………….. triangles.
Solution :
equiangular.

Multiple Choice Questions

Question 1.
In equilateral ΔABC, AD is altitude. Then 4AD² equals.
(a) 2BD²
(b) 2DC²
(c) BC²
(d) 3AB²
Solution :
(d) 3AB²

In ΔADB and ΔADC
AB = AC
∠ADB = ∠ADC
AD = AD
∴ ΔADB ≅ ΔADC
∴ BD = CD (CPCT)

In right ΔADB AB² = AD² + BD²
AB² = AD² + \(\frac {1}{4}\)AB²
⇒ 4AD² = 3AB²
So correct choice is (d)

Question 2.
In rhombus PQRS, PQ² + QR² + RS² + SP² = ?
(a) OP² + OQ²
(b) OQ² + OR²
(c) OR² + OS²
(d) PR² + QS²

Solution :
(d) PR² + QS²

4PQ² = PR² + QS²
4QR² = PR² + QS²
4RS² = PR² + QS²
4PS² = PR² + QS²
∴ PQ² + QR² + RS² + PS² = PR² + QS²
So correct choice is (d)

Question 3.
In figure, DE || BC, AD = 2.4 cm, AE = 3.2 cm, CE = 4.8 cm. The value of BD is :

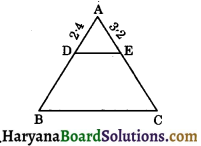
(a) 3.6 cm
(b) 4.2 cm
(c) 4.0 cm
(d) None of these.
Solution :
(a) 3.6 cm

Given AD = 2.4 cm
AE = 3.2 cm
EC = 4.8 cm
Let DB = x
We know that \(\frac{\mathrm{AD}}{\mathrm{BD}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)

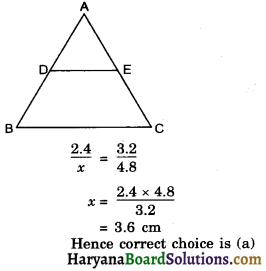
Hence correct choice is (a)

Question 4.
In the given figure, ∠BAC = 90° and AD ⊥ BC, then,
[NCERT Exemplar Problems]
(a) BD.CD = AD²
(b) AB.AC = BC²
(c) BC.CD = BC²
(d) AB.AC = AD²

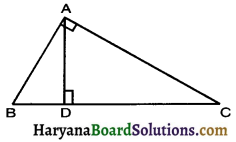
Solution :
(a) BD.CD = AD²

Since
ΔBDA ~ ΔADC
⇒ \(\frac{\mathrm{BD}}{\mathrm{AD}}=\frac{\mathrm{AD}}{\mathrm{CD}}\)
⇒ AD² = BD.CD
So correct choice is (a).

Question 5.
If ΔABC – ΔEDF and ΔABC is not similar to ADEF, then which of the following is not true?
[NCERT Exemplar Problems]
(a) BC.EF = AC.FD
(b) AB.EF = AC.DE
(c) BC.DE = AB.EF
(d) BC.DE = AB.FD.
Solution :
(c) BC.DE = AB.EF

ΔABC ~ ΔEDF
ΔABC not similar to ΔDEF
ΔABC ~ ΔEDF