HBSE 10th Class Maths Important Questions Chapter 14 सांख्यिकी

Haryana State Board HBSE 10th Class Maths Important Questions Chapter 14 सांख्यिकी Important Questions and Answers.

Haryana Board 10th Class Maths Important Questions Chapter 14 सांख्यिकी

परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न :

प्रश्न 1.
किसी स्कूल की कक्षा X के 30 विद्यार्थियों द्वारा गणित के एक पेपर में, 100 में से प्राप्त किए गए अंक नीचे एक सारणी में दिए गए हैं। इन विद्यार्थियों द्वारा प्राप्त अंकों का माध्य ज्ञात कीजिए ।

हल :
यहाँ पर,

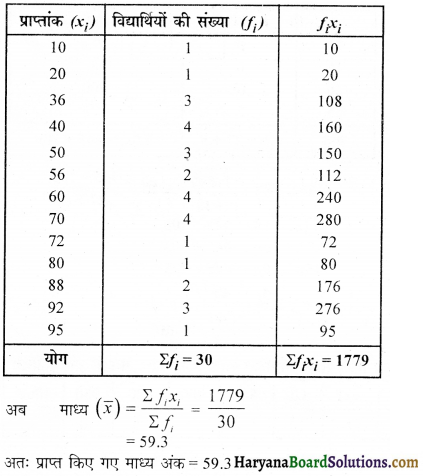
प्रश्न 2.
निम्नलिखित बारंबारता बंटन का माध्य ज्ञात कीजिए-

हल :
यहाँ पर,

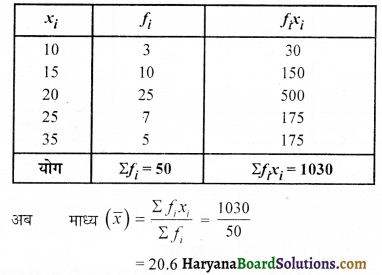
प्रश्न 3.
यदि निम्नलिखित बारंबारता बंटन का माध्य 15 हो तो p का मान ज्ञात करो –

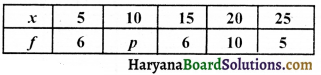
हल :
यहाँ पर,

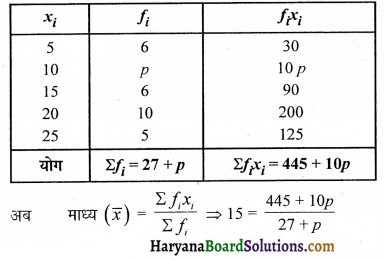
⇒ 15 (27 + p) = 445 + 10p
⇒ 405 + 1.5p = 445 + 10p
⇒ 15p – 10p = 445 – 405
⇒ 5p = 40
⇒ P = \(\frac {40}{5}\) = 8

प्रश्न 4.
कल्पित माध्य विधि से निम्नलिखित आँकड़ों की माध्य मजदूरी ज्ञात कीजिए-

हल :
माना कल्पित माध्य (a) = 900
तो d_i = x_i – a = x_i – 900

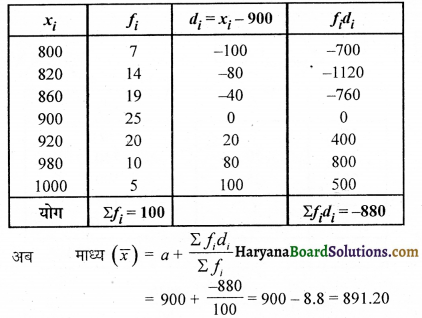
अतः दिए गए आँकड़ों की माध्य मजदूरी = 891.20 रु०

प्रश्न 5.
निम्नलिखित सारणी में ग्रामीण क्षेत्र के विद्यालयों में महिला शिक्षकों के प्रतिशत बंटन को दर्शाती है। महिला शिक्षकों का माध्य प्रतिशत ज्ञात कीजिए :

हल :
यहाँ पर,
माना कल्पित माध्य (a) = 50
तथा वर्ग-माप (h) = 10 तो u₁ = \(\frac{x_i-a}{h}=\frac{x_i-50}{10}\)

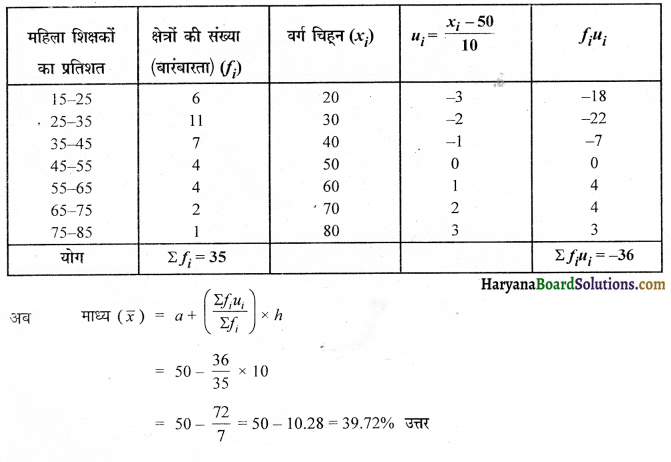
प्रश्न 6.
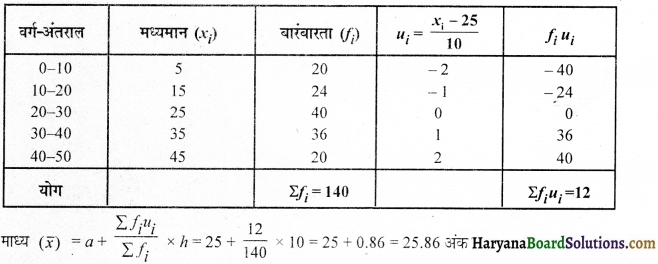
किसी परीक्षा के 140 विद्यार्थियों द्वारा प्राप्त अंक निम्नलिखित सारणी में दर्शाए गए हैं-

तीनों विधियों अर्थात् प्रत्यक्ष विधि, कल्पित माध्य विधि और पग- विचलन विधि के द्वारा माध्य अंकों का परिकलन कीजिए ।
हल :
(i) प्रत्यक्ष विधि :

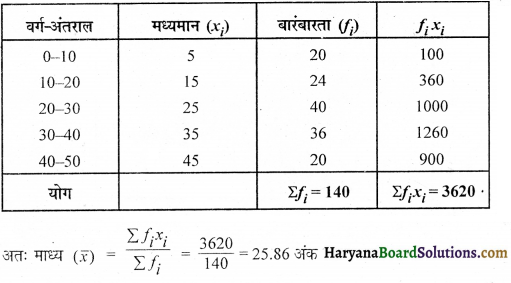
(ii) कल्पित माध्य विधि : माना कल्पित माध्य (a) = 25 तो d_i = x_i – a = x_i – 25

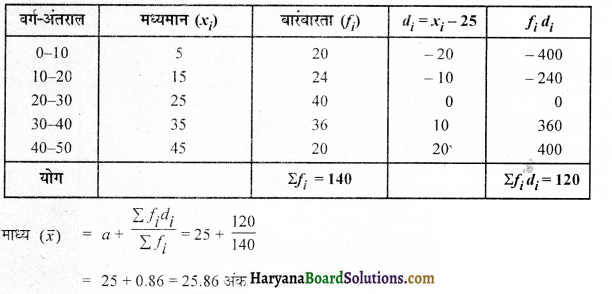
(iii) पग-विचलन विधि : कल्पित माध्य (a) = 25, h = 10 तो u_i = \(\frac{x_i-a}{h}=\frac{x_i-25}{10}\)

प्रश्न 7.
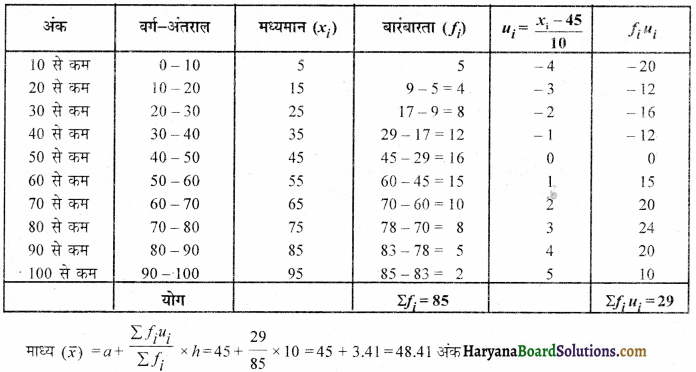
निम्नलिखित आंकड़ों से माध्य ज्ञात कीजिए-

अंक	विद्यार्थियों की संख्या
10 से कम 20 से कम 30 से कम 40 से कम 50 से कम 60 से कम 70 से कम 80 से कम 90 से कम 100 से कम	5 9 17 29 45 60 70 78 83 85

हल :
माना कल्पित माध्य (a) = 45, h = 10 तो u_i = \(\frac{x_i-a}{h}=\frac{x_i-45}{10}\)

प्रश्न 8.
वर्ष 2000-2001 के लिए किसी नगर के साप्ताहिक निर्वाह खर्च सूचकांक निम्नानुसार हैं-

निर्वाह खर्च सूचकांक	सप्ताहों की संख्या
140-150 150-160 160-170 170-180 180-190 190-200	5 10 20 9 6 2
योग	52

माध्य साप्ताहिक निर्वाह खर्च सूचकांक का परिकलन कीजिए ।
हल :
माना कल्पित माध्य (a) = 175, h = 10 तो u_i = \(\frac{x_i-a}{h}=\frac{x_i-175}{10}\)

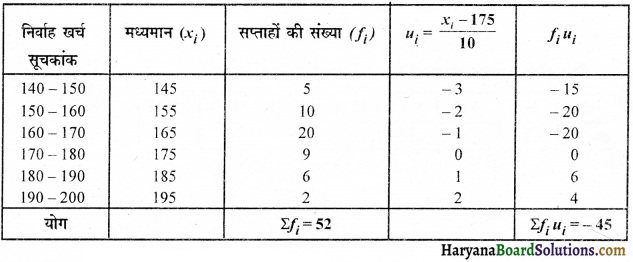
मध्य (\(\bar{x}\)) = a + \(\frac{\sum f_i u_i}{\sum f_i}\) × h = 175 + \(\frac {-45}{52}\) × 10 = 175 – 8.7 = 166.3 (लगभग)

प्रश्न 9.
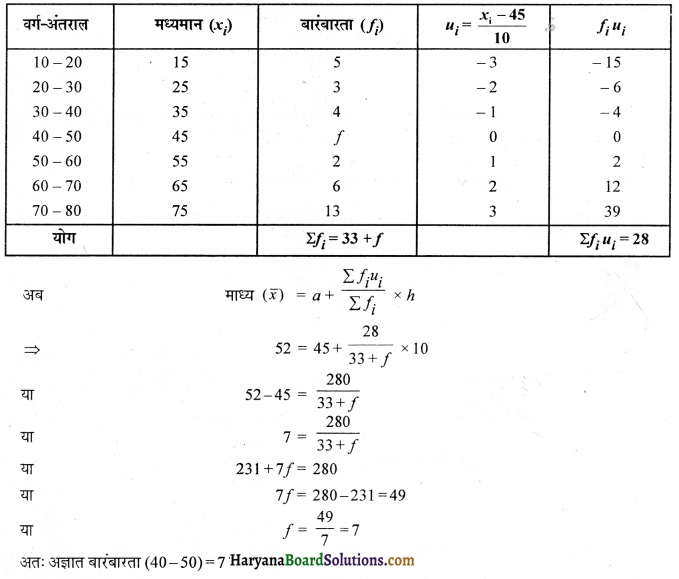
निम्नलिखित बारंबारता बंटन में वर्ग – अंतराल (40-50) की बारंबारता अज्ञात है । यह ज्ञात है कि बंटन का माध्य 52 है। अज्ञात बारंबारता ज्ञात कीजिए ।

हल :
माना अज्ञात बारंबारता = f, माध्य (\(\bar{x}\)) = 52
कल्पित माध्य (a) = 45, h = 10

प्रश्न 10.
निम्नलिखित वर्गीकृत बारंबारता बंटन का बहुलक ज्ञात कीजिए-

हल :
यहाँ पर अधिकतम वर्ग बारंबारता 23 है तथा इस बारंबारता का संगत वर्ग : 12-15 है।
⇒ बहुलक वर्ग = 12-15
बहुलक वर्ग की निम्न सीमा (l) = 12
वर्ग-माप = 3
बहुलक वर्ग की बारंबारता (f₁) = 23
बहुलक वर्ग से ठीक पहले वाले वर्ग की बारंबारता (f₀) = 10
बहुलक वर्ग के ठीक बाद में आने वाले वर्ग की बारंबारता (f₂) = 21
अब बहुलक = l + (\(\frac{f_1-f_0}{2 f_1-f_0-f_2}\)) × h
= 12 + (\(\frac{23-10}{2(23)-10-21}\)) × 3
= 12 + \(\frac {13}{15}\) × 3 = 12 + 2.6 = 14.6

प्रश्न 11.
निम्नलिखित बारंबारता बंटन का बहुलक ज्ञात कीजिए-

हल :
यहाँ पर बहुलक ज्ञात करने के लिए आँकड़ों को सतत वर्ग-अंतरालों में बदलना पड़ेगा क्योंकि सूत्र में वर्ग-अंतरालों को सतत माना गया है जो निम्नलिखित होंगे-

वर्ग-अंतराल	बारंबारता (f)
0.5-4.5 4.5-8.5 8.5-12.5 12.5-16.5 16.5-20.5 20.5-24.5 24.5-28.5 28.5-32.5 32.5-36.5 36.5-40.5	2 5 8 9 12 14 14 15 11 13

यहाँ पर अधिकतम वर्ग बारंबारता 15 है तथा इस बारंबारता का संगत वर्ग 28.5 -32.5 है।
⇒ बहुलक वर्ग = 28.5 – 32.5
बहुलक वर्ग की निम्न सीमा (l) = 28.5
वर्ग-माप (h) = 4
बहुल वर्ग की बारंबारता (f₁) = 15
बहुलक वर्ग से ठीक पहले वाले वर्ग की बारंबारता (f₀) = 14
बहुलक वर्ग के ठीक बाद में आने वाले वर्ग की बारंबारता (f₂) = 11
अब बहुलक = l + (\(\frac{f_1-f_0}{2 f_1-f_0-f_2}\)) × h
= 28.5 + (\(\frac{15-14}{2(15)-14-11}\)) × 4
= 28.5 × \(\frac {1}{5}\) × 4
= 28.5 + 0.8
= 29.3

प्रश्न 12.
निम्नलिखित आँकड़ों का माध्यक 525 है। यदि बारंबारताओं का योग 100 है, तो x और y का मान ज्ञात कीजिए।

वर्ग-अंतराल	बारंबारता (f)
0-100 100-200 200-300 300-400 400-500 500-600 600-700 700-800 800-900 900-1000	2 5 x 12 17 20 Y 9 7 4

हल :
यहाँ पर,

वर्ग-अंतराल	बारंबारता (f)	संचयी बारंबारता (cf)
0-100 100-200 200-300 300-400 400-500 500-600 600-700 700-800 800-900 900-1000	2 5 X 12 17 20 Y 9 7 4	2 7 7 + x 19 + x 36 + x 56 + x 56 + x + y 65 + x + y 72 + x + y 76 + x + y

प्रश्नानुसार, n = 100 ⇒ \(\frac{n}{2}=\frac{100}{2}\) = 50 जो कि वर्ग-अंतराल 500-600 में आता है
⇒ 76 + x + y = 100 ⇒ x + y = 24 ………………(i)
क्योंकि, माध्यक 525 है, जो वर्ग 500-600 में स्थित है ।
अतः, l = 500, f = 20, cf = 36 + x, h = 100
अब माध्यक = l + (\(\frac{\frac{n}{2}-c f}{f}\)) × h
⇒ 525 = 500 + (\(\frac{50-36-x}{20}\)) × 100
या 525 – 500 = (14 – x) × 5
या 25 = 70 – 5x
या 5x = 70 – 25 = 45
अतः x = 9
समीकरण (i) 9 + y = 24
⇒ y = 24 – 9 = 15
अतः x = 9 व y = 15

प्रश्न 13.
किसी स्कूल की कक्षा X की 51 लड़कियों की ऊँचाइयों का एक सर्वेक्षण किया गया और निम्नलिखित आँकड़े प्राप्त किए गए-

माध्यक ऊँचाई ज्ञात कीजिए ।
हल :

ऊँचाई (cm में)	बारम्बारता (f)	संचयी बारम्बारता (cf)
140 से कम 140-145 145-150 150-155 155-160 160-165	4 7 18 11 06 05	4 11 29 40 46 51

यहाँ n = 51
⇒ \(\frac{n}{2}=\frac{51}{2}\) = 25.5 जोकि वर्ग अन्तराल 145 – 150 में आता है।
अतः माध्यक वर्ग = 145 – 150
अब माध्यक वर्ग की निम्न सीमा (l) = 145
वर्गमाप (h) = 5
माध्यक वर्ग से ठीक पहले वाले वर्ग की संचयी बारम्बारता (cf) = 11
माध्यक वर्ग की बारम्बारता (f) = 18
अब माध्यक = l + (\(\frac{\frac{n}{2}-c f}{f}\)) × h
= 145 + (\(\frac{25.5-11}{18}\)) × 5
= 145 + \(\frac {72.5}{18}\)
= 145 + 4.03
= 149.03 cm

प्रश्न 14.
एक प्रवेश परीक्षा में 230 विद्यार्थियों द्वारा प्राप्त अंकों की बारंबारता बंटन निम्नलिखित है-

एक ही अक्ष पर ‘से कम’ तथा ‘से अधिक’ विधि द्वारा संचयी बारंबारता वक्र बनाएँ तथा माध्यक ज्ञात कीजिए ।
हल :
दी गई बारंबारता बंटन का एक कम प्रकार की संचयी बारंबारता बंटन सारणी व ‘से अधिक’ प्रकार की संचयी बारंबारता बंटन सारणी निम्नलिखित प्राप्त होगी-

प्राप्तांक	संचयी बारंबारता
450 से कम 500 से कम 550 से कम 600 से कम 650 से कम 700 से कम 750 से कम 800 से कम	2 55 (20 + 35) 95 (55 + 40) 127 (95 + 32) 151 (127 + 24) 178(151 + 27) 196(178 + 18) 230(196 + 34)

प्राप्तांक	संचयी बारंबारता
400 से अधिक 450 से अधिक 500 से अधिक 550 से अधिक 600 से अधिक 650 से अधिक 700 से अधिक 750 से अधिक	230 210 175 135 103 79 52 34

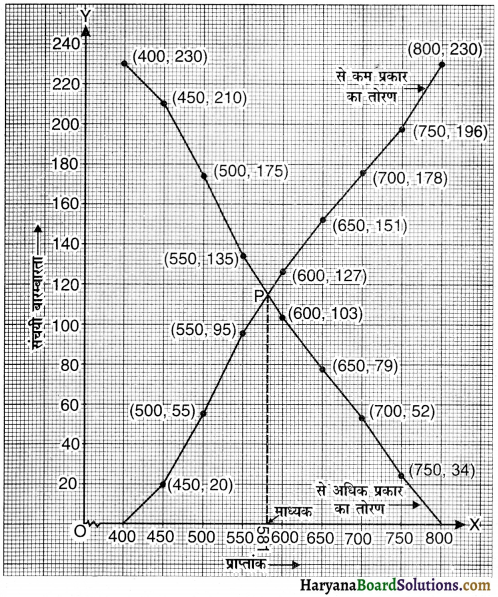
अब ग्राफ पेपर पर बिन्दुओं (450, 20), (500, 55), (550, 95), (600, 127), (650, 151), (700, 178), (750, 196) व (800, 230) को आलेखित कर मुक्त हस्त से मिलाकर ‘से कम’ प्रकार का तोरण खींचिए।

इसी प्रकार बिन्दुओं (400, 230), (450, 210), (500, 175), (550, 135), (600, 103), (650, 79), (700, 52) व (750, 34) को आलेखित कर मुक्त हस्त से मिलाकर ‘से अधिक’ प्रकार का तोरण खींचिए।

दोनों तोरणों का कटाव बिन्दु P माध्यक 581 (लगभग) प्रदान करता है ।

प्रश्न 15.
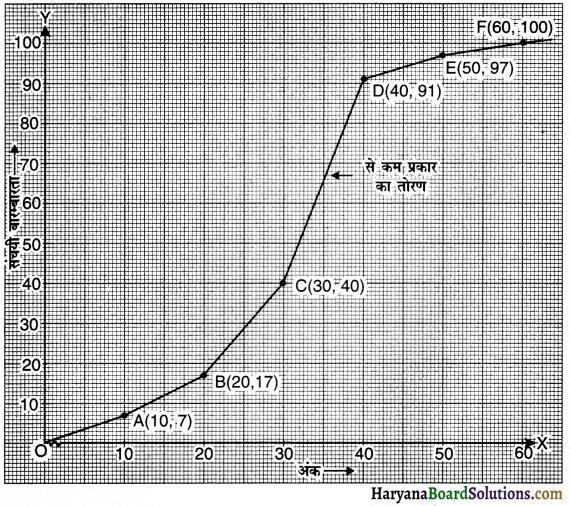
निम्नलिखित बारंबारता बंटन के लिए ‘से कम’ प्रकार का तोरण खींचिए –

हल :
दी गई बारंबारता बंटन सारणी को एक कम प्रकार की संचयी बारंबारता बंटन सारणी में बदलने पर प्राप्त होगा-

अंक	संचयी बारंबारता
10 से कम 20 से कम 30 से कम 40 से कम 50 से कम 60 से कम	7 17 (7+10)40 (17+23) 91 (40+51) 97 (91+6) 100 (97 +3)

अब बिन्दुओं A(10, 7), B(20, 17), C (30, 40), D(40, 91), E(50, 97) व F (60, 100) को आलेखित कर मुक्त हस्त से मिलाकर ‘से कम’ प्रकार का तोरण निम्नलिखित होगा –

बहुविकल्पीय प्रश्न :

प्रश्न 1.
निम्नलिखित में से कौन-सा केन्द्रीय प्रवृत्ति का माप नहीं है-
(A) माध्य
(B) माध्यक
(C) बहुलक
(D) मानक विचलन
हल :
(D) मानक विचलन

प्रश्न 2.
यदि प्रेक्षणों
x₁, x₂, x₃ ………………… x_n की बारंबारताएँ क्रमशः f₁, f₂, f₃ ……………. f_n हों तो इनका माध्य होगा-

हल :

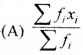
प्रश्न 3.
किसी महाविद्यालय के दस विद्यार्थियों के प्रतिदिन के जेब खर्च (रुपयों में) क्रमशः निम्नलिखित हैं-
26, 27, 20, 29, 21, 23, 25, 30, 28, 21
माध्य प्रतिदिन जेब खर्च होगा-
(A) 25 रु०
(B) 24 रु०
(C) 26 रु०
(D) 25.50 रु०
हल :
(A) 25 रु०

प्रश्न 4.
किसी पाठशाला की दसवीं कक्षा के 10 विद्यार्थियों का भार (कि०ग्रा० में) निम्नलिखित है-
38, 42, 43, 40, 47, 45, 55, 39, 41, 50 इनका माध्य होगा-
(A) 42 कि०ग्रा०
(B) 43 कि०ग्रा०
(C) 44 कि०ग्रा०
(D) 45 कि०ग्रा०
हल :
(C) 44 कि०ग्रा०

प्रश्न 5.
दसवीं कक्षा के एक विद्यार्थी के छः भिन्न-भिन्न विषयों में प्राप्त अंक निम्नानुसार हैं-
70, 76, 82, 78, 83 और 85
इनका माध्य होगा-
(A) 78
(B) 79
(C) 77
(D) 80
हल :
(B) 79

प्रश्न 6.
दसवीं कक्षा के पाँच विद्यार्थियों की मध्यमान ऊँचाई 161 सें०मी० है । यदि उनमें से चार विद्यार्थियों की ऊँचाई (सें०मी० में) 165, 159, 156 और 162 हो तो पाँचवें विद्यार्थी की ऊँचाई होगी-
(A) 163 cm
(B) 164 cm
(C) 162 cm
(D) 161 cm
हल :
(A) 163 cm

प्रश्न 7.
संचयी बारंबारता सारणी निम्न में से क्या ज्ञात करने के लिए बनाई जाती है ?
(A) माध्य
(B) माध्यक
(C) बहुलक
(D) इनमें से कोई नहीं
हल :
(B) माध्यक

प्रश्न 8.
प्रथम 7 सम संख्याओं का माध्य होगा-
(A) 8
(B) 7
(C) 6
(D) 4
हल :
(A) 8

प्रश्न 9.
9 प्रेक्षणों का माध्य 35 ज्ञात किया गया। बाद में पता चला कि एक प्रेक्षण 81 को गलती से 18 पढ़ लिया गया था। इन प्रेक्षणों का सही माध्य होगा-
(A) 42
(B) 41
(C) 40
(D) 39
हल :
(A) 42

प्रश्न 10.
किसी वर्ग – अंतराल की ऊपरी तथा निचली वर्ग सीमाओं का औसत क्या कहलाता है ?
(A) बारंबारता
(C) संचयी बारंबारता
(B) वर्ग चिह्न
(D) माध्यक
हल :
(B) वर्ग चिह्न

प्रश्न 11.
वर्ग – अंतराल 20-25 का वर्ग चिह्न होगा-
(A) 22.0
(B) 22.5
(C) 23.0
(D) 23.5
हल :
(B) 22.5

प्रश्न 12.
वर्ग- अंतराल 40-55 का वर्ग चिह्न होगा-
(A) 43.5
(B) 45.5
(C) 47.5
(D) 49.5
हल :
(C) 47.5

प्रश्न 13.
वर्ग- अंतराल 20-60 का वर्ग चिह्न होगा-
(A) 42
(B) 45
(C) 35
(D) 40
हल :
(D) 40

प्रश्न 14.
प्रथम 6 सम संख्याओं का माध्य क्या है ?
(A) 8
(B) 7
(C) 6
(D) 12
हल :
(B) 7

प्रश्न 15.
प्रथम 6 विषम संख्याओं का माध्य क्या होगा ?
(A) 8
(B) 7
(C) 6
(D) 4
हल :
(C) 6

प्रश्न 16.
किसी भी बारंबारता बंटन के लिए माध्य से विचलनों का बीजगणितीय योग होता है-
(A) सदैव धनात्मक
(B) शून्य
(C) सदैव ऋणात्मक
(D) एक शून्येत्तर संख्या
हल :
(B) शून्य

प्रश्न 17.
वर्गीकृत आँकड़ों का माध्य ज्ञात करने की विधि है –
(A) प्रत्यक्ष – विधि
(B) कल्पित- माध्य विधि
(C) पग-विचलन विधि
(D) उपरोक्त तीनों
हल :
(D) उपरोक्त तीनों

प्रश्न 18.
निम्नलिखित बारंबारता बंटन का माध्य क्या होगा ?

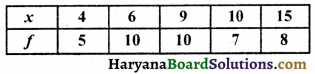
(A) 6
(B) 7
(C) 8
(D) 9
हल :
(D) 9

प्रश्न 19.
निम्नलिखित बारंबारता. बंटन का माध्य क्या होगा ?

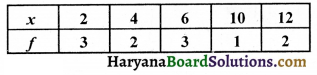
(A) 6
(B) 7
(C) 8
(D) 9
हल :
(A) 6

प्रश्न 20.
निम्नलिखित बारंबारता बंटन का माध्य क्या होगा ?

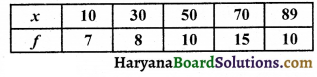
(A) 50
(B) 52.5
(C) 55
(D) 60
हल :
(C) 55

प्रश्न 21.
अध्ययन का वह क्षेत्र जिसमें आँकड़ों के प्रस्तुतिकरण, विश्लेषण तथा निर्वचन पर विचार किया जाता है, उसे कहा जाता है-
(A) सांख्यिकी
(B) क्षेत्रमिति
(C) त्रिकोणमिति
(D) ज्यामिति
हल :
(A) सांख्यिकी

प्रश्न 22.

वर्ग – अंतराल	बारंबारता
0-5 5-10 10-15 15-20 20-25 25-30 30-35	5 12 11 8 1 1 2
कुल	40

प्रत्येक वर्ग- अंतराल की माप है-
(A) 10
(B) 5
(C) 35
(D) 12
हल :
(B) 5

प्रश्न 23.
प्रश्न नं० 22 की सारणी में चौथे वर्ग-अंतराल की निम्न वर्ग सीमा है-
(A) 15
(B) 20
(C) 17.5
(D) 8
हल :
(A) 15

प्रश्न 24.
प्रश्न नं० 22 की सारणी में अंतिम वर्ग – अंतराल की उच्च वर्ग सीमा है-
(A) 30
(B) 32.5
(C) 35
(D) 2
हल :
(C) 35

प्रश्न 25.
प्रश्न नं० 22 की सारणी में तीसरे वर्ग – अंतराल का वर्ग चिह्न है-
(A) 10
(B) 15
(C) 11
(D) 12.5
हल :
(D) 12.5

प्रश्न 26.
प्रश्न नं० 22 की सारणी में अधिकतम बारंबारता वाला वर्ग- अंतराल है-
(A) 0-5
(B) 5-10
(C) 10-15
(D) 15-20
हल :
(B) 5-10

प्रश्न 27.
नीचे की सारणी में 400 नियॉन लैंपों के जीवनकाल दिए गए हैं-

जीवनकाल (घंटों में)	लैंपों की संख्या
300-400 400-500 500-600 600-700 700-800 800-900 900-1000	14 56 60 86 74 62 48

उपरोक्त सारणी में 700 घंटों से अधिक जीवनकाल वाले लैंपों की संख्या है-
(A) 74
(B) 136
(C) 184
(D) 110
हल :
(D) 110

प्रश्न 28.
प्रथम 7 प्राकृत संख्याओं का माध्य क्या है ?
(A) 8
(B) 7
(C) 4
(D) 3
हल :
(C) 4

प्रश्न 29.
निम्नलिखित आँकड़ों का बहुलक क्या है ?
12, 16, 8, 12, 8, 12, 16, 10, 12, 16, 18, 16, 8, 16
(A) 12
(B) 16
(C) 8
(D) 10
हल :
(B) 16

प्रश्न 30.
प्रथम पाँच प्राकृत संख्याओं का माध्य होगा-
(A) 3
(B) 3.5
(C) 4.0
(D) 4.5
हल :
(A) 3

प्रश्न 31.
5 संख्याओं का माध्य 20 है। यदि इनमें से एक संख्या निकाल दी जाए, तो शेष संख्याओं का माध्य 23 हो जाता है । निकाली गई संख्या होगी-
(A) 8
(B) 7
(C) 6
(D) 5
हल :
(A) 8

प्रश्न 32.
यदि परीक्षा पूरी करने में किसी विशेष समूह द्वारा लिया गया समय मिनटों में क्रमशः 17, 19, 20, 22, 24, 24, 28, 30, 30, 36 हो तथा इनका माध्य 25 हो तो कितने विद्यार्थियों ने माध्य से अधिक समय लिया ?
(A) तीन
(B) चार
(C) पाँच
(D) छह
हल :
(B) चार

प्रश्न 33.
…………………. दिए हुए प्रेक्षणों में वह मान है जो सबसे अधिक बार आता है ?
(A) माध्य
(B) माध्यक
(C) बहुलक
(D) (A) व (B) दोनों
हल :
(C) बहुलक

प्रश्न 34.
किसी गेंदबाज़ द्वारा 10 क्रिकेट मैचों में लिए गए विकेटों की संख्याएँ निम्नलिखित हैं-
2 6 4 5 0 2 1 3 2 3
इन आँकड़ों का बहुलक होगा-
(A) 1
(B) 2
(C) 3
(D) 4
हल :
(B) 2

प्रश्न 35.
निम्नलिखित आँकड़ों का बहुलक क्या होगा ?
3, 2, 3, 4, 0, 3, 1, 3
(A) 2
(B) 3
(C) 4
(D) 1
हल :
(B) 3

प्रश्न 36.
निम्नलिखित आँकड़ों का बहुलक क्या होगा ?
2.5, 2.3, 2.2, 2.2, 2.4, 2.7, 2.6, 2.5, 2.3, 2.2, 2.5, 2.2
(A) 2.5
(B) 2.4
(C) 2.3
(D) 2.2
हल :
(D) 2.2

प्रश्न 37.
निम्नलिखित आँकड़ों का माध्यक क्या है ?
34, 32, 48, 38, 24, 30, 27, 21, 35
(A) 24
(B) 32
(C) 21
(D) 48
हल :
(B) 32

प्रश्न 38.
निम्नलिखित बारम्बारता सारणी में बहुलक वर्ग होगा :

(A) 0 – 10
(B) 20 – 30
(C) 50 – 60
(D) 40 – 50
हल :
(D) 40 – 50

प्रश्न 39.
निम्नलिखित आँकड़ों का बहुलक वर्ग क्या होगा ?

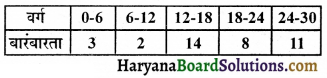
(A) 6 – 12
(B) 0 – 6
(C) 24 – 30
(D) 12 – 18
हल :
(D) 12 – 18

प्रश्न 40.
निम्नलिखित आँकड़ों का बहुलक क्या है ?
10, 8, 16, 10, 16, 13, 10, 19, 9, 10
(A) 19
(B) 10
(C) 16
(D) 8
हल :
(B) 10

प्रश्न 41.
निम्नलिखित आँकड़ों का बहुलक होगा-
25, 29, 24, 25, 29, 25, 34, 35, 25, 39
(A) 25
(B) 29
(C) 35
(D) 39
हल :
(A) 25

प्रश्न 42.
निम्नलिखित बारंबारता बंटन का बहुलक वर्ग होगा-

(A) 20-40
(B) 40-60
(C) 60-80
(D) 80-100
हल :
(B) 40-60

प्रश्न 43.
निम्नलिखित बारंबारता बंटन का बहुलक वर्ग होगा-

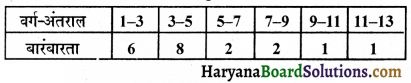
(A) 1 – 3
(B) 3 – 5
(C) 5 – 7
(D) 7 – 9
हल :
(B) 3 – 5

प्रश्न 44.
बहुलक ज्ञात करने का सूत्र है-

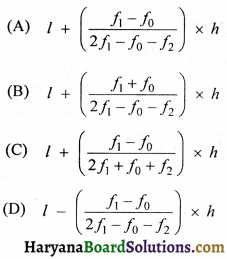
हल :

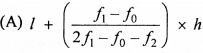
प्रश्न 45.
माध्यक ज्ञात करने का सूत्र है-

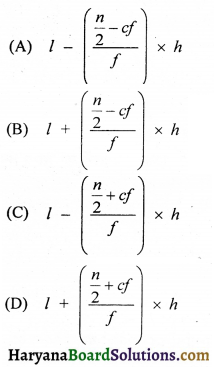
हल :

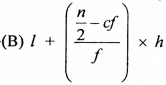
प्रश्न 46.
बारंबारता बंटन के माध्य, माध्यक व बहुलक के बीच उचित संबंध है-
(A) बहुलक = 3 माध्यक – माध्य
(B) बहुलक = 2 माध्यक – माध्य
(C) बहुलक = माध्यक – 2 माध्य
(D) बहुलक = 3 माध्यक – 2 माध्य
हल :
(D) बहुलक = 3 माध्यक – 2 माध्य

प्रश्न 47.
एक कक्षा के 9 विद्यार्थियों के अंक निम्नलिखित हों तो माध्यक होगा-
21, 24, 27, 30, 32, 34, 35, 38, 48
(A) 30
(B) 32
(C) 34
(D) 33
हल :
(B) 32

प्रश्न 48.
निम्नलिखित आँकड़ों से 10 श्रमिकों के प्रतिदिन की मजदूरी (रुपयों में) का माध्यक होगा-
8, 9, 11, 14, 15, 17, 18, 20, 22, 25
(A) 15
(B) 17
(C) 16
(D) 17.5
हल :
(C) 16

प्रश्न 49.
नीचे किसी लड़ाकू जहाज के मशीन के पुर्जों के 15 टुकड़ों का जीवनकाल (घंटों में) दिया है। इसका माध्यक होगा-
694, 696, 699, 705, 710, 712, 715, 716, 719, 724, 725, 728, 729, 734, 745
(A) 716
(B) 715.5
(C) 717.5
(D) 719
हल :
(A) 716

प्रश्न 50.
निम्नलिखित आँकड़ों का माध्यक वर्ग क्या होगा ?

(A) 10-30
(B) 30-60
(C) 60-80
(D) 0-10
हल :
(B) 30-60

प्रश्न 51.
निम्नलिखित आँकड़ों का माध्यक वर्ग क्या होगा ?

(A) 135-140
(B) 140-145
(C) 145-150
(D) 150-155
हल :
(C) 145-150

प्रश्न 52.
प्रथम 7 विषम संख्याओं का माध्य क्या है ?
(A) 13
(B) 11
(C) 9
(D) 7
हल :
(D) 7

प्रश्न 53.
निम्नलिखित आँकड़ों का माध्यक वर्ग होगा :

(A) 0-10
(B) 30-40
(C) 40-50
(D) 20-30
हल :
(C) 40-50

प्रश्न 54.
आलेखीय विधि से माध्यक ज्ञात करने के लिए उचित ग्राफ होता है ?
(A) बारंबारता वक्र
(B) तोरण
(C) बारंबारता बहुभुज
(D) आयत चित्र
हल :
(B) तोरण

प्रश्न 55.
किसी बारंबारता बंटन का बहुलक किस आलेखीय विधि से ज्ञात किया जाता है?
(A) बारंबारता बहुभुज
(B) बारंबारता वक्र
(C) आयत चित्र
(D) तोरण
हल :
(C) आयत चित्र