HBSE 10th Class Maths Important Questions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन

Haryana State Board HBSE 10th Class Maths Important Questions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Important Questions and Answers.

Haryana Board 10th Class Maths Important Questions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन

परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न :

प्रश्न 1.
धातु की बनी एक घनाभ के आकार की टंकी की लंबाई, चौड़ाई और ऊँचाई क्रमशः 3 m, 2m और 1.5m है; उसका (i) आयतन और (ii) उसे बनाने में लगी धातु का क्षेत्रफल ज्ञात करें ।
हल :
यहाँ पर,
घनाभ के आकार की टंकी की लंबाई (l) = 3 m
घनाभ के आकार की टंकी की चौड़ाई (b) = 2 m
घनाभ के आकार की टंकी की ऊँचाई (h) = 1.5 m
(i) घनाभ के आकार की टंकी का आयतन = lbh = 3 × 2 × 1.5m³
= 9m³

(ii) घनाभ के आकार की टंकी को बनाने में लगी धातु का क्षेत्रफल = 2 [lb + bh + hl]
= 2 [3 × 2 + 2 × 1.5 + 1.5 × 3 ] m²
= 2[6 + 3 + 4.5] m²
= 2 × 13.5 m²
= 27m²

प्रश्न 2.
घन का एक किनारा 6 cm है । इसका आयतन और पृष्ठीय क्षेत्रफल ज्ञात करें ।
हल :
यहाँ पर
घन का किनारा (भुजा) = 6 cm
(i) घन का आयतन (भुजा)³ = (6)³ cm³
= 6 × 6 × 6 cm³
= 216 cm³

(ii) घन का पृष्ठीय क्षेत्रफल = 6(भुजा)²
= 6(6)² cm²
= 6 × 6 × 6 cm²
= 216 cm²

प्रश्न 3.
एक घन का आयतन 1728 cm³ है ।
(i) उसकी कोर, (ii) उसका पृष्ठीय क्षेत्रफल ज्ञात कीजिए ।
हल :
यहाँ पर,
घन का आयतन = 1728 cm³
(i) घन की कोर (भुजा) = \(\sqrt[3]{1728}\) = \(\sqrt[3]{12 \times 12 \times 12}\) = \(\sqrt[3]{12^3}\) = 12 cm
(ii) घन का पृष्ठीय क्षेत्रफल 6 (भुजा)² = 6 × 12 × 12 = 864 cm²

प्रश्न 4.
एक लंब वृत्तीय बेलन के आधार का व्यास 28 cm और उसकी ऊँचाई 21 cm है ।
(i) वक्र पृष्ठ,
(ii) संपूर्ण पृष्ठ,
(iii) आयतन ज्ञात कीजिए ।
हल :
यहाँ पर,
लंब वृत्तीय बेलन के आधार का व्यास = 28 cm
लंब वृत्तीय बेलन के आधार की त्रिज्या (r) = \(\frac {28}{2}\) = 14 cm
लंब वृत्तीय बेलन की ऊँचाई (h) = 21 cm
(i) लंब वृत्तीय बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πrh
= 2 × \(\frac {22}{7}\) × 14 × 21 cm²
= 1848 cm²

(ii) लंब वृत्तीय बेलन का संपूर्ण पृष्ठीय क्षेत्रफल = 2πr (r + h)
= 2 × \(\frac {22}{7}\) × 14 (14 + 21) cm²
= 88 × 35 = 3080 cm²

(iii) लंब वृत्तीय बेलन का आयतन = πr²h
= \(\frac {22}{7}\) × 14 × 14 × 21 cm³
= 12936 cm³

प्रश्न 5.
एक लंब वृत्तीय बेलन के आधार का व्यास 14 cm और ऊँचाई 10 cm है। इसका आयतन तथा संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात करें ।
हल :
यहाँ पर,
लंब वृत्तीय बेलन के आधार का व्यास = 14 cm
लंब वृत्तीय बेलन के आधार की त्रिज्या (r) = \(\frac {14}{2}\) = 7 cm
लंब वृत्तीय बेलन की ऊँचाई (h) = 10 cm
(i) लंब वृत्तीय बेलन का आयतन = πr²h
= \(\frac {22}{7}\) × 7 × 7 × 10 cm³
= 1540 cm³

(ii) लंब वृत्तीय बेलन का संपूर्ण पृष्ठीय क्षेत्रफल = 2πr(r + h)
= 2 × \(\frac {22}{7}\) × 7 (7 + 10) cm²
= 44 × 17 = 748 cm²

प्रश्न 6.
एक लंब वृत्तीय शंकु के आधार की त्रिज्या और उसकी ऊँचाई क्रमशः 7 cm और 24 cm हैं। शंकु का आयतन और संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए ।
हल :
यहाँ पर,
शंकु के आधार की त्रिज्या (r) = 7 cm
शंकु की ऊँचाई (h) = 24 cm
शंकु की तिर्यक ऊँचाई (l) = \(\sqrt{r^2+h^2}\) = \(\sqrt{(7)^2+(24)^2}\)
= \(\sqrt{49+576}\)
= \(\sqrt{625}\)
= 25 cm

(i) शंकु का आयतन = \(\frac {1}{3}\)πr²h
= \(\frac{1}{3} \times \frac{22}{7}\) × 7 × 7 × 24 cm³
= 1232 cm³

(ii) शंकु का संपूर्ण पृष्ठीय क्षेत्रफल = πr (r + l)
= \(\frac {22}{7}\) × 7 (7 + 25) cm²
= 22 × 32 = 704 cm²

प्रश्न 7.
धातु के एक गोले का व्यास 8.4 cm है। उसका आयतन और पृष्ठीय क्षेत्रफल ज्ञात कीजिए ।
हल :
यहाँ पर,
गोले का व्यास = 8.4 cm
गोले की त्रिज्या (r) = \(\frac {8.4}{2}\)
= 4.2 cm

(i) गोले का आयतन = \(\frac {4}{3}\)πr³
= \(\frac{4}{3} \times \frac{22}{7}\) × 4.2 × 4.2 × 4.2 cm³
= 310.46 cm³

(ii) गोले का पृष्ठीय क्षेत्रफल = 4πr²
= 4 × \(\frac {22}{7}\) × 4.2 × 4.2 cm²
= 221.76cm²

प्रश्न 8.
एक खोखले अर्धगोलीय बर्तन के अंतः और बाह्य व्यास क्रमशः 42 cm और 45.5 cm हैं। उसकी धारिता तथा उसका बाहरी वक्र पृष्ठ ज्ञात कीजिए ।
हल :
यहाँ पर,
अर्धगोलीय बर्तन का अंतः व्यास = 42 cm
अर्धगोलीय बर्तन की अंतः त्रिज्या (r) = \(\frac {42}{2}\) = 21cm
अर्धगोलीय बर्तन का अंतः आयतन = \(\frac {2}{3}\)πr³ = \(\frac{2}{3} \times \frac{22}{7}\) × 21 × 21 × 21 cm³
= 19404 cm³
अतः अर्धगोलीय बर्तन की धारिता = \(\frac{19404}{1000}\)लीटर
= 19.404 लीटर
अब अर्धगोलीय बर्तन का बाह्य व्यास = 45.5 cm
अर्धगोली बर्तन की बाह्य त्रिज्या (R) = \(\frac {45.5}{2}\) cm
= \(\frac{455}{20}=\frac{91}{4}\) cm
अर्धगोलीय बर्तन का बाह्य पृष्ठीय क्षेत्रफल = 2πR²
= 2 × \(\frac{22}{7} \times \frac{91}{4} \times \frac{91}{4}\)cm²
= 3253.25 cm²

प्रश्न 9.
2m व्यास वाला 14 m गहरा एक कुआँ खोदा गया है। उससे निकली हुई मिट्टी को कुएँ के चारों ओर 5m चौड़ाई तक समान रूप से फैलाकर एक चबूतरा बनाया गया है । चबूतरे की ऊँचाई ज्ञात कीजिए ।
हल :
यहाँ पर,
कुएँ का व्यास = 2m
⇒ कुएँ की त्रिज्या (r) = \(\frac {2}{2}\) = 1m
कुएँ की गहराई (h) = 14 m
∴ कुएँ से निकली मिट्टी का आयतन = πr²h
= \(\frac {22}{7}\) × 1 × 1 × 14 = 44 m³
चंबूतरे सहित कुएँ की बाह्य त्रिज्या (R) = 5 + 1 = 6 m
चबूतरे के तल का क्षेत्रफल = बाह्य वृत्त का क्षेत्रफल – अंतः वृत्त का क्षेत्रफल

प्रश्न 10.
एक अर्धगोलाकार कटोरी, जिसकी आंतरिक त्रिज्या 9 cm है, द्रव से भरी है । इस द्रव को बेलनाकार छोटी बोतलों में भरना है, जबकि प्रत्येक बोतल के आधार का व्यास 3 cm और ऊँचाई 4 cm है । कटोरी को खाली करने के लिए कितनी बोतलों की आवश्यकता होगी ?
हल :
यहाँ पर
अर्धगोलाकार कटोरी की आंतरिक त्रिज्या (R) = 9cm
अर्धगोलाकार कटोरी का आयतन = \(\frac {2}{3}\)πR³
= \(\frac{2}{3} \times \frac{22}{7}\) × 9 × 9 × 9 cm³
कटोरी में द्रव का आयतन = \(\frac{2}{3} \times \frac{22}{7}\) × 9 × 9 × 9 cm³
छोटी बोतल की त्रिज्या (r) = \(\frac {3}{2}\)cm
छोटी बोतल की ऊँचाई (h) = 4 cm

प्रश्न 11.
एक 8.25m ऊँचा तम्बू 30 m व्यास वाले अधार तथा 5.5 m ऊँचाई वाले बेलन पर समान आधार के शंकु को जोड़कर बनाया गया है। 45 रु० प्रति वर्ग m की दर से तम्बू में लगे कपड़े (कैनवास) का मूल्य ज्ञात कीजिए ।
हल :

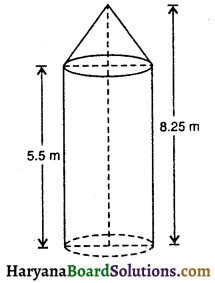
यहाँ पर,
बेलनाकार भाग का व्यास = 30m
बेलनाकार भाग की त्रिज्या (r₁) = \(\frac {30}{2}\) = 15 m
बेलनाकार भाग की ऊँचाई (h₁) = 5.5m
बेलनाकार भाग का वक्र पृष्ठीय क्षेत्रफल = 2πr₁h₁
= 2 × \(\frac {22}{7}\) × 15 × 5.5m²
= \(\frac {3630}{7}\)m²
शंक्वाकार भाग का व्यास = 30 m
शंक्वाकार भाग की त्रिज्या (r₂) = \(\frac {30}{2}\) m = 15 m
शंक्वाकार भाग की ऊँचाई (h₂) = (8.25 – 5.5) m = 2.75m

प्रश्न 12.
पेट्रोल की एक बेलनाकार टंकी के आधार का व्यास 21 cm और लंबाई 18 cm है। वह शंक्वाकार सिरों से जुड़ी है, जिनमें से प्रत्येक की अक्ष लंबाई 9 cm है । टंकी की धारिता ज्ञात कीजिए ।
हल :

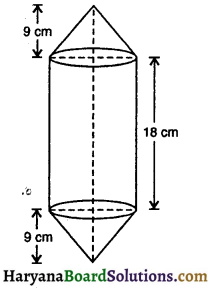
यहाँ पर,
बेलनाकार भाग का व्यास = 21 cm
बेलनाकार भाग की त्रिज्या (r₁) = \(\frac {21}{2}\) m
बेलनाकार भाग की लंबाई (h₁) = 18 cm
बेलनाकार भाग का आयतन = πr₁²h₁
= \(\frac{22}{7} \times \frac{21}{2} \times \frac{21}{2}\) × 18cm³
= 6237 cm³
शंक्वाकार सिरों की त्रिज्या (r₂) = \(\frac {21}{2}\) cm
शंक्वाकार सिरों की ऊँचाई (h₂) = 9 cm
दोनों शंक्वाकार सिरों का आयतन = 2 × \(\frac {1}{3}\)πr₁²h₂
= 2 × \(\frac{1}{3} \times \frac{22}{7} \times \frac{21}{2} \times \frac{21}{2}\) × 9 cm³
= 2079 cm³
अतः टंकी का कुल आयतन = [6237 + 2079] cm³
= 8316 cm³

प्रश्न 13.
एक बर्तन एक खोखले बेलन के रूप में है जिसकी पेंदी उसी के आधार पर बना एक गोलार्ध है । बेलन की गहराई 43 m है और गोलार्ध का व्यास 3.5 m है। उस बर्तन का आयतन और आंतरिक पृष्ठ ज्ञात कीजिए ।
हल :

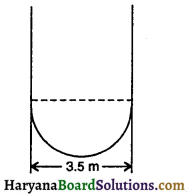
यहाँ पर,
बर्तन के बेलनाकार भाग की गहराई (h) = 4\(\frac {2}{3}\) = \(\frac {14}{3}\)m
बर्तन के बेलनाकार भाग का व्यास = 3.5 m
बर्तन के बेलनाकार भाग की त्रिज्या (r₁) = \(=\frac{35}{10 \times 2}=\frac{7}{4}\)
बर्तन के बेलनाकार भाग का आयतन = πr₁²h
= \(\frac{22}{7} \times \frac{7}{4} \times \frac{7}{4} \times \frac{14}{3}=\frac{539}{12}\)m³
बर्तन के बेलनाकार भाग का वक्र पृष्ठीय क्षेत्रफल = 2πr₁h
= 2 × \(\frac{22}{7} \times \frac{7}{4} \times \frac{14}{3}=\frac{154}{3}\)
बर्तन के अर्धगोलाकार भाग का व्यास = 3.5m
बर्तन के अर्धगोलाकार भाग की त्रिज्या (r₂) = \(\frac{35}{10 \times 2}=\frac{7}{4}\) m
बर्तन के अर्धगोलाकार भाग का आयतन = \(\frac {2}{3}\)πr₂³
= \(\frac{2}{3} \times \frac{22}{7} \times \frac{7}{4} \times \frac{7}{4} \times \frac{7}{4}=\frac{539}{48}\)m³

प्रश्न 14.
एक गोदाम का आकार आकृति के अनुसार है। गोदाम की चौड़ाई की ओर का ऊर्ध्वाधर अनुप्रस्थ-परिच्छेद 7m × 3m माप का एक आयत है जिसके ऊपर 3.5 m त्रिज्या का अर्धवृत्त है। घनाभ के आकार वाले भाग की आंतरिक माप 10m × 7m × 3m हैं। गोदाम का आयतन और उसके फर्श को छोड़कर संपूर्ण आंतरिक पृष्ठ का क्षेत्रफल ज्ञात कीजिए ।

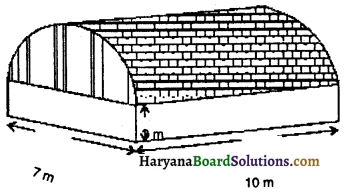
हल :
यहाँ पर,
गोदाम के घनाभाकार भाग का आयतन = l × b × h
= 10 × 7 × 3 m³
= 210 m³
गोदाम के अर्धबेलनाकार भाग की त्रिज्या (r) = \(\frac {7}{2}\)m
गोदाम के अर्धबेलनाकार भाग की लंबाई (h) = 10 m
गोदाम के अर्धबेलनाकार भाग का आयतन = \(\frac {1}{2}\)πr²h
= \(\frac{1}{2} \times \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\) × 10 m³
= 192.5 m³
अतः गोदाम का आयतन = (210 + 192.5) m³
= 402.5m³
गोदाम की चारदीवारी का क्षेत्रफल
= 2 (l + b) × h
= 2 (10 + 7) × 3m²
= 2 × 17 × 3 = 102m²
गोदाम के अर्धबेलनाकार भाग का वक्र पृष्ठीय क्षेत्रफल =\(\frac {1}{2}\)(2πrh)
= \(\frac{22}{7} \times \frac{7}{2}\) × 10 = 110m²
गोदाम के दो अर्धवृत्तों का क्षेत्रफल = 2(\(\frac {1}{2}\)πr²)
= \(\frac {22}{7}\) × 3.5 × 3.5 m²
= 3.5 m²
गोदाम का कुल अंतः पृष्ठीय क्षेत्रफल = (102 + 110 + 38.5) m²
= 250.5m²

प्रश्न 15.
एक ठोस लंब वृत्तीय बेलन, जिसकी ऊँचाई 10cm और आधार की त्रिज्या 6 cm हैं, से उसी ऊँचाई और उसी आधार का एक लंब वृत्तीय शंकु काटकर हटा दिया जाता है। शेष ठोस का आयतन ज्ञात कीजिए ।
हल :
यहाँ पर,
बेलन की ऊँचाई (h) = 10cm
बेलन की त्रिज्या (r) = 6 cm
बेलन का आयतन = πr²h
= \(\frac {22}{7}\) × 6 × 6 × 10 = \(\frac {7290}{7}\)cm³
शंकु की ऊँचाई (h₁) = 10 cm
शंकु की त्रिज्या (r₁) = 6 cm

प्रश्न 16.
एक जूस (juice) बेचने वाला अपने ग्राहकों को संलग्न आकृति में दर्शाए गिलासों में जूस देता था । बेलनाकार गिलास का आंतरिक व्यास 5 cm था, परंतु गिलास के निचले आधार (तली) एक उभरा हुआ अर्धगोला था, जिससे गिलास की धारिता कम हो जाती थी । यदि एक गिलास की ऊँचाई 10 cm थी, तो गिलास की आभासी (apparent) धारिता तथा उसकी वास्तविक धारिता ज्ञात कीजिए । (π = 3. 14 लीजिए )
हल :

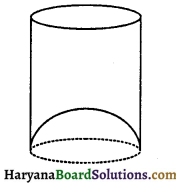
यहाँ पर,
गिलास का आंतरिक व्यास (d) = 5 cm
गिलास की आंतरिक त्रिज्या (r) = \(\frac {5}{2}\)cm
∴ गिलास की आंतरिक ऊँचाई (h) = 10 cm
गिलास की आभासी धारिता = πr²h
= 3.14 × \(\frac {5}{2}\) × \(\frac {5}{2}\) × 10 cm³ = 196.25cm³
आधार में उपस्थित अर्धगोले की त्रिज्या (r₁) = \(\frac {5}{2}\)cm
आधार में उपस्थित अर्धगोले का आयतन = \(\frac {2}{3}\)πr³
= \(\frac {2}{3}\) × 3.14 × \(\frac {5}{2}\) × \(\frac {5}{2}\) × \(\frac {5}{2}\) cm³ = 32.71 cm³
अतः गिलास की वास्तविक धारिता = आभासी धारिता – अर्धगोले का आयतन
= (196.25 – 32.71) cm³
= 163.54 cm³

प्रश्न 17.
एक बिल्डिंग का आन्तरिक भाग एक बेलन के आकार का है जिसके आधार की त्रिज्या 12 m और ऊँचाई 3.5 m है एक शंकु समान आधार और तिर्यक ऊँचाई 12.5 m के द्वारा आरोपित है। बिल्डिंग की धारिता ज्ञात कीजिए ।
हल :

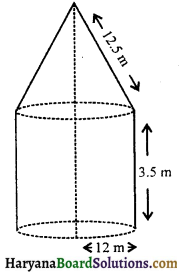
यहाँ पर
बिल्डिंग के बेलनाकार भाग की त्रिज्या (r) = 12 m
बिल्डिंग के बेलनाकार भाग की ऊँचाई (h) = 3.5m
बिल्डिंग के बेलनाकार भाग की धारिता = πr²h
= \(\frac {22}{7}\) × 12 × 12 × 3.5m³
= 1584 m³
बिल्डिंग के शंकु वाले भाग की त्रिज्या (r₁) = 12m
बिल्डिंग के शंकु वाले भाग की तिर्यक ऊँचाई (l) = 12.5 m
बिल्डिंग के शंकु वाले भाग की ऊँचाई (h) = \(\sqrt{l^2-r^2}\)
= \(\sqrt{(12.5)^2-(12)^2}\)
= \(\sqrt{156.25-144}\)
= \(\sqrt{12.25}\)
= 3.5m
बिल्डिंग के शंकु वाले भाग की धारिता = \(\frac {1}{3}\)πr₁²h
= \(\frac{1}{3} \times \frac{22}{7}\) × 12 × 12 × 3.5 m³
= 528 m³
बिल्डिंग की कुल धारिता = (1584 + 528) m³
= 2112m ³

प्रश्न 18.
5.6 सेमी त्रिज्या वाले एक धातु के गोले को पिघलाकर 6 सेमी त्रिज्या वाले एक बेलन के रूप में ढाला जाता है । बेलन की ऊँचाई ज्ञात कीजिए ।
हल :
यहाँ पर,
धातु के गोले की त्रिज्या (r) = 5.6 सेमी
⇒ धातु के गोले का आयतन = \(\frac {4}{3}\)πr³
= \(\frac {4}{3}\)π(5.6)³सेमी³
धातु के गोले को पिघलाकर बने बेलन की त्रिज्या (r) = 6 सेमी
माना धातु के गोले को पिघलाकर बने बेलन की ऊँचाई = H सेमी
धातु के गोले को पिघलाकर बने बेलन का आयतन = πR²H
= π(6)²H सेमी³
= 36πH सेमी³
प्रश्नानुसार,
36πH = \(\frac {4}{3}\)π(5.6)³
⇒ H = \(\frac{4}{3} \times \frac{1}{36}\) × 5.6 × 5.6 × 5.6
= 6.50 सेमी
अतः धातु के गोले को पिघलाकर बने बेलन की ऊँचाई = 6.50 सेमी

प्रश्न 19.
यदि 45 cm ऊँची एक बाल्टी के सिरों की त्रिज्याएँ 28 cm और 7 cm हों, तो उसकी धारिता, वक्र पृष्ठीय क्षेत्रफल और संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए ।
हल :
यहाँ पर,
बाल्टी की ऊँचाई (h) = 45 cm
बाल्टी के एक सिरे की त्रिज्या (r₁) = 28 cm
बाल्टी के दूसरे सिरे की त्रिज्या (r₂) = 7 cm

प्रश्न 20.
एक शंकु की ऊँचाई 30 cm है। उसके शिखर की ओर से एक छोटा शंकु उसके आधार के समांतर एक तल द्वारा काटा गया है। यदि छोटे शंकु का आयतन दिए हुए शंकु के आयतन का \(\frac {1}{27}\) हो, तो आधार से कितनी ऊँचाई पर उसे काटा गया है ?
हल :

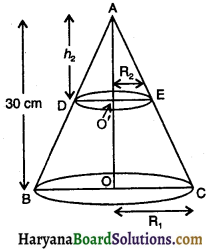
यहाँ पर,
शंकु की ऊँचाई(h₁) = 30 cm
माना शीर्ष से h₂ ऊँचाई पर एक शंकु काटा जाता है, जिसकी त्रिज्या R₂ है ।
क्योंकि ΔADO’ ~ ΔABO

जितनी ऊँचाई से शंकु काटा गया = 30 – 10 = 20 cm
∴ शंकु के आधार से 20 cm ऊँचाई पर दूसरे शंकु को काटा गया है।

प्रश्न 21.
एक खिलौना एक अर्धगोले के ऊपर उसी अर्धव्यास का शंकु रखकर बनाया गया है। यदि शंकु आकार भाग के आधार का अर्धव्यास 7 cm और ऊँचाई 24 cm हो तो खिलौने की सतह का पृष्ठीय क्षेत्रफल तथा 2 रु० प्रति वर्ग cm की दर से इसकी सतह को पॉलिश कराने का खर्च ज्ञात करें।
हल :

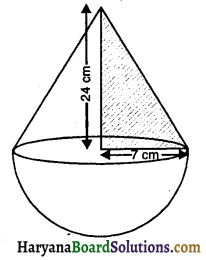
यहाँ पर,
अर्धगोले की त्रिज्या (r) = 7 cm
अर्धगोले का पृष्ठीय क्षेत्रफल = 2πr²
= 2 × \(\frac {22}{7}\) × 7 × 7 cm²
= 308 cm²
शंकु वाले भाग की त्रिज्या (R) = 7 cm
शंकु वाले भाग की ऊँचाई (H) = 24 cm
शंकु वाले भाग की तिर्यक ऊँचाई (L) = \(\sqrt{\mathrm{R}^2+\mathrm{H}^2}\)
= \(\sqrt{(7)^2+(24)^2}\)
= \(\sqrt{49+576}\)
= \(\sqrt{625}\) = 25 cm
शंकु वाले भाग का वक्र पृष्ठीय क्षेत्रफल = πRL
= \(\frac {22}{7}\) × 7 × 25 cm²
= 550 cm²
खिलौने का कुल क्षेत्रफल = (308 + 550) = 858 cm²
1 cm² सतह को पॉलिश कराने का खर्च = 2 रु०
858cm² सतह को पॉलिश कराने का खर्च = 858 × 2रु० = 1716 रु०

प्रश्न 22.
किसी धातु की चादर का बना एक बर्तन एक शंकु के छिन्नक के आकार का है। इसकी ऊँचाई 16 cm तथा निचले और ऊपरी सिरों की त्रिज्याएँ 8 cm और 10 cm हैं। बर्तन का आयतन तथा इसकी पृष्ठीय क्षेत्रफल ज्ञात करें।
हल :

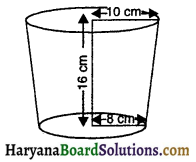
यहाँ पर,
बर्तन की ऊँचाई (h) = 16 cm
बर्तन के एक सिरे की त्रिज्या (r₁) = 10 cm
बर्तन के दूसरे सिरे की त्रिज्या (r₂) = 8 cm

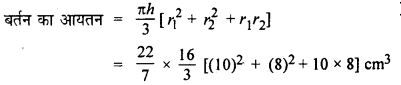
बहुविकल्पीय प्रश्न :

प्रश्न 1.
l लंबाई, b चौड़ाई व h ऊँचाई वाले किसी घनाभ का संपूर्ण पृष्ठीय क्षेत्रफल होगा-
(A) lbh
(B) 2lbh
(C) 2 (lb + bh + hl)
(D) lb + bh + hl
हल :
(C) 2 (lb + bh + hl)

प्रश्न 2.
l भुजा वाले किसी धन का संपूर्ण पृष्ठीय क्षेत्रफल होगा-
(A) l³
(B) 6l²
(C) 2l³
(D) 12l²
हल :
(B) 6l²

प्रश्न 3.
l लंबाई, b चौड़ाई व h ऊँचाई वाले किसी घनाभ की चारदीवारी का क्षेत्रफल होगा-
(A) 2 (l + b) h
(B) (l + b) h
(C) 2 (b + h) l
(D) lbh
हल :
(A) 2 (l + b) h

प्रश्न 4.
l लंबाई, b चौड़ाई व h ऊँचाई वाले किसी घनाभ का आयतन होगा-
(A) 2 (lb + bh + hl)
(B) lb + bh + hl
(C) 2lbh
(D) lbh
हल :
(D) lbh

प्रश्न 5.
l भुजा वाले घन का आयतन होगा-
(A) l³
(B) 6l²
(C) 2l³
(D) 12l²
हल :
(A) l³

प्रश्न 6.
l लंबाई, b चौड़ाई व h ऊँचाई वाले किसी घनाभ का विकर्ण होगा-
(A) \(\sqrt{l+b+h}\)
(B) \(\sqrt{l^2+b^2+h^2}\)
(C) \(\sqrt{lbh}\)
(D) \(\sqrt{2(l b+b h+h l)}\)
हल :
(B) \(\sqrt{l^2+b^2+h^2}\)

प्रश्न 7.
a भुजा वाले घन का विकर्ण होगा-
(A) 6a²
(B) a³
(C) \(\sqrt{3}\) a
(D) \(\sqrt{2}\) a
हल :
(C) \(\sqrt{3}\) a

प्रश्न 8.
10 cm भुजा वाले दो घन सिरे से सिरे तक जोड़े जाते हैं। इस प्रकार प्राप्त घनाभ का पृष्ठीय क्षेत्रफल होगा-
(A) 500 cm²
(B) 1000 cm²
(C) 2000 cm²
(D) 2000 cm³
हल :
(B) 1000 cm²

प्रश्न 9.
एक भूमिगत जलाशय घनाभ के आकार का है, जिसकी विमाएँ 48 m, 36m और 28m हैं। जलाशय का आयतन होगा-
(A) 48384m²
(B) 48384m³
(C) 8160m³
(D) 8160m²
हल :
(B) 48384m³

प्रश्न 10.
घनाभ, जिसकी लम्बाई, चौड़ाई और ऊँचाई क्रमश: 12m, 10m और 8m का आयतन है-
(A) 592m³
(B) 960m³
(C) 480m³
(D) इनमें से कोई नहीं
हल :
(B) 960m³

प्रश्न 11.
48 cm × 36 cm माप की एक धातु की आयताकार चद्दर है। इसके प्रत्येक कोने से 8 cm भुजा का वर्ग काटकर निकाल लिया गया है । शेष चद्दर से ऊपर से खुला एक संदूक बनाया गया है। संदूक का आयतन ज्ञात कीजिए ।
(A) 5120 cm³
(B) 5120 cm²
(C) 13824 cm²
(D) 13824 cm³
हल :
(A) 5120 cm³

प्रश्न 12.
घनाभ, जिसकी लम्बाई, चौड़ाई और ऊँचाई क्रमशः 10m, 8m और 5m का आयतन है-
(A) 400m³
(B) 200m³
(C) 3000m³
(D) इनमें से कोई नहीं
हल :
(A) 400m³

प्रश्न 13.
एक घन का आयतन 1728 घन cm है, उसकी कोर की लंबाई होगी-
(A) 12 cm
(B) 12 m
(C) 144 cm
(D) 864cm
हल :
(A) 12 cm

प्रश्न 14.
5 cm भुजा वाले 3 घन सिरे से सिरे तक जोड़े जाते हैं । इस प्रकार प्राप्त घनाभ का पृष्ठीय क्षेत्रफल होगा-
(A) 375 cm³
(B) 375 cm²
(C) 350 cm²
(D) 350 cm³
हल :
(C) 350 cm²

प्रश्न 15.
घनाभ, जिसकी लम्बाई, चौड़ाई और ऊँचाई क्रमश: 13m, 10m और 8m का आयतन है-
(A) 1040 m³
(B) 1060 m³
(C) 1020 m³
(D) इनमें से कोई नहीं
हल :
(A) 1040m³

प्रश्न 16.
तीन घन जिनकी कोरें क्रमशः 3, 4 व 5 cm हैं, को पिघलाकर एक घन बनाया जाता है, तो नए घन की कोर होगी-
(A) 6 cm
(B) 12 cm
(C) 8 cm
(D) 3 cm
हल :
(A) 6 cm

प्रश्न 17.
घनाभ, जिसकी लम्बाई, चौड़ाई और ऊँचाई क्रमशः 10m, 8m और 6m का आयतन है-
(A) 460m³
(B) 480m³
(C) 520m³
(D) इनमें से कोई नहीं
हल :
(B) 480m³

प्रश्न 18.
त्रिज्या 2 cm तथा 7 cm ऊँचाई वाले बेलन का वक्र पृष्ठीय क्षेत्रफल होगा-
(A) 88 cm²
(B) 88 cm
(C) 88 cm³
(D) 44 cm²
हल :
(A) 88 cm²

प्रश्न 19.
r त्रिज्या व h ऊँचाई वाले बेलन का आयतन होगा-
(A) 2πr (r + h)
(B) 2πrh
(C) πr²h
(D) 2πr²h
हल :
(C) πr²h

प्रश्न 20.
एक लंब वृत्तीय बेलन के आधार का व्यास 28 cm और उसकी ऊँचाई 21 cm है। उसका वक्र पृष्ठीय क्षेत्रफल होगा-
(A) 588 वर्ग cm
(B) 1848 वर्ग cm
(C) 924 वर्ग cm
(D) 1386 वर्ग cm
हल :
(B) 1848 वर्ग cm

प्रश्न 21.
एक बेलन के आधार की त्रिज्या 14 सेमी और ऊँचाई 6 सेमी है, तो उसका आयतन है :
(A) 196 π
(B) 392 π
(C) 1176 π
(D) इनमें से कोई नहीं
हल :
(C) 1176 π

प्रश्न 22.
एक लंब वृत्तीय बेलन के आधार की त्रिज्या 14m और ऊँचाई 21 m है, उसका संपूर्ण पृष्ठीय क्षेत्रफल होगा-
(A) 1848 m²
(C) 3080 m³
(B) 1848 m²
(D) 5080 m³
हल :
(C) 3080 m²

प्रश्न 23.
एक बेलन के आधार की त्रिज्या 2.1 सेमी और ऊँचाई 5 सेमी है, तो उसका आयतन है :
(A) 22.05 π
(B) 7.35 π
(C) 21 π
(D) इनमें से कोई नहीं
हल :
(A) 22.05 π

प्रश्न 24.
यदि R और खोखले लंब वृत्तीय बेलन की बाह्य और अंतः त्रिज्याएँ हों तो उसमें लगी धातु का आयतन होगा-
(A) 2πh (R² – r²)
(B) 2π (R + r)h
(C) πh (R² + r²)
(D) πh (R² – r²)
हल :
(D) πh (R² – r²)

प्रश्न 25.
r त्रिज्या तथा h ऊँचाई वाले लंब वृत्तीय शंकु की तिर्यक ऊँचाई होगी-
(A) \(\sqrt{r^2+h^2}\)
(B) \(\sqrt{r^2-h^2}\)
(C) \(\sqrt{2\left(r^2+h^2\right)}\)
(D) \(\sqrt{2\left(r^2-h^2\right)}\)
हल :
(A) \(\sqrt{r^2+h^2}\)

प्रश्न 26.
r त्रिज्या तथा l तिर्यक ऊँचाई वाले शंकु का वक्र पृष्ठीय क्षेत्रफल होगा-
(A) 2 πrl
(B) πrl
(C) πr (r + l)
(D) \(\frac {1}{3}\)πr²l
हल :
(B) πrl

प्रश्न 27.
त्रिज्या, h ऊँचाई तथा / तिर्यक ऊँचाई वाले शंकु का संपूर्ण पृष्ठीय क्षेत्रफल होगा-
(A) 2 πrl
(B) πrl
(C) πr (r + l)
(D) \(\frac {1}{3}\)πr²h
हल :
(C) πr (r + l)

प्रश्न 28.
r त्रिज्या, h ऊँचाई तथा l तिर्यक ऊँचाई वाले शंकु का आयतन होगा-
(A) 2 πrl
(B) πrl
(C) πr (r + l)
(D) \(\frac {1}{3}\)πr²h
हल :
(D) \(\frac {1}{3}\)πr²h

प्रश्न 29.
एक शंकु के आधार की त्रिज्या 4 सें०मी० और ऊँचाई 3 सें०मी० है, तो उसका पृष्ठीय क्षेत्रफल होगा (π = \(\frac {22}{7}\)) :
(A) 20 सें०मी०²
(B) 20π सें०मी०²
(C) 30π सें०मी०²
(D) इनमें से कोई नहीं
हल :
(D) 20π सें०मी०²

प्रश्न 30.
एक शंकु के आधार की त्रिज्या 7 सेमी और ऊँचाई 6 सेमी है, तो उसका आयतन है (π = \(\frac {22}{7}\)) :
(A) 924 सेमी³
(B) 308 सेमी³
(C) 1232 सेमी³
(D) इनमें से कोई नहीं
हल :
(B) 308 सेमी³

प्रश्न 31.
एक शंकु के आधार की त्रिज्या 3.5 सेमी और ऊँचाई 9 सेमी है, तो उसका आयतन है :
(A) 36.75 π
(B) 110.25 π
(C) 330.75 π
(D) इनमें से कोई नहीं
हल :
(A) 36.75 π

प्रश्न 32.
2 m व्यास वाला 14 m गहरा एक कुआँ खोदा गया है। उससे निकाली हुई मिट्टी को कुएँ के चारों ओर 5 m चौड़ाई तक समान रूप से फैलाकर एक चबूतरा बनाया गया है । चबूतरे की ऊँचाई होगी-
(A) 0.4 m
(B) 1.0 m
(C) 1.5 m
(D) 2.0 m
हल :
(A) 0.4m

प्रश्न 33.
50 वृत्ताकार प्लेटों, जिसमें से प्रत्येक की त्रिज्या 7 cm और मोटाई cm है, को एक-दूसरे के ऊपर रखकर एक ठोस वृत्ताकार बेलन बनाया जाता है। इस प्रकार बने बेलन का संपूर्ण पृष्ठीय क्षेत्रफल होगा-
(A) 1408 वर्ग cm
(B) 1408 घन cm
(C) 3850 वर्ग cm
(D) 3850 घन cm
हल :
(A) 1408 वर्ग cm

प्रश्न 34.
एक घन का आयतन 216 मी.³ है, तो इसकी भुजा की लम्बाई होगी :
(A) 6 मी.
(B) 6 मी.³
(C) 12 मी.
(D) 12 मी.²
हल :
(A) 6 मी.

प्रश्न 35.
2 सें. मी. त्रिज्या तथा 7 सें.मी. ऊँचाई वाले बेलन का आयतन है :
(A) 88 सें.मी.³
(B) 88 सें.मी.²
(C) 88 सें.मी.
(D) \(\frac {352}{21}\) सें.मी.²
हल :
(A) 88 सें.मी.³

प्रश्न 36.
आधार की त्रिज्या 12 dm तथा तिर्यक ऊँचाई 9 dm वाले लंब वृत्तीय शंकु का संपूर्ण पृष्ठीय क्षेत्रफल होगा-
(A) \(\frac {2376}{7}\)cm²
(B) \(\frac {2376}{7}\)dm²
(C) 792 cm²
(D) 792 dm²
हल :
(D) 792 dm²

प्रश्न 37.
आधार की त्रिज्या 24m तथा ऊँचाई 10 m वाले शंक्वाकार तंबू की तिर्यक ऊँचाई होगी-
(A) 34m
(B) 14m
(C) 26m
(D) 24 m
हल :
(C) 26m

प्रश्न 38.
वक्र पृष्ठीय क्षेत्रफल 528 cm² तथा तिर्यक ऊँचाई 21 cm वाले लंब वृत्तीय शंकु के आधार की त्रिज्या होगी –
(A) 16 cm
(B) 8 cm
(C) 6 cm
(D) 4 cm
हल :
(B) 8 cm

प्रश्न 39.
एक शंक्वाकार गुम्बज की तिर्यक ऊँचाई और आधार की त्रिज्या क्रमशः 25m तथा 7m है। इस गुम्बज का वक्र पृष्ठीय क्षेत्रफल होगा-
(A) 550 m²
(B) 550 cm²
(C) 704 m²
(D) 704 cm²
हल :
(A) 550m²

प्रश्न 40.
r त्रिज्या वाले गोले का पृष्ठीय क्षेत्रफल ज्ञात करने का सूत्र होगा-
(A) 2πr²
(B) 3πr²
(C) 4πr²
(D) πr²
हल :
(C) 4πr²

प्रश्न 41.
r त्रिज्या वाले अर्धगोले का वक्र पृष्ठीय क्षेत्रफल ज्ञात करने का सूत्र है-
(A) 3πr²
(B) 4πr²
(C) πr²
(D) 2πr²
हल :
(D) 2πr²

प्रश्न 42.
r त्रिज्या वाले अर्धगोले का संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात करने का सूत्र है-
(A) 3πr²
(B) 4πr²
(C) πr²
(D) 2πr²
हल :
(A) 3πr²

प्रश्न 43.
r त्रिज्या वाले गोले का आयतन होगा-
(A) \(\frac {1}{3}\)πr³
(B) \(\frac {4}{3}\)πr³
(C) \(\frac {2}{3}\)πr³
(D) 4πr³
हल :
(B) \(\frac {4}{3}\)πr³

प्रश्न 44.
r त्रिज्या वाले अर्धगोले का आयतन होगा-
(A) \(\frac {1}{3}\)πr³
(B) \(\frac {4}{3}\)πr³
(C) \(\frac {2}{3}\)πr³
(D) 4πr³
हल :
(C) \(\frac {2}{3}\)πr³

प्रश्न 45.
2.1 cm त्रिज्या वाले गोले का आयतन होगा-
(A) 3880.8 cm³
(B) 388.08 cm³
(C) 3.8808 cm³
(D) 38.808 cm³
हल :
(D) 38.808 cm³

प्रश्न 46.
36πcm³ आयतन वाले गोले की त्रिज्या होगी –
(A) 3 cm
(B) 6 cm
(C) 1.5 cm
(D) 4.5 cm
हल :
(A) 3 cm

प्रश्न 47.
3 cm त्रिज्या वाले अर्धगोले का आयतन है :
(A) \(\frac {198}{7}\)cm³
(B) \(\frac {792}{7}\)cm³
(C) \(\frac {396}{7}\)cm³
(D) \(\frac {198}{14}\)cm³
हल :
(C) \(\frac {396}{7}\)cm³

प्रश्न 48.
एक खोखले अर्धगोलीय बर्तन के अंतः और बाह्य व्यास क्रमशः 42 cm और 45.5 cm हैं। उसकी धारिता होगी-
(A) 17.404 लीटर
(B) 18.404 लीटर
(C) 19.404 लीटर
(D) 20.404 लीटर
हल :
(C) 19.404 लीटर

प्रश्न 49.
धातु के एक गोले का अर्धव्यास 4.2 cm है। उसका पृष्ठीय क्षेत्रफल होगा-
(A) 220.76 वर्ग cm
(B) 221.76 वर्ग cm
(C) 222.76 वर्ग cm
(D) 223.76 वर्ग cm
हल :
(B) 221.76 वर्ग cm

प्रश्न 50.
4.2 cm की त्रिज्या वाले गोले का आयतन होगा-
(A) 310.46 घन cm
(B) 305.46 घन cm
(C) 309.46 घन cm
(D) 300.46 घन cm
हल :
(A) 310.46 घन cm

प्रश्न 51.
यदि एक गोले का व्यास 2R हो तो उसका संपूर्ण पृष्ठीय क्षेत्रफल होगा-
(A) πR²
(B) 2πR²
(C) 3πR²
(D) 4πR²
हल :
(D) 4πR²

प्रश्न 52.
धातु के एक गोले का व्यास 6 cm है । गोले को पिघलाकर एक समान वृत्तीय अनुप्रस्थ- परिच्छेद वाला तार बनाया गया है। यदि तार की लंबाई 36 m हो, तो उसकी त्रिज्या होगी-
(A) 0.1 cm
(B) 1 cm
(C) 0.1mm
(D) 0.01 cm
हल :
(A) 0.1 cm

प्रश्न 53.
सीसे के एक ठोस गोले, जिसकी त्रिज्या 8 cm है, से 1 cm त्रिज्या वाली कितनी गोलियाँ बनाई जा सकती हैं?
(A) 512
(B) 256
(C) 522
(D) 532
हल :
(A) 512

प्रश्न 54.
एक शंकु 8.4 cm ऊँचा है और उसके आधार की त्रिज्या 2.1 cm है। उसे पिघलाकर एक गोले के रूप में ढाला जाता है । गोले की त्रिज्या होगी –
(A) 6.3 cm
(B) 8.4 cm
(C) 4.2 cm
(D) 2.1 cm
हल :
(D) 2.1 cm

प्रश्न 55.
धातु के एक गोले की अंतः और बाह्य त्रिज्याएँ क्रमशः 3 cm और 5 cm हैं । उसको पिघलाकर 105 cm ऊँचाई वाला एक ठोस लंब वृत्तीय बेलन बनाया जाता है। बेलन के आधार का व्यास होगा-
(A) 5 cm
(B) 6 cm
(C) 7 cm
(D) 8 cm
हल :
(C) 7 cm

प्रश्न 56.
एक घन के आयतन और उस गोले के आयतन का अनुपात क्या होगा जो घन में ठीक समा सके ?
(A) 2 : π
(B) 3 : π
(C) 4 : π
(D) 6 : π
हल :
(D) 6 : π

प्रश्न 57.
r त्रिज्या वाले एक ठोस गोले को पिघलाकर r ऊँचाई के एक टोस शंकु के आकार में ढाला जाता है । शंकु के आधार की त्रिज्या होगी-
(A) 2r
(B) 3r
(C) r
(D) 4r
हल :
(A) 2r

प्रश्न 58.
एक धातु के शंकु को समान त्रिज्या के बेलन के आकार में बदला जाता है। यदि बेलन की ऊँचाई 5 cm हो तो शंकु की ऊँचाई होगी-
(A) 10 cm
(B) 15 cm
(C) 20 cm
(D) 25 cm
हल :
(B) 15 cm

प्रश्न 59.
यदि प्रत्येक गोले की त्रिज्या 3 cm है जिन्हें पिघलाकर 45 cm ऊँचाई व 4 cm व्यास का एक टोस धातु का बेलन बनाया जाता है, तो गोलों की संख्या होगी-
(A) 8
(B) 7
(C) 6
(D) 5
हल :
(D) 5

प्रश्न 60.
एक खिलौना 3.5 cm की त्रिज्या वाले गोलार्ध पर बने शंकु के आकार का है। खिलौने की कुल ऊँचाई 15.5 cm है । इसका संपूर्ण पृष्ठीय क्षेत्रफल होगा-
(A) 7.7 cm²
(C) 214.5 cm²
(B) 137.5 cm²
(D) 214.5 cm³
हल :
(C) 214.5 cm²

प्रश्न 61.
पेट्रोल की एक बेलनाकार टंकी के आधार का व्यास 21 cm और लंबाई 18 cm है। वह शंक्वाकार सिरों से जुड़ी है, जिनमें से प्रत्येक की अक्ष लंबाई 9 cm है। टंकी की धारिता होगी –
(A) 8316 cm³
(B) 8216 cm³
(C) 8116 cm³
(D) 8016 cm³
हल :
(A) 8316 cm³

प्रश्न 62.
एक बॉयलर (boiler) बेलनाकार है जिसकी लंबाई 3m है और उसके प्रत्येक सिरे पर 2 m व्यास का एक गोलार्ध है। बॉयलर का आयतन होगा-
(A) 13\(\frac {13}{21}\)
(B) 13\(\frac {10}{21}\)
(C) 13\(\frac {11}{21}\)
(D) 13\(\frac {12}{21}\)
हल :
(A) 13\(\frac {13}{21}\)

प्रश्न 63.
एक छत से, जिसका आकार 22m × 18m है, वर्षा का पानी बहकर नाली द्वारा एक बेलनाकार बर्तन में गिरता है । यदि बर्तन का व्यास 2.4m तथा बर्तन में पानी की ऊँचाई 1.4 m हो तो cm में वर्षा की माप होगी-
(A) 1.3 cm
(B) 1.4 cm
(C) 1.5 cm
(D) 1.6 cm
हल :
(D) 1.6 cm

प्रश्न 64.
यदि शंकु के छिन्नक के वृत्तीय आधारों की त्रिज्याएँ r₁ व r₂ (r₁ > r₂), ऊँचाई h तथा तिर्यक ऊँचाई l हों तो उसका आयतन होगा-
(A) \(\frac {1}{3}\)πh(r₁² + r₁r₂ + r₂²)
(B) π[(r₁ + r₂)l + r₁² + r₂²]
(C) π(r₁ + r₂)l
(D) \(\frac {1}{3}\)πh(r₁² – r₁r₂ + r₂²)
हल :
(A) \(\frac {1}{3}\)πh(r₁² + r₁r₂ + r₂²)

प्रश्न 65.
यदि शंकु के छिन्नक के वृत्तीय आधारों की त्रिज्याएँ r₁ व r₂ (जहाँ r₁ > r₂) व तिर्यक ऊँचाई l हों तो इसका वक्र पृष्ठीय क्षेत्रफल होगा-
(A) 2π(r₁ + r₂) l
(B) π(r₁ + r₂) l
(C) π[(r₁ + r₂)l + r₁² + r₂²]
(D) \(\frac {π}{3}\)h(r₁² + r₁r² + r₂²)
हल :
(B) π(r₁ + r₂) l

प्रश्न 66.
यदि शंकु के छिन्नक के वृत्तीय आधारों की त्रिज्याएँ r₁ व r₂ (जहाँ 1/2) तथा तिर्यक ऊँचाई / हो तो छिन्नक का संपूर्ण पृष्ठीय क्षेत्रफल होगा-
(A) 2π(r₁ + r₂) l
(B) π(r₁ + r₂) l
(C) π[(r₁ + r₂)l + r₁² + r₂²]
(D) \(\frac {π}{3}\)h(r₁² + r₁r₂ + r₂²)
हल :
(C) π[(r₁ + r₂)l + r₁² + r₂²]

प्रश्न 67.
एक जलाशय लंब वृत्तीय शंकु के छिन्नक के आकार में है। इसका ऊपरी सिरा 8 m तथा पेंदी वाला सिरा 4m चौड़ा है। यदि यह 6m गहरा हो तो इसकी क्षमता होगी-
(A) 176 m³
(B) 196 m³
(C) 110m³
(D) 352 m³
हल :
(A) 176m³

प्रश्न 68.
एक 6 cm ऊँचाई वाले शंकु के छिन्नक के आधारों की त्रिज्याएँ 14 cm व 6 cm हैं। इसकी तिर्यक ऊँचाई होगी-
(A) 8 cm
(B) 10cm
(C) 12 cm
(D) 20 cm
हल :
(B) 10cm

प्रश्न 69.
एक 24 cm ऊँचाई वाले शंकु के छिन्नक के आधारों की त्रिज्याएँ 10 cm व 3 cm हैं। इसकी तिर्यक ऊँचाई होगी-
(A) 13 cm
(B) 12 cm
(C) 25 cm
(D) 24 cm
हल :
(C) 25 cm

प्रश्न 70.
एक 12 cm ऊँचाई वाले शंकु के छिन्नक के आधारों की त्रिज्याएँ 9 cm व 4 cm हैं। इसकी तिर्यक ऊँचाई होगी-
(A) 26 cm
(B) 6.5 cm
(C) 24 cm
(D) 13 cm
हल :
(D) 13 cm