HBSE 10th Class Maths Important Questions Chapter 12 वृतों से संबंधित क्षेत्रफल

Haryana State Board HBSE 10th Class Maths Important Questions Chapter 12 वृतों से संबंधित क्षेत्रफल Important Questions and Answers.

Haryana Board 10th Class Maths Important Questions Chapter 12 वृतों से संबंधित क्षेत्रफल

परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न :

प्रश्न 1.
एक कोल्हू का बैल 3m लंबी रस्सी से बंधा हुआ है। वह 14 चक्करों में कितनी दूरी तय करेगा ?
हल :
यहाँ पर,
कोल्हू के बैल के वृत्ताकार पथ की त्रिज्या (r) = 3 m
बैल द्वारा वृत्ताकार पथ पर 1 चक्कर में तय दूरी = 2πr
= 2 × \(\frac {22}{7}\) × 3m = \(\frac {132}{7}\)m
अतः बैल द्वारा वृत्ताकार पथ पर 14 चक्करों में तय दूरी = \(\frac {132}{7}\) × 14 m
= 264 m

प्रश्न 2.
समान केंद्र वाले दो वृत्तों की त्रिज्याएँ 350m और 490m हैं। इनकी परिधियों में कितना अंतर है ?
हल :
यहाँ पर,
पहले वृत्त की त्रिज्या (r₁) = 350 m
∴ पहले वृत्त की परिधि (c₁) = 2πr₁
= 2 × \(\frac {22}{7}\) × 350m
= 2200m
दूसरे वृत्त की त्रिज्या (r₂) = 490m
∴ दूसरे वृत्त की परिधि (c₂) = 2πr₂
= 2 × \(\frac {22}{7}\) × 490m
= 3080m
अतः दोनों वृत्तों की परिधियों में अंतर = c₂ – c₁
= (3080 – 2200) m
= 880m

प्रश्न 3.
एक वृत्ताकार तालाब के अनुदिश 90 cm चौड़ी एक पटरी बनी हुई है। एक व्यक्ति पटरी के बाहरी किनारे के अनुदिश 66 cm लंबे डग भरता हुआ चल रहा है। 400 डगों में वह एक चक्कर पूरा कर लेता है । तालाब की त्रिज्या कितनी है ?
हल :
यहाँ पर, व्यक्ति द्वारा 1 डग भरने में तय लंबाई = 66 cm
व्यक्ति द्वारा 400 डगों को भरने में तय लंबाई = 66 × 400 cm = 26400 cm
अतः पटरी की बाहरी परिधि (c) = 26400 cm
पटरी की बाहरी त्रिज्या (r) = \(\frac{c}{2 \pi}=\frac{26400}{2 \times \frac{22}{7}}\) cm
= \(\frac{26400 \times 7}{2 \times 22}\)
= 4200 cm
पटरी की चौड़ाई = 90 cm
∴ तालाब की त्रिज्या = (4200 – 90) cm
= 4110 cm = 41.1m

प्रश्न 4.
(i) 4 cm त्रिज्या वाले एक वृत्त के एक त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए, जिसका कोण 30° है। (π = 3.14 का प्रयोग करते हुए)
(ii) 7 सेमी त्रिज्या वाले एक वृत्त के त्रिज्यखंड (sector) का क्षेत्रफल ज्ञात कीजिए जिसका केन्द्र पर कोण 30° हो।
(iii) 6 सेमी त्रिज्या और 60° कोण वाले वृत्त के त्रिज्यखंड का क्षेत्रफल ज्ञात कीजिए ।
हल :
(i) यहाँ पर, वृत्त की त्रिज्या (r) = 4 cm
त्रिज्यखण्ड का कोण (θ) = 30°
∴ त्रिज्यखण्ड का क्षेत्रफल = \(\frac {θ}{360°}\) × πr²
= \(\frac {30}{360}\) × 3.14 × 4 × 4
= 4.19 cm²

(ii) यहाँ पर,
वृत्त की त्रिज्या (r) = 7 सेमी
त्रिज्यखण्ड का कोण (θ) = 30°
∴ त्रिज्यखण्ड का क्षेत्रफल = \(\frac {θ}{360}\) × πr²
= \(\frac{30}{360} \times \frac{22}{7}\) × 7 × 7
= \(\frac {77}{6}\) सेमी²

(iii) यहाँ पर,
वृत्त की त्रिज्या (r) = 6 सेमी
त्रिज्यखण्ड का कोण (θ) = 60°
∴ त्रिज्यखण्ड का क्षेत्रफल = \(\frac {θ}{360}\) × πr²
= \(\frac{60}{360} \times \frac{22}{7}\) × 6 × 6
= \(\frac {132}{7}\) सेमी²

प्रश्न 5.
भुजाओं 30 cm और 40 cm वाली, धातु की एक आयताकार शीट में से जितनी बड़ी से बड़ी वृत्ताकार काटी जा सकती थी, काट ली गई है। शेष शीट का क्षेत्रफल ज्ञात कीजिए ।
हल :
दी गई शीट में से काटी गई बड़ी से बड़ी
वृत्ताकार शीट का व्यास (d) = 30 cm
काटी गई वृत्ताकार शीट की त्रिज्या (r) = \(\frac {30}{2}\)cm = 15 cm
∴ वृत्ताकार शीट का क्षेत्रफल (A) = πr²
= \(\frac {22}{7}\) × 15 × 15 cm²
= \(\frac {4950}{7}\) cm²
= 707.14 cm²
दी गई आयताकार शीट का क्षेत्रफल = लंबाई × चौड़ाई
= 40 × 30 cm²
= 1200 cm²
अतः शेष शीट का क्षेत्रफल = (1200 – 707.14) cm²
= 492.86 cm²

प्रश्न 6.
व्यास 150 cm वाले किसी कुएँ के चारों ओर पत्थर की एक मेड़ बनी है । यदि इस मेड़ के बाहरी घेरे की लंबाई 660 cm हो, तो इस मेड़ की चौड़ाई ज्ञात कीजिए ।
हल :

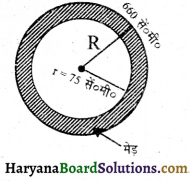
यहाँ पर,
मेड़ के बाहरी घेरे की लंबाई = परिधि (c) = 660 cm
∴ मेड़ के बाहरी घेरे की त्रिज्या (r₁) = \(\frac{\mathrm{c}}{2 \pi}=\frac{660}{2 \times \frac{22}{7}}\) cm
= \(\frac{660 \times 7}{2 \times 22}\)cm = 105 cm
मेड़ के अंदर घेरे का व्यास (d) = 150 cm
मेड़ के अंदर घेरे की त्रिज्या (r₂) = \(\frac {150}{2}\)cm = 75cm
अतः मेड़ की चौड़ाई = r₁ – r₂
= (105 – 75)cm = 30cm

प्रश्न 7.
एक वृत्तीय बाग की त्रिज्या 70 मी० है। इसके गिर्द बाहर की ओर एक 3.5 मी० चौड़ी सड़क बनी है। सड़क बनाने पर क्या व्यय होगा, जबकि व्यय की दर 20 रु० प्रति वर्ग मी० हो ?
हल :
वृत्तीय बाग की अंदर की त्रिज्या = 70 मी०
वृत्तीय बाग का अंदर का = π × (त्रिज्या)²
= \(\frac {22}{7}\) × 70 × 70 = 15400 वर्ग मी०

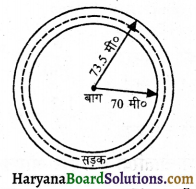
वृत्तीय बाग की बाहर की त्रिज्या = 70 + 3.5 = 73.5 मी०
वृत्तीय बाग का बाहर का क्षेत्रफल = π × (त्रिज्या)²
= \(\frac {22}{7}\) × (73.5)²
= \(\frac {22}{7}\) × 73.5 × 73.5
= 16978.50 वर्ग मी०
सड़क का क्षेत्रफल = बाहर का क्षेत्रफल – अंदर का क्षेत्रफल
= 16978.50 – 15400 वर्ग मी०
= 1578.50 वर्ग मी०
1 वर्ग मी० सड़क बनाने पर खर्च = 20 रु०
1578.50 वर्ग मी० सड़क बनाने पर खर्च = 20 × 1578.50
= 31570 रुपए

प्रश्न 8.
एक वृत्ताकार मैदान के चारों ओर तार लगाया गया है। तार लगाने का खर्च 12 रु० प्रति मी० की दर से 2640 रु० है । इसके बाद मैदान को 0.50 रु० प्रति वर्ग मी० की दर से जोता गया है। मैदान की जुताई में कितना धन खर्च होगा ? (π = \(\frac {22}{7}\) लीजिए)
हल :
यहाँ पर, यदि व्यय 12 रु० हो तो बाड़ की लंबाई = 1 m
यदि व्यय 1 रु० हो तो बाड़ की लंबाई = \(\frac {1}{12}\) m
यदि व्यय 2640 रु० हो तो बाड़ की लंबाई = \(\frac {1}{12}\) × 2640m = 220 m
⇒ वृत्ताकार मैदान की परिधि = 220 m
⇒ 2πr = 220 m [जहाँ r मैदान की त्रिज्या]
⇒ 2 × \(\frac {22}{7}\) × r = 220m
⇒ r = 200 × \(\frac {1}{2}\) × \(\frac {7}{22}\) = 35m
वृत्ताकार मैदान का क्षेत्रफल = πr² = \(\frac {22}{7}\) × 35 × 35m²
= 3850m²
1m² मैदान की जुताई का व्यय = 0.50 रु०
3850m² मैदान की जुताई का व्यय = 3850 × 0.50 रु०
= 1925 रु०

प्रश्न 9.
एक वृत्ताकार ट्रैक की आंतरिक परिधि 220m है। यदि ट्रैक की चौड़ाई प्रत्येक स्थान पर 7m हो तो 2 रु० प्रति m की दर से बाह्य वृत्त के चारों ओर तार लगाने के खर्च की गणना कीजिए ।
हल :

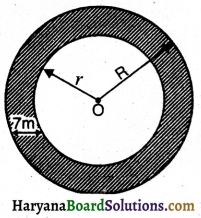
यहाँ पर,
माना वृत्ताकार पथ की बाह्य त्रिज्या = R m
तथा वृत्ताकार पथ की आंतरिक त्रिज्या = r m
वृत्ताकार पथ की आंतरिक परिधि = 220m
⇒ 2πr = 220
⇒ 2 × \(\frac {22}{7}\) × r = 220m
⇒ r = 220 × \(\frac{1}{2} \times \frac{7}{22}\) = 35m
पथ की चौड़ाई = 7 m
∴ वृत्ताकार पथ की बाह्य त्रिज्या (R) = r + 7 = (35 + 7)m = 42 m
वृत्ताकार पथ की बाह्य परिधि = 2π R
= 2 × \(\frac {22}{7}\) × 42m = 264 m
1m बाह्य पथ पर तार लगाने का व्यय = 2 रु०
264m बाह्य पथ पर तार लगाने का व्यय = 264 × 2 रु०
= 528 रु०

प्रश्न 10.
21 cm त्रिज्या के वृत्त से 150° कोण वाला त्रिज्यखंड काटा गया है । त्रिज्यखंड की संगत चाप की लंबाई और क्षेत्रफल ज्ञात कीजिए ।
हल :
यहाँ पर,
वृत्त के त्रिज्यखंड की त्रिज्या (r) = 21cm
त्रिज्यखंड की चाप द्वारा केंद्र पर अंतरित कोण (θ) = 150°

प्रश्न 11.
एक घड़ी की मिनट की सुई 10 cm लंबी है । मिनट की सुई द्वारा प्रातः 9 बजे से 9.35 बजे तक रचित क्षेत्रफल ज्ञात कीजिए ।
हल :
यहाँ पर,
मिनट की सुई की लंबाई (r) = 10 cm
मिनट की सुई द्वारा 9 बजे से 9.35 बजे तक तय कोण (θ) = (\(\frac {360}{60}\) × 35)°
= 210°
अतः मिनट की सुई द्वारा 9 बजे से 9.35 बजे तक तय क्षेत्रफल = \(\frac {θ}{360}\) × πr²
= \(\frac{210}{360} \times \frac{22}{7}\) × 10 × 10 cm²
= 183.3 cm²

प्रश्न 12.
एक वृत्त के चाप की लंबाई 5π है तथा त्रिज्यखंड 20π cm² के क्षेत्रफल से घिरा है । वृत्त की त्रिज्या ज्ञात कीजिए।
हल :

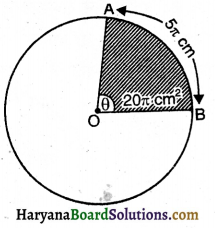
यहाँ पर, माना वृत्त का केंद्र O तथा वृत्त की त्रिज्या l cm है।
प्रश्नानुसार,
चाप AB की लंबाई = 5πcm
⇒ \(\frac {θ}{360}\) × 2πr = 5π
⇒ r = \(\frac{360}{\theta} \times \frac{1}{2}\) × 5 = \(\frac {900}{θ}\) …………….(i)
तथा त्रिज्यखंड OAB का क्षेत्रफल = 20π cm²
⇒ \(\frac {θ}{360}\) × πr² = 20π
⇒ r² = 20 × \(\frac {360}{θ}\) = \(\frac {7200}{θ}\) …………….(ii)
समीकरण (ii) को समीकरण (i) से भाग करने पर,
\(\frac{r^2}{r}=\frac{7200}{\theta} \times \frac{\theta}{900}\)
⇒ r = 8
अतः वृत्त की त्रिज्या = 8

प्रश्न 13.
14 cm त्रिज्या वाले वृत्त की एक जीवा केंद्र पर समकोण बनाती है, वृत्त के लघु तथा दीर्घ वृत्तखंडों के क्षेत्रफल ज्ञात कीजिए ।
हल :

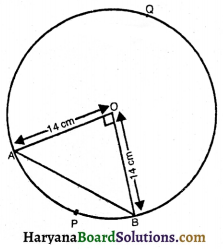
यहाँ पर, वृत्त की त्रिज्या (r) = 14 cm
माना जीवा AB द्वारा वृत्त के केंद्र पर अंतरित कोण (θ) = 90°
संगत लघु वृत्तखंड (APB) का क्षेत्रफल = (त्रिज्यखंड OAPB – समकोण ΔOAB) का क्षेत्रफल
= [\(\frac {θ}{360}\) × πr² – \(\frac {1}{2}\) × OA × OB]
= [\(\frac{90}{360} \times \frac{22}{7}\) × 14 × 14 – \(\frac {1}{2}\) × 14 × 14]cm²
= [154 – 98]cm² = 56 cm²
संगत दीर्घ वृत्तखंड AQB का क्षेत्रफल = वृत्त का क्षेत्रफल – लघुखंड का क्षेत्रफल
= [πr² – 56]cm²
= [\(\frac {22}{7}\) × 14 × 14 – 56]cm²
= [616 – 56] cm²
= 560 cm²

प्रश्न 14.
एक 70m × 52m माप के आयताकार मैदान के कोने में एक घोड़े को 21m लंबी रस्सी से घास चरने के लिए बाँधा गया है। वह कितने क्षेत्रफल में घास चर सकता है? (π = 3. 14 लीजिए)
हल :

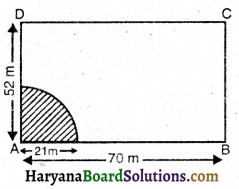
प्रश्नानुसार, छायांकित भाग उस क्षेत्रफल को दर्शाता है, जिसे घोड़ा चर सकता है।
अब छायांकित भाग (चतुर्थांश) के वृत्त की त्रिज्या (r) = 21m
छायांकित भाग (चतुर्थांश) का क्षेत्रफल = \(\frac{\pi r^2}{4}\)
= \(\frac{1}{4} \times \frac{22}{7}\) × 21 × 21 m²
= \(\frac {693}{2}\) = 346.5m²

प्रश्न 15.
संलग्न आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए ।
हल :

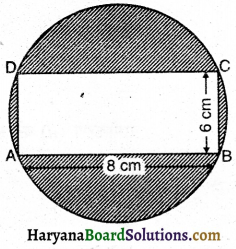
आकृति अनुसार,
वृत्त का व्यास (AC) = आयत ABCD का विकर्ण
= \(\sqrt{(\mathrm{AB})^2+(\mathrm{BC})^2}\)
= \(\sqrt{(8)^2+(6)^2}\)
= \(\sqrt{64+36}\)
= \(\sqrt{100}\) = 10 cm
वृत्त की त्रिज्या (r) = \(\frac{\mathrm{AC}}{2}=\frac{10}{2}\) = 5cm
∴ वृत्त का क्षेत्रफल = πr²
= 3.14 × 5 × 5 cm² = 78.50 cm²
आयत ABCD का क्षेत्रफल = AB × BC
= 8 × 6 cm²
= 48 cm²
अतः छायांकित भाग का क्षेत्रफल = वृत्त का क्षेत्रफल – आयत ABCD का क्षेत्रफल
= (78.50 – 48) cm²
= 30.50 cm²

प्रश्न 16.
एक समबाहु त्रिभुज का क्षेत्रफल 49\(\sqrt{3}\) cm² है। प्रत्येक शीर्ष को केंद्र मानकर त्रिभुज की भुजा की लंबाई की आधी त्रिज्या लेकर वृत्त खींचे गए हैं, जैसा कि संलग्न आकृति में दर्शाया गया है । त्रिभुज के उस भाग का क्षेत्रफल ज्ञात कीजिए जो वृत्तों में सम्मिलित नहीं है (\(\sqrt{3}\) = 1.73 लीजिए)
हल :

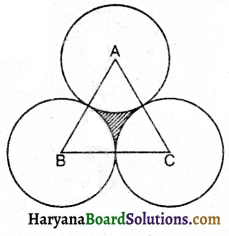
यहाँ पर,
समबाहु त्रिभुज का क्षेत्रफल = 49\(\sqrt{3}\) cm²
⇒ \(\frac{\sqrt{3}}{4}\) (भुजा)² = 49\(\sqrt{3}\)
⇒ (भुजा)² = 49\(\sqrt{3}\) × \(\frac{4}{\sqrt{3}}\) = 196 = (14)²
⇒ भुजा = 14 cm
∴ प्रत्येक वृत्त की त्रिज्या (r) = \(\frac {14}{2}\) = 7 cm
प्रत्येक त्रिज्यखंड का कोण (θ) = 60° (समबाहु त्रिभुज का प्रत्येक कोण)
तीनों त्रिज्यखंडों का क्षेत्रफल = 3[\(\frac {θ}{360}\) × πr²] = 3[\(\frac{60}{360} \times \frac{22}{7}\) × 7 × 7]cm²
= 77 cm²
अतः छायांकित क्षेत्रफल जो वृत्तों में सम्मिलित नहीं है = ΔABC का क्षेत्रफल – तीनों त्रिज्यखंडों का क्षेत्रफल
= (49 × 1.73 – 77 ) cm²
= 7.77 cm²

प्रश्न 17.
एक वृत्त की परिधि ज्ञात कीजिए जिसका क्षेत्रफल 6.16 cm² है।
हल :
यहाँ पर
वृत्त का क्षेत्रफल = 6.16 cm²
⇒ πr² = 6.16
⇒ r² = \(\frac {616}{π}\)
⇒ r² = \(\frac{6.16 \times 7}{22}\) = 1.96
⇒ r = \(\sqrt{1.96}\) = 1.4 cm
अतः वृत्त की परिधि = 2πr
= 2 × \(\frac {22}{7}\) × 1.4 = 8.8 cm

प्रश्न 18.
वृत्त का क्षेत्रफल क्या है, जिसकी परिधि 11 cm भुजा के एक वर्ग के परिमाप के बराबर है?
हल :
यहाँ पर,
वर्ग की भुजा = 11 cm
वर्ग का परिमाप = 4 × भुजा
= 4 × 11 = 44 cm
प्रश्नानुसार,
वृत्त की परिधि = वर्ग का परिमाप
2πr = 44
r = \(\frac {44}{2π}\)
= \(\frac{44}{2} \times \frac{7}{22}\) = 7 cm
अतः वृत्त का क्षेत्रफल = πr² = \(\frac {22}{7}\) × 7 × 7
= 154 cm²

प्रश्न 19.
अर्ध-वृत्ताकार डिजाइन के टुकड़े की परिधि 72 cm है। इसका क्षेत्रफल ज्ञात कीजिए ।
हल :
माना अर्धवृत्ताकार डिजाइन के टुकड़े की त्रिज्या = r cm
दिया है अर्धवृत्ताकार डिजाइन के टुकड़े की परिधि = 72 cm
⇒ \(\frac {1}{2}\)(2πr) = 72
⇒ πr = 72
⇒ r = \(\frac {72}{π}\)cm
अर्धवत्ताकार डिजाइन के टुकड़े का क्षेत्रफल = \(\frac {1}{2}\)πr²
= \(\frac {1}{2}\) × π × \(\frac {72}{π}\) × \(\frac {72}{π}\)
= \(\frac {1}{2}\) × \(\frac{72 \times 72 \times 7}{22}\)
= 824.73 cm²

प्रश्न 20.
एक वृत्त की परिधि व्यास से 33.6 cm अधिक है । वृत्त का क्षेत्रफल ज्ञात कीजिए ।
हल :
मान लीजिए वृत्त की त्रिज्या = r cm
∴ व्यास = 2r cm तथा परिधि = 2πr cm
दिया गया है कि वृत्त की परिधि उसके व्यास से 33.6 cm अधिक है। अर्थात्
परिधि = व्यास + 33.6
⇒ 2πr = 2r + 33.6
⇒ 2(\(\frac {22}{7}\))r = 2r + 33.6
⇒ 44r = 14r + 235.2
⇒ 30r = 235.2
⇒ r = \(\frac {235.2}{30}\) = 7.84 cm
वृत्त का क्षेत्रफल = πr²
= \(\frac {22}{7}\) × 7.84 × 7.84
= 22 × 1.12 × 7.84 cm²
= 193.18 cm²

बहुविकल्पीय प्रश्न :

प्रश्न 1.
एक वृत्त के अनुदिश एक बार चलने में तय की दूरी को कहा जाता है-
(A) त्रिज्या
(B) व्यास
(C) परिधि
(D) क्षेत्रफल
हल :
(C) परिधि

प्रश्न 2.
वृत्त की परिधि और व्यास का अनुपात है :
(A) 2π : 1
(B) 7 : 1
(C) 1 : 1
(D) इनमें से कोई नहीं
हल :
(B) π : 1

प्रश्न 3.
π एक ……………….. संख्या है।
(A) परिमेय
(B) सम
(C) विषम
(D) अपरिमेय
हल :
(D) अपरिमेय

प्रश्न 4.
वृत्त की परिधि और त्रिज्या का अनुकूल है :
(A) 2π : 1
(B) π : 1
(C) 1 : 1
(D) इनमें से कोई नहीं
हल :
(A) 2π : 1

प्रश्न 5.
अर्धवृत्त में बना प्रत्येक कोण होता है-
(A) 45°
(B) 60°
(C) 90°
(D) 180°
हल :
(C) 90°

प्रश्न 6.
संलग्न आकृति में केंद्र वाले वृत्त के अंतर्गत एक समबाहु त्रिभुज ABC है तो ∠BOC = ∠COA = ∠AOB का मान होगा-

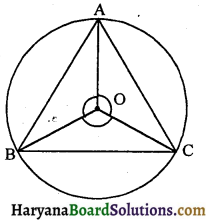
(A) 60°
(C) 30°
(B) 90°
(D) 120°
हल :
(D) 120°

प्रश्न 7.
7 cm त्रिज्या वाले वृत्त की परिधि होगी :
(A) 154 cm²
(B) 154 cm
(D) 44cm²
(C) 44 cm
हल :
(D) 44 cm

प्रश्न 8.
d व्यास वाले वृत्त की परिधि होगी-
(A) πd²
(B) 2πd
(C) πd
(D) πd²
हल :
(C) πd

प्रश्न 9.
3.5 cm त्रिज्या वाले वृत्त की परिधि होगी :
(A) 22 cm
(B) 22 cm²
(C) 44 cm²
(D) 44 cm
हल :
(A) 22 cm

प्रश्न 10.
उस वृत्त की त्रिज्या क्या होगी जिसकी परिधि 44 से.मी. हो ?
(A) 14 cm
(B) 7 cm
(C) 49 cm
(D) 28 cm
हल :
(B) 7 cm

प्रश्न 11.
यदि π = 3.14 हो तो 2.5 cm त्रिज्या वाले वृत्त की परिधि होगी-
(A) 15.7 m
(B) 15.7 cm
(C) 1.57 m
(D) 1.57 cm
हल :
(B) 15.7 cm

प्रश्न 12.
यदि π = 3.14 हो तो 12.56 cm परिधि वाले वृत्त का व्यास होगा-
(A) 8 cm
(B) 6 cm
(C) 4 cm
(D) 2 cm
हल :
(C) 4 cm

प्रश्न 13.
एक वृत्ताकार सिक्के का व्यास 2 cm है । इसकी परिधि होगी-
(A) \(\frac {22}{7}\) cm
(B) \(\frac {11}{7}\) cm
(C) \(\frac {88}{7}\) cm
(D) \(\frac {44}{7}\) cm
हल :
(D) \(\frac {44}{7}\) cm

प्रश्न 14.
गारे के उस वृत्ताकार गड्ढे का व्यास क्या होगा जिसकी परिधि 220 cm है ?
(A) 70 cm
(B) 140 cm
(C) 35 cm
(D) 17.5 cm
हल :
(A) 70 cm

प्रश्न 15.
यदि π = 3.14 हो तो 75.36 cm परिधि वाली खाने की किसी प्लेट की त्रिज्या होगी-
(A) 24 cm
(B) 12 cm
(C) 6 cm
(D) 17.5 cm
हल :
(D) 3 cm

प्रश्न 16.
एक कोल्हू का बैल 3m लंबी रस्सी से बँधा हुआ है, वह एक चक्कर में दूरी तय करेगा-
(A) \(\frac {33}{7}\) m
(B) \(\frac {66}{7}\) m
(C) \(\frac {132}{7}\) m
(D) \(\frac {264}{7}\) m
हल :
(C) \(\frac {132}{7}\) m

प्रश्न 17.
दो पहियों की त्रिज्याओं में अनुपात 3 : 4 है। इनकी परिधियों में अनुपात होगा-
(A) 6 : 4
(B) 3 : 8
(C) \(\frac {3}{2}\) : 4
(D) 3 : 4
हल :
(D) 3 : 4

प्रश्न 18.
वृत्त के व्यास व त्रिज्या में क्या संबंध होता है ?
(A) व्यास = 2 × त्रिज्या
(B) त्रिज्या = 2 × व्यास
(C) व्यास = त्रिज्या / 2
(D) व्यास = 4 × त्रिज्या
हल :
(A) व्यास = 2 × त्रिज्या

प्रश्न 19.
7 cm त्रिज्या के वृत्त का क्षेत्रफल होगा :
(A) 154 cm
(B) 154 cm²
(C) 44 cm
(D) 44 cm²
हल :
(B) 154 cm²

प्रश्न 20.
त्रिज्या r वाले अर्धवृत्त का क्षेत्रफल होगा-
(A) πr²
(B) \(\frac {1}{2}\)πr²
(C) 2πr²
(D) 2πr
हल :
(B) \(\frac {1}{2}\)πr²

प्रश्न 21.
त्रिज्या r वाले वृत्त के चतुर्थांश का क्षेत्रफल होगा-
(A) πr²
(B) \(\frac {1}{2}\)πr²
(C) \(\frac {1}{4}\)πr²
(D) 4πr²
हल :
(C) \(\frac {1}{4}\)πr²

प्रश्न 22.
यदि एक वृत्त का परिमाप और क्षेत्रफल संख्यात्मक रूप में बराबर हों तो उस वृत्त की त्रिज्या होगी-
(A) 2 मात्रक
(B) π मात्रक
(C) 4 मात्रक
(D) 7 मात्रक
हल :
(A) 2 मात्रक

प्रश्न 23.
दो वृत्तों की त्रिज्याएँ क्रमशः 12cm व 7cm हैं । उस वृत्त की त्रिज्या क्या होगी जिसकी परिधि इन दोनों वृत्तों की परिधियों के योग के बराबर है?
(A) 5cm
(B) 9.2cm
(C) 19cm
(D) 17cm
हल :
(C) 19cm

प्रश्न 24.
दो वृत्तों की त्रिज्याएँ क्रमशः 15cm व 10cm हैं । उस वृत्त की त्रिज्या क्या होगी जिसकी परिधि इन दोनों वृत्तों की परिधियों के योग के बराबर है?
(A) 5cm
(B) 19cm
(C) 25cm
(D) 17cm
हल :
(C) 25cm

प्रश्न 25.
दो वृत्तों की त्रिज्याएँ क्रमशः 17cm व 9cm हैं । उस वृत्त की त्रिज्या क्या होगी जिसकी परिधि इन दोनों वृत्तों की परिधियों के योग के बराबर है?
(A) 8cm
(B) 16cm
(C) 13cm
(D) 26cm
हल :
(D) 26cm

प्रश्न 26.
दो वृत्तों की त्रिज्याएँ क्रमशः 4cm व 3cm हैं । उस वृत्त की त्रिज्या क्या होगी जिसका क्षेत्रफल इन दोनों वृत्तों के क्षेत्रफलों के योग के बराबर है?
(A) 5cm
(B) 3.5cm
(C) 7cm
(D) 1cm
हल :
(A) 5cm

प्रश्न 27.
दो वृत्तों की त्रिज्याएँ क्रमशः 8cm व 6cm हैं। उस वृत्त की त्रिज्या क्या होगी जिसका क्षेत्रफल इन दोनों वृत्तों के क्षेत्रफलों के योग के बराबर है?
(A) 14cm
(B) 12cm
(C) 10cm
(D) 2cm
हल :
(C) 10cm

प्रश्न 28.
दो वृत्तों की त्रिज्याएँ क्रमशः 12cm व 9cm हैं । उस वृत्त की त्रिज्या क्या होगी जिसका क्षेत्रफल इन दोनों वृत्तों के क्षेत्रफलों के योग के बराबर है?
(A) 21cm
(B) 15cm
(C) 10.5cm
(D) 7.5cm
हल :
(B) 15cm

प्रश्न 29.
उस वृत्ताकार खेत की परिधि क्या होगी जिस पर 24 रु० प्रति मीटर की दर से बाड़ लगाने का व्यय 5280 रु० है?
(A) 110m
(B) 440m
(C) 330m
(D) 220m
हल :
(D) 220m

प्रश्न 30.
उस वृत्ताकार खेत की परिधि क्या होगी जिस पर 25 रु० प्रति मीटर की दर से बाड़ लगाने का व
(A) 220m
(B) 330m
(C) 440m
(D) 110m
हल :
(A) 220m

प्रश्न 31.
उस वृत्ताकार खेत की परिधि क्या होगी जिस पर 20 रु० प्रति मीटर की दर से बाड़ लगाने का व्यय 5000 रु० है?
(A) 500m
(B) 250m
(C) 125m
(D) 375m
हल :
(B) 250m

प्रश्न 32.
200 cm व्यास वाले वृत्त का क्षेत्रफल होगा-
(A) \(\frac {22}{7}\)mm²
(B) \(\frac {22}{7}\)dm²
(C) \(\frac {22}{7}\)cm²
(D) \(\frac {22}{7}\)m²
हल :
(D) \(\frac {22}{7}\)m²

प्रश्न 33.
154 cm² क्षेत्रफल वाले वृत्त की त्रिज्या होगी –
(A) 7 cm
(B) 14 cm
(C) 3.5 cm
(D) 1.75 cm
हल :
(A) 7 cm

प्रश्न 34.
\(\frac {2200}{7}\)dm² क्षेत्रफल वाले वृत्त की त्रिज्या होगी –
(A) 20 cm
(B) 10 dm
(C) 20 dm
(D) 10 cm
हल :
(B) 10 dm

प्रश्न 35.
π का मान 3.14 लेते हुए उस वृत्त की त्रिज्या ज्ञात कीजिए जिसका क्षेत्रफल 314 cm² है
(A) 20 dm
(B) 20 cm
(C) 10 cm
(D) 10 dm
हल :
(C) 10 cm

प्रश्न 36.
10 cm व्यास वाली वृत्ताकार प्लेट का क्षेत्रफल होगा-
(A) \(\frac {550}{7}\)cm²
(B) \(\frac {5500}{7}\)cm²
(C) \(\frac {275}{7}\)cm²
(D) \(\frac {2750}{7}\)cm²
हल :
(A) \(\frac {550}{7}\)cm²

प्रश्न 37.
0.50 रु० प्रति वर्ग मीटर की दर 3850m² क्षेत्रफल को जोतने का व्यय होगा-
(A) 1925 रु०
(B) 19.25 रु०
(C) 192.5 रु०
(D) 19250 रु०
हल :
(A) 1925 रु०

प्रश्न 38.
संलग्न आकृति के दो संकेंद्रीय वृत्तों की त्रिज्याएँ क्रमशः 10.5cm व 21cm हैं। इनके बीच घिरे छायांकित क्षेत्र का क्षेत्रफल होगा-

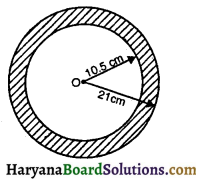
(A) 346.5 cm²
(B) 1039.5 cm²
(C) 693.0 cm²
(D) 1732.5cm²
हल :
(B) 1039.5 cm²

प्रश्न 39.
दो संकेंद्रीय वृत्तों जिनकी त्रिज्याएँ R तथा r हों, के बीच घिरे क्षेत्र का क्षेत्रफल होगा-
(A) 2π (R – r)
(B) 2π (R² – r²)
(C) π(R² – r²)
(D) π(R² + r²)
हल :
(C) π(R² – r²)

प्रश्न 40.
यदि किसी वृत्त की त्रिज्या को दुगुना कर दिया जाए तो प्राप्त वृत्त के क्षेत्रफल का दिए गए वृत्त के क्षेत्रफल से अनुपात होगा-
(A) 1 : 2
(B) 1 : 3
(C) 1 : 4
(D) 1 : 9
हल :
(C) 1 : 4

प्रश्न 41.
यदि किसी वृत्त की त्रिज्या को तीन गुणा कर दिया जाए तो प्राप्त वृत्त के क्षेत्रफल का दिए गए वृत्त के क्षेत्रफल से अनुपात होगा-
(A) 1 : 3
(B) 1 : 9
(C) 2 : 3
(D) 2 : 9
हल :
(B) 1 : 9

प्रश्न 42.
यदि किसी वृत्त की त्रिज्या को चार गुणा कर दिया जाए तो प्राप्त वृत्त के क्षेत्रफल का दिए गए वृत्त के क्षेत्रफल से अनुपात होगा-
(A) 1 : 4
(B) 1 : 9
(C) 1 : 16
(D) 1 : 8
हल :
(C) 1 : 16

प्रश्न 43.
वृत्तीय क्षेत्र का वह भाग जो दो त्रिज्याओं और संगत चाप से घिरा हो, उसे वृत्त का एक ………………… कहा जाता है ।
(A) त्रिज्यखंड
(B) अर्धवृत्त
(C) वृत्तखंड
(D) परिमाप
हल :
(A) त्रिज्यखंड

प्रश्न 44.
वृत्तीय क्षेत्र का वह भाग जो एक जीवा और संगत चाप के बीच में परिबद्ध हो, उसे कहा जाता है-
(A) त्रिज्यखंड
(B) क्षेत्रफल
(C) परिमाप
(D) वृत्तखंड
हल :
(D) वृत्तखंड

प्रश्न 45.
संलग्न आकृति में छायांकित क्षेत्र कहलाता है-

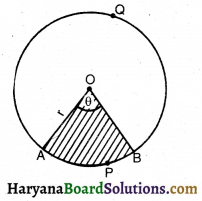
(A) लघु त्रिज्यखंड
(B) दीर्घ त्रिज्यखंड
(C) लघु वृत्तखंड
(D) दीर्घ वृत्तखंड
हल :
(A) लघु त्रिज्यखंड

प्रश्न 46.
प्रश्न 45 की आकृति में क्षेत्र OAQB कहलाता है-
(A) लघु त्रिज्यखंड
(B) दीर्घ त्रिज्यखंड
(C) लघु वृत्तखंड
(D) दीर्घ वृत्तखंड
हल :
(B) दीर्घ त्रिज्यखंड

प्रश्न 47.
संलग्न आकृति में, यदि O वृत्त का केंद्र तथा PQ, एक जीवा हो तो छायांकित भाग को कहा जाता है-

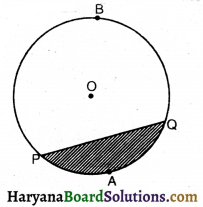
(A) लघु त्रिज्यखंड
(B) दीर्घ त्रिज्यखंड
(C) लघु वृत्तखंड
(D) दीर्घ वृत्तखंड
हल :
(C) लघु वृत्तखंड

प्रश्न 48.
संलग्न आकृति में, यदि AB वृत्त की जीवा तथा O वृत्त का केंद्र हो, तो छायांकित भाग कहलाता है-

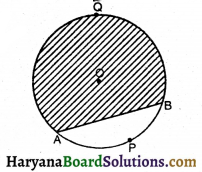
(A) लघु त्रिज्यखंड
(B) दीर्घ त्रिज्यखंड
(C) लघु वृत्तखंड
(D) दीर्घ वृत्तखंड
हल :
(D) दीर्घ वृत्तखंड

प्रश्न 49.
त्रिज्या r वाले वृत्त के एक त्रिज्यखंड जिसका कोण अंशों में θ है, उसके संगत चाप की लंबाई होगी-
(A) \(\frac {θ}{360}\) × 2πr
(B) \(\frac {θ}{360}\) × πr
(C) \(\frac {θ}{360}\) × πr²
(D) \(\frac {θ}{360}\) × 2πr²
हल :
(A) \(\frac {θ}{360}\) × 2πr

प्रश्न 50.
त्रिज्या r वाले वृत्त के एक त्रिज्यखंड जिसका कोण अंशों में θ है, का क्षेत्रफल होगा –
(A) \(\frac {θ}{360}\) × 2πr
(B) \(\frac {θ}{360}\) × πr
(C) \(\frac {θ}{360}\) × πr²
(D) \(\frac {θ}{360}\) × 2πr²
हल :
(C) \(\frac {θ}{360}\) × πr²

प्रश्न 51.
त्रिज्या R वाले वृत्त के उस दीर्घ त्रिज्यखंड का क्षेत्रफल जिसका कोण θ° है, होगा –
(A) \(\frac {θ}{360}\) × πR²
(B) \(\frac {θ}{180}\) × πR²
(C) (\(\frac{360-\theta}{360}\)) × πR²
(D) इनमें से कोई नहीं
हल :
(C) (\(\frac{360-\theta}{360}\)) × πR²

प्रश्न 52.
त्रिज्या r वाले वृत्त के उस त्रिज्यखंड का क्षेत्रफल जिसका कोण 1° है-
(A) πr² / 360
(B) πr² / 180
(C) 2πr / 360
(D) 2πr² / 360
हल :
(A) πr² / 360

प्रश्न 53.
6cm त्रिज्या वाले एक वृत्त के उस त्रिज्यखंड का क्षेत्रफल क्या होगा, जिसका कोण 60° है ?
(A) \(\frac {132}{7}\) cm³
(B) \(\frac {132}{7}\) cm²
(C) \(\frac {132}{7}\) cm
(D) \(\frac {44}{7}\) cm²
हल :
(B) \(\frac {132}{7}\) cm²

प्रश्न 54.
22cm परिधि वाले वृत्त के चतुर्थांश का क्षेत्रफल होगा-
(A) \(\frac {77}{2}\)cm²
(B) \(\frac {77}{4}\)cm²
(C) \(\frac {77}{6}\)cm²
(D) \(\frac {77}{8}\)cm²
हल :
(D) \(\frac {77}{8}\)cm²

प्रश्न 55.
एक घड़ी की मिनट की सुई जिसकी लंबाई 14cm है। इसके द्वारा 5 मिनट में रचित क्षेत्रफल होगा-
(A) \(\frac {154}{9}\)cm²
(B) \(\frac {154}{6}\)cm²
(C) \(\frac {154}{3}\)cm²
(D) \(\frac {154}{5}\)cm²
हल :
(C) \(\frac {154}{3}\)cm²

प्रश्न 56.
किसी वृत्त का क्षेत्रफल क्या होगा, यदि इसकी त्रिज्या 7cm हो ?
(A) 154 cm
(B) 154 cm²
(C) 44 cm²
(D) 44 cm
हल :
(B) 154 cm²

प्रश्न 57.
r त्रिज्या वाले वृत्त का एक चाप केंद्र पर 60° का कोण अंतरित करता है, चाप की लंबाई क्या होगी ?
(A) \(\frac {πr}{3}\) cm
(B) \(\frac {2πr}{3}\) cm²
(C) πr² / 3 cm²
(D) \(\frac {πr}{3}\) cm ²
हल :
(A) \(\frac {πr}{3}\) cm

प्रश्न 58.
त्रिज्या 21cm वाले वृत्त के उस त्रिज्यखंड का क्षेत्रफल क्या होगा जो केंद्र पर 60° का कोण अंतरित करता है –
(A) 115.5 cm²
(B) 462 cm²
(C) 231 cm²
(D) 693 cm²
हल :
(C) 231 cm²

प्रश्न 59.
वृत्त की त्रिज्या 14 cm है, तो उसकी परिधि होगी-
(A) 44 cm
(B) 44 cm²
(C) 88 cm
(D) 88 cm²
हल :
(C) 88 cm

प्रश्न 60.
14 cm त्रिज्या वाले वृत्त के त्रिज्याखंड का क्षेत्रफल होगा जिसका कोण 60° हो :
(A) \(\frac {308}{3}\) cm³
(B) \(\frac {308}{3}\) cm
(C) \(\frac {308}{3}\) cm²
(D) \(\frac {22}{3}\) cm²
हल :
(A) \(\frac {308}{3}\) cm³

प्रश्न 61.
p भुजा वाले समबाहु त्रिभुज का क्षेत्रफल होगा-
(A) \(\frac{\sqrt{3}}{4}\)p
(B) \(\frac{\sqrt{3}}{2}\)p²
(C) \(\frac{\sqrt{3}}{4}\)p²
(D) \(\frac{\sqrt{3}}{4}\)p³
हल :
(C) \(\frac{\sqrt{3}}{4}\)p²

प्रश्न 62.
संलग्न आकृति में, यदि O वृत्त का केंद्र, PQ = 24 cm तथा PR = 7cm हो तो ARPQ का क्षेत्रफल होगा-

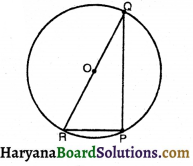
(A) 84 cm²
(B) 168 cm²
(C) 42 cm²
(D) 63 cm²
हल :
(A) 84 cm²