HBSE 10th Class Maths Important Questions Chapter 10 वृत्त

Haryana State Board HBSE 10th Class Maths Important Questions Chapter 10 वृत्त Important Questions and Answers.

Haryana Board 10th Class Maths Important Questions Chapter 10 वृत्त

परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न :

प्रश्न 1.
सिद्ध कीजिए कि वृत्त के किसी बिंदु पर स्पर्श रेखा स्पर्श बिंदु से जाने वाली त्रिज्या पर लंब होती है ।
हल :

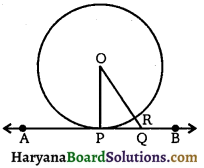
दिया है – एक वृत्त C (O, R) के बिंदु P पर AB एक स्पर्श रेखा है ।
सिद्ध करना है – OP ⊥ AB
रचना – स्पर्श रेखा AB पर P के अलावा अन्य कोई बिंदु Q लेकर इसे वृत्त के केंद्र O से मिलाओ ।
प्रमाण – हम जानते हैं कि किसी बिंदु 0 से किसी रेखा AB की न्यूनतम दूरी, रेखा AB पर लंब की लंबाई के बराबर होगी । अतः यह सिद्ध करने के लिए कि OP ⊥ AB है, हमें केवल यह सिद्ध करना ही पर्याप्त होगा कि OP, बिंदु O से रेखा AB पर स्थित अन्य किसी भी बिंदु को मिलाने वाले रेखाखंडों में से सबसे छोटा है ।
आकृति अनुसार,
OP = OR (वृत्त की त्रिज्या )
OQ = OR + RQ
⇒ OQ > OR
⇒ OQ > OP [∵ OR = OP]
⇒ OP < OQ
अतः वृत्त के केंद्र O से रेखा AB पर स्थित किसी भी अन्य बिंदु को मिलाने वाला रेखाखंड OP से बड़ा होगा ।
OP, बिंदु O से AB की न्यूनतम दूरी है ।
OP ⊥ AB (इति सिद्धम्)

प्रश्न 2.
सिद्ध कीजिए कि किसी वृत्त पर, इसके किसी बाह्य बिंदु से खींची गई दोनों स्पर्श रेखाएँ समान लंबाई की होती हैं।
हल :

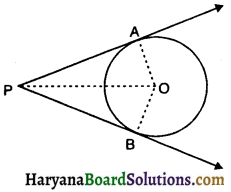
दिया है- O केंद्र के वृत्त के बाह्य बिंदु P से PA और PB दो स्पर्श रेखाएँ खींची गई हैं।
सिद्ध करना है – PA = PB
रचना – OP, OA, OB को मिलाओ ।
प्रमाण – PA वृत्त की स्पर्श रेखा है और OA त्रिज्या है ।
∴ ∠OAP = 90°
इसी प्रकार, ∠OBP = 90°
अब, दो समकोण ΔPAO और ΔPBO में,
कर्ण OP = कर्ण OP (उभयनिष्ठ)
OA = OB (एक ही वृत्त की त्रिज्याएँ)
∴ ΔPAO ≅ ΔPBO (समकोण – कर्ण – भुजा सर्वांगसमता के नियम से)
इस प्रकार, PA = PB [इति सिद्धम्]

प्रश्न 3.
सिद्ध कीजिए कि किसी वृत्त की दो समांतर स्पर्श रेखाओं के स्पर्श बिंदुओं को मिलाने वाला रेखाखंड वृत्त का व्यास होता है ।
हल :

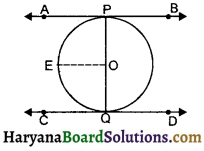
दिया है-माना दो समांतर स्पर्श रेखाएँ AB और CD एक वृत्त जिसका
केंद्र O है को P और Q पर स्पर्श करती हैं ।
सिद्ध करना है – PQ वृत्त का व्यास है ।
रचना – केंद्र O से OE || AB खींचो |
प्रमाण – क्योंकि PA || OE (रचना से)
∴ ∠APO + ∠EOP = 180° (तिर्यक रेखा के एक ओर बने कोण) ……………..(i)
परंतु हम जानते हैं कि स्पर्श रेखा और वृत्त की त्रिज्या के बीच बना कोण समकोण होता है-
∴ ∠APO = 90°
समीकरण (i) से,
90° + ∠EOP = 180°
या ∠EOP = 180° – 90° = 90° ……………..(ii)
इसी प्रकार हम सिद्ध कर सकते हैं कि
∠EOQ = 90° ……………..(iii)
समीकरण (ii) व (iii) से,
∠EOP + ∠EOQ = 90° + 90° = 180°
अतः POQ एक सरल रेखा है ।
अर्थात् POQ वृत्त का व्यास है । [इति सिद्धम्]

प्रश्न 4.
3 cm त्रिज्या वाले वृत्त के केंद्र से 5 cm दूर स्थित एक बिंदु से स्पर्श रेखा की लंबाई ज्ञात कीजिए ।
हल :

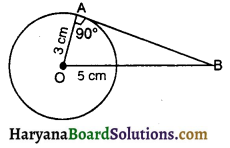
वृत्त की त्रिज्या (AO) = 3cm
वृत्त के केंद्र से बिंदु की दूरी (OB) = 5cm
स्पर्श रेखा (AB) की लंबाई = ?
∠OAB = 90°
[∵ वृत्त के किसी बिंदु पर स्पर्श रेखा स्पर्श बिंदु से होकर जाने वाली त्रिज्या पर लंब होती है ।]
∴ ΔBAO एक समकोण त्रिभुज है । अतः पाइथागोरस प्रमेय से,
OB² = OA² + AB²
या (5)² = (3)² + (AB)²
या 25 – 9 = (AB)²
या AB = \(\sqrt{16}\)
या AB = 4 cm
∴ स्पर्श रेखा की लंबाई = 4 cm

प्रश्न 5.
सिद्ध कीजिए कि दो संकेंद्रीय वृत्तों में बड़े वृत्त की जीवा जो छोटे वृत्त को स्पर्श करती है, स्पर्श बिंदु पर समद्विभाजित होती है ।
हल :

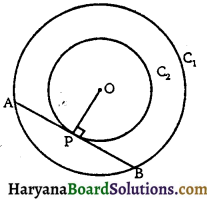
दिया है – केंद्र O वाले दो संकेंद्रीय वृत्त C₁ और C₂ हैं। इनमें बड़े वृत्त C₁ की जीवा AB छोटे वृत्त C₂ को बिंदु P पर स्पर्श करती है ।
सिद्ध करना है – AP = BP
रचना – OP को मिलाएँ ।
प्रमाण – वृत्त C₂ के स्पर्श बिंदु P पर AB एक स्पर्श रेखा है और OP एक त्रिज्या है।
∴ OP ⊥ AB
अब AB वृत्त C₁ की एक जीवा है और OP ⊥ AB है। अतः OP जीवा AB को समद्विभाजित करेगी क्योंकि केंद्र से जीवा पर खींचा गया लंब उसे समद्विभाजित करता है ।
⇒ AP ⊥ BP (इति सिद्धम्)

प्रश्न 6.
दो संकेंद्रीय वृत्तों में सिद्ध कीजिए कि बाह्य वृत्त की वे सभी जीवाएँ, जो आंतरिक वृत्त को स्पर्श करती हैं, समान लंबाई की होती हैं ।
हल :

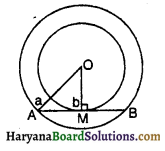
दिया है- दो संकेंद्रीय वृत्त जिनका केंद्र 0 है तथा बाह्य वृत्त की त्रिज्या a और आंतरिक वृत्त की त्रिज्या b है | AB बाह्य वृत्त की एक जीवा है ।
सिद्ध करना है – बाह्य वृत्त की सभी जीवाएँ जो आंतरिक वृत्त को स्पर्श करती हैं, समान लंबाई की होती हैं ।
रचना – OM ⊥ AB तथा बाह्य वृत्त की त्रिज्या OA खींचो ।
प्रमाण – समकोण ΔOAM में,
AM = \(\sqrt{O A^2-O M^2}\) = \(\sqrt{a^2-b^2}\) (पाइथागोरस प्रमेय द्वारा)
अतः AB = 2 AM = 2\(\sqrt{a^2-b^2}\)
जोकि स्थिर है क्योंकि वृत्त की त्रिज्याएँ दी हुई हैं और बदल नहीं सकती ।
अतः इस प्रकार बाह्य वृत्त की सभी जीवाओं की लंबाइयाँ जो अंतःवृत्त को स्पर्श करती हैं, बराबर होती हैं।

प्रश्न 7.
केंद्र O वाले वृत्त पर बाह्य बिंदु T से दो स्पर्श रेखाएँ TP तथा TQ खींची गई हैं । सिद्ध कीजिए कि ∠PTQ = 2 ∠OPQ है |
हल :

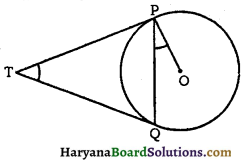
दिया है – केंद्र O वाला एक वृत्त, एक बाह्य बिंदु T तथा वृत्त पर दो स्पर्श रेखाएँ TP और TQ, जहाँ P, Q स्पर्श बिंदु हैं ।
सिद्ध करना है – ∠PTQ = 2∠OPQ.
प्रमाण – माना ∠PTQ = θ
हम जानते हैं कि वृत्त के किसी बाह्य बिंदु से खींची गई स्पर्श रेखाएँ समान होती हैं।
∴ TP = TQ
अतः TPQ एक समद्विबाहु त्रिभुज है ।
∴ ∠TPQ = ∠TQP = \(\frac {1}{2}\) (180° – θ)
= 90°- \(\frac {θ}{2}\)
परंतु त्रिज्या और स्पर्श रेखा के बीच बना कोण 90° होता है ।
∴ ∠OPT = 90°
इसी प्रकार,
∠OPQ = ∠OPT – ∠TPQ
= 90° – (90° – \(\frac {θ}{2}\))
= \(\frac {θ}{2}\) = \(\frac {1}{2}\)∠PTQ
⇒ ∠PTQ = 2∠OPQ [इति सिद्धम्]

प्रश्न 8.
एक रेखा l दो संकेंद्रीय वृत्तों को जिनका केंद्र O है, A, B, C और D पर प्रतिच्छेदित करती है (देखिए संलग्न आकृति) । सिद्ध कीजिए कि AB = CD है ।
हल :

दिया है – O केंद्र वाले दो संकेंद्रीय वृत्तों को रेखा l बिंदु A, B, C तथा D पर प्रतिच्छेद करती है।
सिद्ध करना है – AB = CD
रचना – OM ⊥ l खींचों ।
प्रमाण – हम जानते हैं कि वृत्त के केंद्र से जीवा पर डाला गया लंब जीवा समद्विभाजित करता है ।
⇒ AM = MD …………..(i)
तथा BM = MC …………..(ii)
समीकरण (ii) को (i) में से घटाने पर,
AM – BM = MD – MC
⇒ AB = CD (इति सिद्धम्)

प्रश्न 9.
सिद्ध कीजिए कि चक्रीय चतुर्भुज के सम्मुख कोणों के किसी भी युग्म का योग 180° होता है ।
हल :

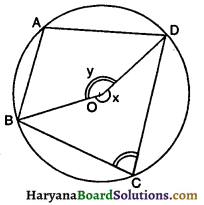
दिया है – एक चक्रीय चतुर्भुज ABCD है।
सिद्ध करना है- ∠BAD + ∠BCD = 180°
तथा ∠ADC + ∠CBA = 180°
रचना-माना कि शीर्षों A, B, C और D से जाने वाले वृत्त का केंद्र O है । OB और OD को मिलाइए ।
प्रमाण-
∠BAD = \(\frac {1}{2}\)∠BOD
= \(\frac {1}{2}\)x ……….(i)
(∵ किसी चाप द्वारा वृत्त के शेष भाग पर बना कोण केंद्र पर बने कोण का आधा होता है ।)
और ∠BCD = \(\frac {1}{2}\)∠BOD
= \(\frac {1}{2}\)y ……….(ii)
समीकरण (i) और (ii) को जोड़ने पर,
∠BAD + ∠BCD = \(\frac {1}{2}\)x + \(\frac {1}{2}\)y
= \(\frac {1}{2}\)(x + y)
= \(\frac {1}{2}\) × 360° = 180° ( x + y = 360°)
∵ चतुर्भुज के कोणों का योग 360° है,
∠ADC + ∠CBA = 360° – (∠BAD + ∠BCD)
= 360° – 180° = 180°
अतः चक्रीय चतुर्भुज के सम्मुख कोणों के किसी युग्म का योग 180° होता है । [इति सिद्धम्]

प्रश्न 10.
दो वृत्त एक बिंदु P पर बाह्यतः स्पर्श करते हैं । P पर खींची गई स्पर्श रेखा के एक बिंदु T से वृत्तों पर स्पर्श रेखाएँ TQ तथा TR खींची जाती हैं, जहां Q, R क्रमशः स्पर्श बिंदु हैं । सिद्ध कीजिए कि TQ = TR है ।
हल :
दिया है- वृत्त C’ केंद्र O’ तथा वृत्त C केंद्र 0 परस्पर बिंदु P पर बाह्यतः स्पर्श करते हैं । P पर दोनों वृत्तों की उभयनिष्ठ स्पर्श रेखा है। उभयनिष्ठ स्पर्श रेखा m के किसी बिंदु T से स्पर्श रेखा TQ वृत्त C’ पर तथा TR वृत्त C पर खींची गई है।

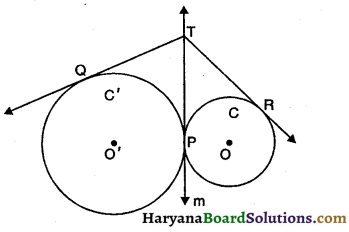
सिद्ध करना है – TQ =TR
प्रमाण – बाह्य बिंदु T से, TP तथा TQ, C’ पर स्पर्श रेखाएँ हैं,
∴ TP = TQ …………..(i)
इसी प्रकार, TP तथा TR बाह्य बिंदु T से वृत्त C पर स्पर्श रेखाएँ हैं,
∴ TP = TR …………..(ii)
समीकरण (i) और (ii) से,
TQ = TR [इति सिद्धम्]

प्रश्न 11.
एक बिंदु P वृत्त के केंद्र से 13 cm की दूरी पर है। P से वृत्त पर खींची गई स्पर्श रेखा की लंबाई 12 cm है। वृत्त की त्रिज्या ज्ञात कीजिए ।
हल :

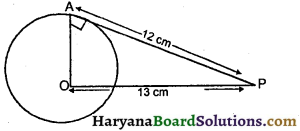
वृत्त के केंद्र 0 से बिंदु P की दूरी (OP) = 13 cm
स्पर्श रेखा (PA) की लंबाई = 12 cm
वृत्त की त्रिज्या (OA) = ?
∠OAP = 90° [∵ वृत्त के किसी बिंदु पर स्पर्श रेखा स्पर्श बिंदु से होकर जाने वाली त्रिज्या पर लंब होती है]
अब समकोण ΔOAP में पाइथागोरस प्रमेय से, OA = \(\sqrt{(\mathrm{OP})^2-(\mathrm{PA})^2}\) = \(\sqrt{(13)^2-(12)^2}\) cm = \(\sqrt{169-144}\) cm
= \(\sqrt{25}\) = 5 cm
अतः वृत्त की त्रिज्या (OA) = 5 cm

प्रश्न 12.
5 सें०मी० त्रिज्या के वृत्त की 8 सें०मी० लम्बी एक जीवा PQ है । P और Q पर स्पर्श रेखाएँ परस्पर एक बिन्दु T पर प्रतिच्छेद करती हैं । TP की लम्बाई ज्ञात कीजिए, यदि वृत्त का केन्द्र O है ।
हल :

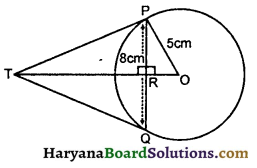
माना संलग्न आकृति में, TP = x व TR =y
समकोण ΔPRO में,

प्रश्न 13.
एक बिंदु से वृत्त पर खींची गई स्पर्श रेखा की लंबाई ज्ञात कीजिए जहाँ पर बिंदु की केंद्र से 25 cm की दूरी है । वृत्त की त्रिज्या 7 cm दी हुई है।
हल :

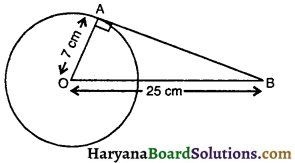
यहाँ पर वृत्त की त्रिज्या (OA) = 7 cm
वृत्त के केंद्र से बिंदु की दूरी (OB) = 25 cm
स्पर्श रेखा (AB) की लंबाई = ?
∠OAB = 90°
[∵ वृत्त के किसी बिंदु पर स्पर्श रेखा स्पर्श बिंदु से होकर जाने वाली त्रिज्या पर लंब होती है ]
अब समकोण ΔOAB में पाइथागोरस प्रमेय से,
AB = \(\sqrt{(\mathrm{OB})^2-(\mathrm{OA})^2}=\sqrt{(25)^2-(7)^2}\) cm
= \(\sqrt{625-49}\) = \(\sqrt{576}\) = 24 cm
अतः स्पर्श रेखा की लंबाई = 24 cm

बहुविकल्पीय प्रश्न :

प्रश्न 1.
वृत्त के किन्हीं दो बिंदुओं को मिलाने वाले रेखाखंड को कहा जाता है-
(A) वृत्त की त्रिज्या
(B) वृत्त की जीवा
(C) वृत्त की चाप
(D) वृत्त का केंद्र
हल :
(B) वृत्त की जीवा

प्रश्न 2.
वृत्त का व्यास उसकी त्रिज्या से ……………. होता है
(A) दो गुना
(B) तीन गुना
(C) आधा
(D) एक तिहाई
हल :
(A) दो गुना

प्रश्न 3.
वृत्त की सबसे बड़ी जीवा होती है-
(A) त्रिज्या
(B) दीर्घ चाप
(C) लघु चाप
(D) व्यास
हल :
(D) व्यास

प्रश्न 4.
किसी वृत्त की कितनी अधिकतम स्पर्श रेखाएँ हो सकती हैं?
(A) केवल एक
(B) दो
(C) अपरिमित
(D) कोई स्पर्श रेखा नहीं
हल :
(C) अपरिमित

प्रश्न 5.
एक चाप …………… होता है जब इसके सिरे एक व्यास के सिरे हों ।
(A) अर्धव्यास
(B) अर्धवृत्त
(C) लघु वृत्तखंड
(D) दीर्घ वृत्तखंड
हल :
(B) अर्धवृत्त

प्रश्न 6.
दो वृत्त सर्वांगसम होते हैं यदि उनकी ……………. बराबर हैं ।
(A) त्रिज्याएँ
(B) जीवाएँ
(C) चाप
(D) लंब रेखाएँ
हल :
(A) त्रिज्याएँ

प्रश्न 7.
सर्वांगसम वृत्तों की बराबर …………… उनके केंद्रों पर बराबर कोण अंतरित करती हैं।
(A) त्रिज्याएँ
(B) जीवाएँ
(C) अर्धव्यास
(D) लंब रेखाएँ

(B) जीवाएँ

प्रश्न 8.
आकृति में, रेखा PQ को निम्नलिखित में से किस नाम से पुकारते हैं?

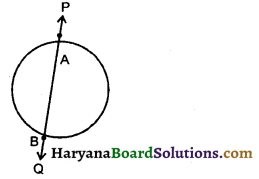
(A) छेदक रेखा
(B) प्रतिच्छेदी रेखा
(C) स्पर्श रेखा
(D) व्यास
हल :
(A) छेदक रेखा

प्रश्न 9.
यदि एक बिंदु P से O केन्द्र वाले किसी वृत्त पर PA, PB स्पर्श रेखाएँ परस्पर 60° के कोण पर झुकी हों, तो ∠POA बराबर है-
(A) 100°
(B) 90°
(C) 80°
(D) 60°
हल :
(D) 60°

प्रश्न 10.
एक वृत्त के केंद्र से एक जीवा को समद्विभाजित करने के लिए खींची गई रेखा जीवा पर ………….. कोण बनाती है।
(A) 180°
(B) 60°
(C) 120°
(D) 90°
हल :
(D) 90°

प्रश्न 11.
केन्द्र 0 वाले वृत्त पर दो स्पर्श रेखाएँ PQ और PR हैं। यदि ∠QPR = 46°, तो ∠QOR हैं :
(A) 160°
(B) 150°
(C) 135°
(D) 134°
हल :
(D) 134°

प्रश्न 12.
निम्नलिखित में से कौन-सा कथन सत्य है ?
(A) वृत्त की बराबर जीवाएँ केंद्र पर बराबर कोण अंतरित करती हैं
(B) वृत्त के केंद्र से किसी जीवा पर खींचा गया लंब जीवा को समद्विभाजित करता है
(C) तीन असरेख बिंदुओं से होकर एक और केवल ही एक वृत्ताता है
(D) उपरोक्त सभी
हल :
(D) उपरोक्त सभी

प्रश्न 13.
संलग्न आकृति में एक रेखा l दो संकेंद्रीय वृत्तों को जिनका केंद्र O है, A, B, C और D पर प्रतिच्छेदित करती है तो, निम्नलिखित में से कौन-सा कथन सत्य है ?

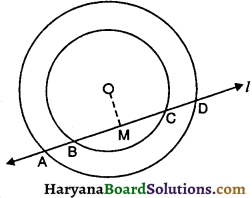
(A) AB = BC
(B) AB = BD
(C) AB = CD
(D) AB = MD
हल :
(C) AB = CD

प्रश्न 14.
वृत्त की किसी चाप द्वारा केंद्र पर अंतरित कोण उस चाप द्वारा वृत्त के शेष भाग पर स्थित किसी बिंदु पर अंतरित कोण का ………….. होता है ।
(A) तीन गुना
(B) दो गुना
(C) आधा
(D) एक-तिहाई
हल :
(B) दो गुना

प्रश्न 15.
संलग्न आकृति में, यदि 0 वृत्त का केंद्र हो तो निम्नलिखित में से कौन-सा संबंध सही है ?

(A) ∠AOB = ∠ACB
(B) ∠AOB = \(\frac {1}{2}\)∠ACB
(C) ∠AOB = 2∠ACB
(D) ∠AOB = \(\frac {1}{3}\)∠ACB
हल :
(C) ∠AOB = 2∠ACB

प्रश्न 16.
अर्धवृत्त में बना कोण ……………. होता है ।
(A) दो समकोण
(B) अर्ध-समकोण
(C) पूर्ण-कोण
(D) समकोण
हल :
(D) समकोण

प्रश्न 17.
आकृति में, 5 सेमी त्रिज्या वाले एक वृत्त के बिन्दु P पर स्पर्श रेखा PQ केन्द्र O से जाने वाली एक रेखा से बिन्दु Q पर इस प्रकार मिलती है कि OQ = 13 सेमी है, PQ की लम्बाई है:

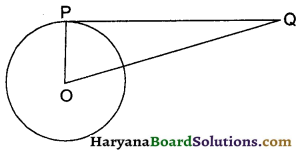
(A) 12 सेंमी०
(B) 9 सेंमी ०
(C) \(\sqrt{194}\) सेंमी०
(D) इनमें से कोई नहीं
हल :
(A) 12 सेंमी०

प्रश्न 18.
चक्रीय चतुर्भुज के सम्मुख कोणों के किसी युग्म का योग ……………… होता है।
(A) 180°
(B) 90°
(C) 360°
(D) 120°
हल :
(A) 180°

प्रश्न 19.
संलग्न आकृति में, यदि O वृत्त का केंद्र हो तो ∠x का मान होगा-

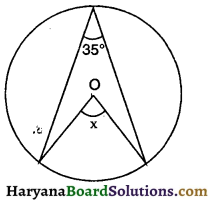
(A) 17\(\frac {1}{2}\)°
(B) 35°
(C) 70°
(D) 52\(\frac {1}{2}\)°
हल :
(C) 70°

प्रश्न 20.
आकृति में, O केन्द्र वाले वृत्त पर TP तथा TQ दो स्पर्श रेखाएँ इस प्रकार हैं कि ∠POQ = 115° है, तो ∠PTQ का मान है :

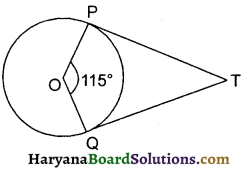
(A) 80°
(B) 85°
(C) 75°
(D) 65°
हल :
(D) 65°

प्रश्न 21.
संलग्न आकृति में, यदि O वृत्त का केंद्र हो तो ∠x का मान होगा-

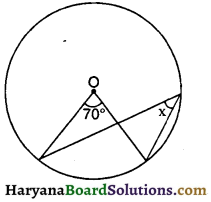
(A) 140°
(B) 70°
(C) 35°
(D) 105°
हल :
(C) 35°

प्रश्न 22.
एक बाह्य बिन्दु T से TP तथा TQ, केन्द्र O वाले किसी वृत्त पर दो स्पर्श रेखाएँ इस प्रकार हैं कि ∠OPQ = 70° है, तो ∠PTQ का मान है :

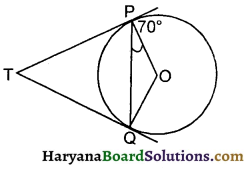
(A) 140°
(B) 35°
(C) 110°
(D) 90°
हल :
(C) 110°

प्रश्न 23.
संलग्न आकृति में A, B, C एक वृत्त पर तीन बिंदु हैं। यदि ∠AOB = 70° तथा ∠AOC = 130°, तो ∠BAC का मान होगा-

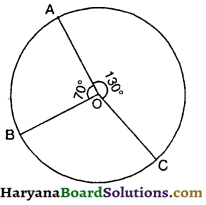
(A) 80°
(B) 120°
(C) 160°
(D) 130°
हल :
(C) 160°

प्रश्न 24.
वह रेखा जो वृत्त को केवल एक बिंदु पर स्पर्श करती है उसे वृत्त की कहा जाता है-
(A) छेदक रेखा
(B) लंब रेखा
(C) स्पर्श रेखा
(D) अस्पर्श रेखा
हल :
(C) स्पर्श रेखा

प्रश्न 25.
वह रेखा जो वृत्त को दो भिन्न-भिन्न बिंदुओं पर प्रतिच्छेदित करती है उसे कहा जाता है-
(A) छेदक रेखा
(B) लंब रेखा
(C) स्पर्श रेखा
(D) प्रमुख रेखा
हल :
(A) छेदक रेखा

प्रश्न 26.
वृत्त की स्पर्श रेखा स्पर्श बिंदु से होकर जाने वाली ……………. पर लंब होती है ।
(A) चाप
(B) त्रिज्या
(C) जीवा
(D) त्रिज्याखंड
हल :
(B) त्रिज्या

प्रश्न 27.
वृत्त के बाहर स्थित बिंदु से वृत्त पर …………………. स्पर्श रेखाएँ खींची जा सकती हैं।
(A) केवल एक
(B) केवल दो
(C) केवल तीन
(D) कोई नहीं
हल :
(B) केवल दो

प्रश्न 28.
वृत्त के ऊपर स्थित बिंदु से वृत्त पर ………………….. स्पर्श रेखाएँ खींची जा सकती हैं।
(A) केवल एक
(B) केवल दो
(C) केवल तीन
(D) कोई नहीं
हल :
(A) केवल एक

प्रश्न 29.
वृत्त के व्यास के छोर पर खींची गई स्पर्श रेखाएँ ……………. होती हैं ।
(A) लंबवत्
(B) छेदक
(C) समांतर
(D) असमांतर
हल :
(C) समांतर

प्रश्न 30.
वृत्त के अभ्यंतर में स्थित बिंदु से वृत्त पर …………… स्पर्श रेखाएँ खींची जा सकती हैं।
(A) शून्य
(B) केवल एक
(C) दो
(D) तीन
हल :
(A) शून्य

प्रश्न 31.
वृत्त का केंद्र दो स्पर्श रेखाओं के बीच के कोण के ……………….. पर स्थित होता है ।
(A) समत्रिभाजक
(B) समद्विभाजक
(C) समचतुर्भाजक
(D) असमद्विभाजक
हल :
(B) समद्विभाजक

प्रश्न 32.
किसी बाह्य बिंदु से किसी वृत्त पर खींची गई स्पर्श रेखाओं की …………….. बराबर होती हैं-
(A) चौड़ाइयाँ
(B) ऊँचाइयाँ
(C) लंबाइयाँ
(D) (A) व (B) दोनों
हल :
(C) लंबाइयाँ

प्रश्न 33.
संलग्न आकृति में, AB और CD वृत्त की दो जीवाएँ बिंदु P पर प्रतिच्छेद करती हैं । निम्नलिखित में से कौन-सा तथ्य सही होगा ?

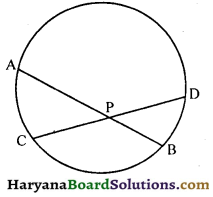
(A) PC.AC = PD.DB
(B) AC.DB = PA.PB
(C) PA.PC = PD.PB
(D) PA.PB = PC.PD
हल :
(D) PA.PB = PC.PD

प्रश्न 34.
संलग्न आकृति में, यदि PAB किसी वृत्त की एक छेदक रेखा हो जो इसे A तथा B पर प्रतिच्छेद करती है तथा PT एक स्पर्श रेखा हो तो PA.PB बराबर होगी-

(A) PA²
(B) PO²
(C) PB²
(D) PT²
हल :
(D) PT²

प्रश्न 35.
एक वृत्त एक चतुर्भुज ABCD की सभी भुजाओं को स्पर्श करता हो तो वृत्त के केंद्र पर सम्मुख भुजाओं द्वारा अंतरित कोण होंगे-
(A) संपूरक
(B) पूरक
(C) शून्य
(D) पूर्ण
हल :
(A) संपूरक

प्रश्न 36.
यदि वृत्त के बाहर किसी बिन्दु P से वृत्त के ऊपर खींची गई स्पर्श रेखा की लम्बाई 15 cm हो और वृत्त की त्रिज्या 8 cm हो, तो बिन्दु P की वृत्त के केन्द्र से दूरी है :
(A) 7 cm
(B) 23 cm
(C) 17 cm
(D) 7.5 cm
हल :
(C) 17 cm

प्रश्न 37.
यदि एक बिंदु P से O केंद्र वाले किसी वृत्त पर PA, PB स्पर्श रेखाएँ परस्पर 80° के कोण पर झुकी हों, तो ∠POB बराबर है :
(A) 100°
(B) 80°
(C) 70°
(D) 50°
हल :
(D) 50°

प्रश्न 38.
वृत्त के किसी बिंदु पर स्पर्श रेखा स्पर्श बिंदु से जाने वाली त्रिज्या के बीच का कोण होगा-
(A) 45°
(B) 90°
(C) 180°
(D) 60°
हल :
(B) 90°

प्रश्न 39.
एक बिंदु A वृत्त के केंद्र से 5 cm दूर स्थित है। A से वृत्त पर खींची गई स्पर्श रेखा की लंबाई 4 cm है । वृत्त की त्रिज्या होगी-
(A) 3 cm
(B) 4 cm
(C) 5 cm
(D) 8 cm
हल :
(A) 3 cm

प्रश्न 40.
दो वृत्त एक बिंदु P पर बाह्यतः स्पर्श करते हैं । P पर खींची गई स्पर्श रेखा के एक बिंदु T से वृत्तों पर स्पर्श रेखाएँ TQ तथा TR खींची जाती हैं, जहाँ Q, R क्रमशः स्पर्श बिंदु हैं, तो निम्नलिखित में से कौन-सा कथन सत्य होगा ?
(A) TQ = TR
(B) TQ = 2 TR
(C) TR = 2 TQ
(D) TQ = \(\frac {1}{2}\)TR
हल :
(A) TQ = TR

प्रश्न 41.
यदि किसी बिन्दु P की वृत्त के केन्द्र से दूरी 13 cm है और वृत्त की त्रिज्या 5cm है, तो P से वृत्त पर खींची गई स्पर्श रेखा की लम्बाई है :
(A) 8 cm
(B) 6.5 cm
(C) 9 cm
(D) 12 cm
हल :
(D) 12 cm

प्रश्न 42.
एक वृत्त पर समांतर स्पर्श रेखाओं की अधिकतम संख्या है :
(A) 1
(B) 2
(C) 3
(D) 4
हल :
(B) 2

प्रश्न 43.
संलग्न आकृति में, यदि TP, TQ केन्द्र O वाले किसी वृत्त पर दो स्पर्श रेखाएँ इस प्रकार हैं कि ∠POQ = 110° है तो ∠PTQ बराबर है-

(A) 90°
(B) 80°
(C) 70°
(D) 60°
हल :
(C) 70°