Haryana State Board HBSE 10th Class Maths Important Questions Chapter 9 त्रिकोणमिति का अनुप्रयोग Important Questions and Answers.
Haryana Board 10th Class Maths Important Questions Chapter 9 त्रिकोणमिति का अनुप्रयोग
परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न :
प्रश्न 1.
1.5 m लम्बा एक आदमी एक चिमनी से 28.5m की दूरी पर है। उसकी आँखों से चिमनी के शिखर का उन्नयन कोण 45° है । चिमनी की ऊँचाई बताइए ।
हल :
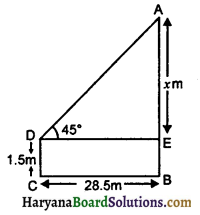
माना AB एक चिमनी है तथा CD एक आदमी है जिसकी ऊँचाई 1.5 m है जो चिमनी से 28.5m की दूरी पर खड़ा है । इस प्रकार उन्नयन ∠ADE = 45° है ।
अब समकोण त्रिभुज ADE में, \(\frac {AE}{DE}\) = tan 45°
⇒ \(\frac {AE}{CB}\) = 1
⇒ AE = 28.5 × 1
= 28.5 m
अतः चिमनी की ऊँचाई (AB) = AE + BE
= AE + CD
= (28.5 + 1.5) m
= 30m
![]()
प्रश्न 2.
मीनार के आधार से 40m की दूरी पर भूमि पर एक बिंदु से मीनार की चोटी का उन्नयन कोण 30° है और मीनार की चोटी पर रखी पानी की टंकी के ऊपरी सिरे का उन्नयन कोण 45° है। ज्ञात कीजिए-
(i) मीनार की ऊँचाई ।
(ii) टंकी की गहराई ।
हल :
मान लो, AB (= h) मीनार की ऊँचाई, BC पानी की टंकी की गहराई है, पानी की टंकी से उन्नयन कोण 30° वनता है और टंकी के ऊपरी सिरे से 45° का कोण बनता है ।
समकोण ΔAOB में,
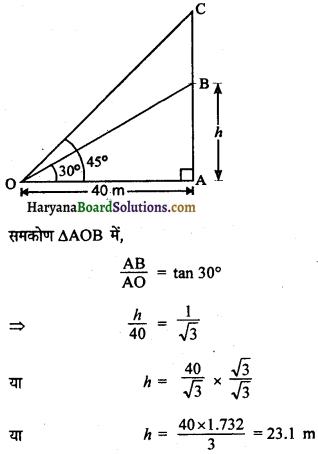
समकोण ΔCAO में,
\(\frac {CA}{AO}\) = tan 45°
या \(\frac {CA}{40}\) = 1
या AC = 40 m
∴ BC = AC – AB
= 40 – 23.1
= 16.9 m
∴ मीनार की ऊँचाई = 23.1 m
पानी की टंकी की गहराई =16.9m
प्रश्न 3.
100 m ऊँचे एक प्रकाश स्तंभ की चोटी से एक प्रेक्षक समुद्र में एक जहाज को ठीक अपनी ओर आते हुए देखता है । यदि जहाज का अवनमन कोण 30° से बदलकर 45° हो जाता है, तो प्रेक्षण की इस अवधि में जहाज द्वारा तय की गई दूरी ज्ञात कीजिए ।
हल :
मान लीजिए, A और B जहाज की दो स्थितियाँ हैं। मान लीजिए प्रेक्षण की अवधि में जहाज द्वारा तय की गई दूरी d m है, अर्थात् AB = d m है।
मान लीजिए, प्रेक्षक बिंदु O पर है ( आकृति में) स्पष्टतः OC = 100 m है।
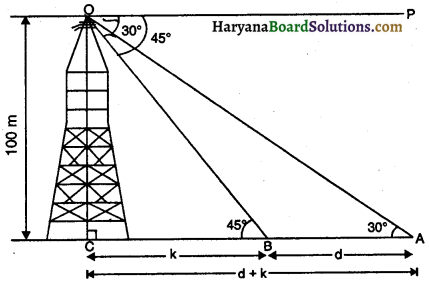
माना B से C की दूरी km है। बिंदु O से A और B के अवनमन कोण क्रमशः 30° और 45° ज्ञात हैं
अतः ∠AOP = 30°, ∠BOP = 45°
⇒ ∠AOP = ∠OAC = 30°
तथा ∠POB = ∠OBC = 45°
समकोण ΔOCB में,
\(\frac {k}{100}\) = cot 45° = 1
या k = 100
समकोण ΔOCA में,
\(\frac{d+k}{100}\) = cot 30° = \(\sqrt{3}\)
∴ d + k = 100\(\sqrt{3}\)
या d + 100 = 100\(\sqrt{3}\)
या d = 100\(\sqrt{3}\) – 100 = 100(\(\sqrt{3}\) – 1) = 100(1.732 – 1)
= 100 × 0.732 = 73.2 m
अतः जहाज द्वारा A से B तक तय की गई दूरी 73.2m है ।
![]()
प्रश्न 4.
भूमि के बिन्दु P से एक 10 मी ऊँचे भवन के शिखर का उन्नयन कोण 30° है। भवन के शिखर का उन्नयन कोण 45° है। ध्वज की लम्बाई और बिन्दु P से भवन की दूरी ज्ञात कीजिए ।
हल :
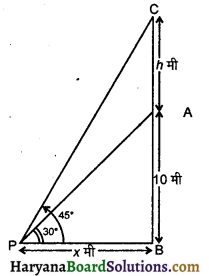
यहाँ पर,
AB एक 10 मी ऊँचा भवन है जिसके शिखर A पर AC ध्वज लगा है ।
अब भवन की ऊँचाई (AB) = 10 मी
माना ध्वज की लंबाई (AC) = h मी
तथा बिन्दु P से B की दूरी = x मी
समकोण ΔABP में,
\(\frac {AB}{PB}\) = tan 30°
⇒ \(\frac{10}{x}=\frac{1}{\sqrt{3}}\) मी
या x = 10\(\sqrt{3}\)
समकोण ΔCBP में,
\(\frac {BC}{PB}\) = tan45°
⇒ \(\frac{h+10}{x}\) = 1
या x = h + 10
10\(\sqrt{3}\) = h + 10 (समीकरण (i) से)
h = 10\(\sqrt{3}\) – 10
h = 10(\(\sqrt{3}\) – 1) मी
अतः ध्वज की लंबाई = 10(\(\sqrt{3}\) – 1) मी
बिन्दु P से भवन की दूरी = 10\(\sqrt{3}\) मी
प्रश्न 5.
एक समतल जमीन पर खड़ी मीनार की छाया उस स्थिति में 40 मी अधिक लम्बी हो जाती है जबकि सूर्य का उन्नयन कोण 60° से घटकर 30° हो जाता है। मीनार की ऊँचाई ज्ञात कीजिए ।
हल :
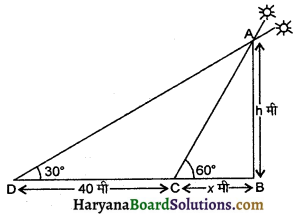
माना AB = h मी मीनार की ऊँचाई है। जब सूर्य का उन्नयन कोण 30° है तो मीनार की छाया DB है और जब सूर्य का उन्नयन कोण 60° है तो मीनार की छाया CB है ।
अतः DC = 40 मी

प्रश्न 6.
आँधी चलने से दो भागों में टूटे हुए एक वृक्ष का ऊपरी भाग भूमि से 30° का कोण बनाता है। वृक्ष का ऊपरी सिरा जिस स्थान पर भूमि को छूता है वह स्थान वृक्ष के आधार – बिंदु से 10m की दूरी पर है | वृक्ष ऊँचाई ज्ञात कीजिए ।
हल :
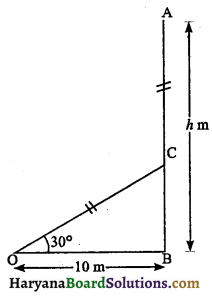
मान लीजिए AB = h m वृक्ष की ऊँचाई है । AC टूटे हुए वृक्ष का एक भाग है।
तब ∠COB = 30° तथा OB = 10m
समकोण ΔCOB में,
tan 30° = \(\frac {CB}{OB}\)
या \(\frac{1}{\sqrt{3}}\) = \(\frac {CB}{10}\)
या \(\sqrt{3}\)CB = 10
या CB = \(\frac{10}{\sqrt{3}}\) ………………(i)
इसी प्रकार, समकोण ΔCOB में,

![]()
प्रश्न 7.
एक सड़क, 50m ऊँची मीनार के आधार तक, सीधी जाती है। मीनार की चोटी से सड़क पर खड़ी दो कारों के अवनमन कोण क्रमश: 30° और 60° हैं। दोनों कारों के बीच की दूरी ज्ञात कीजिए और बताइए कि प्रत्येक कार मीनार के आधार से कितनी दूरी पर है ?
हल :
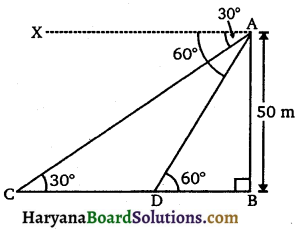
मान लीजिए, AB (= 50m) मीनार की ऊँचाई है तथा C और D सड़क पर खड़ी दो कारों की स्थिति है ।
∠CAX = 30° तथा ∠DAX = 60°
⇒ ∠CAX = ∠CAB = 30°
तथा ∠DAX = ∠ADB = 60°
समकोण ΔACB में,


अब, CB = CD + DB
= 57.74 + 28.87 = 86.61 m
अतः दोनों कारों के बीच की दूरी = 57.74m
पहली कार की मीनार के आधार से दूरी = 86.61 m
दूसरी कार की मीनार के आधार से दूरी = 28.87 m
![]()
प्रश्न 8.
एक बिजली मिस्त्री को एक 5 m ऊँचे खंभे पर आ गई खराबी की मरम्मत करनी है। मरम्मत का काम करने के लिए उसे खंभे के शिखर से 1.3m नीचे एक बिन्दु तक पहुँचने के लिए प्रयुक्त सीढ़ी की लम्बाई कितनी होनी चाहिए जिससे कि क्षैतिज से 60° के कोण पर झुकने से वह अपेक्षित स्थिति तक पहुँच जाये और यह भी बताइए कि खंभे का पाद-बिन्दु कितनी दूरी पर सीढ़ी के पाद-बिन्दु से होना चाहिए ? (\(\sqrt{3}\) = 1.73)
हल :
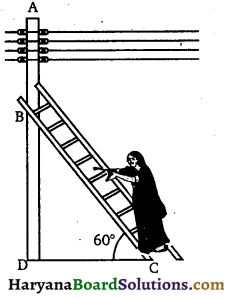
आकृति अनुसार बिजली मिस्त्री को खम्भे AD पर बिन्दु B तक पहुँचना है।
अतः BD = AD – AB
= (5 – 1.3) m = 3.7 m
यहाँ पर BC सीढ़ी को प्रकट करता है । हमें इसकी लम्बाई अर्थात् समकोण ΔBDC का कर्ण ज्ञात करना है।
अब समकोण ΔBDC में

अतः उसे सीढ़ी के पाद को खम्भे से 2.14 m की दूरी पर रखना चाहिए ।
प्रश्न 9.
नदी के पुल पर एक बिंदु से, नदी के सम्मुख किनारों पर अवनमन कोण क्रमशः 30° व 45° हैं । यदि पुल की ऊँचाई किनारों से 3m हो, तो नदी की चौड़ाई ज्ञात कीजिए ।
हल :
आकृति में, A और B नदी के सम्मुख किनारों के बिंदुओं को प्रकट करते हैं, जिससे कि AB नदी की चौड़ाई है। 3 m की ऊँचाई पर बने पुल पर एक बिंदु P है अर्थात् DP = 3m है। हम नदी की चौड़ाई ज्ञात करना चाहते हैं जो कि ΔAPB की भुजा AB की लंबाई है।
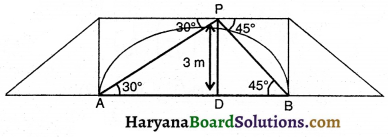
अब AB = AD + DB
समकोण ΔAPD में ∠A = 30°
∴ tan 30° = \(\frac {PD}{AD}\)
या \(\frac{1}{\sqrt{3}}\) = \(\frac {3}{AD}\)
या AD = 3\(\sqrt{3}\) m
अब समकोण ΔPBD में ∠B = 45° है ।
tan 45° = \(\frac {PD}{DB}\)
या 1 = \(\frac {3}{DB}\)
या DB = 3m
अतः AB = AD + BD = (3\(\sqrt{3}\) + 3) m = 3 (\(\sqrt{3}\) + 1) m
इस प्रकार, नदी की चौड़ाई = 3 (\(\sqrt{3}\) + 1) m
![]()
प्रश्न 10.
दो मीनारों के बीच की क्षैतिज दूरी 140 m है। दूसरी मीनार की चोटी से पहली मीनार की चोटी का उन्नयन कोण 30° है। यदि दूसरी मीनार की ऊँचाई 60m है, तो पहली मीनार की ऊँचाई ज्ञात कीजिए ।
हल :
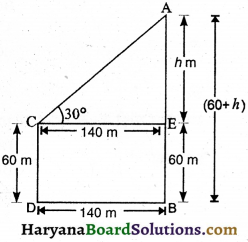
माना AB और CD दो मीनारें हैं ।
दूसरी मीनार की ऊँचाई (CD) = 60 m
और दोनों मीनारों के बीच की दूरी,
DB = 140 m
माना AE = h m
अब CE = DB = 140 m
EB = CD = 60 m
तो पहली मीनार की ऊँचाई (AB) = (60 + h) m
समकोण ΔAEC में,

अतः पहली मीनार की ऊँचाई = 60 + h
= 60 + 80.83 = 140.83 m
प्रश्न 11.
धरती पर एक मीनार ऊर्ध्वाधर खड़ी हैं। धरती के एक बिन्दु से, जो मीनार के पाद-बिन्दु से 15m दूर है, मीनार के शिखर का उन्नयन कोण 60° है। मीनार की ऊँचाई ज्ञात कीजिए ।
हल :
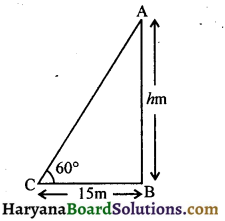
माना मीनार AB का शिखर A तथा पाद- बिन्दु B है जिसकी ऊँचाई hm है। बिन्दु C मीनार के पाद-बिन्दु B से 15 m की दूरी पर है।
प्रश्नानुसार
AB = hm
BC = 15m
∠ACB = 60°
समकोण ΔABC में
\(\frac {AB }{BC}\) = tan 60°
⇒ \(\frac {h}{15}\) = \(\sqrt{3}\)
⇒ h = 15\(\sqrt{3}\)m
अतः मीनार की ऊँचाई (AB) = \(\sqrt{3}\)m.
![]()
प्रश्न 12.
एक हवाई जहाज से जो कि 200m की ऊँचाई पर है, एक नदी के दोनों तटों पर आमने-सामने के दो बिंदुओं के अवनमन कोण क्रमशः 45° तथा 60° हैं। नदी की चौड़ाई ज्ञात कीजिए ।
हल :
माना हवाई जहाज बिंदु P पर स्थित है जिसकी भूमि के स्थित बिंदु M से ऊँचाई 200m है।
माना बिंदु A और B नदी के किनारों पर विपरीत दिशाओं में स्थित दो बिंदु हैं जिनके अवनमन कोण 60° व 45° हैं।
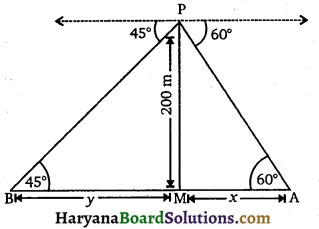
माना AM = x m
तथा BM = y m

बहुविकल्पीय प्रश्न :
प्रश्न 1.
sin θ° का मान होता है-
(A) शून्य
(B) \(\frac {1}{2}\)
(C) \(\frac{1}{\sqrt{2}}\)
(D) \(\frac{\sqrt{3}}{2}\)
हल :
(A) शून्य
![]()
प्रश्न 2.
sin 45° का मान होता है-
(A) शून्य
(B) \(\frac {1}{2}\)
(C) \(\frac{1}{\sqrt{2}}\)
(D) \(\frac{\sqrt{3}}{2}\)
हल :
(C) \(\frac{1}{\sqrt{2}}\)
प्रश्न 3.
sin 90° का मान होता है-
(A) शून्य
(B) \(\frac {1}{2}\)
(C) \(\frac{\sqrt{3}}{2}\)
(D) 1
हल :
(D) 1
प्रश्न 4.
θ के किस मान के लिए cosθ = \(\frac {1}{2}\) होगा ?
(A) 30°
(B) 45°
(C) 60°
(D) 90°
हल :
(C) 60°
प्रश्न 5.
θ के किस मान के लिए tan θ और cot θ का मान बराबर होगा-
(A) 30°
(C) 60°
(B) 45°
(D) 90°
हल :
(B) 45°
![]()
प्रश्न 6.
ΔABC में, ∠B समकोण है, AB = 12 cm और ∠A = 30° है आकृति अनुसार BC का मान होगा-
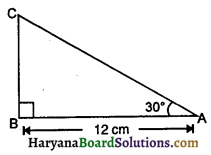
(A) 4\(\sqrt{3}\)cm
(B) 8\(\sqrt{m}\) cm
(C) 2\(\sqrt{m}\) cm
(D) \(\sqrt{m}\) cm
हल :
(A) 4\(\sqrt{3}\) cm
प्रश्न 7.
प्रश्न 6 की त्रिभुज में AC का मान होगा-
(A) 4\(\sqrt{3}\) cm
(B) 2\(\sqrt{3}\) cm
(C) 8\(\sqrt{3}\) cm
(D) 3\(\sqrt{3}\) cm
हल :
(C) 8\(\sqrt{3}\) cm
प्रश्न 8.
समकोण ΔABC में ∠C = 90°, ∠A = 30° तथा AB = 10 cm हो तो BC का मान होगा-
(A) 10 cm
(B) 5\(\sqrt{3}\) cm
(C) 5\(\sqrt{2}\) cm
(D) 5 cm
हल :
(D) 5 cm
प्रश्न 9.
समकोण ΔABC में ∠C = 90°, ∠A = 30° तथा AB = 10 cm हो तो AC का मान होगा-
(A) 10 cm
(B) 5\(\sqrt{3}\) cm
(C) 5\(\sqrt{2}\) cm
(D) 5 cm
हल :
(B) 5\(\sqrt{3}\) cm
![]()
प्रश्न 10.
एक मीनार भूमि पर ऊर्ध्वाधर खड़ी है। भूमि पर मीनार के आधार से 20m दूरी पर स्थित एक बिंदु से उसकी चोटी का उन्नयन कोण 60° है। मीनार की ऊँचाई होगी-
(A) 20\(\sqrt{3}\) m
(B) 20\(\sqrt{2}\) m
(C) \(\frac{20 \sqrt{3}}{3}\)
(D) \(\frac{20 \sqrt{2}}{2}\)
हल :
(A) 20\(\sqrt{3}\) m
प्रश्न 11.
एक सीढ़ी एक दीवार पर इस प्रकार टिकी है कि उसका ऊपरी सिरा दीवार के शिखर को छूता है। सीढ़ी का निचला सिरा दीवार से 2m की दूरी पर है। सीढ़ी भूमि के साथ 60° का कोण बनाती है। दीवार की ऊँचाई होगी-
(A) \(\frac{2 \sqrt{3}}{3}\)
(B) 2\(\sqrt{2}\) m
(C) 2\(\sqrt{3}\) m
(D) \(\sqrt{2}\) m
हल :
(C) 2\(\sqrt{3}\) m
प्रश्न 12.
भूमि पर स्थिर एक ऊर्ध्वाधर बाँस के ऊपरी सिरे से एक तनी हुई रस्सी बांधी गई है और रस्सी का दूसरा सिरा भूमि पर स्थिर किया गया है । सर्कस का एक कलाकार भूमि से रस्सी पर चढ़ रहा है। बांस की ऊँचाई 12 m है और रस्सी भूमि से 30° का कोण बनाती है । कलाकार द्वारा बाँस के ऊपरी सिरे पर पहुँचने में तय की गई दूरी होगी-
(A) 6m
(B) 12m
(C) 18m
(D) 24 m
हल :
(D) 24 m
![]()
प्रश्न 13.
संलग्न आकृति में x का मान होगा-
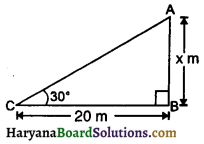
(A) \(\frac{20 \sqrt{3}}{3}\) m
(B) 20\(\sqrt{3}\) m
(C) \(\frac{10 \sqrt{3}}{3}\) m
(D) 10\(\sqrt{3}\) m
हल :
(A) \(\frac{20 \sqrt{3}}{3}\) m
प्रश्न 14.
संलग्न त्रिभुज में x का मान होगा-
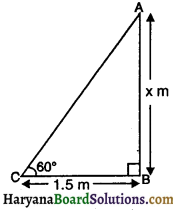
(A) \(\frac{1.5 \sqrt{3}}{3}\) m
(B) 1.5\(\sqrt{3}\) m
(C) 3\(\sqrt{3}\) m
(D) \(\frac{1.5 \sqrt{3}}{3}\) m
हल :
(B) 1.5\(\sqrt{3}\) m
प्रश्न 15.
संलग्न त्रिभुज ABC में AC का मान होगा-
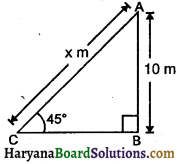
(A) \(\frac{10 \sqrt{2}}{3}\) m
(B) \(\frac{10 \sqrt{3}}{3}\) m
(C) 10\(\sqrt{2}\) m
(D) 5\(\sqrt{2}\) m
हल :
(C) 10\(\sqrt{2}\) m
![]()
प्रश्न 16.
संलग्न त्रिभुज AOB में h का मान होगा-
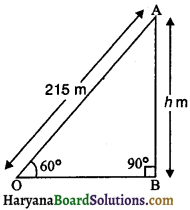
(A) \(\frac{215 \sqrt{2}}{2}\) m
(B) \(\frac{215 \sqrt{2}}{3}\) m
(C) \(\frac{215 \sqrt{3}}{3}\) m
(D) \(\frac{215 \sqrt{3}}{2}\) m
हल :
(D) \(\frac{215 \sqrt{3}}{2}\) m
प्रश्न 17.
सूर्य का उन्नयन कोण क्या होगा जब किसी ऊर्ध्वाधर खंभे की छाया की लंबाई खंभे की ऊँचाई के बराबर हो —
(A) 45°
(B) 30°
(C) 60°
(D) 90°
हल :
(A) 45°
प्रश्न 18.
किसी मीनार के आधार से a और b की दूरियों पर एक ही रेखा में स्थित दो बिंदुओं क्रमशः P और Q से देखने पर, मीनार के ऊपरी सिरे के उन्नयन कोण पूरक पाए जाते हैं। मीनार की ऊँचाई होगी-
(A) ab
(B) \(\sqrt{ab}\)
(C) \(\frac {a}{b}\)
(D) \(\sqrt{\frac{a}{b}}\)
हल :
(B) \(\sqrt{ab}\)
![]()
प्रश्न 19.
एक छड़ तथा उसकी छाया के बीच 1 : \(\sqrt{3}\) का अनुपात है, सूर्य का उन्नयन कोण होगा-
(A) 30°
(B) 45°
(C) 60°
(D) 90°
हल :
(A) 30°
प्रश्न 20.
संलग्न त्रिभुज ABC में AB की लंबाई होगी-
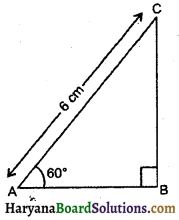
(A) 6 cm
(B) 6\(\sqrt{3}\) cm
(C) 3 cm
(D) 3\(\sqrt{3}\) cm
हल :
(C) 3 cm
प्रश्न 21.
एक मीनार 100\(\sqrt{3}\)m ऊँची है। इसके आधार से 100m दूर स्थित किसी बिंदु से इसके शिखर का उन्नयन कोण होगा-
(A) 30°
(B) 45°
(C) 60°
(D) 90°
हल :
(C) 60°
![]()
प्रश्न 22.
एक पतंग की डोर 100 m लंबी है तथा यह आसमान में उड़ते समय क्षैतिज तल से 60° का कोण बनाती है। यह मानते हुए कि पतंग की डोर बिल्कुल सीधी तनी हुई है। पतंग की क्षैतिज से ऊँचाई होगी-
(A) 50\(\sqrt{3}\) m
(B) 100\(\sqrt{3}\) m
(C) \(\frac{100 \sqrt{3}}{3}\) m
(D) \(\frac{50 \sqrt{3}}{3}\) m
हल :
(A) 50\(\sqrt{3}\) m
प्रश्न 23.
एक दीवार के सहारे खड़ी एक सीढ़ी का उन्नयन कोण दीवार से 9.5m दूर जमीन पर स्थित एक बिंदु से 60° है। सीढ़ी की लंबाई होगी-
(A) 9.5m
(B) 19m
(C) 9.5\(\sqrt{3}\) m
(D) 9.5\(\sqrt{2}\) m
हल :
(B) 19m
प्रश्न 24.
बिजली का एक खंभा 10m ऊँचा है। खंभे को सीधा लंबवत् रखने के लिए स्टील के तार का एक सिरा खंभे की चोटी से बँधा है और दूसरा, भूमि पर स्थिर किया गया है । यदि स्टील का तार खंभे के आधार बिंदु से होकर जाने वाले क्षैतिज के साथ 45° का कोण बनाए, तो बिजली के खंभे के आधार से कितनी दूरी पर भूमि पर स्थिर बिंदु है?
(A) 10\(\sqrt{3}\) m
(B) 20\(\sqrt{3}\) m
(C) 10m
(D) 20m
हल :
(C) 10m
प्रश्न 25.
एक मीनार जमीन पर सीधी खड़ी है। मीनार के आधार से 50m की दूरी पर जमीन पर स्थित एक बिंदु से मीनार की चोटी का उन्नयन कोण 60° है। मीनार की ऊँचाई होगी-
(A) \(\frac{50}{\sqrt{3}}\) m
(B) 100 m
(C) 100\(\sqrt{3}\) m
(D) 50\(\sqrt{3}\) m
हल :
(D) 50\(\sqrt{3}\) m
![]()
प्रश्न 26.
दो खंभों जिनकी ऊँचाई 25 m और 19m हैं, के शीर्ष एक तार से जुड़े हैं । यदि तार क्षैतिज के साथ 30° का कोण बनाती हो तो तार की लंबाई होगी-
(A) 6m
(B) 12 m
(C) 8m
(D) 10m
हल :
(B) 12 m
प्रश्न 27.
धरती पर एक मीनार ऊर्ध्वाधर खड़ी है। धरती के एक बिंदु से जो मीनार के पाद- बिंदु से 15m दूर है, मीनार के शिखर का उन्नयन कोण 60° हो तो मीनार की ऊँचाई होगी-
(A) 15 \(\sqrt{3}\) m
(B) 15m
(C) \(\frac{15}{\sqrt{3}}\)
(D) 30 \(\sqrt{3}\) m
हल :
(A) 15 \(\sqrt{3}\) m