Haryana State Board HBSE 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Intext Questions and Answers.
Haryana Board 8th Class Maths Solutions Chapter 11 क्षेत्रमिति Intext Questions
(पाठगत प्रश्न – पृष्ठ 177-178)
प्रश्न 1.
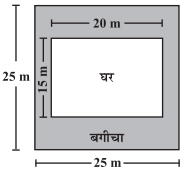
यह एक आयताकार बगीचे की आकृति है 3 जिसकी लम्बाई 30 मीटर और चौड़ाई 20 मीटर है (आकृति देखिए।
(i) इस बगीचे को चारों ओर से घेरने वाली बाड़ की लम्बाई क्या है?
(ii) कितनी भूमि बगीचे द्वारा व्याप्त है।
(iii) बगीचे के परिमाप के साथ-साथ अन्दर की तरफ एक मीटर चौड़ा रास्ता है जिस पर सीमेंट लगवाना है। यदि 4 वर्गमीटर (m2) क्षेत्रफल पर सीमेंट लगवाने के लिए एक बोरी सीमेंट चाहिए तो इस पूरे रास्ते पर सीमेंट लगवाने के लिए कितनी सीमेंट की बोरियों की आवश्यकता है?
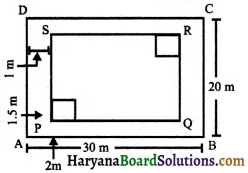
(iv) जैसा कि आरेख (आकृति देखिए) में दर्शाया गया है। इस बगीचे में फूलों की दो आयताकार क्यारियाँ हैं, जिनमें से प्रत्येक का आकार 1.5 m × 2 m है और शेष बगीचे के ऊपर घास है। घास द्वारा घिरा हुआ क्षेत्रफल ज्ञात कीजिए।
हल:
(i) बगीचे को चारों ओर से घेरने वाली बाड़ की लम्बाई
= बगीचे का परिमाप
= 2(लम्बाई + चौड़ाई)
= 2 (30+ 20) मीटर
= 2 × 50 मीटर
= 100 मीटर
(ii) बगीचे द्वारा व्याप्त भूमि = बगीचे का क्षेत्रफल
= लम्बाई × चौड़ाई
= (30 × 20) मी2
= 600 मी2
(iii) यहाँ, AB की लम्बाई = 30 मीटर,
चौड़ाई = QR = 20 मी
ABCD का क्षेत्रफल = (30 × 20) मी2 = 600 मी2
लम्बाई PQ = (30 मी – 2 मी)= 28 मी
चौड़ाई QR = (20 मी – 2 मी)= 18 मी
∴ PQRS का क्षेत्रफल = (28 × 18) मी2 = 504 मी2
अब, सीमेंट लगवाने वाले रास्ते का क्षेत्रफल
= ABCD का क्षेत्रफल – PQRS का क्षेत्रफल = (600 – 504) मी2
= 96 मी2
सीमेंट की बोरियों की संख्या की गणना-

= \(\frac{96}{4}\)
= 24 : अतः 24 बोरी सीमेंट की आवश्यकता होगी।
(iv) 1.5 मी × 2 मी आकार वाले 2 आयताकार फूल लगी क्यारियों का क्षेत्रफल
= (2 × 1.5 × 2) मी2
= 2 × 3 मी2 = 6 मी2
घास द्वारा घिरा हुआ क्षेत्रफल = ABCD का क्षेत्रफल – 2 फूल लगी क्यारियों का क्षेत्रफल
= (504 – 6) मी2
= 498 मी2
∴ घास लगे भाग का क्षेत्रफले = 498 मी2

(पृष्ठ 178)
प्रश्न 1.
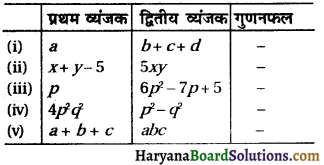
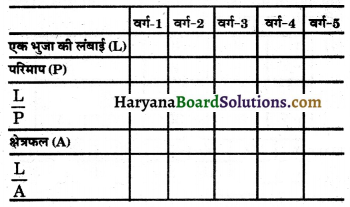
निम्नलिखित का मिलान कीजिए-
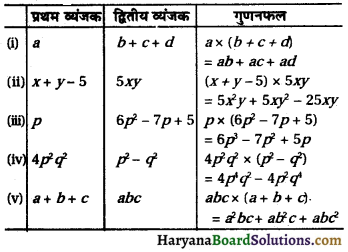
हल:
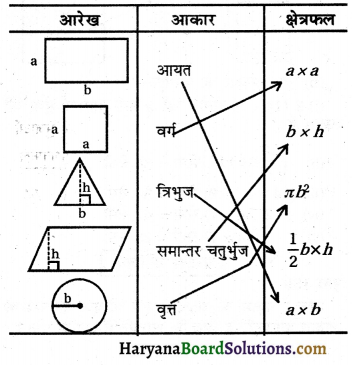
उपर्युक्त दी गई आकृतियों में से प्रत्येक के परिमाप के लिए व्यंजक (सूत्र) निम्नलिखित हैं-
आयत : 2(a+b)
वर्ग : 4a
त्रिभुज : तीनों भुजाओं का योग
समान्तर चतुर्भुज : 2 × आसन्न भुजाओं का योग
वृत्त . : 2πb
(प्रयास कीजिए – पृष्ठ 179)
प्रश्न 1.
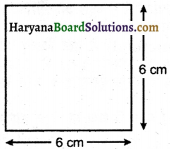
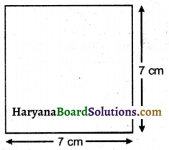
(a) निम्नलिखित आकृतियों का उनके क्षेत्रफलों से मिलान कीजिए
(b) प्रत्येक आकार का परिमाप लिखिए।
हल:
(a) आकृतियों का उनके क्षेत्रफलों से मिलान निम्न प्रकार है
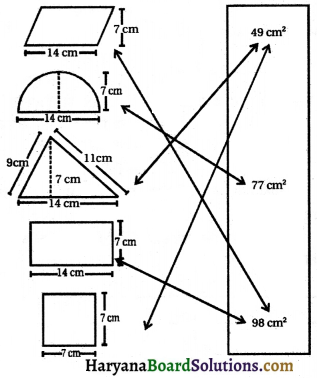
(b) संगत आकार का परिमाप
(i) 2(14 + a) सेमी, जहाँ a सेमी आसन्न भुजा की लम्बाई है।
(ii) (\(\frac{22}{7}\) × 4 + 14) सेमी = 36 सेमी
(iii) (14 + 11 + 9) सेमी = 34 सेमी
(iv) 2 (14 + 7) सेमी = 42 सेमी
(v) (4 × 7) सेमी = 28 सेमी
(प्रयास कीजिए – पृष्ठ 180)
प्रश्न 1.
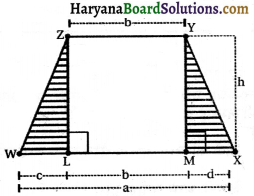
नजमा की बहन के पास भी एक समलम्ब के आकार का प्लॉट है जैसा कि आकृति में दर्शाया गया है। इसे तीन भागों में बाँटिए। दर्शाइए कि समलम्ब =WXYZ का क्षेत्रफल = h
(\(\frac{a+b}{2}\)
हल:
माना कि बिन्दु Z तथा बिन्दु Y से WX पर डाले गए लम्ब के पाद क्रमशः L तथा M हैं।
तब, WXYZ समलम्ब का क्षेत्रफल = समकोण AWLZ का क्षेत्रफल + आयत LMYZ का क्षेत्रफल + समकोण ΔMXY का क्षेत्रफल
=
\(\frac{1}{2}\)(WL × ZL) + LM × MY × \(\frac{1}{2}\) (MX × YM)
= \(\frac{1}{2}\)(WL × h) + LM × h + \(\frac{1}{2}\)(MX × h) [∵ ZL = MY = h]
= \(\frac{1}{2}\) h × (WL + 2LM + MX)
= \(\frac{1}{2}\)h × (WL + LM + MX + LM)
= \(\frac{1}{2}\)h × (WX + ZY)
[∵ WL + LM + MX = WX और LM = ZY]
= \(\frac{1}{2}\)h × (a + b) = h\(\frac{a+b}{2}\)

प्रश्न 2.
यदि h = 10 cm, c = 6 cm, b = 12 cm, d =4 cm, तो इसके प्रत्येक भाग का मान अलग-अलग ज्ञात कीजिए और WXYZ का क्षेत्रफल ज्ञात करने के लिए इनका योग कीजिए। h, a तथा b का मान व्यंजक \(\frac{a+b}{2}\) में रखते हुए इसका सत्यापन कीजिए।
हल:
स्पष्टतः, h = 10 cm, c = 6 cm, b = 12 cm तथा d =4cm लेने पर a = c + b + d = (6 + 12 + 4) cm = 22 cm
समलम्ब WXYZ का क्षेत्रफल = ΔWLZ का क्षेत्रफल + आयत LMYZ का क्षेत्रफल + ΔMXY का क्षेत्रफल
= \(\frac{1}{2}\) × c × h + b × h + \(\frac{1}{2}\) × d × h
= (\(\frac{1}{2}\) × 6 × 10 + 12 × 10 + \(\frac{1}{2}\) × 4 × 10) cm2
= (30 + 120 + 20) cm2
= 170 cm2
और सूत्र के अनुसार-
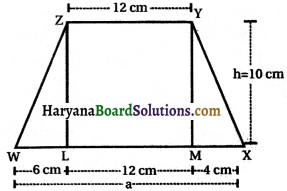
समलम्ब WXYZ का क्षेत्रफल = \(\frac{h \times (a+b)}{2}\)
= \(\frac{10 \times (22+12)}{2}\) cm2
= 5 × 34 cm2
= 170 cm2
अतः, क्षेत्रफल सत्यापित होता है।
(पृष्ठ 181)
प्रश्न 1.
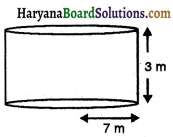
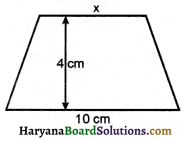
निम्नलिखित समलम्बों का क्षेत्रफल ज्ञात कीजिए-
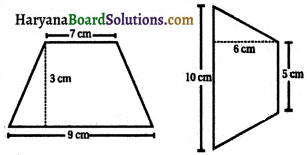
हल:
(i) क्षेत्रफल = \(\frac{1}{2}\)(9 + 7) × 3 cm2
= \(\frac{1}{2}\) × 16 × 3cm2
= 8 × 3 cm2
= 24 cm2
(ii) क्षेत्रफल = \(\frac{1}{2}\)(10 + 5) × 6 cm2
= \(\frac{1}{2}\) × 15 × 6 cm2
= 15 × 3 cm2
= 45 cm2
(पृष्ठ 182)
प्रश्न 1
हम जानते हैं कि 2 0समान्तर चतुर्भुज भी एक चतुर्भुज है। आइए, इसे भी हम दो त्रिभुजों में है विभक्त करते हैं और इन दोनों त्रिभुजों का क्षेत्रफल ज्ञात करते हैं। इस प्रकार समान्तर चतुर्भुज का क्षेत्रफल भी ज्ञात करते हैं। क्या यह सूत्र आपको पूर्व में ज्ञात सूत्र से मेल खाता है? (आकृति देखिए)
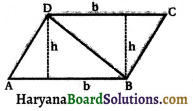
हल:
समान्तर चतुर्भुज PORS का क्षेत्रफल = ΔPQS का क्षेत्रफल + ΔQRS का क्षेत्रफल
= \(\frac{1}{2}\) × b × h + \(\frac{1}{2}\) × b × h
= \(\frac{1}{2}\) × (b + b) × h
= \(\frac{1}{2}\) × 2b × h = bh
हम समलम्ब के क्षेत्रफल का सूत्र जानते हैं। आइए इसका प्रयोग करते हैं।
समान्तर चतुर्भुज PQRS का क्षेत्रफल = \(\frac{1}{2}\) × (समान्तर भुजाओं का योग) × इन भुजाओं के बीच की दूरी
= \(\frac{1}{2}\) × (b + b) × h
= \(\frac{1}{2}\) × 2b × h = bh
हाँ, यह सूत्र हमें पूर्व में ज्ञात सूत्र से मेल खाता है।
(सोचिए, चर्चा कीजिए और लिखिए – पृष्ठ 183)
प्रश्न 1.
समान्तर चतुर्भुज का विकर्ण खींचकर इसे दो सर्वांगसम त्रिभुजों में बाँटा जाता है। क्या समलम्ब को भी दो सर्वांगसम त्रिभुजों में बाँटा जा सकता है?
हल:
एक समलम्ब को दो सर्वांगसम त्रिभुजों में नहीं बाँटा जा सकता है।

(प्रयास कीजिए – पृष्ठ 183)
प्रश्न 1.
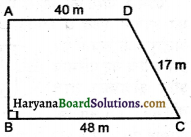
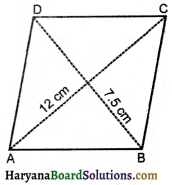
निम्नलिखित चतुर्भुजों का क्षेत्रफल ज्ञात कीजिए (आकृति देखिए)
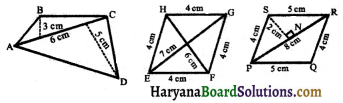
हल:
(i) चतुर्भुज ABCD का क्षेत्रफल = क्षेत्रफल (ΔABC) + क्षेत्रफल (ΔACD)
= (\(\frac{1}{2}\) × 6 × 3 + \(\frac{1}{2}\) × 6 × 5) cm2
= (3 × 3 + 3 × 5) cm2
= (9 + 15) cm2 = 24 cm2
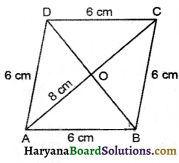
(ii) चतुर्भुज EFGH का क्षेत्रफल = समचतुर्भुज EFGH का क्षेत्रफल
= \(\frac{1}{2}\) × EG × FH
= (\(\frac{1}{2}\) × 7 × 6) cm2
= 21 cm2
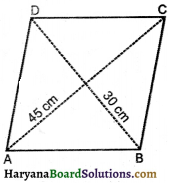
(iii) चतुर्भुज PQRS का क्षेत्रफल = समान्तर चतुर्भुज PQRS का क्षेत्रफल
= 2 × ΔPSR का क्षेत्रफल
= 2 × \(\frac{1}{2}\) × PR × SN
= (8 × 2) cm2
= 16 cm2
(पृष्ठ 184)
प्रश्न 1.
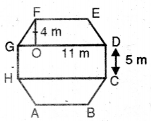
(i) निम्नलिखित बहुभुजों (आकृति देखिए) का क्षेत्रफल ज्ञात करने के लिए इन्हें विभिन्न भागों (त्रिभुजों एवं समलम्बों) में विभाजित कीजिए।
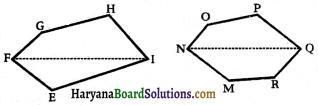
हल:
बहुभुज EFGHI को जैसा कि आकृति में दिखाया गया है, अलग-अलग भागों में बाँटा जाता है।
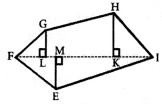
बहुभुज EFGHI का क्षेत्रफल = क्षेत्रफल (ΔEFI) + क्षेत्रफल (ΔFLG) + क्षेत्रफल (समलम्ब LKHG) + क्षेत्रफलं (ΔHKI)
= \(\frac{1}{2}\) × FI × EM + latex]\frac{1}{2}[/latex] × FL × GL + \(\frac{1}{2}\)(KH + LG) × LK + \(\frac{1}{2}\) × KI × KH
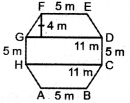
बहुभुज MNOPQR को जैसा कि आकृति में दिखाया गया है, अलग-अलग भागों में N B बाँटा जाता है।
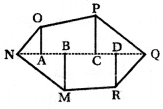
बहुभुज MNOPQR का क्षेत्रफल = क्षेत्रफल (MBN) + क्षेत्रफल (समलम्ब MBDR) + क्षेत्रफल (ΔRDQ) + क्षेत्रफल (ΔFCQ) + क्षेत्रफल (समलम्ब CPOA) + क्षेत्रफल (ΔOAN)
= \(\frac{1}{2}\) × BN × MB + \(\frac{1}{2}\) ×(DR+MB) × BD + \(\frac{1}{2}\) × QD × RD +
\(\frac{1}{2}\) × CQ × PC + \(\frac{1}{2}\) × (CP + AO) × AC + \(\frac{1}{2}\) × NA × OA

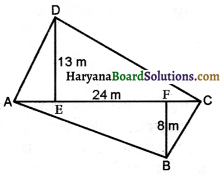
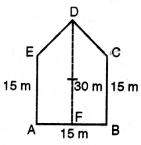
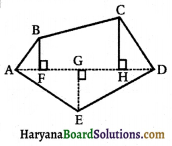
(ii) बहुभुज ABCDE को विभिन्न भागों में बाँटा गया है जैसा कि आकृति में दर्शाया गया है। यदि AD = AE = 8 cm, AH = 6 cm, AG = 4 cm, AF = 3 cm और BF = 2 cm, CH = 3cm, EG = 2.5 cm तो इसका क्षेत्रफल ज्ञात कीजिए।
हल:
बहुभुज ABCDE का क्षेत्रफल = ΔAFB का क्षेत्रफल + समलम्ब FBCH का क्षेत्रफल + ΔCHD का क्षेत्रफल + ADE का क्षेत्रफल
= \(\frac{1}{2}\) × AF × BF + \(\frac{1}{2}\) × (BF + CH) × FH + \(\frac{1}{2}\) × HD × CH +
\(\frac{1}{2}\) × AD × GE
= \(\frac{1}{2}\) × 3 × 2 cm2 + \(\frac{1}{2}\) × (2 + 3) × 3 cm2 + \(\frac{1}{2}\) × 2 × 3 cm2 + \(\frac{1}{2}\) × 8 × 2.5 cm2
[∵ FH = AH – AF= (6 – 3) cm = 3 cm और HD = AD – AH= (8 – 6) cm = 2 cm]
= (3 + \(\frac{1}{2}\) + 3 + 10) cm2
= (\(\frac{6+15+6+20}{2}\)) cm2
= \(\frac{47}{2}\) cm2
= \(23 \frac{1}{2}\) cm2
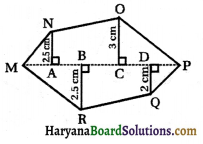
(iii) यदि MP = 9cm, MD = 7 cm, MC = 6 cm, MB = 4 cm, MA = 2 cm तो बहुभुज MNOPQR (आकृति देखिए) का क्षेत्रफल ज्ञात कीजिए। NA, OC, QD एवं RB विकर्ण MP पर खींचे गए लम्ब हैं।
हल:
बहुभुज MNOPQR का क्षेत्रफल = ΔMAN का क्षेत्रफल + समलम्ब ΔNOC का क्षेत्रफल + ΔOCP का क्षेत्रफल + ΔMBR का क्षेत्रफल + समलम्ब RBDQ का क्षेत्रफल + ΔQDP का क्षेत्रफल
= \(\frac{1}{2}\) × MA × AN + \(\frac{1}{2}\) × (AN + CO) × AC + \(\frac{1}{2}\) × CP × CO + \(\frac{1}{2}\) × MB × RB + \(\frac{1}{2}\) × (RB+QD) + \(\frac{1}{2}\) × BD + \(\frac{1}{2}\) × DP × QD
= \(\frac{1}{2}\) × 2 × 2.5 cm2 + \(\frac{1}{2}\) × (2.5 + 3) × 4 cm2 +1 × 3 × 3 cm2 + \(\frac{1}{2}\) × 4 × 2.5 cm2 + \(\frac{1}{2}\) × (2.5 + 2) × 3 cm2 + \(\frac{1}{2}\) × 2 × 2 cm2
[∵ AC = MC – MA = (6 – 2) =4 cm, CP = MP- MC = (9 – 6) cm = 3 cm, BD = MD – MB = (7 – 4)= 3 cm और DP = MP – MD = (9 – 7) cm = 2 cm]
= (2.5 + 11 + 4.5 + 5 + 6.75 + 2) cm2
= 31.75 cm2

(सोचिए, चर्चा कीजिए और लिखिए – पृष्ठ 188)
प्रश्न 1.
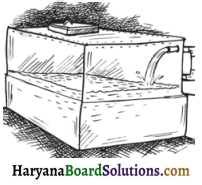
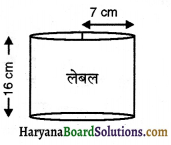
संलग्न आकृति में दर्शाए गए ठोस को बेलन कहना क्यों गलत है?

हल:
क्योंकि बेलन की वृत्ताकार सर्वांगसम फलकें होती हैं जो एकदूसरे के समान्तर होती हैं । इसलिए दिए गए ठोस को बेलन कहना गलत है।
(प्रयास कीजिए – पृष्ठ 189)
प्रश्न 1.
निम्नलिखित घनाभों (आकृति देखिए) का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए
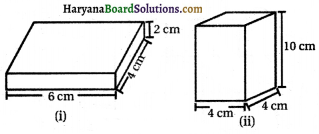
हल:
(i) दिया गया हैलम्बाई (l) = 6cm, चौड़ाई (b) =4cm तथा ऊँचाई (h) =2 cm
∴ घनाभ का कुल पृष्ठीय क्षेत्रफल = 2 (lb + bh + hl)
= 2(6 × 4 + 4 × 2 + 2 × 6)
= 2 (24 + 8 + 12)
= 2 × 44
= 88 cm2
(ii) दिया गया हैलम्बाई (l) = 4 cm, चौड़ाई (b) = 4 cm तथा ऊँचाई (h) = 10 cm
∴ घनाभ का कुल पृष्ठीय क्षेत्रफल
= 2 (lb + bh + hl)
= 2 (4 × 4 + 4 × 10 + 10 × 4)
= 2 (16 + 40 + 40)
= 2(56 + 40)
= 192 cm2

(सोचिए, चर्चा कीजिए और लिखिए – पृष्ठ 190)
प्रश्न 1.
क्या हम कह सकते हैं कि घनाभ का कुल पृष्ठीय क्षेत्रफल = पार्श्व पृष्ठीय क्षेत्रफल + 2 × आधार का क्षेत्रफल?
हल:
अतः घनाभ का कुल पृष्ठीय क्षेत्रफल = पार्श्व पृष्ठीय क्षेत्रफल + 2 × आधार का क्षेत्रफल।
प्रश्न 2.
यदि हम किसी घनाभ [आकृति (i)) की ऊँचाई और आधार की लम्बाई को परस्पर बदलकर एक दूसरा घनाभ [आकृति (ii)] प्राप्त कर लें तो क्या पार्श्व पृष्ठीय क्षेत्रफल बदल जाएगा?
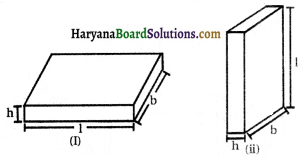
हल:
घनाभ (i) का पार्श्व क्षेत्रफल = 2(l + b) h
और घनाभ (ii) का पार्श्व पृष्ठीय क्षेत्रफल = 2(h + b) × l
स्पष्ट रूप से, ये परिणाम भिन्न हैं।
अतः, घनाभ की स्थिति को बदलने से इसका पार्श्व पृष्ठीय क्षेत्रफल बदल जाता है।
(प्रयास कीजिए – पृष्ठ 191)
प्रश्न 1.
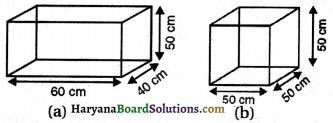
घन A का पृष्ठीय क्षेत्रफल और घन B का पाव पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
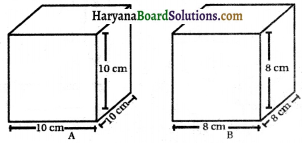
हल:
घन (A) का पृष्ठीय क्षेत्रफल = 6l2
= 6(10)2 cm2
= 600 cm2
घन (B) का पार्श्व पृष्ठीय क्षेत्रफल = 4(side)2
= 4(8)2
= 4 × 64
= 256 cm2
(सोचिए, चर्चा कीजिए और लिखिए – पृष्ठ 191)
प्रश्न 1.
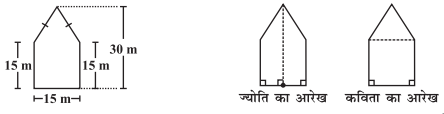
(i) b भुजा वाले दो घनों को मिलाकर एक घनाभ बनाया गया है (आकृति)। इस घनाभ का पृष्ठीय क्षेत्रफल क्या है? क्या यह 12b2 है? क्या ऐसे तीन घनों को मिलाकर बनाए गए घनाभ का पृष्ठीय क्षेत्रफल 18b2 है? क्यों?
(ii) न्यूनतम पृष्ठीय क्षेत्रफल का घनाभ निर्मित करने के लिए समान भुजा वाले 12 घनों को किस प्रकार व्यवस्थित करेंगे?
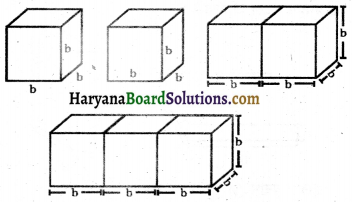
(iii) किसी घन के पृष्ठीय क्षेत्रफल पर पेंट करने के पश्चात् उस घन को समान विमाओं वाले 64 घनों में काटा जाता है (आकृति)। इनमें से कितने घनों का कोई भी फलक पेंट नहीं हुआ है? कितने घनों का 1 फलक पेंट हुआ है? कितने घनों के 2 फलक पेंट हुए हैं? कितने घनों के तीन फलक पेंट हुए हैं?

हल:
(i) दो घनों को मिलाने से हमें एक घनाभ प्राप्त
जिसकी लम्बाई, L = b + b = 2b इकाई
चौड़ाई, B = b इकाई
ऊँचाई, H = b इकाई
∴ घनाभ का पृष्ठीय क्षेत्रफल = 2 (LB + BH + LH)
= 2(2b × b + b × b + 2b × b) वर्ग इकाई
= 2(2b2 + b2 + 2b2) वर्ग इकाई = 10b2 वर्ग इकाई
इसलिए, यह 12b2 नहीं है।
तीन घन को क्रमनुसर मिलाया जाये, तब इस प्रकार प्राप्त घनाभ की विमाएँ निम्न होंगी :
L = लम्बाई = 3b, B = चौड़ाई = b और H = ऊँचाई = b
∴ घनाभ का पृष्ठीय क्षेत्रफल = 2(LB + BH + LH)
= 2(3b × b + b × b + 3b × b) वर्ग इकाई
= 2(3b2 + b2 + 3b2) वर्ग इकाई
= 14b2 वर्ग इकाई
इसलिए, यह = 18b2 नहीं है।

(ii) बराबर भुजाओं के 12 घनों को मिलाने से निम्न घनाभ प्राप्त होता होता है :
(b) 
इस स्थिति में : l = 12b, b = b तथा h = b
∴ इसका पृष्ठीय क्षेत्रफल = 2(12b × b + b × b + 12b × b)
= 2(12b2 + b2 + 12b2)
= 2 × 25b2
= 50b2

इस स्थिति में : l = 6b, b = b तथा h = 2b
∴ इसका पृष्ठीय क्षेत्रफल = 2(6b × b + b × 2b + 6b × 2b)
= 2(6b2 + 2b2 + 12b2)
= 2 × 20b2
= 40b2
(c) 
इस स्थिति में : l = 4b, b = b तथा h = 3b
∴ इसका पृष्ठीय क्षेत्रफल = 2(4b × b + b × 3b + 4b × 3b)
= 2(4b2 + 3b2 + 12b2)
= 2 × 19b2
= 38b2
अतः, सबसे कम पृष्ठीय क्षेत्रफल के लिए घनों को, चित्र के व्यवस्थित किया जा सकता है।
(iii) घनों की संख्या, जिनकी एक भी फलक पेंट नहीं किया गया है = 16
घनों की संख्या, जिनकी एक फलक पेंट किया गया है = 24
घनों की संख्या, जिनकी दो फलक पेंट किए गए हैं = 16
घनों की संख्या, जिनकी तीन फलकें पेंट किए गए हैं = 8

(प्रयास कीजिए – पृष्ठ 193)
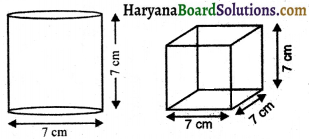
प्रश्न 1.
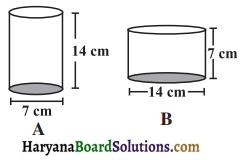
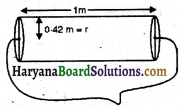
निम्नलिखित बेलनों का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए
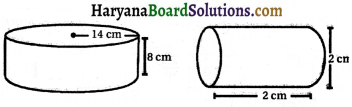
हल:
(i) प्रशनुसार , r = 14 cm और h = 8 cm
∴ कुल पृष्ठीय क्षेत्रफल = 2πrh + 2πr2
= (2 × \(\frac{22}{7}\) × 14 × 8 + 2 × \(\frac{22}{7}\) × 14 × 14) cm2
= (704 + 1232) cm2
= 1936 cm2
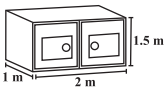
(ii) चित्रानुसार, r = 7, m = 1 m तथा h = 2 m
कुल पृष्ठीय क्षेत्रफल = 2πrh + 2πr2
= (2 × \(\frac{22}{7}\) × 1 × 2 + 2 × \(\frac{22}{7}\) × 1 × 1) m2
= (\(\frac{88}{7}\) +\(\frac{44}{7}\)) m2
= \(\frac{132}{7}\) m2
= \(18 \frac{6}{7}\) m2

(सोचिए, चर्चा कीजिए और लिखिए – पृष्ठ 193)
प्रश्न 1.
नोट कीजिए कि किसी बेलन का पार्श्व पृष्ठीय (वक्र पृष्ठीय)क्षेत्रफल, आधार की परिधि- बेलन की ऊँचाई के समान होता है। क्या हम घनाभ के पार्श्व पृष्ठीय क्षेत्रफल को आधार का परिमाप x घनाभ की ऊँचाई के रूप में लिख सकते हैं?
हल:
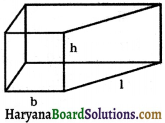
हम जानते हैं कि घनाभ का पार्श्व पृष्ठीय क्षेत्रफल = 2(l + b) × h
= आधार का परिमाप × ऊँचाई इस प्रकार, हम एक घनाभ के पार्श्व पृष्ठीय क्षेत्रफल को आधार का परिमाप × घनाभ की ऊँचाई के रूप में लिख सकते हैं।
(पृष्ठ 196)
प्रश्न 1.
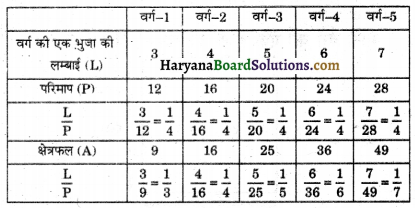
समान आकार (प्रत्येक घन की लम्बाई समान) वाले 36 घन लीजिए, एक घनाभ बनाने के लिए उन्हें व्यवस्थित कीजिए। आप इन्हें अनेक रूपों में व्यवस्थित कर सकते हैं। निम्नलिखित सारणी पर विचार कीजिए
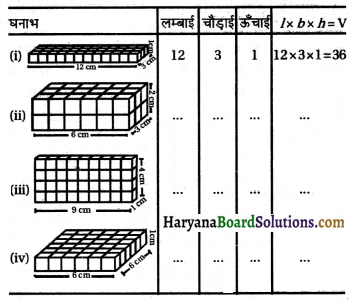
हल:
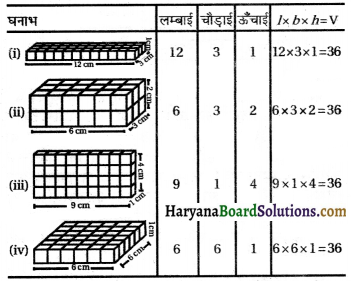
हम देखते हैं कि इन घनाभों को बनाने के लिए हमने 36 घनों का प्रयोग किया है। इसलिए प्रत्येक स्थिति में इसका आयतन 36 घन इकाई है। स्पष्ट रूप से, यह लम्बाई × चौड़ाई × ऊँचाई के बराबर है।

(प्रयास कीजिए – पृष्ठ 197)
प्रश्न 1.
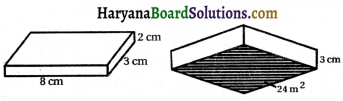
निम्नलिखित घनाभों (आकृति) का आयतन ज्ञात कीजिए
हल:
(i) घनाभ का आयतन = (8 × 3 × 2) cm3
= 48 cm3
(ii) घनाभ का आयतन = आधार का क्षेत्रफल × ऊँचाई
= (24 × \(\frac{3}{100}\)) m
= 0.72 m3
(प्रयास कीजिए – पृष्ठ 197)
प्रश्न 1.
निम्नलिखित घनों का आयतन ज्ञात कीजिए-
(a) 4 cm भुजा वाला
(b) 1.5 m भुजा वाला
हल:
(a) घन का आयतन = (भुजा)3
= (4)3 cm3
= 64 cm3
(b) घन का आयतन = (भुजा)3
= (1.5)3 m3
= 3.375 m3
(सोचिए, चर्चा कीजिए और लिखिए – पृष्ठ 197-198)
प्रश्न 1.
एक कम्पनी बिस्कुट बेचती है। बिस्कुटों को पैक करने के लिए घनाभाकार डिब्बों का उपयोग किया जा रहा है। डिब्बा A → 3 cm × 8 cm × 20 cm, डिब्बा B → 4 cm × 12 cm × 10 cm. डिब्बे का कौन-सा आकार कम्पनी के लिए आर्थिक दृष्टि से लाभदायक रहेगा? क्यों? क्या आप ऐसे किसी और आकार (विमाएँ) के डिब्बे का सुझाव दे सकते हैं जिसका आयतन इनके समान हो परन्तु इनकी तुलना में आर्थिक दृष्टि से अधिक लाभदायक हो?
हल:
डिब्बा A :
आयतन = (3 × 8 × 20) cm3
= 480 cm3
पृष्ठीय क्षेत्रफल = 2(3 × 8 + 8 × 20 + 20 × 3) cm2
= 2(24 + 160 + 60) cm2
= 2 × 244 cm3
= 488 cm2
डिब्बा B:
आयतन = (4 × 12 × 10) cm2
= 480 cm2
पृष्ठीय क्षेत्रफल
= 2(4 × 12+ 12 × 10 + 10 × 4) cm2
= 2(48 + 120+ 40) cm2
= 2 × 208 cm = 416 cm2
स्पष्ट है कि B प्रकार के डिब्बे का आयतन = A प्रकार के डिब्बे का आयतन
परन्तु, B प्रकार के डिब्बे का पृष्ठीय क्षेत्रफल A प्रकार के डिब्बे के पृष्ठीय क्षेत्रफल से कम है।
∴ डिब्बा B में कम सामग्री लगेगी।
इसलिए डिब्बा B आर्थिक रूप से अधिक लाभदायक है। एक अन्य प्रकार का डिब्बा जिसका आकार 8 cm × 6 cm × 10 cm है अर्थात् आयतन 480 cm3 है।
इसका पृष्ठीय क्षेत्रफल = 2(48 + 60 + 80) cm2
= 2 (188) cm2
= 376 cm2
स्पष्ट है कि इस डिब्बे का पृष्ठीय क्षेत्रफल डिब्बा B से भी कम है। इसलिए यह दिए गए दोनों प्रकार के डिब्बों से आर्थिक रूप से अधिक लाभदायक है।

(प्रयास कीजिए – पृष्ठ 198)
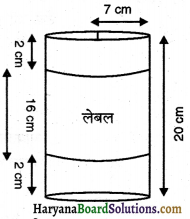
प्रश्न 1.
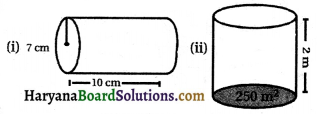
नीचे दिए बेलनों का आयतन ज्ञात कीजिए
हल:
(i) बेलन का आयतन = πr2h
जहाँ r = 7 cm, h = 10 cm
= (\(\frac{22}{7}\) × 7 × 7 × 10) cm3
= (2 × 70) cm3
= 1540 cm3
(ii) बेलन का आयतन = (आधार का क्षेत्रफल) x ऊँचाई
= (250 × 2) m3
= 500 m3
![]()
![]()
![]()
![]()
![]()