Haryana State Board HBSE 8th Class Maths Solutions Chapter 8 राशियों की तुलना Intext Questions and Answers.
Haryana Board 8th Class Maths Solutions Chapter 8 राशियों की तुलना Intext Questions
प्रश्न 1.
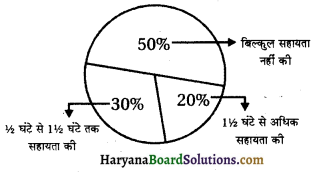
एक प्राथमिक विद्यालय में अभिभावकों से पूछा गया कि वे अपने बच्चों के गृहकार्य में सहायता करने के लिए प्रतिदिन कितने घंटे व्यतीत करते हैं। 90 अभिभावकों ने \(\frac{1}{2}\) घंटे से 1\(\frac{1}{2}\) घंटे तक सहायता की। जितने समय के लिए अभिभावकों ने अपने बच्चों की सहायता करना बताया उसके अनुसार अभिभावकों का वितरण संलग्न आकृति में दिखाया गया है जो इस प्रकार है 20% ने प्रतिदिन 1\(\frac{1}{2}\) घंटे से अधिक सहायता की, 30% ने \(\frac{1}{2}\) घंटे से 1\(\frac{1}{2}\) घंटे तक सहायता की, 50% ने बिल्कुल सहायता नहीं की।
इसके आधार पर निम्नलिखित प्रश्नों के उत्तर दीजिए
(i) कितने अभिभावकों का सर्वे किया गया?
(ii) कितने अभिभावकों ने कहा कि उन्होंने सहायता नहीं की?
(iii) कितने अभिभावकों ने कहा कि उन्होंने 1\(\frac{1}{2}\) घंटे से अधिक सहायता की?
हल:
(i) माना कि सर्वे किए गए अभिभावकों की संख्या = x
∴ \(\frac{1}{2}\) घंटे से 1\(\frac{1}{2}\) घण्टे तक सहायता करने वाले अभिभावकों की संख्या = कुल अभिभावकों का 30%
= x का 30%
= \(\frac{x × 30}{100}\) = \(\frac{3x}{10}\) ……….(i)
परन्तु \(\frac{1}{2}\) घंटे से 1\(\frac{1}{2}\) घण्टे तक सहायता करने वाले अभिभावकों की संख्या = 90 (दिया है) ….(ii)
अत:
\(\frac{3x}{10}\) = 90
x = \(\frac{90 \times 10}{3}\) = 300
अत: 300 अभिभावकों का सर्वे किया गया।
(ii) 50% ने बिल्कुल सहायता नहीं की
अतः बिल्कुल सहायता न करने वाले अभिभावकों की संख्या
= 300 × 50% = 150
(iii) 1\(\frac{1}{2}\) घण्टे से अधिक सहायता करने वाले अभिभावकों की संख्या
= कुल संख्या का 20 प्रतिशत
= 300 x 20 = 60
![]()
(प्रयास कीजिए – पृष्ठ 129-130)
प्रश्न 1.
एक दुकान 20% बट्टा देती है। निम्नलिखित में से प्रत्येक का विक्रय मूल्य क्या होगा?
(a) ₹120 अंकित मूल्य वाली एक पोशाक।
(b) ₹750 अंकित मूल्य वाले एक जोड़ी जूते।
(c) ₹ 250 अंकित मूल्य वाला एक थैला।
हल :
(a) दिया है- अंकित मूल्य = ₹ 120 बट्टा = 20%
बट्टा = ₹ 120 का 20%
= ₹120 × \(\frac{20}{100}\)
= ₹ 24
विक्रय मूल्य = अंकित मूल्य – बट्टा
= ₹(120 – 24)
= ₹96
अत: एक पोशाक का विक्रय मूल्य = ₹96
(b) दिया हैअंकित मूल्य = ₹750 बट्टा = 20%
बट्टा = ₹750 का 20%
= ₹120 × \(\frac{750 × 20 }{100}\)
= ₹ 150
विक्रय मूल्य = अंकित मूल्य – बट्टा
= ₹ (750 – 150)
= ₹ 600
अतः एक जोड़ी जूते का विक्रय मूल्य = ₹600
(c) दिया है-
अंकित मूल्य = ₹250 बट्टा = 20% बट्टा = ₹ 250 का 20%
= ₹ 250 का 20%
= ₹250 × \(\frac{250 × 20 }{100}\)
= ₹ 50
विक्रय मूल्य = अंकित मूल्य – बट्टा
= ₹(250-50)
= ₹200
अतः एक थैला का विक्रय मूल्य = 200
![]()
प्रश्न 2.
₹ 15000 अंकित मूल्य वाली एक मेज ₹14400 में उपलब्ध है। बट्टा और बट्टा प्रतिशत ज्ञात कीजिए।
हल :
दिया अंकित मूल्य = ₹ 15000
विक्रय मूल्य = ₹ 14400
बट्टा = ₹(15000 – 14400)
= ₹600
बट्टा प्रतिशत = = \(\frac{600}{15000}\) × 100
= 4%
प्रश्न 3.
एक अलमारी 5% बट्टे पर ₹ 5225 में बेची जाती है। अलमारी का अंकित मूल्य ज्ञात कीजिए।
हल :
माना अलमारी का मूल्य = ₹ 100
बट्टा = अंकित मूल्य का 5%
= 100 रुपए का 5% = = ₹ 5
विक्रय मूल्य = अंकित मूल्य – बट्टा
=₹ (100 – 5)
= ₹ 95
जब विक्रय मूल्य 95 रुपए तो अंकित मूल्य = ₹ 100
जब विक्रय मूल्य 1 रुपया तो अंकित मूल्य = latex]\frac{100}{95}[/latex]
जब विक्रय मूल्य 5225 तो अंकित मूल्य
= ₹ (\(\frac{100}{95}\) × 5225 )
= ₹5500
अत: अलमारी का अंकित मूल्य = ₹5500
![]()
(प्रयास कीजिए – पृष्ठ 131)
प्रश्न 1.
यदि लाभ की दर 5% है तो निम्नलिखित का विक्रय मूल्य ज्ञात कीजिए
(a) 700 रुपए की एक साइकिल जिस पर ऊपरी खर्च 50 रुपए है।
हल:
(a) साइकिल का क्रय मूल्य = ₹700 रुपए
ऊपरी खर्च = ₹50 रुपए
∴ कुल क्रय मूल्य = ₹(700 + 50) = ₹ 750
लाभ = 5%
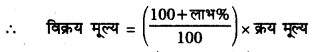
= ₹ \(\left(\frac{100+5}{100} \times 750\right)\)
= ₹ \(\left(\frac{105}{100} \times 750\right)\)
= ₹ 787.50 रुपए
(b) 1150 रुपए में खरीदा गया एक घास काटने का यंत्र जिस पर 50 रुपए परिवहन व्यय के रूप में खर्च किए गए हैं।
हल:
घास काटने के यंत्र का क्रय मूल्य
= ₹ 1150
ऊपरी खर्च = ₹ 50
∴ कुल क्रय मूल्य = ₹ (1150 + 50)
= ₹ 1200
लाभ = 5%
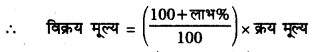
= ₹ \(\left(\frac{100+5}{100} \times 1200\right)\)
= ₹ (105 × 12)
= ₹ 1260
(c) 560 रुपए में खरीदा गया एक पंखा जिस पर 40 रुपए मरम्मत के लिए खर्च किए गए हैं।
हल:
पंखे का क्रय मूल्य = ₹ 560
ऊपरी खर्च = ₹ 40
∴ कुल क्रय मूल्य = ₹ (560 + 40) रुपए = ₹ 600
लाभ = 5%
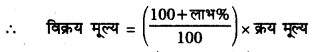
= ₹ \(\left(\frac{100+5}{100} \times 600\right)\)
= ₹ (105 × 6)
= ₹ 630
![]()
(प्रयास कीजिए – पृष्ठ 132)
प्रश्न 1.
एक दुकानदार ने दो टेलीविजन सेट 10,000 रुपए प्रति सेट की दर से खरीदे। उसने एक को 10% हानि से और दूसरे को 10% लाभ से बेच दिया। ज्ञात कीजिए कि कुल मिलाकर उसे इस सौदे में लाभ हुआ अथवा हानि।
हल:
पहले टेलीविजन सेट के लिए
क्रय मूल्य = ₹ 10,000
और हानि = 10%
![]()
= ₹ \(\left(\frac{100-10}{100} \times 10000\right)\)
= ₹ (90 × 100)
= ₹ 9000
दूसरे टेलीविजन सेट के लिए
क्रय मूल्य = ₹ 10000
और लाभ = 10%
![]()
= ₹ \(\left(\frac{100+10}{100} \times 10000\right)\)
= ₹ (110 × 100)
= ₹ 11000
दो टेलीविजन सेट के लिए कुल क्रय मूल्य = ₹ 20000
और कुल विक्रय मूल्य = ₹ (11000 + 9000)
= ₹ 20000
क्योंकि विक्रय मूल्य = क्रय मूल्य
अतः, उसे न लाभ हुआ न ही हानि।
![]()
सोचिए, चर्चा कीजिए और लिखिए (पृष्ठ 133)
प्रश्न 1.
किसी संख्या को दुगुना करने पर उस संख्या में 100% वृद्धि होती है। यदि हम उस संख्या को आधा कर दें तो कितना प्रतिशत ह्रास होगा?
हल:
माना संख्या x, तो इसका आधा = \(\frac{x}{2}\)

प्रश्न 2.
2400 रुपए की तुलना में 2000 रुपए कितना प्रतिशत कम है? क्या यह प्रतिशत उतना ही है, जितना 2000 रुपए की तुलना में 2400 रुपए अधिक है?
हल:
पहली स्थिति में :

नहीं, यह समान नहीं है।
![]()
(प्रयास कीजिए – पृष्ठ 135)
प्रश्न 1.
5% वार्षिक दर से 15,000 रुपए का 2 वर्ष के अंत में ब्याज और भुगतान की जाने वाली कुल राशि ज्ञात कीजिए।
हल:
दिया है, P= 15000 रुपए, R = 5% प्रति वर्ष और T = 2 वर्ष
माना I ब्याज और A मिश्रधन है तो
I = \(\frac{P×R×T}{100}\)
अतः I = \(\frac{15000×5×2}{100}\)
= ₹ (150 × 10
= ₹ 1500
A = P + I
अतः A = ₹ (15000 + 1500)
= ₹ 16500
(प्रयास कीजिए – पृष्ठ 138)
प्रश्न 1.
8,000 रुपए का 2 वर्ष के लिए 5% वार्षिक दर से चक्रवृद्धि ब्याज ज्ञात कीजिए यदि ब्याज वार्षिक संयोजित होता है।
हल:
दिया है, P = 8000 रुपए, R = 5% प्रति वर्ष और n= 2 वर्ष
∴ 2 वर्ष बाद मिश्रधन (A) = \(\mathrm{P}\left(1+\frac{\mathrm{R}}{100}\right)^{n}\)
= ₹ \(\left[8000 \times\left(1+\frac{5}{100}\right)^{2}\right]\)
= ₹ \(\left(8000 \times \frac{21}{20} \times \frac{21}{20}\right)\)
= ₹ (20 × 21 × 21)
= ₹ 8820
और चक्रवृद्धि ब्याज = A – P
= ₹ (8820 – 8000)
= ₹ 820
![]()
(प्रयास कीजिए – पृष्ठ 139)
प्रश्न 1.
निम्नलिखित में ब्याज संयोजन के लिए समय अवधि और दर ज्ञात कीजिए
1. 1\(\frac{1}{2}\) वर्ष के लिए 8% वार्षिक दर पर उधार ली गई एक राशि पर ब्याज अर्धवार्षिक संयोजित किया जाता है।
2. 2 वर्ष के लिए 4% वार्षिक दर पर उधार ली गई एक राशि पर ब्याज अर्धवार्षिक संयोजित किया जाता है।
हल:
दिया है-
ब्याज की दर = 8% प्रति वर्ष
= \(\frac{8}{2}\)% = 4% प्रति अर्ध वार्षिक
समय = 1\(\frac{1}{2}\) वर्ष = 3 आधे वर्ष
2.
दिया है,
ब्याज की दर = 4% प्रति वर्ष
= \(\frac{4}{2}\)% = 2% प्रति अर्ध वार्षिक
समय = 2 वर्ष = 4 आधे वर्ष
![]()
(सोचिए, चर्चा कीजिए और लिखिए – पृष्ठ 139)
प्रश्न 1.
एक राशि 16% वार्षिक दर पर 1 वर्ष के लिए उधार ली जाती है। यदि ब्याज प्रत्येक तीन महीने बाद संयोजित किया जाता है, तो 1 वर्ष में कितनी बार ब्याज देय होगा?
हल:
दिया हैब्याज की दर = 16% प्रति वर्ष
= \(\frac{16}{4}\) % प्रति तिमाही
= 4% प्रति तिमाही ।
समय = 1 वर्ष = 4 तिमाही
अतः, ब्याज एक वर्ष में 4 बार 4% की दर से देय होगा।
(प्रयास कीजिए – पृष्ठ 140)
प्रश्न:
निम्नलिखित के लिए भुगतान की जाने वाली राशि ज्ञात कीजिए
1. ₹ 2400 पर 5% वार्षिक दर से ब्याज वार्षिक संयोजन करते हुए 2 वर्ष के अंत में।
2. ₹ 1800 पर 8% वार्षिक दर से ब्याज तिमाही संयोजन करते हुए 1 वर्ष के अंत में।
हल:
1. दिया है, P = ₹ 2400, R= 5% प्रति वर्ष
और n = 2 वर्ष
∴ 2 वर्ष बाद मिश्रधन = \(\mathrm{P}\left(1+\frac{\mathrm{R}}{100}\right)^{n}\)
= ₹ \(\left[2400 \times\left(1+\frac{5}{100}\right)^{2}\right]\)
= ₹ \(\left(2400 \times \frac{21}{20} \times \frac{21}{20}\right)\)
= ₹ (6 × 21 × 21)
= ₹ 2646
2.
दिया है, मूलधन = ₹ 1800
दर = 8% वार्षिक = 2% प्रति तिमाही
समय = 1 वर्ष = 4 तिमाही
∴ मिश्रधन = [1800 ×
= ₹ \(\left[1800 \times\left(1+\frac{2}{100}\right)^{4}\right]\)
= ₹ \(\left(1800 \times \frac{51}{50} \times \frac{51}{50} \times \frac{51}{50} \times \frac{51}{50}\right)\)
= ₹ \(\frac{121773618}{62500}\)
= ₹ 1948.38
![]()
(प्रयास कीजिए – पृष्ठ 142)
प्रश्न 1.
₹ 10,500 मूल्य की एक मशीन का 5% की दर से अवमूल्यन होता है। एक वर्ष पश्चात् इसका मूल्य ज्ञात कीजिए।
हल:
यहाँ, P = ₹ 10500, अवमूल्यन = 5% वार्षिक, n= 1 वर्ष
1 वर्ष बाद घटा मूल्य = 10500 ×
= ₹ \(\left[10500 \times\left(1-\frac{5}{100}\right)^{1}\right]\)
= ₹ \(\left(10500 \times \frac{95}{100} \right)\)
= ₹ 9975
प्रश्न 2.
एक शहर की वर्तमान जनसंख्या 12 लाख है। यदि वृद्धि की दर 4% है तो 2 वर्ष पश्चात् शहर की जनसंख्या ज्ञात कीजिए।
हल:
माना 2 वर्ष पश्चात् जनसंख्या P, है।
तो, P2 = ₹ \(\left[P \times\left(1+\frac{4}{100}\right)^{2}\right]\)
= \(\left[P \times\left(\frac{104}{100}\right)^{2}\right]\)
= 1200000 × \(\frac{26}{25} \times \frac{26}{25}\)
= 1920 × 676
= 1297920
अतः, 2 वर्ष बाद जनसंख्या = 1297920