HBSE 8th Class Maths Solutions Chapter 7 घन और घनमूल Intext Questions

Haryana State Board HBSE 8th Class Maths Solutions Chapter 7 घन और घनमूल Intext Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 7 घन और घनमूल Intext Questions

(प्रयास कीजिए – पृष्ठ 119)

प्रश्न 1.
निम्नलिखित संख्याओं में से प्रत्येक के घन के इकाई का अंक ज्ञात कीजिए
(i) 3331
(ii) 8888
(iii) 149
(iv) 1005
(v) 1024
(vi) 77
(vii) 5022
(viii) 53
हल:

(प्रयास कीजिए – पृष्ठ 119)

प्रश्न 1.
निम्न प्रतिरूप का प्रयोग करते हुए, निम्नलिखित संख्याओं को विषम संख्याओं के योग के रूप में व्यक्त कीजिए
(a) 6³
(b) 8³
(c) 7³
हल:
प्रतिरूप-
1 = 1 = 1³
3 + 5 = 8 = 2³
7 + 9 + 11 = 27 = 3³
13 + 15 + 17 + 19 = 64 = 4³
21 + 23 + 25 + 27 + 29 = 125 = 5³
हल:
दिए गए प्रतिरूप का प्रयोग करके पर,
(a) 6³ = 31 + 33 + 35 + 37 + 39 + 41 = 216
(b) 8³ = 57 + 59 + 61 + 63 + 65 + 67+ 69 + 71 = 512
(c) 7³ = 43 + 45 + 47 + 49 + 51 + 53 + 55 = 343

प्रश्न 2.
निम्नलिखित प्रतिरूप को देखिए
2³ – 1³ = 1 + 2 × 1 × 3
3³ – 2³ = 1 + 3 × 2 × 3
4³ – 3³ = 1 + 4 × 3 × 3
उपरोक्त प्रतिरूप का प्रयोग करते हुए निम्नलिखित के मान ज्ञात कीजिए
(i) 7³ – 6³
(ii) 12³ – 11³
(iii) 20³ – 19³
(iv) 51³ – 50³
हल:
दिए गए प्रतिरूप का प्रयोग करके
(i) 7³ – 6³ = 1 + 7 × 6 × 3 = 1 + 126 = 127
(ii) 12³ – 11³ = 1 + 12 × 11 × 3 = 1 + 396 = 397.
(iii) 20³ – 19³ = 1 + 20 × 19 × 3 = 1 + 1140 = 1141
(iv) 51³ – 50³ = 1 + 51 × 50 × 3 = 1 + 7650 = 7651

(प्रयास कीजिए – पृष्ठ 120)

प्रश्न 1.
निम्नलिखित में से कौनसी संख्याएँ पूर्ण घन हैं?
(i) 400
(ii) 3375
(iii) 8000
(iv) 15625
(v) 9000
(vi) 6859
(vii) 2025
(viii) 10648
हल:
(i) 400 का अभाज्य गुणनखंड करने पर

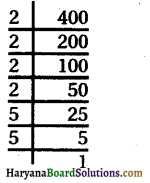
400 = \(\underline{2 \times 2 \times 2}\) × 2 × 5 × 5
चूँकि अभाज्य गुणनखंडों के त्रिक बनाने पर 2 × 5 × 5 शेष बचते हैं।
अतः 400 एक पूर्ण घन संख्या नहीं है।

(ii) 3375
3375 का अभाज्य गुणनखंड करने पर

3375 = \(\underline{3 \times 3 \times 3}\) × \(\underline{5 \times 5 \times 5}\)
चूँकि 3375 के अभाज्य गुणनखंडों के त्रिक बनाने पर कोई भी गुणनखण्ड नहीं बचता है।
अतः 3375 एक पूर्ण घन संख्या नहीं है।

(iii) 8000
8000 का अभाज्य गुणनखंड करने पर-

8000 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × \(\underline{5 \times 5 \times 5}\)
चूँकि 8000 के अभाज्य गुणनखंडों के त्रिक बनाने पर कोई भी गुणनखण्ड नहीं बचता है।
अतः 8000 एक पूर्ण घन संख्या नहीं है।

(iv) 15625
15625 का अभाज्य गुणनखंड करने पर-

15625 = \(\underline{5 \times 5 \times 5}\) × \(\underline{5 \times 5 \times 5}\)
चूँकि 15625 के अभाज्य गुणनखंडों के त्रिक बनाने पर कोई भी गुणनखण्ड नहीं बचता है।
अतः 15625 एक पूर्ण घन संख्या नहीं है।

(v) 9000
9000 का अभाज्य गुणनखंड करने पर-

9000 = \(\underline{5 \times 5 \times 5}\) × 3 × 3 × \(\underline{5 \times 5 \times 5}\)
चूँकि 9000 के अभाज्य गुणनखंडों के त्रिक बनाने पर 3 × 5 शेष बचते है।
अतः 9000 एक पूर्ण घन संख्या नहीं है।

(vi) 6859
6859 का अभाज्य गुणनखंड करने पर-

6859 = \(\underline{19 \times 19 \times 19}\)
चूँकि 6859 के अभाज्य गुणनखंडों के त्रिक बनाने पर कोई भी गुणनखण्ड नहीं बचता है।
अतः 6859 एक पूर्ण घन संख्या है।

(vii) 2025
2025 का अभाज्य गुणनखंड करने पर-

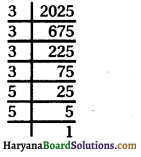
2025 = \(\underline{3 \times 3 \times 3}\) × 3 × 5 × 5
चूँकि 2025 के अभाज्य गुणनखंडों के त्रिक बनाने पर कोई भी गुणनखण्ड नहीं बचता है।
अतः 2025 एक पूर्ण घन संख्या है।

(vii) 10648
10648 का अभाज्य गुणनखंड करने पर-

10648 = \(\underline{2 \times 2 \times 2}\) × \(\underline{11 \times 11 \times 11}\)
चूँकि गुणनखंडों के त्रिक बनाने पर कोई भी गुणनखण्ड नहीं बचता है।
अतः 10648 एक पूर्ण घन संख्या है।

(सोचिए, चर्चा कीजिए और लिखिए – पृष्ठ 121)

प्रश्न 1.
जाँच कीजिए कि निम्नलिखित में से कौनसी संख्याएँ पूर्ण घन हैं-
(i) 2700
(ii) 16000
(iii) 64000
(iv) 900
(v) 125000
(vi) 36000
(vii) 21600
(viii) 10000
(ix) 27000000
(x) 1000
इन पूर्ण घनों में आप क्या प्रतिरूप देखते हैं?
हल:
(i) 2700 के अभाज्य गुणनखण्ड करने पर-
2700 = 2 × 2 × \(\underline{3 \times 3 \times 3}\) × 5 × 5
चूँकि अभाज्य गुणनखंडों के त्रिक बनाने पर 2 × 2 × 5 × 5 शेष बचते है।
अतः 2700 एक पूर्ण घन संख्या नहीं है।

(ii) 16000 के अभाज्य गुणनखण्ड करने पर-
16000 = 2 × 2 × 2 × 2 × 10 × 10 × 10
= 2 × 2 × 2 × 2 × 2 × 2 × 2 × 5 × 5 × 5
= 2 × \(\underline{2 \times 2 \times 2}\) × \(\underline{5 \times 5 \times 5}\)
चूँकि 16000 के अभाज्य गुणनखंडों के त्रिक बनाने पर 2 × 2 × 5 × 5 शेष बचते है।
अतः 16000 एक पूर्ण घन संख्या नहीं है।

(iii) 64000 के अभाज्य गुणनखण्ड करने पर-
64000 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 5 × 5 × 5
= \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) ×\(\underline{2 \times 2 \times 2}\) × \(\underline{5 \times 5 \times 5}\)
चूँकि 64000 के अभाज्य गुणनखंडों त्रिक बनाने पर कोई भी गुणनखण्ड नहीं बचता है।
अतः 64000 एक पूर्ण घन संख्या है।

(iv) 900 के अभाज्य गुणनखण्ड करने पर-
900 = 9 × 100 = 3 × 3 × 10 × 10
= 3 × 3 × 2 × 5 × 2 × 5
= 2 × 2 × 3 × 3 × 5 × 5
चूँकि 900 के अभाज्य गुणनखंडों कोई त्रिक नहीं बचता है।
अतः 900 एक पूर्ण घन संख्या नहीं है।

(v) 125000 के अभाज्य गुणनखण्ड करने पर-
125000 = 125 × 1000
= \(\underline{2 \times 2 \times 2}\) × \(\underline{5 \times 5 \times 5}\) × \(\underline{5 \times 5 \times 5}\)
चूँकि 125000 के अभाज्य गुणनखंडों त्रिक बनाने पर कोई भी गुणनखण्ड नहीं बचता है।
अतः 125000 एक पूर्ण घन संख्या है।

(vi) 36000 के अभाज्य गुणनखण्ड करने पर-
36000 = 36 × 1000
= 6 × 6 × 10 × 10 × 10
= 2 × 3 × 2 × 3 × 2 × 5 × 2 × 5 × 2 × 5
= \(\underline{2 \times 2 \times 2}\) × 2 × 2 × 3 × 3 × \(\underline{5 \times 5 \times 5}\)
चूँकि 125000 के अभाज्य गुणनखंडों त्रिक बनाने पर 2 × 2 × 3 × 3 शेष बचते है।
अतः 125000 एक पूर्ण घन संख्या नहीं है।

(vii) 21600 के अभाज्य गुणनखण्ड करने पर-
21600 = 216 × 100 = 6 × 6 × 6 × 10 × 10
= 2 × 3 × 2 × 3 × 2 × 3 × 2 × 5 × 2 × 5
= \(\underline{2 \times 2 \times 2}\) × 2 × 2 × \(\underline{3 \times 3 \times 3}\) × \(\underline{5 \times 5 \times 5}\)
चूँकि 21600 के अभाज्य गुणनखंडों त्रिक बनाने पर 2 × 2 × 3 × 3 शेष बचते है।
अतः 21600 एक पूर्ण घन संख्या नहीं है।

(viii) 10000 के अभाज्य गुणनखण्ड करने पर-
10000 = 10 × 10 × 10 × 10
= 2 × 5 × 2 × 5 × 2 × 5 × 2 × 5
= \(\underline{2 \times 2 \times 2}\) × 2 × 2 × \(\underline{3 \times 3 \times 3}\) × \(\underline{5 \times 5 \times 5}\)
चूँकि 10000 के अभाज्य गुणनखंडों त्रिक बनाने पर 2 × 2 × 3 × 3 शेष बचते है।
अतः 10000 एक पूर्ण घन संख्या नहीं है।

(ix) 27000000 के अभाज्य गुणनखण्ड करने पर-
27000000 = 27 × 10 × 10 × 10 × 10 × 10 × 10
= 3 × 3 × 3 × 2 × 5 × 2 × 5 × 2 × 5 × 2 × 5 × 2 × 5 × 2 × 5
= \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × \(\underline{3 \times 3 \times 3}\) × \(\underline{5 \times 5 \times 5}\) × \(\underline{5 \times 5 \times 5}\)
चूँकि 27000000 के अभाज्य गुणनखंडों पूर्ण त्रिक बन पर जाते है।
अतः 27000000 एक पूर्ण घन संख्या है।

(x) 1000 के अभाज्य गुणनखण्ड करने पर-
1000 = 10 × 10 × 10
= 2 × 5 × 2 × 5 × 2 × 5
= \(\underline{2 \times 2 \times 2}\) × \(\underline{5 \times 5 \times 5}\)
चूँकि 1000 के अभाज्य गुणनखंडों पूर्ण त्रिक बन पर जाते है।
अतः 1000 एक पूर्ण घन संख्या है।

उपर्युक्त पूर्ण घन संख्याओं 64000, 125000, 27000000 तथा 1000 में हमें यह प्रतिरूप देखने को मिलता है कि इनके अन्त में तीन अथवा छः शून्य हैं। अत: 64,125, 27 तथा 1 भी पूर्ण घन संख्याएँ है।

(सोचिए, चर्चा कीजिए और लिखिए – पृष्ठ 123)

प्रश्न 1.
बताइए कि सत्य है या असत्य-किसी पूर्णांक m के लिए m² < m³ होता है। क्यों?
हल:
माना m = 2 या 3 लेने पर
जब m = 2:
m² = 2 × 2 = 4 और m³ = 2² = 2 × 2 × 2 = 8
स्पष्ट है, 4 < 8 अर्थात् m² < m³

जब m = 3:
m² = 3² = 3 × 3 = 9 और m³ = 3³ = 3 × 3 × 3 = 27
9 < 27, अर्थात् m² < m³

m माना 1 लेने पर
m² = 1² = 1 × 1 = 1 और m³ = 1³ = 1 × 1 × 1 = 1
तो m2 = m3
अतः, हम कह सकते हैं कि धन पूर्णांक (प्राकृत संख्या) के लिए m > 1, m² < m³ सत्य है।
अब, माना m = – 1, -2 लेने पर

जब m = -1:
m² = (-1)² = – 1 × – 1 = 1
और m³ = (-1)³ = – 1 × – 1 × – 1 = – 1
स्पष्ट है, 1 > – 1, अर्थात् m2 > m3

जब m = – 2:
m² = (-2)² = – 2 × – 2 = 4 और
m³ = (-2)³ = – 2 × – 2 × – 2 = – 8
4 > -8, अर्थात् m² > m³

अतः हम कह सकते हैं कि किसी ऋण पूर्णांक m के लिए m² < m³ असत्य है।