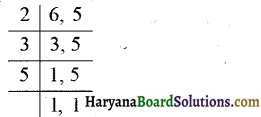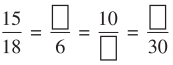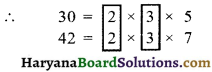Class 6

Haryana State Board HBSE 6th Class Maths Solutions Chapter 3 संख्याओं के साथ खेलना InText Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 3 संख्याओं के साथ खेलना InText Questions

पृष्ठ सं. 51 से (प्रयास कीजिए)

प्रश्न 1.
45, 30 और 36 के सम्भावित गुणनखण्ड ज्ञात कीजिए।
हल :
45 के सम्भावित गुणनखण्डों के लिए,
45 = 1 × 45
45 = 3 × 15
45 = 5 × 9
45 = 9 × 5
यहाँ पर रुकें, क्योंकि 5 तथा 9 पहले आ चुके हैं।
अत: 45 के सम्भावित गुणनखण्ड 1, 3, 5, 9, 15 तथा 45 हैं। उत्तर

30 के सम्भावित गुणनखण्डों के लिए,
30 = 1 × 30
30 = 2 × 15
30 = 3 × 10
30 = 5 × 6
30 = 6 × 5
यहाँ पर रुकें, क्योंकि 5 तथा 6 पहले आ चुके हैं।
अतः 30 के सम्भावित गुणनखण्ड 1, 2, 3, 5, 6, 10, 15 तथा 30 है। उत्तर

अब, 36 के सम्भावित गुणनखण्ड के लिए,
36 = 1 × 36
36 = 2 × 18
36 = 3 × 12
36 = 4 × 9
36 = 6 × 6
यहाँ पर रूकें, क्योंकि दोनों गुणज 6 समान हैं।
अत: 36 के सम्भावित गुणनखण्ड 1, 2, 3, 4, 6, 9, 12, 18 तथा 36 हैं। उत्तर

पृष्ठ सं. 55 से

प्रश्न 1.
ध्यान दीजिए कि 2 × 3 + 1 = 7 एक अभाज्य संख्या है। यहाँ के एक गुणज में 1 जोड़कर एक अभाज्य संख्या प्राप्त की गई है। क्या आप इस प्रकार से कुछ और अभाज्य संख्याएँ ज्ञात कर सकते हैं?
हल :
इसी प्रकार की कुछ और अभाज्य संख्याएँ –
2 × 1 + 1 = 3, जो कि एक अभाज्य संख्या है।
2 × 2 + 1 = 5, जो कि एक अभाज्य संख्या है।
2 × 5 + 1 = 11, जो कि एक अभाज्य संख्या है।
2 × 6 + 1 = 13, जो कि एक अभाज्य संख्या है।
2 × 8 + 1 = 17, जो कि एक अभाज्य संख्या है।
2 × 9 + 1 = 19, जो कि एक अभाज्य संख्या है।

पृष्ठ सं. 59 से

प्रश्न 1.
क्या 7221 संख्या 3 से विभाज्य है?
हल:
संख्या के अंकों का योग = 7 + 2 + 2 + 1 = 12, जो कि 3 से विभाज्य है।
∴ 7221 संख्या 3 से विभाज्य है। उत्तर

पृष्ठ सं. 60 से

प्रश्न 1.
क्या 73512 संख्या 8 से विभाज्य है?
हल :
73512 में 512.8 से विभाज्य है। इसलिए 73512 संख्या 8 से विभाज्य है। [∵ हम जानते हैं कि यदि किसी संख्या के इकाई, दहाई और सैकड़े के अंकों से बनी संख्या 8 से विभाज्य हो, तो वह संख्या 8 से विभाज्य होती है। यहाँ पर 512 ÷ 8 = 64]

पृष्ठ सं. 62 से

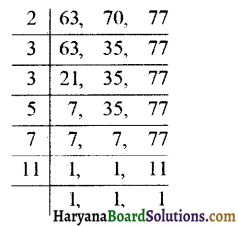
प्रश्न 1.
निम्न युग्मों के उभयनिष्ठ या सार्व गुणनखण्ड क्या हैं?
(a) 8, 20
(b) 9, 15
हल :
(a) 8 के गुणनखण्ड = 1, 2, 4 और 8 और
20 के गुणनखण्ड = 1, 2, 4, 5, 10 और 20
∴ 8 और 20 के उभयनिष्ठ गुणनखण्ड 1, 2 और 4 हैं। उत्तर

(b) 9 के गुणनखण्ड = 1, 3 और 9
15 के गुणनखण्ड = 1, 3, 5 और 15
∴ 9 और 15 के उभयनिष्ठ गुणनखण्ड 1 और 3 हैं। उत्तर

प्रश्न 2.
निम्न के सार्व गुणनखण्ड ज्ञात कीजिए।
(a) 8, 12, 20
(b) 9, 15, 21
उत्तर :
(a) 8, 12, 20
हम देखते हैं कि
8 = 1 × 8
8 = 2 × 4
∴ 8 के सभी गुणनखण्ड 1, 2, 4 और 8 हैं।
अब,
12 = 1 × 12
12 = 2 × 6
12 = 3 × 4
∴ 12 के सभी गुणनखण्ड 1, 2, 3, 4, 6 और 12 हैं।
पुनः,
20 = 1 × 20
20 = 2 × 10
20 = 4 × 5
∴ 20 के सभी गुणनखण्ड 1, 2, 4, 5, 10 और 20 हैं।
अत: 8, 12 और 20 के सार्व गुणनखण्ड 1, 2, 4 हैं उत्तर

(b) 9, 15, 21 हम देखते हैं कि
9 = 1 × 9
9 = 3 × 3
∴ 9 के सभी गुणनखण्ड 1, 3 और 9 हैं।
अब, 15 = 1 × 15
15 = 3 × 5
∴ 15 के सभी गुणखण्ड 1, 3, 5 और 15 हैं।
पुनः, 21 = 1 × 21
21 = 3 × 7
∴ 21 के सभी गुणनखण्ड 1, 3, 7 और 21 हैं।
अतः 9, 15 और 21 के सार्व गुणनखण्ड 1 और 3 हैं।

पृष्ठ सं. 65 से

प्रश्न 1.
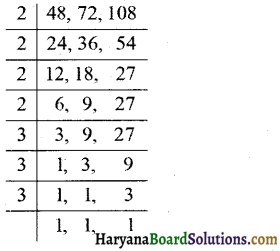
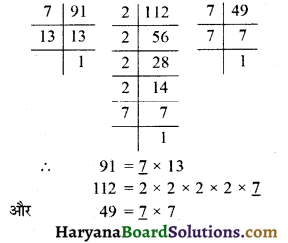
16, 28 और 38 के अभाज्य गुणनखण्ड लिखिए।
हल:

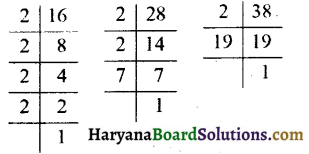
अत:, 16 के अभाज्य गुणनखण्ड = 2 × 2 × 2 × 2
28 के अभाज्य गुणनखण्ड = 2 × 2 × 7
38 के अभाज्य गुणनखण्ड = 2 × 19

पृष्ठ सं. 66 से

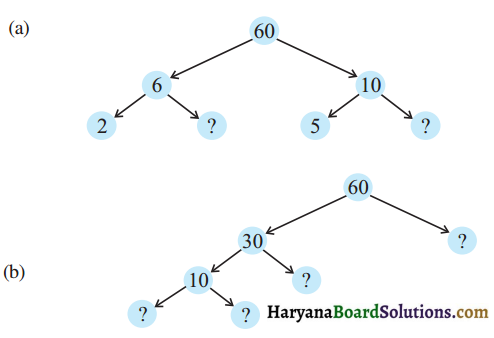
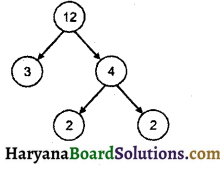
प्रश्न 1.
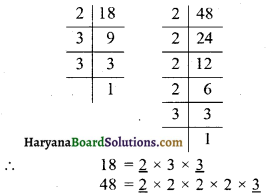
गुणनखण्ड वृक्ष बनाइए-
(a) 8
(b) 12
हल :
(a) 8 का गुणनखण्ड. वृक्ष

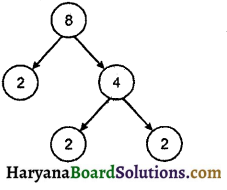
(b) 12 का गुणनखण्ड वृक्ष

पृष्ठ सं. 68 से

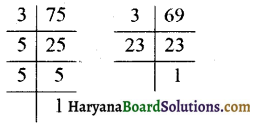
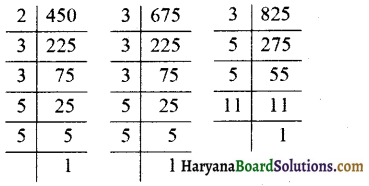
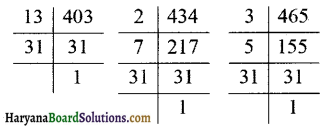
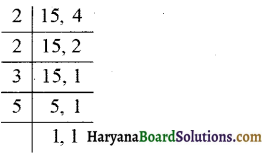
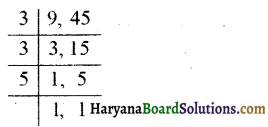
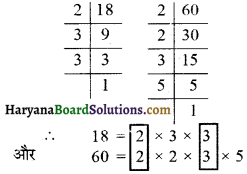
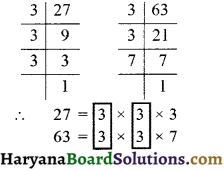
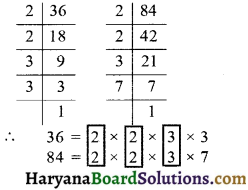
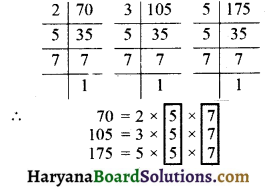
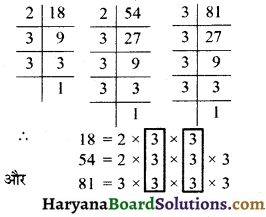
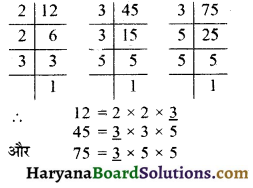
प्रश्न 1.
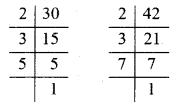
निम्न का म.स. ज्ञात कीजिए
(i) 24 और 36
(ii) 15, 25 और 30
(iii) 8 और 12
(iv) 12, 16 और 28
हल :
(i) दी गई संख्याओं के अभाज्य गुणनखण्ड करने पर,

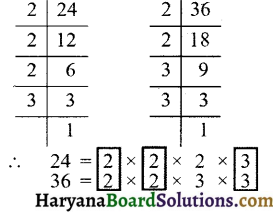
दी गई संख्याओं में सार्व गुणनखण्ड 2, 2 और 3 हैं।
∴ अभीष्ट म.स. = 2 × 2 × 3 = 12. उत्तर

(ii) दी गई संख्याओं के अभाज्य गुणनखण्ड करने पर,

दी गई संख्याओं में सार्व गुणनखण्ड 5 है।
∴ अभीष्ट म.स. = 5 उत्तर

(iii) दी गई संख्याओं के अभाज्य गुणनखण्ड करने पर,

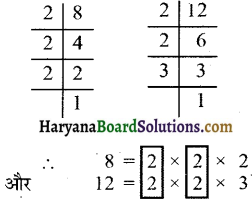
दी गई संख्याओं में सार्वगु नखण्ड 2 दो बार आ रहा
∴ अभीष्ट म.स. = 2 × 2 = 4. उत्तर

(iv) दी गई संख्याओं के अभाज्य गुणनखण्ड करने पर

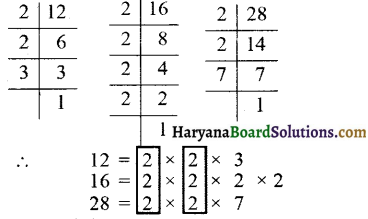
दी गई संख्याओं में सार्व गुणनखण्ड 2 दो बार आ रहा है।
∴ अभीष्ट म.स. = 2 × 2 = 4. उत्तर

पृष्ठ सं. 69 से

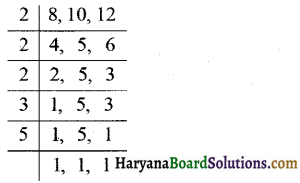
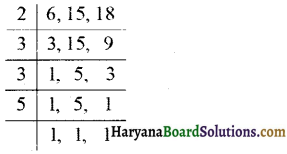
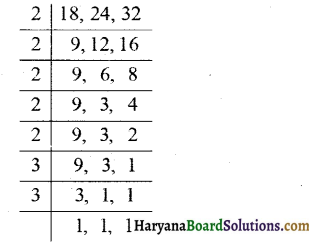
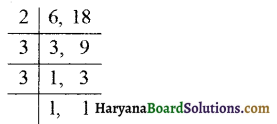
प्रश्न 1.
(a) 8 और 12 ल.स. क्या है?
(b) 4 और 9 का ल.स. क्या है?
(c) 6 और 9 का ल.स. क्या है?
हल :
(a) 8 और 12 का ल.स.

8 और 12 का ल.स. = 2 × 2 × 2 × 3 = 24. उत्तर

(b) 4 और 9 का ल.स.

4 और 9 का ल.स. = 2 × 2 × 3 × 3
= 36 उत्तर

(c) 6 और 9 का ल.स.

6 और 9 का ल.स. = 2 × 3 × 3 = 18. उत्तर

Haryana State Board HBSE 6th Class Maths Solutions Chapter 12 अनुपात और समानुपात Ex 12.3 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 12 अनुपात और समानुपात Exercise 12.3

प्रश्न 1.
यदि 7 मीटर कपड़े का मूल्य ₹ 1470 हो, तो 5 मीटर कपड़े का मूल्य ज्ञात कीजिए।
हल :
7 मीटर कपड़े का मूल्य = ₹ 1470
∴ 1 मीटर कपड़े का मूल्य = ₹ \(\frac{1470}{7}\) = ₹ 2160
∴ 5 मीटर कपड़े का मूल्य = 210 × 5.
= ₹ 1050 उत्तर

प्रश्न 2.
एकता 10 दिन में ₹ 3000 अर्जित करती है। 30 दिन में वह कितना अर्जित करेगी?
हल :
∵ 10 दिनों में एकता अर्जित करती है = ₹ 3000
∴ 1 दिन में एकता अर्जित करेगी = \(\frac{₹ 3000}{10}\) = ₹ 300
∴ 30 दिनों में एकता अर्जित करेगी = 300 × ₹ 30
= ₹ 9000। उत्तर

प्रश्न 3.
यदि पिछले 3 दिन में 276 मिमी वर्षा होती है, तो एक सप्ताह (7 दिन) में कितने सेमी वर्षा होगी? यह मानते हुए कि वर्षा उसी गति से हो रही है।
हल :
∵ 3 दिन में बारिश = 276 मिमी
1 दिन में बारिश = \(\frac{276}{3}\) मिमी = 92 मिमी
∴ 1 सप्ताह (7 दिन) में बारिश = 92 × 7 मिमी
= 644 मिमी। उत्तर

प्रश्न 4.
5 किग्रा गेहूँ का मूल्य ₹ 91.50 है, तो :
(a) 8 किग्रा गेहूँ का मूल्य क्या होगा?
(b) ₹ 183 में कितना गेहूँ खरीदा जा सकता है ?
हल :
(a) ∵ 5 किग्रा गेहूँ का मूल्य = ₹ 91.50
∴ 1 किग्रा गेहूँ का मूल्य = ₹ \(\frac{91.30}{5}\) = ₹ 18.30
∴ 8 किग्रा गेहूँ का मूल्य = 18.30 × 8 रु. = 146.40 रु.। उत्तर

(b) ∵ ₹ 91.50 रु. में गेहूं खरीदा = 5 किग्रा
∴ ₹ 1 में गेहूं खरीदा = \(\frac{5}{91.5}\) किग्रा
= \(\frac{50}{915}\) किग्रा = \(\frac{10}{183}\) किग्रा
∴ ₹ 183 में गेहूँ खरीदा = \(\left(\frac{10}{183} \times 183\right)\) किग्रा
. = 10 किग्रा। उत्तर

प्रश्न 5.
पिछले 30 दिनों में तापमान 15° सेल्सियस गिरता है। यदि तापमान की गिरावट इसी गति से जारी रहे तो, अगले 10 दिनों में तापमान कितने डिग्री गिरेगा?
हल :
30 दिन में तापमान गिरता है = 15° सेल्सियस
∴ 1 दिन में तापमान गिरता है = \(\left(\frac{15}{30}\right)^{\circ}\) से.
= \(\left(\frac{1}{2}\right)^{\circ}\)
∴ अगले 10 दिन में तापमान गिरेग = \(\left(\frac{1}{2} \times 10\right)^{\circ}\)
= 5° संल्सियस। उत्तर

प्रश्न 6.
शाइना 3 महीने का किराया ₹ 15000 देती है। उसे पूरे वर्ष का किराया कितना देना होगा, यदि वर्ष भर किराया समान रहे ?
हल :
∵ 3 माह का किराया = ₹ 15000
∴ 1 माह का किराया = ₹ \(\frac{15000}{3}\) = 5000
∴ 1 साल (12 माह) का किराया = ₹ (5000 × 12)
= ₹ 60,000। उत्तर

प्रश्न 7.
4 दर्जन केलों का मूल्य ₹ 180 है। ₹ 90 में कितने केले खरीदे जा सकते हैं ?
हल :
₹180 में केले खरीदे जाते हैं = 4 दर्जन
= 48 केले
∴ 1 रु. में केले खरीदे जाते हैं = \(\frac{48}{180}\)
∴ ₹ 90 में केले खरीदे जा सकते हैं = \(\frac{48}{180}\) × 90
= 24 केले उत्तर

प्रश्न 8.
72 पुस्तकों का भार 9 किग्रा है। ऐसी 40 पुस्तकों का भार कितना होगा?
हल :
∵ 72 पुस्तकों का भार = 9 किग्रा
∴ 1 पुस्तक का भार = \(\frac{9}{72}\) किग्रा
∴ 40 पुस्तकों का भार = \(\left(\frac{1}{8} \times 40\right)\) किग्रा
= 5 किग्रा। उत्तर

प्रश्न 9.
एक ट्रक में 594 किमी चलने पर 108 लीटर डीजल लगता है। 1650 किमी की दूरी तय करने में कितने लीटर डीजल लगेगा?
हल :
∵ 594 किमी चलने पर डीजल का खर्चा
= 108 लीटर
∴ 1 किमी चलने पर डीजल का खर्चा = \(\frac{108}{594}\) लीटर
= \(\frac{2}{11}\) लीटर
∴ 1650 किमी चलने पर डीजल खर्चा = \(\left(\frac{2}{11} \times 1650\right)\)
= (2 × 150) ली.
= 300 लीटर। उत्तर

प्रश्न 10.
राजू ने ₹ 150 में 10 पेन और मनीष ने ₹ 84 में 7 पेन खरीदे। ज्ञात कीजिए किसने पेन सस्ते खरीदे ?
हल :
∵ राजू ने 10 पेन खरीदे = ₹ 150 में
∴ राजू ने 1 पेन खरीदा = ₹ \(\frac{150}{10}\) = ₹ 15 में
∵ मनीष ने 7 पेन खरीदे = ₹ 84 में
∴ मनीष ने 1 पेन खरीदेगा = ₹ \(\frac{84}{7}\) = ₹ 12 में
अतः 12 < 15
∴ मनीष ने पेन सस्ते खरीदे। उत्तर

प्रश्न 11.
अनीश ने 6 ओवर में 42 रन बनाए और अनूप ने 7 ओवर में 63 रन बनाए। एक ओवर में किसने अधिक रन बनाए ?
हल :
∵ अनीश ने 6 ओवर में रन बनाए = 42
∴ अनीश ने 1 ओवर में रन बनाए = \(\frac{42}{6}\) = 7
∵ अनूप ने 7 ओवर में रन बनाए = 63
∴ अनूप ने 1 ओवर में रन बनाए = \(\frac{63}{7}\) = 9
अतः 9 > 7
∴ अनूप ने प्रति ओवर ज्यादा रन बनाए। उत्तर

Haryana State Board HBSE 6th Class Maths Solutions Chapter 11 बीजगणित InText Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 11 बीजगणित InText Questions

एक समीकरण क्या है?

(पृष्ठ सं. 258 से)

प्रश्न 1.
समीकरणों के कुछ उदाहरण नीचे दिए जा रहे हैं (कुछ समीकरणों में समबद्ध चर भी दिए गये है) :
वांछित रिक्त स्थानों को भरएि :
x + 10 = 30 (चर x)
p – 3 = 7 (चर p)
3n = 21 (चर …)
\(\frac{t}{5}\) = 4 (चर …)
2l + 3 = 7 (चर …)
2m – 3 = 5 (चर …)
हल :
रिक्त स्थान निम्न प्रकार भरे जाएँगे :
x + 10 = 30 (चर x)
p – 3 = 7 (चर p)
3n = 21 (चर n)
\(\frac{t}{5}\) = 4 (चर t)
2l + 3 = 7 (चर l)
2m – 3 = 5 (चर m)

एक समीकरण का इल

(पृष्ठ सं. 259 से)

प्रश्न 1.
निम्नलिखित सारणी की प्रविष्टियों को पूरा कीजिए और स्पष्ट कीजिए कि आपके उत्तर हाँ/नहीं क्यों हैं ?

स्पष्टीकरण :
1. x = 10 के लिए : x + 10 = 10 + 10 ⇒ 20 ≠ 30
2. x = 30 के लिए : x + 10 = 30 + 10 ⇒ 40 ≠ 30
3. x = 20 के लिए : x + 10 = 20 + 10 ⇒ 30 = 30
4. p = 5 के लिए : p – 3 = 5 – 3 ⇒ 2 ≠ 7
5. p = 15 के लिए : p – 3 = 15 – 3 = 15 ≠ 7
6. p = 10 के लिए : p – 3 = 10 – 3 ⇒ 7 = 7
7. n = 9 के लिए : 3n = 3 × 9 ⇒ 27 ≠ 21
8. n = 7 के लिए : 3n = 3 × 7 ⇒ 21 = 21
9. t = 25 के लिए : \(\frac{t}{5}\) = \(\frac{25}{5}\) ⇒ 5 ≠ 4
10. t = 20 के लिए : \(\frac{t}{5}\) = \(\frac{20}{5}\) ⇒ 4 = 4
11. l = 5 के लिए : 2l + 3 = 2 × 5 + 3 ⇒ 13 ≠ 7
12. l = 1 के लिए : 2l + 3 = 2 × 1 + 3 ⇒ 5 ≠ 7
13. l = 2 के लिए : 2l + 3 = 2 × 2 + 3 ⇒ 7 = 7

Haryana State Board HBSE 6th Class Maths Solutions Chapter 3 संख्याओं के साथ खेलना Ex 3.7 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 3 संख्याओं के साथ खेलना Exercise 3.7

प्रश्न 1.
रेणु 75 किग्रा और 69 किग्रा भारों वाली दो खाद की बोरियों खरीदती है। भार के उस बट्टे का अधिकतम मान ज्ञात कीजिए जो दोनों बोरियों के भारों को पूरा-पूरा माप ले।
हल :
75 किग्रा और 69 किग्रा भार वाली दो खाद की बोरियों के लिए भार के उस बट्टे का अधिकतम मान 75 और 69 का म.स. होगा।

∴ 75 = 3 × 5 × 5
69 = 3 × 23
अभीष्ट म.स. = 3
अतः भार के उस बट्टे का अधिकतम मान जो दोनों बोरियों के भारों को पूरा-पूरा माप ले = 3 किया। उत्तर

प्रश्न 2.
तीन लड़के एक ही स्थान से एक साथ कदम उठाकर चलना प्रारम्भ करते हैं। उनके कदमों की माप क्रमश: 63 सेमी, 70 सेमी और 77 सेमी है। इनमें से प्रत्येक कितनी न्यूनतम दूरी तय करे कि वह दूरी पूरे-पूरे कदमों में तय हो जाए?
हल :
तीन लड़के एक ही स्थान से एक साथ चलते हैं व उनके कदमों की माप क्रमशः 63 सेमी, 70 सेमी, 77 सेमी है। न्यूनतम दूरी के लिए ल.स. ज्ञात करना होगा :

∴ अभीष्ट ल.स. = 2 × 3 × 3 × 5 × 7 × 11
= 6930 सेमी
= 69.30 मीटर
∴ प्रत्येक द्वारा तय की गई न्यूनतम दूरी
= 69.30 मीटर। उत्तर

प्रश्न 3.
किसी कमरे की लम्बाई, चौड़ाई और ऊंचाई क्रमशः 825 सेमी,675 सेमी और 450 सेमी है। ऐसा सबसे लम्बा फीता (tape) ज्ञात कीजिए जो कमरे की तीनों विमाओं (dimensions) को पूरा-पूरा माप ले।
हल :
सबसे बड़ा फीता जो तीनों विमाओं को पूरा-पूरा माप सके 825,675 और 450 का म.स. होगा।

∴ 450 = 2 × 3 × 3 × 5 × 5
675 = 3 × 3 × 3 × 5 × 5 और
825 = 3 × 5 × 5 × 11
∴ 450, 675 और 825 का म.स. = 3 × 5 × 5 = 75
∴ सबसे बड़े फीते की अभीष्ट लम्बाई = 75 सेमी। उत्तर

प्रश्न 4.
6, 8 और 12 से विभाज्य तीन अंकों की सबसे छोटी संख्या ज्ञात कीजिए।
हल :
6, 8 और 12 से विभाज्य तीन अंकों की सबसे छोटी संख्या ज्ञात करने के लिए ल.स. ज्ञात करना होगा :

अभीष्ट ल.स. = 2 × 2 × 2 × 3 = 24
∵ तीन अंकों की सबसे छोटी संख्या 100 है।
अब 100 को 24 से भाग देने पर,

∴ 100 से बड़ी (3 अंकों वाली) जो कि 24 से विभाज्य हो, वह संख्या
= 100 + (24 – 4) = 120
अतः अभीष्ट संख्या = 120. उत्तर

प्रश्न 5.
8, 10 और 12 से विभाज्य तीन अंकों की सबसे बड़ी संख्या ज्ञात कीजिए।
हल :
8, 10 और 12 से विभाज्य संख्या उनका ल.स. ही होगा :

ल.स. = 2 × 2 × 2 × 3 × 5 = 120
अब तीन अंकों की सबसे बड़ी संख्या 999 है। इसमें 120 का भाग देने पर,

∴ 3 अंकों की सबसे बड़ी संख्या जो 120 से पूर्णतया विभाज्य हो, वह संख्या = 999 – 39 = 960
अतः अभीष्ट संख्या = 960. उत्तर

प्रश्न 6.
तीन विभिन्न चौराहों की ट्रैफिक लाइट (traffic lights) क्रमशः प्रत्येक 48 सेकण्ड, 72 सेकण्ड और 108 सेकण्ड बाद बदलती है। यदि वे एकसाथ प्रातः 7 बजे बदलें, तो वे पुनः एक साथ कब बदलेंगी?

हल :
जब ट्रैफिक लाइटें पुनः अपने आप बदलेंगी, का अभीष्ट समय 48, 72 और 108 का ल.स. होगा :

ल. स. = 2 × 2 × 2 × 2 × 3 × 3 × 3
= 432 सेकण्ड
अत: अभीष्ट समय = 432 सेकण्ड या 7 मिनट 12 सेकण्ड
अतः ट्रैफिक लाइट पुनः एकसाथ 7 बजकर 7 मिनट 12 सेकण्ड बाद बदलेंगी। उत्तर

प्रश्न 7.
तीन टैंकरों में क्रमशः 403 लीटर, 434 लीटर और 465 लीटर डीजल है। उस बर्तन की अधिकतम धारिता ज्ञात कीजिए जो इन तीनों टैंकरों के डीजल को पूरा-पूरा माप देगा।
हल :
बर्तन की अधिकतम धारिता 403, 434 और 465 लीटर का म.स. है,
हम देखते हैं कि

∴ 403 = 13 × 31,
434 = 2 × 7 × 31
और 465 = 3 × 5 × 31
अभीष्ट म.स. = 31
अत: उस बर्तन की अधिकतम धारिता = 31 लीटर। उत्तर

प्रश्न 8.
वह सबसे छोटी संख्या ज्ञात कीजिए जिसे 6, 15 और 18 से भाग देने पर प्रत्येक दशा में 5 शेष रहे।
हल :
6, 15 और 18 से विभाजित होने वाली सबसे छोटी संख्या उनका ल स. होगा परन्तु अभीष्ट संख्या ल.स. से 5 अधिक होनी चाहिए।

ल.स. = 2 × 3 × 3 × 5 = 90
इस प्रकार अभीष्ट संख्या = (90 + 5) = 95. उत्तर

प्रश्न 9.
चार अंकों की वह सबसे छोटी संख्या ज्ञात कीजिए जो 18, 24 और 32 से विभाज्य है।
हल :
चार अंकों की सबसे छोटी संख्या जो 18, 24 और 32 से विभाजित हो, उनका ल.स. होगा,

ल.स. = 2 × 2 × 2 × 2 × 2 × 3 × 3 = 288.
अब, चार अंकों की सबसे छोटी संख्या 1000 है। इसमें 288 का भाग देने पर,

∴ चार अंकों की सबसे छोटी संख्या जो 288 से पूर्णतया विभाज्य हो।
= 1000 + (288 – 136)
= 1000 + 152
= 1152
अत: 4 अंकों की सबसे छोटी संख्या जो 18, 24 तथा 32 से विभाज्य है = 1152. उत्तर

प्रश्न 10.
निम्नलिखित संख्याओं का ल.स. ज्ञात कीजिए जिनमें एक संख्या सदैव 3 का एक गुणज है :
(a) 9 और 4
(b) 12 और 5
(c) 6 और 5
(d) 15 और 4
प्राप्त ल.स. में एक सामान्य गुण का अवलोकन कीजिए। क्या ल.स. प्रत्येक स्थिति में दोनों संख्याओं का गुणनफल है? क्या हम यह निष्कर्ष निकाल सकते हैं कि दो संख्याओं का ल.स. सदैव 3 का एक गुणज है ?
हल :
पहले हम संख्याओं का ल.स. ज्ञात करते हैं।
(a)

ल.स. = 2 × 2 × 3 × 3 = 36.

(b)

ल.स. = 2 × 2 × 3 × 5 = 60.

(c)

ल.स. = 2 × 3 × 5 = 30.

(d)

ल.स. = 2 × 2 × 3 × 5 = 60
इस प्रकार हम देखते हैं कि सभी प्रश्नों से प्राप्त ल.स. दो संख्याओं का गुणनफल है और यह सदैव 3 का गुणज भी है।

प्रश्न 11.
निम्नलिखित संख्याओं का ल.स.ज्ञात कीजिए जिनमें एक संख्या दूसरी संख्या का एक गुणनखण्ड है।
(a) 5, 20
(b) 6, 18
(c) 12, 48
(d) 9, 45
प्राप्त परिणामों में आप क्या देखते हैं?
हल :
(a) पहले हम संख्याओं का ल.स. ज्ञात करते हैं।

∴ ल.स. = 2 × 2 × 5 = 20.

(b)

∴ ल.स. = 2 × 3 × 3 = 18.

(c)

∴ ल.स. = 2 × 2 × 2 × 2 × 3 = 48.

(d)

∴ ल.स. = 3 × 3 × 5 = 45
इस प्रकार हम देखते हैं कि दो संख्याओं का ल.स. बड़ी संख्या होगी यदि एक संख्या दूसरी का गुणनखण्ड है। उत्तर

Haryana State Board HBSE 6th Class Maths Solutions Chapter 12 अनुपात और समानुपात Ex 12.2 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 12 अनुपात और समानुपात Exercise 12.2

प्रश्न 1.
क्या निम्न राशियाँ समानुपात में हैं :
(a) 15, 45, 40, 120
(b) 33, 121, 9, 96
(c) 24, 28, 36, 48
(d) 32, 48, 70, 210
(e) 4, 6, 8, 12
(f) 33, 44, 75, 100
हल :
(a) 15 : 45 और 40 : 120
चरम पदों का गुणनफल = 15 × 120 = 1800
मध्य पदों का गुणनफल = 45 × 40 = 1800
अतः चरम पदों का गुणनफल = मध्य पदों का गुणनफल
∴ 15, 45, 40, 120 समानुपात में हैं। उत्तर

(b) 33 : 121 और 9 : 96
चरम पदों का गुणनफल = 33 × 96 = 3168
मध्य पदों का गुणनफल = 121 × 9 = 1089
स्पष्ट है, चरम पदों का गुणनफल ≠ मध्य पदों का गुणनफल
इसलिए 33 : 121 और 9 : 96 समानुपात में नहीं हैं। उत्तर

(c) 24 : 28 और 36 : 48
चरम पदों का गुणनफल = 24 × 48 = 1152
मध्य पदों का गुणनफल = 28 × 36 = 1008
चरम पदों का गुणनफल ≠ मध्य पदों का गुणनफल
∴ 24 : 28 : 36 : 48 समानुपात में नहीं हैं। उत्तर

(d) 32 : 48 और 70 : 210
चरम पदों का गुणनफल = 32 × 210 = 6720
मध्य पदों का गुणनफल = 48 × 70 = 3360
चरम पदों का गुणनफल ≠ मध्य पदों का गुणनफल
∴ 32 : 48 और 70 : 210 समानुपात में नहीं हैं। उत्तर

(e) 4 : 6 और 8 : 12
चरम पदों का गुणनफल = 4 × 12 = 48
मध्य पदों का गुणनफल = 6 × 8 = 48
चरम पदों का गुणनफल = मध्य पदों का गुणनफल
∴ 4 : 6 और 8 : 12 समानुपात में हैं। उत्तर

(f) 33 : 44 और 75 : 100
33 : 44 और 75 : 100
चरम पदों का गुणनफल = 33 × 100 = 3300
मध्य पदों का गुणनफल = 44 × 75 = 3300
चरम पदों का गुणनफल = मध्य पदों का गुणनफल
∴ 33 : 40 और 75 : 100 समानुपात में हैं। उत्तर

प्रश्न 2.
निम्न में से प्रत्येक कथनों के आगे सत्य या असत्य लिखिए :
(a) 16 : 24 : : 20 : 30
(b) 21 : 6 : : 35 : 10
(c) 12 : 18 : : 28 : 12
(d) 8 : 9 : : 24 : 27
(e) 5.2 : 3.9 : : 3 : 4
(f) 0.9 : 0.36 : : 10 : 4
हल :
(a) सत्य [क्योकि 16 × 30 = 24 × 20 = 480]
(b) सत्य [क्योंकि 21 × 10 = 6 × 35 = 210]
(c) असत्य [क्योंकि 12 × 12 ≠ 18 × 28]
(d) सत्य [क्योंकि 8 × 27 = 9 × 24 = 216]
(e) असत्य [क्योंकि 5.2 × 4 ≠ 3.9 × 3]
(f) सत्य [क्योंकि 0.9 × 4 = 0.36 × 10 = 3.6]

प्रश्न 3.
क्या निम्न कथन सही हैं ?
(a) 40 व्यक्ति : 200 व्यक्ति = ₹ 15 : ₹ 75
(b) 7.5 लीटर : 15 लीटर = 5 किग्रा : 10 किग्रा
(c) 99 किग्रा : 45 किग्रा = ₹ 44 : ₹ 20
(d) 32 मीटर : 64 मीटर = 6 सेकण्ड : 12 सेकण्ड
(e) 45 किमी : 60 किमी = 12 घण्टे : 15 घण्टे।
हल :
(a) 40 व्यक्ति : 200 व्यक्ति = 40 : 200
= \(\frac{400}{200}=\frac{1}{5}\)
और ₹ 15 : ₹ 75 = 15 : 75 = \(\frac{15}{75}=\frac{1}{5}\)
स्पष्ट है, \(\frac{1}{5}=\frac{1}{5}\)
अतः दिया हुआ कथन सही है। उत्तर

(b) 7.5 लीटर : 15 लीटर = 7.5 : 15
\(\frac{7.5}{15}=\frac{75}{150}=\frac{1}{2}\)
और 5 किग्रा : 10 किग्रा = 5 : 10
= \(\frac{5}{10}=\frac{1}{2}\)
स्पष्ट है, \(\frac{1}{2}=\frac{1}{2}\)
अतः दिया हुआ कथन सही है। उत्तर

(c) 99 किग्रा : 45 किग्रा = 99 : 45 = \(\frac{99}{45}=\frac{11}{5}\)
और ₹ 44 : ₹ 20 = 44 : 20 = \(\frac{44}{20}=\frac{11}{5}\)
स्पष्ट है, \(\frac{11}{5}=\frac{11}{5}\)
अतः दिया हुआ कथन सही है। उत्तर

(d) 32 मी. : 64 मी. = 32 : 64 = \(\frac{32}{64}=\frac{1}{2}\)
और 6 सेकण्ड : 12 सेकण्ड = 6 : 12 = \(\frac{6}{12}=\frac{1}{2}\)
स्पष्ट है, \(\frac{1}{2}=\frac{1}{2}\)
अतः दिया हुआ कथन सही है। उत्तर

(e) 45 किमी : 60 किमी = 45 : 60 = \(\frac{45}{60}=\frac{3}{4}\)
और 12 घण्टे : 15 घण्टे = 12 : 15 = \(\frac{12}{15}=\frac{4}{5}\)
स्पष्ट है \(\frac{3}{4} \neq \frac{4}{5}\)
अतः दिया हुआ कथन सही नहीं है। उत्तर

प्रश्न 4.
जाँचिए कि क्या निम्न अनुपात, समानुपात बनाते हैं। यदि समानुपात बनता हो, तो मध्य पद और चरम पद भी लिखिए :
(a) 25 सेमी: 1 मीटर और ₹ 40 : ₹ 160
(b) 39 लीटर : 65 लीटर और 6 बोतल : 10 बोतल
(c) 2 किग्रा : 80 किग्रा और 25 ग्राम : 625 ग्राम
(d) 200 मिली : 2.5 लीटर और ₹ 4 : ₹ 50।
हल :
(a) 25 सेमी : 1 मीटर = 25 सेमी : 100 सेमी
(∵ 1 मीटर = 100 सेमी)
= 25 : 100
= \(\frac{25}{100}=\frac{1}{4}\)
और ₹40 : ₹ 160 = 40 : 160
= \(\frac{40}{160}=\frac{1}{4}\)
स्पष्ट है, \(\frac{1}{4}=\frac{1}{4}\)
∴ 25 सेमी : 1 मीटर और ₹ 40 : ₹ 160 समानुपात में हैं।
इनके मध्य पद 100 और 40 तथा चरम पद 25 और 160 हैं। उत्तर

(b) 39 लीटर : 65 लीटर = 39 : 65 = \(\frac{39}{65}=\frac{3}{5}\)
और 6 बोतल : 10 बोतल = 6 : 10 = \(\frac{6}{10}=\frac{3}{5}\)
स्पष्ट है, \(\frac{3}{5}=\frac{3}{5}\)
इस प्रकार 39 लीटर : 65 लीटर और 6 बोतल : 10 : बोतल समानुपात में हैं।
∴ इनके मध्य पद 65 और 6 और चरम पद 39 और 10 हैं। उत्तर

(c) 2 किग्रा : 80 किग्रा = 2 : 80 = \(\frac{2}{80}=\frac{1}{40}\)
और 25 ग्रा. 625 ग्रा. = 25 : 625 = \(\frac{25}{625}=\frac{1}{25}\)
स्पष्ट है, \(\frac{1}{40} \neq \frac{1}{25}\)
∴ 2 किग्रा : 80 किग्रा और 25 ग्राम : 625 ग्राम समानुपात में नहीं हैं। उत्तर

(d) 200 मिली : 2.5 लीटर
(∵ 1 लीटर = 100 मिली)
= 200 मिली : 2500 मिली
= 200 : 2500
= \(\frac{200}{2500}=\frac{2}{25}\)
और ₹ 4 : ₹ 50 = 4 : 50
= \(\frac{4}{50}=\frac{2}{25}\)
स्पष्ट है, \(\frac{2}{25}=\frac{2}{25}\)
∴ 200 मिली : 2.5 लीटर और ₹4 : ₹ 50 समानुपात में हैं।
इनके मध्य पद 2.5 और 4 तथा चरम पद 200 और 50 हैं। उत्तर

ऐकिक विधि :

और अभीष्ट इकाइयों का मान = (1 इकाई का मान) × (इकाइयों की संख्या)

Haryana State Board HBSE 6th Class Maths Solutions Chapter 12 अनुपात और समानुपात Ex 12.1 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 12 अनुपात और समानुपात Exercise 12.1

प्रश्न 1.
एक कक्षा में 20 लड़कियाँ और 15 लड़के हैं। अनुपात ज्ञात कीजिए :
(a) लड़कियों की संख्या का लड़कों की संख्या से।
(b) लड़कियों की संख्या का कुल विद्यार्थियों की संख्या से।
हल :
लड़कियों की संख्या = 20
लड़कों की संख्या = 15
कक्षा में कुल विद्यार्थियों की संख्या = (20 + 15) = 35
(a) लड़कियों की संख्या का लड़कों की संख्या के अनुपात
= 20 : 15 [पहली और दूसरी राशि के म.स. = 5 से भाग देने पर]
= \(\frac{20 \div 5}{15 \div 5}=\frac{4}{3}\)
=4 : 3 उत्तर

(b) लड़कियों की संख्या का कुल विद्यार्थियों की संख्या से अनुपात
= 20 : 35 [पहली और दूसरी राशि के म.स. = 5 से भाग देने पर]
= \(\frac{20 \div 5}{35 \div 5}=\frac{4}{7}\)
= 4 : 7 उत्तर

प्रश्न 2.
30 विद्यार्थियों की कक्षा में 6 फुटबाल, 12 क्रिकेट और बाकी टेनिस पसन्द करते हैं। अनुपात ज्ञात कीजिए:
(a) फुटबाल पसंद करने वालों की संख्या का टेनिस पसन्द करने वालों की संख्या से।
(b) क्रिकेट प्रेमियों का कुल विद्यार्थियों की संख्या से।

हल :
छात्रों की कुल संख्या = 30
फुटबाल प्रेमियों की संख्या = 6
किक्रेट प्रेमियों की संख्या = 12
टेनिस प्रेमियों की संख्या = 30 – (6 + 12)
= 30 – 18 = 12

(a) फुटबाल पसन्द करने वालों की संख्या का टेनिस पसन्द करने वालों की संख्या से अनुपात
= 6 : 12 [पहली और दूसरी राशि के म.स. = 6 से भाग देने पर]
= 1 : 2

(b) क्रिकेट प्रेमियों का कुल विद्यार्थियों की संख्या से अनुपात
= 12 : 30 [पहली और दूसरी राशि के म.स. = 6 से भाग देने पर]
= 2 : 5 उत्तर

प्रश्न 3.
आकृति को देखकर अनुपात निकालिए :

(a) आयत के अन्दर के सभी त्रिभुजों की संख्या का वृत्तों की संख्या से।
(b) आयत के अंदर के सभी वर्गों की संख्या का सभी आकृतियों से।
(c) आयत के अन्दर के सभी वृत्तों की संख्या का सभी आकृतियों से।
हल :
दी गई आकृति से देखते हैं कि
त्रिभुजों की संख्या = 3
वृत्तों की संख्या = 2
वर्गों की संख्या = 2
आकृतियों की कुल संख्या = 3 + 2 + 2 = 7
(a) त्रिभुजों की संख्या का वृत्तों की संख्या से अनुपात
= 3 : 2 उत्तर

(b) वर्गों की संख्या का सभी आकृतियों से अनुपात
= 2 : 7 उत्तर

(c) वृत्तों की संख्या का सभी आकृतियों से अनुपात
= 2 : 7 उत्तर

प्रश्न 4.
हामिद और अख्तर ने एक घण्टे में क्रमश: 9 किमी और 12 किमी की दूरी तय की। हामिद और अख्तर की चालों का अनुपात ज्ञात कीजिए।
हल :
हम जानते हैं कि

हामिद की चाल = \(\frac{9}{1}\) = 9 किमी/घण्टा
अख्तर की चाल = \(\frac{12}{1}\) = 12 किमी/घण्टा
∴ हामिद और अख्तर की चालों का अनुपात . = 9 : 12 [दोनों राशियों को उनके म.स. = 3 से भाग देने पर]
= 3 : 4. उत्तर

प्रश्न 5.
रिक्त स्थानों को भरिए :

[क्या ये तुल्य अनुपात हैं?]
हल :

प्रश्न 6.
निम्न में से प्रत्येक का अनुपात ज्ञात कीजिए :
(a) 81 का 108 से
(b) 98 का 63 से
(c) 33 किमी का 121 किमी से
(d) 30 मिनट का 45 मिनट से
हल :
(a) 81 का 108 से = 81 : 108
= 3 : 4 उत्तर
[पहली और दूसरी राशि को उनके म.स. = 27 से भाग देने पर]

(b) 98 का 63 से = 98 : 63
= 14 : 9 उत्तर
[पहली और दूसरी राशि को उनके म.स. = 7 से भाग देने पर]

(c) 33 किमी का 121 किमी से = 33 : 121
= 3 : 11 उत्तर
[पहली और दूसरी राशि को उनके म.स. = 11 से भाग देने पर]

(d) 30 मिनट का 45 मिनट से = 30 : 45 .
= 2 : 3 उत्तर
[पहली व दूसरी राशि को उनके म.स. = 15 से भाग देने पर]

प्रश्न 7.
निम्न में से प्रत्येक का अनुपात ज्ञात कीजिए :
(a) 30 मिनट का 1.5 घंटे
(b) 40 सेमी का 1.5 मी
(c) 55 पैसे का 1 रुपया
(d) 500 मिली का 2 लीटर
हल :
(a) 30 मिनट का 1.5 घण्टे से (∵ 1 घण्टा = 60 मिनट)
= 30 मिनट : 1.5 × 60 मिनट
= 30 मिनट : 90 मिनट
= 30 : 90 = 1 : 3 उत्तर
[पहली और दूसरी राशि को उनके म.स. = 30 से भाग देने पर]

(b) 40 सेमी का 1.5 मीटर (∵ 1 मीटर = 100 सेमी)
= 40 सेमी : 1.5 × 100 सेमी
= 40 सेमी : 150 सेमी
= 40 : 150
= 4 : 15 उत्तर
[पहली और दूसरी राशि को उनके म.स. = 10 से भाग देने पर]

(c) 55 पैसे का 1 रुपया (∵ 1 रुपया = 100 पैसे)
= 55 पैसे : 1 × 100 पैसे
= 55 पैसे : 100 पैसे
= 55 : 100 = 11 : 20 उत्तर
[पहली और दूसरी राशि को उनके म.स. = 5 से भाग देने पर]

(d) 500 मिली का 2 लीटर (∵ 1 लीटर = 100 मिली)
= 500 मिली : 2 × 1000 मिली
= 500 मिली : 2000 मिली
= 500 : 2000
= 1 : 4 उत्तर
[पहली और दूसरी राशि को उनके म.स. = 500 से भाग देने पर]

प्रश्न 8.
एक वर्ष में सीमा ₹ 1,50,000 कमाती है और ₹ 50,000 की बचत करती है। प्रत्येक का अनुपात ज्ञात कीजिए :
(a) सीमा द्वारा किया गया व्यय और उसकी बचत का
(b) सीमा द्वारा की गई बचत और उसके द्वारा किए गए व्यय का
हल :
सीमा की आय = ₹ 1,50,000
सीमा की बचत = ₹ 50,000
सीमा का व्यय = 1,50,000 – 50,000
= ₹ 1,00,000

(a) सीमा द्वारा किया गया व्यय और उसकी बचत का अनुपात
= 1,00,000 : 50,000
= 2 : 1 उत्तर
[पहली और दूसरी राशि को उनके म.स. = 50,000 से भाग देने पर]

(b) सीमा द्वारा की गई बचत और उसके द्वारा किए गए व्यय का अनुपात
= ₹ 50,000 : ₹ 1,00,000
= 1 : 2 उत्तर
[पहली और दूसरी राशि को उनके म.स. = 50,000 से भाग देने पर]

प्रश्न 9.
एक विद्यालय में 3300 विद्यार्थी और 102 शिक्षक हैं। शिक्षकों की संख्या का विद्यार्थियों की संख्या से अनुपात ज्ञात कीजिए।
हल :
शिक्षकों की संख्या = 102
विद्यार्थियों की संख्या = 3300
∴ शिक्षकों की संख्या का विद्यार्थियों की संख्या से अनुपात
= 102 : 3300 = 17 : 550
[पहली और दूसरी संख्या के उनके म.स. = 6 से भाग देने पर]

प्रश्न 10.
एक कॉलेज में 4320 विद्यार्थियों में से 2300 लड़कियाँ हैं। अनुपात निकालिए:
(a) लड़कियों की संख्या और कुल विद्यार्थियों की संख्या का
(b) लड़कों की संख्या और लड़कियों की संख्या का
(c) लड़कों की संख्या और कुल विद्यार्थियों की संख्या का
हल :
विद्यार्थियों की कुल संख्या = 4320
लड़कियों की संख्या = 2300
∴ लड़कों की संख्या = 4320 – 2300
= 2020

(a) लड़कियों की संख्या और कुल विद्यार्थियों की संख्या का अनुपात = 2300 : 4320
= 115 : 216
[पहली और दूसरी संख्या को उनके म.स. = 20 से भाग देने पर]

(b) लड़कों की संख्या लड़कियों की संख्या का अनुपात = 2020 : 2300
= 101 : 115
[पहली और दूसरी संख्या को उनके म.स. = 20 से भाग देने पर]

(c) लड़कों की संख्या और कुल विद्यार्थियों की संख्या का अनुपात
= 2020 : 4320 = 101 : 216
[पहली और दूसरी संख्या को उनके म.स. = 20 से भाग देने पर] उत्तर

प्रश्न 11.
एक विद्यालय के 1800 विद्यार्थियों में से 750 ने बास्केट बाल, 800 ने क्रिकेट और शेष ने टेबल टेनिस खेलना पसन्द किया है। यदि एक छात्र केवल एक खेल चुने, तो अनुपात ज्ञात कीजिए :

(a) बास्केट बाल खेलने वालों और टेबल टेनिस खेलने वालों का।
(b) क्रिकेट खेलने वालों और बास्केट बाल खेलने वालों का।
(c) बास्केट बाल खेलने वालों और कुल विद्यार्थियों का।
हल :
विद्यार्थियों की कुल संख्या = 1800
बास्केट बाल खेलने वाले छात्रों की संख्या = 750
किक्रेट खेलने वाले छात्रों की संख्या = 800
∴ टेबल टेनिस खेलने वाले छात्रों की संख्या = 1800 – (750 + 800)
= 1800 – 1550 = 250

(a) बास्केट बॉल खेलने वालों और टेबल टेनिस खेलने वालों का अनुपात = 750 : 250 = 3 : 1 उत्तर
[पहली और दूसरी संख्या को उनके म.स. = 250 से भाग देने पर]

(b) क्रिकेट खेलने वालों और बास्केट बॉल खेलने वालों का अनुपात
= 800 : 750 = 16 : 15 उत्तर
[पहली और दूसरी संख्या को उनके म.स. = 50 से भाग देने पर]

(c) बास्केट बाल खेलने वालों और कुल विद्यार्थियों का अनुपात
= 750 : 1800 = 5 : 12 . उत्तर
[पहली और दूसरी संख्या को उनके म.स. = 150 से भाग देने पर]

प्रश्न 12.
एक दर्जन पेन का मूल्य ₹ 180 है और 8 बॉल पेन का मूल्य ₹ 56 है। पेन के मूल्य का बॉल पेन के मूल्य से अनुपात ज्ञात कीजिए।
हल :
∵ 1 दर्जन (12) पेन का मूल्य = ₹ 180
∴ 1 पेन का मूल्य = \(\frac{180}{12}\) = ₹ 15
∵ 8 बॉल पेन का मूल्य = ₹ 56
∴ 1 बॉल पेन का मूल्य = ₹\(\frac{56}{8}\) = ₹ 7
अतः पेन के मूल्य का बॉल पेन के मूल्य से अनुपात
= 1 पेन का मूल्य : 1 बॉल पेन का मूल्य
= ₹ 15 : ₹ 7 = 15 : 7 उत्तर

प्रश्न 13.
कथन को देखें : एक हॉल की चौड़ाई और लंबाई का अनुपात 2 : 5 है। निम्न सारणी को पूरा कीजिए जो कि हॉल की कुछ संभव चौड़ाई व लम्बाई दिखाती है :

हल :

प्रश्न 14.
शीला और संगीता के बीच 20 पेनों को 3 : 2 में बाँटिए।
हल :
दोनों राशियों के अनुपातों का योग = 3 + 2 = 5
पेनों की कुल संख्या = 20
∴ शीला को प्राप्त पेन = \(\frac{3}{5}\) × 20 = 3 × 4 = 12
और संगीता को प्राप्त पेन = \(\frac{2}{5}\) × 20 = 2 × 4 = 8.
अतः शीला को 12 पैन और संगीता को 8 पैन उत्तर

प्रश्न 15.
एक माता अपनी बेटी श्रेया और भूमिका में 36 रुपयों को उनकी आयु के अनुपात में बाँटना चाहती है। यदि श्रेया की आयु 15 वर्ष और भूमिका की आयु 12 वर्ष हो, तो श्रेया और भूमिका को कितना-कितना मिलेगा ?
हल :
श्रेया की आयु = 15 वर्ष
भूमिका की आयु = 12 वर्ष
श्रेया और भूमिका की आयु का अनुपात = 15 : 12 = 5 : 4
∵ माता 36 रुपयों को उनकी आयु के अनुपात में बाँटना चाहती है।
∴ अनुपातों का योग = 5 + 4 = 9
श्रेया का हिस्सा = \(\frac{5}{9}\) × 36
= 5 × 4 = 20 रुपये
भूमिका का हिस्सा = \(\frac{4}{9}\) × 36.
=4 × 4 = 16 रुपये

प्रश्न 16.
पिता की वर्तमान आयु 42 वर्ष और उसके पुत्र की 14 वर्ष है। अनुपात ज्ञात कीजिए:
(a) पिता की वर्तमान आयु का और पुत्र की वर्तमान आयु से;
(b) पिता की आयु का पुत्र की आयु से, जब पुत्र 12 वर्ष का था;
(c) 10 वर्ष बाद की पिता की आयु का 10 वर्ष बाद पुत्र की आयु से;
(d) पिता की आयु का पुत्र की आयु से, जब पिता 30 वर्ष का था।
हल :
पिता की वर्तमान आयु = 42 वर्ष
पुत्र की वर्तमान आयु = 14 वर्ष
(a) पिता और उसके पुत्र की वर्तमान आयु का अनुपात
= 42 वर्ष : 14 वर्ष
= 42 : 14 [दोनों राशियों को उनके
म.स. = 14 से भाग देने पर] उत्तर
= 3 : 1

(b) जब 2 साल पहले पुत्र की आयु 12 वर्ष थी तब पिता की आयु = (42 – 2) = 40 वर्ष
अभीष्ट अनुपात = 40 वर्ष : 12 वर्ष
= 40 : 12 = 10 : 3 उत्तर
[दोनों राशियों को उनके म.स. = 4 से भाग देने पर]

(c) 10 वर्ष बाद,
पिता की आयु = (42 + 10) वर्ष = 52 वर्ष
पुत्र की आयु = (14 + 10) वर्ष = 24 वर्ष
10 वर्ष बाद पिता और पुत्र की आयु का अनुपात
= 52 वर्ष : 24 वर्ष
= 52 : 24 उत्तर
= 13 : 6 [दोनों राशियों को उनके म.स. = 4 से भाग देने पर]

(d) जब पिता 30 वर्ष का था, यानि कि (12 वर्ष पहले) तब पुत्र की आयु = (14 – 12) वर्ष = 2 वर्ष
∴ अभीष्ट अनुपात = 30 वर्ष : 2 वर्ष
= 30 : 2 उत्तर
= 15 : 1 [दोनों राशियों को उनके म.स. = 2 से भाग देने पर]

Haryana State Board HBSE 6th Class Maths Solutions Chapter 3 संख्याओं के साथ खेलना Ex 3.6 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 3 संख्याओं के साथ खेलना Exercise 3.6

प्रश्न 1.
निम्नलिखित संख्याओं के म.स. ज्ञात कीजिए :
(a) 18, 48
(b) 30, 42
(c) 18, 60
(d) 27, 63
(e) 36, 84
(f) 34, 102
(g) 70, 105, 175
(h) 91, 112, 49
(i) 18, 54, 81
(j) 12, 45, 75
हल :
(a) दी गई संख्याओं के अभाज्य गुणनखण्ड करने पर

दी गई संख्याओं में सार्व गुणनखण्ड 2 और 3 हैं।
∴ अभीष्ट म.स. = 2 × 3 = 6. उत्तर

(b) दी गई संख्याओं के अभाज्य गुणनखण्ड करने पर,


दी गई संख्याओं में सार्व गुणनखण्ड 2 और 3 हैं।
∴ अभीष्ट म.स. = 2 × 3 = 6. उत्तर

(c) दी गई संख्याओं के अभाज्य गुणनखण्ड करने पर

दी गई संख्याओं में सार्व गुणनखण्ड 2 और 3 हैं।
∴ अभीष्ट म.स. = 2 × 3 = 6. उत्तर

(d) दी गई संख्याओं के अभाज्य गुणनखण्ड करने पर,

दी गई संख्याओं में सार्व गुणनखण्ड 3 दो बार आ रहा है।
∴ अभीष्ट म.स. = 3 × 3 = 9. उत्तर

(e) दी गई संख्याओं के अभाज्य गुणनखण्ड करने पर

दी गई संख्याओं में सार्व गुणनखण्ड 2 (दो बार) और 3 एक बार आ रहा है।
∴ अभीष्ट म.स. = 2 × 2 × 3 = 12. उत्तर

(f) दी गई संख्याओं के अभाज्य गुणनखण्ड करने पर

दी गई संख्याओं में सार्व गुणनखण्ड 2 और 17 हैं।
∴ अभीष्ट म.स. = 2 × 17 = 34. उत्तर

(g) दी गई संख्याओं के अभाज्य गुणनखण्ड करने पर

दी गई संख्याओं के सार्व गुणनखण्ड 5 और 7 हैं।
∴ अभीष्ट म.स. = 5 × 7 = 35. उत्तर

(h) दी गई संख्याओं के अभाज्य गुणनखण्ड करने पर

दी गई संख्याओं में सार्व गुणनखण्ड 7 एक बार आ रहा हैं।
∴ अभीष्ट म.स. = 7 उत्तर

(i) दी गई संख्याओं के अभाज्य गुणनखण्ड करने पर,

दी गई संख्याओं में सार्व गुणनखण्ड 3 दो बार आ रहा
∴ अभीष्ट म.स. = 3 × 3 = 9. उत्तर

(j) दी गई संख्या के अभाज्य गुणनखण्ड करने पर

दी गई संख्याओं में सार्व गुणनखण्ड 3 एक बार आ रहा है।
∴ अभीष्ट म.स. = 3 उत्तर

प्रश्न 2.
निम्न का म.स. क्या है ?
(a) दो क्रमागत संख्याएँ
(b) दो क्रमागत सम संख्याएँ
(c) दो क्रमागत विषम संख्याएँ।
हल :
(a) दो क्रमागत संख्याओं का म.स. = 1
(b) दो क्रमागत सम संख्याओं का म.स. = 2
(c) दो क्रमागत विषम संख्याओं का म.स. = 1

प्रश्न 3.
अभाज्य गुणनखण्डन द्वारा दो सह-अभाज्य संख्याओं 4 और 15 का म. स. इस प्रकार ज्ञात किया गया :
4 = 2 × 2 और 15 = 3 × 5
चूंकि इन गुणनखण्डों में कोई अभाज्य सार्व गुणनखण्ड नहीं है, इसलिए 4 और 15 का म.स. शून्य है। क्या यह उत्तर सही है ? यदि नहीं, तो सही म.स. क्या है?
हल :
यह उत्तर सही नहीं है। 4 तथा 15 का म.स. निम्न प्रकार ज्ञात कर सकते हैं।
4 = 1 × 2 × 2
और 15 = 1 × 3 × 5
अतः म.स. = 1
वास्तव में दो सह-अभाज्य संख्याओं का म.स. सदैव 1 होता है। इसलिए 4 तथा 15 का म.स. 1 होगा। क्योंकि 4 तथा 15 दोनों सह-अभाज्य संख्याएँ हैं। उत्तर

Haryana State Board HBSE 6th Class Maths Solutions Chapter 3 संख्याओं के साथ खेलना Ex 3.5 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 3 संख्याओं के साथ खेलना Exercise 3.5

प्रश्न 1.
निम्नलिखित में से कौन-से कथन सत्य हैं ?
(a) यदि कोई सख्या 3 से विभाज्य है, तो वह १ से भी विभाज्य होती है।
(b) यदि एक संख्या 9 से विभाज्य है, तो वह 3 से भी अवश्य विभाज्य होगी।
(c) एक संख्या 18 से भी विभाज्य होती है, यदि वह 3 और 6 दोनों से विभाज्य हो।
(d) यदि एक संख्या 9 और 10 दोनों से विभाज्य हो, तो वह 90 से भी विभाज्य होगी।
(e) यदि दो संख्याएँ सह-अभाज्य हों, तो इनमें से कम-से-कम एक अवश्य ही अभाज्य संख्या होगी।
(f) से विभाज्य सभी संख्याएँ 8 से भी अवश्य विभाज्य होनी चाहिए।
(g) 8 से विभाज्य सभी संख्याएँ 4 से विभाज्य होनी चाहिए।
(h) यदि कोई संख्या दो संख्याओं को अलग-अलग पूरा-पूरा विभाजित करती है, तो वह उनके योग को भी पूरा-पूरा विभाजित करेगी।
(i) यदि कोई संख्या दो संख्याओं के योग को पूरी तरह विभाजित करती है, तो वह उन दोनों संख्याओं को अलग-अलग भी विभाजित करेगी।
हल :
(a) असत्य,
(b) सत्य,
(c) असत्य,
(d) सत्य,
(e) असत्य,
(f) असत्य,
(g) सत्य,
(h) सत्य,
(i) असत्य।

प्रश्न 2.
यहाँ 60 के लिए दो भिन्न-भिन्न गुणनखण्ड वृक्ष दिए हैं। इनमें अज्ञात संख्याएँ लिखिए।

हल :
(a) ∵ 6 = 2 × 3 और 10 = 5 × 2
∴ अज्ञात संख्याएँ 3 और 2 हैं। उत्तर
(b) 60 = 30 × 2
30 = 10 × 3
10 = 2 = 5
∴ अज्ञात संख्याएँ 2, 3, 2 और 5 हैं।

प्रश्न 3.
एक भाज्य संख्या के अभाज्य गुणनखण्ड में किन गुणनखण्डों को सम्मिलित नहीं किया जाता है ?
हल :
एक भाज्य संख्या के अभाज्य गुणनखण्ड में, 1 और स्वयं वह संख्या को सम्मिलित नहीं किया जाता है। उत्तर

प्रश्न 4.
चार अंकों की सबसे बड़ी संख्या लिखिए और उसे अभाज्य गुणनखण्डन के रूप में व्यक्त कीजिए।
हल :
चार अंकों की सबसे बड़ी संख्या = 9999
अभाज्य गुणनखण्ड करने पर,

∴ 9999 के अभाज्य गुणनखण्ड = 3 × 3 × 11 × 101. उत्तर

प्रश्न 5.
पाँच अंकों की सबसे छोटी संख्या लिखिए और उसे अभाज्य गुणनखण्डन के रूप में व्यक्त कीजिए।
हल :
पाँच अंकों की सबसे छोटी संख्या = 10000
अभाज्य गुणनखण्ड करने पर,

∴ 10000 के अभाज्य गुणनखण्ड
= 2 × 2 × 2 × 2 × 5 × 5 × 5 × 5. उत्तर

प्रश्न 6.
1729 के सभी अभाज्य गुणनखण्ड ज्ञात कीजिए और उन्हें आरोही क्रम में व्यवस्थित कीजिए। अब दो क्रमागत अभाज्य गुणनखण्डों में यदि कोई सम्बन्ध है, तो लिखिए।
हल :
अभाज्य गुणन करने पर,

1729 के अभाज्य गुणनखण्डों को आरोही क्रम में व्यवस्थित करने पर
∴ 1729 के अभाज्य गुणनखण्ड = 7 × 13 × 19
दो क्रमागत अभाज्य गुणनखण्डों के बीच सम्बन्ध बताता है कि दो क्रमागत अभाज्य गुणनखण्डों के बीच अन्तर 6 है। उत्तर

प्रश्न 7.
तीन क्रमागत संख्याओं का गुणनफल सदैव 6 से विभाज्य होता है। इस कथन को कुछ उदाहरणों की सहायता से स्पष्ट कीजिए।
हल :
तीन क्रमागत संख्याओं का गुणनफल निम्न प्रकार है:
1 × 2 × 3 = 6
11 × 12 × 13 = 1716
2 × 3 × 4 = 24
17 × 18 × 19 = 5814
3 × 4 × 5 = 60
20 × 21 × 22 = 9240
∵ प्रत्येक गुणनफल में इकाई के अंक 6.4 तथा 0 हैं।
∴ प्रत्येक 2 से विभाज्य है।
और इन गुणनफलों के अंकों का योग 6, 9, 12, 15 तथा 18 है जो कि 3 से विभाज्य है।
∴ प्रत्येक गुणनफल 6 से विभाज्य है।
अत: तीन क्रमागत संख्याओं का गुणनफल सदैव 6 से विभाज्य होता है। उत्तर

प्रश्न 8.
दो क्रमागत विषम संख्याओं का योग 4 से विभाज्य होता है। कुछ उदाहरण लेकर इस कथन का सत्यापन कीजिए।
हल :
दो क्रमागत विषम संख्याओं का योग करने पर,
3 + 5 = 8
5 + 7 = 12
7 + 9 = 16
53 + 55 = 108
55 + 57 = 112
57 + 59 = 116
प्रत्येक योग में इकाई व दहाई के स्थान के अंकों से बनी संख्याएँ 8, 12, 16 हैं, जो कि 4 से विभाज्य हैं।
∴ प्रत्येक दो क्रमागत विषम संख्याओं का योग 4 से विभाज्य होता है।

प्रश्न 9.
निम्न में से किन व्यंजकों में अभाज्य गुणनखण्ड किए गए हैं:
(a) 24 = 2 × 3 × 4
(b) 56 = 1 × 7 × 2 × 2 × 2
(c) 70 = 2 × 5 × 7
(d) 54 = 2 × 3 × 9
हल :
(a) में 4 के और गुणनखण्ड हो सकते हैं। अत: ये अभाज्य गुणनखण्ड नहीं हैं।
(b) में अन्य और गुणनखण्ड नहीं हो सकते हैं। अत: ये अभाज्य गुणनखण्ड हैं।
(c) में अन्य और गुणनखण्ड नहीं हो सकते हैं। अत: ये अभाज्य गुणनखण्ड हैं।
(d) में 9 के और गुणनखण्ड हो सकते हैं। अतः ये अभाज्य गुणनखण्ड नहीं है।
अत: (b) और (c) में अभाज्य गुणनखण्ड किए गए हैं। उत्तर

प्रश्न 10.
बिना भाग किए ज्ञात कीजिए कि क्या 25110 संख्या 45 से विभाज्य है ?
हल :
संख्या 45 = 5 × 9, जहाँ 5 और 9 सह-अभाज्य संख्याएँ हैं।
∴ 25110 की भाजकता की जाँच 5 और 9 से करने पर,
25110 में इकाई का अंक = 0
∴ यह संख्या 5 से विभाज्य है।
संख्या के अंकों का योग = 2 + 5 + 1 + 1 + 0 = 9, जो कि 9 से विभाज्य है।
∴ यह संख्या भी 9 से विभाज्य है।
अत: 25110 संख्या 45 से विभाज्य है।

प्रश्न 11.
संख्या 18, 2 और 3 दोनों से विभाज्य है। यह 2 × 3 = 6 से भी विभाज्य है। इसी प्रकार, एक संख्या 4 और 6 दोनों से विभाज्य है। क्या हम कह सकते हैं कि यह संख्या 4 × 6 = 24 से भी विभाज्य होगी? यदि नहीं, तो अपने उत्तर की पुष्टि के लिए एक उदाहरण दीजिए।
हल :
यह जरूरी नहीं है, क्योंकि 12, 36, 60 इत्यादि संख्याएँ 4 और 6 दोनों से विभाज्य हैं। परन्तु ये संख्याएँ 4 × 6 = 24 से विभाज्य नहीं हैं।

प्रश्न 12.
मैं चार भिन्न-भिन्न अभाज्य गुणनखण्डों वाली सबसे छोटी संख्खा हूँ। क्या आप मुझे ज्ञात कर सकते हैं?
हल :
चार भिन्न-भिन्न अभाज्य छोटी संख्याएँ 2, 3, 5 और 7 हैं।
∴ अभीष्ट संख्या = 2 × 3 × 5 × 7 = 210. उत्तर

Haryana State Board HBSE 6th Class Maths Solutions Chapter 10 क्षेत्रमिति Ex 10.3 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 10 क्षेत्रमिति Exercise 10.3

प्रश्न 1.
उन आयतों का क्षेत्रफल ज्ञात कीजिए जिनकी भुजाएँ नीचे दी गई हैं:
(a) 3 सेमी और 4 सेमी
(b) 12 मीटर और 21 मीटर
(c) 2 किमी और 3 किमी
(d) 2 मीटर और 70 सेमी
हल :
(a) आयत की लम्बाई = 4 सेमी
आयत की चौड़ाई = 3 सेमी
आयत का क्षेत्रफल = लम्बाई × चौड़ाई
= 4 सेमी × 3 सेमी
= 12 वर्ग सेमी उत्तर

(b) आयत की लम्बाई = 21 मीटर
आयत की चौड़ाई = 12 मीटर
आयत को क्षेत्रफल = लम्बाई × चौड़ाई
= 21 मीटर × 12 मीटर
= 252 वर्ग मीटर उत्तर

(c) आयत की लम्बाई = 3 किमी
आयत की चौड़ाई = 2 किमी
आयत का क्षेत्रफल = लम्बाई × चौड़ाई
= 3 किमी × 2 किमी
= 6 वर्ग किमी उत्तर

(d) आयत की लम्बाई = 2 मीटर = 2 × 100 सेमी
= 200 सेमी
आयत की चौड़ाई = 70 सेमी
आयत का क्षेत्रफल = लम्बाई × चौड़ाई
= 200 सेमी × 70 सेमी
= 14000 वर्ग सेमी उत्तर

प्रश्न 2.
उन वर्गों का क्षेत्रफल ज्ञात कीजिए जिनकी भुजाएं निम्नलिखित हैं :
(a) 10 सेमी
(b) 14 सेमी
(c) 5 मी
हल :
(a) वर्ग की भुजा = 10 सेमी
वर्ग का क्षेत्रफल = (भुजा)²
= 10 × 10 वर्ग सेमी
= 100 वर्ग सेमी उत्तर

(b) वर्ग की भुजा = 14 सेमी
वर्ग का क्षेत्रफल = 14 × 14 वर्ग सेमी
= 196 वर्ग सेमी उत्तर

(c) वर्ग की भुजा = 5 मीटर
वर्ग का क्षेत्रफल = भुजा × भुजा
= 5 × 5 वर्ग मीटर
= 25 वर्ग मीटर उत्तर

प्रश्न 3.
तीन आयतों की विमाएं निम्नलिखित हैं :
(a) 9 मीटर और 6 मीटर
(b) 3 मीटर और 17 मीटर
(c) 4 मीटर और 14 मीटर
इनमें से किसका क्षेत्रफल सबसे अधिक है और किसका सबसे कम ?
हल :
(a) आयत का क्षेत्रफल = (9 × 6) वर्ग मीटर
= 54 वर्ग मीटर

(b) आयत का क्षेत्रफल = (3 × 17) वर्ग मीटर
= 51 वर्ग मीटर

(c) आयत का क्षेत्रफल = (4 × 14) वर्ग मीटर
= 56 वर्ग मीटर
तीनों आयतों के क्षेत्रफलों से स्पष्ट है कि 56 सबसे बड़ी संख्या और 51 सबसे छोटी संख्या है।
∴ आयत (c) का सबसे बड़ा क्षेत्रफल है और आयत (b) का सबसे कम क्षेत्रफल है। उत्तर

प्रश्न 4.
50 मीटर लम्बाई वाले एक आयताकार बगीचे का क्षेत्रफल 300 वर्ग मीटर है। बगीचे की चौड़ाई ज्ञात कीजिए।
हल :
आयताकार बगीचे का क्षेत्रफल = 300 वर्ग मीटर
आयताकार बगीचे की लम्बाई = 50 मीटर
हम जानते हैं कि
आयत का क्षेत्रफल = लम्बाई × चौड़ाई

अतः बगीचे की चौड़ाई = 6 मीटर उत्तर

प्रश्न 5.
500 मीटर लम्बाई तथा 200 मीटर चौड़ाई वाले एक आयताकार भूखण्ड पर 8 रु. प्रति 100 वर्ग मीटर की दर से टाइल लगाने का व्यय ज्ञात कीजिए।
हल :
आयताकार भूखण्ड का क्षेत्रफल = ल. × चौ.
= 500 × 200 वर्ग मीटर
= 100000 वर्ग मीटर
∵ 100 वर्ग मीटर भूखण्ड पर टाइल लगाने का व्यय = ₹ 8
∴ 1 वर्ग मीटर भूखण्ड पर टाइल लगाने का व्यय = ₹ \(\frac{8}{100}\)
∴ 100000 वर्ग मीटर भूखण्ड पर टाइल लगाने का व्यय
= ₹ \(\frac{8}{100}\) × 100000
= ₹ 8,000
अतः टाइल लगाने का व्यय ₹ 8,000 है। उत्तर

प्रश्न 6.
एक मेज के ऊपरी पृष्ठ की माप 2 मीटर × 1 मीटर 50 सेमी है। मेज का क्षेत्रफल वर्ग मीटर में ज्ञात कीजिए।
हल :
मेज की ऊपरी सतह की लम्बाई = 2 मीटर
मेज की ऊपरी सतह की चौड़ाई = 1 मीटर 50 सेमी
= 1.50 मीटर
मेज का क्षेत्रफल = लम्बाई × चौड़ाई
= 2 × 1.50 वर्ग मीटर
= 3 वर्ग मीटर उत्तर

प्रश्न 7.
एक कमरे की लम्बाई 4 मीटर 25 सेमी तथा चौड़ाई 3 मीटर 50 सेमी है। कमरे के फर्श को ढकने के लिए कितने वर्ग मीटर गलीचे की आवश्यकता होगी?
हल :
कमरे की लम्बाई = 4 मीटर 25 सेमी
= 4.25 मीटर
कमरे की चौड़ाई = 3 मीटर 50 सेमी = 3.50 मीटर कमरे के फर्श को ढकने के लिए गलीचे की आवश्यकता
= कमरे के फर्श का क्षेत्रफल
= लम्बाई × चौड़ाई
= (4.25 × 3.50) वर्ग मीटर
= 14.875 वर्ग मीटर उत्तर

प्रश्न 8.
एक फर्श की लम्बाई 5 मीटर तथा चौड़ाई 4 मीटर है। 3 मीटर भुजा वाले एक वर्गाकार गलीचे को फर्श पर बिछाया गया है। फर्श के उस भाग का क्षेत्रफल ज्ञात 3 मीटर कीजिए जिस पर गलीचा नहीं बिछा है।
हल :
कमरे के फर्श की लम्बाई = 5 मीटर
और कमरे के फर्श की चौड़ाई = 4 मीटर
कमरे के फर्श का क्षेत्रफल = (5 × 4) वर्ग मीटर
= 20 वर्ग मीटर
वर्गाकार गलीचे का क्षेत्रफल = भुजा × भुजा
= 3 × 3 वर्ग मी = 9 वर्ग मीटर
फर्श के उस भाग का क्षेत्रफल जिस पर गलीचा नहीं बिछा है
= कमरे के फर्श का क्षेत्रफल – गलीचे का क्षेत्रफल
= (20 – 9) वर्ग मीटर = 11 वर्ग मीटर उत्तर

प्रश्न 9.
5 मीटर लम्बाई तथा 4 मीटर चौड़ाई वाले एक आयताकार भूखण्ड पर 1 मीटर भुजा वाली वर्गाकार फूलों की 5 क्यारियाँ बनाई जाती हैं। भूखण्ड के शेष भाग का क्षेत्रफल ज्ञात कीजिए।
हल :
आयताकार भूखण्ड का क्षेत्रफल
= लम्बाई × चौड़ाई
= 5 मीटर × 4 मीटर = 20 वर्ग मीटर
वर्गाकार 1 क्यारी का क्षेत्रफल = भुजा × भुजा
= 1 × 1 वर्ग मीटर
= 1 वर्ग मीटर
∴ 5 वर्गाकार क्यारियों का क्षेत्रफल = 5 × 1 वर्ग मीटर
= 5 वर्ग मीटर
भूखण्ड के शेष भाग का क्षेत्रफल
= 20 वर्ग मीटर – 5 वर्ग मीटर
= 15 वर्ग मीटर उत्तर

प्रश्न 10.
निम्नलिखित आकृतियों को आयतों में तोडिए। इनका क्षेत्रफल ज्ञात कीजिए (भुजाओं की माप सेमी में दी गई है)।

हल :
(a) माना आकृति को A, B, C और D आयतों में विभाजित किया जाता है :

आयत (A) का क्षेत्रफल
= (3 × 3) वर्ग सेमी
= 9 वर्ग सेमी

आयत (B) का क्षेत्रफल
= (1 × 2) वर्ग सेमी
= 2 वर्ग सेमी

आयत (C) का क्षेत्रफल = (3 × 3) वर्ग सेमी.
= 9 वर्ग सेमी

आयत (D) का क्षेत्रफल = (4 × 2) वर्ग सेमी = 8 वर्ग सेमी
∴ आकृति का कुल क्षेत्रफल = आयत A का क्षे. + आयत B का क्षे. + आयत C का क्षे. + आयत D का क्षे.
= (9 + 2 + 9 + 8) वर्ग सेमी
= 28 वर्ग सेमी उत्तर

(b) दी गई आकृति को A, B और C आयतों में विभाजित कर क्षेत्रफल ज्ञात करते हैं :

आयत (A) का क्षेत्रफल
= (2 × 1) वर्ग सेमी
= 2 वर्ग सेमी
आयत (B) का क्षेत्रफल = (5 × 1) वर्ग सेमी
= 5 वर्ग सेमी
आयत (C) का क्षेत्रफल = (2 × 1) वर्ग सेमी
= 2 वर्ग सेमी
∴ आकृति का कुल क्षेत्रफल = तीनों आयतों के क्षेत्रफलों का योग
= (2 + 5 + 2) वर्ग सेमी
= 9 वर्ग सेमी उत्तर

प्रश्न 11.
निम्नलिखित आकृतियों को आयतों में तोड़िए और प्रत्येक का क्षेत्रफल ज्ञात कीजिए (भुजाओं की माप सेमी में दी गई है) :

हल :
(a) दी गई आकृति को A, B दो आयतों में तोड़कर प्रत्येक का क्षेत्रफल ज्ञात करने पर,

आयत (A) का क्षेत्रफल
= (10 × 2) वर्ग सेमी
= 20 वर्ग सेमी
आयत (B) का क्षेत्रफल
= (10 × 2) वर्ग सेमी
= 20 वर्ग सेमी
∴ आकृति का कुल क्षेत्रफल = (20 + 20) वर्ग सेमी
= 40 वर्ग सेमी उत्तर

(b) दी गई आकृति को 7 सेमी भुजा वाले 5 वर्गों में तोड़कर क्षेत्रफल ज्ञात करने पर,

प्रत्येक वर्ग का क्षेत्रफल
= भुजा × भुजा
= 7 × 7 वर्ग सेमी
= 49 वर्ग सेमी
∴ 5 वर्गों का क्षेत्रफल = 49 × 5 वर्ग सेमी
अतः दी गयी आकृति का क्षेत्रफल = 245 वर्ग सेमी। उत्तर

(c) दी गई आकृति को दो आयतों A और B में तोड़कर प्रत्येक का क्षेत्रफल ज्ञात करने पर,

आयत (A) का क्षेत्रफल
= (5 × 1) वर्ग सेमी
= 5 वर्ग सेमी
∴ आयत (B) का क्षेत्रफल
= (4 × 1) वर्ग सेमी
= 4 वर्ग सेमी
∴ आकृति का कुल क्षेत्रफल
= आयत A का क्षे. + आयत B का क्षे.
= 5 वर्ग सेमी + 4 वर्ग सेमी = 9 वर्ग सेमी उत्तर

प्रश्न 12.
एक टाइल की माप 5 सेमी × 12 सेमी है। एक क्षेत्र को पूर्णतया ढकने के लिए ऐसी कितनी टाइलों की आवश्यकता होगी, जिसकी लम्बाई और चौड़ाई क्रमशः है
(a) 144 सेमी और 100 सेमी
(b) 70 सेमी और 36 सेमी है।
हल :
(a) क्षेत्र का क्षेत्रफल = लम्बाई × चौड़ाई
= 144 सेमी × 100 सेमी
= 14400 वर्ग सेमी

एक टाइल का क्षेत्रफल = 5 सेमी × 12 सेमी
= 60 वर्ग सेमी

(b) क्षेत्र का क्षेत्रफल = लम्बाई × चौड़ाई
= 70 सेमी × 36 सेमी
= 2520 वर्ग सेमी
एक टाइल का क्षेत्रफल = 5 सेमी × 12 सेमी
= 60 सेमी

Haryana State Board HBSE 6th Class Maths Solutions Chapter 3 संख्याओं के साथ खेलना Ex 3.4 Textbook Exercise Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 3 संख्याओं के साथ खेलना Exercise 3.4

प्रश्न 1.
निम्न के सार्व गुणनखण्ड ज्ञात कीजिए :
(a) 20 और 28
(b) 15 और 25
(c) 35 और 50
(d) 56 और 120
हल :
(a) हम देखते हैं कि
20 = 1 × 20
20 = 2 × 10
20 = 4 × 5
∴ 20 के सभी गुणनखण्ड 1, 2, 4, 5, 10 और 20 हैं।
इसी प्रकार, 28 = 1 × 28
28 = 2 × 14
28 = 4 × 7
∴ 28 के सभी गुणनखण्ड 1, 2, 4, 7, 14 और 28 है।
अत: 20 और 28 के सार्व गुणनखण्ड 1, 2 और 4 हैं। उत्तर

(b) हम देखते हैं कि
15 = 1 × 15
15 = 3 × 5
∴ 15 के सभी गुणनखण्ड 1, 3, 5 और 15 हैं।
इसी प्रकार, 25 = 1 × 25
25 = 5 × 5
∴ 25 के सभी गुणनखण्ड 1, 5 और 25 हैं।
अत: 15 और 25 के सार्व गुणनखण्ड 1 और 5 हैं। उत्तर

(c) हम देखते हैं कि
35 = 1 × 35
35 = 5 × 7
∴ 35 के सभी गुणनखण्ड 1, 5, 7 और 35 हैं।
इसी प्रकार, 50 = 1 × 50
50 = 2 × 25
50 = 5 × 10
∴ 50 के सभी गुणनखण्ड 1, 2, 5, 10, 25 और 50 हैं।
∴ 35 और 50 के सार्व मुणनखण्ड 1 और 5 हैं। उत्तर

(d) हम देखते हैं कि
56 = 1 × 56
56 = 2 × 28
56 = 4 × 14
56 = 7 × 8
∴ 56 के सभी गुणनखण्ड 1, 2, 4, 7, 8, 14, 28 और 56 हैं।
इसी प्रकार, 120 = 1 x 120
120 = 2 × 60
120 = 3 × 40
120 = 4 × 30
120 = 5 × 24
120 = 6 × 20
120 = 8 × 15
120 = 10 × 12
∴ 120 के सभी गुणनखण्ड 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60 और 120 हैं।
अत: 56 और 120 के सार्व गुणनखण्ड 1, 2, 4 और 8 हैं। उत्तर

प्रश्न 2.
निम्न के सार्व गुणनखण्ड ज्ञात कीजिए :
(a) 4, 8 और 12
(b) 5, 15 और 25
हल :
(a) हम देखते हैं कि
4 = 1 × 4
4 = 2 × 2
∴ 4 के सभी गुणनखण्ड 1, 2 और 4 हैं।
अब, 8 = 1 × 8 ,
8 = 2 × 4
8 के सभी गुणनखण्ड 1, 2, 4 और 8 हैं।
पु: 12 = 1 × 12
12 = 2 × 6
12 = 3 × 4
∴ 12 के सभी गुणनखण्ड 1, 2, 3, 4, 6 और 12 हैं।
अतः 4, 8 और 12 के सार्व गुणनखण्ड 1,2 और 4 हैं। उत्तर

(b) हम देखते हैं कि
5 = 1 × 5
∴ 5 के सभी गुणनखण्ड 1 और 5 हैं।
अब, 15 = 1 × 15
15 = 3 × 5
∴ 15 के सभी गुणनखण्ड 1, 3, 5 और 15 हैं।
पुनः, 25 = 1 × 25
25 = 5 × 5
∴ 25 के सभी गुणनखण्ड 1, 5 और 25 हैं।
अत: 5, 15 और 25 के सार्व गुणनखण्ड 1 और 5 हैं। उत्तर

प्रश्न 3.
निम्न के प्रथम तीन सार्व गुणज ज्ञात कीजिए :
(a) 6 और 8
(b) 12 और 18
हल :
(a) 6 के गुणज = 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72 …..
और 8 के गुणज = 8, 16, 24, 32, 40, 48, 56, 64, 72, …………..
अत: 6 और 8 के प्रथम तीन सार्व गुणज = 24, 48 और 72 हैं।

(b) 12 के गुणज = 12, 24, 36, 48, 60, 72, 84, 96, 108…….
और 18 के गुणज = 18, 36, 54, 72, 90, 108, ……..
अत: 12 और 18 के प्रथम तीन सार्व गुणज 36, 72 और 108 हैं। उत्तर

प्रश्न 4.
100 से छोटी ऐसी सभी संख्याएँ लिखिए जो 3 और 4 के सार्व गुणज हैं।
हल :
3 और 4 के उभयनिष्ठ गुणज 3 × 4 का गुणज = 12 है।
∴ 100 से छोटी सभी संख्याएँ जो 3 और 4 के सार्व गुणज हैं:
12, 24, 36, 48, 60, 72, 84 और 96. उत्तर

प्रश्न 5.
निम्नलिखित में से कौन-सी संख्याएँ सह-अभाज्य हैं ?
(a) 18 और 35
(b) 15 और 37
(c) 30 और 415
(d) 17 और 68
(e) 216 और 215
(f) 81 और 16
हल :
(a) 18 के गुणनखण्ड = 1, 2, 3, 6, 9 और 18
तथा 35 के गुणनखण्ड = 1, 5, 7 और 35 हैं।
∵ 18 और 35 का सार्व गुणनखण्ड 1 है।
अतः 18 और 35 सह-अभाज्य संख्याएँ हैं। उत्तर

(b) 15 के गुणनखण्ड 1, 3, 5 और 15 हैं तथा 37 के गुणनखण्ड 1 और 37 हैं।
∵ 15 और 37 का सार्व गुणनखण्ड 1 है।
अतः 15 और 37 सह-अभाज्य संख्याएँ हैं। उत्तर

(c) 30 के गुणनखण्ड = 1, 2, 3, 5, 6, 10, 15 और 30
तथा 415 के गुणनखण्ड = 1, 5, 83 और 415
∵ 30 और 415 के सार्व गुणनखण्ड 1 और 5 हैं।
अत: 30 और 415 सह-अभाज्य संख्याएँ नहीं हैं। उत्तर

(d) 17 के गुणनखण्ड = 1 और 17
तथा 68 के गुणनखण्ड = 1, 4, 17 और 68
∵ 17 और 68 के सार्व गुणनखण्ड 1 और 17 है।
अतः 17 और 68 सह-अभाज्य संख्याएँ नहीं हैं। उत्तर

(e) 216 के गुणनखण्ड = 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 27, 36, 54, 72, 108 और 216 हैं
तथा 215 के गुणनखण्ड = 1, 5, 43 और 215 हैं
∵ 216 और 215 का सार्व गुणनखण्ड 1 है।
अत: 216 और 215 सह-अभाज्य संख्याएँ हैं।

(f) 81 के गुणनखण्ड = 1, 3, 9, 27 और 81
तथा 16 के गुणनखण्ड = 1, 2, 4, 8 और 16
∵ 81 और 16 का सार्व गुणनखण्ड 1 है।
अत: 81 और 16 सह-अभाज्य संख्याएँ हैं। उत्तर

प्रश्न 6.
एक संख्या 5 और 12 दोनों से विभाज्य है। किस अन्य संख्या से यह संख्या सदैव विभाजित होगी?
हल :
दी गई संख्या 5 और 12 दोनों से विभाज्य है तब यह संख्या एक अन्य संख्या 5 × 12 = 60 से सदैव विभाजित होगी। अर्थात् वह अन्य संख्या 60 है जिससे दी गई संख्या सदैव विभाजित होगी। उत्तर

प्रश्न 7.
एक संख्या 12 से विभाज्य है। और कौन-सी संख्याएँ हैं जिनसे यह संख्या विभाज्य होगी?
हल :
12 के गुणनखण्ड = 1, 2, 3, 4, 6 और 12 संख्या 12 से विभाज्य है।
∴ यह संख्या 12 के गुणनखण्डों से भी विभाज्य होगी।
अत: वह संख्या 1, 2, 3 और 4 और 6 से भी विभाज्य होगी। उत्तर

Haryana State Board HBSE 6th Class Maths Solutions Chapter 13 सममिति InText Questions and Answers.

Haryana Board 6th Class Maths Solutions Chapter 13 सममिति InText Questions

प्रयास कीजिए (पृष्ठ सं. 283 से)

प्रश्न 1.
आपके ज्यामिति बॉक्स में दो सेट स्क्वेयर हैं। क्या ये सममित हैं ?
हल :
ज्यामिति बॉक्स में दो सेट स्क्वेयर हैं :
(i) 30° – 60° – 90° सेट स्क्वे यर
(ii) 45° – 45° – 90° सेट स्क्वे यर।
हाँ, ये सेट स्कवेयर सममित हैं।

प्रश्न 2.
अपनी कक्षा में उपलब्ध कुछ वस्तुओं की सूची बनाइए, जैसे श्यामपट्ट (black board), मेज, दीवार, पाठ्यपुस्तक इत्यादि। इनमें से कौन-सी वस्तुएँ सममित हैं और कौन-सी सममित नहीं हैं? क्या आप उनमें से सममित वस्तुओं की सममित रेखाएँ पहचान सकते हैं ?
हल :
कक्षा में उपलब्ध कुछ वस्तुओं की सूची निम्न प्रकार है :
श्यामपट्ट, डस्टर, चॉक, कुर्सी, मेज, दरवाजा, पंखा, बल्ब, कूड़ेदान आदि।
हाँ, ये सभी वस्तुएँ सममित हैं. उन्हें सममित रेखा पर पहचान सकते हैं।

पृष्ठ सं. 285 से

एक पतंग
आपके ज्यामिति बॉक्स में दो सेट स्क्वेयर में से एक के कोणों की माप 30°, 60° और 90° है।

ऐसे ही दो समान सेट स्क्वेयर लीजिए। उन्हें आपस में मिलाकर रखिए और एक पतंग बनाइए, जैसा आकृति में दिखाया गया है।

प्रश्न 1.
इस आकृति में कितनी सममित रेखाएँ हैं? क्या आप सोचते हैं कि कुछ आकृतियों में एक से अधिक सममित रेखाएँ होती हैं।
हल :
इस आकृति में केवल एक ऊर्ध्वाधर रेखा सममित रेखा है।
हाँ, कुछ आकृतियों में एक से अधिक सममित रेखाएँ होती हैं।

एक आयत :
आयत को लम्बाई की ओर मोड़ते हैं जिससे कि एक आधा भाग, दूसरे आधे भाग को पूर्णतया टैंक ले।

प्रश्न 2.
क्या यह मोड़ एक सममित रेखा है? क्यों ?
हल :
हाँ, यह मोड़ एक सममित की रेखा है, क्योंकि इस प्रकार बनी आकृति के दोनों भाग पूर्णतः समान हैं। इसको खोलकर पुनः एक बार चौड़ाई की ओर से समान तरीके से मोड़ते हैं।

प्रश्न 3.
क्या यह दूसरा मोड़ भी सममित रेखा है? क्यो ?
हल :
हाँ, यह दूसरा मोड़ भी सममित रेखा है, क्योंकि इस प्रकार बनी आकृति के दोनों भाग पूर्णतः समान है।

प्रश्न 4.
क्या ये दो रेखाएँ सममित रेखाएँ हैं ?
हल :
हाँ, ये दो रेखाएँ सममित रेखाएँ हैं।

प्रयास कीजिए (पृष्ठ सं. 285 से)

प्रश्न 1.
दो या अधिक सेट स्क्वेयर को मिलाकर आप जितनी भी आकृतियाँ बना सकते हैं, बनाइए। इन्हें वांकित कागज पर बनाइए और इनकी सममित रेखाएँ बताइए।
हल :
(i) दो समान सेट स्क्वे यरों 30°, 60° और 90° को मिलाने से निम्न आकृतियाँ प्राप्त होती हैं :

इन आकृतियों को सममित रेखा द्वारा दर्शाया गया है।

(ii) दो समान सेट स्क्वे यरों 45°, 45° और 90° को मिलाने से अग्र आकृतियाँ प्राप्त होती हैं :

समकोण समुद्विबाहु त्रिभुज इन आकृतियों की सममित रेखा, बिन्दुकित रेखा द्वारा दर्शाई गई है।

(iii) तीन समान सेट स्क्वे यरों 45° – 45° – 90 को मिलाने पर निम्न आकृति प्राप्त होती है :

पृष्ठ सं. 291 से

प्रश्न 1.
यदि आप दर्पण के सामने 100 सेमी की दरी पर हैं। आपका प्रतिबिम्ब कहाँ होगा? यदि आप दर्पण की ओर चलते हैं, तो आपका प्रतिबिम्ब किस प्रकार चलता
हल :
यदि हम दर्पण के सामने 100 सेमी की दूरी पर है तो हमारा प्रतिबिम्ब हमसे 200 सेमी दूरी पर बनेगा। पुनः हम दर्पण की ओर चलते है, तो हमारा प्रतिबिम्ब दोगुनी गति से चलता हम प्रतीत होगा।