Haryana State Board HBSE 10th Class Home Science Solutions Chapter 5 धन का प्रबन्ध Textbook Exercise Questions and Answers.
Haryana Board 10th Class Home Science Solutions Chapter 5 धन का प्रबन्ध
अति लघु उत्तरीय प्रश्न –
प्रश्न 1.
पारिवारिक आय से आप क्या समझते हैं ?
उत्तर :
सभी प्रकार की आय का आयोजन नियंत्रण व मूल्यांकन करना, जिससे परिवार के लिए अधिकतम सन्तुष्टि की प्राप्ति हो सके, उसे पारिवारिक आय कहते हैं।
प्रश्न 2.
मौद्रिक आय किसे कहते हैं ?
उत्तर :
आय के कई साधन हैं। वेतन से प्राप्त मुद्रा, व्यापार से प्राप्त मुद्रा, ज़मीन मकान के किराये से प्राप्त मुद्रा आदि। किसी भी साधन से प्राप्त मुद्रा, मौद्रिक आय कहलाती है।

प्रश्न 3.
आत्मिक आय से आप क्या समझते हैं ?
उत्तर :
विभिन्न स्रोतों से प्राप्त मौद्रिक तथा वास्तविक आय के व्यय से प्राप्त होने वाली सन्तुष्टि आत्मिक आय कहलाती है।
प्रश्न 4.
आवश्यक व्यय कौन-कौन से हैं ? आवश्यकताओं के वर्ग भी बताइये।
उत्तर :
भोजन, वस्त्र, आवास, शिक्षा एवं चिकित्सा पर किये व्यय आवश्यक व्यय माने जाते हैं। आवश्यकताओं के वर्ग निम्नलिखित हैं –
- अनिवार्य आवश्यकताएं (जीवन रक्षक आवश्यकताएँ)
- निपुणता-रक्षक आवश्यकताएँ
- प्रतिष्ठा-रक्षक आवश्यकताएँ
- आराम संबंधी आवश्यकताएँ
- विलासिता संबंधी आवश्यकताएँ।
प्रश्न 5.
व्यय किसे कहते हैं ?
उत्तर :
अपने परिवार के लक्ष्यों की प्राप्ति हेतु तथा आवश्यकताओं को पूर्ण करने के लिए विभिन्न साधनों से आय को किस प्रकार और कितना विभिन्न आवश्यकताओं पर खर्च किया जाता है, उसे व्यय कहते हैं।
प्रश्न 6.
परिवार की आय को कौन-कौन-से दो भागों में बांटा जा सकता है ?
उत्तर :
परिवार की आय को दो भागों में विभाजित किया जाता है-प्रत्यक्ष और अप्रत्यक्ष। प्रत्यक्ष आय वह है जो पैसे के रूप में प्राप्त होती है जैसे वेतन, दुकान की कमाई। अप्रत्यक्ष आय जो किसी नौकरी करने वाले व्यक्ति को सुविधाओं के रूप में मिलती है जैसे मकान, मुफ्त दवाइयाँ, डॉक्टरी सहायता आदि।

प्रश्न 7.
खर्च कितने प्रकार के हो सकते हैं ?
उत्तर :
परिवार को भिन्न – भिन्न जगहों से आय प्राप्त होती है उसको कहां और कितना प्रयोग किया जाता है को खर्च कहा जाता है। खर्च तीन प्रकार के होते हैं –
1. निर्धारित खर्च जैसे मकान का किराया, बच्चों की फीस।
2. अर्द्ध-निर्धारित खर्च-जो बढ़ता-घटता रहता है; जैसे कपड़े, भोजन और दवाइयों का खर्च।
3. गैर-निर्धारित खर्च-जिनको घटाया या बिल्कुल बन्द किया जा सकता है; जैसे मनोरंजन, हार-शृंगार आदि।
प्रश्न 8.
बजट से आप क्या समझते हैं ?
उत्तर :
पारिवारिक आय के अनुसार घर के खर्च का पहले से भी अनुमान लगाने को बजट कहा जाता है या आय और खर्च का लेखा-जोखा बजट कहलाता है। बजट लिखित या मौखिक भी हो सकता है।
प्रश्न 9.
खर्च की आवश्यक और अनावश्यक मदें कौन-कौन सी हैं ?
उत्तर :
खर्च की आवश्यक और अनावश्यक मदें निम्नलिखित हैं –
(क) आवश्यक मदें-घर, भोजन और कपड़े।
(ख) कम आवश्यक मदें-घर को चलाने के लिए खर्चे बच्चों की पढाई, डॉक्टरी सहायता, मनोरंजन और अन्य फुटकर खर्च और बचत।
(ग) खर्च की अवश्यक मदें ये वे खर्चे हैं जिनसे आसानी से बचा जा सकता है। मनोरंजन का खर्च, हार-श्रृंगार का खर्च और धार्मिक खर्चे आदि।
प्रश्न 10.
बचत से आप क्या समझते हो ?
उत्तर :
घर की आय में से वह भाग जिसको प्रत्येक महीने आय में से बचा लिया जाता है उसको बचत कहते हैं। बचत प्रत्येक परिवार के लिए इसलिए आवश्यक है ताकि बीमारी, दुर्घटना, बुढ़ापे आदि के लिए पैसा इकट्ठा हो सके।

प्रश्न 11.
बचत करने के किन्हीं चार ढंगों के बारे में बताएं।
उत्तर :
पुराने समय में गहने और सोने के रूप में ही बचत की जाती थी। परन्तु आजकल बचत करने के लिए नए ढंग हैं जो न केवल मनुष्य को बचत करने में सहायक होते हैं बल्कि वह बचत मनुष्य की आय का एक अन्य साधन भी बन जाती है; जैसे जीवन बीमा, निश्चित काल का जमा खाता, डाकघर बचत खाता और भविष्य निधि फण्ड योजना आदि।
प्रश्न 12.
व्यक्ति का व्यवसाय बजट पर कैसे प्रभाव डालता है ?
उत्तर :
कई व्यक्तियों को अपनी नौकरी या बिजनैस करके कई स्थानों पर जाना पड़ता है। इसलिए उनको कई ऐसी वस्तुओं पर खर्च करना पड़ता है जिनकी साधारण व्यक्ति को आवश्यकता नहीं होती जैसे सूटकेस, बढ़िया कपड़े और मोबाइल आदि। इन सभी बातों का प्रभाव बजट पर पड़ता है।
प्रश्न 13.
गृहिणी की योग्यता बजट पर कैसे प्रभाव डालती है ?
उत्तर :
समझदार गृहिणियां अपनी योग्यता और कुशलता से कम आय में परिवार की आवश्यकताएं पूर्ण करके बचत कर लेती हैं। जैसे घर कपड़े सिल कर,पुराने कपड़ों की मरम्मत करके, घर में आचार चटनियां बनाकर या घर में सब्जियां उगा कर पारिवारिक बजट को प्रभावित करती हैं।
प्रश्न 14.
बजट कितनी प्रकार का हो सकता है ?
उत्तर :
पारिवारिक बजट तीन प्रकार का होता है –
- बचत बजट (Surplus Budget) – इसमें आय अधिक और खर्च कम होता है।
- सन्तुलित बजट (Balanced Budget) – इसमें आय और खर्च बराबर होते हैं।
- घाटे का बजट (Deficit Budget) – इसमें आय कम और खर्च अधिक होता है।

प्रश्न 15.
प्रतिदिन का हिसाब रखना बजट बनाने के लिए क्यों आवश्यक है ?
अथवा
प्रतिदिन का हिसाब-किताब रखना क्यों जरूरी है ?
उत्तर :
रोज़ाना खर्च का हिसाब रखने से गृहिणी को यह पता लगता है कि खर्च बजट के अनुसार हो रहा है। यदि किसी मद पर खर्च अधिक हो जाए तो किसी और से घटाकर उसको सन्तुलित किया जाता है।
प्रश्न 16.
बजट के प्रकार लिखिए, तथा बताइये कि सबसे अच्छा बजट कौन-सा माना जाता है ?
उत्तर :
पारिवारिक आय-व्यय के हिसाब से बजट तीन प्रकार के होते हैं –
- सन्तुलित बजट
- बचत का बजट
- घाटे का बजट।
बचत का बजट सर्वाधिक अच्छा बजट माना जाता है।
प्रश्न 17.
पारिवारिक बजट से आप क्या समझते हैं ?
उत्तर :
पारिवारिक आय तथा व्यय में सन्तुलन लाने के लिए आय का सही उपयोग करना अत्यन्त आवश्यक है, इसलिए गृहिणी को धन व्यय करने से पहले परिवार में विभिन्न साधनों या स्रोतों से होने वाली पूरी आय (आमदनी) तथा इस आय को विभिन्न मदों पर खर्च करने की पूरी योजना बना लेनी चाहिए। इस प्रकार परिवार में किसी निश्चित अवधि के लिए पर्व अनुमानित आय-व्यय के विस्तत विवरण को पारिवारिक बजट कहते हैं।

प्रश्न 18.
बजट योजना किन तत्त्वों पर निर्भर करती है ?
उत्तर :
बजट योजना निम्न चार तत्त्वों पर निर्भर करती है –
- परिवार की आय।
- परिवार का लक्ष्य।
- परिवार की तात्कालिक आवश्यकताएँ।
- परिवार की भावी आवश्यकताएँ।
प्रश्न 19.
बजट-निर्माण के मुख्य चरण क्या हैं ?
उत्तर :
बजट-निर्माण के मुख्य चरण निम्नलिखित हैं –
- परिवार के सभी स्रोतों से प्राप्त मासिक आय को जोड़ना।
- परिवार की आवश्यकताओं की सूची उनकी प्राथमिकता के आधार पर बना लेना।
- पारिवारिक परिस्थितियों के अनुसार प्रत्येक आवश्यकता के लिए आय का प्रतिशत निर्धारित करना और अन्त में कुल खर्च का अनुमान लगाना।
- कुछ धन भविष्य के लिए अथवा आकस्मिक खर्च के लिए बचाया जाना।
प्रश्न 20.
बजट सम्बन्धी ऐन्जिल का सिद्धान्त क्या है ?
उत्तर :
ऐन्जिल के सिद्धान्त के अनुसार जैसे-जैसे आय बढ़ती है –
- भोजन पर व्यय का प्रतिशत घटता है तथा अन्य आरामदेह वस्तुओं पर व्यय का प्रतिशत बढ़ता है।
- मकान, वस्त्र, विद्युत् पर व्यय उतना ही रहता है, उसमें परिवर्तन नहीं होता।
- विलासिता, शिक्षा, स्वास्थ्य, मनोरंजन, सांस्कृतिक आवश्यकताओं पर व्यय का प्रतिशत बढ़ जाता है।

प्रश्न 21.
निम्न व उच्च वर्ग के बजट में क्या अन्तर है ?
उत्तर :
निम्न व उच्च वर्ग के बजट में निम्नलिखित अन्तर है –
- निम्न वर्ग में भोजन की मद में अधिक खर्च होता है जबकि उच्च वर्ग में भोजन की मद पर खर्च का प्रतिशत कम रहता है।
- उच्च वर्ग में शिक्षा तथा मनोरंजन पर प्रतिशत व्यय अधिक होता है जबकि निम्न वर्ग में इन मदों का प्रतिशत व्यय कम रहता है।
- उच्च परिवार में बचत का प्रतिशत अधिक होता है, जबकि निम्न परिवार में बचत नहीं के बराबर ही होती है।
प्रश्न 22.
गृहिणी को परिवार के आय-व्यय का सन्तुलन बनाए रखने के लिए किन-किन बातों पर ध्यान देना चाहिए ?
उत्तर :
परिवार के आय-व्यय का सन्तुलन बनाए रखने के लिए अग्र बातों पर ध्यान देना चाहिए –
- परिवार की आय के साधन।
- आय को प्रभावित करने वाले तत्त्व।
- परिवार के आवश्यक व्यय।
- व्यय को प्रभावित करने वाले तत्त्व।
- आय के साधनों का सम्भावित विकास।
- आय के साधनों को विकसित कर व्यय-योजना द्वारा रहन-सहन का स्तर उन्नत करना।
- बुद्धिमत्तापूर्ण व्यय, बचत के लाभ तथा ऋण से हानियाँ।
- आय-व्यय का सन्तुलित बजट।
- घरेलू हिसाब रखना।
- बचत के साधन अपनाना।
- बचत का सही उपयोग।
- आवश्यक कागज़-पत्रों की सम्भाल।

प्रश्न 23.
बचत के प्रमुख लक्ष्य क्या हैं ?
अथवा
बचत करना क्यों आवश्यक है ?
अथवा
बचत के लाभ लिखें।
उत्तर :
बचत के प्रमुख लक्ष्य निम्नलिखित हैं –
- आय बन्द हो जाने पर एक साधन-नौकरी छूट जाने या व्यवसाय में घाटा हो जाने पर बचत की राशि ही काम आती है।
- चोरी हो जाने, आग लग जाने एवं महंगाई बढ़ने पर बचत का सदुपयोग किया जाता है।
- आकस्मिक दुर्घटना या बीमारी तथा बुढ़ापे में कार्य करने की असमर्थता के समय बचत ही काम आती है।
- मकान खरीदने, बनवाने या जमीन खरीदने के लिए बचत का प्रयोग किया जाता है।
- बच्चों की ऊँची शिक्षा में बचत का उपयोग किया जाता है।
- सामाजिक तथा धार्मिक कार्यों पर भी बचत का उपयोग होता है।
- राष्ट्र के विकास तथा रक्षा के साधनों पर बचत का उपयोग होता है।
- मुद्रा-स्फीति पर नियंत्रण के लिए बचत करना आवश्यक है।

प्रश्न 23.
(A). बचत क्यों की जानी चाहिए ?
उत्तर :
देखें प्रश्न 23 का उत्तर।
प्रश्न 24.
बचत किसे कहते हैं ? बचत तथा विनियोग के साधनों के नाम लिखिए।
उत्तर :
धन को किसी भी समय इकट्ठा जमा करने या फिर नियमित समय के अन्तर पर धीरे-धीरे एकत्रित करने को बचत कहा जाता है। बचत तथा विनियोग के प्रमुख साधन अग्रलिखित हैं –
- बैंक (Banks)
- डाकघर बचत खाता (Post Office Savings Account)
- जीवन बीमा (Life Insurance)
- भविष्य निधि योजना (Provident Fund)
- यूनिट्स (Units)
- राष्ट्रीय बचत सर्टिफिकेट (National Savings Certificate)
- लॉटरी, चिट व्यवस्था आदि (Lottery and Chit System)
- सहकारी संस्थाएँ (Co-operative Societies)
- कम्पनियों में पैसा लगाना (Investing in Companies)।
प्रश्न 24. (A)
बचत किसे कहते हैं ?
उत्तर :
देखें प्रश्न 24 का उत्तर।

प्रश्न 25.
बचत के विनियोजन में किन बातों का ध्यान रखना आवश्यक तथा लाभकारी होता है ?
अथवा
बचत किए हुए धन को निवेश करते समय आप किन-किन बातों को ध्यान में रखेंगे।
उत्तर :
बचत के विनियोजन में निम्न दो बातों का ध्यान रखना आवश्यक तथा लाभकारी होता है –
1. जिस संस्था में धन जमा करना है, वह विश्वसनीय हो।
2. विश्वसनीय संस्थाओं की ब्याज की दरें जानकर, जिस संस्था में ब्याज की दर अधिक हो, उसी में बचत का धन जमा करना चाहिए।
प्रश्न 26.
बचत के विनियोजन के लिए सरकारी तथा गैर-सरकारी संस्थाओं की सूची बनाइये।
उत्तर :
बैंक, डाकखाना, बीमा, प्रॉवीडेन्ट फण्ड, यूनिट ट्रस्ट, सहकारी समितियाँ, हिस्से (शेयर्स), चिट फण्ड कम्पनियाँ आदि।
प्रश्न 27.
बैंक में रुपया जमा करने के क्या लाभ हैं ?
उत्तर :
बैंक में रुपया जमा करने के निम्नलिखित लाभ हैं –
- बचत का धन सुरक्षित रहता है।
- आवश्यकता होने पर धन निकाला भी जा सकता है।
- बचत के धन पर ब्याज भी मिलता है।
- इस धन को देश के विकास के लिए विभिन्न उत्पादक कार्यों में लगाया जाता है।

प्रश्न 28.
बचत खाता किसके नाम पर खोला जा सकता है ?
उत्तर :
बचत खाता निम्नलिखित नामों से खोला जा सकता है –
- किसी बालिग व्यक्ति के नाम पर।
- संरक्षता में किसी नाबालिग के नाम पर।
- दो या अधिक व्यक्तियों के नाम पर (संयुक्त खाता)। एक वर्ष से अधिक के नाबालिग बच्चे के नाम पर बचत खाते में धनराशि नकद, चैक या ड्राफ्ट के रूप में जमा कराई जा सकती है।
प्रश्न 29.
आवश्यकता पड़ने पर बैंक से धन किस प्रकार निकाला जा सकता है ? बचत खाते से धन निकालने के बैंक के क्या नियम होते हैं ?
उत्तर :
आवश्यकता पड़ने पर बैंक से चैक द्वारा या निकासी फार्म (Withdrawal form) की सहायता से धन निकाला जा सकता है। बैंक से धन निकालने के निम्न नियम होते हैं –
- जमाकर्ता अपने बचत खाते में 3 महीने में 30 बार धन निकाल सकता है।
- आवश्यकता पड़ने पर बैंक जमाकर्ता को 30 बार से अधिक बार धन निकालने की अनुमति दे सकता है।
- किसी भी समय यदि बचत खाते में पाँच सौ रुपये से कम होंगे तो जमाकर्ता से एक रुपया प्रति छः माह की दर से वसूल किया जाता है।
- जमाकर्ता द्वारा अपने बचत खाते से एक महीने में एक या अधिक बार निकाली गई कुल राशि 10,000 से अधिक नहीं होनी चाहिए।
- चैक बुक उन्हीं जमाकर्ता को दी जाती है जिनके बचत खाते में ₹ 500 या उससे अधिक रहते हैं।
प्रश्न 30.
पास बुक क्या होती है ?
उत्तर :
हर बचत खातेदार को एक पास बुक या पुस्तिका दी जाती है जिसमें बचत बैंक के नियम दिये होते हैं तथा खातेदार का नाम, पता तथा खाता नम्बर आदि विवरण होते हैं। बैंक से धन निकालते समय या जमा कराते समय पास बुक को साथ दिया जाता है जिससे राशि सम्बन्धी सभी आवश्यक विवरण बैंक द्वारा उसी समय दर्ज कर दिये जाते हैं।

प्रश्न 31.
भविष्य निधि योजना से क्या अभिप्राय है ?
उत्तर :
यह योजना नौकरी करने वाले सभी वर्ग के कर्मचारियों के लिए है। प्रत्येक कर्मचारी अपने वेतन में से अनिवार्य रूप से इस योजना में राशि विनियोजित करता है।
प्रश्न 32.
स्कूल बचत बैंक योजना क्या होती है ?
उत्तर :
स्कूल बचत बैंक योजना (संचायिका योजना) स्कूल के बच्चों का ऐसा बचत बैंक होता है जिसका नियमन वे स्वयं करते हैं। इससे बच्चों में नियमित बचत करने की आदत का विकास होता है, साथ ही उन्हें पैसे रखने का हिसाब भी आ जाता है। इस प्रकार स्कूली बच्चों द्वारा जमा की गई धनराशि का खाता विद्यालय के नाम से खोला जाता है।
प्रश्न 33.
यूनिट ट्रस्ट क्रय करके किस प्रकार बचत की जाती है ?
उत्तर :
भारतीय संसद् ने एक अधिनियम 1964 में लागू कर ‘यूनिट ट्रस्ट ऑफ़ इण्डिया’ की स्थापना की थी। यूनिट एक प्रकार की अंशपूँजी होती है। इसकी कीमत ₹ 10 होती है परन्तु इसका क्रय-विक्रय मूल्य कम व अधिक होता रहता है। ट्रस्ट को उद्योगों से जो लाभ होता है उसका 90% यूनिट क्रय करने वालों में लाभांश के रूप में प्रतिवर्ष 30 जून को बाँट दिया जाता है। सन् 1983 में विधवाओं, अपंगों और 55 वर्ष से अधिक आयु वाले व्यक्तियों को लाभांश प्रतिमास देने की सुविधा हो गई है। इसमें कम से-कम ₹ 5,000 जमा करने पड़ते हैं। इसका लाभ बैंक या डाकघर से प्राप्त किया जा सकता है।

प्रश्न 34.
परिवार के लिए धन की बचत करने के कोई चार लाभ लिखें।
उत्तर :
देखें प्रश्न 7 दीर्घ उत्तरीय प्रश्न का उत्तर।
प्रश्न 35.
बचत का निवेश करने की किन्हीं छः संस्थाओं की सूची बनाएं।
उत्तर :
देखें प्रश्न 8, दीर्घ उत्तरीय प्रश्न का उत्तर।
प्रश्न 36.
व्यय योजना बनाने से परिवार को होने वाले कोई दो लाभ लिखें।
उत्तर :
1. आकस्मिक खर्चों का अनुमान लगाना सरल हो जाता है।
2. व्यय योजना बनाने से बचत करने की प्रेरणा मिलती है।
प्रश्न 37.
बचत और विनियोग के दो साधन बताएं।
उत्तर :
बैंक, बीमा, शेयरस, यूनिट ट्रस्ट।

प्रश्न 38.
आवश्यक व्यय तथा अनावश्यक व्यय कौन-कौन से हैं ? दो उदाहरण दें ?
उत्तर :
आवश्यक व्यय : बच्चों की फीस, घर का किराया। अनावश्यक व्यय : घूमने जाना, फिल्म देखने जाना।
प्रश्न 39.
अनावश्यक व्यय कौन-कौन से हैं?
उत्तर :
देखें उपरोक्त प्रश्नों में।
प्रश्न 40.
यूनिट ट्रस्ट ऑफ इण्डिया की स्थापना कब हुई ?
उत्तर :
देखें उपरोक्त प्रश्न।
लघ उत्तरीय प्रश्न –
प्रश्न 1.
धन के प्रबन्ध के महत्त्व की विवेचना कीजिए।
उत्तर :
धन एक भौतिक साधन है। प्रत्येक परिवार के लिए इसकी मात्रा भिन्न-भिन्न होते हुए भी परिवार के लिए इसकी मात्रा सीमित भी होती है और यह परिवार पर ही निर्भर करता है कि वह किस प्रकार से अपने इस सीमित धन से अधिक-से-अधिक आवश्यकताएँ पूरी कर सकें। धन का जीवन में एक महत्त्वपूर्ण साधन है। प्रत्येक व्यक्ति को जीवन की विभिन्न सुख-सुविधाएँ जुटाने के लिए धन पर निर्भर रहना पड़ता है। दिन-प्रतिदिन मनुष्य को जीवन में अनेक आवश्यकताओं का अनुभव होता है। मनुष्य की आवश्यकताएं तीन प्रकारों में बाँटी जा सकती हैं; जैसे कि-अति आवश्यक आवश्यकताएँ (Needs or Essential Requirements); आरामदायक आवश्यकताएँ (Comforts) तथा विलासितापूर्ण आवश्यकताएँ (Luxuries)।
इन सभी आवश्यकताओं को मनुष्य अपनी सामर्थ्य के अनुसार पूर्ण करने का प्रयत्न करता है। परिवार की सम्पूर्ण व्यवस्था का संचालन धन पर ही निर्भर है। धन एक प्रकार का ऐसा सुविधाजनक साधन है जो कि मनुष्य को उन वस्तुओं को खरीदने में मदद करता है जिनके प्रयोग से उसकी आवश्यकताओं की सन्तुष्टि होती है। धन के उचित उपयोग के लिए धन के प्रबन्ध’ (Money Management) का सही ज्ञान होना अति आवश्यक है।
धन-प्रबन्ध के द्वारा ही पारिवारिक आय का योजनाबद्ध उपयोग सम्भव है। धन प्रबन्ध इस प्रकार करना चाहिए कि आय तथा व्यय में सन्तुलन हो तथा थोड़ी बहुत बचत की जा सके जो कि भविष्य में काम आ सके और परिवार की आकस्मिक आवश्यकताओं को पूरा करने में भी सहायता दे सके। उचित धन प्रबन्ध परिवार के भविष्य को सुखमय तथा सुविधाजनक बनाने में सहायक होता है। इसके लिए आय के समस्त साधनों का पूरा ज्ञान होना अति आवश्यक है क्योंकि व्यय बहुत कुछ आय की राशि पर ही निर्भर करता है।

प्रश्न 2.
पारिवारिक आय की क्या विशेषताएं हैं ?
उत्तर :
पारिवारिक आय की प्रमुख विशेषताएँ निम्नलिखित हैं –
- पारिवारिक आय राष्ट्रीय की आय पर निर्भर करती है।
- आय का वितरण देशवासियों में समान रूप से नहीं होता। समाज में आय की विषमताओं के कारण निम्न वर्ग, मध्यम वर्ग एवं उच्च वर्ग समाज बन जाता है।
- जिस वर्ग का व्यक्ति होता है उसके अनुसार उसकी आय निर्धारित होती है। जैसे-कृषक वर्ग, व्यापारी वर्ग, शिक्षक वर्ग, डॉक्टर या अभियन्ता वर्ग आदि।
- व्यक्ति की कुशलता एवं उसके व्यक्तिगत गुणों पर उसकी आय निर्भर करती है।
- पारिवारिक आय परिवार में आय अर्जित करने वाले सदस्यों की संख्या पर निर्भर करती है।
- शिक्षित व्यक्तियों की आय अशिक्षित व्यक्तियों से अधिक होती है।
- परिवार में सदस्यों की संख्या कम रहने पर एक निश्चित आय अधिक लगती है परन्तु परिवार में सदस्यों की संख्या यदि बढ़ जाती है तब वही निश्चित आय कम लगती है।
- एक परिवार के लिए जितनी आय पर्याप्त होगी इसकी कोई सीमा निश्चित नहीं होती।
प्रश्न 3.
आय वर्ग कितने प्रकार के हैं ? विवेचना कीजिए।
उत्तर :
हर परिवार की अलग-अलग आय होती है, जिसके आधार पर वह अपनी भिन्न-भिन्न जरूरतों को पूर्ण करने में सफल होते हैं। किसी भी परिवार के जीवन-स्तर का अनुमान उसकी पारिवारिक आय से सरलता से लगाया जा सकता है। आय की मात्रा के आधार पर परिवारों को मुख्यत: तीन आय-वर्गों में विभाजित किया जा सकता है –
- निम्न आय वर्ग (Low Income Group)
- मध्यम आय वर्ग (Middle Income Group)
- उच्च आय वर्ग (High Income Group)
सामान्यतः ये तीन आयु-वर्ग मान्य हैं, परन्तु इनमें कोई भी निश्चित विभाजन रेखा नहीं खींची जा सकती; जैसे कि निम्न और मध्यम वर्ग के बीच के वर्ग को निम्न-मध्यम आय वर्ग भी कहा जा सकता है और इससे उच्च और मध्यम वर्ग के बीच में उच्च-मध्यम आय-वर्ग आ सकता है। कितनी आय वाले परिवार को इनमें से किस वर्ग में रखा जाए यह भी पूरी तरह से निश्चित नहीं किया जाता है और यह समय-समय पर बदलता रहता है।
यही नहीं, विभिन्न अर्थशास्त्रियों के भी इसके बारे में भिन्न-भिन्न मत हैं। इसके साथ ही कोई परिवार कहाँ रहता है यानी रहने के स्थान पर, वस्तुओं की उपलब्धि तथा परिवार की उन्हें खरीदने की क्षमता (Purchasing Power) भी भिन्न-भिन्न होती है। उदाहरणार्थ बड़े शहरों में उसी धन की मात्रा से कम वस्तुएँ, सुख-सुविधाएँ तथा आवश्यकताओं को पूरा किया जा सकता है, जबकि गाँवों या छोटे शहरों में उतने ही धन से अधिक पारिवारिक आवश्यकताओं को सुविधापूर्वक पूरा किया जा सकता है।
फिर भी मान्य नियमों के आधार पर परिवार की आय को देखते हुए विभिन्न परिवारों को निम्न, मध्यम व उच्च आय वर्गों में बाँटने के लिए आगे दी गई विभाजन सीमा ली जा सकती है –
निम्न आय वर्ग – ₹ 800 मासिक तक।
मध्यम आय वर्ग – ₹ 800 से ₹ 2,000 मासिक तक।
उच्च आय वर्ग – ₹ 2,000 या ₹ 2,500 से ऊपर।

प्रश्न 4.
व्यय कितने प्रकार के होते हैं ?
उत्तर :
जो कुछ भी हम खर्च करते हैं उसको तीन भागों में विभाजित किया जा सकता है –
निर्धारित व्यय – निर्धारित व्यय प्रतिमाह करने पड़ते हैं। ऐसे खर्च की राशि प्रायः निश्चित रहती है, जैसे-मकान का किराया, बिजली का खर्च, बीमे की किस्तें, आय कर, शिक्षा शुल्क आदि। ऐसे व्यय में किसी प्रकार की कटौती करना असम्भव रहता है।
अर्ध-निर्धारित – व्यय-कछ ऐसे व्यय होते हैं जिनको करना अनिवार्य होता है पर इनकी धनराशि में कमी या वृद्धि की जा सकती है। कमी या वृद्धि परिवार के सदस्यों की आमदनी व परिस्थिति पर निर्भर करती है। आमदनी बढ़ने पर खाने तथा वस्त्र पर अधिक व्यय किया जा सकता है, इसके विपरीत आमदनी कम हो जाने पर सादा भोजन या सादा वस्त्रों पर जीवित रहा जा सकता है।
अन्य व्यय – कुछ ऐसे व्यय होते हैं जो व्यक्ति विशेष की आमदनी पर निश्चित होते हैं। धन की कमी होने पर ऐसे व्यय बन्द किए जा सकते हैं तथा आमदनी बढ़ने पर उन्हें फिर किया जा सकता है। मनोरंजन व सांस्कृतिक कार्यक्रमों पर आय के अनुसार ही खर्च होने लगता है तथा आय कम होने पर उन्हें बन्द किया जा सकता है।
आकस्मिक व्यय – ये व्यय ऐसे होते हैं जो अतिथियों के आगमन, बीमारी, दुर्घटना आदि के कारण उत्पन्न हो जाते हैं। इनकी पूर्ति करना भी आवश्यक होता है।

प्रश्न 5.
व्यय को सीमित रखने के लिए गृहिणी को किन बातों का ध्यान देना चाहिए ?
उत्तर :
व्यय को सीमित रखने के लिए गृहिणी को अग्रलिखित बातों पर ध्यान देना चाहिए –
- प्रत्येक गृहिणी को घर की आय का पूर्ण ज्ञान होना चाहिए ताकि वह ठीक बजट बना सके और खर्च भी उसी के अनुसार कर सके।
- प्रत्येक गृहिणी को घर में परिस्थितियों का ज्ञान होना चाहिए। परिवार में व्यक्तियों की संख्या, उनकी उम्र, उनकी आवश्यकताएँ, बच्चों की शिक्षा-श्रेणी आदि का ज्ञान गृहिणी को होना चाहिए।
- गृहिणी को पारिवारिक बजट बनाने का ज्ञान होना चाहिए।
- प्रतिदिन के व्यय का हिसाब रखा जाना चाहिए जिससे यह पता रहे कि किस मद में कितना खर्च हो चुका है और कितना भाग शेष बचा है। इससे अनावश्यक खर्चों को रोका जा सकता है।
- थोक क्रय करना चाहिए। इससे पूरे माह का सामान क्रय हो जाता है। सामान का मूल्य भी सस्ता रहता है और सामान ढोने आदि का खर्च भी बच जाता है।
- गृहिणी को बाजार भाव का ज्ञान भी होना चाहिए जिससे ठगे जाने की सम्भावना नहीं रहती।
- आवश्यक वस्तुओं की खरीददारी ही करनी चाहिए।
- वस्तुओं को सदैव नकद खरीदना चाहिए। उधार खरीदने की आदत से व्यय असीमित हो जाता है।
- मितव्ययिता के साथ खर्च करने की आदत होनी चाहिए।

प्रश्न 6.
व्यय को प्रभावित करने वाले तत्त्व कौन-से होते हैं ?
उत्तर :
परिवार पर किए गए व्यय निम्नलिखित तत्त्वों से प्रभावित होते हैं –
1. परिवार का ढाँचा – हमारे देश में दो प्रकार की परिवार व्यवस्था है। संयुक्त परिवार व्यवस्था तथा एकाकी परिवार व्यवस्था। संयुक्त परिवार में कुछ मदों जैसे मकान का किराया, नौकर का पारिश्रमिक, भोजन, विद्युत् आदि के खर्च सम्मिलित रूप से एक जगह हो जाते हैं। ऐसे परिवार में सम्मिलित व्यय का बोझ परिवार के सभी सदस्यों पर पड़ता है। एकाकी परिवार में सभी खर्चे एक ही व्यक्ति की आय से ही करने पड़ते हैं। संयुक्त परिवार में एकाकी की तुलना में अधिक बचत की जा सकती है।
2. परिवार के सदस्यों की संख्या – एक व्यक्ति की आय और परिवार में सदस्यों की अधिक संख्या वाली स्थिति में बचत की सम्भावना नहीं के बराबर होती है।
3. बच्चों की संख्या – जिस परिवार में बच्चे अधिक होते हैं, उसमें खर्च अधिक होते हैं। इसलिए कहते हैं-‘कम बच्चे सुखी, परिवार’।
4. रहन-सहन का स्तर – जिस परिवार के रहन-सहन का स्तर ऊँचा होता है वैसे परिवार को अपने स्तर को बनाए रखने के लिए अधिक खर्च करना पड़ता है।
5. परिवार के सदस्यों के व्यवसाय – परिवार के सदस्यों के व्यवसाय भी खर्च को प्रभावित करते हैं। व्यवसाय को सुचारू रूप से चलाने के लिए भी व्यवसाय में धन खर्च करते रहना पड़ता है।
6. सामाजिक तथा धार्मिक परम्पराएँ – प्रत्येक समाज तथा परिवार में ऐसी सामाजिक तथा धार्मिक परम्पराएँ होती हैं जिन्हें न चाहते हुए भी मानना पड़ता है और उन्हें निभाने में खर्च होता है। हमारे भारतीय समाज में आए दिन उत्सव होते हैं, जैसे-अन्नप्राशन, मुंडन, जनेऊ, विवाह, नामकरण, गृह-प्रवेश, मरणोपरान्त तेरहवीं आदि। इन उत्सवों को मनाने तथा सगे-सम्बन्धियों को भोज इत्यादि देने में बजट से अलग बहुत अधिक खर्च करना पड़ता है। आज ये सब खर्च व्यर्थ माने जाते हैं।
7. गृहिणी की योग्यता एवं कुशलता – बुद्धिमानी से खर्च करने पर परिवार को अधिक सुख-सुविधाएँ प्राप्त होती हैं। यदि गृहिणी कुशल है और वह सोच-समझकर खर्च करती है तो वह परिवार को सुख व शान्ति दे सकती है।

प्रश्न 7.
बचत के प्रमुख लक्षण क्या हैं ?
उत्तर :
बचत के प्रमुख लक्षण निम्न हैं –
- अन्य बन्द हो जाने पर, आय साधन-नौकरी छूट जाने या व्यवसाय में घाटा हो जाने पर बचत की राशि ही काम आती है।
- चोरी हो जाने, आग लग जाने एवं महँगाई बढ़ने पर बचत का सदुपयोग किया जाता है।
- आकस्मिक दुर्घटना या बीमारी तथा बुढ़ापे में कार्य की असमर्थता के समय बचत ही काम आती है।
- मकान खरीदने, बनवाने या जमीन खरीदने के लिए बचत का ही उपयोग किया जाता है।
- बच्चों की ऊँची शिक्षा में बचत का उपयोग किया जाता है।
- सामाजिक तथा धार्मिक कार्यों पर भी बचत का उपयोग होता है।
- राष्ट्र के विकास तथा रक्षा के साधनों पर बचत का उपयोग होता है।
- मुद्रा-स्फीति पर नियन्त्रण के लिए बचत करना आवश्यक है।
प्रश्न 8.
पारिवारिक बजट किस प्रकार बनाया जाता है?
उत्तर :
पारिवारिक बजट बनाने के लिए निम्न प्रकार तैयारी करते हैं
1. बजट बनाने से पूर्व निम्न सूचनाएँ एकत्रित की जाती हैं –
- परिवार के सभी सदस्यों की संख्या (स्त्री, पुरुष, बच्चे, बूढ़े आदि)।
- परिवार के सदस्यों की विभिन्न साधनों से होने वाली आय।
- परिवार के बजट की अवधि-मासिक बजट बनाना है या वार्षिक।
2. सूचनाएँ एकत्रित करने के बाद खर्चों के बारे में अनुमान लगाया जाता है। यह देखना होता है कि किन-किन मदों पर खर्च होना है। उपभोग की जाने वाली वस्तुओं की मात्रा तथा संख्या की सूची बनाई जाती है। वस्तुओं के मूल्य तथा उन पर व्यय किए गए कुल धन का पता लगाया जाता है।
3. पूरी सूची तैयार करने के बाद यह देखते हैं कि विभिन्न मदों पर आय का कितना प्रतिशत खर्च किया गया है। अन्त में आय में से व्यय निकालकर कुल बचत हुई या नहीं, यह देखते हैं। यदि व्यय अधिक है तो इसे किस प्रकार पूरा किया जा सकता है, यह देखते हैं। बजट बनाते समय आय का विभाजन इस प्रकार करना चाहिए जिससे आवश्यकताओं की पूर्ति करने के बाद कुछ धन भावी आवश्यकताओं के लिए भी बच जाए।

प्रश्न 9.
गृहिणी मितव्ययिता कैसे कर सकती है?
उत्तर :
घर में मितव्ययिता के लिए कुछ सुझाव निम्नलिखित हैं –
- अति आवश्यक वस्तुओं को ही खरीदना चाहिए।
- खरीददारी सदैव नगद करनी चाहिए, उधार कभी नहीं लेना चाहिए।
- सामान सदैव विश्वास की व अच्छी दुकानों से ही खरीदना चाहिए।
- पौष्टिक गुणों वाले सस्ते खाद्य-पदार्थ ही प्रयोग में लाने चाहिएं।
- फसल के समय अधिक सामग्री (जैसे-गेहूँ, चावल) खरीदकर उसे विधिपूर्वक सुरक्षित रखना चाहिए। फल व सब्जियों का संरक्षण करना चाहिए।
- प्रतिकूल मौसम में सस्ता सामान (जैसे-गर्मी में ऊन) खरीदना चाहिए।
- जल, ईंधन तथा बिजली का सावधानी से प्रयोग करना चाहिए। बेकार में इन्हें बरबाद नहीं करना चाहिए।
- घर की वस्तुओं की नियमपूर्वक देखभाल, सफ़ाई तथा मरम्मत करते रहना चाहिए।
- बच्चों के लिए ट्यूटर रखने के बजाय उन्हें परिवार के सदस्यों द्वारा खुद पढ़ाया जाना चाहिए।
- घर के कामों में भी सदस्यों को हाथ बँटाना चाहिए और नौकर कम-से-कम रखने चाहिए।
प्रश्न 10.
भारत में पारिवारिक बजट बनाने में क्या कठिनाइयाँ सामने आती हैं ?
उत्तर :
भारत में पारिवारिक बजट बनाने में निम्न कठिनाइयाँ सामने आती हैं
1. गृहिणियों में शिक्षा का अभाव – भारत में अधिकांश गृहिणियाँ या तो अशिक्षित हैं या बहुत कम पढ़ी-लिखी हैं। इस कारण उन्हें बजट बनाने का ज्ञान नहीं है।
2. बजट बनाने का आलस्य – बहुत-सी गृहिणियाँ बजट बनाने को एक अतिरिक्त कार्य समझती हैं। इस प्रकार आलस्य बजट बनाने में एक कठिनाई है।
3. गृहिणियों में व्याप्त अन्धविश्वास – भारत की अधिकांश गृहिणियाँ अन्धविश्वासों तथा कुप्रथाओं को मान्यता देती हैं, इस कारण वे परिवार की आय और व्यय की बातों को खुलकर नहीं कह पाती हैं।
4. उचित सम्पर्क का अभाव – सरकारी कर्मचारियों और साधारण जनता का सीधा सम्पर्क न होने के कारण जनता बजट बनाने की ओर विशेष ध्यान नहीं देती है।

प्रश्न 11.
परिवार के लिए खरीदी जाने वाली वस्तुओं को कितनी श्रेणियों में बाँटा जा सकता है?
अथवा
क्रय के कितने स्वरूप हैं?
उत्तर :
परिवार के लिए क्रय की जाने वाली वस्तुओं के चार स्वरूप हैं जो अग्रलिखित –
1. दैनिक क्रय – दैनिक क्रय में वे सभी वस्तुएँ आती हैं जिन्हें हम इकट्ठा खरीदकर नहीं रख सकते। उन्हें प्रतिदिन ही खरीदना चाहिए, जैसे-दूध, दही, पनीर, मक्खन, फल, सब्जी, अण्डे आदि। बहुधा ये वस्तुएं नियमित रूप से एक-दो बेचने वालों से ही खरीदी जाती हैं। इनमें से बहुत से बेचने वाले घर पर ही सामान दे जाते हैं। फल तथा ये सभी वस्तुएं मिश्रित दुकानों से खरीदनी चाहिए क्योंकि अनेक दुकानों से खरीदने पर वस्तुएँ अच्छी मिलती हैं।
2. मासिक उपयोग का सामान या आवधिक क्रय – पूरे माह के लिए सामान खरीद लिया जाता है। इसमें वे सभी वस्तुएँ खरीद ली जाती हैं जिनके खराब होने की सम्भावना नहीं रहती है और जिन्हें बार-बार खरीदे जाने से समय, धन, श्रम अधिक लगता है, जैसे अनाज, दालें, गुड़, साबुन आदि। कपड़े भी साल में दो-तीन बार इकट्ठे ही क्रय करके बनवा लिये जाते हैं। इस क्रय का बजट में स्थान होता है। इन वस्तुओं को भी निश्चित और हमेशा एक दुकान से नहीं खरीदना चाहिए।
3. आकस्मिक क्रय – इसके अन्तर्गत वे सभी वस्तएँ आती हैं जो कि आकस्मिक स्थिति में खरीदी जाती हैं, जैसे-अचानक बीमार पड़ने पर दवाइयाँ, इन्जेकशन, किसी के यहाँ से शादी का निमन्त्रण आने पर उपहार, भेंट आदि आकस्मिक रूप से खरीदी जाती हैं।
4. कदाचित् क्रय – इसके अन्तर्गत वे वस्तुएँ आती हैं जो कि कभी-कभी खरीदी जाती हैं। कई परिवार तो उन्हें जीवन में एक ही बार खरीद सकते हैं, जैसे-मकान, जमीन, मोटर-कार, फ्रिज, आभूषण। इनका खरीदा जाना बचत पर निर्भर करता है।

प्रश्न 12.
डाकघर बचत बैंक में खाता खोलने की विधि बताइये।
उत्तर :
खाता खोलने के लिए अपनी सुविधानुसार निकटतम डाकघर में जाकर निर्धारित फार्म भरकर तथा धनराशि (जो जमा करनी हो या कम-से-कम पाँच रुपये) देकर खाता खुलवाया जा सकता है। डाकघर का अधिकारी उस व्यक्ति के नाम पास बुक बना देता है तथा जमा की गई राशी को पास बुक में चढ़ाकर मोहर लगा देता है। अब इस पास बुक की सहायता से कभी भी रुपये जमा कराये जा सकते हैं। एक व्यक्ति द्वारा खोले गये खाते में अधिक-से-अधिक ₹ 25,000 तथा दो व्यक्तियों के संयुक्त खाते में अधिक-से-अधिक ₹ 50,000 जमा हो सकते हैं। पास बुक खो जाने पर खातेदान प्रार्थना-पत्र निर्धारित शुल्क देकर नई पास-बुक बनवा सकता है।
प्रश्न 13.
भविष्य निधि (प्रॉवीडेन्ट फण्ड) क्या होती है? यह कितने प्रकार की होती है ?
उत्तर :
भविष्य निधि नौकरी करने वाले की अनिवार्य बचत योजना होती है। इस योजना के अन्तर्गत प्रति माह वेतन से निश्चित धनराशि काटकर जमा कर ली जाती है। यह दो प्रकार की होती है –
1. अनिवार्य भविष्य निधि योजना (Compulsory Provident Fund) यह योजना गैर-सरकारी, अर्द्ध-सरकारी स्कूलों, कॉलेजों, फैक्ट्रियों, फर्मों, कारखानों के कर्मचारियों पर लागू होती है। इसमें संस्था प्रत्येक कर्मचारी के वेतन से निश्चित हिसाब से पैसा काटकर भावी खाते में जमा कर देती है। कार्यरत रहने पर की गई जमा राशि का सेवा-निवृत्ति के बाद भुगतान कर दिया जाता है। यदि सेवक की। जाती है, तो उसके वारिसों को उक्त धनराशि दी जाती है। यदि उच्च शिक्षा, लम्बी बीमारी, आवास-गृह हेतु धन की आवश्यकता होती है तो उसे आंशिक भुगतान लेकर प्राप्त किया जा सकता है।
2. सामान्य भविष्य निधि योजना (General Provident Fund) यह योजना सरकारी कर्मचारियों पर लागू होती है। इसमें वेतन से निश्चित धन प्रति मास काटकर शासकीय कोष में जमा कर दिया जाता है। यदि कोई व्यक्ति अधिक राशि जमा करवाना चाहता है तो उसकी स्वेच्छा से अधिक काट लिया जाता है। शासकीय कर्मचारी की सेवा मुक्ति के बाद जमा राशि ब्याज सहित उसे वापस लौटा दी जाती है। यदि कर्मचारी की मृत्यु हो जाती है, तो उसके द्वारा उल्लेख किए गए वारिस को भुगतान कर दिया जाता है।

प्रश्न 14.
परिवार की आय से आप क्या समझते हो? आय कितनी तरह की हो सकती है?
अथवा
पारिवारिक आय कितने प्रकार की होती है ? प्रत्येक का 2-2 पंक्तियों में वर्णन करें।
उत्तर :
परिवार की आय को दो भागों में विभाजित किया जाता है-प्रत्यक्ष और अप्रत्यक्ष ।
प्रत्यक्ष आय – जो आय पैसे के रूप में घर आती है, उसको प्रत्यक्ष आय कहा जाता है। यह किसी दुकान से रोजाना की बचत, महीने का वेतन, छिमाही फसलों की कमाई या फैक्टरियों वालों का मुनाफ़ा आदि के रूप में हो सकती है। इसके अतिरिक्त अपने मकान का किराया, ज़मीन का वार्षिक ठेका (आय), बैंक का ब्याज आदि को भी प्रत्यक्ष आय कहा जाता है।
अप्रत्यक्ष आय – यह आय उन सुविधाओं के कारण होती है जो किसी भी नौकरी करने वाले को मिली हों और उनके न मिलने से घर वालों को आय में से खर्च करना पड़े जैसे कि सरकारी घर, मुफ्त दवाइयां या डॉक्टरी सहायता, बिना फ़ीस से बच्चों की पढ़ाई पर, सरकारी कार आदि।
प्रश्न 14. (A)
पारिवारिक आय कितने प्रकार की होती है ?
उत्तर :
देखें प्रश्न 14 का उत्तर।
प्रश्न 15.
खर्च से आप क्या समझते हो? खर्च को कौन-कौन से भागों में बांटा जा सकता है?
उत्तर :
खर्च परिवार की आय और उसकी आवश्यकताओं पर निर्भर करता है। कुछ खर्च ऐसे होते हैं जो परिवार को चाहे आय आधिक हो या कम करने ही पड़ते हैं पर कुछ खर्चे ऐसे होते हैं जिनको आय बढ़ने या घटने से बढ़ाये या घटाये जा सकते हैं जैसे मनोरंजन और हार-श्रृंगार का खर्चा । खर्च को तीन भागों में विभाजित किया जा सकता है –
1. निश्चित खर्च-जैसे मकान का किराया, बिजली का बिल, स्कूल की फीस आदि वे खर्च हैं जो निश्चित होते हैं।
2. अर्द्ध-निश्चित खर्च-ये वे खर्च हैं जो आवश्यक होते हैं परन्तु इनमें परिवर्तन किया जा सकता है जैसे मकान का रख-रखाव, कपड़े और खाने पीने आदि का खर्च।
3. अतिरिक्त खर्च-ये वे खर्च हैं जो आय बढ़ने से बढ़ाए और घटने से घटाए या बन्द किए जा सकते हैं जैसे मनोरंजन और हार भंगार पर खर्च आदि।

प्रश्न 15. (A)
निर्धारित व्यय व अर्धनिर्धारित व्यय में क्या अन्तर है ?
उत्तर :
देखें प्रश्न 15 का उत्तर।
प्रश्न 16.
घर के खर्चों को तुम कौन-कौन से मदों में बांटोगे?
उत्तर :
घर में कई प्रकार की वस्तुओं पर खर्च किया जाता है। घर के खर्च को मुख्य रूप में दो सूचियों में विभाजित किया जा सकता है
1. आवश्यक सूची-इस सूची में घर, भोजन, कपड़े, दवाई, बच्चों की पढ़ाई पर खर्चा आदि शामिल हैं। यह खर्चा प्रत्येक स्थिति में करना ही पड़ता है जिससे परिवार के आवश्यक खर्चे पूरे हो सकें।
2. कम आवश्यक सूची-इस सूची में मनोरंजन, हार-शृंगार, सैर-सपाटा, सामाजिक और धार्मिक समागमों के खर्चे शामिल होते हैं। ये खर्चे ऐसे होते हैं जिनको कुछ समय के लिए टाला भी जा सकता है और पैसा न होने की सूरत में ये खर्चे बन्द भी किए जा सकते हैं।
प्रश्न 17.
बचत क्यों और कैसे की जा सकती है?
उत्तर :
परिवार की आय में से खर्च के पश्चात् जो बचता है उसको बचत कहा जाता है। प्रत्येक मनुष्य को अपनी आय का कुछ प्रतिशत भाग अवश्य बचाना चाहिए। निम्नलिखित कारणों से बचत करनी आवश्यक होती है
1. अचानक बीमारी – कई बार घर का कोई सदस्य अचानक किसी गम्भीर बीमारी का शिकार हो सकता है और उसका इलाज कराने के लिए काफ़ी धन की आवश्यकता पड़ती है और ऐसी स्थिति में बचत काम आती है।
2. परिवार पालक की मृत्यु – कई बार किसी दुर्घटना या बीमारी कारण पारिवारिक मुखिया की अचानक मृत्यु हो सकती है जिससे परिवार की आय बन्द या कम हो सकती है। ऐसी स्थिति में बचत काम आती है।
3. अचानक घाटा – व्यापार करने वाले लोगों को कई बार व्यापार में बहुत अधिक घाटा पड़ जाता है और उनके पास आय का साधन नहीं रहता। ऐसी स्थिति में बचत ही काम आती है।
4. भविष्य की आवश्यकताएं – प्रत्येक परिवार की अपनी भविष्य की आवश्यकताएं होती हैं जैसे बच्चों की उच्च शिक्षा, विवाह शादियों और मकान बनाने आदि के लिए धन की आवश्यकता पड़ती है। इन कामों के लिए बचाया हुआ धन प्रयोग किया जाता है।
5. सुरक्षित बुढ़ापे के लिए – बुढ़ापा एक कुदरती अवस्था है। इस अवस्था में मनुष्य कमाई करने के योग्य नहीं रहता, इसलिए इस समय उसको अपने खर्चे भोजन, कपड़े, आवास और दवाइयों के लिए धन की आवश्यकता होती है जोकि की गई बचत में से ही पूरी की जा सकती है।

प्रश्न 18.
खर्च पर कौन-कौन से तत्त्व प्रभाव डालते हैं?
अथवा
व्यय को प्रभावित करने वाले तत्त्व लिखें।
उत्तर :
पारिवारिक आवश्यकताएं, मनोरंजन और अन्य सामाजिक और धार्मिक कार्यों पर प्रयोग की गई धन राशि को खर्च कहा जाता है। प्रत्येक परिवार के खर्चे भिन्न-भिन्न होते हैं। खर्च पर निम्नलिखित तत्त्व प्रभाव डालते हैं –
1. पारिवारिक सदस्यों की संख्या-यदि परिवार के सदस्यों की संख्या अधिक है तो खर्च भी अधिक होगा इसके अतिरिक्त सदस्यों की आयु और स्वास्थ्य से भी खर्च का सम्बन्ध है।
2. परिवार का सामाजिक स्तर-समाज में परिवार का क्या स्तर है इससे भी परिवार के खर्च पर प्रभाव पड़ता है। समाज में ऊँचा स्तर रखने वाले परिवारों को सामाजिक और धार्मिक कार्यों में अधिक योगदान देना पड़ता है।
3. व्यवसाय – व्यक्ति का व्यवसाय भी उनके खर्च को प्रभावित करता है जैसे राजनीतिज्ञ और व्यापार करने वाले लोगों को अपने व्यवसाय की सफलता के लिए क्लबों, मनोरंजन, महत्त्वपूर्ण लोगों की खातिरदारी पर खर्च करना पड़ता है।
इन तत्त्वों के अतिरिक्त व्यक्ति का स्वभाव, आदतें, दोस्ती का घेरा और मानसिक स्तर भी उसके खर्च को प्रभावित करते हैं।
प्रश्न 19.
प्रतिदिन का हिसाब लिखना क्यों ज़रूरी है और कैसे रखा जाता है?
अथवा
प्रतिदिन का हिसाब-किताब रखना क्यों ज़रूरी है?
उत्तर :
रोज़ाना हिसाब रखना सीमित आय वालों के लिए अति आवश्यक है, क्योंकि रोजाना हिसाब रखने से गृहिणी को यह पता चलता रहता है कि क्या खर्च बजट के अनुसार हो रहा है। यदि खर्चा बढ़ जाए तो गृहिणी को उसी दिन मालूम हो जाता है और दूसरे दिन वह जहां हो सके खर्चा कम कर के बजट को संतुलित कर सकती है। रोज़ाना हिसाब लिखने से गृहिणी परिवार के अन्य सदस्यों को साथ-साथ खर्चे के बारे में सावधान करती रहती है जिससे परिवार के दूसरे सदस्य भी फिजूलखर्ची नहीं करते।
हिसाब रखना-हर रोज़ का हिसाब रखने के लिए एक कापी या डायरी का प्रयोग किया जा सकता है। प्रतिदिन का हिसाब रखने के लिए हर रोज़ एक सफे (पेज) का प्रयोग करना चाहिए। पेज पर तारीख डाल कर चीज़ का ब्योरा अच्छी तरह देकर उसका रेट और कुल रकम लिखनी चाहिए। अगर किसी को सेवा फल के तौर पर कोई रकम दी जाए तो वह भी लिख लेनी चाहिए। महीने के अन्त में हर मद पर हुए खर्चे को अलग-अलग कर लेना चाहिए ताकि पता चल जाए कि किसी मद पर फजूल खर्च तो नहीं हुआ।

प्रश्न 20.
खर्च की कौन-सी मदों से उच्च आय वालों का प्रतिशत खर्च कम आय वालों से अधिक होता है?
उत्तर :
खर्चे की मदें अमीर और ग़रीब दोनों की एक ही हैं परन्तु उच्च आय वर्ग, कम आय वालों से कई मदों पर अधिक खर्च करते हैं। जैसे भोजन, कपड़े, मनोरंजन और घर चलाना। भोजन में उच्च आय वर्ग महंगे भोजन पदार्थों का प्रयोग करते हैं और इसके साथ साथ उनका बाहर भोजन करने का खर्च अधिक होता है।
इस तरह कपड़ों और जूतों पर भी इस वर्ग का खर्च अधिक होता है। अमीर या उच्च आय वर्ग के लोग महंगे और संख्या में अधिक कपड़े बनाते हैं। इसके साथ ही जूते भी कपड़ों से मिलते या मेल खाते खरीदते हैं इसलिए इस तरह उनका कपड़ों के ऊपर कुल खर्चा अधिक हो जाता है। इसके अतिरिक्त उच्च आय वर्ग के लोग कम आय वालों से मनोरंजन पर अधिक खर्च करते हैं। वह सैर-सपाटे, फिल्मों, हार-शृंगार, सिगरेट, शराब आदि के खर्चे बढ़ा लेते हैं। इसके अतिरिक्त सामाजिक और धार्मिक कामों पर भी अधिक खर्च करते हैं। इसके साथ-साथ उनके नौकरों, पेट्रोल और टेलीफोनों के खर्चे भी बढ़ जाते हैं।
प्रश्न 21.
धन निवेश करने की किसी एक योजना के बारे में लिखें।
उत्तर :
देखें दीर्घ उत्तरीय प्रश्न 8 का उत्तर।

प्रश्न 22.
पारिवारिक व्यय का ब्योरा रखने के कोई दो लाभ बताएं।
उत्तर :
1. व्यय का ब्योरा रखने से मितव्ययिता आती है।
2. हिसाब रखने से बचत करने की प्रेरणा मिलती है।
प्रश्न 23.
कोई दो ऐसे तथ्य बतायें जो निवेश संस्था चुनने से पूर्व आप ध्यान में रखेंगे ?
उत्तर :
1. आयकर से छुटकारा-हमें वहां धन लगाना चाहिए जहां पर आयकर से छूट मिलती हो। विभिन्न बचत योजनाओं में आयकर छूट का प्रतिशत भिन्न-भिन्न होता है। अधिक प्रतिशत छूट वाला विकल्प उत्तम रहेगा।
2. आसान उपलब्धि-जैसे ही धन वापसी का समय आये तो धन वापसी आसान होनी चाहिए।
प्रश्न 24.
व्यय को प्रभावित करने वाले चार कारक बताएँ।
उत्तर :
देखें उपरोक्त प्रश्नों में।
दीर्घ उत्तरीय प्रश्न –
प्रश्न 1.
पारिवारिक आय कितने प्रकार की होती है? उदाहरण सहित वर्णन कीजिए।
उत्तर :
आय का मुख्य साधन है-‘काम के बाद प्राप्त होने वाला धन’। लेकिन इसके अतिरिक्त परिवार को अन्य स्रोतों से भी धन प्राप्त हो सकता है।
पारिवारिक आय को मुख्यतः तीन भागों में विभाजित किया जा सकता है –
- मौद्रिक आय (Money Income)
- वास्तविक आय (Real Income) प्रत्यक्ष आय
- आत्मिक आय (Psychic Income) अप्रत्यक्ष आय
मौद्रिक आय, ‘प्रत्यक्ष’ व ‘अप्रत्यक्ष’ दोनों तरह की वास्तविक आय तथा उनके उपभोग से प्राप्त मनोवैज्ञानिक सन्तुष्टि के योग को कुल आय (Total Income) कहते हैं।
1. मौद्रिक आय (Money Income) परिवार के सभी सदस्यों को किसी भी प्रकार से मुद्रा के रूप में प्राप्त हुई आय को मौद्रिक आय कहते हैं। इसके अन्तर्गत परिवार के सभी सदस्यों को सभी साधनों से प्राप्त वेतन, व्यापार, उद्योग-धन्धों से प्राप्त धन, मकान से प्राप्त किराया, बचत किए हुए धन से प्राप्त ब्याज या और किसी भी रूप में हुए लाभ आते हैं। इस प्रकार से प्राप्त धन परिवार की आवश्यकताओं को पूरा करने के लिए किसी भी समय प्रयोग में लाया जा सकता है।
2. वास्तविक आय (Real Income) किसी भी समय पर मनुष्य की विभिन्न आवश्यकताओं को पूर्ण करने के लिए उपलब्ध वस्तुएँ तथा सुख-सुविधाओं को वास्तविक आय कहा जा सकता है। यह आय समयानुसार परिवर्तनशील होती है। इसमें परिवार के किसी भी सदस्य को अपने कार्य-स्थल से धन के अतिरिक्त प्राप्त होने वाली वस्तुएँ तथा सुविधाएँ भी सम्मिलित होती हैं और इस प्रकार यह एक नियत समय के लिए निर्धारित होती है।
यह आय दो प्रकार की होती है –
(i) वास्तविक प्रत्यक्ष आय (Real Direct Income)
(ii) वास्तविक अप्रत्यक्ष आय (Real Indirect Income)
(i) वास्तविक प्रत्यक्ष आय – परिवार को वास्तविक प्रत्यक्ष रूप से होने वाली आय मुख्यतः वस्तुओं एवं सुविधाओं के रूप में ही प्राप्त होती है उदाहरणतः कई बार कार्य-स्थल से वेतन के अलावा कुछ ओर सुविधाएँ, जैसे कि रहने के लिए घर, कार, औषधि खर्चा, टेलीफोन का खर्चा, आने-जाने का खर्चा, यूनीफार्म (Uniform), नौकर आदि भी मिलते हैं और इस प्रकार यह परिवार के लिए प्रत्यक्ष आय का ही एक साधन है। इसी प्रकार गाँवों में किसानों की भूमि में खेती करने पर उनकी मेहनत के बदले उन्हें नगद पैसे के स्थान पर अधिकतर भूमि में हुई उपज में से एक हिस्सा दे दिया जाता है। यह भी परिवार के लिए प्रत्यक्ष आय ही है।
(ii) वास्तविक अप्रत्यक्ष आय-इस प्रकार की आय मुख्यतः परिवार के सदस्यों के ज्ञान व निपुणता के फलस्वरूप प्राप्त होती है उदाहरणार्थ परिवार को किसी सदस्य के बिजली व उपकरण ठीक करने के काम जानने से घर में बिजली या फिर कोई उपकरण बिगड़ जाने पर उसे ठीक करने के लिए बाहर से किसी व्यक्ति को बुलवाने पर होने वाले धन को बचाया जा सकता है। अन्य उदाहरणों में घर में बागबानी करके कुछ फल व सब्जियाँ आदि उगाकर तथा घर में ही कपड़े आदि सिलकर दर्जी को दी जाने वाली सिलाई से बचत की जा सकती है।
घर में इसी प्रकार से यदि गृहिणी अन्य कार्य, जैसे-घरेलू उपयोग के लिए फल-सब्जियों का संरक्षण करना, घर में कपड़े धोना आदि स्वयं करे तो वह परिवार के लिए एक प्रकार से अप्रत्यक्ष रूप से आय अर्जित कर रही है। इस प्रकार संक्षेप में यह कहा जा सकता है कि वास्तविक आय वह आय होती है जो परिवार को सुविधाओं के रूप में प्राप्त होती है और जिनके प्राप्त न होने पर परिवार को अपनी मौद्रिक आय में से खर्च करना पड़ता है।
3. आत्मिक आय (Psychic Income) विभिन्न स्रोतों से प्राप्त मौद्रिक तथा वास्तविक आय के व्यय से प्राप्त होने वाली सन्तुष्टि आत्मिक आय कहलाती है, हालांकि इस प्रकार की आय का कोई भी मापदण्ड नहीं है क्योंकि किसी भी आय के व्यय से किसी मनुष्य को कितनी सन्तुष्टि होती है, इसका माप लगाना अति कठिन है। यही नहीं, हर मनुष्य या परिवार को एक निश्चित मात्रा में किए गए व्यय से प्राप्त सन्तुष्टि भिन्न-भिन्न होती है परन्तु फिर भी आत्मिक आय में वृद्धि के लिए धन-प्रबन्ध का समुचित उपयोग बहुत ही आवश्यक है।

प्रश्न 1. (A)
मौद्रिक आय से आप क्या समझते हैं ?
(B) मौद्रिक आय के चार उदाहरण दें।
उत्तर :
देखें प्रश्न 1 का उत्तर।
प्रश्न 2.
पारिवारिक आय की सम्पूर्ति करने की आवश्यकता क्यों पड़ती है ? आय की सम्पूर्ति करने के विभिन्न तरीकों का विस्तृत वर्णन कीजिए।
उत्तर :
परिवार चाहे किसी भी आय वर्ग का हो, उसे धन को समझदारी से प्रयोग करना चाहिए। हमारी दिन प्रतिदिन की अनगिनत आवश्यकताएँ होती हैं और उन आवश्यकताओं को पूरा करने के लिए आय के साधन सीमित होते हैं। इस कारण केवल पारिवारिक आय तथा व्यय में सन्तुलन लाना बहुत कठिन हो जाता है, अपितु बचत की तो गुंजाइश ही नहीं रह जाती। इन सबके अतिरिक्त परिवार की आकस्मिक आवश्यकताओं को पूरा करना भी बहुत ही आवश्यक हो जाता है जिसके लिए पारिवारिक आय की सम्पूर्ति की आवश्यकता पड़ती है। पारिवारिक आय की सम्पूर्ति निम्नलिखित तरीकों द्वारा की जा सकती है –
1. गृह-उद्योगों द्वारा (Through Household Production) – गृहिणी घर में कुछ साधारण उद्योगों द्वारा धन में वृद्धि कर सकती है। उदाहरणार्थ अगर गृहिणी सिलाई कढ़ाई में निपुण हो तो उसे चाहिए कि वह घर के सभी कार्यों को सम्पन्न कर कुछ खाली समय अवश्य निकाल ले। इस समय का सदुपयोग वह कपड़ों की सिलाई करके और उन कपड़ों को बेचकर, कुछ धन बचाकर आय की सम्पूर्ति अवश्य कर सकती है। इसी प्रकार मौसम में फल तथा सब्जियों का संरक्षण करके बाज़ार में बेचना, पापड़-बड़ियाँ आदि बनाकर बेचना भी कुछ अन्य उदाहरण हैं। न केवल गृहिणी ही, वरन् घर का कोई भी सदस्य अपनी कुशलता, निपुणता तथा क्षमता का सही उपयोग करके पारिवारिक आय की सम्पूर्ति करने में सहायक हो सकता है।
2. पार्ट-टाइम नौकरी द्वारा (Through Part-Time Jobs) – गृहिणी या घर का कोई भी अन्य सदस्य कोई पार्ट-टाइम नौकरी कर ले तो परिवार की आय में वृद्धि की जा सकती है और आर्थिक स्थिति में सुधार लाया जा सकता है। अत: गृहिणी को चाहिए कि गृह-संचालन में समय की उचित व्यवस्था करके कुछ समय बचाकर पार्ट-टाइम नौकरी करे जिससे कि परिवार का जीवन-स्तर ऊँचा उठाया जा सके।
3. परिवार की वास्तविक आय में बढ़ोत्तरी करना (Increase in the Real Income of the Family) परिवार की मौद्रिक आय के साथ-साथ वास्तविक आय में भी वृद्धि की जा सकती है। घर के आगे या पीछे पड़े खाली स्थान पर गृह-वाटिका बनाई जा सकती है, जिसमें विभिन्न प्रकार के फल तथा सब्जियाँ उगाई जा सकती हैं। इस प्रकार फल व सब्जियों पर व्यय होने वाले धन को बचाकर उसका उपयोग अन्य आवश्यक कार्यों के लिए किया जा सकता है।
उपरोक्त के अलावा पारिवारिक आय त में निम्नलिखित बातें भी सहायक होती हैं –
- समय का उचित विभाजन – गृह कार्यों का परिवार के सदस्यों में उचित विभाजन कर गृहिणी निर्धारित समय में गृह कार्य समाप्त कर बाहर भी कार्य कर सकती है या गृह उद्योग से आय को बढ़ा सकती है।
- श्रम एवं समय की बचत के साधनों का प्रयोग – इन साधनों द्वारा समय की बचत होती है जिसे अन्य गृह व्यवसाय में लगाकर धन उपार्जन किया जा सकता है।
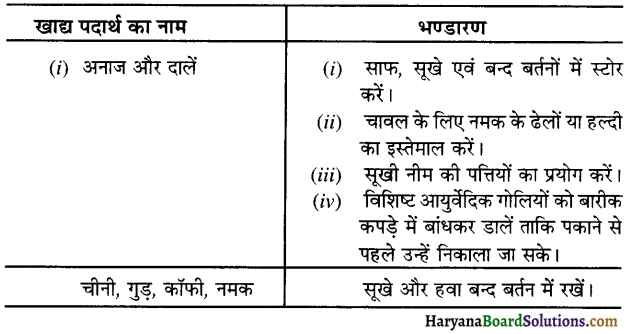
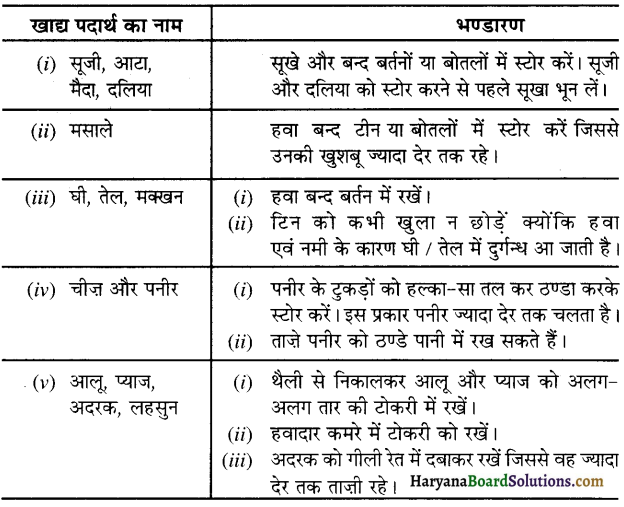
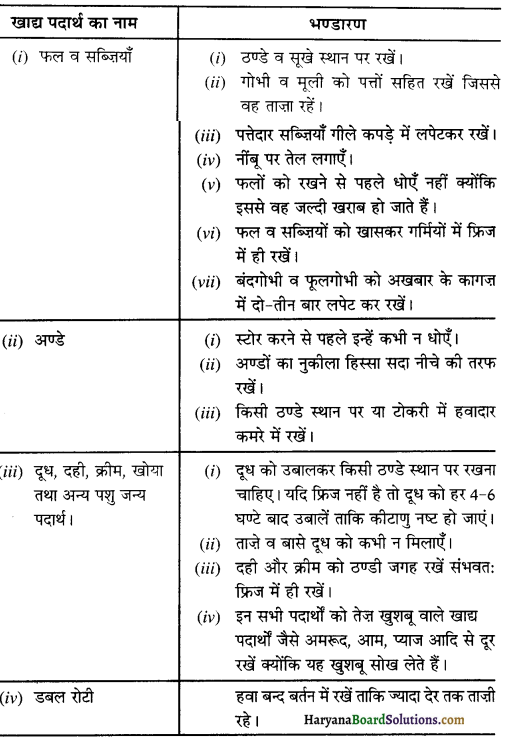
- खाद्य – पदार्थों का संरक्षण एवं संग्रहीकरण-मौसम के अनुसार खाद्य-पदार्थों का संरक्षण तथा संग्रहीकरण कर व्यय में मितव्ययिता की जा सकती है जैसे – मौसम में अनाज सस्ते होते हैं, मौसमी फलों तथा सब्जियों को सॉस, चटनी, जैम, अचार, मुरब्बों आदि के रूप में संरक्षित करना।
- धन का मितव्यय-विवेकपूर्ण व्यय से बचत होती है।
- बचत किए हुए धन का उचित विनियोग-बचत के उचित विनियोग से धन में वृद्धि होती है। ब्याज के रूप में अतिरिक्त आय की वृद्धि होती है। अतः बचत का उचित विनियोग भी आवश्यक है। ब्याज से आय की कमी की पूर्ति होती है।
इस प्रकार उपरोक्त तरीकों से अर्जित सम्पूर्ण आय से परिवार की आवश्यकताओं को किसी सीमा तक पूरा किया जा सकता है, परन्तु साथ ही यह भी ज़रूरी है कि गृहिणी अपनी पारिवारिक आय का योजनापूर्वक उपयोग करे। अधिकतर गृहिणियाँ बिना योजना के ही धन का व्यय करती रहती है, जिसके कारण महीने के अन्त में कई महत्त्वपूर्ण कार्य अधूरे ही रह जाते हैं और परिवार के सभी लक्ष्यों की पूर्ति होना सम्भव नहीं हो पाता है। गृहिणी को चाहिए कि बचत का बजट बनाए जिससे पारिवारिक आय का कुछ अंश आकस्मिक आवश्यकताओं के लिए बचत के रूप में संग्रहित हो सके।
इस प्रकार यह कहा जा सकता है कि पारिवारिक आय तथा व्यय में सन्तुलन लाने के लिए आय की सम्पूर्ति करना परिवार के लिए सहायक है। अत: किसी भी परिवार को सुखमय बनाने के लिए पारिवारिक आय का सही उपयोग तथा आवश्यकता पड़ने पर पारिवारिक आय को विभिन्न तरीकों से बढ़ाना भी अत्यन्त आवश्यक होता है।

प्रश्न 2.A.
आय की सम्पूर्ति के तरीके बताएं।
उत्तर :
देखें प्रश्न 2 का उत्तर।
प्रश्न 3.
परिवार का हिसाब रखने के क्या लाभ होते हैं ?
अथवा
परिवार में आय-व्यय का विवरण रखना क्यों आवश्यक है ?
उत्तर :
परिवार की अर्थ – व्यवस्था को ठीक बनाए रखने के लिए परिवार की आय तथा विभिन्न उद्देश्यों को ध्यान में रखकर बजट बना लेना ही पर्याप्त नहीं होता है, बल्कि विभिन्न मदों पर खर्च किए जाने वाले पैसे का हिसाब-किताब रखना भी बहुत ज़रूरी होता है। घर में इतने प्रकार के खर्चे होते हैं, ‘सभी को याद रखना सम्भव नहीं होता और मानसिक बोझ लदा रहता है। बाजार का हिसाब-किताब रखने के लिए अलग से कापी होनी चाहिए। कापी के ऊपर के पृष्ठ पर ‘बाज़ार का हिसाब’ लिखना चाहिए। प्रत्येक वस्तु का मूल्य अलग-अलग लिखकर उससे प्रतिदिन के खर्च का जोड़ रात को लिख लिया जाए।
कई दिन का हिसाब यदि एक साथ लिखा जाता है तो इसमें भूलने का भय रहता है। हिसाब लिखते समय पृष्ठ के ऊपर तिथि एवं दिन अवश्य लिखना चाहिए। प्रत्येक कापी के पृष्ठ पर केवल एक दिन का हिसाब लिखने से देखने में आसानी होती है। हिसाब की कापी भी एक निर्धारित स्थान पर ही रखनी चाहिए। इससे कापी ढूँढ़ने में व्यर्थ में समय नष्ट नहीं होता और ढूँढने में कठिनाई भी नहीं होती। महीने के शुरू में ही गृह-स्वामिनी को खर्च का ब्योरा बना लेने से सुविधा रहती है तथा व्यर्थ की मदों पर फ़िजूल खर्च का भी भय नहीं रहता।
परिवार में आय-व्यय के विवरण रखने से निम्नलिखित लाभ होते हैं –
1. विभिन्न मदों के लिए निश्चित की गई धनराशि की उपयुक्तता का पता चलता है। यदि धनराशि कम पड़ जाती है तो इस बात का ध्यान रखा जा सकता है कि अगली बार बजट बनाते समय उस मद के लिए अधिक धनराशि नियत की जा सके। इसके विपरीत यदि निर्धारित धनराशि अधिक हो तो उससे सही करने में सहायता मिलती है।
2. कई पदार्थ, जैसे-अखबार, दूध आदि का मूल्य नकद नहीं चुकाया जाता है और महीने के अन्त में ही रकम का भुगतान किया जाता है। यदि नियमित रूप से दैनिक हिसाब लिखा हुआ हो तो भुगतान करने में परेशानी नहीं होती।
3. परिवार के विभिन्न सदस्यों की इच्छाओं-आकांक्षाओं का पता चल जाता है।
4. नई गृहस्थी की पारिवारिक आवश्यकताओं का ज्ञान हो जाता है।
5. आकस्मिक खर्चों का अनुमान लगाना सरल हो जाता है।
6. महीने के प्रारम्भिक दिनों में हाथ में अधिक पैसा होने से अधिक खर्चा हो जाता है। यदि दैनिक हिसाब लिखा हो तो आगामी दिनों में व्यय को सीमित करके सन्तुलित किया जा सकता है।
7. महीने भर बाजार से उधार सामान लेते रहने वाले परिवार में तो हिसाब-किताब लिखना और भी आवश्यक हो जाता है, जिससे दुकानदार किसी प्रकार की हेराफेरी न कर सके।
8. खर्चे का हिसाब-किताब रखने से मितव्ययिता आती है।
9. हिसाब रखने से गृहिणी को बचत करने की प्रेरणा मिलती है।
10. हिसाब रखने से नौकर की चोरी की आदत को बढ़ावा नहीं मिलता।

प्रश्न 4.
घरेलू हिसाब-किताब की विभिन्न विधियाँ कौन-सी हैं ? संक्षेप में बताइए।
उत्तर :
परिवार में हिसाब-किताब की कुछ विधियाँ निम्नलिखित हैं –
1. पारिवारिक वित्त योजना – इसे बजट विधि भी कहते हैं। इस विधि के अन्तर्गत परिवार की सारी आय को एकत्रित करके बजट के अनुसार विभिन्न मदों में बाँट देते हैं। पूरा पैसा गहस्वामी या गृहिणी दोनों में से किसी के हाथ में होता है, या दोनों मिलकर खर्चा करते हैं।
2. आबंटन विधि – इस विधि में यह तय कर लिया जाता है कि आय का कितना भाग पारिवारिक खर्च के लिए है और वह गृहिणी को दे दिया जाता है। शेष अंश गृहस्वामी मकान के किराये तथा वैयक्तिक खर्चे के लिए अपने पास रख लेता है।
3. बराबर वेतन विधि – इस विधि में परिवार की आय में से परिवार के सभी प्रकार के खर्चों के लिए अपेक्षित धनराशि निकाल ली जाती है। शेष धन को पति-पत्नी वैयक्तिक खर्चे के लिए बराबर बाँट लेते हैं।
4. आय-व्यय की बराबर बाँट विधि-इस विधि के अन्तर्गत पूरी आय तथा खर्चों को दो बराबर-बराबर भागों में बाँट लिया जाता है। आय और व्यय का एक भाग पत्नी के तथा दूसरा भाग पति के हिस्से रहता है। जिन घरों में पति व पत्नी दोनों कमाते हैं, वहाँ इस पद्धति का प्रचलन अधिक है।
5. वितरण विधि – इस विधि में पूरी आय सामान्यतः गृहस्वामी के हाथ में रहती है और सभी उसी से अपनी आवश्यकतानुसार पैसा माँगते हैं।
6. अलग – अलग लिफाफों में पैसे रखना-खर्च के हिसाब-किताब की एक सरल विधि यह है कि बजट में जिस-जिस मद के लिए जितनी धनराशि निश्चित की गई है उसे अलग-अलग लिफाफों में डालकर लिफाफे पर मद का नाम लिख लिया जाता है। जिस समय जो खर्च करना होता है, उस समय उसी लिफाफे में से पैसे निकालकर खर्च कर लिया जाता है। इस विधि से महीने के अन्त में यह तो पता आसानी से चल जाता है कि किस मद में कितना खर्च हुआ है, परन्तु मद का पूरा हिसाब नहीं रखा जा सकता है।
7. अलग – अलग कार्ड बनाना-खर्चे का हिसाब-किताब रखने की यह अच्छी विधि है। इस विधि में विभिन्न प्रकार के खर्चों के लिए अलग-अलग कार्ड बना लिए जाते हैं, जैसे-दूध वाले के लिए कार्ड, धोबी के लिए अलग कार्ड, किराने वाले के लिए कार्ड आदि। इस विधि का दोष यह है कि कार्ड के खोने की सम्भावना रहती है और वर्ष भर में इतने कार्ड एकत्रित हो जाते हैं कि वार्षिक खर्च का आसानी से पता नहीं लगता।
8. खर्च की कापी बनाना – इस विधि में एक कापी, डायरी या रजिस्टर में प्रतिदिन विभिन्न मदों पर होने वाले खर्च को लिख लिया जाता है, जिससे प्रतिदिन का कुल व्यय निकल सकता है। दूध, अखबार, धोबी आदि के लिए महीने के शुरू में ही तारीख डालकर लेखा बना लिया जाता है तथा प्रतिदिन की मात्रा और मूल्यों को भर देते हैं। महीने के अन्त में इनका जोड़ निकाल लेते हैं।

प्रश्न 5.
दूध का हिसाब रखना क्यों आवश्यक है ? इसके क्या नियम हैं ? दूध वाले के हिसाब-किताब का नमूना बनाइये।
उत्तर :
दूध का पैसा प्रतिदिन के हिसाब से भी चुकता किया जाता है, परन्तु इसमें असुविधा होती है। बड़े-बड़े शहरों में जहाँ सरकारी डेरियाँ होती हैं, वहां दूध की मात्रा प्रतिदिन के हिसाब से निर्धारित की जाती है। उपभोक्ता यदि इससे कम व अधिक लेना चाहता है तो नहीं ले सकता, अतः दूध का सीधा हिसाब होने से इसमें हिसाब रखने की आवश्यकता नहीं होती। भारतवर्ष में अधिकतर प्राइवेट डेरियों तथा दुकानों से दूध आता है। दूध ग्वालों द्वारा घरों में लाया जाता है जो कि अधिकतर अनपढ़ होते हैं। दूध का हिसाब रखना गृहिणी के लिए जरूरी हो जाता है। हिसाब न रखने से यह पता नहीं चल सकता कि किस दिन दूध कम या अधिक आया, किस दिन नहीं लिया गया तथा महीने में कुल दूध कितना लिया गया। इससे डेयरी वाला हिसाब में गड़बड़ी कर सकता है। दूध की मात्रा ज्यादा बतलाकर अधिक रुपये ले सकता है।
दूध का हिसाब रखने के नियम –
- दूध का हिसाब रखने के लिए अलग कापी हो।
- दूध का हिसाब प्रतिदिन लिख लेना चाहिए।
- हिसाब की कापी के प्रत्येक पृष्ठ का प्रयोग करें जिससे वह व्यर्थ में नष्ट न हो।
- इसके लिए हिसाब-किताब की तालिका अवश्य बनाई जाए।
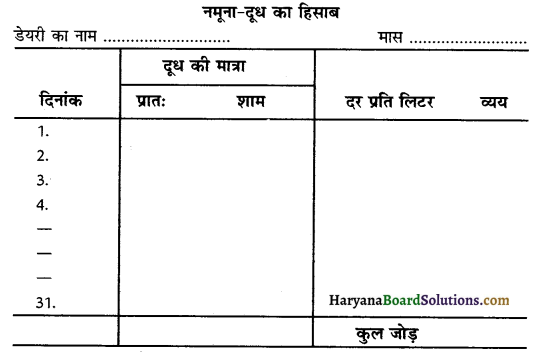

प्रश्न 6.
बचत की आवश्यकता क्यों होती है ?
उत्तर :
बचत की आवश्यकता निम्न उद्देश्यों की पूर्ति के लिए होती है –
1. आपात्कालीन स्थितियों के लिए-भविष्य अनिश्चित होता है तथा परिवार के लिए कई ऐसी स्थितियाँ आ सकती हैं जिनका सामना करने के लिए अतिरिक्त धन की आवश्यकता पड़ती है
(i) बीमारी-परिवार का कोई भी सदस्य जब किसी गम्भीर रोग से ग्रस्त हो जाता है तो उसकी चिकित्सा के लिए धन की आवश्यकता पड़ती है। ऐसी संकटकालीन स्थिति में परिवार द्वारा पहले से बचाया हुआ धन ही काम आता है।
(ii) किसी दुर्घटना के कारण असमर्थता-कई बार दुर्घटना से गृहस्वामी अपंग हो जाता है तथा काम करने योग्य नहीं रहता है। ऐसी स्थिति का सामना करने के लिए बचत किए गए धन की आवश्यकता होती है।
(iii) आय बन्द होना या कम होना-कई कारणों से, जैसे-नौकरी छूटना, व्यापार बन्द होना या व्यापार में घाटा होने से आय बन्द हो जाती है या कम हो जाती है लेकिन अन्य व्यय उतना ही रहता है। ऐसी स्थिति में बचत किया हुआ धन बहुत काम आता है और जब तक दूसरी नौकरी या व्यापार करते हैं तब तक इसी राशि से व्यय को सीमित करके काम चलाया जा सकता है।
(iv) गृहस्वामी का निधन हो जाने पर-मानव जीवन अस्थिर है। गृहस्वामी के निधन के बाद परिवार को आर्थिक संकट का सामना करना पड़ता है। ऐसी परिस्थिति से बचत की गई राशि, जैसे-जीवन बीमा आदि परिवार को आर्थिक संरक्षण प्रदान करती है।
(v) अन्य आकस्मिक दुर्घटनाएँ-घर में आग लग जाने के कारण या चोरी हो जाने के कारण परिवार की आर्थिक स्थिति खराब हो जाती है तथा इस क्षति को बचत किए गए धन द्वारा ही पूरा किया जा सकता है।
2. सुरक्षित भविष्य के लिए नौकरी से अवकाश – प्राप्ति के बाद जो निवृत्त वेतन मिलता है वह परिवार की सभी आवश्यकताओं की पूर्ति हेतु काफ़ी नहीं होता है, अतः आर्थिक रूप से सुरक्षित भविष्य के लिए बचत करना बहुत आवश्यक है।
3. पारिवारिक लक्ष्यों की पूर्ति के लिए – प्रत्येक परिवार के जीवन लक्ष्य होते हैं, जैसे-बच्चों के लिए उच्च शिक्षा आदि। सीमित आय द्वारा इन लक्ष्यों की पूर्ति करना असम्भव-सा है। यदि पहले ही जब बच्चे छोटे हों और परिवार पर आर्थिक दबाव अधिक न हो, आय का कुछ अंश बचाकर उचित रूप से जमा करते जाएँ तो बच्चों के बड़े होने तक उनकी शिक्षा के लिए काफ़ी धन हो जाता है।
4. पारिवारिक जीवन स्तर को ऊँचा उठाने के लिए – आज के भौतिक गुण में परिवार के जीवन स्तर की मापक कुछ भौतिक वस्तुएँ, जैसे-फ्रिज, रंगीन टी० वी०, कार आदि हैं। सीमित आय में इनको खरीदना तो कठिन है परन्तु बचत करके यदि धन इकट्ठा कर लिया जाए तो यह परिवार को उपलब्ध हो सकती हैं।
5. अन्य आकस्मिक खर्चों के लिए – परिवार के कई आकस्मिक खर्च, जैसे अतिथि आगमन, विवाह आदि के कारण होते हैं। ऐसी स्थिति में बचत की धनराशि ही काम आती है।

प्रश्न 7.
परिवार द्वारा बचत कौन-कौन से माध्यम से की जाती है ? संक्षेप में वर्णन कीजिए।
अथवा
बचत किए हुए धन के विनियोग के विभिन्न साधनों के बारे में लिखिए।
उत्तर :
परिवार के द्वारा बचाई गई धनराशि बचत कहलाती है। इसे गृहिणी को ऐसे काम में लगाना चाहिए जिससे कुछ आय भी अर्जित हो तथा धन भी सुरक्षित रहे। बचत विनियोग के विभिन्न साधन हैं। सुरक्षा तथा आय की दृष्टि से प्रमुख साधन अग्रलिखित हैं –
- बैंक
- बीमा
- डाकखाना
- राष्ट्रीय बचत प्रमाण-पत्र
- यूनिट ट्रस्ट क्रय करके।
1. बैंक – पहले समय में लोग बैंक में रुपया जमा करवाने से घबराते थे। उन्हें इस बात का डर रहता था कि बैंक फेल हो जाए और रकम न दे तो उनकी रकम डूब जाएगी, परन्तु आजकल ऐसा नहीं होता। आज प्रायः अधिकांश बैंकों का राष्ट्रीयकरण हो गया है और राष्ट्रीयकृत बैंकों पर भी रिज़र्व बैंक ऑफ़ इण्डिया का पूर्ण नियन्त्रण है। अत: बैंकों में जमा राशि की पूर्ण सुरक्षा रहती है।
बैंक एक ऐसी राष्ट्रीयकृत संस्था है जो मनुष्य की धन सम्बन्धी समस्याओं के निराकरण में सहयोग देती है। बैंक लोगों के धन को जमा करने का कार्य करती है। आवश्यकता पड़ने पर बैंक लोगों को अनेक कार्यों हेतु उधार रुपया देने की व्यवस्था करती है जिसके लिए ब्याज की दर बहुत कम होती है।
इसके अतिरिक्त बैंक में जमा रुपयों को समय-समय पर निकालने की सुविधा, औद्योगिक व्यवसायों के सम्पादन, कीमती वस्तुओं की सुरक्षा के लिए लॉकर्स की सुविधा, चैक, बिल, हुण्डी, ड्राफ्ट से भुगतान की सुविधा प्राप्त होती है।
2. जीवन बीमा – जीवन बीमा अनिवार्य रूप से बचत का उत्तम माध्यम है। यह व्यक्ति को सुरक्षा प्रदान करता है। जीवन बीमा एक ऐसा करार या बन्ध-पत्र होता है जिसमें भावी अनिश्चित विपत्तियों या विशेष घटना घटने पर बीमा धारक या उसके उत्तराधिकारी को एक पूर्व निश्चित धनराशि प्रदान की जाती है। इसके लिए उसे प्रति मास निश्चित किस्त देनी पड़ती है। बीमा निगम एक ऐसी संस्था है जो साधन एवं सुरक्षा प्रदान कर जोखिम को समाप्त करती है तथा अनिश्चित वातावरण को निश्चित वातावरण में परिवर्तित करती है।
3. डाकघर बचत बैंक – डाकघर बचत को सुरक्षित रखने तथा उसका पूर्ण लाभ उठाने में सहायक होता है। डाकघर में कम-से-कम राशि 2 रुपये तक जमा की जा सकती है। डाकघर, बैंक की भी भूमिका निभाते हैं। भारतीय सरकार ने डाकघर बचत बैंक की स्थापना इस दृष्टिकोण से की है कि लोग सरलतापूर्वक बचत कर सकें तथा उनमें बचत की आदत बन सके। इसमें दो व्यक्ति मिलकर रुपया जमा कर सकते हैं तथा नाबालिग बच्चों के नाम से भी माता-पिता खाता खोल सकते हैं।

4. राष्ट्रीय बचत प्रमाण – पत्र-राष्ट्रीय बचत प्रमाण-पत्र की योजना 10 जून, 1966 से शुरू की गई है। ये बचत प्रमाण-पत्र ₹10, ₹ 100 तथा ₹ 1,000 की कीमत के डाकघर से खरीदे जा सकते हैं। अवधि की समाप्ति पर इस रकम पर ₹ 8 प्रति सैंकड़ा की दर से रुपया जमा करने वाले को वापस लौटा दिया जाता है। ये विभिन्न वर्षीय पत्र होते हैं।
5. यूनिट्स – भारतीय संसद् ने एक अधिनियम 1964 में लागू कर ‘यूनिट ट्रस्ट ऑफ़ इण्डिया’ की स्थापना की थी। यूनिट एक प्रकार की अंशपूँजी होती है। इसकी कीमत ₹ 10 होती है। इसके द्वारा यूनिट क्रय करके बचत की जाती है। पोस्ट ऑफिस में आवेदन-पत्र देकर यूनिट्स को क्रय किया जा सकता है। यूनिट से मिलने वाले धन को विभिन्न उद्योगों में विनिमय किया जा सकता है। इसका लाभ बैंक या डाकघर से प्राप्त विभिन्न उद्योगों में विनिमय किया जा सकता है। इसका लाभ बैंक या डाकघर से प्राप्त किया जा सकता है।
6. अनिवार्य समय बचत खाता – इसमें एक निश्चित समयावधि के लिए खाते में धन जमा करवाया जाता है। इससे जमाकर्ता को प्रतिवर्ष निर्धारित ब्याज मिलता रहता है। निश्चित अवधि के पश्चात् ही जमाराशि वापस मिलती है। यह जमा खाता अकेले व्यक्ति द्वारा, संयुक्त रूप से, अल्पवयस्क और विक्षिप्त व्यक्ति के अभिभावक द्वारा खोला जा सकता है।
7. उपहार कूपन्स – यह कूपन ₹ 500, ₹ 1,000, ₹ 5,000 तथा ₹ 10,000 के मिलते हैं। कोई भी व्यक्ति उपहार के रूप में इन्हें किसी अल्पवयस्क या वयस्क व्यक्ति को दे सकता है।
8. दस-वर्षीय रक्षा जमा बाण्ड – यह रिज़र्व बैंक तथा स्टेट बैंक की कुछ शाखाओं और शासकीय कोषालय से खरीदे जा सकते हैं। एक वयस्क अधिक-से-अधिक ₹ 35,000 के और दो वयस्क संयुक्त रूप से ₹ 70,000 के बाण्ड खरीद सकते हैं। इनकी क्रय करने की तिथि से एक वर्ष तक भुगतान नहीं होता है तथा इसके पश्चात् नियमानुसार कटौती काटकर इच्छा से राशि वापिस ली जा सकती है।।
9. प्रीमियम इनामी बाण्ड – ये इनामी बाण्ड ₹ 5 से लेकर ₹ 100 तक के होते हैं। इनकी राशि का भुगतान पाँच वर्ष से पहले नहीं हो सकता है। इन पर इनाम की राशि भी प्राप्त होती है। ये रिज़र्व बैंक, स्टेट बैंक की शाखाओं, शासकीय कोषालयों तथा डाकखानों से प्राप्त किए जा सकते हैं।
10. लॉटरी चिट व्यवस्था – इसमें जान-पहचान वाले व्यक्ति मिलकर प्रतिमास निश्चित राशि देकर कुछ धन इकट्ठा करते हैं। इनमें से जिन व्यक्तियों को धन की आवश्यकता होती है वह चिट पर नाम लिखकर डालते हैं। चिट उठाने पर जिसका नाम आता है, उसे ही धन मिल जाता है, लेकिन आगामी सभी किस्तें जमा करवाते रहनी पड़ती है।
11. कम्पनियों में हिस्सा खरीदना – कई कम्पनियाँ अपने शेयर बेचती हैं। ये शेयर खरीदने पर प्रतिवर्ष धनराशि के हिसाब से लाभांश (Dividend) मिलता रहता है।
12. सहकारी संस्थाएँ – कुछ व्यक्ति मिलकर सहकारी संस्थाएं बनाकर व्यापार आदि करते हैं। जो लाभ होता है उसे आपस में लगाई गई धनराशि के हिसाब से बाँट लेते हैं। सहकारी संस्थाओं को पंजीकृत होने के पश्चात् सरकार की ओर से भी कई प्रकार की सुविधाएँ प्राप्त होती हैं।
नोट – यहां दी गई सभी रुपयों की सीमा अथवा दर सरकार की तथा बैंक या डाकखाने द्वारा तय किए नियमों अनुसार कम या अधिक हो सकती है।

प्रश्न 7.
(A) बचत किए हुए धन के निवेश के किसी एक साधन के बारे में लिखिए।
(B) बचत करना क्यों आवश्यक है ? बचत के विभिन्न तरीकों के बारे में बताइए।
उत्तर :
देखें प्रश्न 7 का उत्तर।
प्रश्न 8.
डाकघर में किन-किन तरीकों से बचत की जाती है ?
उत्तर :
1. डाकघर बचत बैंक (Postal Saving Bank Account) डाकघर में भी रुपया जमा करके बचत की जाती है। सरकार ने डाकघर में बचत बैंक का निर्माण इसलिए किया है कि लोग सरलतापूर्वक रुपया जमा कर सकें तथा उनमें बचत की प्रवृत्ति पैदा हो सके। देहाती क्षेत्रों में जहाँ बैंक की शाखाएँ नहीं हैं, परिवारों के लिए यह सुविधा बहत कल्याणकारी है। डाकघर बचत बैंक में कोई भी व्यक्ति स्वयं के नाम पर नाबालिग के नाम पर जिसका संरक्षक है, खाता खोल सकता है। इसमें दो व्यक्ति संयुक्त रूप से भी खाता खोल सकते हैं। यह खाता पाँच रुपए जमा करवा कर खोला जा सकता है।
डाकघर बचत बैंक में ब्याज की दर बदलती रहती है। डाकघर बचत बैंक में खाता खोलने को प्रोत्साहित करने के लिए कई इनामी योजनाएं भी निकाली गई हैं। इनमें प्रत्येक ऐसे व्यक्ति को इनाम के लिए रखा जा सकता है जिसकी कम-से-कम ₹ 200 की राशि डाकघर में जमा हो। एक व्यक्ति के नाम में अधिक-से-अधिक ₹ 25,000 तथा संयुक्त खाते में ₹ 50,000 जमा हो सकते हैं। जमा राशि केवल उसी डाकघर से निकाली जा सकती है, जहाँ पर खाता खोला गया है। ब्याज 31 मार्च के बाद वर्ष में एक बार जोड़ा जाता है। बैंक की तरह डाकघर भी खाता खोलने वाले को पास बुक देता है जिसमें प्रत्येक जमा तथा निकाली गई राशि का लेखा होता है। माता-पिता या अभिभावक स्वयं नाबालिग के नाम पर खाता खोल सकते हैं।
2. डाकघर सावधि संचयी योजना (Cumulative Scheme) बैंक की तरह इसमें भी सी० टी० डी० जमा खाते खोले जाते हैं। ये 5, 10, 15 वर्ष के लिए खोले जाते हैं। इसमें प्रतिमाह ₹ 5 से ₹ 100 तक की राशि जमा की जा सकती है।
- इस योजना के अन्तर्गत कोई भी एक व्यक्ति या दो व्यक्ति मिलकर खाता खोल सकते हैं।
- यह जमा खाता निश्चित अवधि के लिए खोला जाता है। इसमें ब्याज की दरें बदलती रहती हैं।
- ब्याज का भुगतान प्रति वर्ष किया जाता है परन्तु ब्याज की गणना छमाही की जाती है।
3. डाकघर मियादी खाता (Postal Fixed Deposit) – यह खाता डाकघर में अकेले या संयुक्त रूप में खोला जा सकता है। यह 1, 2, 3, 5 या 10 वर्ष तक के लिए खोला जा सकता है। इसमें ₹ 50 से लेकर ₹ 25,000 तक जमा किए जा सकते हैं।
4. राष्ट्रीय बचत प्रमाण – पत्र (National Saving Certificates) ये प्रमाण-पत्र 10, 100, 1,000 की कीमत के डाकघर से खरीदे जा सकते हैं। ये रकम 10 वर्ष के बाद ₹ 8 प्रति सैंकड़ा की दर से ब्याज सहित जमा करने वाले को दे दी जाती है।
5. बारह-वर्षीय राष्ट्रीय रक्षा – पत्र-ये रक्षा-पत्र ₹ 5, 10, 15, 50, 100, 500, 1000, 5,000 तथा ₹ 25,000 की कीमतों के डाकघर से खरीदे जा सकते हैं। इसमें वार्षिक दर से ब्याज दिया जाता है। एक व्यक्ति 35,000 के तथा दो व्यक्ति एक साथ मिलकर 50,000 के 12 वर्षीय राष्ट्रीय रक्षा-पत्र खरीद सकते हैं।
उपरोक्त के अलावा डाकघर की सहायता से विविध प्रकार के बचत प्रमाण-पत्र तथा खातों द्वारा बचत की जा सकती है। पाँच वर्षीय राष्ट्रीय विकास पत्र, सामाजिक सुरक्षा पत्र, राष्ट्रीय बचत वार्षिक पत्र आदि इसी प्रकार के बचत पत्र हैं।

प्रश्न 9.
जीवन बीमा क्या है ? इसके प्रमुख उद्देश्य व लाभ बताइए।
उत्तर :
जीवन बीमा बचत का सर्वोत्तम साधन है। जीवन बीमा निगम द्वारा दिया गया एक बन्ध-पत्र होता है जिसमें भावी अनिश्चित आपत्तियों या घटना घटित होने पर बीमाधारक को या उसके उत्तराधिकारी को एक पूर्व निश्चित धनराशि निगम द्वारा दी जाती है।
जीवन बीमा के उद्देश्य व लाभ जीवन बीमा के मुख्य उद्देश्य या लाभ निम्नलिखित हैं –
1. परिवार को आर्थिक संरक्षण प्रदान करना – बीमेदार के निधन पर उसके द्वारा नियुक्त परिवार के सदस्य को बीमा की राशि दी जाती है जिससे परिवार आर्थिक संकट का सामना कर सके।
2. वृद्धावस्था में आर्थिक सुरक्षा – वृद्धावस्था में बीमे द्वारा प्राप्त धनराशि आर्थिक संरक्षता प्रदान करती है।
3. विवाह, शिक्षा आदि के लिए आर्थिक सहायता – जीवन बीमा अपनी विशेष पॉलिसी के द्वारा परिवार के विभिन्न उद्देश्यों, विवाह, शिक्षा आदि के लिए आर्थिक सहायता प्रदान करता है।
4. बचत की आदत डालना – जीवन बीमा बचत के लिए विवश करके परिवार के सदस्यों में नियमित बचत करने की आदत डालता है।
5. सम्पत्ति कर चुकाना – बीमेदार के निधन के बाद सम्पत्ति कर चुकाने के लिए सम्पत्ति को बेचने की आवश्यकता नहीं पड़ती है, जीवन बीमा सम्पत्ति कर के लिए धन की व्यवस्था करता है।
6. बीमेदार को व्यापार आदि के लिए ऋण देना-आर्थिक संकट में या व्यापार आदि के लिए बीमा निगम बीमेदार की पॉलिसी की जमानत लेकर ऋण भी देता है।
7. अन्य बचत योजनाओं की अपेक्षा अधिक लाभ पहुँचाना-जीवन बीमा अन्य बचत योजनाओं से अधिक लाभ पहुंचाती है –
- बीमेदार की मृत्यु के बाद उसके परिवार को आर्थिक सुरक्षा प्राप्त होती है।
- बीमे में जमा करवाई गई धनराशि पर आयकर की छूट होती है।
- बीमेदार ने यदि किसी से ऋण लिया हो, तब भी उसके निधन के बाद बीमे की राशि उत्तराधिकारी को दी जाती है और इस प्रकार यह राशि लेनदारों से पूर्ण रूप से सुरक्षित होती है।
- बीमेदार के व्यवस्था करने पर उसके निधन के बाद बीमे की धनराशि उत्तराधिकारी को किस्तों में दी जाती है और जिससे पूर्ण राशि का एक साथ अपव्यय न हो।

प्रश्न 10.
धन का सदुपयोग करने के लिए एक परिवार को क्या-क्या करना चाहिए (कोई तीन उपाय)?
उत्तर :
धन का सदुपयोग करने के लिए परिवार को निम्न कार्य करने चाहिए –
- धन से सोना चांदी खरीद कर रख लेना चाहिए।
- बैंक में बचत खाता खोल लेना चाहिएं।
- निश्चित अवधि जमा योजना में पैसे लगाने चाहिए।
- वस्तुएँ आवश्यकतानुसार खरीदनी चाहिएं ना कि दिखावे के लिए।
- डाकखाने की विभिन्न बचत योजनाओं में पैसा लगाना चाहिए जैसे किसान विकास पत्र, राष्ट्रीय बचत योजना, डाक घर मासिक आय योजना।
- भविष्य निधि, बीमा पॉलिसी आदि में भी धन लगाया जा सकता है।
- वस्तुओं को ऑफ सीजन में खरीद कर भी पैसे की बचत की जा सकती है।
प्रश्न 11.
(A) बचत करना क्यों आवश्यक है ? बचत के किन्हीं चार साधनों के नाम बताएं।
(B) बचत किसे कहते हैं ? इसके साधनों के नाम लिखें।
(C) बचत करना क्यों आवश्यक है ? बचत करने के विभिन्न तरीकों के बारे में बताइए।
उत्तर :
देखें उपरोक्त प्रश्नों में।
एक शब्द/एक वाक्य वाले प्रश्न –
(क) निम्न का उत्तर एक शब्द में दें –
प्रश्न 1.
मकान का किराया कैसा खर्च है ?
उत्तर :
निर्धारित खर्च।

प्रश्न 2.
पारिवारिक आय व्यय के हिसाब से बजट कितने प्रकार का है ?
उत्तर :
तीन प्रकार का।
प्रश्न 3.
यूनिट ट्रस्ट ऑफ़ इण्डिया की स्थापना कब हुई ?
उत्तर :
1964.
प्रश्न 4.
आय को कितने भागों में बांटा जा सकता है ?
उत्तर :
तीन।
प्रश्न 5.
बजट योजना कितने तत्त्वों पर निर्भर है ?
उत्तर :
चार।
(ख) रिक्त स्थान भरो –
1. अवकाश काल का उचित प्रयोग करके हम आत्मिक आय, पारिवारिक आय तथा
………… आय को बढ़ा सकते हैं।
2. ………….. का बजट उत्तम रहता है।
3. खर्चे का हिसाब-किताब रखने से …………. आती है।
4. आयु बढ़ने के साथ-साथ खर्चों में …………. होती है।
उत्तर :
1. मौद्रिक
2. बचत
3. मितव्ययता
4. वृद्धि।

(ग) निम्न में ठीक तथा गलत बताएं –
1. विवेकपूर्ण व्यय से बचत होती है।
2. हमारे देश में दो प्रकार की परिवार व्यवस्था है।
3. शिक्षित व्यक्तियों की आय अशिक्षित व्यक्तियों से अधिक होती है।
4. आवश्यक वस्तुओं की खरीददारी ही करनी चाहिए।
उत्तर :
1. ठीक
2. ठीक
3. ठीक
4. ठीक।
बहु-विकल्पीय प्रश्न –
प्रश्न 1.
खर्च कितने प्रकार के होते हैं –
(A) एक
(B) दो
(C) तीन
(D) चार।
उत्तर :
तीन।
प्रश्न 2.
पारिवारिक बजट के प्रकार हैं –
(A) बचत बजट
(B) सन्तुलित बजट
(C) घाटे का बजट
(D) उपरोक्त सभी।
उत्तर :
उपरोक्त सभी।

प्रश्न 3.
यूनिट ट्रस्ट ऑफ़ इण्डिया की स्थापना कब की गई ?
(A) 1962
(B) 1964
(C) 1971
(D) 1980
उत्तर :
1964.
प्रश्न 4.
आय को मुख्यतः कितने भागों में बांट सकते हैं ?
(A) एक
(B) दो
(C) तीन
(D) चार।
उत्तर :
तीन।
प्रश्न 5.
आत्मिक आय से आप क्या समझते हैं –
(A) विभिन्न स्रोतों से प्राप्त आय के व्यय से होने वाली सन्तुष्टि
(B) विभिन्न स्रोतों से प्राप्त धन
(C) प्राप्त सेवाएं और सुविधाएं
(D) उपरिलिखित सभी।
उत्तर :
विभिन्न स्रोतों से प्राप्त आय के व्यय से होने वाली सन्तुष्टि।
प्रश्न 6.
परिवार की आय को कैसे बढ़ाया जा सकता है –
(A) अंशकालिक नौकरी करके
(B) परिवार की आय में बढ़ोत्तरी करके
(C) गृह उद्योगों की शुरुआत द्वारा
(D) उपरिलिखित सभी।
उत्तर :
उपरिलिखित सभी।

प्रश्न 7.
अवकाश काल का उचित प्रयोग करके हम ……………. को बढ़ा सकते हैं।
(A) आत्मिक आय
(B) पारिवारिक आय
(C) मौद्रिक आय
(D) उपरिलिखित सभी।
उत्तर :
उपरिलिखित सभी।
प्रश्न 8.
सुरक्षित भविष्य के लिए क्या करना चाहिए –
(A) बचत करना
(B) खुलकर खर्च करना
(C) उधार लेना
(D) धन का दान देना।
उत्तर :
बचत करना।
प्रश्न 9.
आयु बढ़ने के साथ-साथ खर्चों में ……… होती है।
(A) वृद्धि
(B) कमी
(C) कोई फ़र्क नहीं पड़ता
(D) उपरिलिखित में से कोई नहीं।
उत्तर :
वृद्धि।

प्रश्न 10.
किस प्रकार का बजट उत्तम रहता है –
(A) घाटे का बजट
(B) बचत का बजट
(C) सन्तुलित बजट
(D) उपरिलिखित सभी।
उत्तर :
बचत का बजट।
प्रश्न 11.
संयुक्त परिवार में खर्च …………… होता है।
(A) कम
(B) अधिक
(C) सामान्य
(D) कोई भी नहीं।
उत्तर :
कम।
प्रश्न 12.
खर्च की आवश्यक मद कौन-सी है –
(A) घर
(B) भोजन
(C) कपड़े
(D) उपरिलिखित सभी।
उत्तर :
उपरिलिखित सभी।

प्रश्न 13.
खर्च कितने प्रकार के होते हैं –
(A) निर्धारित खर्च
(B) अर्द्ध-निर्धारित खर्च
(C) गैर-निर्धारित खर्च
(D) उपरिलिखित सभी।
उत्तर :
उपरिलिखित सभी।
प्रश्न 14.
ऐन्जिल के सिद्धान्त के अनुसार जैसे-जैसे आय बढ़ती है, भोजन पर व्यय का प्रतिशत ……………. है।
(A) घटता
(B) बढ़ता
(C) उतना ही रहता है
(D) कोई भी नहीं।
उत्तर :
घटता।
प्रश्न 15.
निम्नलिखित में से कौन-सी प्राथमिक आवश्यकता नहीं है ?
(A) आवास
(B) भोजन
(C) कपड़ा
(D) शिक्षा।
उत्तर :
शिक्षा।

प्रश्न 16.
बचत की आवश्यकता क्यों होती है ?
(A) सुरक्षित भविष्य के लिए
(B) आपात स्थिति का सामना करने के लिए
(C) परिवार के रहन-सहन का स्तर बढ़ाने के लिए
(D) उपर्युक्त सभी के लिए।
उत्तर :
उपर्युक्त सभी के लिए।
प्रश्न 17.
परिवार के द्वारा जिन साधनों और सुविधाओं का प्रयोग किया जाता है, वह उसकी कौन-सी आय कहलाती है ?
(A) आत्मिक आय
(B) वास्तविक आय
(C) मौद्रिक आय
(D) इनमें से कोई भी नहीं।
उत्तर :
आत्मिक आय
प्रश्न 18.
निम्नलिखित मदों में व्यय करने के लिए आप किसको सबसे अधिक प्राथमिकता देंगे ?
(A) विदेश यात्रा के लिए जाना
(B) सर्दियों के लिए पर्याप्त ऊनी कपड़ों की खरीददारी
(C) रेफ्रिजरेटर खरीदना
(D) नया सोफा सेट खरीदना।
उत्तर :
सर्दियों के लिए पर्याप्त ऊनी कपड़ों की खरीददारी।

प्रश्न 19.
जीवन बीमा पॉलिसी कराना कहलाता है –
(A) निवेश
(B) व्यय करना
(C) बचत
(D) इनमें से कोई भी नहीं।
उत्तर :
बचत।
प्रश्न 20.
सुरक्षित भविष्य के लिए क्या करना चाहिए ?
(A) बचत करना
(B) खुलकर खर्च करना
(C) उधार लेना
(D) धन का दान देना।
उत्तर :
बचत करना।
प्रश्न 21.
निम्नलिखित मदों में से व्यय करने के लिए आप किसको सबसे अधिक प्राथमिकता देंगे ?
(A) छुट्टियाँ बिताने के लिए कहीं बाहर जाना
(B) बच्चों के लिए पौष्टिक भोजन की खरीद
(C) मिक्सर ग्राइंडर की खरीद
(D) साधारण पर्दे बदलने के लिए नए फैन्सी पर्दो की खरीद।
उत्तर :
बच्चों के लिए पौष्टिक भोजन की खरीद।

प्रश्न 22.
निम्न में से कौन-सा कथन बचत से सम्बन्धित है ?
(A) आपकी माता द्वारा आपको दिए गए पैसे
(B) आपके पिता का वेतन
(C) आप प्रतिदिन दस रुपये एक डिब्बे में डालते हैं
(D) अण्डे बेचकर आपको धन मिलता है।
उत्तर :
आप प्रतिदिन दस रुपये एक डिब्बे में डालते हैं।
प्रश्न 24.
ऐंजिल के अनुसार, जैसे-जैसे आय बढ़ती है, मकान, वस्त्र, विद्युत् पर व्यय में ……………… ।
(A) परिवर्तन नहीं होता है
(B) परिवर्तन होता है
(C) लाभ होता है
(D) हानि होती है।
उत्तर :
परिवर्तन नहीं होता है।
प्रश्न 25.
संयुक्त परिवार में खर्च कम और आय …………. होती है।
(A) कम
(B) सामान्य
(C) अधिक
(D) ऊपरलिखित सभी।
उत्तर :
अधिक।

प्रश्न 26.
कौन-सा बजट सबसे उत्तम रहता है ?
(A) घाटे का बजट
(B) बचत का बजट
(C) संतुलित बजट
(D) ऊपरलिखित सभी।
उत्तर :
बचत का बजट।
प्रश्न 27.
ऐंजिल के अनुसार, जैसे-जैसे आय बढ़ती है, भोजन पर व्यय का प्रतिशत
(A) घटता
(B) बढ़ता
(C) सामान्य
(D) ऊपरलिखित सभी।
उत्तर :
घटता।

प्रश्न 28.
संयुक्त परिवार में खर्च आय अधिक होती है।
(A) ज्यादा
(B) कम
(C) सामान्य
(D) ऊपरलिखित सभी।
उत्तर :
कम।
प्रश्न 29.
परिवार की आय को कौन-कौन से दो भागों में बाँटा जा सकता है ?
(A) मौद्रिक आय व मानसिक रूप से प्राप्त आय
(B) प्रत्यक्ष व अप्रत्यक्ष आय
(C) मौद्रिक आय व अप्रत्यक्ष आय
(D) अप्रत्यक्ष आय व मानसिक रूप से प्राप्त आय।
उत्तर :
मौद्रिक आय व मानसिक रूप से प्राप्त आय।
प्रश्न 30.
डाकखाने में कितने रुपयों से खाता खोला जा सकता है ?
(A) कम से कम ₹ 1000 से
(B) कम से कम ₹ 2000 से
(C) कम से कम ₹ 5000 से
(D) कम से कम ₹ 50 से।
उत्तर :
कम से कम ₹ 50 से।

प्रश्न 31.
आमदनी में से ………… को बचत कहते हैं।
(A) खर्च की गई रकम
(B) उधार ली गई रकम
(C) बचाई गई रकम
(D) ऊपरलिखित सभी।
उत्तर :
बचाई गई रकम।
प्रश्न 32.
बजट योजना किस तत्त्व पर निर्भर करती है ?
(A) परिवार की आय
(B) परिवार का लक्ष्य
(C) परिवार की तत्कालीन आवश्यकताएँ
(D) ऊपरलिखित सभी।
उत्तर :
ऊपरलिखित सभी।
धन का प्रबन्ध HBSE 10th Class Home Science Notes
धन का प्रबन्ध –
→ परिवार की आय को प्रत्यक्ष और अप्रत्यक्ष दो किस्मों में विभाजित किया जाता है।
→ घर की आवश्यकताओं के लिए प्रयोग की धन राशि को खर्च कहा जाता है।
→ खर्च निर्धारित और गैर-निर्धारित होता है।
→ पारिवारिक आमदन के अनुसार खर्च के अनुमान को बजट कहा जाता है।
→ आमदन में से बचाई गई रकम को बचत कहते हैं।
→ कुशल गृहिणी कम आमदन से भी बढ़िया घर चला सकती है।
→ बजट तीन किस्मों का होता है-बचत बजट, संतुलित बजट और घाटे का बजट।
→ बचत अवश्य करनी चाहिए। इसमें परिवार के सदस्यों की भलाई है।
→ संयुक्त परिवारों में खर्च कम और आय अधिक होती है।

परिवार के लिए सबसे महत्त्वपूर्ण बात यह है कि वह अपने वित्तीय साधनों का प्रयोग इस ढंग से करे कि अधिक-से-अधिक लाभ प्राप्त हो सके। प्रत्येक मनुष्य अपने ज्ञान, योग्यताओं का प्रयोग करके अपने जीवन का गुजारा करता है। एक विशेष समय में जैसे कि सप्ताह, महीना, साल में परिवार द्वारा कमाई गई आय को पारिवारिक आय कहा जाता है।
इस पारिवारिक आय को इस ढंग से खर्च करना चाहिए कि परिवार के सभी सदस्य सन्तुष्ट, खुश और तन्दुरुस्त रहें। इसलिए एक समझदार गृहिणी को आय और खर्च में सन्तुलन रखने के लिए बजट बनाना चाहिए।
![]()
![]()
![]()



![]()
![]()
![]()
![]()