HBSE 10th Class Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.1

Haryana State Board HBSE 10th Class Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.1 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Exercise 8.1

प्रश्न 1.
ΔABC में, जिसका कोण B समकोण है, AB = 24cm और BC = 7 cm है। निम्नलिखित का मान ज्ञात कीजिए
(i) sin A, cos A
(ii) sin C, cos C
हल :

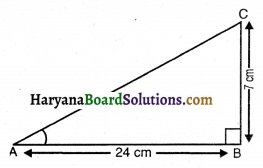
यहाँ पर, ΔABC में कोण B समकोण है।
AB = 24 cm
BC = 7 cm

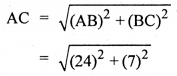
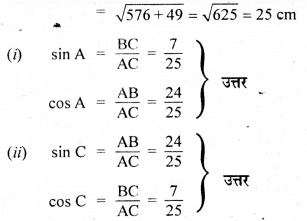
प्रश्न 2.
संलग्न आकृति में, tan P- cot R का मान ज्ञात कीजिए।
हल :

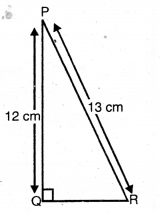
दी गई आकृति के अनुसार, ΔPQR में ∠Q समकोण है।
PQ = 12 cm
PR = 13 cm

प्रश्न 3.
यदि sin A = \(\frac{3}{4}\), तो cos A और tan A का मान परिकलित कीजिए।
हल :

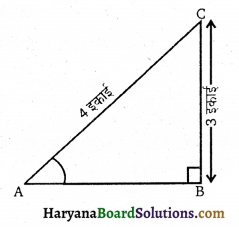
माना ΔABC में ∠B समकोण है, तो
BC = 3 इकाई
AC = 4 इकाई

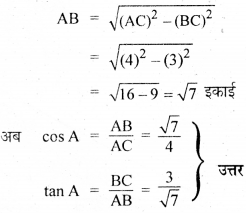
प्रश्न 4.
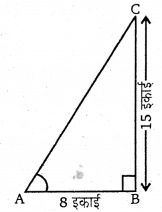
यदि 15 cot A = 8 हो तो sin A और sec A का मान ज्ञात कीजिए।
हल :
माना ΔABC में ∠B समकोण है, तो
15 cotA = 8.
या cot A = \(\frac{8}{15}=\frac{\mathrm{AB}}{\mathrm{BC}}\)
AB = 8 इकाई
BC = 15 इकाई

प्रश्न 5.
यदि sec θ = 13/12 हो तो अन्य सभी त्रिकोणमितीय अनुपात परिकलित कीजिए।
हल :

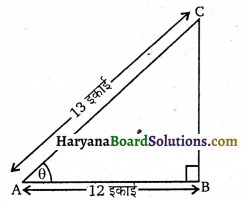
माना ΔABC में ∠B समकोण है तथा ∠A =θ तो
sece = 12 = AB
AC = 13 इकाई
AB = 12 इकाई

प्रश्न 6.
यदि ∠A और ∠B न्यून कोण हो, जहाँ cos A = cos B, तो दिखाइए कि ∠A = ∠B.
हल :

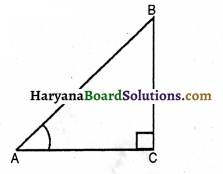
माना ABC एक त्रिभुज है, जिसका ∠C समकोण है तथा ∠A व ∠B न्यून कोण हैं।
अब समकोण ΔACB में
cos A = \(\frac{\mathrm{AC}}{\mathrm{AB}}\)
cos B = \(\frac{\mathrm{BC}}{\mathrm{AB}}\)
परंतु प्रश्नानुसार,
cos A = cos B
\(\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{\mathrm{BC}}{\mathrm{AB}}\)
या AC = BC
क्योंकि ΔACB में, AC = BC इसलिए ∠A = ∠B [∵ समकोण भुजाओं के सम्मुख कोण बराबर होते हैं।]

प्रश्न 7.
यदि cot θ = \(\frac{7}{8}\) तो (i) \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}\)
(ii) cot²θ का मान निकालिए।
हल :

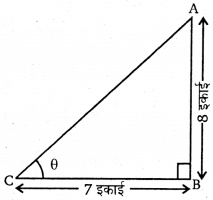
माना ABC एक त्रिभुज है जिसका ∠B समकोण तथा ∠ACB = θ है।
cot θ = \(\frac{7}{8}=\frac{\mathrm{BC}}{\mathrm{AB}}\)
BC = 7 इकाई
AB = 8 इकाई

(ii) cot²θ = \(\left(\frac{\mathrm{BC}}{\mathrm{AB}}\right)^{2}=\left(\frac{7}{8}\right)^{2}=\frac{49}{64}\)

प्रश्न 8.
यदि 3 cotA = 4, तो जाँच कीजिए कि \(\frac{1-\tan ^{2} A}{1+\tan ^{2} A}\) = cos²A – sin²A है या नहीं।
हल :

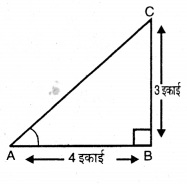
माना ABC एक त्रिभुज है, जिसका ∠B समकोण तथा ∠A न्यून कोण है। दी गई आकृति के अनुसार,
3 cot A = 4
या cos A = \(\frac{4}{3}=\frac{A B}{B C}\)
AB = 4 इकाई
BC = 3 इकाई

प्रश्न 9.
त्रिभुज ABC में, जिसका कोण B समकोण है, यदि tan A = \(\frac{1}{\sqrt{3}}\) , तो निम्नलिखित के मान ज्ञात कीजिए-
(i) sin A cos C + cos A sin C
(ii) cos A cos C- sin A sin C
हल :

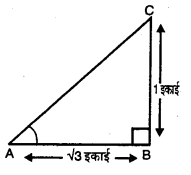
त्रिभुज ABC में ∠B समकोण है तथा
tan A = \(\frac{1}{\sqrt{3}}=\frac{\mathrm{BC}}{\mathrm{AB}}\)
BC = 1 इकाई
AB = √3 इकाई

प्रश्न 10.
ΔPQR में, जिसका कोण Q समकोण है, PR + QR = 25cm और PQ = 5cm है। sin P, cos P और tan P के मान ज्ञात कीजिए।
हल :

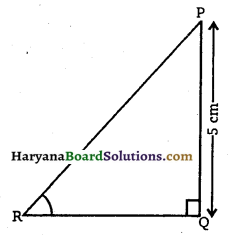
ΔPQR में ∠Q समकोण है तथा
PR + OR = 25cm
और PQ = 5cm
माना PR = x cm
तो QR = (25-x) cm
हम जानते हैं कि पाइथागोरस प्रमेय अनुसार,
PR² = PQ² + QR²
x² = (5)² + (25-x)²
x² = 25 + 625 + x² – 50x
50x = 650
x = 650/50 = 13 cm
PR = 13 cm
और QR = 25 – 13 = 12 cm

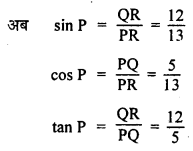
प्रश्न 11.
बताइए कि निम्नलिखित कथन सत्य हैं या असत्य। कारण सहित अपने उत्तर की पुष्टि कीजिए।
(i) tan A का मान सदैव 1 से कम होता है।
(i) कोणA के किसी मान के लिए sec A = \(\frac{12}{5}\)
(iii) cos A, कोण A के cosecant के लिए प्रयुक्त एक संक्षिप्त रूप है।
(iv) cot A, cot और A का गुणनफल होता है।
(v) किसी भी कोण 8 के लिए sin θ = \(\frac{4}{3}\)
हल :
(i) असत्य, क्योंकि tan A का मान शून्य से अनंत तक होता है।
(ii) सत्य।
(iii) असत्य, क्योंकि cos A कोण A के cosine के लिए प्रयुक्त एक संक्षिप्त रूप है न कि cosecant के लिए।
(iv) असत्य, क्योंकि cotA को कोण A के cotangent का संक्षिप्त रूप माना जाता है न कि cot और A का गुणनफल।
(v) असत्य, क्योंकि किसी भी कोण θ के लिए sinθ का मान 0 और 1 के बीच होता है।