Haryana State Board HBSE 7th Class Maths Solutions Chapter 7 त्रिभुजों की सर्वांगसमता InText Questions and Answers.
Haryana Board 7th Class Maths Solutions Chapter 7 त्रिभुजों की सर्वांगसमता InText Questions
पृष्ठ सं. 152-153
प्रश्न 1.
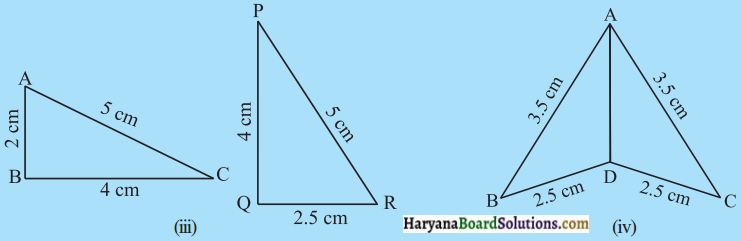
आकृतियों में त्रिभुजों की भुजाओं की लम्बाइयाँ दर्शाई गई हैं। S.S.S. सर्वांगसमता प्रतिबंध का प्रयोग करके बताइए कि कौन-कौन से त्रिभुज-युग्म सर्वांगसम हैं। सर्वागसमता की स्थिति में, उत्तर को सांकेतिक रूप में लिखिए :
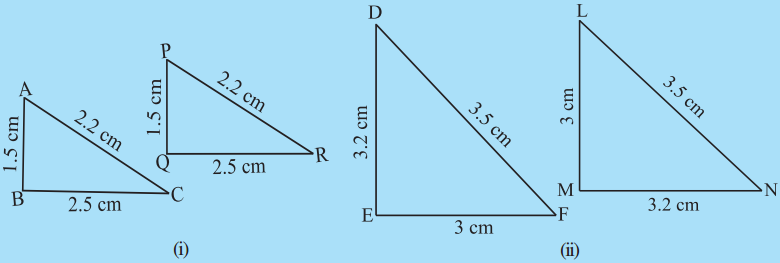
हल :
(i) ΔABC और ΔPQR में,
AB = PQ = 15 सेमी
BC = QR = 2.5 सेमी
CA = RP = 2.2 सेमी
S.S.S. सर्वांगसमता से,
ΔABC ≅ ΔPQR
(ii) ΔDEF और ΔLMN में,
EF ≠ MN
अत: ये त्रिभुज सर्वांगसम नहीं हैं।
(iii) ΔABC और ΔPQR में
BC ≠ QR
अत: ये त्रिभुज सर्वांगसम नहीं हैं।
(iv) ΔADB और Δ ADC में,
AD = AD (उभयनिष्ठ)
DB = DC = 2.5 सेमी और
BA = CA = 3.5 सेमी
∴ S.S.S. सर्वांगसमता से,
ΔADB ≅ ΔADC.

प्रश्न 2.
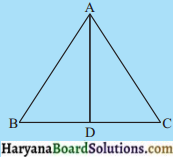
आकृति में, AB = AC और D, \(\overline{B C}\) का मध्य बिंदु है।
(i) ΔADB और ΔADC में बराबर भागों के तीन युग्म बताइए।
(ii) क्या ΔADB ≅ ΔADC है? कारण दीजिए।
(iii) क्या ∠B = ∠C है? क्यों?
हल :
(i) ΔADB और ΔADC में,
AD = AD, (उभयनिष्ठ)
AB = AC, (दिया है)
और DB = DC,
[∵ D, \(\overline{B C}\) का मध्य बिन्दु है]
(ii) S.S.S. सर्वांगसमता प्रतिबन्ध से ।
ΔADB ≅ ΔADC
(iii) ∠B = ∠C है।
क्योंकि सर्वांगसम त्रिभुजों के संगत कोण समान होते हैं।
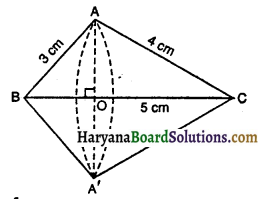
प्रश्न 3.
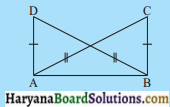
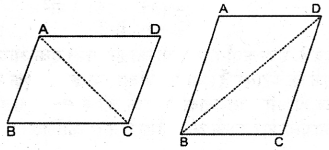
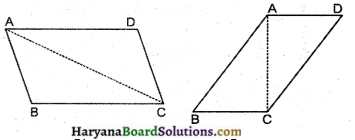
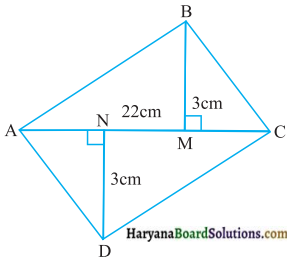
आकृति में, AC = BD और AD = BCहै। निम्नलिखित कथनों में कौन-सा कथन सत्य है?
(i) ΔABC ≅ ΔABD
(ii) ΔABC ≅ ΔBAD
हल :
(i) ΔABC ≅ ΔABD नहीं लिख सकते
AB = AB [सही है]
BC = BD, [सही नहीं है।
और CA = DA, [सही नहीं है]
(ii) ΔABC ≅ ΔBAD लिख सकते हैं।
AB = AB [उभयनिष्ठ]
BC = AD [दिया है]
और CA = DB, [दिया है]

पृष्ठ सं. 156 (इन्हें कीजिए)
प्रश्न 1.
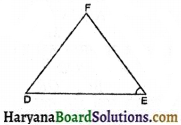
ΔDEF की भुजाओं \(\overline{D E}\) और \(\overline{E F}\) का अंतर्गत कोण कौन-सा है?
हल :
ΔDEF को भुजाओं \(\overline{D E}\) और \(\overline{E F}\) का अंतर्गत कोण ∠DEF है।
प्रश्न 2.
S.A.S. सर्वांगसमता प्रतिबंध का उपयोग करके आप ΔPQR ≅ ΔFED स्थापित करना चाहते हैं। यह दिया गया है कि PQ = FE और RP = DF है। सर्वांगसमता को स्थापित करने के लिए अन्य किस तथ्य या सूचना की आवश्यकता होगी?
हल :
ΔPQR ≅ ΔFED को स्थापित करने के लिए अन्य तथ्य ∠P = ∠F की आवश्यकता होगी।
प्रश्न 3.
आकृति में, त्रिभुजों के युग्मों में कुछ भागों की माप अंकित की गई है। S.A.S. सर्वांगसमता प्रतिबंध का उपयोग करके, इनमें वेयुग्म छाँटिए जोसर्वांगसम हैं। सर्वांगसम त्रिभुजों की स्थिति में उन्हें सांकेतिक रूप में भी लिखिए।
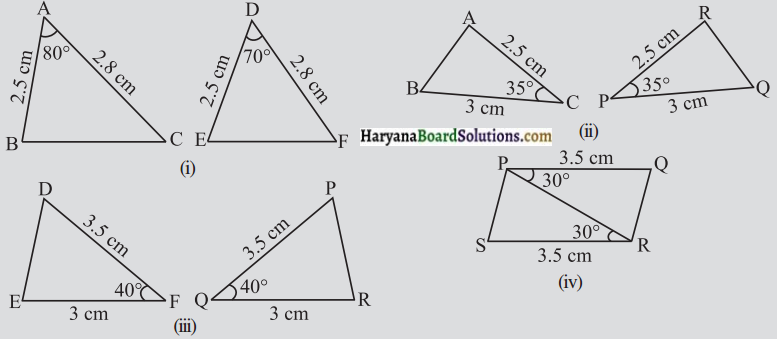
हल :
(i) ΔABC और ΔDEF में,
∠A ≠ ∠D
अतः ये दोनों Δ सर्वांगसम नहीं हैं।
(ii) ΔACB और ΔRPQ में,
AC = RP = 2.5 सेमी
∠C = ∠P = 35° और
CB = PQ = 3 सेमी
∴ S.A.S. सर्वांगसमता से,
ΔACB ≅ ΔRPQ
(iii) ΔDEF और ΔPQR में,
DE = PQ = 3.5 सेमी
∠F = ∠Q = 40°
सेमी EF = RQ = 3 सेमी
∴ SAS सर्वांगसमता से,
ΔDFE ≅ ΔPQR
(iv) ΔRSP और ΔPQR में,
RS = PQ = 3.5 सेमी
∠PRS = ∠RPQ = 30°
और RP = PR
∴ S.A.S. सर्वांगसमता से,
ΔRSP ≅ ΔPQR.

प्रश्न 4.
आकृति में, \(\overline{A B}\) और \(\overline{C D}\) एक-दूसरे को O पर समद्विभाजित करती हैं।
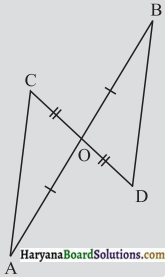
(i) दोनों त्रिभुजों AOC और BOD में बराबर भागों के तीन युग्मों को बताइए।
(ii) निम्न कथनों में से कौन-से कथन सत्य हैं ?
(a) ΔAOC ≅ ΔDOB
(b) ΔAOC ≅ ΔBOD
हल :
(i) ΔAOC और ΔBOD के बराबर भागों के तीन युग्म निम्न हैं:
OA = OB
OC = OD और
∠AOC = ∠BOD
(ii) सही विकल्प (b) है।
पृष्ठ सं. 158
प्रश्न 1.
ΔMNP में कोणों, M तथा Nके अंतर्गत भुजा क्या है ?
हल :
ΔMNP में कोणों M तथा N के अंतर्गत भुजा MN है।

प्रश्न 2.
A.S.A. सर्वांगसमता प्रतिबंध का उपयोग करके आप ΔDEF ≅ ΔMNP स्थापित करना चाहते हैं। आपको दिया गया है कि ∠D = ∠M और ∠F = ∠P इस सर्वांगसमता को स्थापित करने के लिए और कौन-से तथ्य की आवश्यकता है ? (खाका आकृति बनाकर कोशिश कीजिए।
हल:
ΔDEF ≅ ΔMNP
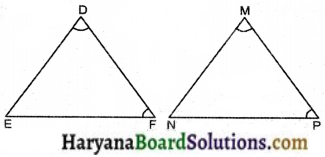
स्थापित करने के लिए दिए गए प्रतिबन्धों के अतिरिक्त भुजा DF = भुजा MP की आवश्यकता होगी।
प्रश्न 3.
निम्न आकृतियों में, त्रिभुजों के कुछ भागों की माप अंकित की गई है। A.S.A. सांगसमता प्रतिबंध का उपयोग करके बताइए कौन-से त्रिभुजों के युग्म सर्वांगसम हैं। सांगसमता की स्थिति में, उत्तर को सांकेतिक रूप में लिखिए।
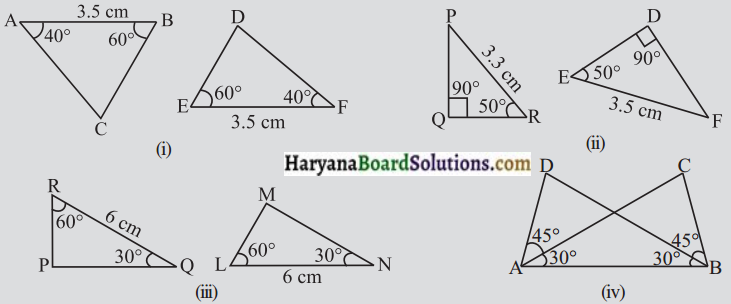
हल :
(i) ΔABC और ΔFED में,
∠A = ∠F = 40°
AB = FE = 3.5 सेमी
और
∠B = ∠E = 60°
∴ A.S.A. सर्वांगसमता से,
ΔABC ≅ ΔFED
(ii) ΔPQR और ΔEDF में,
PR ≠ EF
∴ A.S.A. सर्वांगसमता से,
अतः ये त्रिभुज सर्वांगसम नहीं है।
(iii) ΔPQR और MNL में,
∠R = ∠L = 60°
QR = NL = 6 सेमी और
∠Q = ∠N = 30°
∴ A.S.A. सर्वांगसमता से,
ΔPQR ≅ ΔMNL
(iv) ΔABC और ΔBAD में,
∠CAB = ∠DBA = 30°
AB = BA और
∠ABC = ∠BAD = 75°,
(∵ 30° + 45° = 75°)
∴ A.S.A. सर्वांगसमता से,
ΔABC ≅ ΔBAD

प्रश्न 4.
दो त्रिभुजों के कुछ भागों की माप नीचे दी गई हैं। A.S.A. सर्वांगसमता प्रतिबंध का उपयोग करके जाँचिए कि क्या ये दोनों त्रिभुज सर्वांगसम हैं या नहीं। सर्वांगसमता की स्थिति में उत्तर को सांकेतिक रूप में भी लिखिए :
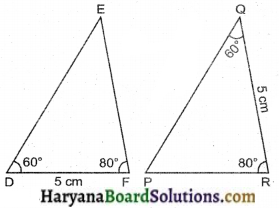
| ∆DEF | ∆PQR |
| (i) ∠D = 60º, ∠F = 80º, DF = 5 सेमी | ∠Q = 60º, ∠R = 80º, QR = 5 सेमी |
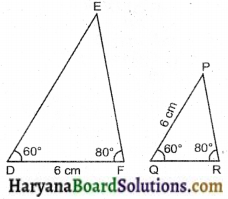
| (ii) ∠D = 60º, ∠F = 80º, DF = 6 सेमी | ∠Q = 60º, ∠R = 80º, QP = 6 सेमी |
| (iii) ∠E = 80º, ∠F = 30º, EF = 5 सेमी | ∠P = 80º, PQ = 5 cm, ∠R = 30º सेमी |
हल :
(i) ΔDEF और ΔQPR में,
∠D = ∠Q
DF = QR और
∠F = ∠R = 80°
∴ A.S.A. सर्वांगसमता से,
ΔDEF ≅ ΔQPR
(ii) ∵ समान कोणों के बीच समान भुजा नहीं है।
∴ ये त्रिभुज सर्वांगसम नहीं हैं।
(iii) ΔDEF और ΔQPR में,
∠E = ∠P = 80°
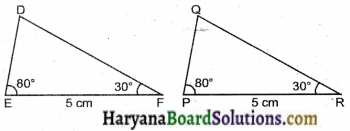
EF = PR = 5 सेमी और
∠F = ∠R = 30°
∴ A.S.A. सर्वांगसमता से,
ΔDEF ≅ ΔQPR.
प्रश्न 5.
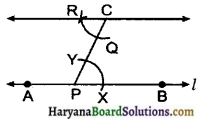
आकृति में, किरण AZ, ∠DAB तथा ∠DCB को समद्विभाजित करती है।
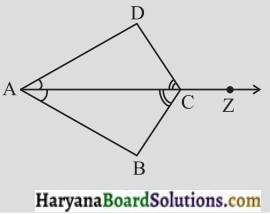
(i) त्रिभुजों BAC और DAC में बराबर भागों के तीन युग्म बताइए।
(ii) क्या ΔBAC ≅ ΔDAC हैं ? कारण दीजिए।
(iii) क्या AB = AD है ? अपने उत्तर का उचित कारण दीजिए।
(iv) क्या CD = CBहै? कारण दीजिए।
हल :
(i) ΔBAC तथा ΔDAC में तीन समान युग्म हैं।
∠BAC = ∠DAC, AC = AC और ∠BCA = ∠DCA.
(ii) हाँ, A.S.A. सर्वांगसमता से,
ΔBAC ≅ ΔDAC.
(iii) हाँ, AB = AD [∵ सर्वांगसम त्रिभुजों में संगत भुजाएँ समान होती हैं]
(iv) हाँ, CD = CB, [∵ सर्वांगसम त्रिभुजों में संगत भुजाएँ समान होती हैं]

पृष्ठ सं. 160 – 161
प्रश्न 1.
आकृतियों में, त्रिभुजों के कुछ भागों की माप दी गई हैं। R.H.S. सर्वांगसमता प्रतिबंध का उपयोग करके बताइए कि कौन-कौन से त्रिभुज युग्म सर्वांगसम हैं ? सर्वांगसम त्रिभुजों की स्थिति में, उन्हें सांकेतिक रूप में लिखिए।
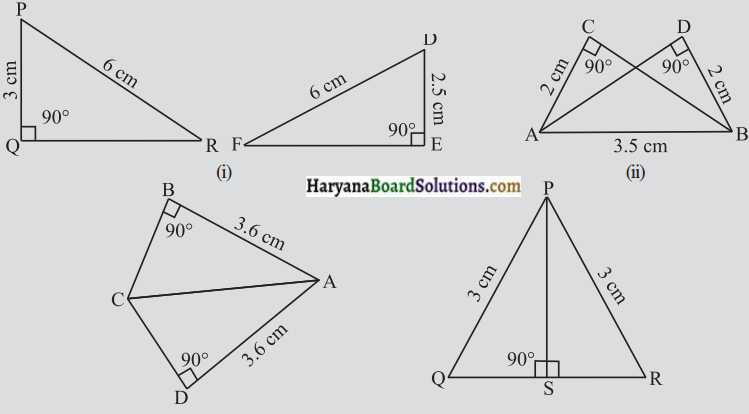
हल :
(i) ΔPQR और ΔDEF में,
PQ ≠ DE
अतः ये त्रिभुज सांगसम नहीं हैं।
(ii) ΔCAB और ΔDBA में,
∠C = ∠D = 90°
AB = BA = 3.5 सेमी और
CA = DB = 2 सेमी
∴ R.H.S. सर्वांगसमता से,
ΔCAB ≅ ΔDBA.
(iii) ΔABC और ΔADC में,
∠B = ∠D = 90°
कर्ण AC = कर्ण AC और
AB = AD = 3.6 सेमी
∴ R.H.S. सर्वांगसमता से,
ΔABC ≅ ΔADC
(iv) ΔPSQ और ΔPSR में,
∠PSQ = ∠PSR = 90°
कर्ण PQ = कर्ण PR = 3 सेमी
और PS = PS
∴ R.H.S. सांगसमता से,
ΔPSQ ≅ ΔPSR.
प्रश्न 2.
R.H.S. सर्वांगसमता प्रतिबंध से ΔABC ≅ ΔRPQ स्थापित करना है। यदि यह दिया गया हो कि ∠B = ∠P= 90° और AB = RP है, तो अन्य किस और सूचना की आवश्यकता है?
हल :
R.H.S. सर्वांगसमता प्रतिबन्ध से ΔABC ≅ ΔRPQ स्थापित करने के लिए दिए गए प्रतिबन्धों के अतिरिक्त हमें कर्ण AC = कर्ण AC को समान करने की आवश्यकता है।
प्रश्न 3.
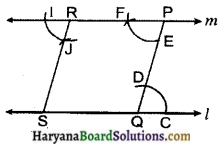
आकृति में, BD और CE, ΔABC के शीर्ष लंब हैं और BD = CE.
(i) ΔCBD और ΔBCE में, बराबर भागों के तीन बुग्म बताइए।
(ii) क्या ΔCBD ≅ ΔBCE है ? क्यों अथवा क्यों नहीं ?
(iii) क्या ∠DCB = ∠EBC है ? क्यों या क्यों नहीं ?
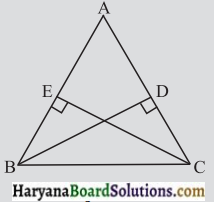
हल :
(i) ΔCBD और ΔBCE में बराबर भागों के तीन युग्म हैं :
CB = BC
∠CDB = ∠BEC
और BD = CE
(ii) R.H.S. सर्वांगसमता से,
ΔCED ≅ ΔBCE.
(iii) हाँ, ∠DCB = ∠EBC, (∵ सर्वांगसम त्रिभुजों के संगत कोण समान होते हैं)

प्रश्न 4.
ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC और AD इसका एक शीर्षलंब है।
(i) ΔADB और ΔADC में, बराबर भागों में तीन युग्म बताइए।
(ii) क्या ΔADB ≅ ΔADC है ? क्यों अथवा क्यों नहीं ?
(iii) क्या ∠B = ∠C है? क्यों या क्यों नहीं ?
(iv) क्या BD = CD है ? क्यों या क्यों नहीं ?
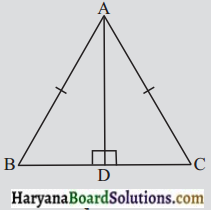
हल :
(i) ΔADB और ΔADC में, बराबर भागों के तीन युग्म निम्न हैं:
AD = AD
∠ADB = ∠ADC
और AB = AC.
(ii) R.H.S. सर्वांगसमता से,
ΔADB ≅ ΔADC.
(iii) हाँ, ∠B = ∠C
(∵ सर्वांगसम त्रिभु के संगत कोण समान होते हैं)
(iv) हाँ, BD = CD, (∵ सर्वांगसम त्रिभुजों की संगत भुजाएँ समान होती हैं)
![]()
![]()





























 = \(\frac{12}{0.3}\) = 40
= \(\frac{12}{0.3}\) = 40