Haryana State Board HBSE 7th Class Maths Solutions Chapter 10 प्रायोगिक ज्यामिती Ex 10.1 Textbook Exercise Questions and Answers.
Haryana Board 7th Class Maths Solutions Chapter 10 प्रायोगिक ज्यामिती Ex 10.1
प्रश्न 1.
एक रेखा (मान लीजिए AB) खींचिए और इसके बाहर स्थित कोई बिन्दु C लीजिए। केवल पैमाना (रूलर) और परकार का प्रयोग करते हुए, C से होकर AB के समान्तर एक रेखा खींचिए।
हल :
रचना के पद :
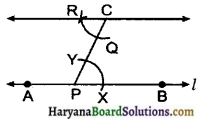
1. रेखा AB पर कोई बिन्दु P लेते हैं।
2. AB के बाहर कोई बिन्दु C लिया और CP को मिलाया।
3. P को केन्द्र मानकर एक चाप खींचा जो AB और PC को क्रमशः X और Y पर काटते हैं।
4. केन्द्र C को और तीसरे चरण की त्रिज्या के बराबर एक चाप खींचा जो PC को Q पर काटता है।
5. केन्द्र Q से XY के बराबर त्रिज्या से एक चाप खींचा जो चरण 4 में R पर काटता हैं।
6. CR को मिलाया और इसको दोनों दिशाओं में बढ़ाने पर अभीष्ट रेखा प्राप्त होगी।
∴ ∠RCQ = ∠XPY (एकान्तर कोण)
∴ AB || CR.
![]()
प्रश्न 2.
एक रेखा l खींचिए और l पर स्थित किसी भी बिन्दु पर l पर लम्ब खींचिए। इस लम्ब रेखा पर एक बिंदु x लीजिए जो l से 4 सेमी की दूरी पर हो। Xसे होकर l के समान्तर एक रेखा m खींचिए।
हल :
रचना के पद :
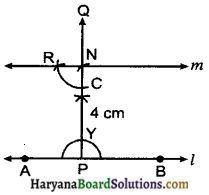
1. एक रेखा l खींचते हैं और उस पर कोई बिन्दु P लेते हैं।
2. P को केन्द्र मानकर उचित त्रिज्या का एक चाप खींचते हैं जो l को A व B बिन्दु पर काटता है।
3. A को केन्द्र मानकर AP त्रिज्या से अधिक त्रिज्या लेकर ऊपर की ओर चाप खींचते हैं।
4. अब B को केन्द्र मानकर चरण 3 के बराबर त्रिज्या का चाप खींचते हैं जो पहले चाप को C बिन्दु पर काटता है।
5. PC को मिलाते हुए आगे Q तक बढ़ाया। तब PQ⊥l.
6. P को केन्द्र मानकर 4 सेमी की त्रिज्या लेकर एक चाप खींचते हैं जो PQ को N पर काटता है। तब
PN = 4 सेमी।
7. बिन्दु N पर ∠RNP = ∠BPN बनाया।
8. NR को मिलाते हुए आगे बढ़ाया। इस प्रकार l के समान्तर m रेखा प्राप्त होगी।
∠RNP = ∠BPN (एकान्तर कोण)
∴ NR || l
⇒ m || l.
![]()
प्रश्न 3.
मान लीजिए l एक रेखा है और P एक बिन्दु है जो l पर स्थित नहीं है। Pसे होकर l के समान्तर एक रेखा m खींचिए। अब Pको के किसी बिंदुए से जोडिए। m पर कोई अन्य बिन्दु R चुनिए। R से होकर, PQ के समान्तर एक रेखा खींचिए। मान लीजिए यह रेखा, रेखा l से बिंदु S पर मिलती है। समान्तर रेखाओं के इन दोनों युग्मों से क्या आकृति बनती है ?
हल :
रचना के पद :
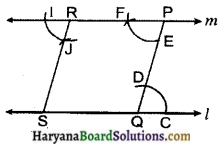
1. एक रेखा l खींचते हैं। इसके बाहर कोई बिन्दु P लेते हैं।
2. रेखा l पर दूसरा बिन्दु 0 लेते हैं।
3. PQ को मिलाया।
4. Q को केन्द्र मानकर एक चाप खींचते हैं जो l को क्रमशः C और D बिन्दु पर काटता है।
5. P को केन्द्र मानकर चरण 4 की त्रिज्या का चाप खींचते हैं जो PQ को E बिन्दु पर काटता है।
6. अब E बिन्दु को केन्द्र मानकर CD त्रिज्या के बराबर एक चाप खींचते हैं जो पहले चाप को F बिन्दु पर काटता है।
7. PF को मिलाते हुए दोनों दिशाओं में आगे बढ़ाया।
8. इस प्रकार एक अभीष्ट रेखा m प्राप्त होगी।
9. रेखा m पर कोई बिन्दु R लिया।
10. R से PQ के समान्तर RS रेखा खींची।
इस प्रकार प्राप्त आकृति PQRS एक समान्तर चतुर्भुज होगा।