HBSE 10th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल और आयतन Ex 13.5

Haryana State Board HBSE 10th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल और आयतन Ex 13.5 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल और आयतन Exercise 13.5

प्रश्न 1.
व्यास 3mm वाले ताँबे के एक तार को 12cm लंबे और 10cm व्यास वाले एक बेलन पर इस प्रकार लपेटा जाता है कि वह बेलन के वक्र पृष्ठ को पूर्णतया ढक लेता है। तार की लंबाई और द्रव्यमान ज्ञात कीजिए, यह मानते हुए कि ताँबे का घनत्व 8.88 g प्रति cm³ है।
(π = 3.14 लीजिए)
हल :
यहाँ पर, प्रश्नानुसार स्पष्ट होता है कि बेलन पर तार को एक बार लपेट देने पर उसकी लंबाई का 3mm (0.3cm) भाग ढक जाता है।
बेलन की पूरी लंबाई ढकने के लिए आवश्यक लपेटों की संख्या =
= \(\frac{12}{0.3}\) = 40
क्योंकि एक लपेट में तार की लंबाई बेलन के सिरे की परिधि के बराबर है
अब बेलन की त्रिज्या (r) = \(\frac{10}{2}\)cm = 5cm
= 2πr = 2 x 3.14 x 5cm = 31.4 cm
40 लपेटों में लगी तार की लंबाई (h) = 40 x 31.4 = 1256 cm
ताँबे की तार की त्रिज्या (r₁) = \(\frac{3}{2}\)mm = \(\frac{3}{20}\) cm
ताँबे की तार का आयतन = πr₁²h
= 3.14 x \(\frac{3}{20}\) x \(\frac{3}{20}\) x 1256 cm³
= 88.74 cm³
1 cm³ ताँबे की तार का द्रव्यमान = 8.88g
88.74 cm³ ताँबे की तार का द्रव्यमान = 88.74 x 8.88 g=788 g (लगभग)

प्रश्न 2.
एक समकोण त्रिभुज, जिसकी भुजाएँ 3cm और 4cm हैं (कर्ण के अतिरिक्त), को उसके कर्ण के परितः घुमाया जाता है। इस प्रकार प्राप्त द्वि-शंकु (double cone) के आयतन और पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
(π का मान जो भी उपयुक्त लगे, प्रयोग कीजिए।)
हल :

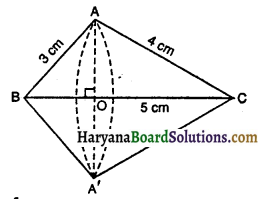
माना
ΔABC, ∠A पर समकोण है
जिसमें
AB = 3 cm
AC = 4 cm
कर्ण (BC) = \(\sqrt{(3)^{2}+(4)^{2}}\)
\(\sqrt{9+16}=\sqrt{25}\) = 5 cm
समकोण त्रिभुज को कर्ण BC के गिर्द घुमाने पर बने द्विशंकु के उभयनिष्ठ आधार की त्रिज्या AO या A’O है।
शंकु BAA’ की ऊँचाई BO तथा तिर्यक ऊँचाई 3 cm है।
शंकु CAA’ की ऊँचाई CO तथा तिर्यक ऊँचाई 4 cm है।
समकोण त्रिभुजों AOB तथा BAC में,
∠B= ∠B (उभयनिष्ठ)
∠BOA = ∠BAC = 90°
इसलिए, ΔAOB तथा ΔCAB समरूप हैं।


इसी प्रकार
द्विशंकु का पृष्ठीय क्षेत्रफल = शंकु (BAA’ + CAA’) का पृष्ठीय क्षेत्रफल
= π(AO) (AB) + π(AO)(AC)
= \(\frac{22}{7} \times \frac{12}{5}\) [3 +4] cm
= \(\frac{22}{7} \times \frac{12}{5}\) x 7 cm² = \(\frac{264}{5}\) cm² = 52.8cm²

प्रश्न 3.
एक टंकी, जिसके आंतरिक मापन 150cm x 120cm x 110cm हैं, में 129600 cm³ पानी है। इस पानी में कुछ छिद्र वाली ईंटें तब तक डाली जाती हैं, जब तक कि टंकी पूरी ऊपर तक भर न जाए। प्रत्येक ईंट अपने आयतन का \(\frac{1}{17}\) पानी सोख लेती है। यदि प्रत्येक ईंट की माप 22.5cm x 7.5cm x 6.5cm हैं, तो टंकी में कुल कितनी ईंटें डाली जा सकती हैं, ताकि उसमें से पानी बाहर न बहे?
हल :
यहाँ पर,
दी गई टंकी का आयतन = 150 x 120 x 110 cm³
= 1980000 cm³
दी गई टंकी में उपस्थित पानी का आयतन = 129600 cm³
दी गई प्रत्येक ईंट का आयतन = 22.5 x 7.5 x 6.5 cm³
= 1096.875 cm³
टंकी में डाली जा सकने वाली ईंटों की संख्या = n
माना ईंटों द्वारा सोखे जाने वाले पानी का आयतन = nx + x 1096.875 cm³
= 64.522 n cm³
टंकी में शेष बचे पानी का आयतन = [129600 – 64.522 n] cm³
प्रश्नानुसार
टंकी में शेष बचे पानी का आयतन + n ईंटों का आयतन = टंकी का आयतन
[129600 – 64.522 n] +1096.875 n = 1980000
[1096.875-64.522]n = 1980000 – 129600
1032.353n = 1850400
n = \(\frac{1850400}{1032.353}\)= 1792.41 – missing 1792
अतः आवश्यक ईंटों की संख्या = 1792

प्रश्न 4.
किसी महीने के 15 दिनों में, एक नदी की घाटी में 10 cm वर्षा हुई। यदि इस घाटी का क्षेत्रफल 7280km2 है, तो दर्शाइए कि कुल वर्षा लगभग तीन नदियों के सामान्य पानी के योग के समतुल्य थी, जबकि प्रत्येक नदी 1072 km लंबी, 75m चौड़ी और 3 m गहरी है।
हल :
यहाँ पर, दी गई घाटी का क्षेत्रफल = 7280 km²
= 7280 x 1000 x 1000 m² = 7280000000 m²
घाटी में 15 दिनों में हुई वर्षा से ऊँचाई (h)= 10cm = \(\frac{10}{100} m=\frac{1}{10} m\)
घाटी में हुई वर्षा का कुल आयतन = क्षेत्रफल – ऊँचाई
= 7280000000 x \(\frac{1}{10}\) m³ = 728000000 m³
दी गई प्रत्येक नदी की लंबाई (l) = 1072 km = 1072000 m
दी गई प्रत्येक नदी की चौड़ाई (b) = 75m
दी गई प्रत्येक नदी की गहराई (h) = 3m
दी गई प्रत्येक नदी का आयतन = 1072000 x 75 x 3 m³
= 241200000 m³
तीनों नदियों में समा सकने वाले जल का आयतन = 3 x 241200000 m³
= 723600000 m³
अतः घाटी में हुई वर्षा का आयतन तीनों नदियों में समा सकने वाले जल के आयतन के लगभग बराबर है।

प्रश्न 5.
टीन की बनी हुई एक तेल की कुप्पी 10cm लंबे एक बेलन में एक शंकु के छिन्नक को जोड़ने से बनी है। यदि इसकी कुल ऊँचाई 22cm है, बेलनाकार भाग का व्यास 8cm है और कुप्पी के ऊपरी सिरे का व्यास 18cm है, तो इसके बनाने में लगी टीन की चादर का क्षेत्रफल ज्ञात कीजिए। (देखिए संलग्न आकृति।)
हल :

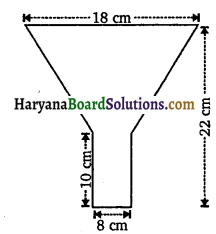
यहाँ पर,
कुप्पी के बेलनाकार भाग का व्यास = 8 cm
कुप्पी के बेलनाकार भाग की त्रिज्या (r₁) = \(\frac{8}{2}\) = 4cm
कुप्पी के बेलनाकार भाग की ऊँचाई (h₁) = 10 cm
कुप्पी के बेलनाकार भाग का पृष्ठीय क्षेत्रफल = 2 πr₁h₁
= 2 x \(\frac{22}{7}\) x 4 x 10 cm²
= \(\frac{1760}{7}\) cm₂
कुप्पी के शंकु रूपी छिन्नक वाले भाग के लिए,
r₁ = \(\) = 9 cm
r₂ = \(\) = 4 cm
h₂ = 22 – 10 = 12 cm

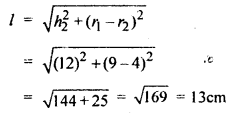
पृष्ठीय क्षेत्रफल = π(r₁ + r₂)l
= \(\frac{22}{7}\) (9 + 4) x 13 cm² = \(\frac{22}{7}\) x 13 x 13 cm²
= \(\frac{3718}{7}\) cm²
अतः कीप को बनाने में लगी टीन की चादर का कुल पृष्ठीय क्षेत्रफल
=\(\left(\frac{1760}{7}+\frac{3718}{7}\right) \mathrm{cm}^{2}=\frac{5478}{7}\) cm²
= 782,5\(\frac{4}{7}\) cm²

प्रश्न 6.
शंकु के एक छिन्नक के लिए, पूर्व स्पष्ट किए संकेतों का प्रयोग करते हुए, वक्र पृष्ठीय क्षेत्रफल और संपूर्ण पृष्ठीय क्षेत्रफल के निम्न सूत्रों को सिद्ध कीजिए,
(i) वक्र पृष्ठीय क्षेत्रफल = π(r₁ +r₂)l
(ii) संपूर्ण पृष्ठीय क्षेत्रफल = \(\pi\left(r_{1}+r_{2}\right) l+\pi r_{1}^{2}+\pi r_{2}^{2}\)
हल :

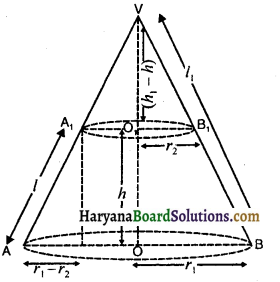
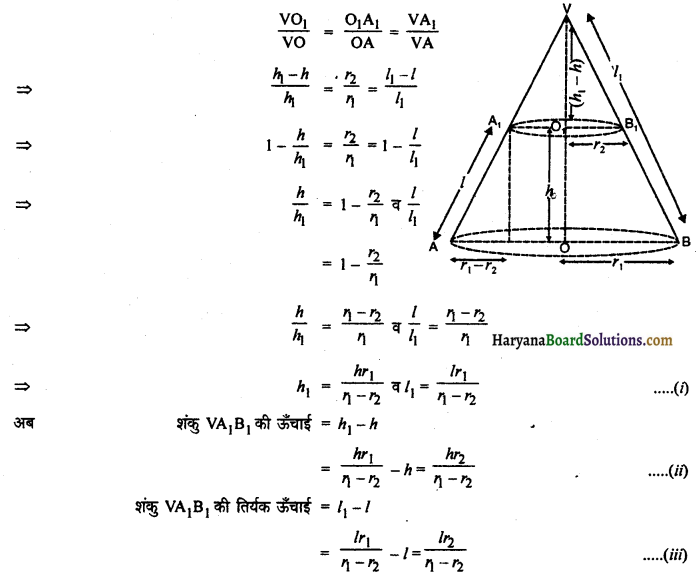
माना AB B₁A₁ छिन्नक की ऊँचाई h, तिर्यक ऊँचाई । तथा वृत्ताकार आधारों की त्रिज्याएँ r₁ व r₂ हैं।
(जहाँ r₁ > r₂)
माना शंकु VAB में, तिर्यक ऊँचाई (VA) = l₁
ऊँचाई (VO) = h₁
तो शंकु VA₁B₁ में,
तिर्यक ऊँचाई (VA₁) = l₁ – l
ऊँचाई (VO₁) = h₁ – h
क्योंकि समकोण ΔVOA व ΔVO₁A₁ समरूप हैं।
πr₁l₁ – πr₂(l₁ – l)

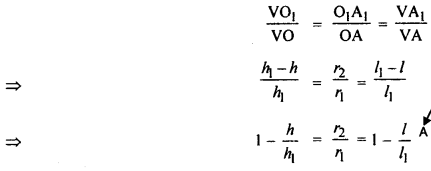
= π(r₁ +r₂)l (इति सिद्धम्)
(i) छिन्नक का वक्र पृष्ठीय क्षेत्रफल = (शंकु VAB – शंकु VA₁B₁)का वक्र पृष्ठीय क्षेत्रफल


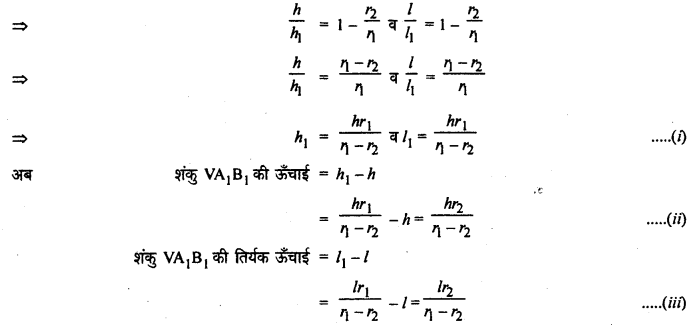
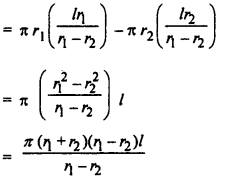
(ii) छिन्नक का संपूर्ण पृष्ठीय क्षेत्रफल = छिन्नक का वक्र पृष्ठीय क्षेत्रफल + (नीचे वाले वृत्ताकार आधार + ऊपरी वृत्ताकार शीष) का क्षेत्रफल = \(\pi\left(r_{1}+r_{2}\right) l+\pi r_{1}^{2}+\pi r_{2}^{2}\) (इति सिद्धम्)

प्रश्न 7.
शंकु के एक छिन्नक के लिए, पूर्व स्पष्ट किए संकेतों का प्रयोग करते हुए, आयतन का निम्न सूत्र सिद्ध कीजिए, आयतन = \(\frac{1}{3} \pi h\left[r_{1}^{2}+r_{1} r_{2}+r_{2}^{2}\right]\)
हल :
माना ABB₁A₁ छिन्नक की ऊँचाई h, तिर्यक ऊँचाई । तथा वृत्ताकार आधारों की त्रिज्याएँ r₁ व r₂ हैं
(जहाँ r₁ > ₂ )।
माना शंकु VAB में, तिर्यक ऊँचाई (VA) = l₁
ऊँचाई (VO) = h₁
तो शंकु VA₁B₁ में,
तिर्यक ऊँचाई (VA₁) = l₁ – l
ऊँचाई (VO₁) = h₁ – h
क्योंकि समकोण ΔVOA व ΔVO₁A₁ समरूप हैं।